Abstract
This study presents results of mapping three-dimensional (3-D) variations of the electrical conductivity in depths ranging from 400 to 1200 km using 6 years of magnetic data from the Swarm and CryoSat-2 satellites as well as from ground observatories. The approach involves the 3-D inversion of matrix Q-responses (transfer functions) that relate spherical harmonic coefficients of external (inducing) and internal (induced) origin of the magnetic potential. Transfer functions were estimated from geomagnetic field variations at periods ranging from 2 to 40 days. We study the effect of different combinations of input data sets on the transfer functions. We also present a new global 1-D conductivity profile based on a joint analysis of satellite tidal signals and global magnetospheric Q-responses.

Similar content being viewed by others
Introduction
Understanding 3-D physical properties of the Earth’s mantle on a global scale is an outstanding problem of modern geophysics. There exist only two direct methods that can determine the distribution of physical properties in the mantle: seismic and electromagnetic (EM) methods. Seismic tomography provides a variety of global 3-D velocity models (Debayle and Ricard 2012; Lekic and Romanovicz 2011; Ritsema et al. 2011; Schaeffer and Lebedev 2013, among others), but the interpretation of seismic velocities alone leads to ambiguities. Additionally, seismic velocities are only weakly sensitive to the hydrogen content (Buchen et al. 2018; Fei et al. 2017; Schulze et al. 2018, among others).
The goal of EM sounding methods is to identify spatial variations of the electrical conductivity in the Earth’s interior. Since the conductivity is sensitive to temperature, chemical composition and hydrogen content (Karato and Wang 2013; Khan 2016; Yoshino 2010, among others) its knowledge helps understanding the Earth’s origin as well as its past evolution and recent dynamics. Constraining the 3-D conductivity distribution in the mantle is conventionally performed by means of Geomagnetic Depth Sounding (GDS). Until now GDS studies most often rely on the long-period variations of magnetic field of magnetospheric origin coming from a global network of geomagnetic observatories. From these data local C-responses (Banks 1969) (see also Appendix A of this paper explaining the concept) are estimated at a number of periods and then inverted for mantle conductivity. There are numerous studies (Chen et al. 2020; Khan et al. 2011; Munch et al. 2018; Schultz and Larsen 1990; Zhang et al. 2020, among others) that performed 1-D inversions of local C-responses at a number of locations in order to detect lateral variations in the mantle conductivity.
In addition, a few semi-global (Koyama et al. 2006, 2014; Shimizu et al. 2010; Utada et al. 2009) and global (Kelbert et al. 2009; Li et al. 2020; Semenov and Kuvshinov 2012; Sun et al. 2015) 3-D mantle conductivity models have been derived by means of an inversion of local C-responses. A few comments on the recovered 3-D models are relevant at this point. First, due to limited frequency band, local C-responses, and thus models based on them have limited sensitivity in the crust and upper mantle (Grayver et al. 2017; Kelbert et al. 2008; Püthe and Kuvshinov 2014). Second, the family of 3-D models produced until now are rather divergent. This discrepancy is mostly due to the inherent strong non-uniqueness of the inverse problem arising from spatial sparsity and irregularity of data distribution, limited period range, and inconsistency of the assumed external field model, which is based on a too simplistic assumptions about the geometry of the magnetospheric ring current. Indeed, there has long been evidence for a more complex structure and asymmetry of the magnetospheric source (Balasis and Egbert 2006; Luhr et al. 2017; Olsen and Kuvshinov 2004, among others).
To overcome the former problem, Püthe et al. (2014) introduced a new type of transfer functions (TFs) that are capable of handling sources of arbitrary complexity. These TFs relate the expansion coefficients describing the source globally with a locally measured magnetic (or/and electric) field, hence these TFs are referred to as global-to-local (G2L) TFs. Guzavina et al. (2019) and Munch et al. (2020) estimated and inverted “vertical magnetic” G2L TFs at several continental geomagnetic observatories in terms of local 1-D conductivity distributions and revealed noticeable lateral variations in mantle conductivity. Note that the term “vertical magnetic” stresses the fact that G2L TFs under consideration relate the global expansion coefficients to the local vertical magnetic field component.
However, regardless of whether local C-responses or global-to-local transfer functions are used, the spatially uneven distribution of observatories with only a few stations in oceanic regions precludes obtaining a cogent global 3-D model of mantle conductivity of uniform lateral resolution from observatory data. In contrast to ground-based data, satellite-borne measurements provide better spatio-temporal data coverage. With the Swarm satellite constellation mission (Olsen and Floberghagen 2018), the possibility of obtaining global images of 3-D mantle heterogeneities, especially in oceanic regions, was considered as attainable. Bearing this in mind, mapping 3-D electrical conductivity of the Earth’s mantle has been identified as one of the scientific objectives of the Swarm satellite mission.
A major challenge when working with satellite data is the fact that, due to constantly moving platform, one cannot use the local response or global-to-local transfer functions concepts discussed above. Instead, in the course of the Swarm mission preparation, two alternative approaches, both based on an inversion of the induced coefficients of a spherical harmonic (SH) expansion of the magnetic potential due to signals of magnetospheric origin, have been developed. Both the time-domain (Velimsky 2013) and the frequency-domain (Püthe and Kuvshinov 2013) approaches yield promising results in 3-D model studies. However, a 3-D inversion of internal coefficients has an inherent shortcoming since it requires a precise description of the magnetospheric source, i.e., good knowledge of the time series of the inducing SH coefficients. However, in reality the source is inevitably determined with uncertainty. This may lead to artifacts in resulting 3-D mantle conductivity images.
Püthe and Kuvshinov (2014) presented the concept of an alternative 3-D inverse solution that alleviates this problem. The inversion scheme is based on an analysis of array of transfer functions, hereinafter denoted as Q-matrix or matrix Q-response. The frequency-dependent Q-matrix relates external (inducing) and induced SH coefficients of the magnetic potential describing the signals of magnetospheric origin (Olsen 1999). This scheme avoids complications with actual description of the source. Only the geometry of the source, namely the specific set of SH terms that are significant for its description, is assumed a priori (in analogy with the plane wave source geometry assumption in magnetotellurics). Data analysis also allows the researchers for a direct estimation of uncertainties, which can be incorporated into the inversion scheme. Moreover, the approach permits the use of intermittent data, e.g., data from different satellite missions that are separated in time.
In this paper, we implement the matrix Q-responses concept to constrain the 3-D mantle conductivity distribution using 6 years of satellite and observatory magnetic data. Most of the satellite data come from the Swarm mission, but we also exploit magnetic data from the Cryosat-2 satellite. As shown by Olsen et al. (2020), platform magnetometer data like those from CryoSat-2 are a highly valuable augmentation to data from dedicated geomagnetic missions like CHAMP and Swarm. As we will see, Cryosat-2 data indeed allows us to improve the determination of inducing and induced SH coefficients discussed above.
The paper is organized as follows. In “Data” section, we shortly describe the ground-based and satellite magnetic data used in this study. In “Methodology” section, we discuss the concept of matrix Q-responses and explain how these responses are numerically predicted. Estimation of matrix Q-responses requires in its turn retrieving time series of SH inducing and induced coefficients which is explained in “Estimating inducing and induced coefficients” section. Derivation of experimental matrix Q-responses from the recovered time series is presented in “Estimating matrix Q-responses” section. In “Obtaining background 1-D conductivity model” section, we determine global 1-D conductivity profile which we use as starting and background conductivity distribution during 3-D inversion. “Obtaining 3-D conductivity model” section provides details of 3-D inverse solution and presents the results of the inversion. A summary and final remarks are given in “Concluding remarks” section. Finally in “Outlook” section, we discuss potential ways to improve the recovery of 3-D conductivity structures in the mantle. Four appendices detail some aspects of the paper.
Data
Observatory data
Hourly means of three components of magnetic field (vector data) from 161 worldwide distributed geomagnetic observatories for the period 25 November 2013 to 31 December 2019 were utilized for estimation of time series of SH inducing and induced coefficients. The observatory data had been checked for trends, jumps, spikes and other errors (Macmillan and Olsen 2013). Figure 1 shows the locations of these observatories.
Satellite data
Most of the satellite data come from the Swarm mission. The data include vector magnetic field measurements decimated to 1-min sampling rate from two of the three Swarm satellites, namely Alpha and Bravo, for the same time interval as for the observatory data. Data from the third satellite, Charlie, that flies nearby Alpha are not included into the analysis since this data set would be significantly redundant to that from Alpha, at least from the GDS perspective. Additionally, we used 5 years (25 November 2013 to 31 December 2018) of calibrated 1-min data from the CryoSat-2 satellite (Olsen et al. 2020). Note that satellites move with a speed of \(\sim 7.7\) km/s, and thus 1-min temporal sampling corresponds to \(\sim 460\) km spatial interval.
Methodology
Concept of matrix Q-responses
We begin by stating Maxwell’s equations in the frequency domain
where \({{\vec {B}}} \equiv {{\vec {B}}}({{\vec {r}}}, \omega )\) and \({{\vec {E}}} \equiv {{\vec {E}}}({{\vec {r}}}, \omega )\) are the Fourier transforms of the magnetic and electric fields, respectively; \({{\vec {r}}} =(r, \vartheta , \varphi )\) with r, \(\vartheta \) and \(\varphi \) being distance from Earth’s center, colatitude and longitude; and \(\omega = 2\pi /T\) is angular frequency with T as period. \({{\vec {j}}}^{ext} \equiv {{\vec {j}}}^{ext}({{\vec {r}}}, \omega )\) is the Fourier transform of an impressed (extraneous) source current density. \(\sigma ({{\vec {r}}})\) is the conductivity distribution in the media and \(\mu _{0}\) is the magnetic permeability of free space. This formulation neglects displacement currents, which can be ignored in the considered period range of hours and longer. Also note that we adopted the Fourier convention
In a source-free region above the conducting Earth, but below the region enclosed by the current \({{\vec {j}}}^{\text {ext}}\) (in our case the magnetosphere), Eq. (1) reduces to \(\nabla \times {{\vec {B}}}=0\). Therefore, \({{\vec {B}}}\) is a potential field and can be written as a gradient of a scalar magnetic potential V, i.e.,
Since \({{\vec {B}}}\) is solenoidal, i.e., \(\nabla \cdot {{\vec {B}}} = 0\), V satisfies Laplace’s equation \(\nabla ^2 V = 0\), and can be represented as sum of external (inducing) and internal (induced) parts,
where both parts are expanded in series of spherical harmonics (SH):
Here, \(a=6371.2\) km is Earth’s mean radius, \(\varepsilon _{n}^{m}(\omega )\) and \(\iota _{k}^{l}(\omega ; \sigma )\) are the SH coefficients of the inducing and induced parts of the potential, respectively, and \(Y_{n}^{m}\) is the spherical harmonic of degree n and order m,
with \(P_n^{|m|}(\cos \vartheta )\) being the Schmidt quasi-normalized associated Legendre function of degree n and order |m|. For brevity, we will use the convention
where \(N_{\text {ext}}\) and \(N_{\text {int}}\) are the maximum degree of inducing and induced coefficients, respectively. Further note that in Eq. (7) we explicitly specify that \(V^{int}\) and \(\iota _n^m\) depend on subsurface conductivity \(\sigma \), and in Eqs. (6)–(7) we use different indices for external (inducing) and internal (induced) coefficients to account for the Earth’s 3-D conductivity distribution. In contrast, for a 1-D Earth model (that is, conductivity depends only on depth), every inducing coefficient produces exactly one induced coefficient of the same degree and order, and these coefficients are linearly related through the scalar Q-response defined as
Further, \(Q_{n}\) is independent of the order m (e.g., Bailey 1969) and can be calculated analytically using appropriate recurrence formulas. Based on the Srivastava (1966) formalism, Parkinson (1983) presents such formulas for layered spherical Earth’s model with piece-wise constant conductivity. There also exist recursions for other layered Earth’s models, for example, for a conductivity distribution that obeys a power law within each layer (cf. Kuvshinov and Semenov 2012).
It follows from Eqs. (4)–(10) that the magnetic field above or on the surface of the Earth (\(r \ge a\)) can be written as
Here \({{\vec {B}}}_H = (B_\vartheta , B_\varphi )\) and \(\nabla _\perp \) denotes the angular part of the gradient, i.e.,
with \({{\vec {e}}}_\vartheta \) and \({{\vec {e}}}_\varphi \) as the unit tangential vectors of the spherical coordinate system.
In case of a 3-D conductivity distribution, every inducing coefficient \(\varepsilon _{n}^{m}\) generates an infinite series of induced coefficients \(\iota _{k}^{l}\); thus we can write
where the \(Q_{kn}^{lm}\) forms a two-dimensional array of transfer functions we refer to as “matrix Q-response” or “Q-matrix” (Olsen 1999). The magnetic field above or on the surface of Earth reads
Modeling matrix Q-responses
A 3-D inversion of observed (i.e., estimated from the data) matrix Q-responses involves multiple computations (predictions) of these responses for given 3-D conductivity models. This requires solving numerically Maxwell’s equations (1)–(2), and thus an elaboration on the form of current density term \({{\vec {j}}}^{\text {ext}}\). Since we work with the magnetospheric ring current as a source we can assume that the source current flows in a thin shell of infinitesimal radius \(a+\delta r\) as \(\delta r \rightarrow 0\) (that is, just above the Earth’s surface), and the shell is surrounded by an insulator. Then \({{\vec {j}}}^{\text {ext}}\) collapses to the sheet current density \({{\vec {J}}}^{\text {ext}}\). Since the current density is a solenoidal field, one can write \({{\vec {J}}}^{\text {ext}}\) in the form of a stream function \(\Psi \)
where \({\vec {e}}_r\) is the unit radial vector, and \(\times \) stands for the vector product. The stream function \(\Psi \) can be expanded in terms of the coefficients \(\varepsilon _n^m\) as (Schmucker 1985)
By substituting Eq. (18) into Eq. (17) the sheet current density \({{\vec {J}}}^{\text {ext}}\) reads
Note that \({{\vec {J}}}^{ext}\) described by Eq. (19) produces exactly the external magnetic field \({{\vec {B}}}^{\text {ext}}\) at the surface of the Earth (see Appendix G of Kuvshinov and Semenov (2012) for details). In particular, \(B_r^{\text {ext}}\) at the surface of the 3-D Earth’s is obtained from Eq. (15) as
and correspondingly, the induced part of the radial component at the surface of the 3-D Earth reads
where \({{\vec {r}}}_a = (a, \vartheta , \varphi )\). We can further define
as the inducing and induced parts of the radial component (at \(r=a\)) generated for a given 3-D conductivity distribution by spherical harmonic sources with unit amplitude \(\varepsilon _n^m(\omega )=1\), namely
Since \(B_{n,r}^{m,\text {int}}=B_{n,r}^{m}-B_{n,r}^{m,\text {ext}}\), we compute (predict) the matrix Q-responses by making use of the orthogonality of the spherical harmonics \(Y_k^l\)
Here \(\Omega \) is the complete solid angle, \(\text {d}\Omega =\sin \vartheta \text {d}\vartheta \text {d}\varphi \), \({Y}_k^{l^*}\) denotes complex conjugation of \(Y_k^l\), and \(\left\| Y_k^l\right\| ^{2}\) is the squared norm of the spherical harmonic \(Y_k^l\). For calculating \(B_{n,r}^{m}\) in a given 3-D conductivity model we utilize the global EM forward solver x3dg (Kuvshinov 2008) which numerically solves the corresponding Maxwell’s equations
using the integral equation (IE) approach with contracting IE kernel (Pankratov and Kuvshinov 2016). The mathematical machinery underlying the x3dg solver is extensively described in Kuvshinov and Semenov (2012).
Determination of responses from magnetic field observations consists of two stages: (i) time series of SH coefficients of inducing and induced parts of the magnetic potential are determined from the satellite and observatory data and (ii) matrix Q-responses are estimated from these time series. The following two sections provide details of each stage.
Estimating inducing and induced coefficients
First, the core, lithosphere and ionosphere magnetic field, as given by the Comprehensive Inversion (CI; Sabaka et al. 2018) are subtracted from the vector magnetic field data. The residual field variations in the period range between a few days and a few months are assumed to contain the signals of magnetospheric origin. Subtraction of ionospheric signals allowed us to use both day and night residual data, thus substantially increasing the amount of available data.
Data poleward of \(\pm 55^\circ \) geomagnetic latitude were heavily down-weighted by a factor \(0.01\sin (\vartheta )\) to suppress the negative influence of auroral ionospheric currents. Time series of SH inducing and induced coefficients were then estimated from the three components of magnetic field using its real-valued representation that reads
where \(q_{n}^m\), \(s_{n}^m\) and \(g_{k}^l\), \(h_{k}^l\) stand for the inducing and induced coefficients, respectively, that are determined in the geomagnetic dipole coordinate system. Since it is assumed that the signals under consideration are governed by dynamics of the distant magnetospheric ring current which mostly flows in (geomagnetic) equatorial plane, the dominant coefficients in the above expansions are of degree 1 and order 0. These coefficients were estimated in 1.5-h time bins, roughly corresponding to a single satellite orbit. The remaining coefficients were estimated in time bins of 6 h in order to improve the spatial resolution and avoid overfitting. With these settings, the coefficients for the jth time (either 1.5 or 6 h) bin are estimated by solving the following minimization problem
where \(B_{\alpha }^{\text {ext}}\) and \(B_{\alpha }^{\text {int}}\) correspond to the terms with \(\sum \nolimits _{n=1}^{N_{\text {ext}}}\sum \nolimits _{m=1}^n\) and \(\sum \nolimits _{k=1}^{N_{\text {int}}}\sum \nolimits _{l=1}^k\) summation, respectively, in Eqs. (28)–(30) and \({\mathbf {q}}_j, {\mathbf {s}}_j, {\mathbf {g}}_j, {\mathbf {h}}_j\) are vectors of estimated coefficients. For example, for \({\mathbf {q}}_j\), it reads
where the superscript T denotes the transpose of a vector. The notation \(t \in D_j\) means that we take all available measurements in time bin, \(D_j\), which reads
where \(\Delta t\) is either 1.5 or 6 h. The absence of dependence on time t in \(B_{\alpha }^{\text {ext}}\) and \(B_{\alpha }^{\text {int}}\) in Eq. (31) implies that we assume that coefficients do not vary within a time bin \(D_j\). Note also that for satellite data \({{\vec {r}}} \equiv {{\vec {r}}}(t)\), since satellite moves in time. The weights in Eq. (31) are defined as follows:
Our choice of \(N_{\text {ext}}\) is based on the following consideration. Since the magnetospheric ring current is located a few Earth’s radii away from the Earth, its hypothetical small-scale structures are filtered out when the signal approaches the Earth and low orbit satellites such as Swarm and CryoSat-2. In view of this, \(N_{\text {ext}} = 2\) appears a reasonable option. The choice of \(N_{\text {int}}\) is mostly constrained by spatio-temporal coverage of input data sets. Our statistical analysis (not shown here) indicates that we can determine coefficients up to degree \(N_{\text {int}} =3\). Therefore, we need to estimate \(N_{\text {ext}}(N_{\text {ext}}+2)+N_{\text {int}}(N_{\text {int}}+2) = 23\) coefficients for every time bin. Since the problem (31) is linear with respect to the coefficients, we used a Huber-weighted robust regression method (Aster et al. 2018) to solve it.
Figure 2 presents the determined time series of inducing and induced coefficients up to degree \(N_{\text {ext}} = 2\). Note that the sixth-year time series were recovered using Swarm and observatory data only, since CryoSat-2 data were not available for us at the time of this study. We observe that the dominant coefficients are indeed of degree 1 and order 0. Additionally, in agreement with theory, the induced coefficients are a fraction of the inducing coefficients.
Further, we would like to study the influence of different input data sets on the quality of the recovered time series. We tried five data combinations:
-
Observatories,
-
Swarm,
-
Swarm + CryoSat-2,
-
Swarm + observatories,
-
Swarm + CryoSat-2 + observatories.
We calculated multiple squared coherency (MSC) between inducing and induced coefficients for all combinations. Frequency-dependent real-valued MSC is a measure that assesses the extent to which the output signal (in our case time series of induced SH coefficients of a given degree k and order l) can be predicted from all input signals (in our case eight time series of inducing SH coefficients), using the assumed linear model stated by Eq. (14). MSC varies between 0 and 1, and for ideal linear system it is equal to one. Thus, the higher MSC the higher the correlation between inducing and induced coefficients. In the absence of systematic biases and correlated noise, the higher MSC would indicate the statistically more reliable estimates of coefficients.
Figure 3 shows the MSC for all combinations of the data sets. Justification of the choice of the period range for which we estimated MSC is given in the next section. Further note that in order to make the time-domain and frequency-domain presentations consistent, we use a complex-valued notation for the time series of coefficients in the remainder of the paper. In this notation, vector magnetic field is given as
where \({\text {Re}}\) denote real part, \(\varepsilon _{n}^m\) and \(q_n^m, s_n^m\) are related as
and similarly \(\iota _{k}^l\) can be written via \(g_k^l\) and \(h_k^l\) as
It is seen from the figure that MSC is highest when both satellite and observatory data sets are used to calculate MSC. MSC obtained using only observatory data is noticeably lower than MSC derived entirely from satellite data. Likewise, MSC estimated from the Swarm and CryoSat-2 data sets combination is higher than MSC obtained using only Swarm data. However, adding observatory data to the Swarm or Swarm + CryoSat-2 data levels the difference. With this exercise we aimed to demonstrate that satellite data are indeed indispensable for better separation/description of inducing and induced coefficients.
Finally, we note that the highest MSC is observed for the coefficient \(\iota _1^0\), as expected. The lowest MSC is obtained for the coefficient \(\iota _2^0\); this is probably due to the fact that the major part of the variance in \(n=2~ m=0\) coefficients is due to annual and seasonal variability (cf. Fig. 2) which is outside of the considered period range.
Estimating matrix Q-responses
The Q-matrix is estimated row-wise for a given k and l and at a given frequency \(\omega \) by solving a minimization problem
where \({{\mathbf {Q}}}_{k}^{l}\) stands for the row elements of Q-matrix, i.e.,
and the vector \({\varvec{{\mathcal {E}}}}_i\) contains estimates of the time spectra (for a given frequency \(\omega \)) of all inducing coefficients at i-th segment of the full time time series, i.e.,
Similarly, \(\iota _{k,i}^l\) is an estimate of the time spectra of the individual induced coefficient at the i-th segment of the corresponding full time series. The length of the time segments depends on \(\omega \) and in general is a multiple of the associated period \(P = 2\pi /\omega \). Short segments increase \(N_{\text {seg}}\), but in turn also increase the spectral leakage. We found a segment length of 3P to be an optimal value in practice. Furthermore, the time segments overlap to improve statistical efficiency and are tapered before performing the Fourier transform to further decrease the spectral leakage (e.g., Chave and Jones 2012). Since the problem (39) is linear with respect to elements of \({{\mathbf {Q}}}_{k}^{l}\), we used the Huber-weighted robust regression method (Aster et al. 2018) to find the minimizing estimate. The uncertainties of the estimates are calculated by using the jack-knife approach. Repeating regression analysis for each k and l pair, we eventually obtained the estimates for all, \(N_{\text {ext}}(N_{\text {ext}}+2)\times N_{\text {int}}(N_{\text {int}}+2) = 8 \times 15\), elements of Q-matrix and their uncertainties.
We note here that the matrix Q-responses are estimated at log-spaced periods. The shortest period was chosen to be two days to avoid the influence of different ionospheric sources. The longest period is constrained by the length of the time series. For a reliable statistical estimate, the number of time segments must significantly exceed the number of dependent variables, \(N_{\text {ext}}\). In our case, we have 6 years of data and \(N_{\text {ext}}\) = 8. Using segments with a length of 3P, an overlap of 50 percent, and requiring the number of segments to be at least \(4 N_{\text {ext}}\), the maximum period at which we can estimate matrix Q-responses is \(\approx 40\) days.
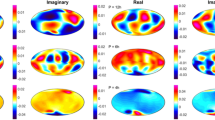
Figure 4 shows estimated “diagonal” matrix Q-responses. Since diagonal responses are dominant, they are the most well resolved components. Additionally, Fig. 4 shows the “upper limit” responses from the perfectly conducting Earth model (see details in Appendix B), as well as the “best fit” responses from the recovered 3-D model (will be discussed later in the paper).
Estimated “diagonal” (dominant) matrix Q-responses (circles and triangles with error bars). Also shown are the “upper limit” responses from a perfectly conducting Earth model (dashed lines), and the responses from the recovered 3-D model (solid lines). Real and imaginary parts of the responses are depicted by blue and red colors, respectively
Obtaining background 1-D conductivity model
As we already discussed in “Introduction” section, with magnetic field variations of magnetospheric origin one can constrain the 3-D conductivity distribution at depths approximately between 400 and 1600 km. Due to the non-linearity and non-uniqueness of the inverse problem, the choice of the background 1-D model within and outside this depth range is crucial for obtaining plausible 3-D conductivity distribution. In this section, we will obtain the background 1-D model that will be used as a starting and background model during inversion of matrix Q-responses. The present section, in its methodological part, closely follows the scheme outlined by (Grayver et al. 2017). It is based on a joint quasi 1-D inversion of the magnetic signature of oceanic tidal signals and “magnetospheric” Q-responses. Here the term “quasi” is used to stress the fact that during 1-D inversion the 3-D forward modeling operator is exploited to account for the effects arising from laterally variable oceanic bathymetry and sediment thickness. The 3-D forward modeling operator used to estimate these effects has already been introduced in the previous section. We also note here that the oceanic tidal signals are included into our analysis in order to constrain the conductivity in the upper mantle (depths between 10 and 400 km).
Determination of the \(M_2\) magnetic tidal signal
The tidally generated flow of the electrically conductive seawater in Earth’s main magnetic field produces electric currents in the oceans, which in turn produce EM field in the subsurface. The magnetic field measured on the coast, at the sea bottom and with satellites thus contain information about the subsurface electrical conductivity. In contrast to the conventional EM sources of ionospheric and magnetospheric origin (which are inductively coupled with the Earth due to the insulating atmosphere between the source and the Earth), the unique characteristic of the motion-induced electric currents in the oceans is its galvanic coupling with the oceanic lithosphere. This enhances the sensitivity to resistive subsurface structures (Schnepf et al. 2015; Velimsky et al. 2018) since the induced fields are influenced by the toroidal (galvanic) part of the primary tidal EM field. Despite small amplitude (a few nT), tidal magnetic signals due to the semi-diurnal lunar \(M_2\) tide (of period of 12 h and 25 min) have been reliably extracted from magnetic satellite measurements using the Comprehensive Inversion (CI) approach based on a simultaneous estimation of the different contributions (in the core, lithosphere, ionosphere, etc.) and selection of data for geomagnetic quiet periods (Sabaka et al. 2015, 2016, 2020). The radial component, \(B_r^{\text {M2}}\), of the \(M_2\) magnetic tidal signal was synthesized from the estimated \(M_2\) SH coefficients, \(\tau _{n}^m\), at mean satellite altitude (h = 430 km) on a \(2^\circ \times 2^\circ \) grid. The expansion of the \(M_2\) signal in the CI model is based on a potential representation given by
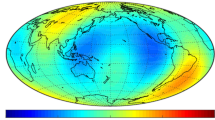
The upper panel of Fig. 5 shows the magnitude of the observed (i.e., synthesized from the estimated SH coefficients) \(M_2\) radial magnetic field component.
Top and middle: global maps of magnitudes of the observed and predicted (modeled) \(M_2\) radial magnetic field component. Predicted fields are obtained using the “joint” 1-D conductivity profile shown in Fig. 7. Bottom: residuals, i.e., magnitude of the difference between observed and predicted \(M_2\) radial magnetic field. Values are shown for a mean satellite altitude of \(h = 430\hbox { km}\)
Estimating dominant Q-response
As already discussed, the \(n=1\) and \(m=0\) term is largest in a SH expansion of the signals of magnetospheric origin. To derive a global 1-D conductivity profile we use the corresponding diagonal elements of the matrix Q-response, namely the response that relates the inducing \(\varepsilon _1^0\), and induced, \(\iota _1^0\), coefficients. Hereinafter we call those as the “dominant” Q-response. To estimate this response, we first estimate time series of inducing and induced coefficients up to spherical harmonic degrees \(N_{\text {ext}}=2\) and \(N_{\text {int}}=3\), respectively (see Section “Estimating inducing and induced coefficients”). Since the model we work with consists of a surface thin layer of laterally variable (2-D) conductance on top of a 1-D conductivity structure (cf. Fig. 6), the problem becomes intrinsically 3-D and requires the implementation of Eq. (14) to estimate the desired \(Q_{11}^{00}\). To this end we solve the minimization problem
where
As discussed in “Estimating inducing and induced coefficients” section, 6 years of magnetic data allows us to estimate \(Q_{11}^{00}\) up to periods of \(\approx 40\) days. In addition, and together with \(Q_{11}^{00}\), we estimate seven responses: \(Q_{1\,-1}^{0\,-1}, Q_{1\,1}^{0\,1}, ..., Q_{1\,2}^{0\,2}\). However, the amplitude of these responses are much smaller than \(Q_{11}^{00}\). Therefore, in order to utilize longer periods, we resort to the “uni-variate” minimization problem
This allows us to estimate \(Q_{11}^{00}\) up to periods of about one year. To verify the validity of this approach we also performed an estimation of \(Q_{11}^{00}\) using Eq. (43) and compared the results in the period range where both responses overlap (2–30 days). The observed difference (not shown here) between both uni- and multi-variate responses are negligible, thus reaffirming the use of a uni-variate approach for estimating \(Q_{11}^{00}\). Circles with error bars in Fig. 8 depict the estimated \(Q_{11}^{00}\) (the results shown with solid lines will be explained later).
Modeling tidal signals and the dominant Q-response
Joint inversion of magnetic tidal signals and \(Q_{11}^{00}\) responses requires their multiple prediction for a given conductivity model. To accurately predict (calculate) magnetic fields/responses due to tidally induced oceanic or magnetospheric electric currents, it is essential to account for the conductivity of non-uniform oceans (Kuvshinov 2008). To this end, we added a thin shell of laterally variable conductance (corresponding to oceans and continents) on top of a 1-D mantle conductivity model (Fig. 6). As discussed in the “Modeling matrix Q-responses” section, we calculate the EM field by using the global EM forward code x3dg (Kuvshinov 2008), which numerically solves Eqs. (1)−(2).
The extraneous current density, \(\vec {j}^{ext}\), induced by the tidal forces, is confined to the ocean and given by
where \({{\vec {r}}}_a = (a, \vartheta , \varphi )\), and \(\vartheta \), and \(\varphi \) are geographic colatitude and longitude, respectively, \(\sigma _s\) is the depth-averaged conductivity of seawater, \(\vec {B}^{\text {main}}\) is Earth’s main (core) magnetic field, \(\vec {v} = \vec {u}/h\), h is the height of the water column and \(\vec {u}\) is the depth-integrated seawater velocity of the \(M_2\) tidal mode. \(\vec {B}^{\text {main}}\) is calculated using the World Magnetic Model (Chulliat et al. 2015), \({\vec {u}}\) is taken from the HAMTIDE ocean tidal model (Taguchi et al. 2014), and \(\sigma _s\) is derived from ocean salinity and temperature data given by the World Ocean Atlas 2009; see Grayver et al. (2016) for more detail about the individual terms of Eq. (46) and their uncertainties.
In case of \(Q_{11}^{00}(\omega ; \sigma )\), the extraneous source is given by a sheet current density, parameterized using a single \(Y_1^0 = \cos \vartheta \) spherical harmonic. Following Eq. (24), it reads
Once the corresponding radial component of the magnetic field, \(B_{1,r}^{0, \text {pred}}\), is computed at Earth’s surface, \(Q_{11}^{00, \text {pred}}(\omega ; \sigma )\) is obtained as
where \(\vartheta \) and \(\varphi \) are geomagnetic colatitude and longitude, respectively. To obtain Eq. (48), we used Eqs. (22) and (25) with
Joint stochastic 1-D inversion of tidal signals and dominant Q-responses
We consider a 1-D conductivity model consisting of \(M = 46\) layers of fixed thicknesses (see second column in Table 1) and a core of fixed conductivity of \(10^5\) S/m. We aim at estimating the conductivity values \(\sigma _1, \sigma _2, \cdots , \sigma _M\) by solving a non-linear inverse problem, formulated as the minimization task
where \(\phi _d\) is the data misfit, \(\lambda \) and \(\phi _r\) are a regularization parameter and a regularization term, respectively, and \({\mathbf {m}} = [\ln \sigma _1, \ln \sigma _2, \cdots , \ln \sigma _M]\) is the vector of model parameters. Solving the logarithm of conductivity ensures positivity of the arguments. The data misfit in Eq. (50) reads
where \(\omega _i\) corresponds to periods between 1.5 and 150 days with number of frequencies \(N_{\text {1D}} = 27\), and \({{\vec {r}}}_{j} = (a+h, \vartheta _j, \varphi _j)\) are \(2^\circ \times 2^\circ \) grid points, with number of grid points \(N_{\text {grid}} = 90 \times 180\). We do not have experimental estimates for \(\delta B_r^{\text {M2}}\), but in order to make the second term dimensionless and compatible with the first term we introduce \(\delta B_r^{\text {M2}}({{\vec {r}}}_{j},\omega _{\text {M2}}) = 0.1\) nT. As discussed by Grayver et al. (2017) and Munch et al. (2020), normalizing with the numbers of actual measurements (\(N_{\text {1D}}\) and \(N_{\text {grid}}\)) is an important aspect that helps equalize the contribution of different input data sets.
The regularization term reads
where \({\mathbf {l}}_i\) is the regularization operator of the i-th model parameter. In our implementation it approximates the first derivative with respect to the model parameters; in other words it corresponds to the differences in log-conductivities between neighboring layers. The scalar \(p_m\) controls the norm of the regularization term; by varying \(p_m\) one retrieves different regularization norms, ranging from a smooth \(L_2\)-norm (\(p_m = 2\)) to the structurally sparse \(L_1\)-norm (\(p_m = 1\)) solutions. The regularization parameter \(\lambda \) was determined by means of an L-curve analysis (Hansen 1992). \(p_m\) was set to 1.5 which provides a good balance between sharp conductivity contrasts and smooth models (Grayver and Kuvshinov 2016).
The minimization problem described by Eq. (50) is solved by means of a global stochastic optimization technique (Covariance Matrix Adaptation Evolution Strategy (CMAES); Hansen and Ostermeier (2001)). The details of the CMAES algorithm used in our inversion are described in Grayver and Kuvshinov (2016).
Figure 7 shows mantle conductivity models estimated by inverting the dominant Q-responses and tidal radial magnetic field separately and jointly. The obtained models generally follow previous results (Grayver et al. 2017), demonstrating that joint inversion allows us to resolve the conductivity of the upper mantle, the mantle transition zone, and the lower mantle. Table 1 lists the estimated (layered) 1-D conductivity model along with the 95 % confidence interval for each layer.
The middle panel in Fig. 5 shows a map of the magnitude of the predicted (modeled) \(M_2\) radial magnetic field at mean satellite altitude of h = 430 km. This predicted field is obtained using the estimated “joint” 1-D profile shown in Fig. 7. Comparing estimated and predicted fields we conclude that they match remarkably well. The bottom panel of this figure shows a global map of residuals, i.e., the magnitude of the difference between the predicted and the observed \(M_2\) radial magnetic field, which is small in most regions of the world.
Finally, the solid curves in Fig. 8 present predicted dominant Q-responses calculated using the “joint” 1-D profile of Fig. 7. We see that predicted responses agree very well with the data-based responses at all periods.
Estimated (circles) dominant Q-responses and their uncertainties (error bars), and model predictions (solid curves). Predictions are for the 1-D profile obtained by jointly inverting the dominant Q-responses and tidal radial magnetic field (cf. Fig. 7). Positive and negative values correspond to real and imaginary parts of the Q-response, respectively
Obtaining 3-D conductivity model
Concept of the 3-D inversion
Similar to the 1-D inversion described in the previous section, we formulate the 3-D inverse problem as a minimization task described by Eq. (50), where the data misfit \(\phi _d({\mathbf {m}})\) reads
Here \(\omega _i\) correspond to periods between 2 and 37.25 days with number of frequencies \(N_{\text {3D}} = 17\). The model vector \({\mathbf {m}}\) contains the 3-D conductivity distribution structure of the Earth’s mantle that we want to determine, the parameterization of which will be specified in the next section. The form of the regularization term \(\phi _r({\mathbf {m}})\) depends on the desired level of smoothness and model parameterization, as discussed later in the paper.
In contrast to 1-D inversion where we were able to invoke a stochastic optimization technique—and thus to quantify the uncertainty of the obtained 1-D model—for the 3-D inversion, we exploit a deterministic approach owing to the high computational cost of the problem. Due to the non-linearity of EM inverse problems, iterative descent methods (e.g., Nocedal and Wright 2006) are typically the methods of choice for deterministic inversions. These methods require a computation of the gradient of the penalty function \(\phi \) with respect to the model parameters, i.e.,
While the gradient of the regularization term is easily calculated analytically, calculation of the data misfit gradient is more challenging. The straightforward option—a brute-force numerical differentiation—requires extremely high computational loads and is approximate by nature. A much more efficient way to rigorously calculate the gradient of the misfit is provided by an adjoint source approach; see e.g., Pankratov and Kuvshinov (2010a). It allows the calculation of the misfit gradient for the price of only a few additional forward calculations (i.e., numerical solutions of Maxwell’s equations) excited by a specific (adjoint) source. Each inverse problem setting requires explicit formulas for the adjoint source. The corresponding formulas for our inverse problem are presented in Appendix C.
Numerical implementation
The derivations presented so far neither depend on the choice of the forward solver (which numerically solves Maxwell’s equations (1)–(2) for a given conductivity model and a given source) nor on the optimization method used to solve the inverse problem. In this section, we describe how we numerically implement the inversion concept outlined in the previous section.
For the forward computations, the 3-D conductivity structure \(\sigma \) is discretized at a spherical grid consisting of \(n_r\times n_\vartheta \times n_\varphi \) volume cells; the conductivity in each cell is assumed to be constant.
The most expensive part—in terms of computational loads—of our forward solution (based on IE approach) is the calculation of Green’s tensors. However, these tensors depend on the chosen 1-D background conductivity, but not on the 3-D conductivity distribution in the model (Kuvshinov and Semenov 2012). This gives a possibility to make the inversion algorithm much more computationally efficient by isolating the computation of Green’s tensors from the rest of the forward calculations, such that it does not need to be repeated in each iteration of the optimization procedure. A parallelization with respect to \(N_{\text {3D}}\) frequencies and to \(N_{\text {ext}}(N_{\text {ext}}+2)\) elementary sources \({{\vec {j}}}_n^{m}\) has been implemented to further optimize the computational load.
The inversion domain is divided into \(N_r\) layers of possibly variable thicknesses, which do not necessarily coincide with the \(n_r\) layers used for the forward modeling. Since our data are transfer functions relating SH coefficients of the magnetic potential, it is most natural to also parameterize the model domain in terms of spherical harmonics, as done previously by e.g., Kelbert et al. (2008). Within each layer the conductivity is thus defined as a finite sum of spherical harmonics up to a cut-off degree L, i.e., the number of model parameters \(N_m\) is given by \(N_m=N_r(L+1)^2\). Derivation and a detailed description of this parameterization is presented in Appendix D.
As mentioned in section “Concept of the 3-D inversion”, we stabilize the inversion with a regularization term \(\phi _r\). A parametrization with spherical harmonics automatically yields a smooth solution. Due to the low cut-off degree L, an additional natural regularization is included in the parametrization. Further smoothing is performed by multiplication of the coefficients by a factor \(l(l+1)\). Radial smoothing, i.e., regularization across layer boundaries, was omitted in this study.
An inversion is usually initiated using strong regularization. Once the convergence rate flattens, the value of the regularization parameter \(\lambda \) is decreased, and the results obtained with the previous \(\lambda \) are used as starting model. This gradual adaptation of the amount of regularization constrains the solution to be close to the global minimum in every stage of the iterative inversion process. This, in turn, facilitates convergence and prevents stepping into a local minimum.
To minimize the penalty function our inversion code offers the option to choose between several popular optimization methods: non-linear conjugate gradients, quasi-Newton and limited-memory quasi-Newton (LMQN). Our tests (not shown here) revealed that the LMQN method is superior to other methods in terms of computational cost. Our implementation of the method follows Nocedal and Wright (2006). The iterative formula for updating the model vector \({\mathbf {m}}\) is
where \(H^{(k)}\) is an approximation to the inverse Hessian matrix, updated at every iteration k, using the limited-memory Broyden–Fletcher–Goldfarb–Shanno formula (e.g., Nocedal and Wright 2006). The step length \(\alpha ^{(k)}\) is computed by an inexact line search and chosen to satisfy the Wolfe conditions (Nocedal and Wright 2006).
Results of 3-D inversion
As discussed earlier matrix Q-responses were estimated in the period range between 2 and 37.25 days. This means—following the skin depth concept (e.g., Weidelt 1972)—that with these responses we constrain the 3-D conductivity distribution at mid-mantle depths. Specifically, we search for conductivity variations in the depth range between 410 and 1200 km. We parametrize the 3-D conductivity distribution at these depths by three spherical layers of 260, 230, and 300 km thickness. The thickness and position of the first layer was chosen to coincide with the mantle transition zone (depths 410 – 670 km) where seismic studies show compositional changes. The thicknesses of the two lower layers are taken to be compatible with those used in other global 3-D EM inversions (Kelbert et al. 2009; Semenov and Kuvshinov 2012; Sun et al. 2015). To remain compatible with the cut-off degree for the induced SH coefficients, the conductivity in the mantle was parameterized by spherical harmonics up to degree three.
The nonuniform layers are embedded in a (fixed) background 1-D conductivity profile obtained in the “Obtaining background 1-D conductivity model” section.
To account for the effects of the nonuniform distribution of oceans and continents we included in the model a thin surface layer describing laterally variable conductance (cf. the right panel of Fig. 6).
Forward calculations were performed on a \(5^\circ \times 5^\circ \) lateral grid; results of our model experiments (not shown here) indicate that higher spatial resolution does not lead to improved results since the matrix Q-responses are estimated up to very low degree and for periods longer than 2 days.
Figure 9 shows the final 3-D model.
The model show significant deviations of conductivity from the global 1-D conductivity profile in the Pacific Ocean region, particularly at depths between 410 and 670 km. Following many inversion runs, which entailed testing different model parameterization (in terms of number of layers and cut-off degree of SH expansion) and different number of Q-matrix elements included in the inversion, the “Pacific Ocean” anomaly appeared to be a robust feature. However, we would like to stress that the 3-D model is poorly constrained in polar regions where the data are heavily downweighted when estimating inducing and induced coefficients. By purpose we do not compare our model with the global 3-D models obtained from ground-based (observatory) data (Kelbert et al. 2009; Semenov and Kuvshinov 2012; Sun et al. 2015) since these models are inconclusive in the Pacific Ocean due to the lack of ground-based data in this region.
Concluding remarks
This paper presents methodological developments and results related to detecting three-dimensional (3-D) variations of the electrical conductivity at mid-mantle depths (410 – 1200 km) using 6 years of Swarm, CryoSat-2 and observatory magnetic field data. As far as we know this is one of the first endeavors to image 3-D mantle conductivity from space. The reader is referred to the paper of Velimsky and Knopp (2020) in the same issue where an alternative 3-D model based on different inversion concept is presented and discussed.
Our approach relies on the estimation and inversion of matrix Q-responses. These responses relate spherical harmonic coefficients of inducing and induced parts of the magnetic potential. The limited spatio-temporal resolution of the data allows us to estimate time series of SH inducing and induced coefficients only up to degrees 2 and 3, respectively. This, by the nature of the case, restricts the lateral resolution of the resulting 3-D conductivity models.
The presented results show significant deviations of conductivity from 1-D conductivity profile in the Pacific Ocean region. Many inversion settings were investigated in order to test the robustness of this feature. These included varying model parameterization and number of Q-matrix elements included in the inversion. We refrain, however, from speculation on the origin of this anomaly, noting that the agreement between estimated and predicted responses is not fully satisfactory for many elements of the Q-matrix. This is in particular due to the fact that the estimated responses occasionally take unrealistic values, indicating that the determination of time series of SH inducing and induced coefficients is far from perfect and requires further improvement. In “Outlook” section, we discuss how the global 3-D EM mapping of mantle conductivity could be advanced.
We also obtained a new 1-D conductivity profile that is global for depths larger than 400 km (since based on the inversion of global long-period Q-responses) but semi-global (i.e., confined to the oceans) at shallower depths (since based on an inversion of tidal signals). As expected, this new 1-D profile is close to that obtained by Grayver et al. (2017) where a similar approach was used, although utilizing different input data sets. Bearing in mind that this approach: (i) is most consistent in terms of proper accounting for the ocean effect and including magnetospheric source terms other than \(P_1^0\), and (ii) allows for constraining the 1-D electrical structure of the mantle throughout its full depth range, we recommend the use of the 1-D conductivity profile presented here or in (Grayver et al. 2017) instead of that obtained by Kuvshinov and Olsen (2006) and Püthe et al. (2015).
Outlook
In spite of continuous and dedicated efforts, the difficult task of global 3-D determination of mantle conductivity structures remains a challenging problem. We discuss below some potential ways to improve the determination of 3-D structures on a global scale.
Alternative approaches to estimate time series of inducing and induced coefficients
As seen in section “Estimating matrix Q-responses”, many elements of the Q-matrix are poorly resolved. The most probable reason for this is an imperfect estimation of the inducing and induced coefficients. Note again that the induced coefficients are responsible for 3-D conductivity effects, and one 3-D effect that strongly influences the results but cannot be properly addressed by the “separation” (Gauss) method exploited in this paper is the so-called ocean induction effect (Kuvshinov 2008). Recall that the Gauss method is based on a simultaneous analysis of radial and horizontal magnetic field components. Given deficient spatio-temporal distribution of observatory and Swarm data, with Gauss method one is able to recover only low SH coefficients both in the inducing and induced parts. But induced radial magnetic field requires higher SH degrees for its proper description, since this component is strongly affected by the (localized) ocean effect.
There exists an alternative approach to isolate the inducing part of the signals from the induced part. It exploits the pre-computed EM fields/responses induced by “elementary” extraneous currents in an a priori model of known conductivity; commonly this model includes oceans and continents of laterally variable conductance underlain by a layered (1-D) medium. This approach has been routinely used for the last two decades to retrieve the inducing part of the signals in the frequency domain. In particular, the concept was used in analyses of ground-based (Guzavina et al. 2019; Koch and Kuvshinov 2015; Kuvshinov et al. 1999, among others) and satellite (Chulliat et al. 2016; Sabaka et al. 2013, 2015, 2020, among others) magnetic data of ionospheric origin (assumed to be mostly periodic). It was also used for analysis of aperiodic ground-based data of magnetospheric origin (Honkonen et al. 2018; Munch et al. 2020; Olsen and Kuvshinov 2004; Püthe and Kuvshinov 2013; Püthe et al. 2014). Note that the latter studies aimed to explore the spatio-temporal evolution of the induced EM field, and time-domain results in these studies were obtained by converting the frequency-domain results into the time domain by means of a Fourier transform (FT).
In the context of this study we are interested in isolating inducing and induced parts of (aperiodic) signals of magnetospheric origin. This prompts a two-step procedure for retrieving time series of the corresponding SH coefficients. The procedure is based on the fact that the magnetic horizontal components are much less influenced by 3-D effects compared to the radial component (Kuvshinov 2008). Thereby, by analyzing the horizontal magnetic components and assuming an a priori Earth’s conductivity model, one determines time series of inducing coefficients. Note, that to account for time-domain induction effects in satellite data the FT approach hardly works, since satellites move in space. But retrieving the inducing coefficients can be done directly in the time domain using a concept of impulse responses (Svetov 1991). We notice here that as applied to geomagnetic field modeling this concept was already used by Maus and Weidelt (2004), Olsen et al. (2005) and Thomson and Lesur (2007) but invoking a simplified setting, assuming a 1-D conductivity and a magnetospheric source described by one single spherical harmonic. With the retrieved time series of external (inducing) SH coefficients, one determines in a second step the induced coefficients by analyzing the magnetic radial component only. Efficient implementation of this two-step approach is discussed in Grayver et al. (2020).
Exploiting data from non-dedicated satellite missions
In the context of 3-D EM induction studies we strive for a precise and detailed description of the spatio-temporal structure of inducing and induced signals. From this perspective, the ideal geomagnetic satellite mission would consist of a large number of low Earth orbiting (LEO) satellites (in polar, circular orbits) uniformly separated in local time (that is, in longitude). This configuration allows for detecting both latitudinal and longitudinal variability of the signals. The more satellites, the higher the resolution of the recovered inducing and induced signals, in time and space. The existing dedicated Swarm constellation mission comprises two satellites (Alpha and Bravo) with varying local time separation between zero and six hours, thus limiting detection of longitudinal variability of the signals. Olsen et al. (2020) and Stolle et al. (2020) used data collected by the CryoSat-2 and GRACE-FO satellites, respectively, and demonstrated that platform magnetometers do provide valuable geomagnetic field measurements, given that vector magnetic field can be properly calibrated. These platform magnetometers are present onboard many LEO satellites, as a part of their attitude control system. In this study, we used calibrated CryoSat-2 data in addition to Swarm and observatory data, and observe that these data indeed improve the recovery of the aforementioned signals. However, improvement by adding data from one single satellite is limited. Obviously, more data from LEO satellites in orbits with different local times are necessary for a substantial improvement; for instance, usage of duly calibrated data from satellites like the Iridium-Next and Spire constellation could be promising.
Another opportunity are dedicated satellite constellations with low-inclined satellites (e.g., Hulot et al. 2020) which will enable researchers to better characterize the complex spatio-temporal nature of the ionospheric and magnetospheric signals.
Multi-response, multi-source and multi-resolution global 3-D imaging
The 3-D results presented in this paper rely on an analysis of magnetic field variations of periods longer than one day, generated by the magnetospheric ring current. As the penetration depth of EM field depends on period, these variations are sensitive to depths greater than 400 km. To constrain 3-D conductivity distribution at shallower depths the analysis of EM field variations at periods shorter than one day are required. In the period range of daily variations (4 to 24 hours) these variations are primarily periodic and the dominating source in this period range is the (mid-latitude) ionospheric current system forced by solar heating of the ionosphere (Yamazaki and Maute 2017). Variations at periods shorter than 4 h—which are mostly aperiodic—also originate in the ionosphere, and can be spatially approximated by a vertically incident plane wave of arbitrary polarization, at least at mid-latitudes (Chave and Jones 2012). Analysis of variations in a period range as wide as practicable would provide an opportunity for imaging the 3-D conductivity structures of the Earth throughout its full depth range—from the crust down to the lower mantle. However, this is a challenging task, because it requires combining transfer functions from sources of different morphology, specifically, long-period (a few days to a few months) matrix Q-responses, daily (4 to 24 hours) and long-period global-to-local transfer functions (Guzavina et al. 2019; Püthe et al. 2014), and shorter period (a few minutes to 3 hours) magnetotelluric (MT) responses—tippers (Morschhauser et al. 2019). The latter three (local) responses are estimated from ground-based data, whereas the (global) matrix Q-responses are estimated from satellite (and observatory) data. As discussed above, the satellite-based matrix Q-responses allow for a global 3-D imaging of mid-mantle conductivity but at rather low (continental-scale) lateral resolution. Ground-based data allow for higher resolution 3-D imaging of the Earth’s mantle in regions with a dense net of continuous observation sites (like in Europe and China), or temporary long-term (like in Australia (Koch and Kuvshinov 2015)) observations. However, bearing in mind an overall very irregular spatial distribution of the ground-based magnetic sites (with substantial gaps in oceanic regions), a proper determination of a global 3-D mantle conductivity model of (uniform) high-resolution is hardly feasible. The above considerations suggest a multi-resolution approach to global 3-D imaging. Specifically, at a first step a low-resolution baseline global 3-D conductivity model at mid-mantle depths is obtained by inverting matrix Q-responses. Wherever possible, large-scale regional 3-D conductivity models in the full depth range are obtained by joint inversion of MT tippers and global-to-local transfer functions. As for oceanic regions, one can decipher local one-dimensional (1-D) conductivity profiles beneath island observatories. The final step of the discussed approach is a compilation of the retrieved global, regional and local models in a global multi-resolution model, for instance, as done by (Alekseev et al. 2015).
So far we discussed the work utilizing only magnetic field data, and confined to onshore observations as ground-based data. However, as discussed earlier, there is an overall deficiency of geomagnetic data in oceanic regions. Data from sea-bottom long-term (with measurement period from a few months to a few years), large-scale MT surveys (Baba et al. 2010, 2017; Suetsugu et al. 2012, among others) can fill, at least partly, this spatial gap. A rather exhaustive summary of available sea-bottom MT data sets is presented in (Guzavina 2020). From these data one can estimate and invert both MT responses (impedance and tipper) and “daily band” global-to-local TFs. It is noteworthy that with sea-bottom long-term MT data it is possible to estimate not only “vertical magnetic” global-to-local TFs, but also TFs relating SH expansion coefficients with local horizontal electric and magnetic fields (Guzavina 2020). Finally, sea-bottom MT data generally comprise detectable tidal signals (Schnepf et al. 2014) which also can be used for constraining conductivity distribution in the lithosphere and upper mantle (Zhang et al. 2019).
In addition one can expand the database for EM sounding of the deep Earth with long-period MT data from a few continental-scale MT projects, such as EarthScope (Schultz 2010), AusLAMP (Chopping et al. 2016) and SinoProbe (Dong and Li 2010).
Finally, multi-year continuous observations of electric field, number of which around the world is constantly growing (Blum et al. 2017; Fujii et al. 2015; Wang et al. 2020) is another promising source of data for the probing deep structures of the Earth.
Availability of data and materials
Swarm and CryoSat-2 data are available from https://earth.esa.int/web/guest/swarm/data-access Ground observatory data are available from ftp://ftp.nerc-murchison.ac.uk/geomag/Swarm/AUX_OBS/hour/.
Change history
20 April 2021
A Correction to this paper has been published: https://doi.org/10.1186/s40623-021-01413-4
Abbreviations
- MT:
-
Magnetotelluric
- G2L:
-
Global-to-local
- 1-D:
-
One-dimensional
- 3-D:
-
Three-dimensional
- SH:
-
Spherical harmonics
References
Abramowitz M, Stegun IA (1964) Handbook of mathematical functions. Dover Press, New York
Alekseev D, Kuvshinov A, Palshin N (2015) Compilation of 3-D global conductivity model of the Earth for space weather applications. Earth Planets Space 67:108–118. https://doi.org/10.1186/s40623-015-0272-5
Aster RC, Borchers B, Thurber CH (2018) Parameter estimation and inverse problems. Elsevier, New York
Baba K, Chen J, Sommer M, Utada H, Geissler WH, Jokat W, Jegen M (2017) Marine magnetotellurics imaged no distinct plume beneath the Tristan da Cunha hotspot in the southern Atlantic Ocean. Tectonophysics 716:52–63.
Baba K, Utada H, Goto T, Kasaya T, Shimizu H, Tada N (2010) Electrical conductivity imaging of the Philippine Sea upper mantle using seafloor magnetotelluric data. Phys Earth Planet In 183:44–62
Bailey R (1969) Inversion of the geomagnetic induction problem. Proc Roy Soc Lond 315:185–194
Balasis G, Egbert G (2006) Empirical orthogonal function analysis of magnetic observatory data: further evidence for non-axisymmetric magnetospheric sources for satellite induction studies. Geophys Res Lett. https://doi.org/10.1029/2006GL025721
Banks R (1969) Geomagnetic variations and the electrical conductivity of the upper mantle. Geophys J R Astr Soc 17:457–487
Blum C, White T, Sauter E, Stewart D, Bedrosian P, Love J (2017) Geoelectric monitoring at the Boulder magnetic observatory. Geosci Instrum Methods Data Syst 6:447–452
Buchen J, Marquardt H, Speziale S, Kawazoe T, Ballaran TB, Kurnosov A (2018) High-pressure single-crystal elasticity of wadsleyite and the seismic signature of water in the shallow transition zone. Earth Planet Sci Lett 498:77–87
Chave A, Jones A (2012) The magnetotelluric method. Theory and practice. Cambridge University Press, New York
Chen C, Kruglyakov M, Kuvshinov A (2020) A new method for accurate and efficient modeling of the local ocean induction effects Application to long-period responses from island geomagnetic observatories. Geophys Res Lett 47(8):e2019GL086. https://doi.org/10.1029/2019GL086351
Chopping, RG, Duan J, Czarnota K, Kemp T (2016) AusLAMP long period magnetotellurics: progress update and new insights into Victorian geology and mineral prospectivity, pp. GP41A–03
Chulliat A, Vigneron P, Hulot G (2016) First results from the swarm dedicated ionospheric field inversion chain. Earth Planets Space. https://doi.org/10.1186/s40623-016-0481-6
Chulliat A et al (2015) The US/UK world magnetic model for 2015-2020, NOAA Technical Report
Debayle E, Ricard Y (2012) A global shear velocity model of the upper mantle from fundamental and higher Rayleigh mode measurements. J Geophys Res 117:1–24
Dong S, Li T (2010) SinoProbe - A multidisciplinary research program of Earth sciences in China, AGU Fall Meeting Abstracts, pp. T42B–08
Fei H, Yamazaki D, Sakurai M, Miyajima N, Ohfuji H, Katsura T, Yamamoto T (2017) A nearly water-saturated mantle transition zone inferred from mineral viscosity. Sci Adv 3:6. https://doi.org/10.1126/sciadv.1603024
Fujii I, Ookawa T, Nagamachi S, Owada T (2015) The characteristics of geoelectric fields at Kakioka, Kanoya, and Memambetsu inferred from voltage measurements during 2000 to 2011. Earth Planets Space 67(1):62–79. https://doi.org/10.1093/gji/ggw063
Grayver A, Kuvshinov A (2016) Exploring equivalence domain in non-linear inverse problems using Covariance Matrix Adaption Evolution strategy and random sampling. Geophys J Int 205:971–987.
Grayver A, Munch F, Kuvshinov A, Khan A, Sabaka T, Toffner-Clausen L (2017) Joint inversion of satellite detected tidal and magnetospheric signals constrains electrical conductivity and water content of the upper mantle and transition zone. Geophys Res Lett 44:6074–6081
Grayver A, Schnepf N, Kuvshinov A, Sabaka T, Manoj C, Olsen N (2016) Satellite tidal magnetic signals constrain oceanic lithosphere-asthenosphere boundary. Sci Adv. https://doi.org/10.1126/sciadv.1600798
Grayver A, Kuvshinov A, Werthmüller D (2020) Time-domain modeling of 3-D earth’s and planetary EM induction effect in ground and satellite observations. J Geophys Res. https://doi.org/10.1029/2020JA028672
Guzavina M, Grayver A, Kuvshinov A (2019) Probing upper mantle electrical conductivity with daily magnetic variations using global to local transfer functions. Geophys J Int 219(3):2125–2147
Guzavina M (2020) Novel approaches for probing upper mantle electrical conductivity using solar quiet variations: Improved data processing and transfer functions, PhD thesis; ETH Zürich
Hansen P (1992) Analysis of discrete ill-posed problems by means of the L-curve. SIAM Review 34:561–580
Hansen N, Ostermeier A (2001) Completely derandomized self-adaptation in evolution strategies. Evol Comput 9(2):159–195
Honkonen I, Kuvshinov A, Rastätter L, Pulkkinen A (2018) Predicting global ground geoelectric field with coupled geospace and three-dimensional geomagnetic induction models. Space Weather. https://doi.org/10.1029/2018SW001859
Hulot G et al (2020) NanoMagSat, a 16U nanosatellite constellation high-precision magnetic project to monitor the Earth’s magnetic field and ionospheric environment, AGU Abstract, DI001-08
Karato S-i, Wang D (2013) Electrical conductivity of minerals and rocks, Physics and Chemistry of the Deep Earth, pp. 145–182
Kelbert A, Egbert G, Schultz A (2008) A nonlinear conjugate 3-D inversion of global induction data. Resolution studies. Geophys J Int 173:365–381
Kelbert A, Schultz A, Egbert G (2009) Global electromagnetic induction constraints on transition-zone water content variations. Nature 460:1003–1007
Khan A (2016) On earth’s mantle constitution and structure from joint analysis of geophysical and laboratory-based data: an example. Surv Geophys 37(1):149–189
Khan A, Kuvshinov A, Semenov A (2011) On the heterogeneous electrical conductivity structure of the Earth’s mantle with implications for transition zone water content. J Geophys Res. https://doi.org/10.1029/2010JB007,458
Koch S, Kuvshinov A (2015) 3-D EM inversion of ground based geomagnetic Sq data. Results from the analysis of Australian array (AWAGS) data. Geophys J Int 200(3):1284–1296. https://doi.org/10.1093/gji/ggu474
Koyama T, Khan A, Kuvshinov A (2014) Three-dimensional electrical conductivity structure beneath Australia from inversion of geomagnetic observatory data: evidence for lateral variations in transition-zone temperature, water content and melt. Geophys J Int 196:1330–1350. https://doi.org/10.1093/gji/ggt455
Koyama T, Shimizu H, Utada H, Ichiki M, Ohtani E, Hae R (2006) Water content in the mantle transition zone beneath the North Pacific derived from the electrical conductivity anomaly, in AGU Geophys Monogr Ser, vol. 168
Kuvshinov A, Avdeev D, Pankratov O (1999) Global induction by Sq and Dst sources in the presence of oceans: bimodal solutions for non-uniform spherical surface shells above radially symmetric earth models in comparison to observations. Geophys J Int 137:630–650
Kuvshinov A, Olsen N (2006) A global model of mantle conductivity derived from 5 years of CHAMP, Ørsted, and SAC-C magnetic data. Geophys Res Lett 33(18):L18,301
Kuvshinov A, Semenov A (2012) Global 3-D imaging of mantle electrical conductivity based on inversion of observatory C-responses - I. An approach and its verification. Geophys J Int 189:1335–1352
Kuvshinov A (2008) 3-D global induction in the oceans and solid Earth: recent progress in modeling magnetic and electric fields from sources of magnetospheric, ionospheric and oceanic origin, Surveys in Geophysics, pp. 10.1007/s10,712–008–9045–z
Lekic V, Romanovicz B (2011) Inferring upper-mantle structure by full waveform tomography with the spectral element method. Geophys J Int 185:799–831
Li S, Weng A, Zhang Y, Schultz A, Li Y, Tang Y, Zou Z, Zhou Z (2020) Evidence of Bermuda hot and wet upwelling from novel three-dimensional global mantle electrical conductivity image, Geochemistry, Geophysics. Geosystems 21:6. https://doi.org/10.1029/2020GC009016
Luhr H, Xiong C, Olsen N (2017) Near-earth magnetic field effects of large-scale magnetospheric currents. Space Sci Rev 206:521–545. https://doi.org/10.1016/j.srt.2018.11.017
Macmillan S, Olsen N (2013) Observatory data and the Swarm mission. Earth Planets Space 65:1355–1362. https://doi.org/10.5047/eps.2013.07.011
Maus S, Weidelt P (2004) Separating the magnetospheric disturbance magnetic field into external and transient internal contributions using a 1d conductivity model of the earth. Geophys Res Lett 31:12
Morschhauser A, Grayver A, Kuvshinov A, Samrock F, Matzka J (2019) Tippers at island geomagnetic observatories constrain electrical conductivity of oceanic lithosphere and upper mantle. Earth Planets Space 71(1):1–9. https://doi.org/10.1186/s40623-019-0991-0
Munch FD, Grayver AV, Guzavina M, Kuvshinov AV, Khan A (2020) Joint inversion of daily and long-period geomagnetic transfer functions reveals lateral variations in mantle water content. Geophys Res Lett 47(10):e2020GL087,222. https://doi.org/10.1029/2020GL087222
Munch F, Grayver A, Kuvshinov A, Khan A (2018) Stochastic inversion of geomagnetic observatory data including rigorous treatment of the ocean induction effect with implications for transition zone water content and thermal structure. J Geophys Res 123:31–51
Nocedal J, Wright SJ (2006) Numerical optimization. Springer, New York
Olsen N (1999) Induction studies with satellite data. Surv Geophys 20:309–340
Olsen N, Albini G, Bouffard J, Parrinello T, Tøfffner-Clausen L (2020) Magnetic observations from CryoSat-2: calibration and processing of satellite platform magnetometer data. Earth Planets Space 72:48. https://doi.org/10.1186/s40623-020-01171-9
Olsen N, Floberghagen R (2018) Exploring Geospace from Space: the Swarm Satellite Constellation Mission. Space Res Today 203:61–71. https://doi.org/10.1016/j.srt.2018.11.017
Olsen N, Kuvshinov A (2004) Modelling the ocean effect of geomagnetic storms. Earth Planets Space 56:525–530. https://doi.org/10.1002/2017SW001735
Olsen N, Sabaka TJ, Lowes F (2005) New parameterization of external and induced fields in geomagnetic field modeling, and a candidate model for IGRF 2005. Earth Planets space 57(12):1141–1149. https://doi.org/10.1186/BF03351897
Pankratov O, Kuvshinov A (2010a) General formalism for the efficient calculation of derivatives of EM frequency domain responses and derivatives of the misfit. Geophys J Int 181:229–249
Pankratov O, Kuvshinov A (2010b) Fast calculation of the sensitivity matrix for responses to the Earth’s conductivity: General strategy and examples. Izvestiya, Phys Solid Earth 46(9):788-804
Pankratov O, Kuvshinov A (2016) Applied mathematics in em studies with special emphasis on an uncertainty quantification and 3-D integral equation modelling. Surv Geophys 37(1):109–147
Parkinson WD (1983) Introduction to Geomagnetism. Scottish Academic Press, Edinburgh
Püthe C, Kuvshinov A (2013) Determination of the 3-D distribution of electrical conductivity in Earth’s mantle from Swarm satellite data: frequency domain approach based on inversion of induced coefficients. Earth Planets Space 65:1247–1256. https://doi.org/10.5047/eps.2013.09.004
Püthe C, Kuvshinov A (2014) Mapping 3-D mantle electrical conductivity from space: a new 3-d inversion scheme based on analysis of matrix q-responses. Geophys J Int 197:768–784. https://doi.org/10.1093/gji/ggu027
Püthe C, Kuvshinov A, Khan A, Olsen N (2015) A new model of Earth’s radial conductivity structure derived from over 10 yr of satellite and observatory magnetic data. Geophys J Int 203(3):1864–1872. https://doi.org/10.1093/gji/ggv407
Püthe C, Kuvshinov A, Olsen N (2014) Handling complex source structures in global EM induction studies: From C-responses to new arrays of transfer functions. J Int Geophys. https://doi.org/10.1093/gji/ggu027
Ritsema J, Deuss A, van Heijst H, Woodhouse J (2011) S40RTS: a degree-40 shear-velocity model for the mantle from new Rayleigh wave dispersion, teleseismic traveltime and normal-mode splitting function measurements. Geophys J Int 184:1223–1236
Sabaka T, Toffner-Clausen L, Olsen N (2013) Use of the comprehensive inversion method for Swarm satellite data analysis. Earth Planets Space 65:1201–1222. https://doi.org/10.5047/eps.2013.09.007
Sabaka T, Olsen N, Tyler R, Kuvshinov A (2015) CM5, a pre-Swarm comprehensive geomagnetic field model derived from over 12 yr of CHAMP, Ørsted, SAC-C and observatory data. Geophys J Int 200:1596–1626. https://doi.org/10.1093/gji/ggu493
Sabaka TJ, Tyler RH, Olsen N (2016) Extracting ocean-generated tidal magnetic signals from Swarm data through satellite gradiometry. Geophys Res Lett 43(7):3237–3245. https://doi.org/10.1002/2016GL068180
Sabaka T, Tøffner-Clausen L, Olsen N, Finlay C (2018) A comprehensive model of Earth’s magnetic field determined from 4 years of Swarm satellite observation. Earth Planets Space 70:2–26. https://doi.org/10.1186/s40623-018-0896-3
Sabaka T, Tøffner-Clausen C, Olsen N, Finlay C (2020) CM6: a comprehensive geomagnetic field model derived from both CHAMP and Swarm satellite observations. Earth Planets Space. https://doi.org/10.1186/s40623-020-01210-5
Schaeffer A, Lebedev S (2013) Global shear-speed structure of the upper mantle and transition zone. Geophys J Int 194:417–449
Schmucker U (1999) A spherical harmonic analysis of solar daily variations in the years 1964–1965: response estimates and source fields for global induction - II.Results. Geophys J Int 136:455–476
Schmucker U (1985) Sources of the geomagnetic field. Landolt-Börnstein, New-Series, 5(2b). Springer-Verlag, Berlin-Heidelberg, pp 31–73
Schnepf NR, Manoj C, Kuvshinov A, Toh H, Maus S (2014) Tidal signals in ocean-bottom magnetic measurements of the Northwestern Pacific: observation versus prediction. Geophys J Int 198(2):1096–1110. https://doi.org/10.1093/gji/ggu190
Schnepf NR, Kuvshinov A, Sabaka T (2015) Can we probe the conductivity of the lithosphere and upper mantle using satellite tidal magnetic signals? GRL 42: https://doi.org/10.1002/2015GL063540
Schultz A (2010) EMScope: a continental scale magnetotelluric observatory and data discovery resource. Data Sci J 8:IGY6–IGY20
Schultz A, Larsen JC (1990) On the electrical conductivity of the mid mantle II. Delineation of heterogeneity by application of extremal inverse solutions, Geophys J Int 101(3):565–580. https://doi.org/10.1111/j.1365-246X.1990.tb05571.x
Schulze K, Marquardt H, Kawazoe T, Ballaran TB, McCammon C, Koch-Müller M, Kurnosov A, Marquardt K (2018) Seismically invisible water in earth’s transition zone? Earth Planet Sci Lett 498:9–16
Semenov A, Kuvshinov A (2012) Global 3-D imaging of mantle electrical conductivity based on inversion of observatory C-responses - II. Data analysis and results. Geophys J Int 191:965–992
Shimizu H, Utada H, Baba K, Koyama T, Obayashi M, Fukao Y (2010) Three-dimensional imaging of electrical conductivity in the mantle transition zone beneath the North Pacific ocean by a semi-global induction study. Phys Earth Planet Int 183:252–269
Srivastava BJ (1966) Theory of the magnetotelluric method of a spherical conductor. Geophys J R Astron Soc 11:373–387
Stolle C, Michaelis I, Xiong C, Rother M, Usbeck T, Yamazaki Y, Rauberg J, Styp-Rekowski K (2020) Observing Earth’s magnetic environment with the GRACE-FO mission. Earth Planets Space 72:48. https://doi.org/10.1186/s40623-021-01364-w
Suetsugu D et al (2012) TIARES Project: Tomographic investigation by seafloor array experiment for the Society hotspot. Earth Planets Space 64:4. https://doi.org/10.5047/eps.2011.11.002
Sun J, Kelbert A, Egbert GD (2015) Ionospheric current source modeling and global geomagnetic induction using ground geomagnetic observatory data. J Geophys Res Solid Earth 120:6771–6796. https://doi.org/10.1002/2015JB012063
Svetov BS (1991) Transfer functions of the electromagnetic field (in russian). Fizika Zemli 1:119–128
Taguchi E, Stammer D, Zahel W (2014) Inferring deep ocean tidal energy dissipation from the global high-resolution data-assimilative HAMTIDE model. J Geophys Res 119(7):4573–4592
Thomson AW, Lesur V (2007) An improved geomagnetic data selection algorithm for global geomagnetic field modelling. Geophys J Int 169(3):951–963
Utada H, Koyama T, Obayashi M, Fukao Y (2009) A joint interpretation of electromagnetic and seismic tomography models suggests the mantle transition zone below Europe is dry. Earth Planet Sci Lett 281:249–257
Velimsky J (2013) Determination of three-dimensional distribution of electrical conductivity in the Earth’s mantle from Swarm satellite data: Time domain approach. Earth Planets Space 65:1239–1246. https://doi.org/10.5047/eps.2013.08.001
Velimsky J, Grayver A, Kuvshinov A, Sachl L (2018) On the modelling of M2 tidal magnetic signatures: effects of physical approximations and numerical resolution. Earth Planets Space 70:10. https://doi.org/10.1186/s40623-018-0967-5
Velimsky J, Knopp O (2020) Lateral variations of electrical conductivity in the lower mantle constrained by Swarm, Cryosat-2, and observatory data. Earth Planets Space 72:48. https://doi.org/10.1186/s40623-020-01334-8
Wang H, Egbert G, Yao Y, Cheng J (2020) Array analysis of magnetic and electric field observatories in China: estimation of magnetotelluric impedances at very long periods. Geophys J Int 222(1):305–326. https://doi.org/10.1093/gji/ggaa169
Weidelt P (1972) The inverse problem of geomagnetic induction. Z Geophys 38:257–289
Yamazaki Y, Maute A (2017) Sq and EEJ-A Review on the daily variation of the geomagnetic field caused by ionospheric dynamo currents. Space Sci Rev 206(1–4):299–405
Yoshino T (2010) Laboratory electrical conductivity measurement of mantle minerals. Surv Geophys 31(2):163–206
Zhang H, Egbert GD, Chave AD, Huang Q, Kelbert A, Erofeeva SY (2019) Constraints on the resistivity of the oceanic lithosphere and asthenosphere from seafloor ocean tidal electromagnetic measurements. Geophys J Int 219(1):464–478. https://doi.org/10.1093/gji/ggz315
Zhang Y, Weng A, Li S, Yang Y, Tang Y, Liu Y (2020) Electrical conductivity in the mantle transition zone beneath Eastern China derived from L1-Norm C-responses. Geophys J Int 221(2):1110–1124. https://doi.org/10.1093/gji/ggaa059
Acknowledgements
We wish to thank ESA for the prompt availability of Swarm L1b data and for providing access to the CryoSat-2 platform magnetometer data and related engineering information. We also wish to thank Christoph Püthe, core member of the team who developed and validated the tools for estimation and inversion of matrix Q-responses. The staff of the geomagnetic observatories and INTERMAGNET are thanked for supplying high-quality observatory data. Susan Macmillan (BGS) is gratefully acknowledged for collating checked and corrected observatory hourly mean values in the AUX\(\_\)OBS database.
Open Access
This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funding
This study has been supported in the framework of Swarm DISC activities, funded by ESA contract no. 4000109587, with support from EO Science for Society.
Author information
Authors and Affiliations
Contributions
AK estimated matrix Q-responses, performed their 3-D inversion and wrote the draft of the manuscript. AG estimated dominant Q-responses and conducted 1-D inversion of these responses and tidal magnetic signals. NiO developed the tool to derive time series of inducing and induced SH coefficients of magnetospheric origin, and calibrated the CryoSat-2 data. LT processed the Swarm, CryoSat-2 and observatory data, and estimated time series of inducing and induced SH coefficients. All co-authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: DOI for the reference ‘Stolle et al. (2020)’ has been changed.
Appendices
Appendix A: Conventional local transfer functions used in GDS
Following Appendix H of (Kuvshinov and Semenov 2012) frequency-domain EM field at the surface of the 1-D Earth can be written as
Here \(Z_n\) is an impedance of underlying 1-D section, \({{\vec {r}}}_a = (a-, \vartheta , \varphi )\) and \(a-\) means that r tends to the surface of the Earth, \(r=a\), from below. Hereinafter we will omit but imply the dependence of the fields and responses on \(\omega \) and \(\sigma \). Also we note that \(Z_n\) depends on r; thus we explicitly write in the above equations that it is calculated on the surface of the Earth. \(Z_n\) is connected with the \(C_n\)-response as
\(C_n\) has a dimension of length and real part of \(C_n\) reflects the depth of penetration of EM field into the Earth (Weidelt 1972). Eqs. (56)–(58) allows us to obtain formulas used in Geomagnetic Depth Sounding
-
1
If the source is described by a single spherical harmonic \(Y^m_n\) and \(m \ne 0\) (and the Earth’s model is 1-D), then—as it is seen from Eqs. (57)–(58)—the \(C_n\)-response can be estimated from the local measurements of magnetic field as
$$\begin{aligned} C_n = \frac{a}{n(n+1)}\frac{\frac{\partial P_n^{|m|}}{\partial \vartheta }}{P^{|m|}_n }\frac{B_r}{B_\vartheta } , \end{aligned}$$(60)or/and
$$\begin{aligned} C_n = \frac{1}{\sin \vartheta }\frac{ima}{n(n+1)}\frac{B_r}{B_\varphi } . \end{aligned}$$(61) -
2
If—along with the magnetic field—the electric field is measured, then —as it is seen from Eqs. (56) and (58)—the \(C_n\)-response can be estimated as
$$\begin{aligned} C_n = -\frac{1}{i\omega } \frac{E_\varphi }{B_\vartheta } , \end{aligned}$$(62)or/and
$$\begin{aligned} C_n = \frac{1}{i\omega }\frac{E_\vartheta }{B_\varphi } . \end{aligned}$$(63) -
3
Formulas (60)–(63) can be useful, for example, when EM field variations due to (ionospheric) Sq source are investigated. Recall that daily Sq variations are assumed to be periodic, and thus they can be represented via their time harmonics with frequencies \(\omega _p = \frac{2\pi p}{P}, p = 1,2,...\), where \(P=24\) hours. For p-th time harmonic the dominant source term is \(Y_{p+1}^p\) (cf. Schmucker (1999)), and thus from the local measurements of Sq field one can estimate \(C_{p+1}\) at frequencies \(\omega _p\).
-
4
If the source is described by a single spherical harmonic \(Y_n^m\), but \(m=0\), then \(B_\varphi = 0\), and thus only formulas (60) and (62) are valid. In particular, when the source is described via harmonic \(Y_1^0 \equiv \cos \vartheta \) then Eq. (60) degenerates to
$$\begin{aligned} C_1 = -\frac{a}{2}\tan \vartheta \frac{B_r}{B_\vartheta } . \end{aligned}$$(64) -
5
If the source is described via a number of spherical harmonics then measuring EM field at a single site is not sufficient to determine the \(C_n\) response(s). In this case the least squares fitting of \(B_r\) and one or both components of horizontal magnetic field \({{\vec {B}}}_H\) at a number of sites (observatories) allows for estimating the responses (Schmucker 1999).
-
6
If we assume that \(Z_n\) depends weakly on the degree n and —to a first approximation—is equal to \(Z_1\), and if, in addition to magnetic field the tangential gradients of the magnetic field are measured (or estimated), then even in the case when the source is described by a number of spherical harmonics the \(C_1\)-response can be estimated from single site measurements of magnetic field and their gradients as
$$\begin{aligned} C_1 = -a \frac{B_r}{\nabla _\perp \cdot {{\vec {B}}}_H} , \end{aligned}$$(65)where \(\nabla _\perp \cdot \) is an angular part of divergence operator. To obtain Eq. (65), we used the following equations
$$\begin{aligned} B_r\approx \,& {} Z_1(a,\omega )\sum \limits _{n,m} (2n+1)n\epsilon _n^m(\omega )\frac{1}{i\omega \mu _0 a - n Z_n(a)} Y^m_n(\vartheta ,\varphi ), \end{aligned}$$(66)$$\begin{aligned} \nabla _\perp \cdot {{\vec {B}}}_{H}= & {} \sum \limits _{n,m} (2n+1)n\epsilon _n^m(\omega ) \frac{i\omega \mu _0}{i\omega \mu _0 a -n Z_n(a) }Y^m_n(\vartheta ,\varphi ) . \end{aligned}$$(67)The latter equation is obtained using equality
$$\begin{aligned} \nabla _\perp \cdot \left( \nabla _\perp Y^m_n \right) = \nabla ^2_\perp Y^m_n = -n(n+1)Y^m_n , \end{aligned}$$(68)where \(\nabla ^2_\perp \) is an angular part of Laplacian operator.
-
7
Finally, the continuity of magnetic field through the Earth’s surface allows us to relate “global” \(C_n\) (at the surface of the Earth) and \(Q_n\). By equating Eqs. (57) and (11), the latter with \(r=a\), we obtain
$$\begin{aligned} C_n = \frac{a}{n+1}\frac{1-\frac{n+1}{n}Q_n}{1+Q_n}, \end{aligned}$$(69)and
$$\begin{aligned} Q_n = \frac{n}{n+1}\frac{a-(n+1)C_n}{a+n C_n} . \end{aligned}$$(70)
Appendix B: Q-responses for two simplistic conductivity models of the Earth
It is instructive to explore the behavior of \(Q_n\) for the Earth’s model of uniform conductivity
It can be shown (Parkinson 1983) that for this Earth’s model \(Q_n\) is given by
where \(J_p\) is Bessel’s function of p-th order, and (propagation) constant k is
Let us look at the behavior of \(Q_n\) for large k. Due to Eq. (73) this gives us an information how \(Q_n\) behaves at high frequencies or/and for high conductivity of the Earth. Using asymptotic for spherical Bessel functions for large value of argument (Abramowitz and Stegun 1964) one obtains
By substituting Eq. (74) into Eq. (11) we have
Note that the latter result is valid for a sphere of any radius, and thus one can obtain an expression for \(Q_n\) for the following simplistic 1-D conductivity Earth’s model which consists of insulating “mantle” of thickness h and perfect conductor underneath
Using the fact that Eq. (11) is now valid for \(r \ge a-h\), and that \(B_r = 0\) due to Eq. (75) one obtains that
From the latter equation it follows that for the model described by Eq. (76), \(Q_n\) is a real-valued quantity which does not depend on \(\omega \). This, in particular, means that in time domain the inducing and induced coefficients are related as
This model is in a routine use by external field researchers since it allows them to account for EM induction in a rather simple manner. Note that in case of any Earth’s model with finite 1-D conductivity distribution the relation between the inducing and induced coefficients in time domain reads as a convolution, i.e.,
The reader can find more details on time-domain modeling of magnetic fields and responses in Grayver et al. (2020).
Appendix C: Constructing adjoint source to calculate the misfit gradient
The content of this and the next appendix closely follows material presented in (Püthe and Kuvshinov 2013).
In this appendix we are interested in estimating gradient of the misfit (53) with respect to model parameters. Taking the total derivative of the data misfit in Eq. (53) yields
Since \(Q_{kn}^{lm,\text {pred}}\) is given by Eq. (25), the only term left to derive is \(\text {d}Q_{kn}^{lm,\text {pred}}\). We first note that, by taking the derivative of Eq. (25), we obtain
where we define
The critical element in Eq. (80) is the total derivative of the radial component of the magnetic field, \(\text {d}B_{n,r}^m\). To investigate this element, let us first define the operator \({\mathbf {G}}^{ej}(\vec {j}^{\text {ext}})\) as the “electric field solution” of Maxwell’s equations (1)–(2) for the current source \(\vec {j}^{\text {ext}}\), i.e., \(\vec {E}\equiv \vec {E}^j={\mathbf {G}}^{ej}(\vec {j}^{\text {ext}})\). Analogously, the operator \({\mathbf {G}}^{bj}(\vec {j}^{\text {ext}})\) represents the “magnetic field solution” of Maxwell’s equations (1)–(2). Note that these operators are universal and do not depend on the type of code solving the forward problem.
In a similar way, we can define the operator \({\mathbf {G}}^{eh}(\vec {h}^{\text {ext}})\) as the electric field solution of an alternative formulation of Maxwell’s equations,
where \(\vec {h}^{\text {ext}}\) describes a distribution of magnetic dipoles. Pankratov and Kuvshinov (2010a) showed that this formulation can be transformed into the more common representation of Maxwell’s equations with a current source, cf. Eqs. (1)–(2). The formulation given by Eqs. (82)–(83) is however convenient in context of the adjoint approach, as will become clear later. An important property of the operators \({\mathbf {G}}^{ej}\), \({\mathbf {G}}^{eh}\) and \({\mathbf {G}}^{bj}\) are their reciprocity relations (Pankratov and Kuvshinov 2010b):
where
denotes a complex-valued bilinear scalar product. In a spherical coordinate system,
Let us now consider Maxwell’s equations (1)–(2) in an Earth’s model with infinitesimally changed conductivity \(\sigma +\text {d}\sigma \), yielding electric and magnetic fields \(\vec {E}+\text {d}\vec {E}\) and \(\vec {B}+\text {d}\vec {B}\), respectively
Further, subtracting Eqs. (1)–(2) from Eqs. (88)–(89) we obtain
Using the operators defined above, we can rewrite Eq. (90) as
Note that we neglected the second order quantity \(\text {d}\sigma \text {d}\vec {E}\). Eqs. (92) and (91) constitute a set of Maxwell’s equations for the infinitesimal fields \(\text {d}\vec {E}\) and \(\text {d}\vec {B}\) excited by the “source” \(\text {d}\sigma {\mathbf {G}}^{ej}(\vec {j}^{\text {ext}})\). Using the operator representation a second time, we obtain an expression for \(\text {d}\vec {B}\)
So far, we did not make any assumptions about the external source current \(\vec {j}^{\text {ext}}\). We are interested in magnetic fields excited by elementary spherical harmonic source described by Eq. (24). This yields the special case of Eq. (93),
Making use of reciprocity relation (85) and the definitions above, Eq. (80) can be rewritten in operator form:
where
is a fictitious magnetic source, consisting of radial magnetic dipoles distributed along Earth’s surface with weights that are equal to \(c_k^l Y_k^{l^*}\).
Substituting the last line of Eq. (95) into Eq. (80) yields
with
With the definition of the bilinear scalar product (87), we can use Eq. (97) to obtain the elements of the data misfit gradient
Here \(\vec {E}^{{u}_n^m}={\mathbf {G}}^{eh}(\vec {u}_n^m)\) and \(\vec {E}_n^m={\mathbf {G}}^{ej}(\vec {j}_n^m)\), or in other words, \(\vec {E}^{{u}_n^m}\) and \(\vec {E}_n^m\) are the “electric field” solutions of Maxwell’s equations (82)–(83) and (26)–(27), respectively. This representation implies a model built from elementary volume cells \(V_j\) each having a piece-wise constant conductivity \(\sigma _j\). The last term in Eq. (99), \(\partial \sigma _j/\partial m_s\), depends on the model parameterization (cf. Pankratov and Kuvshinov (2010a)); note that the Einstein summation convention is implied for j. If the model parameters directly represent the conductivities of each cell, i.e., \(m_s=\sigma _s\), then \(\partial \sigma _j/\partial m_s=\delta _{sj}\), where \(\delta _{sj}\) is Kronecker’s delta. Equation (99) demonstrates the essence of the adjoint approach: in order to calculate the gradient of the data misfit, only one (per frequency and elementary source) additional forward modeling with excitation by the adjoint source \({{\vec {u}}}_n^m\) is required.
Appendix D: Parametrization of the inversion domain
As we discussed in the main text, the inversion domain is divided into \(N_r\) layers of possibly variable thicknesses; \(N_r\) is not necessarily equal to \(n_r\) (i.e., the number of laterally heterogeneous layers relevant for forward modeling), as we might only be interested in recovering the distribution of conductivity in specific layers. However, the layer boundaries coincide with those of the forward modeling domain.
The conductivity of each cell is first normalized as
where \(c_a>0\) and \(c_b>0\) are chosen such that \(s\in [-1,1]\) based on assumptions about minimum and maximum conductivities in the mantle. Solving Eq. (100) for \(\sigma \) yields
We then expand s for each layer by spherical harmonics,
The model vector \({\mathbf {m}}\) is accordingly composed of the coefficients of the SH expansion
Its constituents can be derived from Eq. (102) by making use of the orthogonality of the spherical harmonics, i.e.,
where \(\left\| P_l^m\right\| ^{2}\) is the squared norm of the associated Legendre polynomial \(P_l^m\).
In Appendix C, we presented a formula (Eq. 99) to compute the partial derivative of the data misfit \(\phi _d\) with respect to the model parameters. The equation includes the factor \(\partial \sigma _k/\partial m_j\) (note that different subscripts are used here in order to avoid confusion) and for spherical harmonic parametrization, this term is calculated as
Note that \(m_j\) on the left-hand side of Eq. (108) denotes a model parameter, while on the right-hand side, it denotes the order of the spherical harmonic for this model parameter.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuvshinov, A., Grayver, A., Tøffner-Clausen, L. et al. Probing 3-D electrical conductivity of the mantle using 6 years of Swarm, CryoSat-2 and observatory magnetic data and exploiting matrix Q-responses approach. Earth Planets Space 73, 67 (2021). https://doi.org/10.1186/s40623-020-01341-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-020-01341-9