Main text

Introduction

The mode conversion responsible for radio wave generation has been studied for several decades (e.g., Oya 1971, 1974; LaBelle 2018) and owing to the importance of this subject, it is still an active topic in a lot of research. It is well known that the refractive index is determined by the characteristics of the wave, such as wave frequency and wave normal angle, and by the parameters of the plasma medium, such as number density of plasma and background magnetic field strength (Stix 1992). The mode conversion of slow Z-mode waves (\(\omega_{p} < \omega < \omega_{\text{UHR}}\), where ω, \(\omega_{p}\), and \(\omega_{\text{UHR}}\) are the wave frequency, electron plasma frequency, and upper hybrid resonance frequency, respectively) to left-hand ordinary (LO)-mode waves has been investigated for the purpose of understanding the origin of the planetary radio emissions (Jones 1976, 1980, 1987, 1988), Jovian decametric radiation (Oya 1974; Jones 1977), and auroral kilometric radiation (Benson 1975).

Recent simulation studies investigated the mode conversion process in detail and revealed the condition required for the efficient mode conversion quantitatively (Kim et al. 2005; Kalaee et al. 2009, 2010; Kalaee and Katoh 2014, 2016a, 2019; Horký et al. 2018; Horký and Omura 2019). Jones (1980) considered the condition for the mode conversion under the assumption that the magnetic field direction is perpendicular to the density gradient and derived a formula for the beaming angle of LO-mode waves. Kalaee and Katoh (2014, 2016a) compared the beaming angle proposed by Jones (1980) to the angle obtained by simulation results and proposed an improvement of the beaming angle theory. Kalaee and Katoh (2016b) considered the magnetic field direction arbitrary to the density gradient to generalize the condition for the mode conversion and presented the formula for the beaming angle of LO-mode waves. The sequence of the conversion process from Z-mode to LO-mode waves is illustrated in Fig. 1. First, let us consider a situation where slow Z-mode waves of frequency \(\omega\) propagate toward a region of higher plasma density. These waves become fast Z-mode waves after passing through the layer with \(\omega = \omega_{p}\). Although fast Z-mode waves of frequency \(\omega\) can exist in the higher density region as long as the wave frequency is higher than the Z-mode wave cutoff frequency \(\omega_{{Z - {\text{cutoff}}}}\), the waves change their propagation direction toward the lower density region before reaching the region where \(\omega = \omega_{{Z - {\text{cutoff}}}}\) and then propagate further into the lower density region passing through the layer with \(\omega = \omega_{p}\), where the waves have the possibility to convert into LO-mode waves.

Fig. 1
figure 1

A schematic representation of the slow Z-mode wave propagation in an inhomogeneous plasma and mode conversion processes

Full size image

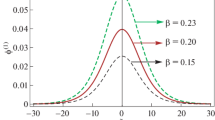
Kalaee et al. (2009) performed several simulations with different steepness and revealed the conversion efficiency as shown in Fig. 2, where L/λ shows the steepness of the inhomogeneity, L is the scale length of the density gradient, and λ is the wavelength of incident waves. For the case in which the two branches of modes are separated, a region of evanescence develops between the two branches, and mode conversion can only take place by the tunneling effect. Therefore, for an efficient mode conversion in this case, the steepness of the inhomogeneity is important (Fig. 2a). However, for the case in which the two mode branches are connected, the steepness is not critical and the conversion efficiency is determined independently of the steepness (Fig. 2b).

Fig. 2
figure 2

Conversion efficiency as a function of the spatial scale of the density gradient in the case of (a) \(\omega = 2.03\omega_{c}\) with \(\theta = 65^{ \circ }\) and (b) \(\omega = 2.03\omega_{c}\) with \(\theta = 58^{ \circ }\). The former case corresponds to the condition that two mode branches are disconnected (there is an evanescent zone between them), while in the latter case two mode branches are connected (Kalaee et al. 2009)

Full size image

In this paper, we focus on the return point of the waves where the plasma density becomes the highest along a ray-path in the mode conversion process. We consider the condition of the mode conversion employing the dispersion relation of cold plasma and Snell’s law. By assuming the conditions in which the two mode branches are connected where the mode conversion can occur with the highest efficiency, we formulate the minimum variation of the plasma frequency needed for this efficient conversion process, which we call “the plasma frequency demand,” and quantify the range of wave frequency of the incident slow Z-mode waves.

Theory and assumptions

First, we review the coupling properties of the Z-mode and LO-mode waves based on the cold plasma theory, and then we extend our discussion to formulate the plasma frequency for the mode conversion processes.

The dispersion relation of waves in a cold plasma is given by

$$n^{2} = n_{\parallel }^{2} + n_{ \bot }^{2} = 1 - \frac{2X(X - 1)}{{2(X - 1) - Y^{2} \sin^{2} \theta \pm \varGamma }} ,$$
(1)

where \(n_{\parallel }\) and \(n_{ \bot }\) are the parallel and perpendicular components of the refractive index, respectively, \(\varGamma = [Y^{4} \sin^{4} \theta + 4(X - 1)^{2} Y^{2} \cos^{2} \theta ]^{{\frac{1}{2}}}\), \(X = (\frac{{\omega_{p} }}{\omega })^{2}\), \(Y = \frac{{\omega_{c} }}{\omega }\), ωc is the electron gyrofrequency, \(\theta\) is the wave normal angle, and the + (−) sign indicates the refractive index of the extraordinary (ordinary) mode. The ordinary and extraordinary modes coalesce under the condition where \(\varGamma\) = 0. This in turn requires that the conditions of \(\theta = 0\) and \(X = 1\) be simultaneously satisfied:

$$\varGamma = \left[ {4\left( {X - 1} \right)^{2} Y^{2} } \right]^{1/2} = 2\left( {X - 1} \right)Y$$
(2)

and

$$n^{2} = n_{\parallel }^{2} = 1 - \frac{2X(X - 1)}{{2\left( {X - 1} \right) + 2\left( {X - 1} \right)Y}} = 1 - \frac{X}{1 + Y} ,$$
(3)

and then for X → 1, \(\varGamma = 0\) and \(n^{2} = n_{\parallel }^{2} = \frac{Y}{1 + Y}\).

That is, at this point (mode conversion point), \(\omega_{p} = \omega\) and the wave normal angle should be zero (\(n_{ \bot }\) = 0). Meanwhile, by considering Snell’s law and the assumption that the external magnetic field is directed perpendicular to the density gradient, the parallel component of the refractive index should be constant during the wave propagation in an inhomogeneous plasma. Figure 3 shows the configuration of the background magnetic field B0, k-vector, and the density gradient ∇N, where B0 is assumed to be perpendicular to ∇N.

Fig. 3
figure 3

Configuration of the background magnetic field, k-vector, and density gradient

Full size image

The above discussion results in a condition for effective mode conversion,

$$n_{\parallel ,inc} = {\text{constant}} = n_{{LO(\omega_{p} = \,\,\omega \,\left| {\,\theta = 0)} \right.}} ,$$
(4)

where \(n_{\parallel ,inc}\) represents the parallel component of the refractive index of the incident wave and \(n_{{\omega_{p} = \omega \left| {\theta = 0} \right.}}\) denotes the LO-mode refractive index at the mode conversion point, where \(\omega_{p} = \omega\) and \(\theta\) = 0. It has been suggested that for a certain incident angle of waves, the two wave mode branches (ordinary and extraordinary) are connected and the condition required for the efficient mode conversion is satisfied. Figure 4 shows the wave normal angle \(\theta\) of the ordinary and extraordinary mode waves of frequency \({\omega \mathord{\left/ {\vphantom {\omega {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }} = 2.1\) as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\), determined from the dispersion relation of cold plasma considering Snell’s law. One case is under the condition that Eq. (4) is satisfied (blue curves) and the other case is under the condition that Eq. (4) is not satisfied (red curves). In the first case, \(n_{\parallel ,inc} = {\text{constant}} = n_{{LO(\omega_{p} = \,\,\omega \,\left| {\,\theta = 0)} \right.}} = 0.567\), while in the second case, \(n_{\parallel ,inc} = {\text{constant}} = 0.714 \ne n_{{LO(\omega_{p} = \,\,\omega \,\left| {\,\theta = 0)} \right.}} = 0.567\). It can be observed from Fig. 4 that in the first case, the two wave modes are coupled (which leads to efficient mode conversion) and in the second case, the two wave modes are decoupled (which leads to weak mode conversion). In the second case, the mode conversion can only occur via the tunneling effect, where the steepness of inhomogeneity becomes important (Kalaee and Katoh 2014). In the first case, where the two wave modes are coupled, the efficient mode conversion can be expected regardless of the steepness of the inhomogeneity (Kalaee et al. 2009). However, even in the first case, the plasma frequency required is crucial in the mode conversion process. Here, one fundamental question arises from the discussion above: how large is the inhomogeneity of plasma required for mode conversion under the condition that Eq. (4) is satisfied? In the next section, we extend our discussion to formulate the plasma frequency required for the efficient mode conversion to occur.

Fig. 4
figure 4

Variation of wave normal angle \(\theta\) as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\) for the incident wave with \({\omega \mathord{\left/ {\vphantom {\omega {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }} = 2.1\). Blue curves are under the condition that Eq. (4) can be satisfied and red curves are under the condition that Eq. (4) cannot be satisfied. RP indicates the return point where the plasma frequency becomes maximum along the ray-path in the inhomogeneous medium

Full size image

Calculation of the plasma frequency demand

We start from the dispersion relation in the cold plasma with Snell’s law, and then we consider the return point. The dispersion relation is given by

$$D (n ,\omega )= An^{4} + Bn^{2} + C = 0 ,$$
(5)

where A, B, and C are coefficients including \(\omega_{p}\), \(\omega_{c}\), \(\omega\), and \(\theta\). The refractive index can be described by the parallel and perpendicular components given by \(n^{2} = n_{\parallel }^{2} + n_{ \bot }^{2}\), where \(\sin \theta = \frac{{n_{ \bot } }}{n}\) and \(\cos \theta = \frac{{n_{\parallel } }}{n}\). Thus, we rewrite Eq. (5) as

$$A\;\left( {n_{\parallel }^{2} + n_{ \bot }^{2} } \right)^{2} - B\left( {n_{\parallel }^{2} + n_{ \bot }^{2} } \right)^{2} + C = 0 ,$$
(6)
$$\begin{aligned} A = S\sin^{2} \theta + P\cos^{2} \theta \hfill \\ B = RL\sin^{2} \theta + PS(1 + \cos^{2} \theta ) \hfill \\ C = PRL \hfill \\ \end{aligned} ,$$
(7)

where \(R = 1 - {{\tilde{\omega }_{p}^{2} } \mathord{\left/ ({\vphantom {{\tilde{\omega }_{p}^{2} } {1 + \tilde{\omega }_{c} )}}} \right. \kern-0pt} {1 + \tilde{\omega }_{c} )}}\), \(L = 1 - {{\tilde{\omega }_{p}^{2} } \mathord{\left/( {\vphantom {{\tilde{\omega }_{p}^{2} } {1 - \tilde{\omega }_{c} )}}} \right. \kern-0pt} {1 - \tilde{\omega }_{c} )}}\), \(P = 1 - \tilde{\omega }_{p}^{2}\), \(S = {{(R + L)} \mathord{\left/ {\vphantom {{(R + L)} 2}} \right. \kern-0pt} 2}\), and \(\tilde{\omega }_{p}\) and \(\tilde{\omega }_{c}\), respectively, describe the plasma frequency and gyrofrequency normalized by the wave frequency \(\omega\). By making use of the above equations, Eq. (6) can be rewritten in the form of

$${\text{S}}n_{ \bot }^{4} +\left[\left({\text{S+P}}\right)n_{\parallel }^{2} - {\text{RL}} - {\text{PS}}\right]n_{ \bot }^{2} + {\text{P}}(n_{\parallel }^{4} - 2{\text{S}}n_{\parallel }^{2} - {\text{RL)}}\;{ = }\; 0.$$
(8)

By considering \(n_{\parallel }\) as a constant (projection on the boundary surface), Eq. (6) is rewritten in the form

$$A^{\prime}n_{ \bot }^{4} + B^{\prime}n_{ \bot }^{2} + C^{\prime} = 0 ,$$
(9)

where \(A^{\prime}\), \(B^{\prime}\), and \(C^{\prime}\) are defined by

$$A^{\prime} = 1 - \tilde{\omega }_{p}^{2} - \tilde{\omega }_{c}^{2}$$
(10)
$$B^{\prime} = \left[ {\left( {1 - \tilde{\omega }_{p}^{2} } \right)\left( {1 - \tilde{\omega }_{c}^{2} } \right) + \left( {1 - \tilde{\omega }_{p}^{2} - \tilde{\omega }_{c}^{2} } \right)} \right] n_{\parallel }^{2} - \left( {1 - \tilde{\omega }_{p}^{2} } \right)^{2} - \left( {1 - \tilde{\omega }_{p}^{2} } \right)\left( {1 - \tilde{\omega }_{p}^{2} - \tilde{\omega }_{c}^{2} } \right) + \tilde{\omega }_{c}^{2}$$
(11)
$$C^{\prime} = \left( {1 - \tilde{\omega }_{p}^{2} } \right)\left[ {n_{\parallel }^{4} \left( {1 - \tilde{\omega }_{c}^{2} } \right)} - 2n_{\parallel }^{2} \left( {1 - \tilde{\omega }_{p}^{2} - \tilde{\omega }_{c}^{2} } \right) + {\left( {1 - \tilde{\omega }_{p}^{2} } \right)^{2} - \tilde{\omega }_{c}^{2}} \right] .$$
(12)

As we are interested in the plasma frequency at the return point (indicated by RP in Figs. 4, 5), we consider the situation in Eq. (9) to find the return point. At the return point, Eq. (9) has two equal, non-zero solutions. The solutions do not correspond to the mode conversion between the ordinary and extraordinary modes, but merely correspond to the return of the extraordinary mode. Thus, for this case, the condition is given by \(D^\prime \;{ = }\;{B^\prime}^{2} \; - \;4A^\prime C^\prime \;{ = }\; 0\). By substituting Eqs. (10), (11), and (12) in Eq. (9) and after simplifications, we obtain

Fig. 5
figure 5

Variations of wave normal angle and \(n_{ \bot }\) as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\) for the incident wave with \({\omega \mathord{\left/ {\vphantom {\omega {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }} = 3.5\) and \(\nabla n \bot \vec{B}\), under the condition that Eq. (4) can be satisfied. \(D^{\prime}{ = }\, 0\) at RP

Full size image
$$D^{\prime}{ = }\tilde{\omega }_{p}^{4} \tilde{\omega }_{c}^{2} \left[ {\tilde{\omega }_{c}^{2} \left( {1 - n_{\parallel }^{2} } \right)^{2} + 4\left( {1 - \tilde{\omega }_{p}^{2} } \right)n_{\parallel }^{2} } \right] = 0$$
(13)

and then

$${\tilde{\omega }_{c}^{2} \left( {1 - n_{\parallel }^{2} } \right)^{2} + 4\left( {1 - \tilde{\omega }_{p}^{2} } \right)n_{\parallel }^{2} } = 0$$
(14)
$$\tilde{\omega }_{c}^{2} \left( {1 - n_{\parallel }^{2} } \right)^{2} = - 4\left( {1 - \tilde{\omega }_{p}^{2} } \right)n_{\parallel }^{2} .$$
(15)

By solving Eq. (15) for \(\tilde{\omega }_{p}\), we obtain

$$\tilde{\omega }_{p}^{2} = 1 + \frac{{\tilde{\omega }_{c}^{2} \left( {1 - n_{\parallel }^{2} } \right)^{2} }}{{4n_{\parallel }^{2} }}$$
(16)

or

$$\left( {\frac{{\omega_{p - RP} }}{{\omega_{c} }}} \right)^{2} = {\left( {\frac{\omega }{{\omega_{c} }}} \right)^{2} + \frac{{\left( {1 - n_{\parallel }^{2} } \right)^{2} }}{{4n_{\parallel }^{2} }}} .$$
(17)

Equations (16, 17) indicate the value of \(\omega_{p}\) at the return point. The initial condition for the occurrence of efficient mode conversion (that the ordinary and extraordinary modes are connected) is

$$n_{\parallel }^{2} = n_{{LO(\omega_{p} = \,\,\omega \,\left| {\,\theta = 0)} \right.}}^{2} = \frac{1}{{1 + \frac{\omega }{{\omega_{c} }}}} .$$
(18)

Finally, by substituting Eq. (18) in Eq. (17), we obtain

$$\left( {\frac{{\omega_{p - RP} }}{{\omega_{c} }}} \right)^{2} = {\left( {\frac{\omega }{{\omega_{c} }}} \right)^{2} + \frac{{\left( {\frac{\omega }{{\omega_{c} }}} \right)^{2} }}{{4\left( {\frac{\omega }{{\omega_{c} }} + 1} \right)}}}$$
(19)

or

$${\frac{{\omega_{p - RP} }}{{\omega_{c} }}} = \left[ {\left( {\frac{\omega }{{\omega_{c} }}} \right)^{2} + \frac{{\left( {\frac{\omega }{{\omega_{c} }}} \right)^{2} }}{{4\left( {\frac{\omega }{{\omega_{c} }} + 1} \right)}}} \right]^{1/2} .$$
(20)

The above equation shows the value of the plasma frequency at the return point in an efficient mode conversion event (the condition Eq. (18) is satisfied). Figure 5 shows another example of efficient mode conversion. The initial angular frequency of the slow Z-mode wave is \(3.5\omega_{c}\) with the wave normal angle \(\theta \le 61.8^{^\circ }\) in the region where \(\omega_{p} < 3.5\omega_{c}\) (\(3.35\omega_{c} < \omega_{p} < 3.5\omega_{c}\)). The plasma frequency at the return point indicated by RP can be obtained from Eq. (20). Here, we define another parameter \(\delta \omega_{p - RP}\), which we call “the plasma frequency demand,” corresponding to the difference between the plasma frequency at the return point and the plasma frequency at the point where \(\omega_{p} = \omega\), which is given by

$$\frac{{\delta \omega_{p - RP} }}{{\omega_{c} }} = {\frac{{\omega_{p - RP} }}{{\omega_{c} }}} - {\left. {\frac{{\omega_{p} }}{{\omega_{c} }}} \right|_{\omega_p = \omega } }.$$
(21)

Using Eqs. (20) and (21), we obtain \(\omega_{p - RP} \approx 3.56\omega_{c}\) and \(\delta \omega_{p - RP} \approx 0.1\omega_{c}\) for the above case, as shown in Fig. 5.

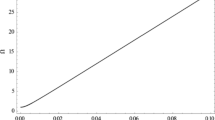
Using Eq. (21), we obtain the values of \(\frac{{\delta \omega_{p - RP} }}{{\omega_{c} }}\) for a wide range of angular frequency of the incident slow Z-mode waves, \(0.1\omega_{c} \le \omega \le 100\omega_{c}\), for the occurrence of efficient mode conversion. The results are shown in Fig. 6 as the blue solid line. The red solid line in Fig. 6 indicates the difference between the plasma frequency at the cutoff of Z-mode waves (\(\omega_{{p - {\text{Z-cutoff}}}}\)) and the frequency of the incident wave, \(({{\delta \omega_{p - {\text{Z-cutoff}}} } \mathord{\left/ {\vphantom {{\delta \omega_{p - Zcutoff} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }} = \frac{{\omega_{{p - {\text{Z-cutoff}}}} - \omega }}{{\omega_{c} }})\), where the Z-mode cutoff frequency is given by \(\omega_{\text{Z-cutoff}} = -\frac{{\omega_{c} }}{2} + \left[ {\frac{{\omega_{c}^{2} }}{4} + \omega_{p - \text{Z-cutoff}}^{2} } \right]^{1/2}\). Under the condition that the efficient mode conversion can occur, the \(\delta \omega_{p - RP}\) required for the mode conversion is not necessarily large compared to the \(\delta \omega_{p - \text{Zcutoff}}\) required to reach the Z-mode cutoff frequency. \(\delta \omega_{p - RP}\) is estimated to range from \(0.01\omega_{c}\) to \(0.12\omega_{c}\) for \(\omega\) ranging from \(0.1\omega_{c}\) to \(100\omega_{c}\).

Fig. 6
figure 6

The blue curve is related to the plasma frequency demand in the occurrence of efficient mode conversion processes (\(\delta \omega_{p} \; = \;\delta \omega_{p - RP}\)). The red curve is related to the plasma cutoff via the angular frequency (\(\delta \omega_{p} = \delta \omega_{p - \text{Zcutoff}}\))

Full size image

Finally, we consider the case where the magnetic field direction is not purely perpendicular to the density gradient and obtain the plasma frequency at the return point numerically. Figure 7 shows variations of the wave normal angle as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\) for the incident wave with \({\omega \mathord{\left/ {\vphantom {\omega {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }} = 3.5\), where the angle \(\alpha\) between ∇N and B0 is \(75^{^\circ }\), under the condition that Eq. (4) is satisfied (the two mode branches are connected). In this example, \(\delta \omega_{p - RP}\) is estimated to be \(0.053\omega_{c}\), which is less than in the case of the previous example (\(\alpha = 90^{^\circ }\)).

Fig. 7
figure 7

Variations of the wave normal angle as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\) under the condition satisfying Eq. (4) where ∇N is not perpendicular to B0

Full size image

Summary

The inhomogeneity plays an important role in the mode conversion process. We aim to quantify the least frequency of plasma under the condition satisfying the efficient mode conversion, which we call “the plasma frequency demand.” We described how the wave that leads to efficient mode conversion propagates in the inhomogeneous plasma. We studied how the ray-path of the Z-mode waves changes before reaching the cutoff frequency and then reflects into the plasma frequency layer with \(\omega_{p} = \omega\). Using the dispersion relation for waves in cold plasma according to Snell’s law, we considered the return point of waves under the assumption that the external magnetic field is directed perpendicular to the density gradient. We obtained the formula to quantify the least plasma frequency required for efficient mode conversion. The results which we obtained are summarized as follows:

  1. 1.

    We formulated the plasma frequency at the reflected point (Eq. 20) and “the plasma frequency demand” for the efficient mode conversion (Eq. 21).

  2. 2.

    The range of \(\delta \omega_{p - RP}\) is between \(0.01\omega_{c}\) and \(0.12\omega_{c}\) for the slow Z-mode of incident waves ranging from \(0.1\omega_{c}\) to \(100\omega_{c}\), under the assumption that the magnetic field direction is purely perpendicular to the density gradient.

  3. 3.

    \(\delta \omega_{p - RP}\) becomes small for the case in which the angle between the magnetic field direction and the density gradient is not purely perpendicular. We obtained \(\delta \omega_{p - RP} \approx 0.053\) with \(\alpha = 75^{^\circ }\) and \(\omega_{p} > \omega_{c}\), which is less than the \(\delta \omega_{p - RP} \approx 0.1\) that we obtained in the case with \(\alpha = 90^{^\circ }\).

Finally, for the case where Eq. (4) is not satisfied, corresponding to the condition in which the two mode branches are separated and an evanescent layer develops between the two wave modes, the mode conversion can occur by the tunneling effect (Kalaee and Katoh 2014). In this case, the steepness of the inhomogeneity plays an important role in controlling the efficiency of the mode conversion.

The relationship between the density gradient and the conversion efficiency suggested by the present study should be examined by comparison with in situ observations. The evaluation of the properties of the observed Z-mode and LO-mode waves and the condition of the ambient plasma, comparing them with those expected from the theoretical consideration, are also important (e.g., Kalaee et al. 2010) to discuss the dominancy of the connected/disconnected cases, the assumption of the spatial distributions of plasma density and background magnetic field, and the frequency/wavenumber spectra of the incident upper hybrid mode waves considering the amplitude ratio between the incident waves and converted radio waves. We need to know the variation of the wave normal angle as a function of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{c} }}} \right. \kern-0pt} {\omega_{c} }}\), as indicated in Fig. 5. For the case of the mode conversion satisfying the matching condition, we expect the variation of the wave normal angle of Z-mode waves in the observation results. The wavenumber spectra can be estimated by the ratio of the wave electric field components to the wave magnetic field components with reference to the dispersion relation. For the intensities of both the incident waves and converted radio waves, we need to carefully select events where we can assume that both the observed radio waves and Z-mode waves in the vicinity of the plasmapause are closely related to each other. Regarding the angle between the direction of the density gradient and the wave normal angle, in a first step, we will assume that the density gradient is perpendicular to the background magnetic field. This assumption is basically acceptable in the equatorial region of the plasmapause. A close comparison between theoretical/simulation studies and observation results is crucial. Arase, the exploration of energization and radiation in geospace (ERG) satellite (Miyoshi et al. 2018) orbits the inner magnetosphere and crosses the plasmapause, where efficient mode conversion can occur. The Arase satellite is capable of observing radio emissions of LO- and Z-mode waves (Kasaba et al. 2017; Kasahara. et al. 2018a; Kumamoto et al. 2018; Matsuda et al. 2018), energetic electrons (Kazama et al. 2017; Kasahara et al. 2018b) serving free energy to excite slow Z-mode waves, and the energy exchange between waves and particles (Katoh et al. 2018; Hikishima et al. 2018). We expect that the comparison between the theory and the Arase satellite observations will enable us to investigate a comprehensive scenario of the mode conversion process. The discussion on the percentage of radio waves satisfying the matching condition is highly important. It is beyond the scope of this study, but it is a very important aspect to be addressed in our future work.