Abstract
We studied ionospheric irregularities caused by midlatitude sporadic-E (Es) in Japan using ionospheric total electron content (TEC) data from a dense GNSS array, GEONET, with a 3D (three-dimensional) tomography technique. Es is a thin layer of unusually high ionization that appears at altitudes of ~ 100 km. Here, we studied five cases of Es irregularities in 2010 and 2012, also reported in previous studies, over the Kanto and Kyushu Districts. We used slant TEC residuals as the input and estimated the number of electron density anomalies of more than 2000 small blocks with dimensions of 20–30 km covering a horizontal region of 300 × 500 km. We applied a continuity constraint to stabilize the solution and performed several different resolution tests with synthetic data to assess the accuracy of the results. The tomography results showed that positive electron density anomalies occurred at the E region height, and the morphology and dynamics were consistent with those reported by earlier studies.

Similar content being viewed by others
Introduction
Sporadic-E, also known as Es, is an ionospheric irregularity, characterized by an extremely high electron density that unpredictably occurs in the E region (~ 100 km altitude) of the ionosphere. It occurs in low-latitude (Jayachandran et al. 1999; Resende and Denardini 2012), midlatitude (Wakabayashi et al. 2005; Maeda and Heki 2014), and high-latitude (Kirkwood and Nilsson 2000) regions and is widely believed to be generated by the vertical shear of zonal winds (Whitehead 1970, 1989). There have been studies on Es over decades to clarify its generation mechanism, structure, time evolution, and distribution using various instruments and techniques.
Previously, Es was often observed with ground-based radars such as ionosonde, coherent scatter radar, and incoherent scatter radar, through oblique and vertical incidence soundings. Miller and Smith (1975, 1978), for instance, revealed a horizontal patchy structure of midlatitude Es with an incoherent scatter radar. In addition to studies that used numerical simulations (Yokoyama et al. 2005), sounding rockets were launched to the height of several hundred kilometers to study Es (Yamamoto et al. 1998; Wakabayashi et al. 2005; Bernhardt et al. 2005; Kurihara et al. 2010). Using a magnesium ion imager onboard a rocket, Kurihara et al. (2010) successfully imaged the patchy frontal structures of Es by scanning the magnesium ion within the layer.
In recent years, Es has been investigated using global navigation satellite systems (GNSSs), such as the global positioning system (GPS), with techniques such as GPS occultation (Garcia-Fernandez and Tsuda 2006) and the ground-based GNSS-total electron content (TEC) method (Maeda and Heki 2014, 2015). TEC corresponds to the number of electrons integrated along the line of sight (LoS) of GNSS microwave signals between satellite and ground receivers. Maeda et al. (2016) and Furuya et al. (2017) used an interferometric synthetic aperture radar (InSAR) to draw detailed 2D maps of Es patches.
The GNSS-TEC method has fairly good resolution in space (~ 20 km) and time (30 s) in Japan owing to the nationwide dense GNSS array (~ 1200 stations), called GNSS Earth Observation Network (GEONET). By utilizing GEONET, Maeda and Heki (2015) found that GNSS-TEC can detect Es patches with critical frequencies (foEs) exceeding 20 MHz as short-term localized enhancements in TEC. They also showed that Es patches often show frontal structure extending dominantly in the east–west direction over tens of kilometers or more. The GNSS-TEC approach, however, only enabled 2D imaging of Es.
Computerized ionospheric tomography is an effective way to study 3D structures of ionospheric electron density (Austen et al. 1988), particularly in a region with densely deployed GNSS stations (Seemala et al. 2014; Chen et al. 2016; Saito et al. 2016). Here, we study the 3D structure of Es irregularities by performing 3D tomography of electron density anomalies using the GNSS-TEC data. We analyze five cases of daytime Es over two different regions, the Kanto and the Kyushu Districts, Japan (Fig. 1a, b), studied earlier in Maeda and Heki (2014, 2015).
Maps showing the distribution of GNSS stations (red dots) and the blocks above the Kanto (a) and the Kyushu (b) Districts, Japan. Blocks extend upwards covering altitudes from 60 to 270 km above the surface. The distribution of LoS penetrating blocks at the altitude of 90–120 km of the satellite–station pairs used for 3D tomography for Case 1 above Kanto (c) and Case 4 above Kyushu (d)
Dataset
We used the raw data files from hundreds of GEONET stations in the two studied regions provided by Geospatial Information Authority of Japan (available online from terras.gsi.go.jp) with 30-s recording intervals. The receivers tracked only GPS satellites before July 2012, but after the GEONET receiver replacements at middle 2012, they have started tracking GLONASS satellites as well.
From Maeda and Heki (2014, 2015), we selected five cases, i.e., Case 1 (Kanto, ~ 8 UT on May 14, 2010), Case 2 (Kanto, ~ 8 UT on May 21, 2010), Case 3 (Kanto, ~ 9 UT on May 13, 2012), Case 4 (Kyushu, ~ 03 UT on May 22, 2010), and Case 5 (Kyushu, ~ 02 UT on June 9, 2013). We used both GPS and GLONASS data for Case 5, and only GPS data were used for the other cases.
Methods
Before the 3D ionospheric tomography calculations (estimation of electron density anomalies of the 3D blocks) were conducted, we derived slant TEC (STEC) residuals to be used as the input data. STEC indicates the number of electrons integrated along the line of sight (LoS) connecting GNSS satellites and ground receivers. We derived STEC from the phase differences between the L1 (~ 1.5 GHz) and L2 (~ 1.2 GHz) microwave carriers. We then modeled STEC changes using the reference curves obtained by fitting cubic polynomials of time to the vertical TEC (VTEC) (Ozeki and Heki 2010), obtaining the STEC anomalies, i.e., the departures from the reference curves, to be used as the input data for the subsequent steps.
We set up the 3D blocks of ionospheric electron density with dimensions of 0.16° in the north–south direction, 0.20° in the east–west direction, and 30 km in the up–down direction, over the two studied regions (Fig. 1a, b). The electron density within a block was assumed to be homogeneous. The LoS penetrates multiple blocks, and the STEC residual can be expressed as the sum of the products of the penetration lengths and electron density anomalies of individual blocks. We calculated the penetration length as the distance between the two intersections of LoS with the block surface by simple geometric calculations. Since the studied area spans only a few degrees in latitude, we considered that the Earth is a sphere (its flattening is neglected) with an average radius. Figure 1c, d shows the geometry of LoS penetrating the blocks at the altitudes of 90–120 km for Cases 1 and 4.
Although the LoS are densely distributed, they do not penetrate all the blocks, especially above the oceanic areas. Hence, we needed to introduce certain constraints to regularize the least-squares inversion. Here, we applied a continuity constraint, i.e., we assumed that neighboring blocks have the same electron density anomalies with a certain allowance for the difference. Suppose block number j is at the east side of block number i; then, we assumed X i and X j , the electron density anomalies of these blocks, satisfy the constraint \(X_{i} - X_{j} = 0.\) One block normally has six neighboring blocks (up, down, north, south, east, and south), and all these pairs were added to the normal matrix as virtual observations (Nakagawa and Oyanagi 1982). We did not constrain the block pairs that were not juxtaposed. The tolerance corresponds to the “observation” error of these virtual data and to the standard deviation of the actual differences between the adjacent blocks. We assumed 0.10 (in 1011 electrons/m3, equivalent to 1 TECU, or 1016 electrons/m2, for a penetration length of 100 km) as the tolerance. The influence of this value on the tomography results will be discussed in the next section. In addition, we also assumed the STEC observation error to be 0.2 TECU. This is a few times as large as the typical error for differential GNSS VTEC measurements (Coster et al. 2013) but is consistent with the post-fit STEC residuals. This will be further discussed together with the accuracy of the 3D tomography results later in this article.
Resolution tests
To investigate the reliability of the 3D tomography solution, we performed both the classical checkerboard resolution test and another test assuming anomalies similar to the expected Es patch. We perform these two resolution tests for Case 1 and Case 4: the Es observed over the Kanto District on May 14, 2010, and the Es observed over the Kyushu District on May 22, 2010, respectively. For these tests, we assumed the same satellite and station distribution as in the real case to synthesize the STEC data. We assumed the electron density anomalies of ±0.60 × 1011 electrons/m3 for the checkerboard test (Figs. 2, 3 input). We assumed no anomalies for the background and 0.60 × 1011 electrons/m3 for the Es-like anomaly in the second test (Figs. 4, 5 input).
Same as Fig. 2, but we assumed Case 4 in the Kyushu District
Same as Fig. 4, but we assumed Case 4 in the Kyushu District
Figure 2 (output) shows the distribution of the anomalies recovered using the synthetic data. It suggests that we could well resolve the spatial structures of the assumed anomaly, but the recovered amplitudes are about two-thirds the input. By comparing the two map views at different altitudes, we see that the resolution at higher altitudes (240–270 km) is slightly worse than that at lower heights (90–120 km). This reflects better coverage (more penetration) of LoS for lower blocks. The output of Fig. 2 also suggests that the resolution is higher above the land area and poorer above the ocean (e.g., southeast part of the low-altitude horizontal view). Last, the boundary between positive and negative anomalies is blurred in the recovered pattern. On the other hand, the result for Case 4 (Fig. 3 output) is worse, i.e., recovered blocks in oceanic area show diagonal stripes, reflecting poor resolution along the NE–SW axis. This is due to the smaller percentage of land area in the Kyushu District within the studied region and to the failure of penetration of these blocks by LoS with a variety of azimuths.
We further demonstrate the robustness of our tomography result by conducting another resolution test, assuming a block-like-positive anomaly in Case 1 (Fig. 4 input) and Case 4 (Fig. 5 input) to check the resolution for a possible 3D spatial structure of Es patches. We set all the blocks to neutral for the plasma density anomaly except in several blocks at 90–120 km height with positive electron density anomalies as strong as the positive anomaly blocks of the checkerboard test. The results (Figs. 4, 5 output) indicated that the accuracy is high enough to allow us to detect the spatial structure of the local stratified ionospheric plasma density in a robust manner. However, in the latitude–height sections the positive anomalies are found to be elongated obliquely upward (Figs. 4e2, 5e2). This is due to the lack of ray paths in the direction perpendicular to the elongation direction of the recovered pattern. Thus, we need to be cautious in interpreting the 3D structure of Es patches in the tomography results.
By using the case of Fig. 4, we tested the influence of different strengths of the continuity constraint. In the results shown in Additional file 1: Fig. S1, weaker constraints (i.e., large values of tolerance) result in an absolute value of the recovered anomaly that is more consistent with the assumption. At the same time, fake anomalies grow in higher altitudes. In contrast, stronger constraints (smaller tolerance) result in a clearer spatial distribution (less fake anomalies), but the recovered anomaly shows much smaller electron density anomalies than the assumption. Considering these two aspects, we employed 0.10 × 1011 electrons/m3 as the constraint strength because of relatively small smear and the discrepancy between the assumed and the recovered amplitudes. Nevertheless, the recovered density anomaly obtained using this constraint is about 1/4 its input, so we need to focus on the amount of electron density anomalies of recovered Es patches.
Results and discussion
Height of Es patches
In Figs. 6, 7, we show the results of 3D tomography for Cases 1 and 4, respectively. We used six satellites and 4,828 LoS for inversion in Case 1, and we used 11 satellites and 10,547 LoS in Case 4. To reduce the random noise, we first performed the inversion at three consecutive time epochs (at UT 8:15, 8:17, 8:19 in Figs. 6, 3:51, 3:53, 3:55 in Fig. 7) and calculated the averages of the results. Considering the horizontal drift of these Es patches (Maeda and Heki 2015), we did not further increase the stacking period. (With longer periods, travel distances of Es patches may exceed the block size.)
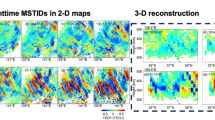
Results of 3D tomography (average of the results at 8:15, 8:17, 8:19 UT) of Case 1 Es patch that occurred on May 14, 2010, above the Kanto District (Maeda and Heki 2014, 2015). Black curves in a describe the tracks (moving northward) of the intersection of LoS with a thin layer at 100-km altitude (black dots show the positions at 8:23 UT, and black squares indicate the GNSS stations) for the station–satellite pairs shown in e. We show the map views at altitudes 90–120 km (a) and 180–210 km (b), and latitude–height profiles at 35.6° N (c) and 35.9° N (d). Time series (red curves) showing VTEC residuals 7:50–09:00 UT from reference curves, observed at eleven GNSS stations (black rectangle in a) with GPS satellite 29, show typical Es signatures as short-period positive pulse around 8.5 UT (e)
Results of 3D tomography (average of 3:51, 3:53, 3:55 UT) of Case 4 Es patch on May 22, 2010, above the Kyushu District (Maeda and Heki 2015). Black curves in a describe the tracks (moving southward) of the intersection of LoS with a thin layer at 100-km altitude (black dots show the positions at 3:51 UT) for the station–satellite pairs shown in e. We show the map views of the results at altitudes 90–120 km (a) and 180–210 km (b), and latitude–height profiles at 31.8° N (c) and 32.0° N (d). Time series (red curves) showing vertical TEC changes 2.5–4.5 UT as residuals from reference curves, observed at ten stations (black rectangles in a), using GPS satellite 24 (e). Clear Es signatures are seen 3.50–3.75 UT as positive pulses
One of the purposes of this study is to justify the estimated heights of the Es irregularities inferred in the previous studies (Maeda and Heki 2014, 2015). The tomography results (Figs. 6a, 7a) clearly show that the high electron density anomalies mainly reside in the second layer from the bottom. Its height 90–120 km corresponds to the E region of the ionosphere. Because the height resolution of the 3D tomography in this study is relatively poor (30 km), we cannot discuss the Es patch thickness. We can also see that the Es patches do not appear in the upper layers (Figs. 6b, 7b). Es patches are also recognized in latitude–height profiles (i.e., 35.6° N for the Kanto and 31.8° N for the Kyushu cases). This is consistent with Maeda and Heki (2014) who inferred that the Es lies at a height ~ 100 km. In Figs. 6e and 7e, we plotted time series of TEC changes at stations shown with black squares in Figs. 6a and 7a. There, we can see that they exhibit pulse-like enhancements when SIPs (sub-ionospheric point, calculated assuming 100 km ionospheric height) overlap with the Es patches recovered by the 3D tomography. The results of other cases corresponding to Figs. 6a and 7a are shown in Fig. 8 (Cases 1–3) and Fig. 9 (Cases 4, 5).
Horizontal drifts of Es patches in three cases (Case 1: May 14, 2010, Case 2: May 21, 2010, and Case 3: May 13, 2012) above the Kanto District inferred by comparing the snapshots at the first epoch (a, c, and e) and 15 min later (b, d, and f). At each epoch, we show the map view (left) and the longitude-height profile (right). Black dashed lines indicate the longitudes used for the profiles
Horizontal drifts of Es patches in two cases (Case 4: May 22, 2010, and Case 5: June 9, 2013) above the Kyushu District inferred by comparing the snapshots at the first epoch (a, c) and 15 min later (b, d). At each epoch, we show the map view (left) and the longitudinal profile (right). Black dashed lines indicate the longitudes used for the profiles
Figures 8 and 9 also show the height-latitude profiles of the results. There, we often see faint positive anomalies to continue obliquely upward from the Es patches at ~ 100 km altitude. One might think that they represent real plasma density anomaly structure extending from the main bodies of Es. However, a similar pattern also appears in the resolution test results with the Es-like structures (Figs. 4e2, 5e2), which suggests that they are artifacts due to the lack of data with LoS perpendicular to the direction of the fake structures.
Horizontal drift of Es patches
We study the horizontal drift of Es patches by comparing the horizontal tomography results at two time epochs separated by 15 min. Figures 8 and 9 show the three cases in Kanto (Cases 1–3) and two cases in Kyushu (Cases 4, 5), respectively. In Cases 1 and 2, the Es move southward, while in Cases 3–5 they move northward, maintaining their altitude of ~ 100 km, with speeds (30–100 m/s) consistent with the earlier report by Maeda and Heki (2015).
Accuracy of tomography results
To assess the accuracy of our tomography results, we discuss two quantities. First, we show formal errors, i.e., the square root of the diagonal components of the covariance matrix, the inverse of the normal matrix, which is related to the non-uniform distribution of the accuracy of the tomography results. Additional file 1: Figure S2 shows relatively high accuracy for blocks at lower altitude (90–120 km) above land, and lower accuracy for high-altitude blocks (240–270 km) above the ocean for Case 1 and Case 4. This is consistent with the results of the classical checkerboard test discussed earlier (Figs. 2, 3). Typical errors are ~ 0.01 × 1011 electrons/m3 at the E layer height in both cases. However, they range from 0.01 × 1011 to 0.02 × 1011 electrons/m3 at an altitude of 240–270 km, and larger errors tend to occur above sea.
Next, we compare the distributions of the post-fit residuals of STEC after inversion (Additional file 1: Fig. S3 bottom panels) with the original STEC anomalies (Additional file 1: Fig. S3 upper panels). In each case, the post-fit residual shows much smaller dispersion, and its standard deviation is similar to the assumed STEC observation errors (0.2 TECU). Hence, the formal errors in Additional file 1: Fig. S2 would not be very unrealistic.
Impact of multi-GNSS
We demonstrate the impact of using multi-GNSS data by comparing the results of the checkerboard test with three different data sets, i.e., (1) GPS and GLONASS, (2) GPS only, and (3) GLONASS only, using Case 5. In the results shown in Fig. 10, it is clear that GPS and GLONASS (top panels) cases show much better recovery of the checkerboard pattern than GPS only (middle) or GLONASS only (bottom) cases in the lower (Fig. 10a1–a3) and upper (Fig. 10b1–b3) ionosphere.
Results of the checkerboard test for Case 5 using both GPS and GLONASS data (top), GPS data only (middle), and GLONASS data only (bottom). In each case, we give map views at two different altitudes, namely 90–120 km (a1–a3) and 240–270 km (b1–b3), and latitude–height profile in (e1–e3), and two longitude-height profiles in (c1–c3, d1–d3)
This is more evident above the land region, but improvements are marginal above the oceanic region. This would imply that the diversity of azimuths of LoS penetrating those blocks was not improved by adding GLONASS satellites. This is inevitable above the ocean as long as we rely on observations from the remote land area. Nevertheless, the results indicate that the combination of GPS and GLONASS improves the result of the 3D tomography. The situation will be further improved by the addition of new GNSS such as Beidou from China, Galileo from the European Union, and Quasi-Zenith Satellite System (QZSS) from Japan.
Conclusions
We studied five cases of daytime midlatitude Es irregularities with the 3D tomography technique using STEC residual data from GEONET GNSS stations. We performed a linear least-squares inversion stabilizing the solution by continuity constraints. We also confirmed the performance of our tomography result by two kinds of resolution tests, i.e., the classical checkerboard test and another test assuming Es-like structures.
By performing 3D tomography for the five cases selected from earlier studies (Maeda and Heki 2014, 2015), we confirmed that the Es patches lie at an altitude ~ 100 km. We also confirmed the earlier reports that Es patches exhibit a frontal shape elongated in the E–W direction. We also confirmed that their horizontal drifts are consistent with earlier studies, and we also demonstrated the usefulness of multi-GNSS for 3D tomography.
References
Austen JR, Franke J, Liu CH (1988) Ionospheric imaging using computerized tomography. Radio Sci 23:299–307
Bernhardt PA, Selcher CA, Siefring C, Wilkens M, Compton C, Bust G, Yamamoto M, Fukao S, Ono T, Wakabayashi M, Mori H (2005) Radio tomographic imaging of sporadic-E layers during SEEK-2. Ann Geophys 23:2357–2368
Chen CH, Saito A, Lin CH, Yamamoto M, Suzuki S, Seemala GK (2016) Medium-scale traveling ionospheric disturbances by three-dimensional ionospheric GPS tomography. Earth Planets Space 68:32. https://doi.org/10.1186/s40623-016-0412-6
Coster A, Williams J, Weatherwax A, Rideout W, Herne D (2013) Accuracy of GPS total electron content: GPS receiver bias temperature dependence. Radio Sci 48:190–196. https://doi.org/10.1002/rds.20011
Furuya M, Suzuki T, Maeda J, Heki K (2017) Midlatitude sporadic-E episodes viewed by L-band split-spectrum InSAR. Earth Planets Space 69:175. https://doi.org/10.1186/s40623-017-0764-6
Garcia-Fernandez M, Tsuda T (2006) A global distribution of sporadic E events revealed by means of CHAMP-GPS occultations. Earth Planets Space 58:33–36
Jayachandran PT, Ram PS, Rao PVSR, Somayajulu VV (1999) Sequential sporadic-E layers at low latitudes in the Indian sector. Ann Geophy 17:519–525
Kirkwood S, Nilsson H (2000) High-latitude sporadic-e and other thin layers—the role of magnetospheric electric fields. Space Sci Rev 91:579–613
Kurihara J, Kurihara YK, Iwagami N, Suzuki T, Kumamoto A, Ono T, Nakamura M, Ishii M, Matsuoka A, Ishisaka K, Abe T, Nozawa S (2010) Horizontal structure of sporadic E layer observed with a rocket borne magnesium ion imager. J Geophys Res 115:2–7. https://doi.org/10.1029/2009JA014926
Maeda J, Heki K (2014) Two-dimensional observations of midlatitude sporadic e irregularities with a dense GPS array in Japan. Radio Sci 49(1):28–35. https://doi.org/10.1002/2013RS005295
Maeda J, Heki K (2015) Morphology and dynamics of daytime mid-latitude sporadic-E patches revealed by GPS total electron content observations in Japan. Earth Planets Space 67(1):89. https://doi.org/10.1186/s40623-015-0257-4
Maeda J, Suzuki T, Furuya M, Heki K (2016) Imaging the midlatitude sporadic E plasma patches with a coordinated observation of spaceborne InSAR and GPS total electron content. Geophys Res Lett 43:1419–1425. https://doi.org/10.1002/2015GL067585
Miller KL, Smith LG (1975) Horizontal structure of mid-latitude sporadic E layers observed by incoherent scatter radar. Radio Sci 10:271–276
Miller KL, Smith LG (1978) Incoherent scatter radar observations of irregular structure in mid-latitude sporadic E layers. J Geophys Res 33:3761–3775
Nakagawa T (1982) Observation data analysis with the least-squares method, UP applied mathematics series, vol 7. Tokyo University Press, Tokyo, p 216 (in Japanese)
Ozeki M, Heki K (2010) Ionospheric holes made by ballistic missiles from North Korea detected with a Japanese dense GPS array. J Geophys Res 115:1–11. https://doi.org/10.1029/2010JA015531
Resende LCA, Denardini CM (2012) Equatorial sporadic E -layer abnormal density enhancement during the recovery phase of the December 2006 magnetic storm: a case study. Earth Planets Space 64:345–351. https://doi.org/10.5047/eps.2011.10.007
Saito S, Suzuki S, Yamamoto M, Chen C H, Saito A (2016) Real-time Ionosphere Monitoring by Three-dimensional Tomography Over Japan. In: Proc. 29th int. tech. meeting, Satellite Division of the Institute of Navigation (ION GNSS + 2016), Portland, Oregon. pp 706–713
Seemala GK, Yamamoto M, Saito A, Chen CH (2014) Three-dimensional GPS ionospheric tomography over Japan using constrained least squares. J Geophys Res Space Phys 119:3044–3052. https://doi.org/10.1002/2013JA019582
Wakabayashi M, Ono T, Mori H, Bernhardt PA (2005) Electron density and plasma waves in mid-latitude sporadic-E layer observed during the SEEK-2 campaign. Ann Geophys 23:2335–2345
Whitehead JD (1970) Production and prediction of sporadic E. Rev Geophys Space Phys 8:65–144
Whitehead JD (1989) Recent work on mid-latitude and equatorial sporadic E. J Atmos Terr Phys 51:401–424
Yamamoto M, Ono T, Oya H, Tsunoda RT, Larsen MF, Fukao S, Yamamoto M (1998) Structures in sporadic-E observed with an impedance probe during the SEEK campaign: comparisons with neutral-wind and radar-echo observations. Geophys Res Lett 25:1781–1784
Yokoyama T, Yamamoto M, Fukao S, Takahashi T, Tanaka M (2005) Numerical simulation of mid-latitude ionospheric E-region based on SEEK and SEEK-2 observations. Ann Geophys 23:2377–2384
Authors’ contributions
INM analyzed the data and wrote the manuscript. KH proposed the initial idea and developed the software. JM proposed the cases appropriate for 3D tomography studies. All authors read and approved the final manuscript.
Acknowledgements
I.N. Muafiry thanks the Indonesia Endowment Fund for Education (LPDP) for supporting his study in Hokkaido University. The authors thank the Geospatial Information Authority (GSI) for GEONET data.
Competing interest
The authors declare that they have no competing interests.
Ethics approval and consent to participate
Not applicable.
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Additional files
Additional file 1: Fig. S1.
Results of the resolution tests assuming the Es-like anomaly shown in Fig. 4 using various values for the continuity constraint. The pattern is reasonably reproduced at 90–120 km altitude for all cases. For weaker constraints (i.e., larger values for the tolerance, right-hand-side panels), the absolute value of the recovered anomaly becomes more consistent with the assumed anomaly, but fake anomalies (smears) increase. We adopted 0.10 × 1011 electrons/m3 as the continuity constraint used in this study.
Additional file 2: Fig. S2.
Formal error distribution of the 3D tomography result of Case 1 (upper panel) and Case 4 (lower panel) for boxes at altitude 90–120 km (a) and 240–270 km (b). They are obtained as square root of the diagonal components of the inverse of the normal matrix. We can see the errors are uniform above the land region, with degradation in the top layer above the oceanic region and along the rim.
Additional file 3: Fig. S3.
Distribution of the input STEC anomalies (orange) and post-fit residuals (blue) for Cases 1–5. The residuals become significantly smaller than the input anomaly data, suggesting that the tomography results reasonably reproduced the observations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Muafiry, I.N., Heki, K. & Maeda, J. 3D tomography of midlatitude sporadic-E in Japan from GNSS-TEC data. Earth Planets Space 70, 45 (2018). https://doi.org/10.1186/s40623-018-0815-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-018-0815-7