Abstract
Sporadic-E (Es) is a layer of ionization that irregularly appears within the E region of the ionosphere and is known to generate an unusual propagation of very high frequency waves over long distances. The detailed spatial structure of Es remains unclear due to the limited spatial resolution in the conventional ionosonde observations. We detect midlatitude Es by interferometric synthetic aperture radar (InSAR), which can clarify the spatial structure of Es with unprecedented resolution. Moreover, we use the range split-spectrum method (SSM) to separate dispersive and nondispersive components in the InSAR image. While InSAR SSM largely succeeds in decomposing into dispersive and nondispersive signals, our results indicate that small-scale dispersive signals due to the total electron content anomalies are accompanied by nondispersive signals with similar spatial scale at the same locations. We also examine the effects of higher-order terms in the refractive index for dispersive media. Both of these detected Es episodes indicate that smaller-scale dispersive effects originate from higher-order effects. We interpret that the smaller-scale nondispersive signals could indicate the emergence of nitric oxide (NO) generated by the reactions of metals, Mg and Fe, with nitric oxide ion (NO+) during the Es.

Similar content being viewed by others
Introduction
While the sporadic-E (Es) layer of the ionosphere has been attracting broad research interest since the 1930s (e.g., Whitehead 1989; Mathews 1998; Haldoupis 2011), there still remain large uncertainties in the dynamics of the Es. Recently, global navigation satellite system (GNSS) receiver data have been used to derive the total electron content (TEC) along the microwave propagation path between the GNSS satellite and receiver. Taking advantage of the dense GNSS receiver network data in Japan, Maeda and Heki (2014, 2015) derived the TEC anomalies associated with midlatitude Es episodes in Japan and demonstrated the detailed morphology and dynamics of Es. In terms of the spatial resolution in the observation of Es, however, satellite-based InSAR imaging is more advantageous than the GNSS network. Maeda et al. (2016) first succeeded in demonstrating an Es episode in Japan using both GNSS TEC and an InSAR image derived from the Advanced Land Observation Satellite/Phased Array L-band Synthetic Aperture Radar (ALOS/PALSAR). ALOS was launched in 2006 by the Japan Aerospace Exploration Agency (JAXA). Another advantage of InSAR imaging is that no receivers have to be deployed on the imaging area, whereas the temporal resolution of InSAR is seriously limited by the satellite’s recurrence interval, which is 46 days in the case of ALOS/PALSAR.
Maeda et al. (2016) attributed the phase anomalies in the InSAR image to the Es episode, given the nearly identical location of the phase anomalies in the InSAR data and those derived from the GNSS TEC data. We should note, however, that GNSS TEC is physically distinct from the InSAR phase anomaly, because the InSAR phase includes the dispersive signal due to TEC and the nondispersive phase delay that has been mostly attributed to polar molecules in the troposphere. In contrast to the dual frequency measurement by GNSS, SAR imaging has been performed with a single carrier frequency, and no operational corrections for the ionosphere have been conducted to date. However, it has been demonstrated that the range split-spectrum method (SSM) could virtually perform dual frequency imaging, thereby allowing for the possible operational correction of the dispersive effects (Brcic et al. 2010; Rosen et al. 2010; Gomba et al. 2016).
Our first objective is to report the results of our application of the SSM to two Es episodes in Japan: the first episode is the one reported by Maeda et al. (2016), and the second one is a new Es episode detected by ALOS2/PALSAR2 launched in 2014, a follow-on mission of JAXA’s ALOS/PALSAR. The second objective is to examine the impact of higher-order terms in the refractive index on the estimates of dispersive signals, which is motivated by the results based only on the conventional first-order refraction index.
Theory and processing methods
Generation of a single look complex image for SSM
While SAR imaging is performed with a single carrier frequency, f 0, the actual waveform of each radar pulse is frequency modulated with its variable instantaneous frequency as a linear function of time. Therefore, it has a finite bandwidth, B w , on the order of 10–100 MHz in the frequency domain, which controls the range resolution (Fig. 1a, left). The actual single look complex (SLC) image is base-banded, and the effect of the carrier frequency is numerically included in the phase value of each slant range pixel (Fig. 1a, right). A key component of SSM is the splitting of the original bandwidth into two sub-bands with new lower and higher carrier frequencies (Fig. 1b), followed by standard InSAR processing at each new carrier frequency (Brcic et al. 2010; Rosen et al. 2010; Gomba et al. 2016). As such, SSM is performed at the expense of range resolution, whereas the azimuth resolution remains the same as in the original SAR image. While Gomba et al. (2016) have detailed the processing steps, we address the procedure for SSM, paying particular attention to the generation of two new SLC images from the original SLC image.
a (Left) original range spectrum with its center frequency f 0 and bandwidth B w . (Right) corresponding base-banded SLC data from a point target at R. Here, T and τ indicate the pulse length and the delay time 2R/c from a target, respectively; c is the speed-of-light. The sinc function is defined as sinc(x) = sin(πx)/πx. b (Left) bandpass-filtered range spectrum with a new higher central frequency f H and bandwidth B H w . (Right) corresponding bandpass SLC data from a point target at R. T H indicates the reduced pulse length. c (Left) base-banded range spectrum with a new higher central frequency f H and bandwidth B H w . (Right) corresponding base-banded SLC data from a point target at R with new center frequency f H
We first apply two bandpass filters along the range axes of the SLC image, so we can split the original B w into two narrower bands; Fig. 1b illustrates the bandpass filtering at higher frequency. The bandpass SLC image, however, is not base-banded and includes the modulated phase that corresponds to the deviation of the new carrier frequency from the original carrier frequency (Fig. 1b, right). We, therefore, need to demodulate the bandpass SLC, so it is base-banded with the new center frequency, f H (Fig. 1c). We perform the demodulation in the time (range) domain, multiplying the conjugate of the demodulated phase at each slant range. We repeat this procedure for the new lower frequency, f L. When we have new SLC images with new higher and lower carrier frequencies, we can perform the standard processing of the differential InSAR.
Estimation of dispersive phases
The refractive index of dispersive media explicitly depends on the carrier frequency, which allows for separating the ionospheric dispersive phase from the nondispersive phase, such as that due to tropospheric propagation delay and ground displacement signals. Following the phase-based GNSS range measurement (Syndergaard 2002; Kim and Tinin 2007; Hernández-Pajares et al. 2014), we write the frequency dependence of the InSAR phase Δϕ as follows:
where \(\Delta \phi_{\text{Nondisp}} ,\,\Delta \phi_{\text{TEC}} ,\,\Delta \phi_{\text{Mag}} ,\,{\text{and}}\,\Delta \phi_{\text{Bend}}\) indicate the contribution from the nondispersive phase, first-order TEC, second-order TEC, and the third-order ray-bending phase, respectively, and f 0 is the original carrier frequency. The second-order TEC term ∆ϕ Mag indicates the Faraday rotation effect by the geomagnetic field and is often dubbed the geomagnetic effect. Although the final term, ∆ϕ Bend, includes the third-order TEC, higher-order geomagnetic, geometric ray-bending, and ray-bending due to the excess path delay and transverse heterogeneity of TEC (Hernández-Pajares et al. 2014), we call it the bending term for simplicity because the former two contributions would be much smaller than the more dominant terms in ∆ϕ TEC and ∆ϕ Mag. In the literature regarding high-precision GNSS positioning, the second-order geomagnetic and the third-order bending effects are estimated to be orders of magnitude smaller than the first-order TEC, whereas these higher-order terms are currently taken into account in the operational GNSS positioning (e.g., Syndergaard 2002; Kedar et al. 2003). Dual frequency phase data for both GNSS and InSAR are used to simply solve for the first two terms of Eq. (1) neglecting higher-order dispersive terms. Equation (13) for SSM in Gomba et al. (2016) is also derived under this assumption.
In contrast to the GNSS phase, the InSAR phase indicates the difference between two acquisition epochs, and the dominant first-order term can be significantly reduced in the InSAR phase. Because the effect of Es is included in either one of the two image acquisitions, and Es indicates an anomalously dense ionized layer in the E region of the ionosphere, the higher-order dispersive terms may have a significant impact on the InSAR phase and may be revealed. In order to solve for the effects of the higher-order terms in addition to the two conventional terms above, we may split the original bandwidth into four bands to match the number of observations to those of the unknowns. However, the elements of the matrix become numerically close to each other. Under the available bandwidth and in the presence of phase noises, the condition number for the resulting matrix becomes unacceptably large, preventing the estimation of the higher-order terms. While estimating four unknowns from two InSAR data sets at the two frequencies is an under-determined problem, we can derive the so-called minimum-norm estimates in such a case (e.g., Menke 2012). Below, we compare the conventional estimates with the minimum-norm estimates. Another reason to consider the effect of higher-order terms in the dispersive phase is that our results based on the conventional scheme do not necessarily result in a distinct separation of dispersive and nondispersive components as shown below.
Results
Es episode on June 28, 2009
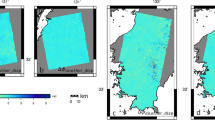
We first apply SSM to the Es event reported by Maeda et al. (2016). Details of the ALOS/PALSAR data sets, the new bandwidth, and frequencies are shown in Table 1. All the SAR data in this study are acquired along descending path, which passes during the local daytime. Figure 2a, b indicates the unwrapped differential interferograms for the higher and lower frequencies, respectively. The processing strategy for the InSAR data is basically the same as that in Maeda et al. (2016) with the exception of the new center frequency and narrower bandwidth in the range axis. Although the nearly one-third bandwidth makes the range resolution nearly three times coarser than the original, we have performed multi-looking with 50 looks in range and 80 looks in azimuth, with a pixel resolution of ~ 250 m. We do not discuss any signals with sizes smaller than ~ 1 km. We used JAXA’s precision orbit data and did not re-estimate, and we did not remove any long-wavelength residual phase trend. Figure 2a, b is quite similar to the original interferogram in Maeda et al. (2016), suggesting that the spatial resolution is sufficient for confirming the structure of the Es. Figure 3a, b shows the estimated nondispersive and dispersive components using Eq. (13) of Gomba et al. (2016) that takes into account only the first-order dispersion. We do not apply any spatial filters in Fig. 3a, b, and the estimated results are shown.
Unwrapped differential interferogram with a new higher frequency and b new lower frequency. The bandwidth is reduced to 9.33 MHz from the original 28 MHz for ALOS/PALSAR fine beam single (FBS) polarization mode. Details of the InSAR data are shown in Table 1
Although we originally expected that the dispersive signal would dominate over the nondispersive signal, we observe significant nondispersive signals that are partly correlated with dispersive signals. Long-wavelength phase trends arise from the east to west both in the dispersive and nondispersive signals, while the EW phase gradient in each signal is the inverse. In addition, we notice small-scale phase anomalies in both the dispersive and nondispersive signals, which are correlated with each other in terms of their locations. A distinct separation between dispersive and nondispersive components does not seem to be successfully performed as was performed at another location (Additional file 1) and as shown by Gomba et al. (2016).
Figure 4 gives the minimum-norm estimates of nondispersive (Fig. 4a), first-order TEC (Fig. 4b), second-order geomagnetic (Fig. 4c), and third-order bending effects (Fig. 4d). The sum of the three dispersive terms is shown in Fig. 4e. Comparing the two estimates of nondispersive effects in Figs. 3a and 4a, the long-wavelength phase slopes across the image are significantly reduced in the minimum-norm estimate in Fig. 4a. The small-scale phase anomalies, however, remain in both Figs. 3a and 4a, whose locations are correlated with those of dispersive signals as noted below. The three dispersive signals indicate interesting characteristics in their spatial distributions. The ENE-WSW-trending phase advance patches near the coastline are commonly observed, suggesting that the first-order term alone cannot capture the entire dispersive signals. We also notice that the small-scale phase anomalies are more significant in the higher-order geomagnetic and bending effects; we do not apply any smoothing filters in Fig. 4.
Minimum-norm estimates of a nondispersive, b first-order TEC, c second-order TEC (geomagnetic), and d third-order effect derived from the ALOS/PALSAR interferograms in Figs. 2a, b. The sum of the dispersive effects b–d is shown in e
Comparing the conventional solutions (Fig. 3a, b) with the minimum-norm solution (Fig. 4a, e), the overall phase anomalies for nondispersive (Figs. 3a and 4a) and dispersive effect (Figs. 3b and 4e) are largely consistent, whereas the long-wavelength EW phase trends are absent in the minimum-norm solutions in contrast to the conventional solutions.
Es episode on May 25, 2016
Next, we describe the second detection of Es by GNSS and InSAR, using ALOS2/PALSAR2 data. To search for the Es episode in Japan, we first examined the ionosonde data at Kokubunji, Wakkanai, and Yamagawa in Japan, and chose the dates when the critical frequencies of Es (foEs) were higher than 15 MHz during the local daytime from May to August in 2015 and 2016, as Es is known to be frequent in the local daytime during the summer. The ionosonde observations were operationally performed by National Institute of Communications and Technology (NICT), Japan. Second, we searched the ALOS-2/PALSAR-2 data sets for observation areas, dates, and times matching the ionosonde data above as closely as possible. Third, we generated a GNSS TEC map whose areas, dates, and times were the same as the above, and if Es was confirmed in the GNSS TEC map, we generated an interferogram. The GNSS TEC map in Fig. 5a indicates the presence of EW-trending TEC anomalies at 3:10 UTC on May 25, 2016, and Fig. 5b, c shows the time series of slant TEC derived from satellite 31 at the station 0388 and 0400, respectively. We detected the phase anomalies in the pair of February 17, 2016 (Master), and May 25, 2016 (Slave), along a track from Okayama to Kagawa. Details of the ALOS2/PALSAR2 data sets are shown in Table 1.
a GNSS TEC anomaly map at 3:10 UT on May 25, 2016, derived from satellites 23, 26, and 31. The imaged area by ALOS2 is shown with a red rectangle. b Slant TEC anomaly time series at the GEONET site 0388 derived from satellite 31. Solid vertical line indicates the image acquisition time by ALOS2. c Same time series at the GEONET site 0400
Figure 6a, b indicates the derived high- and low-frequency interferograms derived by SSM. We first show our estimates of nondispersive (Fig. 7a) and dispersive components (Fig. 7b), which are derived on the assumption of the first-order TEC effect alone for the dispersive component. In contrast to the cases in Figs. 3 and 4, the dispersive phase anomalies are much greater than the nondispersive, notably in the eastern areas. However, we cannot attribute all of the dispersive signals to the Es episode, because it might indicate the TEC in the F region and could be also due to the TEC during the other acquisition date. However, the EW-trending steep phase changes in Fig. 7b are presumably attributable to the Es on May 26, 2016, in light of the GNSS TEC map in Fig. 5a. It seems that the ALOS2/PALSAR2 data could not cover the central part but the eastern edge of the TEC anomalies. Although nondispersive phases are nearly flat over the entire region, there again arise localized and steep phase changes in Fig. 7a, which are closely correlated with those in the dispersive phase of Fig. 7b. This is similar to the observations in the previous case (Figs. 3 and 4).
Unwrapped differential interferogram with a the new higher frequency and b the new lower frequency. The bandwidth is reduced to 11.9 MHz from the original 79 MHz for the ALOS2/PALSAR2 strip map high-resolution (SM1) mode. Details of the InSAR data are shown in Table 1
The minimum-norm estimates of each term are shown in Fig. 8. The nondispersive signals in Fig. 8a are mostly flat as in Fig. 7a, and the localized signals near the phase jump still remain, while the amplitude of the localized signals is reduced. The three dispersive signals in Fig. 8b–d reveal spatial characteristics similar to those in Figs. 4 in terms of spatial scales. Large-scale signals are notable in the lower-order terms (Fig. 8b, c), while small-scale signals are dominant in the higher-order terms (Fig. 8c, d). Comparing the conventional estimates with the minimum-norm estimates, both the conventional dispersive and the summed dispersive signals are largely consistent (Figs. 7b and 8e).
Minimum-norm estimates of a nondispersive, b first-order TEC, c second-order TEC (geomagnetic), and d third-order effect derived from the ALOS2/PALSAR2 interferograms in Fig. 6a, b. The sum of the dispersive effects b–d is shown in e
Discussion
Origin of dispersive and nondispersive signals at the same locations
Regardless of whether we consider the effects of higher-order terms in the refractive index, we have identified small-scale phase anomalies on the order of ~ 5 km or less in both dispersive and nondispersive components at the same locations. The dispersive phases originate in the free electrons associated with the Es, while the nondispersive phases at the same locations with comparable magnitude are unexpected but may indicate some physical processes in the ionosphere. It is unlikely that tropospheric nondispersive signals appear at the same locations because of the huge differences in the height. What does the presence of nondispersive phase suggest?
The origin of refractivity is polarization (e.g., Feynman et al. 1963; Ch. 31 in Vol. 1, Ch. 32 in Vol. 2). The polarization between positive ions and free electrons is responsible for the refractivity, while the dispersive refractivity in the ionosphere is due to the oscillation of free electrons by the external electric field. Positive ions shielded by free electrons cannot oscillate because of their heavier mass and have no dispersive effect. In addition, it is known that nitric oxide ion (NO+) is the most abundant ions in the E region, and metallic ions such as Mg+ and Fe+ are known to be mainly sustaining the Es (e.g., Mathews 1998). While the thermal ionization of meteorites is responsible for the generation of metallic ion, the following chemical reactions with NO+ have been suggested to be equally important (Nagata and Tohmatsu 1973; Feng et al. 2013):
We speculate that the coexistence of dispersive and nondispersive phases may be due to the nitric oxide (NO) molecule according to these reactions, because NO is a well-known polar molecule. Our observation of nondispersive phases may, therefore, validate the reality of the reactions above. In addition, the Es patches shown in this study are highly ionized with foEs well exceeding 15 MHz. In these cases, there must be a substantial transport of metallic ions into the Es region. However, it is unclear how and where such a large amount of metallic ions is deposited (T. Yokoyama, personal communication, November 2, 2015). In addition to the primary ionization by solar UV, reactions of Mg and Fe with NO+ may play a crucial role as a secondary driver for ionization in the daytime E regionIt is also important that highly ionized Es patches occur particularly during daytime when NO+ density is rich. The increase in NO density is also suggested by the depletion of NO+ density at the peak electron density altitude of Es (Nagata and Tohmatsu 1973; Roddy et al. 2004). However, in view of the reduced magnitude of the small-scale nondispersive signals in the minimum-norm estimates (Figs. 4a and 8a), we cannot yet quantitatively evaluate how many NO molecules were generated and need to perform more case studies.
Non-uniqueness of the estimated dispersive and nondispersive signals
Although the conventional scheme to separate dispersive and nondispersive phases solves for two linear equations with two unknowns, we have shown that the two solutions by the conventional scheme are actually not unique and that it may be necessary to estimate higher-order terms for the refractive index. Since the conventional solutions share some characteristics with those derived from the minimum-norm solutions, we prefer the latter minimum-norm solutions, at least in the case of ALOS/PALSAR in Fig. 4, because they do not leave a long-wavelength phase slope in either the dispersive or nondispersive phases. The significant reduction in the long-wavelength phase slopes might be caused by minimizing the norm of the solutions. However, it seems that the higher-order terms in the refractive index allow us to isolate the scale dependence of the dispersive signal on frequency; small-scale dispersive signals are likely due to the higher-order terms. However, we do not claim that it is always necessary to estimate the effects of the higher-order terms. The case studies in Gomba et al. (2016) and our results in the Additional file 1 indicate that the conventional two unknown scheme could successfully separate the dispersive and nondispersive signals, because they do not seem to show any correlated phases in the other signals. Although it is uncertain now why the conventional scheme works in some cases, it is noticed in the Additional file 1 data that the total phase changes due to the dispersive signals are much greater than those we have found in our Es observations. The first-order TEC effect seems to be intrinsically dominant.
Conclusion
We examined two Es episodes in Japan using L-band InSAR SSM. Both cases indicated the presence of dispersive and nondispersive small-scale signals at the same locations, the latter of which might indicate the presence of nitric oxide (NO) molecules generated by the chemical reactions in the Es. While the standard InSAR SSM based only on the first-order TEC term could largely separate the dispersive and nondispersive phases, we might have to consider the effects of higher-order terms in the refractive index, depending on the nature of the dispersive signals.
Abbreviations
- Es:
-
sporadic-E
- VHF:
-
very high frequency
- InSAR:
-
interferometric synthetic aperture radar
- SSM:
-
split spectrum method
- TEC:
-
total electron content
- GNSS:
-
global navigation satellite system
- ALOS:
-
advanced land observation satellite
- PALSAR:
-
phased array L-band synthetic aperture radar
- JAXA:
-
Japan Aerospace Exploration Agency
- SLC:
-
single look complex
- ENE:
-
east–north–east
- WSW:
-
west–south–west
- EW:
-
east–west
- foEs:
-
critical frequencies of Es
- NICT:
-
National Institute of Communications and Technology
References
Brcic R, Parizzi A, Eineder M, Bamler R, Meyer F (2010) Estimation and compensation of ionospheric delay for SAR Interferometry. IEEE IGARSS, Proc. https://doi.org/10.1109/IGARSS.2010.5652231
Feng W, Marsh DR, Chipperfield MP, Janches D, Höffner J, Yi F, Plane JMC (2013) A global atmospheric model of meteoric iron. J Geophys Res Atmos 118:9456–9474. https://doi.org/10.1002/jgrd.50708
Feynman R, Leighton R, Sands M (1963) The Feynman lectures on physics. http://www.feynmanlectures.caltech.edu. California Institute of Technology
Gomba G, Parizzi A, De Zan F, Eineder M, Bamler R (2016) Toward operational compensation of ionospheric effects in SAR Interferograms: the split-spectrum method. IEEE Trans Geosci Remote Sens 54(3):1446–1461. https://doi.org/10.1109/TGRS.2015.2481079
Haldoupis C (2011) A tutorial review on sporadic E layers. In: Abdu MA, Pancheva D, Bhattacharyya A (eds) Aeronomy of the earth’s atmosphere and ionosphere, IAGA special sopron book series 2. Springer Netherlands, Dordrecht. https://doi.org/10.1007/978-94-007-0326-1_29
Hernández-Pajares M, Aragón-Ángel À, Defraigne P, Bergeot N, Prieto-Cerdeira R, García-Rigo A (2014) Distribution and mitigation of higher-order ionospheric effects on precise GNSS processing. J Geophys Res Solid Earth 119:3823–3837. https://doi.org/10.1002/2013JB010568
Kedar S, Hajj GA, Wilson BD, Heflin MB (2003) The effect of the second order GPS ionospheric correction on receiver positions. Geophys Res Lett 30:1829. https://doi.org/10.1029/2003gl017639
Kim BC, Tinin MV (2007) Contribution of ionospheric irregularities to the error of dual-frequency GNSS positioning. J Geod 81:189–199. https://doi.org/10.1007/s00190-006-0099-8
Maeda J, Heki K (2014) Two-dimensional observations of midlatitude sporadic E irregularities with a dense GPS array in Japan. Radio Sci 49:28–35. https://doi.org/10.1002/2013RS005295
Maeda J, Heki K (2015) Morphology and dynamics of daytime mid-latitude sporadic-E patches revealed by GPS total electron content observations. Earth Planets Space 67:89. https://doi.org/10.1186/s40623-015-0257-4
Maeda J, Suzuki T, Furuya M, Heki K (2016) Imaging the midlatitude sporadic E plasma patches with a coordinated observation of spaceborne InSAR and GPS total electron content. Geophys Res Lett 43:1419–1425. https://doi.org/10.1002/2015GL067585
Mathews JD (1998) Sporadic E: current views and recent progress. J Atmos Terr Phys 60(4):413–435
Menke W (2012) Geophysical data analysis: discrete inverse theory. Academic Press, Cambridge
Nagata T, Tohmatsu T (1973) Modern aeronomy (in Japanese). Shokabo, Tokyo
Roddy PA, Earle GD, Swenson CM, Carlson CG, Bullett TW (2004) Relative concentrations of molecular and metallic ions in midlatitude intermediate and sporadic-E layers. Geophys Res Lett 31:L19807. https://doi.org/10.1029/2004GL020604
Rosen P, Hensley S, Chen C (2010) Measurement and mitigation of the ionosphere in L-band Interferometric SAR data. In: Proceedings of the IEEE Radar Conference. https://doi.org/10.1109/RADAR.2010.5494385
Syndergaard S (2002) A new algorithm for retrieving GPS radio occultation total electron content. Geophys Res Lett. https://doi.org/10.1029/2001gl014478
Whitehead JD (1989) Recent work on mid-latitude and equatorial sporadic E. J Atmos Terr Phys 51:401–424
Authors’ contributions
MF, TS, and JM performed SAR image processing, while TS, JM, and KH derived GNSS TEC maps. TS and JM found the Es episodes. MF initially wrote the manuscript. All authors read and approved the final manuscript.
Acknowledgements
PALSAR 1.0 and PALSAR-2 level 1.1 data in this study are shared among PIXEL (PALSAR Interferometry Consortium to Study our Evolving Land Surface) under a cooperative research contract with the Earthquake Research Insitute, University of Tokyo. The ownership of ALOS-2/PALSAR-2 data belongs to JAXA. MF thanks Drs. Dominique Derauw and Giorgio Gomba for discussing the implementation of the range SSM in the earlier stage of this work. We acknowledge two anonymous reviewers, whose comments were helpful in improving the original manuscript.
Availability of data and materials
We generated all the presented InSAR images by processing ALOS/PALSAR level 1.0 and ALOS2/PALSAR2 level 1.1 data, which can be searched and purchased from either RESTEC (https://www.restec.or.jp/en/) or PASCO (http://en.alos-pasco.com). We can share the original level 1.0/1.1 data upon request within a framework of collaboration with our group. We used the processing software developed by Gamma Remote Sensing (https://www.gamma-rs.ch), and the basebanding of band-passed SLC was performed by our originally developed code.
Competing interests
The authors declare that they have no competing interests.
Ethics approval and consent to participate
Not applicable.
Funding
This study was partly funded by Joint Research Program (B), 2015-B-02, at the Earthquake Research Institute, the University of Tokyo, and partly by the Joint Research Program, Suishin 14, of the Japan Arctic Research Network Center.
Publishers’ Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Furuya, M., Suzuki, T., Maeda, J. et al. Midlatitude sporadic-E episodes viewed by L-band split-spectrum InSAR. Earth Planets Space 69, 175 (2017). https://doi.org/10.1186/s40623-017-0764-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-017-0764-6