Abstract
The youngest geomagnetic polarity reversal, the Matuyama–Brunhes (M–B) boundary, provides an important plane of data for sediments, ice cores, and lavas. The geomagnetic field intensity and directional changes that occurred during the reversal also provide important information for understanding the dynamics of the Earth’s outer core, which generates the magnetic field. However, the reversal process is relatively rapid in terms of the geological timescale; therefore, adequate temporal resolution of the geomagnetic field record is essential for addressing these topics. Here, we report a new high-resolution paleomagnetic record from a continuous marine succession in the Chiba composite section of the Kokumoto Formation of the Kazusa Group, Japan, that reveals detailed behaviors of the virtual geomagnetic poles (VGPs) and relative paleointensity changes during the M–B polarity transition. The resultant relative paleointensity and VGP records show a significant paleointensity minimum near the M–B boundary, which is accompanied by a clear “polarity switch.” A newly obtained high-resolution oxygen isotope chronology for the Chiba composite section indicates that the M–B boundary is located in the middle of marine isotope stage (MIS) 19 and yields an age of 771.7 ka for the boundary. This age is consistent with those based on the latest astronomically tuned marine and ice core records and with the recalculated age of 770.9 ± 7.3 ka deduced from the U–Pb zircon age of the Byk-E tephra. To the best of our knowledge, our new paleomagnetic data represent one of the most detailed records on this geomagnetic field reversal that has thus far been obtained from marine sediments and will therefore be key for understanding the dynamics of the geomagnetic dynamo and for calibrating the geological timescale.

.
Similar content being viewed by others
Background
The Earth’s latest magnetic field reversal event, the Matuyama–Brunhes (M–B) boundary, is an important calibration point on the geological timescale, connecting sediments and volcanic rocks, and has therefore been the focus of a number of paleomagnetic studies. During the polarity transition of the M–B boundary as well as other reversals, the Earth’s geomagnetic field intensity dropped significantly (e.g., Valet et al. 2005; Valet and Fournier 2016), resulting in the increased production of cosmogenic radionuclides, including 10Be, in the upper atmosphere (Beer et al. 2002). Hence, the M–B boundary has also been recognized as a positive spike in the 10Be flux recorded in marine sediments (e.g., Suganuma et al. 2010; Valet et al. 2014) and in an Antarctic ice core (Raisbeck et al. 2006; Dreyfus et al. 2008). Therefore, changes in the geomagnetic field intensity and the 10Be production rate in the atmosphere also provide a timescale that has been widely used in the geochronology of marine sediments (e.g., Guyodo and Valet 1999; Yamazaki 1999; Channell and Kleiven 2000; Laj et al. 2000; Stoner et al. 2000; Kiefer et al. 2001; Christl et al. 2003, 2007; Horng et al. 2003; Valet et al. 2005, 2014; Yamazaki and Oda 2005; Yamamoto et al. 2007; Yamazaki and Kanamatsu 2007; Suganuma et al. 2008; Channell et al. 2008, 2009, 2010, 2014, 2016; Inoue and Yamazaki 2010: Macri et al. 2010; Mazaud et al. 2012, 2015). These geomagnetic field intensity data associated with the directional change also contain essential information about the Earth’s magnetic field reversal; however, the nature of the geomagnetic dynamo in the Earth’s outer core remains a controversial topic (e.g., Valet and Fournier 2016). One key issue is that the reversal process is relatively rapid compared to the geological timescale; therefore, adequate temporal resolution is required to describe the reversal process.
The M–B boundary has a frequently cited age of 780 ka, which is derived from astronomically tuned benthic and planktonic oxygen isotope records from the eastern equatorial Pacific (Shackleton et al. 1990). This marine, astronomically dated M–B boundary age, is supported by the 40Ar/39Ar ages of the Maui lavas at 775.6 ± 1.9 ka (Coe et al. 2004; Singer et al. 2005), amended to 781–783 ka by recent revisions to the reference age of the Fish Canyon Tuff sanidine standards for 40Ar/39Ar geochronology (Kuiper et al. 2008; Renne et al. 2011). However, an understanding of post-depositional remanent magnetization (PDRM) processes shows that lock-in of the geomagnetic signal occurs below the sediment–water interface in marine sediments (e.g., Roberts et al. 2013; Suganuma et al. 2011), which then tends to yield older ages for geomagnetic events than for depositions. Because this age offset is thought to be relative to the sedimentation rate (Suganuma et al. 2010), geomagnetic records with higher sedimentation rates should minimize the age offset that can occur due to the PDRM lock-in process. Indeed, younger astrochronological M–B boundary ages of 772–773 ka are given for high-sedimentation-rate records (Channell et al. 2010; Valet et al. 2014), particularly for one of the records with no PDRM lock-in delay detected by Valet et al. (2014). These M–B boundary ages are consistent with the records of cosmogenic nuclides in marine sediments (e.g., Suganuma et al. 2010) and an Antarctic ice core (Dreyfus et al. 2008). Recently, Suganuma et al. (2015) presented a new U–Pb zircon age of 772.7 ± 7.2 ka from a volcanic ash layer just below the M–B boundary in the Chiba composite section (a very rapidly deposited marine sediment) in Japan. This U–Pb zircon age, coupled with an astronomical age for the marine sediment, yields an M–B boundary age of 770.2 ± 7.3 ka. This is the first direct comparison of the astronomical age calibration, U–Pb dating, and geomagnetic reversal records for the M–B boundary; however, there has been no relative paleointensity record from the Chiba composite section, which is a key requirement for calibrating the geological timescale.
In this paper, we performed a high-resolution paleomagnetic analysis for the Yoro-Tabuchi and Yoro-River sections of the main part of the Chiba composite section in the Kokumoto Formation of the Kazusa Group, Japan, to provide very detailed records of the virtual geomagnetic poles (VGP) and the relative paleointensity changes through the M–B boundary. This record provides one of the most detailed descriptions of the M–B polarity transition obtained thus far from marine sediments and will therefore be key for understanding the dynamics of the geomagnetic dynamo and for calibrating the geological timescale.
Methods
Geology of the studied section and samples
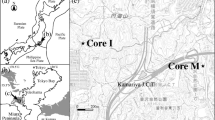
The Kazusa Group, distributed in the southeastern Japanese islands, is one of the thickest (approximately 3000 m) Lower and Middle Pleistocene sedimentary successions (e.g., Ito 1998; Kazaoka et al. 2015) (Fig. 1a). The Kazusa Group is the forearc basin fill of Kazusa; it was developed in response to the west-northwestward subduction of the Pacific plate beneath the Philippine Sea plate along the Japan and Izu-Bonin trenches (e.g., Seno and Takano 1989) and was deposited in the basin plain, submarine fan, slope, shelf, and coastal environments (Katsura 1984; Ito and Katsura 1992). Because the Kanto Basin was uplifted from the southern margin and the marine strata dip gently northward, the strata exposures are particularly good in the central part of the Boso Peninsula (Fig. 1b). The thickest succession (up to 3000 m) crops out along the Yoro-River, where numerous studies based on lithostratigraphy, biostratigraphy, and paleomagnetic and oxygen isotope stratigraphy have been focused. Well-preserved microfossils (e.g., Oda 1977; Sato et al. 1988; Cherepanova et al. 2002) and oxygen isotope stratigraphy (Okada and Niitsuma 1989; Pickering et al. 1999; Tsuji et al. 2005) place the Kazusa Group to the age between 2.4 and 0.45 Ma (Ito et al. 2016). Although the sedimentation rate of the Kazusa Group is generally very high (ca. 2 m/kyr on average) (Kazaoka et al. 2015), sedimentation rates within the group are most likely controlled by the lithological changes (sandstone- and siltstone-dominated units), corresponding to the eustatic sea level changes through the glacial–interglacial cycles.
The Kokumoto Formation represents an expanded and well-exposed sedimentary succession across the Lower–Middle Pleistocene boundary, particularly in the Chiba composite section (Yoro-Tabuchi, Yoro-River, Yanagawa, and Kogusabata sections) (Fig. 1b). The predominant silty beds of the Chiba composite section are intensely bioturbated, and there is a lack of evidence for episodic deposition such as slumps or muddy turbidites, although minor sandy beds are intercalated within the silty section, particularly in the lower part of the section (Nishida et al. 2016). Marine oxygen isotope records reveal continuous deposition from MIS 21 to MIS 18 with glacial and interglacial cycles corresponding to sandstone- and siltstone-dominated units, respectively (Okada and Niitsuma 1989; Pickering et al. 1999; Suganuma et al. 2015). The Byk-E tephra is widely distributed in the area and provides an excellent stratigraphic marker for the Lower–Middle Pleistocene boundary in the Chiba composite section (Suganuma et al. 2015). The Byk-E tephra bed consists of white, glassy, fine-grained ash and has 1–3 cm in thickness (Kazaoka et al. 2015).
In the present study, a suite of rock samples for paleomagnetic and oxygen isotopic analyses was collected from the Yoro-River and Yoro-Tabuchi sections of the main part of the Chiba composite section (Fig. 2) located at 35°17.66′ N, 140°8.79′ E, which outcrops on the gorge walls of the Yoro-River and along a branch creek of the Yoro-River. The Yoro-River section was used be called as the “Tabuchi” section (Kazaoka et al. 2015; Nishida et al. 2016; Suganuma et al. 2015). Since we newly investigated and sampled from the section along a branch creek of the Yoro-River, we named the section as “Yoro-Tabuchi” section and renamed the Tabuchi section as “Yoro-River” section.
Detailed stratigraphic correlations between the Yanagawa, Yoro-River, Yoro-Tabuchi, and Kokusabata sections. The stratigraphic correlations are based on lithological changes and marker tephra beds. The samples for paleomagnetic (thin horizontal bars) and oxygen isotope analyses (light blue squares) are from the Yoro-River and the Yoro-Tabuchi sections in this study. The sample horizons shown on the Yanagawa and Kokusabata sections and the “TBH” series for the paleomagnetic studies on the Yoro-River section were used by Suganuma et al. (2015)
Mini-cores with 1 in. diameters were collected at 213 horizons with a 10-cm stratigraphic interval using a portable engine drill and covering a 29-m succession across the Byk-E tephra bed (Fig. 2). All mini-cores were oriented with a magnetic compass before being removed from the outcrop. Each mini-core was cut into approximately 2-cm-long specimens. The samples for the oxygen isotopic analysis were collected at 72 horizons with a 20-cm stratigraphic interval covering an 18-m succession (Fig. 2). Sandstones were avoided for the sampling.
Paleomagnetic and rock-magnetic measurements
To determine the grain size, the composition of the magnetic materials, and the stability for thermal demagnetization (ThD) analysis, the following rock-magnetic and paleomagnetic measurements were taken in addition to the previous paleomagnetic studies conducted by Suganuma et al. (2015).
Before any other measurements were taken, low-field magnetic susceptibility (volumetric) measurements were taken on all specimens using a Kappabridge susceptibility meter (KLY-3; AGICO, Brno, Czech Republic) at Ibaraki University. The natural remanent magnetization (NRM) was measured using a three-axis cryogenic magnetometer (SRM-760R; 2G Enterprises, USA) installed in a magnetically shielded room at the National Institute of Polar Research (NIPR). Stepwise alternating field demagnetization (AFD) was performed in 2.5- to 10-mT increments up to 80 mT using an AF demagnetizer with a set of static 3-axis AF coils installed on the magnetometer. Stepwise thermal demagnetization (ThD) was performed in 20–50 °C increments up to 700 °C using thermal demagnetizers (TDS-1; Natsuhara-Giken, Japan) at the NIPR.
To evaluate the magnetic grain concentrations in a specimen, remanence after the acquisition of anhysteretic remanent magnetization (ARM) was measured. The ARM acquisition was performed in a 0.03-mT DC field with an 80-mT AF using the SRM-760R magnetometer at the NIPR. The isothermal remanent magnetization (IRM), regarded as saturation IRM (SIRM), was imparted at 1.5 T using a pulse magnetizer (MMPM-9; Magnetic Measurements, UK) at the NIPR. Then, IRM of 0.1 and 0.3 T was acquired in the opposite direction of the initial IRM, and the S-ratio0.1T and S-ratio0.3T were calculated following the definition of Bloemendal et al. (1992).
Magnetic hysteresis was measured with a maximum magnetic field of 0.5 T for selected specimens using an alternating gradient magnetometer (PMC MicroMag 2900 AGM; Lake Shore cryogenics Inc., USA) at the NIPR. The ratio of saturation magnetization to saturation remanence (Mrs/Ms) is commonly used as a proxy for the magnetic grain size of ferrimagnetic particles (Day et al. 1977). Magnetic hysteresis properties were also obtained using first-order reversal curve (FORC) diagrams, which provide enhanced mineral and domain state discrimination (Pike et al. 1999; Roberts et al. 2000; Muxworthy and Roberts 2007).
Thermomagnetic experiments were performed on selected specimens using a thermomagnetic balance (NMB-89; Natsuhara-Giken, Japan) at the Center for Advanced Marine Core Research, Kochi University. The specimens were heated in air and in a vacuum from room temperature up to 700 °C in a field of 300 mT.
Oxygen isotope analysis
The rock samples for the oxygen isotopic analysis were disaggregated primarily using Na2SO4 and partly using a high-voltage pulse power fragmentation system (SELFRAG Lab; SELFRAG AG, Switzerland) installed at the NIPR. The non-magnetic fraction, including foraminiferal tests, was concentrated using an isodynamic separator at Ibaraki University. We manually picked benthic foraminifera from the non-magnetic fraction for each sample. Oxygen isotopic measurements were taken with an MAT 253 mass spectrometer with a Kiel IV carbonate device installed at the Department of Geology and Paleontology, National Museum of Nature and Science. Jcp-1 and NBS-19 were used as standards to calibrate the measured isotopic values to the Vienna Pee Dee Belemnite (VPDB). The standard deviation of the oxygen isotopic measurements was calculated as 0.038‰ from 119 measurements of NBS-19 working standard samples. We used Bolivinita quadrilatera and Cibicides spp., which were the dominant species yielded from this succession, for the isotopic measurements. Okada et al. (2012) reported that B. quadrilatera has δ18O values identical to the genus Uvigerina, which is thought to have an equilibrium δ18O value with the bottom water. Shackleton and Hall (1984) reported 0.64‰ as the average δ18O difference of Uvigerina spp. minus Cibicidoides wuellerstorfi. In the Chiba composite section, Suganuma et al. (2015) used this value to adjust the δ18O measurements of the Cibicides spp., which is a genus closely related to Cibicidoides, to those of the Uvigerina spp. because the average δ18O difference between them (0.74 ± 0.18‰; 95% confidence limit of the average) reasonably matched the value reported by Shackleton and Hall (1984). We therefore corrected the δ18O values of the Cibicides spp. to those of B. quadrilatera by adding 0.64‰, in accordance with Suganuma et al. (2015).
Results
Rock-magnetic characteristics
Hysteresis loops of the representative specimens exhibit no evidence of wasp-waisted characteristics (Fig. 3a), indicating there are no obvious contributions from superparamagnetic grains or high-coercivity magnetic minerals (Roberts et al. 1995; Tauxe et al. 1996). In general, higher and lower values of Mrs/Ms correspond to finer and coarser magnetic grain sizes, respectively. The hysteresis data fall within a limited range of magnetic grain sizes that correspond to pseudo-single-domain (PSD) sizes (Fig. 3b). FORC diagrams indicate limited spreading along the Bu axis and are compatible with fine-grained magnetite with coercivities extending up to ~80 mT (Fig. 3c).
a Hysteresis loops for representative specimens. Red and blue are uncorrected and corrected values for the paramagnetic slopes, respectively. b Day plot of the hysteresis parameters for selected specimens. SD single domain, PSD pseudo-single domain, MD multi-domain, after Dunlop (2002). c FORC diagram for representative specimens
Suganuma et al. (2015) reported the results of rock-magnetic investigations, including thermomagnetic experiments and progressive thermal demagnetization on composite 3-axis IRMs (Lowrie 1990) performed on specimens from the Yoro-River section. Figure 4 shows the typical results of those rock-magnetic investigations using a specimen obtained from 315 cm below the Byk-E bed (drawn using data from Suganuma et al. 2015). According to the results, the thermomagnetic experiments demonstrate that the specimen heated in air has a single Curie temperature at 580 °C with a pronounced increase between 400 and 450 °C, indicating the creation of a ferromagnetic mineral phase. However, the thermomagnetic curve in the cooling process has a lower magnetization compared to the respective heating curve. This finding indicates that the ferromagnetic or ferrimagnetic mineral created between 400 and 450 °C was further altered by continued heating to form a higher Curie/Néel temperature mineral such as hematite. In contrast, the specimen heated in a vacuum has a single Curie/Néel temperature at 580 °C as well as in air but no increase in the magnetization between 400 and 450 °C, and the curve shows an increase in magnetization through the cooling process compared to heating. Progressive ThD in air on composite 3-axis IRMs demonstrates a major decrease in intensity for the 0.03- and 0.5-T components between 450 and 580 °C, which indicates the existence of a magnetic mineral with soft to medium coercivity, likely magnetite or low-Ti titanomagnetite. Subsequently, a small decrease in intensity is observed above 600 °C for all components. This observation indicates that specimens heated in air contain a small contribution from a higher-temperature component, such as hematite. In contrast, specimens heated in a vacuum show that the magnetizations, mostly carried by the 0.03-T and 0.5-T components, are completely demagnetized below 580 °C, which indicates the dominance of magnetite. These results suggest that the main magnetic carrier of those specimens from the Yoro-River section is magnetite dominant, except for the component that is demagnetized and/or decomposed by 400 °C.
a Examples of the thermomagnetic analyses conducted from 100 to 700 °C in air (upper) and in a vacuum (lower). Arrows represent heating and cooling. b Progressive thermal demagnetization of the three-component IRMs (0.03, 0.5, and 1.5 T) in air (upper) and in a vacuum (lower). The sample used for those diagrams is TBH31
In the present study, we performed repeated thermomagnetic experiments in air to determine the upper limit temperature at which the magnetic minerals are not decomposed due to oxidation. For each experiment, the destination temperature was progressively increased from 300 to 500 °C at 50 °C increments to monitor the magnetic stability of the specimens during the heating process. The results show that magnetizations of the specimens are mostly stable up to 400 °C, indicating that a thermal demagnetization at less than 400 °C does not change the magnetic mineralogy of the specimens (Fig. 5).
Examples of the repeated thermomagnetic analysis in air for selected specimens: a is for TBH11 from 0.55 m below the Byk-E bed; b is for TBH31 from 2.55 m below the Byk-E bed. For each analysis, the destination temperature is increased progressively from 300 to 500 °C at 50 °C increments. Numbers shown in the panels inside of the diagrams a and b indicate the destination temperatures in °C
To evaluate the variation in rock-magnetic properties, the magnetic susceptibility (k) and the ARM susceptibility (k ARM) as well as the ratio of both parameters throughout the stratigraphic sequence are shown in Fig. 6. Although several spikes are observed, likely corresponding to tephra and/or sandy layers, these data indicate that the rock-magnetic characteristics are relatively homogeneous throughout the Yoro-Tabuchi and Yoro-River sections (Fig. 6). The values of the S-ratios are also shown in Fig. 6. The S-ratio(0.3T) exhibits a high average value of more than 0.96 with little fluctuation indicating that the magnetic grains mostly consist of low coercivity minerals like magnetites throughout the sections. This finding is consistent with the results of the thermomagnetic and the 3-axis IRM experiments. In contrast, the S-ratio(0.1T) exhibits a little fluctuation with an average value of about 0.78. The fluctuation seems to change coherently with the k/kARM ratio, suggesting that the S-ratio(0.1T) is influenced by the magnetic grain size as well as the k/kARM is. Although a little fluctuation observed on the S-ratio(0.1T), the range of variations (standard deviation) is confined only within 7% of the average value. Those observations on the S-ratios suggest that the sediments from the Yoro-River and the Yoro-Tabuchi sections have a quite homogeneous rock-magnetic property in terms of magnetic mineralogy and the grain size.
Remanent magnetization and rock-magnetic properties of samples from the Yoro-River and Yoro-Tabuchi sections. From top to bottom, relative paleointensity, declination, inclination, maximum angular deviation (MAD) values, the S-ratios, the ratio of ARM susceptibility (k ARM) to magnetic susceptibility (k), and k (red) or k ARM (blue) are shown. Shading represents the polarity transition zone of the M–B boundary. All the properties were derived from the all (213) sample horizons except for the S-ratios which were from the selected 52 horizons (Additional file 1)
Remanent magnetization
Examples of the stepwise alternating field and thermal demagnetization (AFD and ThD) results are shown with Zijderveld diagrams (Zijderveld 1967) in Fig. 7a–e. The results of AFD after ThD at 300 °C are also shown in Fig. 7c, f. The stepwise ThD analysis (up to 700 °C, with 10–50 °C temperature increments) shows that several specimens, especially from the low-paleointensity intervals shown later, do not have components of characteristic remanent magnetization (ChRM) that decay toward the origin (Fig. 7e). In contrast, the AFD analysis (up to 80 mT) after the ThD at 300 °C appears to effectively extract a characteristic component that decays toward the origin (Fig. 7f). This finding indicates that some of the specimens become unstable for ThD analysis at temperatures higher than 300 °C, which is consistent with the thermomagnetic experiments exhibiting an unstable magnetic feature above 400 °C. Characteristic remanent magnetization (ChRM) directions, calculated using principal component analysis (Kirschvink 1980), are deduced using data after the hybrid demagnetization method (AFD after ThD at 300 °C). The ChRM directions are plotted in Fig. 6 with the AFD at 20 mT and the ThD at 300 °C. The maximum angular deviation (MAD) associated with each ChRM calculation generally remains below 10°, although it exhibits a much higher value in some instances. Therefore, we avoided using ChRMs with MADs greater than 15° for the subsequent discussion. The AFD directions show that both inclination and declination appear to reverse polarity at approximately 2 m below the Byk-E tephra, as previous studies have found (Niitsuma 1971; Okada and Niitsuma 1989). In contrast, the hybrid ChRMs, similar to but less scattered than the ThD directions, show the polarity reversal at approximately 1–2 m above the Byk-E tephra, which is almost consistent with Suganuma et al. (2015) (Fig. 6). Inclinations and declinations from the ChRMs distributed for normal and reversed polarity regions are antipodal in a broad sense, which indicates that the Yoro-Tabuchi and Yoro-River sections preserve reliable primary magnetizations through the M–B boundary (Fig. 6). Although, the averages of declination and inclination of the ChRMs from the reversed polarity interval, where the intensities are strong enough, are around 160° and −40°, respectively. This indicates that a tectonic rotation and inclination error can be supposed. The Kanto region, central part of the Honshu island, including the Boso Peninsula has supposed to be undergone a clockwise rotation at around 1 Ma, which is caused by a collision of the Izu massif to the Honshu island, and after 1 Ma, no systematic tectonic rotation has been detected (e.g., Koyama and Kitazato 1989). If the rotation effect remains on the Chiba composite section, the average declination should be more than 180° in opposite to our result. This suggests that the dipole moment has possibly behaved as non-“axial dipole” likely to be prepared the reversal. To evaluate precisely the tectonic rotation and/or inclination error effects, we need to have paleomagnetic data from much wider horizon avoiding reversal-related intervals, which should be done as a future work. In this study, we assume that any effect due to a tectonic rotation and/or inclination error is negligible in our record.
Examples of stepwise a, d alternating field demagnetization (AFD); b, e thermal demagnetization (ThD); and c, f progressive AFD after ThD at 300 °C. The filled and open circles correspond to projections onto the horizontal and vertical planes, respectively. The data points that likely indicate secondary components are shown in gray in (f)
These data indicate that a remarkably deep PDRM lock-in reported by Okada and Niitsuma (1989) most likely originated from an overprint of magnetization due to the formation of secondary magnetic mineral under the sediment surface. Thus, the ThD analyses at 300 °C are effective for removing the secondary component, indicating that the deeper M–B boundary horizons reported by previous studies (Niitsuma 1971; Okada and Niitsuma 1989; Aida 1997) should be revised by the data represented in this study. Accordingly, a detailed VGP path for the Yoro-Tabuchi and Yoro-River sections was established at a 10-cm resolution and clearly identifies the geomagnetic polarity reversal (Fig. 9a).
Relative paleointensity
The concentration-dependent parameters, including k and k ARM, all vary by a factor of less than 4; the magnetic grain-size-dependent parameter k/k ARM varies by a factor of less than 2. The relatively constant concentration and grain size of the magnetic grains satisfy the criteria suggested for the construction of relative paleointensity proxies (e.g., Tauxe 1993). The magnetic-concentration-sensitive parameters, ARM and k, are often used to normalize the NRM for constructing paleointensity proxies (e.g., Valet 2003; Suganuma et al. 2008, 2009). However, the low-temperature component is thought to be a secondary acquired “noise” with respect to the primary magnetic signal, as shown by rock-magnetic experiments. In this study, we use the ARM after ThD at 300 °C as a normalizer for the concentration of magnetic grains that carries a primary signal to avoid the secondary low-temperature component. The ratio of NRM300/ARM300 (both proxies are coercivity fractions between 30 and 50 mT for the NRM and ARM vectors after thermal demagnetization at 300 °C) is used as a paleomagnetic paleointensity proxy. Although a similar method was used by Wu et al. (2015), they used magnetic susceptibility as a normalizer. The uppermost diagram of Fig. 6 displays a prominent low in the relative paleointensity proxy at the directional change zone of the M–B boundary (indicated by a shaded bar).
Oxygen isotope curve and age model
Marine oxygen isotope records of the Kokumoto Formation by Pickering et al. (1999) and Okada and Niitsuma (1989) revealed a continuous sedimentary record from MIS 21 to MIS 18 with glacial and interglacial cycles corresponding to sandstone- and siltstone-dominated units, respectively. Suganuma et al. (2015) established an age model for the Chiba composite section, which was deduced by a comparison between a benthic δ18O record with 1-m stratigraphic resolution and an Atlantic benthic δ18O record (U1308; Channell et al. 2010), indicating that the sedimentation rates during the high-stand period of MIS 19, including the M–B boundary, became quite low—down to 0.32 m/kyr compared to other horizons that reach up to 3 m/kyr. This finding suggests that a δ18O record with a much higher time resolution would be needed to reconstruct a reliable age model, especially during the high-stand period of MIS 19. To meet this demand, we obtained a new 20-cm stratigraphic resolution benthic δ18O record from the Yoro-River and Yoro-Tabuchi sections (Additional file 2). We used this record combined with the record from Suganuma et al. (2015) to establish a new age model for the Chiba composite section. As a target curve to compare with our record, we selected an astronomically tuned eustatic sea level curve deduced by using benthic foraminiferal δ18O and Mg/Ca ratios of the ODP 1123 cores from the South Pacific (Elderfield et al. 2012) to avoid local δ18O variations due to changes in regional seawater temperature. According to the visual correlation between the two curves, we assigned 6 tie points where the sea level curve exhibits peaks or troughs to establish a more reliable age model for the Chiba composite section (Fig. 8; Table 1). This age model matches quite well with that of Suganuma et al. (2015), except for the transgression and the high-stand part of MIS 19, where the resolution of the δ18O record from the Yoro-River and Yoro-Tabuchi sections is substantially improved. The resultant age model and the deduced sedimentation rates are shown in Fig. 8 and indicate that the sedimentation rates basically decrease in the high-stand periods and drastically increase in the low-stand and regression periods. Those observations are thought to be reasonably explained by a sequence stratigraphic interpretation as follows: A high stand providing an additional accommodation place for sediments yields a reduced sedimentation rate on the slope and the basin floor, and a low stand and regression providing movement ahead of a sediment body yields an increased sedimentation rate on the slope and the basin floor. This type of phenomenon is also seen in the variation of sedimentation rates between the interglacial and glacial cycles for the Kazusa Group. Pickering et al. (1999) showed that the average sedimentation rates for the interglacial and glacial cycles from MIS 33 to MIS 17 are 2.1 ± 1.4 and 4.3 ± 2.8 m/kyr, respectively. Although these data could not show a variation in sedimentation rates during an interglacial period due to insufficient resolution, a comparable variation in sedimentation rates observed in this study within an interglacial period cannot be excluded.
High-resolution oxygen isotope stratigraphy from the Yoro-Tabuchi and Yoro-River sections and the age model. VPDB Vienna Pee Dee Belemnite, MIS marine isotope stage. The oxygen isotope data are combined with those of Suganuma et al. (2015) and visually tuned to the eustatic sea level change of Elderfield et al. (2012) based on the Byk-E tephra (red) and major oxygen isotope features. The Matuyama–Brunhes (M–B) boundary age is assigned as 771.7 ka based on this age model. The thickness scale used in Suganuma et al. (2015) was slightly modified to plot the data in Fig. 8 to adjust into the newly measured thickness scale of the Yoro-River section. The thickness of the top horizon down to the Ku2 bed was estimated by an extrapolation using the top thickness in the Kokusabata section multiplied by the ratio of thickness between the Byk-E and Ku2 beds in the Yoro-River and Kokusabata sections
The M–B boundary is detected in the interval showing a sedimentation rate of 61 cm/kyr, which is a relatively low rate compared to other parts of the Chiba composite section, but it might still be high enough to minimize the lock-in effect (Suganuma et al. 2010) and to reconstruct a high-resolution paleomagnetic record during the M–B polarity transition.
Discussion
Matuyama–Brunhes polarity at the Yoro-River and Yoro-Tabuchi sections and the VGP path
The M–B boundary for the Kokumoto Formation and detailed geomagnetic behavior during the polarity transition have been reported by Niitsuma (1971) and Okada and Niitsuma (1989). In these reports, the M–B boundary was considered to be 1–2 m below the Byk-E tephra. In addition, Tsunakawa et al. (1999) reconstructed the geomagnetic field variability during the M–B polarity transition by applying a deconvolution technique using a continuous paleomagnetic record from the Kokumoto Formation. These paleomagnetic data were obtained using only AF demagnetization techniques; however, Suganuma et al. (2015) indicated that these previous studies were not successful in removing the overprint on the magnetic signals based on thermal demagnetization for the specimens from same section and concluded that their VGP records needed revision.
In the present study, a detailed VGP path from the Yoro-River and Yoro-Tabuchi sections was newly established at 10-cm resolution across the M–B boundary (Figs. 6, 9). The VGPs cluster at high latitudes in the Southern Hemisphere from the bottom of the succession up to 0.25 m. Then, the VGP swings to high latitudes in the Northern Hemisphere at 1.95 m after a rebound-like feature at 0.85 m. Subsequently, the VGP exhibits several rebounds between the middle latitudes in the Northern Hemisphere and equatorial regions and then finally settles in the north polar region at a horizon higher than 11.5 m. According to these observations, we define the zone between 0.25 and 1.95 m, where the VGP swings from the southern to the northern high-latitude region, as the directional transition zone of the M–B boundary (shown as a gray bar in Fig. 5). The directional transition zone can be called the “polarity switch” of the M–B boundary (Valet et al. 2012). We also define the midpoint of this zone in the Yoro-River section, which appears 1.10 m above the Byk-E tephra, as the M–B boundary at this section from a magnetostratigraphic point of view. The horizon of the M–B boundary in the Yoro-River section is almost consistent with that shown in a boring core from the vicinity of this section (Hyodo et al. 2016) and in the Yanagawa section (Suganuma et al. 2015).
a VGP path for the M–B boundary derived from the Yoro-Tabuchi and the Yoro-River sections plotted on the Mollweide projection world map. b VGP latitudes plotted along an age scale. Colored small circles used for the data points indicate the ages as follows: purple 762.5–763.5 ka; green 763.5–765.5 ka; blue 765.5–769 ka; red 769–773 ka; and gray 773–794 ka. Arrows in (a) indicate the moving directions of the VGP paths
The VGP path for the M–B boundary from the Yoro-River and Yoro-Tabuchi sections appears to be one of the most detailed illustrations of the geomagnetic polarity reversal obtained from marine sediments. This path shows that the VGP swings back and forth several times after the “polarity switch.” These swings are thought to be “rebounds” after the “polarity switch” (e.g., Valet et al. 2014) corresponding to the M–B boundary. These rebound-like VGP swings contain clustering features in South Asia or the equatorial western Pacific and in North America. The VGP clustering in North America is likely to be consistent with that observed in marine sediment cores from the North Atlantic Ocean 983B (Channell and Kleiven 2000) and the Indian Ocean V16-58 (Clement and Kent 1991) as well as in the Tahitian lavas (Hoffman and Mochizuki 2012).
Relative paleointensity and comparison with other records
The relative paleointensity record from the Yoro-River and Yoro-Tabuchi sections plotted against age is shown in Fig. 10. This record contains a significant paleointensity minimum near the M–B boundary, which indicates that the geomagnetic field was weak, as expected, during the polarity transition, as shown in other studies (e.g., Valet et al. 2005).
Comparison of the relative paleointensity records from the Yoro-Tabuchi and Yoro-River sections with other published paleointensity and 10Be data across the M–B boundary. The relative paleointensity records are from this study, MD90-0961 (Valet et al. 2014), ODP Site 983 (Channell et al. 1998; Channell and Kleiven 2000), IODP Site U1308 (Channell et al. 2010), and PISO-1500 (Channell et al. 2009). The 10Be data are from MD98-2143 (Suganuma et al. 2010), MD90-0961 (Valet et al. 2014), and EPICA Dome C (Raisbeck et al. 2006; Dreyfus et al. 2008). The 10Be flux from the EPICA Dome C ice core is corrected to Antarctic Ice Core Chronology 2012 (Bazin et al. 2013). Note that the 10Be flux records are inverted. This inversion allows us to indicate the age of the paleomagnetic M–B boundary for each record. The M–B boundary ages and transitional intervals (duration of the M–B transition) from MD90-0961 (green), Site U1308 (orange), Site 983 (red), and the Yoro-Tabuchi and Yoro-River sections (blue) are shown by arrows and bars
Figure 10 also compares our relative paleointensity record with the MD90-0961 record from the Indian Ocean (Valet et al. 2014), the ODP Site 983 and the IODP Site U1308 from the Iceland Basin in the North Atlantic (Channell et al. 1998, 2010; Channell and Kleiven 2000), and the paleointensity stack curve of PISO-1500 (Channell et al. 2009). The 10Be data from MD97-2143 (Suganuma et al. 2010), MD90-0961 (Valet et al. 2014), and the EPICA Dome C (Raisbeck et al. 2006; Dreyfus et al. 2008) are also shown for comparison. Although small discrepancies exist in the ages and sharpness of the peaks and valleys, these paleointensity records generally show similar long-term variations and patterns. A distinctive common feature of these records is a paleointensity low at approximately 770–780 ka, which corresponds to the M–B boundary. These consistencies, including the horizons of the M–B boundary and its reversal interval in these records, support the relevance of the oxygen isotope age model for the Chiba composite section.
Unfortunately, a recovery of the paleointensity to the normal level seen before the reversal is not observed in our record due to a shortage of sampling horizons in the upper section. However, the generally observed common variations seen in all relative paleointensity records from widely separated areas with different sedimentary responses to climate changes should represent the true geomagnetic field behavior.
The M–B boundary age
Based on our age model, an age of 771.7 ka is assigned to the M–B boundary in the Yoro-River and Yoro-Tabuchi sections of the Chiba composite section (Fig. 8). The duration of the M–B directional transition zone observed between 0.25 and 1.95 m in our record is estimated to be 2.8 kyr, which is consistent with those of high-resolution marine sedimentary records from the North Atlantic Ocean (2.9–6.2 kyr) (Channell et al. 2010). The M–B boundary “precursor” (Hartl and Tauxe 1996), which predates the M–B boundary by ~18 kyr (e.g., Valet et al. 2014), is not observed in our record.
This M–B boundary age of 771.7 ka is apparently younger than the frequently cited astrochronological age of 777.8–780.1 ka for the M–B boundary based on marine records of low depositional rate (e.g., Shackleton et al. 1990; Lisiecki and Raymo 2005; Pilans and Gibbard 2012). In contrast, Suganuma et al. (2015) recently presented a new U–Pb zircon age of 772.7 ± 7.2 ka from the Byk-E tephra and gave an age of 770.2 ± 7.3 ka for the M–B boundary based on the depositional time interval between the tephra and the M–B boundary. According to our new age model, the sedimentation rate of the section including the M–B boundary is deduced as 61 cm/kyr, which provides an age for the VGP midpoint horizon of the directional transition zone that is 1.8 kyr younger than the depositional age of the Byk-E tephra. Based on this age model, we recalculate the M–B boundary age using the U–Pb zircon age of Byk-E as 770.9 ± 7.3 ka (error includes uncertainty in orbital tuning), showing remarkable consistency with the M–B boundary age of 771.7 ka derived by the correlation of the oxygen isotope records.
The age of 771.7 ka is also consistent with the astrochronological ages obtained from the high-sedimentation-rate records in the North Atlantic (773.1 ka; Channell et al. 2010) and in the equatorial Indian Ocean (772 ka; Valet et al. 2014). Recent reports of the ages of the 10Be flux anomaly from marine sediments in the equatorial Indian (772 ka; Valet et al. 2014) and Pacific (770 ka; Suganuma et al. 2010) Oceans are also consistent with our M–B boundary age estimate. Because the paleomagnetic records from sections with higher sedimentation rates are thought to be less affected by the PDRM lock-in (e.g., Suganuma et al. 2010, 2011), more reliable records with higher sedimentation rates may provide younger M–B boundary ages.
A rapid polarity transition and older M–B boundary ages have recently been reported (Sagnotti et al. 2014, 2016) for the last reversal from a paleolacustrine sequence from the central Apennines, Italy. However, since continental sediments likely behave differently than marine environments, further studies would be needed to compare the reversal timing between the continental and marine records. Although M–B boundary age and reversal duration may depend on the site location or on the local non-dipole field configuration, further investigation of suitable stratigraphic sequences, particularly from marine sediments, is still needed to understand the exact timing and nature of the geomagnetic field reversal.
Conclusions
Despite a long history of paleomagnetic studies, no consensus has been reached on the nature of geomagnetic field reversals. In addition, refining the chronology for geomagnetic polarity reversals, such as the M–B boundary, is very important for precise correlations among sediments, ice cores, and lavas. Because the geomagnetic polarity reversal is a relatively rapid process in terms of the geological timescale, polarity transition records with a higher time resolution are essential to address these topics. In this article, we report a high-resolution paleomagnetic and oxygen isotope record for the M–B polarity transition from a continuous marine succession in the Yoro-River and Yoro-Tabuchi sections of the main part of the Chiba composite section in the Kokumoto Formation of the Kazusa Group in Japan. Rock-magnetic experiments indicate that magnetic carriers contained in the samples are mainly composed of PSD-sized magnetite. The thermomagnetic experiments show that magnetizations of the samples are mostly stable up to 400 °C. The variations in rock-magnetic properties are relatively homogeneous throughout the Yoro-River and Yoro-Tabuchi sections. Progressive alternating field demagnetization after thermal demagnetization at 300 °C reveals a ChRM direction change that indicates a clear “polarity switch” corresponding to the M–B boundary in the section. The relative paleointensity records also show a significant paleointensity minimum near the M–B boundary. A newly obtained high-resolution oxygen isotope chronology indicates that the M–B boundary is located in the middle of MIS 19 and yields an age of 771.7 ka for the boundary. This new M–B boundary age is consistent with the findings based on the latest astronomically tuned high-resolution marine sedimentary records, Antarctic ice cores, and the recalculated age of 770.9 ± 7.3 ka deduced from the U–Pb zircon age of the Byk-E tephra using the new age model based on oxygen isotopes. This record shows one of the most detailed behaviors of the M–B polarity transition that has been obtained thus far from marine sediments and will therefore be key for understanding the dynamics of the geomagnetic dynamo. In addition, the Chiba composite section is one of the candidate sites for the Lower–Middle Pleistocene Boundary GSSP; therefore, this record has certain merit for calibrating the geological timescale, including the use of methods such as astronomical tuning, U–Pb dating, and magnetostratigraphy for the M–B boundary.
Abbreviations
- GSSP:
-
Global Boundary Stratotype Section and Point
- NIPR:
-
National Institute of Polar Research
- M–B boundary:
-
Matuyama–Brunhes boundary
- ChRM:
-
characteristic remanent magnetization
- VGP:
-
virtual geomagnetic pole
- NRM:
-
natural remanent magnetization
- AFD:
-
alternating field demagnetization
- ThD:
-
thermal demagnetization
- ARM:
-
anhysteretic remanent magnetization
- IRM:
-
isothermal remanent magnetization
- SIRM:
-
saturation isothermal remanent magnetization
- MAD:
-
maximum angular deviation
- MIS:
-
marine isotope stage
References
Aida N (1997) Paleomagnetic stratigraphy of the type section (proposed site) for the Lower/Middle Pleistocene Boundary Kokumoto Formation. In: Kawamura M, Oka T, Kondo T (eds) Commemorative volume for Professor Makoto Kato, Commemorative Volume Publication Committee, Sapporo, pp 275–282 (in Japanese with English abstract)
Bazin L, Landais A, Lemieux-Dudon B, Toye Mahamadou Kele H, Veres D, Parrenin F, Martinerie P, Ritz C, Capron E, Lipenkov V, Loutre M-F, Raynaud D, Vinther B, Svensson A, Rasmusse OS, Severi M, Blunier T, Leuenberge RM, Fischer H, Masson-Delmotte V, Chappellaz J, Wolff E (2013) An optimized multi-proxy, multi-site Antarctic ice and gas orbital chronology (AICC2012): 120–800 ka. Clim Past 9:1715–1731
Beer J, Muscheler R, Wagner G, Laj C, Kissel C, Kubik PW, Synal HA (2002) Cosmogenic nuclides during isotope stages 2 and 3. Quat Sci Rev 21:1129–1139
Bloemendal J, King JW, Hall FR, Doh S-J (1992) Rock magnetism of late Neogene and Pleistocene deep-sea sediments: relationship to sediment source, diagenetic processes, and sediment lithology. J Geophys Res 97:4361–4375
Channell JET, Kleiven HF (2000) Geomagnetic palaeointensities and astrochronological ages for the Matuyama–Brunhes boundary and the boundaries of the Jaramillo Subchron: palaeomagnetic and oxygen isotope records from ODP Site 983. Philos Trans R Soc Lond B 358:1027–1047
Channell JET, Hodell DA, McManus J, Lehman B (1998) Orbital modulation of the Earth’s magnetic field intensity. Nature 394:464–468
Channell JET, Hodell DA, Xuan C, Mazaud A, Stoner JS (2008) Age calibrated relative paleointensity for the last 1.5 Myr at IODP Site U1308 (North Atlantic). Earth Planet Sci Lett 274:59–71. doi:10.1016/j.epsl.2008.07.005
Channell JET, Xuan C, Hodell DA (2009) Stacking paleointensity and oxygen isotope data for the last 1.5 Myr (PISO-1500). Earth Planet Sci Lett 283:14–23. doi:10.1016/j.epsl.2009.03.012
Channell JET, Hodell DA, Singer BS, Xuan C (2010) Reconciling astrochronological and 40Ar/39Ar ages for the Matuyama–Brunhes boundary and late Matuyama chron. Geochem Geophys Geosyst 11:Q0AA12, doi:10.1029/2010GC003203
Channell JET, Wright JD, Mazaud A, Stoner JS (2014) Age through tandem correlation of Quaternary relative paleointensity (RPI) and oxygen isotope data at IODP Site U1306 (Eirik Drift, SW Greenland). Quat Sci Rev 88:135–146
Channell JET, Hodell DA, Curtis JH (2016) Relative paleointensity (RPI) and oxygen isotope stratigraphy at IODP Site U1308: North Atlantic RPI stack for 1.2–2.2 Ma (NARPI-2200) and age of the Olduvai Subchron. Quat Sci Rev 131:1–19. doi:10.1016/j.quascirev.2015.10.011
Cherepanova MV, Pushkar VS, Razjigaeva N, Kumai H, Koizumi I (2002) Diatom biostratigraphy of the Kazusa Group, Boso Peninsula, Honshu, Japan. Quat Res (Daiyonki Kenkyu) 41:1–10
Christl M, Strobl C, Mangini A (2003) Beryllium-10 in deep-sea sediments: a tracer for the Earth’s magnetic field intensity during the last 200,000 years. Quat Sci Rev 22:725–739
Christl M, Mangini A, Kubik PW (2007) Highly resolved Beryllium-10 record from ODP Site 1089—a global signal? Earth Planet Sci Lett 257:245–258
Clement BM, Kent DV (1991) A southern hemisphere record of the Matuyama–Brunhes polarity reversal. Geophys Res Lett 18:81–984
Coe RS, Singer BS, Pringle MS, Zhao XX (2004) Matuyama–Brunhes reversal and Kamikatsura event on Maui: paleomagnetic directions, Ar-40/Ar-39 ages and implications. Earth Planet Sci Lett 222:667–684. doi:10.1016/j.epsl.2004.03.003
Day R, Fuller M, Schmidt VA (1977) Hysteresis properties of titanomagnetites: grain-size and compositional dependence. Phys Earth Planet Int 13:260–267
Dreyfus GB, Raisbeck GM, Parrenin F, Jouzel J, Guyodo Y, Nomade S, Mazaud A (2008) An ice core perspective on the age of the Matuyama–Brunhes boundary. Earth Planet Sci Lett 274:151–156
Dunlop DJ (2002) Theory and application of the Day plot (Mrs/Ms versus Hcr/Hc): 1. Theoretical curves and tests using titanomagnetite data. J Geophys Res 107(B3):2056. doi:10.1029/2001JB000486
Elderfield H, Ferretti P, Greaves M, Crowhurst S, McCave IN, Hodell D, Piotrowski AM (2012) Evolution of ocean temperature and ice volume through the Mid-Pleistocene climate transition. Science 337:704–709. doi:10.1126/science.1221294
Guyodo Y, Valet JP (1999) Global changes in intensity of the Earth’s magnetic field during the past 800 kyr. Nature 399(6733):249–252
Hartl P, Tauxe L (1996) A precursor to the Matuyama/Brunhes transition-field instability as recorded in pelagic sediments. Earth Planet Sci Lett 138:121–135
Hoffman KA, Mochizuki N (2012) Evidence of a partitioned dynamo reversal process from paleomagnetic recordings in Tahitian lavas. Geophys Res Lett 39:L06303. doi:10.1029/2011GL050830
Horng CS, Roberts AP, Liang WT (2003) A 2.14-Myr astronomically tuned record of relative geomagnetic paleointensity from the western Philippine Sea. J Geophys Res 108:2059. doi:10.1029/2001JB001698
Hyodo M, Katoh S, Kitamura A, Takasaki K, Matsushita H, Kitaba I, Tanaka I, Nara M, Matsuzaki M, Dettman DL, Okada M (2016) High resolution stratigraphy across the early-middle Pleistocene boundary from a core of the Kokumoto Formation at Tabuchi, Chiba Prefecture, Japan. Quat Int 397:16–26. doi:10.1016/j.quaint.2015.03.031
Inoue S, Yamazaki T (2010) Geomagnetic relative paleointensity chronostratigraphy of sediment cores from the Okhotsk Sea. Palaeogeogr Palaeoclimatol Palaeoecol 291:253–266. doi:10.1016/j.palaeo.2010.02.037
Ito M (1998) Submarine fan sequences of the lower Kazusa Group, a Plio-Pleistocene forearc basin fill in the Boso Peninsula, Japan. Sediment Geol 122:69–938
Ito M, Katsura Y (1992) Inferred glacio-eustatic control for high-frequency depositional sequences of the Plio-Pleistocene Kazusa Group, a forearc basin fill in Boso Peninsula, Japan. Sediment Geol 80:67–75
Ito M, Kameo M, Satoguchi Y, Masuda F, Hiroki Y, Takano O, Nakajima T, Suzuki N (2016) Neogene-Quaternary sedimentary successions. In: Moreno T, Wallis S, Kojima T, Gibbons W (eds) The geology of Japan. Geological Society of London, London, pp 309–337
Katsura Y (1984) Depositional environments of the Plio-Pleistocene Kazusa Group, Boso Peninsula, Japan. Sci Rep Inst Geosci Univ Tsukuba Sect B Geol Sci 5:69–104
Kazaoka O, Suganuma Y, Okada M, Kameo K, Head MJ, Yoshida T, Sugaya M, Kameyama S, Ogitsu I, Nirei H, Aida N, Kumai H (2015) Stratigraphy of the Kazusa Group, Chiba Peninsula, Central Japan: an expanded and highly-resolved marine sedimentary record from the Lower and Middle Pleistocene. Quat Int 383:116–134
Kiefer T, Sarnthein M, Erlenkeuser H, Grootes PM, Roberts AP (2001) North Pacific response to millennial-scale changes in ocean circulation over the last 60 kyr. Paleoceanography 16:179–189
Kirschvink JL (1980) The least-squares line and plane and the analysis of palaeomagnetic data. Geophys J R Astron Soc 62(3):699–718. doi:10.1111/j.1365-246X.1980.tb02601.x
Koyama M, Kitazato H (1989) Paleomagnetic evidence for Pleistocene clockwise rotation in the Oiso Hills: a possible record of interaction between the Philippine Sea plate and northeast Japan. In: Hillhouse JW (ed) Deep structure and past kinematics of accreted terranes, vol 50., Geophysics monographsAmerican Geophysical Union, Washington, pp 249–265
Kuiper KF, Deino A, Hilgen FJ, Krijgsman W, Renne PR, Wijbrans JR (2008) Synchronizing rock clocks of earth history. Science (80-) 320:500–504
Laj C, Kissel C, Mazaud A, Channell JET, Beer J (2000) North Atlantic palaeointensity stack since 75 ka (NAPIS-75) and the duration of the Laschamp event. Philos Trans R Soc Lond A 358:1009–1025
Lisiecki LE, Raymo ME (2005) A Pliocene–Pleistocene stack of 57 globally distributed benthic δ18O records. Paleoceanography 20:PA1003. doi:10.1029/2004PA001071
Lowrie W (1990) Identification of ferromagnetic minerals in a rock by coercivity and unblocking temperature properties. Geophys Res Lett 17:159–162
Macri P, Sagnotti L, Dinarès-Turell J, Caburlotto A (2010) Relative geomagnetic paleointensity of the Brunhes Chron and the Matuyama–Brunhes precursor as recorded in sediment core from Wilkes Land Basin (Antarctica). Phys Earth Planet Int 179:72–86
Mazaud A, Channell JET, Stoner JS (2012) Relative paleointensity and environmental magnetism since 1.2 Ma at IODP site U1305 (Eirik Drift, NW Atlantic). Earth Planet Sci Lett 357–358:137–144
Mazaud A, Channell JET, Stoner JS (2015) The paleomagnetic record at IODP Site U1307 back to 2.2 Ma (Eirik Drift, off south Greenland). Earth Planet Sci Lett 429:82–89
Muxworthy AR, Roberts AP (2007) First-order reversal curve (FORC) diagrams. In: Gubbins D, Herrero-Bervera E (eds) Encyclopedia of geomagnetism and paleomagnetism. Springer, London, pp 266–272
Niitsuma N (1971) Detailed study of the sediments recording the Matuyama–Brunhes geomagnetic reversal. Sci Rep Tohoku Univ 2nd Ser (Geol) 43:1–39
Nishida N, Kazaoka O, Izumi K, Suganuma Y, Okada M, Yoshida T, Ogitsu I, Nakazato H, Kameyama S, Kagawa A, Morisaki M, Nirei N (2016) Sedimentary processes and depositional environments of a continuous marine succession across the Lower–Middle Pleistocene boundary: Kokumoto Formation, Kazusa Group, central Japan. Quat Int 397:3–15
Oda M (1977) Planktonic foraminiferal biostratigraphy of the late Cenozoic sedimentary sequence, Central Honshu, Japan. Sci Rep Tohoku Univ 2nd Ser (Geol) 48:1–76
Okada M, Niitsuma N (1989) Detailed paleomagnetic records during the Brunhes–Matuyama geomagnetic reversal and a direct determination of depth lag for magnetization in marine sediments. Phys Earth Planet Int 56:133–150
Okada M, Tokoro Y, Uchida Y, Arai Y, Saito K (2012) An integrated stratigraphy around the Plio-Pleistocene boundary interval in the Chikura Group, southernmost part of the Boso Peninsula, central Japan, based on data from paleomagnetic and oxygen isotopic analyses. J Geol Soc Jpn 118:97–108 (in Japanese with English abstract)
Pickering KT, Souter C, Oba T, Taira A, Schaaf M, Platzman E (1999) Glacio-eustatic control on deep-marine clastic forearc sedimentation, Pliocene–mid-Pleistocene (c. 1180–600 ka) Kazusa Group, SE Japan. J Geol Soc Lond 156:125–136
Pike CR, Roberts AP, Verosub KL (1999) Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 85:6660–6667
Pilans B, Gibbard PL (2012) The quaternary period. In: Gradstein FM, Ogg JG, Schmitz MD, Ogg GM (eds) The geologic time scale 2012, vol 2. Elsevier, Amsterdam, pp 980–1009
Raisbeck GM, Yiou F, Cattani O, Jouzel J (2006) Be-10 evidence for the Matuyama–Brunhes geomagnetic reversal in the EPICA Dome C ice core. Nature 444:82–84
Renne PR, Balco G, Ludwig KR, Mundil R, Min K (2011) Response to the comment by W.H. Schwarz et al. on “Joint determination of 40 K decay constants and 40Ar∗/40 K for the Fish Canyon sanidine standard, and improved accuracy for 40Ar/39Ar geochronology” by P.R. Renne et al. (2010). Geochim Cosmochim Acta 75:5097–5100. doi:10.1016/j.gca.2011.06.021
Roberts AP, Cui Y, Verosub KL (1995) Wasp-waisted hysteresis loops: mineral magnetic characteristics and discrimination of components in mixed magnetic systems. J Geophys Res 100:17909–17924. doi:10.1029/95JB00672
Roberts AP, Pike CR, Verosub KL (2000) First-order reversal curve diagrams: a new tool for characterizing the magnetic properties of natural samples. J Geophys Res 105:28461–28475
Roberts AP, Taux L, Heslop D (2013) Magnetic paleointensity stratigraphy and high-resolution Quaternary geochronology: successes and future challenges. Quat Sci Rev 61:1–16
Sagnotti L, Scardia G, Giaccio B, Liddicoat JC, Nomade S, Renne PR, Sprain CJ (2014) Extremely rapid directional change during Matuyama–Brunhes geomagnetic polarity reversal. Geophys J Int 199:1110–1124. doi:10.1093/gji/ggu287
Sagnotti L, Giaccio B, Liddicoat JC, Nomade S, Renne PR, Scardia G, Sprain CJ (2016) How fast was the Matuyama–Brunhes geomagnetic reversal? A new subcentennial record from the Sulmona Basin, central Italy. Geophys J Int 204:798–812. doi:10.1093/gji/ggv486
Sato T, Takayama T, Kato M, Kudo T, Kameo K (1988) Calcareous microfossil biostratigraphy of the uppermost Cenozoic formations distributed in the coast of the Japan Sea, part 4: conclusion. J Jpn Assoc Pet Technol 53:474–491 (in Japanese with English abstract)
Seno T, Takano T (1989) Seismotectonics at the trench–trench–trench triple junction off central Honshu. Pure Appl Geophys 129:27–40
Shackleton NJ, Hall MA (1984) Oxygen and carbon isotope stratigraphy of Deep Sea Drilling Project hole 552A: Plio-Pleistocene glacial history. Init Rep Deep Sea Drill Proj 81:599–609
Shackleton NJ, Berger A, Peltier WR (1990) An alternative astronomical calibration of the Lower Pleistocene timescale based on ODP Site 677. Trans R Soc Edinb Earth Sci 81:251–261
Singer BS, Hoffman KA, Coe RS, Brown LL, Jicha BR, Pringle MS, Chauvin A (2005) Structural and temporal requirements for geomagnetic field reversal deduced from lava flows. Nature 434:633–636
Stoner JS, Channell JET, Hillaire-Marcel C, Kissel C (2000) Geomagnetic paleointensity and environmental record from Labrador Sea core MD95-2024: global marine sediment and ice core chronostratigraphy for the last 110 kyr. Earth Planet Sci Lett 183:161–177
Suganuma Y, Yamazaki T, Kanamatsu T, Hokanishi N (2008) Relative paleointensity record during the last 800 ka from the equatorial Indian Ocean: implication for relationship between inclination and intensity variations. Geochem Geophys Geosyst 9:Q02011. doi:10.1029/2007GC001723
Suganuma Y, Yamazaki T, Kanamatsu T (2009) South Asian monsoon variability during the past 800 kyr revealed by rock magnetic proxies. Quat Sci Rev 28:926–938
Suganuma Y, Yokoyama Y, Yamazaki T, Kawamura K, Horng CS, Matsuzaki H (2010) 10Be evidence for delayed acquisition of remanent magnetization in marine sediments: implication for a new age for the Matuyama–Brunhes boundary. Earth Planet Sci Lett 296:443–450
Suganuma Y, Okuno J, Heslop D, Roberts AP, Yamazaki T, Yokoyama Y (2011) Post-depositional remanent magnetization lock-in for marine sediments deduced from Be-10 and paleomagnetic records through the Matuyama–Brunhes boundary. Earth Planet Sci Lett 311:39–52
Suganuma Y, Okada M, Horie K, Kaiden H, Takehara M, Senda R, Kimura J, Kawamura K, Haneda Y, Kazaoka O, Head MJ (2015) Age of Matuyama–Brunhes boundary constrained by U–Pb zircon dating of a widespread tephra. Geology 43:491–494
Tauxe L (1993) Sedimentary records of relative paleointensity of the geomagnetic-field—theory and practice. Rev Geophys 31:319–354
Tauxe L, Mullender TAT, Pick T (1996) Potbellies, wasp-waists, and superparamagnetism in magnetic hysteresis. J Geophys Res 101:571–583. doi:10.1029/95JB03041
Tsuji T, Miyata Y, Okada M, Mita I, Nakagawa H, Sato Y, Nakamizu M (2005) High-resolution chronology of the lower Pleistocene Otadai and Umegase Formations of the Kazusa Group, Boso Peninsula, central Japan: chronostratigraphy of the JNOC TR-3 cores based on oxygen isotope, magnetostratigraphy and calcareous nannofossil. J Geol Soc Jpn 111:1–20 (in Japanese with English abstract)
Tsunakawa H, Okada M, Niitsuma N (1999) Further application of the deconvolution method of post-depositional DRM to the precise record of the Matuyama–Brunhes reversal in the sediments from the Bose Peninsula, Japan. Earth Planets Space 51:169–173. doi:10.1186/BF03352221
Valet JP (2003) Time variations in geomagnetic intensity. Rev Geophys. doi:10.1029/2001RG000104
Valet JP, Fournier A (2016) Deciphering records of geomagnetic reversals. Rev Geophys. doi:10.1002/2015RG000506
Valet JP, Meynadier L, Guyodo Y (2005) Geomagnetic dipole strength and reversal rate over the past two million years. Nature 435:802–880
Valet JP, Fournier A, Courtillot V, Herrero-Bervera E (2012) Dynamical similarity of geomagnetic field reversals. Nature 490:89–93
Valet JP, Bassinot F, Bouilloux A, Bourlès D, Nomade S, Guillou V, Lopes F, Thouveny N, Dewilde F (2014) Geomagnetic, cosmogenic and climatic changes across the last geomagnetic reversal from Equatorial Indian Ocean sediments. Earth Planet Sci Lett 397:67–79
Wu Y, Ouyang T, Qiu S, Rao Z, Zhu Z (2015) A sedimentary paleomagnetic record of the upper Jaramillo transition from the Lantian Basin in China. Earth Planets Space 67:1–12. doi:10.1186/s40623-015-0341-9
Yamamoto Y, Yamazaki T, Kanamatsu T et al (2007) Relative paleointensity stack during the last 250 kyr in the northwest Pacific. J Geophys Res 112:B01104. doi:10.1029/2006JB004477
Yamazaki T (1999) Relative paleointensity of the geomagnetic field during Brunhes Chron recorded in North Pacific deep-sea sediment cores: orbital influence? Earth Planet Sci Lett 169:23–35
Yamazaki T, Kanamatsu T (2007) A relative paleointensity record of the geomagnetic field since 1.6 Ma from the North Pacific. Earth Planets Space 59:785–794. doi:10.1186/BF03352741
Yamazaki T, Oda H (2005) A geomagnetic paleointensity stack between 0.8 and 3.0 Ma from equatorial Pacific sediment cores. Geochem Geophys Geosyst 6:Q11H20. doi:10.1029/2005GC001001
Zijderveld JDA (1967) A.C. demagnetization of rocks: analysis of result. In: Collinson DW, Creer KM, Runcorn SK (eds) Methods in paleomagnetism. Elsevier, New York, pp 254–286
Authors’ contributions
MO proposed the topic and conceived and designed the study. YS assisted in the fieldwork and rock-magnetic experiments, in the discussion of the data, and in the drafting of the manuscript. YH assisted in the fieldwork, carried out the experimental study, and developed the figures. OK assisted in the fieldwork. All authors read and approved the final manuscript.
Author information
Makoto Okada is a professor at Ibaraki University, Japan. He received his Ph.D. from the University of Tokyo. His research interests include magnetostratigraphy and oxygen isotope stratigraphy and their applications in paleoceanography and tectonic events during the Cenozoic time in Japan and the surrounding areas. Yusuke Suganuma is an associate professor at the National Institution for Polar Research, Japan. He received his Ph.D. from the University of Tokyo. His research interests focus on cosmogenic radionuclides and their application in earth sciences, including precise dating of geomagnetic reversals and the growth and decay timing of the Antarctic ice sheets. Yuki Haneda is a Ph.D. student at Ibaraki University. The main themes of his research include magnetostratigraphy and oxygen isotopic stratigraphy of the Upper Pliocene to the Lower Pleistocene distributed around central Japan and their utilization for paleoceanographic environment reconstruction in the northwestern marginal region of the Pacific Ocean during and after Northern Hemisphere glaciation. Osamu Kazaoka is a chief researcher at the Research Institute of Environmental Geology, Chiba Prefecture, Japan. He received his Ph.D. from Osaka City University. He is a specialist in sedimentary geology, particularly in Pleistocene and Holocene marine sequences, and environmental geology focusing on the liquefaction of man-made sedimentary formations.
Acknowledgements
We thank Martin J. Head and Masayuki Hyodo for helpful discussions on this project. We also thank Nozomi Suzuki and Yoshimi Kubota for help with the oxygen isotope measurements at the National Museum of Nature and Science and Yuhji Yamamoto who supported the rock-magnetic measurements at the Kochi Core Center through a joint use system (Grants 15A046, 15B041, 14A017, and 14A018). We are also grateful for the constructive comments from anonymous referees. This work was partially supported by JSPS KAKENHI, Grant Numbers 16H04068 and 15K13581, by a donation from Hisashi Nirei, and by special funding from the Director of the National Institute of Polar Research, Japan.
Competing interests
The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Additional files
40623_2017_627_MOESM1_ESM.xls
Additional file 1 Rock-magnetic and paleomagnetic results from the Yoro-River and Yoro-Tabuchi sections, which were used for Figure 6.
40623_2017_627_MOESM2_ESM.xls
Additional file 2. Oxygen isotope data of benthic species from the Yoro-River and Yoro-Tabuchi sections. The δ18O values of the Cibicides spp. were converted into those of B. quadrilatera by adding 0.64‰.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Okada, M., Suganuma, Y., Haneda, Y. et al. Paleomagnetic direction and paleointensity variations during the Matuyama–Brunhes polarity transition from a marine succession in the Chiba composite section of the Boso Peninsula, central Japan. Earth Planets Space 69, 45 (2017). https://doi.org/10.1186/s40623-017-0627-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-017-0627-1