Abstract
We have investigated the spatial distribution of the static stress drop of similar aftershocks of the 2007 Noto Hanto earthquake, central Japan, and have examined the relationship between the coseismic slip of the mainshock and the static stress drop of the similar aftershocks. The static stress drop is estimated by using the empirical Green’s function method for P- and S-waves. The estimated static stress drop approximately ranges from 5 to 20 MPa, which is a typical range of values for tectonic earthquakes. The static stress drops of the aftershocks in a large slip area of the mainshock tend to be larger than those in a small slip area. This suggests a large difference between the strength and the dynamic stress level in the large slip area and a small difference in the small slip area if the final stress level is equal to the dynamic stress level.
Similar content being viewed by others
Findings
Introduction
Static stress drop, defined as the difference between the initial and residual stress levels, is one of the key parameters for understanding the dynamic characteristics of earthquakes. Many studies have reported that the static stress drop is almost constant for the scale from natural earthquakes to acoustic emission events (e.g., Hiramatsu et al. 2002; Imanishi and Ellsworth 2006; Yoshimitsu et al. 2014). On the other hand, a spatial or temporal fluctuation of the static stress drop has often been recognized as well because the heterogeneity of stress and strength on a ruptured fault determines the value of the static stress drop (e.g., Allmann and Shearer 2007, 2009; Hardebeck and Aron 2009; Oth 2013; Uchide et al. 2014). In particular, the static stress drops of small earthquakes are considered to be good indicators for the heterogeneity of the difference between the strength and the dynamic stress level, because we can assume that the initial stress is equal to the strength at the hypocenter, where the rupture initiates (Yamada et al. 2010).
Allmann and Shearer (2007) found that the patterns of high- and low-stress drop regions along the Parkfield segment of the San Andreas fault were largely unchanged before and after the 2004 M6.0 Parkfield earthquake from the analyses of the static stress drop of small earthquakes. They also reported higher stress drops in the hypocentral region of the 2004 earthquake and lower stress drops in the Middle Mountain asperity and along the creeping fault section. Hardebeck and Aron (2009) found that high stress drops were concentrated around the major locked patch near Oakland on the Hayward fault in California. They suggested that the relationship between fault strength and the strength of the wall rock was complex because the stress drops are directly uncorrelated with the strength of the wall rock geology at depth. Yamada et al. (2010) analyzed the waveform data of small earthquakes which occurred in the source area of the Kīholo Bay earthquake beneath the northwest part of the Island of Hawai‘i. They reported that aftershocks around large slip areas of the mainshock were likely to have larger static stress drops, suggesting that the spatial pattern of stress drop reflects a coherent variation in the difference between the shear strength and the dynamic stress level. However, to confirm that this is a common property of earthquakes, more case studies are needed on the spatial relationship between the static stress drops of aftershocks and the coseismic slip of a mainshock.
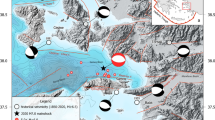
The 2007 Noto Hanto earthquake (MJMA6.9) occurred at 9:41 (Japan Standard Time (JST)) on 25 March 2007, at a depth of 11 km beneath the west coast of the Noto Peninsula, central Japan (Fig. 1), accompanied by uplift and subsidence along the coastline around the source area (Hiramatsu et al. 2008). Several heterogeneous slip models have been proposed for the 2007 Noto Hanto earthquake based on strong motion data (Horikawa 2008), the coseismic crustal movement (Fukushima et al. 2008; Ozawa et al. 2008), and both of these (Asano and Iwata 2007). These models showed that a large coseismic slip area existed from the hypocenter to the shallow part of the fault plane. The aftershocks are distributed not only in the small slip area but also in the large slip area (Horikawa 2008). Thus, this earthquake is a suitable candidate for examining the spatial relationship between the stress drops of aftershocks and the coseismic slip of a mainshock.
The distribution of the epicenters of the mainshock (star) and the aftershocks (circles) and the stations (triangles). Red circles are epicenters of similar aftershocks of which static stress drops are estimated in this study. Note that the epicenters of the similar aftershocks of each group are represented by a single circle
In this study, we estimate the static stress drops of the aftershocks on the fault plane of the 2007 Noto Hanto earthquake and conclude that the static stress drops in a large slip area tend to be larger than those in a small slip area. This relationship provides information on the spatial distribution of the difference between the strength and the dynamic stress level.
Data and method
The Group for the Joint Aftershock Observations of the 2007 Noto Hanto Earthquake operated a dense temporal network around the source region to obtain waveform data of the aftershocks (Sakai et al. 2007). The sampling frequency of the waveform data ranged from 100 to 200 Hz (Sakai et al. 2007). Sakai et al. (2008) relocated the hypocenters of 1318 aftershocks, which occurred between 25 March to 18 April 2007, using this dense network data, and showed a well-defined southeast dipping plane as the source fault. Hiramatsu et al. (2011) examined the waveform data of the 1318 aftershocks and identified 19 groups of similar aftershocks on the source fault which showed high cross-correlation coefficients (≥0.95) of waveforms in the 1–4 Hz frequency band at the same stations and which shared an almost identical source area.
In this study, we apply the procedure of Yamada et al. (2010) to estimate the corner frequency and static stress drop. For the analysis, we selected a pair of earthquakes having a close hypocentral distance and having similar waveforms, indicating that the source mechanism and the propagation path could be considered to be common. Consequently, we tried to analyze the 19 groups of similar aftershocks on the source fault (Hiramatsu et al. 2011) for the analysis.
We used the smallest earthquake (M ≥ 2.0) of each group of similar aftershocks as the empirical Green’s function (EGF) earthquake and used the largest earthquake (M ≥ 2.5) as the target earthquake (TEQ).
We estimate the velocity spectra of P- and S-waves of the vertical component using a Fourier transform. We use a variable-length time window for the P-wave because the arrival time difference between P- and S-waves depends on the hypocentral distance. The duration of the time window of a P-wave ranges from 1.06 to 5.89 s. In contrast, we use a fixed time window with a 1.3-s duration for the S-wave. In order to stabilize the analysis, we obtain the velocity spectra from the seismograms in three moving windows with a 0.08-s interval, following Imanishi and Ellsworth (2006) (Fig. 2a, b).
Examples of the analyses. (Left panels) Velocity waveform of the vertical component of a target earthquake (TEQ) and (center panels) that of an empirical Green’s function (EGF) earthquake. Red, blue, and green bars indicate a time window for the calculation of the deconvolved velocity amplitude spectrum ratio shown in right panels. (Right panels) Deconvolved velocity amplitude spectrum ratio (red, blue, and green lines) and the synthetic spectrum ratio with the optimum parameters (gray line)
We then deconvolve the velocity spectra of the P- or S-waves of the TEQ with that of the EGF earthquake at each station to obtain the spectral ratio of the source which cancels out propagation effects, path and site effects.
The deconvolved velocity amplitude of P- or S-waves \( \left|{\dot{u}}_r(f)\right| \) is approximately described as (Boatwright 1978),
where R r and M 0r are the ratios of the target and EGF earthquakes on the radiation pattern coefficient and the seismic moment, respectively. The subscripts T and E for the corner frequency f C indicate the target and EGF earthquakes. Taking the logarithm of Eq. 1 provides a linear relationship:
We search for the optimum values of f CT , f CE , and R r M 0r , which minimizes the square of the error between the observed spectral ratios from the three moving windows and the calculated one using a grid search (Fig. 2c). In the grid search, we usually use a spectral ratio above 3 Hz, but for some cases a spectral ratio of 1–3 Hz is also used. The smallest corner frequency obtained in this study is 3.8 Hz. Examples of the analysis are shown in Fig. 2.
It is, however, usually difficult to obtain a reliable value of f CE , because the sampling frequency of the waveform records analyzed in this study is not high enough, 100-Hz sampling at most stations, which is inadequate to estimate the corner frequency of smaller earthquakes. Therefore, we estimate only the static stress drop of TEQ based on f CT in this study.
The seismic moment, M 0 (Nm), is calculated with an empirical scaling relationship (Hanks and Kanamori 1979), log10 M 0 = 1.5M L + 9.1, assuming that the local magnitude, M L , is equivalent to the moment magnitude.
We estimate the static stress drop from the corner frequency using the formulae ∆σ = 7/16M 0(f C /0.32V S)3 and ∆σ = 7/16M 0(f C /0.21V S)3 (Madariaga 1976) for the P- and S-waves, respectively, where V S (=3.2 km/s) is the shear wave velocity. These formulae assume that the rupture speed is equal to 0.9Vs and are considered to be appropriate for estimating the static stress drop of small earthquakes (Yamada et al. 2010).
For each TEQ, the static stress drop is estimated from individual waveforms at each station. We average linearly the value of the static stress drop estimated at each station over all the stations considered and obtain the static stress drop for each TEQ. If the number of the stations used for the averaging is less than 3, the resulting estimation of the static stress drop is rejected. We obtained, accordingly, the static stress drop of six TEQs. The estimated static stress drop, together with hypocenter information, of the analyzed earthquakes is summarized in Table 1.
Results
The estimated static stress drops of the six TEQs ranged from 2.5 to 14.0 MPa for P-wave analyses, from 5.2 to 32.2 MPa for S-wave analyses, and from 5.0 to 19.0 MPa for both P- and S-wave analyses (hereafter, referred to as the average case). For both P- and S-wave analyses, all the estimations of static stress drops are averaged across all stations available. These values approximately coincide with the estimated static stress drops of aftershocks of other inland earthquakes in Japan (Ito 2005; Iio et al. 2006), although the estimation procedures used differ from those used in this study. Figure 3 shows a relationship between the local magnitude of the analyzed earthquake and the estimated static stress drop of the average case. Oth (2013) reported a positive dependency of static stress drop on seismic moment for several crustal thrust earthquakes in central Honshu, including the 2007 Noto Hanto earthquake. Our result seems to be consistent with the positive dependency. However, the magnitude range of this study is quite narrow and the number of the data is small, leading easily to an apparent dependence. In fact, if we focus on the static stress drop of a narrow seismic moment range reported previously (e.g., Ide et al. 2003; Imanishi and Ellsworth 2006, Allmann and Shearer 2009), we could find either a positive or a negative dependency of static stress drop on seismic moment. Thus, we consider that the static stress drops estimated in this study do not show any obvious evidence of the dependency of static stress drop on the seismic moment (Fig. 3). The value of the stress drops estimated from P-waves approximately coincides with those from S-waves, although a slight difference is discerned between them (Fig. 4 and Table 1).
Relationship between local magnitude and static stress drop of TEQ analyzed in this study. A dashed line represents a scaling relationship between seismic moment and static stress drop proposed by Nadeau and Johnson (1998)
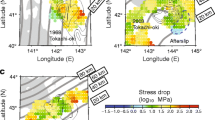
Distribution of the static stress drop of similar aftershocks estimated for P-waves (left panel), S-waves (center panel), both P- and S-waves (right panel), and coseismic slip. The circles show the source locations of similar aftershocks analyzed in this study, and those colors represent the values of the static stress drop. The contours in the background show the coseismic slip distribution of the 2007 Noto Hanto earthquake reported by Horikawa (2008). The interval of the contour lines is 0.5 m
Discussion
The spatial distribution of the six TEQs and the values of the corresponding static stress drops are shown in Fig. 4, together with the coseismic slip distribution of the 2007 Noto Hanto earthquake reported by Horikawa (2008). We can recognize that similar aftershocks with a high static stress drop tend to be distributed over a large slip area, and vice versa, for the estimations for P-waves (Fig. 4a), S-waves (Fig. 4b), and for the average case (Fig. 4c). Following the definition of Horikawa (2008), we define here a large slip area as being an area with a slip ≥1 m and a small slip area as an area with a slip <1 m. For the 2007 Noto Hanto earthquake, as mentioned in the “Introduction” subsection, several slip models have reported a common feature of slip distribution: that is, a large coseismic slip area exists on the fault plane in the shallower part from the hypocenter based on different kinds of data (Fukushima et al. 2008; Ozawa et al. 2008; Asano and Iwata 2007). The absolute values of slip are slightly different between these models, but the pattern of the slip distribution is similar: in other words, the relationship between the slip and the static stress drop approximately holds in spite of the absolute value of the slip, implying that the choice of the slip model does not affect the following discussion.
Figure 5 shows the relationship between the coseismic slip and the average static stress drop of similar aftershocks. For the average case, the average value of the static stress drop in the large slip area is 14.0 ± 1.9 (MPa) and that outside the large slip area is 5.6 ± 0.4 (MPa). The error described here is the standard error of the average value of the static stress drop over all the estimations for both P- and S-wave in each area.
Relationship between the static stress drop of similar aftershocks and the coseismic slip. The static stress drop of similar aftershocks for the average case is plotted on the coseismic displacement of the 2007 Noto Hanto earthquake (Horikawa 2008). The error bar shows the standard error of the average of the static stress drop of each event
We next compare the static stress drops of the aftershocks with that of the mainshock (Fig. 6). For the 2007 Noto Hanto earthquake, the distributions of the slip and the static stress drop of the mainshock are coherent (Horikawa 2008). A large coseismic slip area is characterized by a high coseismic static stress drop, and vice versa. The analyzed events are distributed over both the high, and the low, or negative, coseismic static stress drop areas. Figure 6 shows that similar aftershocks with a high static stress drop tend to occur in the high static stress drop area of the mainshock. This coincides with the results of the Kīholo Bay earthquake (Mw 6.7) reported by Yamada et al. (2010).
Distribution of the static stress drop of similar aftershocks (circles) and that of the mainshock (contours). The static stress drop of similar aftershocks (circles) is plotted over the distribution of the static stress drop of the mainshock (at intervals of 2 MPa) as reported by Horikawa (2008). The gray area shows a negative static stress drop. A star shows the location of the hypocenter of the 2007 Noto Hanto earthquake
Assuming that the similar aftershocks analyzed here are the ruptures of small patches that had little slip during the mainshock, we consider that the stress level of these patches increases in proportion to the surrounding slip, or static stress drop, of the mainshock. The high static stress drop of the aftershocks in the large slip area is likely to imply a spatially large difference between the strength and the dynamic stress level, as suggested by previous studies (e.g., Yamada et al. 2010).
From the perspective of repeating earthquakes, several empirical scaling relationships have been proposed. For example, Nadeau and Johnson (1998) reported a scaling relationship between the slip, d, and the seismic moment, M 0, as d ∝ M 0 1/6. They also proposed an additional scaling of Δσ ∝ M 0 −1/4 between the static stress drop, Δσ, and the seismic moment for repeating earthquakes on a plate interface. However, a comparison between the slip of similar aftershocks of inland earthquakes and the aseismic slip from geodetic observations supports a general scaling of d ∝ M 0 1/3 (Hiramatsu et al. 2011; Hayashi and Hiramatsu 2013). The estimated static stress drop in this study does not support the scaling of Δσ ∝ M 0 −1/4 (Fig. 3). A disagreement with a scaling of Δσ ∝ M 0 −1/4 is also observed for microearthquakes recorded at the SAFOD Pilot Hole at Parkfield (Imanishi and Ellsworth 2006) and repeating acoustic emission events from laboratory experiments (Yoshimitsu et al. 2014).
This disagreement is possibly interpreted by a difference of seismic coupling between small asperities and the surrounding aseismic slip if a constant stress drop applies to repeating earthquakes on the plate interface (Hayashi and Hiramatsu 2013). A 100 % seismic coupling with a constant static stress drop provides d ∝ M 0 1/3 or T r ∝ M 0 1/3, where T r is a recurrence time for repeating earthquakes. The break of this widely accepted scaling for natural earthquakes implies the break of a 100 % seismic coupling or the break of the constant static stress drop, Δσ ∝ M 0 −1/4, as proposed by Nadeau and Johnson (1998). As mentioned above, our data and several lines of previous studies do not support the break of the constant static stress drop. If the seismic coupling is below 100 %, it is not necessary that the scaling of d ∝ M 0 1/3 or T r ∝ M 0 1/3 holds, providing possibly d ∝ M 0 1/6 as proposed by Nadeau and Johnson (1998). If this is the case, repeating earthquakes with a constant static stress drop can possibly occur.
Conclusions
A relationship between the coseismic slip of the mainshock and the static stress drop of similar aftershocks has been examined for the 2007 Noto Hanto earthquake, a large inland earthquake, in central Japan. We have applied the empirical Green’s function method for P- and S-waves to estimate the static stress drop of similar aftershocks. The static stress drops estimated for P-waves coincide with those for S-waves, and those from both waves show a typical value for a tectonic earthquake of 5 to 20 MPa. Similar aftershocks in the large coseismic slip area show a higher static stress drop than those in the small coseismic slip area. The similar aftershock is considered to be the rupture of a small patch with little slip during the mainshock, and its stress level is determined by the coseismic slip or static stress drop. This relationship between the static stress drop and the coseismic slip is possibly interpreted by the spatial distribution of the difference between the strength and the dynamic stress level, if the final stress level is equal to the dynamic stress level.
References
Allmann BP, Shearer PM (2007) Spatial and temporal stress drop variation in small earthquakes near Parkfield, California. J Geophys Res 112, B04305. doi:10.1029/2006JB004395
Allmann BP, Shearer PM (2009) Global variations of stress drop for moderate to large earthquakes. J Geophys Res 114, B01310. doi:10.1029/2008JB005821
Asano K, Iwata T (2007) Source rupture process of the 2007 Noto Hanto earthquake, Japan, obtained from strong ground motion and GPS data. EOS Trans Am Geophys Union 88:S51B–0512
Boatwright J (1978) Detailed spectral analysis of two small New York State earthquakes. Bull Seismol Soc Am 68:1131–1177
Fukushima Y, Ozawa T, Hashimoto M (2008) Fault model of the 2007 Noto Hanto earthquake estimated from PALSAR radar interferometry and GPS data. Earth Planets Space 60:90–104
Hanks TC, Kanamori H (1979) A moment magnitude scale. J Geophys Res 84:2348–2350
Hardebeck JL, Aron A (2009) Earthquake stress drops and inferred fault strength on the Hayward fault, east San Francisco bay, California. Bull Seismol Soc Am 99:1801–1814
Hayashi M, Hiramatsu Y (2013) Spatial distribution of similar aftershocks of a large inland earthquake, the 2000 Western Tottori earthquake, in Japan. Earth Planets Space 65:1587–1592
Hiramatsu Y, Yamanaka H, Tadokoro K, Nishigami K, Ohmi S (2002) Scaling law between corner frequency and seismic moment of microearthquakes: is the breakdown of the cube law a nature of earthquakes? Geophys Res Lett. doi:10.1029/2001GL013849
Hiramatsu Y, Moriya K, Kamiya T, Kato M, Nishimura T (2008) Fault model of the 2007 Noto Hanto earthquake estimated from coseismic deformation obtained by the distribution of littoral organisms and GPS: implication for neotectonics in the northwestern Noto Peninsula. Earth Planets Space 60:903–913
Hiramatsu Y, Hayashi M, Hayashi A, the Group for the Joint Aftershock Observations of the 2007 Noto Hanto Earthquake (2011) Relation between similar aftershocks and ruptured asperity of a large inland earthquake: example of the 2007 Noto Hanto earthquake. Earth Planets Space 63:145–149
Horikawa H (2008) Characterization of the 2007 Noto Hanto, Japan, earthquake. Earth Planets Space 60:1017–1022
Ide S, Beroza GC, Prejean SG, Ellsworth WL (2003) Apparent break in earthquake scaling due to path and site effects on deep borehole recordings. J Geophys Res 108(B5):2271. doi:10.1029/2001JB001617
Iio Y, Katao H, Ueno T, Enescu B, Hirano N, Okada T, Uchida N, Matsumoto S, Matsushima T, Uehira K, Shimizu H (2006) Spatial distribution of static stress drops for aftershocks of the 2005 west off Fukuoka prefecture earthquake. Earth Planets Space 58:1611–1615
Imanishi K, Ellsworth WL (2006) Source scaling relationships of microearthquakes at Parkfield, CA, determined using the SAFOD pilot hole seismic array. In: Abercrombie RE et al (eds) Earthquakes: radiated energy and the physics of earthquake faulting, vol 170, Geophysical monograph series. AGU, Washington D.C, pp 81–90
Ito Y (2005) Mechanisms of aftershock generation. Report of the National Research Institute for Earth Science and Disaster Prevention 68:27–89, in Japanese with English abstract
Madariaga R (1976) Dynamics of an expanding circular fault. Bull Seismol Soc Am 66:639–666
Nadeau RM, Johnson LR (1998) Seismological studies at Parkfield VI: moment release rates and estimates of source parameters for small repeating earthquakes. Bull Seismol Soc Am 88:790–814
Oth A (2013) On the characteristics of earthquake stress release variations in Japan. Earth Planet Sci Lett 377–378:132–141. doi:10.1016/j.epsl.2013.06.037
Ozawa S, Yarai H, Tobita M, Une H, Nishimura T (2008) Crustal deformation associated with the Noto Hanto earthquake in 2007 in Japan. Earth Planets Space 60:95–98
Sakai S, Kato A, Kurashimo E, Iidaka T, Igarashi T, Hirata N, Iwasaki T, Kanazawa T, Watanabe S, Haneda S, Kobayashi M, Miura K, Miura R, Tagami K, Ogino I, Saka M, Watanabe A, Miyakawa K, Katsumata K, Takahashi H, Kasahara M, Honda R, Maeda T, Ichiyanagi M, Yamaguchi T, Kosuga M, Okada T, Nakajima J, Hori S, Nakayama T et al (2007) Aftershock observation for the 2007 Noto Hanto earthquake. Bull Earthq Res Inst Univ Tokyo 82:225–233 (in Japanese with English abstract)
Sakai S, Kato A, Iidaka T, Iwasaki T, Kurashimo E, Igarashi T, Hirata N, Kanazawa T, the Group for the Joint Aftershock Observation of the 2007 Noto Hanto Earthquake (2008) Highly resolved distribution of aftershocks of the 2007 Noto Hanto earthquake by a dense seismic observation. Earth Planets Space 60:83–88
Uchide T, Shearer PM, Imanishi K (2014) Stress drop variations among small earthquakes before the 2011 Tohoku-oki, Japan, earthquake and implications for the main shock. J Geophys Res 119:7164–7147. doi:10.1002/2014JB010943
Wessel P, Smith WHF (1998) New, improved version of generic mapping tools released. Eos Trans AGU 79:579
Yamada T, Okubo PG, Wolfe CJ (2010) Kīholo Bay, Hawai‘i, earthquake sequence of 2006: relationship of the main shock slip with locations and source parameters of aftershocks. J Geophys Res 115, B08304. doi:10.1029/2009JB006657
Yoshimitsu N, Kawakata H, Takahashi N (2014) Magnitude-7 level earthquakes: a new lower limit of self-similarity in seismic scaling relationships. Geophys Res Lett. doi:10.1002/2014GL060306
Acknowledgements
We thank the Earthquake Research Institute, The University of Tokyo, Disaster Prevention Research Institute, Kyoto University, the Japan Meteorological Agency, and the National Research Institute for Earth Science and Disaster Prevention for providing the seismic waveform data collected at each online station. We are grateful to Haruo Horikawa for providing the results. All the figures were produced using the GMT software (Wessel and Smith 1998). The authors are grateful for two anonymous reviewers and the editor Azusa Nishizawa for their comments and suggestions that improved the manuscript.
Author information
Authors and Affiliations
Consortia
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
US conducted the analyses. YH and TY participated in the design of this study and drafted the manuscript. GJAO participated in the design of this study and in the acquisition of the data. All the authors have read and approved the final manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Urano, S., Hiramatsu, Y., Yamada, T. et al. Relationship between coseismic slip and static stress drop of similar aftershocks of the 2007 Noto Hanto earthquake. Earth Planet Sp 67, 101 (2015). https://doi.org/10.1186/s40623-015-0277-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-015-0277-0