Abstract
In the context of the 12th release of the international geomagnetic reference field (IGRF), we present the methodology we followed to design a candidate secular variation model for years 2015–2020. An initial geomagnetic field model centered around 2014.3 is first constructed, based on Swarm magnetic measurements, for both the main field and its instantaneous secular variation. This initial model is next fed to an inverse geodynamo modelling framework in order to specify, for epoch 2014.3, the initial condition for the integration of a three-dimensional numerical dynamo model. The initialization phase combines the information contained in the initial model with that coming from the numerical dynamo model, in the form of three-dimensional multivariate statistics built from a numerical dynamo run unconstrained by data.
We study the performance of this novel approach over two recent 5-year long intervals, 2005–2010 and 2009–2014. For a forecast horizon of 5 years, shorter than the large-scale secular acceleration time scale (∼10 years), we find that it is safer to neglect the flow acceleration and to assume that the flow determined by the initialization is steady. This steady flow is used to advance the three-dimensional induction equation forward in time, with the benefit of estimating the effects of magnetic diffusion. The result of this deterministic integration between 2015.0 and 2020.0 yields our candidate average secular variation model for that time frame, which is thus centered on 2017.5.
Similar content being viewed by others
Background
The international geomagnetic reference field (IGRF) is a series of standard mathematical models produced by the International Association of Geomagnetism and Aeronomy (IAGA). Every 5 years, the new generation of IGRF comprises in particular a forecast of the evolution of the main geomagnetic field for the 5 years to come, in the form of a secular variation model (Hulot et al. 2015, and references therein). That secular variation component is used to compute the value of any geomagnetic element during the 5-year period of operation of the IGRF model. The computation rests on a linear interpolation of the field model from the start of the 5-year period to the time of interest. The latest version of the IGRF, hereafter referred to as the 12th generation of IGRF (IGRF-12), was released in December 2014 (Thébault et al. 2015a). Eight international teams proposed candidate secular variation models. The role of the task force appointed by IAGA was then to assess the quality of the candidate models and to propose a composite model based on those candidates (consult Thébault et al. 2015b, in this issue to see how the evaluation has been carried out for IGRF-12).
Forecasting the evolution of the main geomagnetic field is no trivial matter, since its time evolution is controlled by the complex interaction of fluid flow and magnetic field within Earth’s fluid core (e.g., Roberts and King 2013). The so-called geodynamo is a deterministic system with chaotic dynamics and consequently with a limited horizon of predictability. Estimates of this horizon are in the multidecadal range (Hulot et al. 2010; Lhuillier et al. 2011) that is several times the 5-year IGRF time scale. In addition, the geometric attenuation of the core field, going from the surface of the core to the surface of the Earth, favors its large scales over the smaller ones, effectively filtering out fast small-scale features that may potentially be detrimental to the quality of the forecast. Finally, the typical time scale for the acceleration of these large scales is on the order of 10 years (see e.g., Christensen et al. 2012), meaning that the geomagnetic evolution at 5 years is generally well approximated by a linear trend. These three points combined (multi-decadal horizon of predictability, small scales filtered out, 10-year geomagnetic acceleration time scale) explain why a linear extrapolation is rather successful over the lifetime of an IGRF release, even though unexpected sudden changes in the secular variation, in the form of geomagnetic jerks (Mandea et al. 2010), can at times substantially deteriorate the quality of the prediction.
The models of secular variation submitted to the previous generation of IGRF (Finlay et al. 2010b) were for the most part derived from time-dependent models of the main field itself. In this case, the submitted candidate secular variation was then the instantaneous secular variation at the terminal epoch of the era over which such field models were defined. Those models expressed the time dependency of the internal geomagnetic field either by means of a Taylor expansion or by resorting to splines. An exception was the candidate secular variation model proposed by Kuang et al. (Kuang et al. 2010) in which the time dependency was controlled by an underlying numerical model of the geodynamo. The arsenal of techniques designed in order to combine data with a prognostic numerical model goes by the generic name of data assimilation. Data assimilation, at the heart of numerical weather prediction (e.g., Talagrand et al. 1997), has raised growing interest in the context of terrestrial magnetism over the last decade (Fournier et al. 2010; Hulot et al. 2015).
In their study, Kuang and colleagues assimilated Gauss coefficients from a suite of nested geomagnetic field models spanning the past few millennia. Inspection of their initial results led them to modify their assimilation scheme and to incorporate a predictor-corrector algorithm to apply upon the forecast, the goal of which was to reduce the secular component of the forecast error that came from the numerical model itself (consult Kuang et al. 2010, for details).
We follow here the same philosophy of injecting physical laws, in the form of a numerical model of the geodynamo (to be described below), in order to estimate the average secular variation for the 5 years to come (2015–2020). Instead of relying on geomagnetic field models as “observations” to feed to a sequential assimilation scheme, we use here data from the Swarm constellation (Friis-Christensen et al. 2006) to construct a snapshot model of the field and its secular variation at epoch 2014.3, which we will refer to as the initial model throughout this study. This initial model is used, together with the multivariate statistics characterizing the variability of, and correlations within, the numerical dynamo model (Aubert and Fournier 2011; Fournier et al. 2011), to estimate an initial condition for the subsequent integration of that numerical dynamo model.
This is an instantaneous approach, in the sense that observations of the core field and its secular variation are fed to the numerical model at a single epoch. This strategy is motivated by two factors. First, we wish to resort to Swarm data alone, which cover a limited time span (recall that the Swarm mission was launched on 22nd November 2013). Second, we observe that, even though our sequential data assimilation technology has improved steadily over the past few years (Aubert and Fournier 2011; Fournier et al. 2013), we have not yet arrived to a point where, on interannual to decadal time scales, a sequence of observations assimilated in the past can result in an estimation of the start state for the forecast that is markedly better than that obtained with observations at a single epoch. In their current form, our sequential tools are more suited to analyze the behavior of the geomagnetic field over historical to archaeological time scales, essentially because the uncertainties affecting the corresponding measurements are rather large, which makes the assimilation of a sequence of measurements in time valuable. Dealing with a single epoch offers the possibility to assimilate the secular variation in addition to the field itself, which allows to place tighter constraints on the flow within the core, especially if the secular variation is known to high accuracy, which is the case for recent times. A snapshot initialization (Aubert 2013, 2014) followed by an integration is thus the option we retained for the IGRF. In the following, we describe our plan of action in Section “Methods.” The application of the methodology to design a candidate secular variation model for IGRF-12 is presented in Section “Results and discussion”. A summary and conclusion follow in Section “Conclusions.”
Methods
We describe in the following first how we construct the initial model for epoch 2014.3 from Swarm data and next how this initial model is used in conjunction with a numerical dynamo model to design a candidate secular variation model for IGRF-12.
Construction of the initial model for 2014.3
Data selection and weighting
We consider the Swarm satellite data (Olsen et al. 2013) for satellites A (Alpha), B (Bravo), and C (Charlie) from 26th November 2013 to 12th September 2014. We use systematically the latest version of the data and select in priority the reprocessed data (SW_RPRO_MAGx) then consider the data version 0302 running from November 2013 to 5th July 2014 then the data version 0301 up to 12th September 2014. We also select the data according to the quality flags that are defined in the Level-1b product definition document (National Space Institute, T.U.o.D. 2013) for the scalar measurements (Flags_F), for the vector measurements (Flags_B), the platform (Flags_Platform), and the satellite altitude (Flags_q). Flags_F are selected so that the Absolute Scalar Magnetometer (ASM) is in scalar or vector mode. We reject systematically data with the code 255. Acceptable vector data are those stamped with Flags_B =0 corresponding to the nominal mode of the Vector Field Magnetometer (VFM). We then keep only the data corresponding to a Flag_Platform ≤1, excluding in principle the data measured during the satellite maneuver. Lastly for Flag_q, we insist that at least two of the three satellite star cameras are in operating mode.
In addition, the Swarm scalar and vector Level-1b data are sub-sampled every 10 s, which corresponds to an along-track spacing of about 75 km. We separate the scalar and vector data into mid-latitudes (magnetic latitudes between −52° and 52°) and high latitudes (magnetic latitudes larger than 52° in absolute value). Vector data at polar latitudes are not considered. All scalar and vector data at mid-latitudes are taken in the 23:00–6:00 local time window, in order to minimize the contributions from the ionospheric S q field and to minimize the contamination by plasma bubbles (Park et al. 2013). In contrast, the scalar data in the polar regions are selected for all local times, under the condition that the Sun was at least 10° below the horizon.
Further selection criteria are applied, based on the D st index. The D st index, which measures the activity of the magnetic field generated by the ring current, is requested not to exceed 5 nT in absolute value. In addition, the maximum variation of the D st index during the previous 3 h is requested not to exceed 5 nT in absolute value at both mid- and high latitudes. Also, all scalar and vector data correspond to a planetary Kp index ≤2°. Data selection criteria are summarized in Table 1.
We compute the magnetic field vector and scalar values at the epoch and location of the selected Swarm measurements predicted by the model of Thébault et al. (Thébault et al. 2010). These predictions are then subtracted from the measurements in order to identify strong outliers in the Swarm dataset. The presence of outliers is explained by the fact that quality flags are currently provisional and will be updated later (European Space Agency 2015). When a series of consecutive data contains outliers, the entire day is removed from the analysis. The days identified as containing consistently large outliers are the following ones: 25th and 26th March, 8th April 2014, 11th and 12th September 2014.
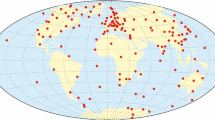
All in all, the number of pointwise data N d used is close to 1,400,000; the statistics of the dataset are summarized in Table 2. In addition, we show the spatial coverage of the ASM (scalar) data from one satellite (Alpha) in Fig. 1.
We attribute some a priori weights to the data. Data are primarily weighted according to their geographic colatitude, θ. We, however, add an extra prior information about the data quality. Let dF denote the difference between the geomagnetic intensity measured by the ASM and the one computed from the 3-component measurement provided by the VFM. We assume that the scalar measurement is correct and assign a weight to each vector measurement in proportion to the absolute value of dF, expressed in nT. For each VFM datum i, this extra weight is defined as
whereas it is 0 for a scalar (F) measurement. We next define the N d ×N d diagonal weight matrix W,
The entries of W imply that scalar data located at the geographical equator are given a weight of 1, whereas scalar data located near the poles have a weight close to 0.5. Similar weights are applied to vector data in perfect agreement with scalar data (those which have dF=0), while vector data with dF≠0 are down-weighted according to formula (1) above.
Parameterization of the initial model
These data are used to construct a global field model for the geomagnetic field B and its time rate-of-change at Earth’s surface as follows: the field is decomposed into its internal and external parts, B i and B e , respectively. We work in spherical coordinates (r,θ,φ) with unit vectors (e r ,e θ ,e φ ). We assume that the internal field B i derives from a potential V i according to
The potential V i is in turn described using spherical harmonics
in which a is the mean radius of the Earth (a=6371.2 km), \({g_{n}^{m}}\) and \({h_{n}^{m}}\) are the Gauss coefficients of degree n and order m, and \(\mathcal {P}_{n}^{m}\) denotes the associated Legendre function of degree n and order m, whose normalization is subject to the Schmidt convention. In the following, g will represent the vector of Gauss coefficients,
in which T denotes the transpose. The static internal part is described up to spherical harmonic N=30, which allows us to take into account the long-wavelength component of the crustal field. The time-varying contribution to B i is modelled up to spherical harmonic degree n=13, using a linear Taylor expansion
in which the dot stands for the time derivative and the central epoch t c is set to 2014.3, roughly the median epoch of the dataset, and keeping in mind that this Taylor expansion is restricted to the first 13 spherical harmonic degrees (\(\dot {{g_{n}^{m}}}=\dot {{h_{n}^{m}}}=0\ \forall n > 13\)). In the following, \(\dot {\mathbf {g}}\) will precisely refer to the vector of non-zero coefficients of the secular variation, and the vector y will denote the vector of Gauss coefficients of the field and the secular variation,
In addition, we co-estimate the static external field B e upto n=2 in the solar magnetic reference frame and assume a time-dependent component of degree n=1 parameterized by the D st index split into its external and internal contributions (Maus and Weidelt 2004; Olsen et al. 2006); consult http://www.ngdc.noaa.gov/stp/geomag/est_ist.html for the provisional indices.
Construction of the initial model; uncertainties
The inverse problem at hand is nonlinear, due to the nonlinear dependency of intensity data to the vector of Gauss coefficients y. We linearize it around an initial guess y 0, which we take to be the candidate proposed by Thébault et al. (Thébault et al. 2010) for the 11th generation of the IGRF (Finlay et al. 2010b). The model vector y for the central epoch t c is estimated by means of an iterative least squares algorithm which aims at minimizing exclusively the misfit to the data, given the a priori weight matrix W. Iterations are governed by
where A i is the design matrix (based on the calculation of the Fréchet derivative around the ith estimate) and d is the data vector of size N d . Three iterations suffice to achieve convergence. They are followed by two extra iterations to update W by an iteratively reweighted least-absolute deviation algorithm to further account for remaining outliers (e.g., Olsen et al. 2000).
The field lines of the axisymmetric part of the field so obtained (the initial model introduced above) are shown in Fig. 2a. Let y o and W o denote the final coefficient vector and weight matrix so obtained. The statistics of the solution are listed in Table 2. Residuals show a bias on the φ-component of the magnetic field. This bias is due to a few measurements clearly identified retrospectively as outliers but that were not removed from the dataset at the time of production of the candidate model. The reweighted scheme aims precisely at downweighting these data and at obtaining a model which is not biased by them. Throughout the inversion, we do not introduce any regularization (either spatial or temporal) in the form of a norm added to the objective function. This rather reckless strategy (the dataset alone can certainly not constrain the field and its secular variation up to degree 13, see the mild slope of the blue spectrum at Earth’s surface in Fig. 4) is motivated by our will to rest on the statistics supplied by the numerical dynamo model (to be detailed below) to constrain those components of the field not controlled by the data. Error covariances on y o are formally controlled by the matrix (e.g., Tarantola and Valette 1982)
Core-field estimate. a The field lines of the axisymmetric component of the initial field model at epoch 2014.3. They are represented down to the core-mantle boundary, under the usual assumption that the mantle is an electrical insulator. The estimate of the magnetic structure in- and outside the core, obtained by Kalman filtering, is shown to the right. b The color map represents the axisymmetric toroidal (azimuthal) field, which is trapped in the core (scale ±2 mT). c The field lines are those of the axisymmetric poloidal field
in which σ o is the root-mean-square misfit to the data (σ o=5.11 nT, see Table 2) and where the design matrix is evaluated around y o (the final set of coefficients). In the following, we will split \(\mathbf {C}_{\mathbf {y}^{o}}\) into \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\), its 195×195 upper left block which corresponds to the coefficients describing the first 13 harmonic degrees of the main field (total number of coefficients N y =195), and \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\), its 195×195 lower right block, which corresponds to the secular variation counterpart of \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\). For subsequent convenience, let us define
and
Both these vectors have a size of N y .
An additional crustal covariance matrix
The main and crustal magnetic fields are not separable for the lowest degrees (n≤13) of the geomagnetic spectrum of interest here. In order to take into account the additional uncertainties on y o due to the crustal field, we assume that, at these scales, the undesired crustal component is mostly induced by the axial dipole field. Building on the approach put forward by Thébault and Vervelidou (Thébault and Vervelidou 2015) to compute the associated crustal error covariance matrix C c , we give ourselves the possibility, in the following, to add C c to \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\) while estimating the magnetic field at the surface (and in the interior) of Earth’s core. For details on the procedure used to compute C c , we refer the reader to the study of Thébault and Vervelidou (Thébault and Vervelidou 2015).
Initialization of the geodynamo state for 2014.3
We now explain how the initial model for epoch 2014.3 can be used to define an initial condition for the integration of a numerical model of the geodynamo starting at this epoch. The overall procedure, termed inverse geodynamo modelling by Aubert (Aubert 2013), is described in detail in its latest implementation by Aubert (2014). We use this latest implementation in this work. In summary, it is a multi-step approach which combines the information coming from the observations, here in the form of y o complemented with its error covariance matrices \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\) and \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) (the former possibly augmented with C c ), with the prior information contained in a numerical model of the geodynamo. The prior information is described by three-dimensional multivariate statistics connecting the variables defining the state of the dynamo, in our case a velocity field u dyn, a magnetic field B dyn, and a buoyancy field C dyn. The numerical model of the geodynamo we resort to is the coupled Earth dynamo model (Aubert et al. 2013). The coupled Earth dynamo can reproduce two of the most salient features of the historical secular variation down-projected at the core-mantle boundary (e.g., Jackson and Finlay 2015), namely its hemispherical dichotomy (the strongest variations occurring in the so-called Atlantic hemisphere) and the westward drift of low-latitude features at a speed of about 15 km/year. In the coupled Earth model, we ascribe these two properties to a bottom-up control of the geomagnetic secular variation by the inner core (consult Aubert et al. 2013, for details).
From a technical standpoint, u dyn and B dyn are both decomposed into their poloidal and toroidal components. The resulting four fields and C dyn are described using a spherical harmonic expansion in the horizontal direction, with truncation at degree and order 133. The radial dependency is treated using second-order finite differences, over a non-uniform grid comprising 160 depth levels in the fluid outer core, and 24 depth levels in the solid inner core. All in all, the number of independent state variables which define the three-dimensional state of the dynamo is close to 107. The dynamo is strongly driven, reaching a level of super-criticality which allows the magnetic Reynolds number to have a value of about 1000, within a factor of 2 of its estimate for Earth. This is a reason for assuming that this model describes fairly well the kinematics of the large-scale secular variation, which is governed by the induction equation. Not all model parameters have a proper Earth-like value, though, in particular the diffusive ones, which hinders the capabilities of the model to account for short-term processes (see below).
The three-dimensional multivariate statistics used in the following are constructed from a collection of 746 quasi-equidistant snapshots of the coupled Earth dynamo taken during a free-run (a numerical integration unconstrained by data) spanning approximately 67,000 years. Numerical integration is performed using a semi-implicit scheme and the adaptive numerical time step required for stability ranges in the free-run between 3 and 11 days. Let C p denote the covariance matrix built from this integration.
Estimate of B dyn
The statistics of the coupled Earth dynamo are first used to estimate the three-dimensional magnetic structure in the core, \(\widehat {\textbf {B}}_{\text {dyn}}\), from the observation of the large-scale poloidal field at the core surface, described by \(\mathbf {y}^{o}_{\text {mf}}\). This is achieved by means of a standard Kalman filter (e.g., Fournier et al. 2010, Section 2, and references therein).
The correlations between the poloidal field at the core surface and the poloidal and toroidal fields inside the core are statistically significant in the coupled Earth dynamo, which explains why a coherent picture of \(\widehat {\textbf {B}}_{\text {dyn}}\) is produced by the Kalman filter (see Fig. 2b, c for an illustration). Note that in the current version of the inverse geodynamo modelling framework, \(\widehat {\textbf {B}}_{\text {dyn}}\) is described up to spherical harmonic degree 30. Further details on Step 1, in particular concerning the correlations mentioned above, are provided in the Appendix.
The knowledge of \(\widehat {\textbf {B}}_{\text {dyn}}\) makes it possible to compute the three-dimensional magnetic diffusion inside the core
in which μ 0 and σ are the magnetic permeability of vacuum and the electrical conductivity of the core, respectively.
Core-surface flow
We now operate at the core surface (radius c=3485 km). We rely on the observation of the secular variation \(\dot {{\mathbf B}}^{o}\) at r=c (described by the set of coefficients \(\mathbf {y}^{o}_{\text {sv}}\)) to estimate the velocity field u s at that radius. This is done by solving a diffusion-free core flow problem,
where ∇ h is the horizontal divergence operator and \(\widehat {B}_{r} \equiv \textbf {e}_{r} \cdot \widehat {\textbf {B}}_{\text {dyn}}\) (consult Holme 2015, for a recent review on the core-flow problem). Note that one crucial advantage of specifying a stress-free condition at the outer boundary of the coupled Earth dynamo is to solve Step 2 exactly at this boundary, thus alleviating the deleterious effects of the Ekman layer induced by a no-slip boundary condition (Aubert 2014). The error budget allocated to solve this problem is divided into two components: errors on the observations are prescribed by \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) (see above), while uncertainties on the flow coefficients are again defined by the second-order statistical moments of the unconstrained free run of the coupled Earth dynamo. As stressed by Aubert (Aubert 2014), expliciting \(\widehat {\textbf {D}}_{\text {dyn}}\) and expanding \(\widehat {\textbf {B}}_{\text {dyn}}\) to spherical harmonic degree 30 allows one to incorporate directly the effects of diffusion and generation of large-scale (observed) secular variation by the interaction of the small-scale (concealed by the crust) B with the large-scale u s (Eymin and Hulot 2005) into the analysis, with no need for an iterative scheme. For illustration, the map of our preferred u s (in a sense to be defined below) is shown in Fig. 3a.
Core-flow estimate. a Core-flow estimate at Earth’s core surface for epoch 2014.3. The gray scale map is that of the toroidal velocity scalar, which measures the amount of local rotation. b The cylindrical radial component of our preferred estimate of the flow inside Earth’s core at the same epoch. Isosurfaces corresponding to +12 km/year and −12 km/year in red and blue, respectively. We are facing the Greenwich meridian (materialized by the black segment in the equatorial plane). The arrow points through the North Pole. These flow estimates are obtained using an inflation factor β=95.7 and are truncated at spherical harmonic degree and order 30 (see text for details)
Estimate of u dyn and C dyn
The third and final step of the analysis consists of estimating the flow and buoyancy fields inside the core, \(\widehat {\textbf {u}}_{\text {dyn}}\) and \(\widehat {C}_{\text {dyn}}\), from u s . This is again achieved by a Kalman filter which downward propagates the information contained in u s by exploiting the long-range correlations present in C p , due in particular to the importance of the Coriolis force in the force balance (Aubert and Fournier 2011).
The Appendix contains additional information on the correlations which enable the propagation of information from the surface of the core downwards in this step. The cylindrical-radial component of our preferred \(\widehat {\textbf {u}}_{\text {dyn}}\) is shown for illustration in Fig. 3b. As anticipated for a rapidly rotating system, the flow shows convincing signs of invariance along the direction of rotation, in the form of columns parallel to the rotation axis. The columns are partially disrupted since thermal and chemical convection in the coupled Earth dynamo is strongly driven. Further inspection of the flow shows that it is mantle bound underneath Indonesia and inner core bound underneath America. This reflects the prior information contained in C p : the boundary conditions applied to the coupled Earth dynamo favor a faster inner core growth (hence a stronger buoyancy release) underneath Indonesia.
The triplet \((\widehat {\textbf {B}}_{\text {dyn}},\widehat {\textbf {u}}_{\text {dyn}},\widehat {C}_{\text {dyn}})\) specifies uniquely an initial condition at epoch 2014.3 for a subsequent integration of the coupled Earth dynamo. Note that this triplet is estimated up to degree 30, whereas the numerical truncation of the numerical model is 133, as recalled above (Aubert et al. 2013). The non-estimated spectral band (30 < n ≤ 133) of the initial condition is simply set to zero and gets populated over the course of the numerical integration by virtue of the nonlinearities of the system. This integration is carried out with a fixed time step of size 2.5 days. The average secular variation (ASV) for the 2015.0-2020.0 time window is given by
The Gauss coefficients representation of the ASV (truncated at harmonic degree 8) can then potentially define a candidate secular variation for IGRF-12.
Results and discussion
The methodology presented in the previous section leaves in principle no room for tuning parameters, save for the scheme through which non-dimensional numerical dynamo quantities are cast into the dimensional world (for this last point, we use robust physical laws presumed to hold both in the numerical models and the Earth’s core, see e.g., Aubert et al. 2013; Fournier et al. 2011). The prior information supplied by C p is determined once-and-for-all; likewise, \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\) and \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) are posterior statistics of the inverse problem solved to estimate \(\mathbf {y}^{o}_{\text {mf}}\) and \(\mathbf {y}^{o}_{\text {sv}}\).
We found, however, that two issues needed be addressed, connected with the unrealistically small uncertainties contained in \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) on the one hand, and in the statistical (as opposed to dynamical) nature of \(\left (\widehat {\textbf {B}}_{\text {dyn}},\widehat {\textbf {u}}_{\text {dyn}},\widehat {C}_{\text {dyn}}\right)\) which can be detrimental to a short-term forecast, on the other hand.
Inflation of C\(_{\mathbf {y}^{o}}^{\text {sv}}\)
The formal uncertainties contained in \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) are unrealistically small, with a root-mean-squared (rms) value of order 0.05 nT/year for the large-scale coefficients. In particular, unmodelled external field variations can cause correlated errors not accounted for in Eq. 9.
In order to achieve statistical compatibility between the observations and the coupled Earth dynamo (i.e., some overlap between the two sources of information), we find it necessary to uniformly inflate \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {sv}}\) by a factor β.
Let \(\widehat {\mathbf {y}}_{\text {sv}}\) denote our estimate of the vector of the Gauss coefficients of the secular variation, of size N y . We define the normalized misfit for the secular variation \(\mathcal {J}_{\text {sv}}\) as
and test different β for the initialization. The corresponding values of \(\mathcal {J}_{\text {sv}}\) are listed in Table 3. Our preferred β is the one (95.7) which yields a \(\mathcal {J}_{\text {sv}}\) close to unity (0.99), in the case where C c is added to \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\) in Step 1. This choice of β leads to uncertainties on the large-scale coefficients of the secular variation of the order of 0.3−0.5 nT/year, with the largest values attained for zonal coefficients. Larger values of β lead to smaller values of \(\mathcal {J}_{\text {sv}}\), at the expense of too much weight given to the prior. This can be seen on the spectra in Fig. 4. If the value of β is too small, the misfit remains large, and too much confidence is placed upon the unregularized initial secular variation (whose spectrum is not steep enough above degree 5). If β is too large, the prior takes over starting from degree 3, which is too large scale. Our preferred value offers a compromise between these two extreme options: the effect of the prior starts to be strongly felt at degree 6 and above. In our view, it seems reasonable to think that the Swarm dataset we selected and the initial model it served to build can give a reliable estimate of the secular variation up to degree 5 at epoch 2014.3.
Mauesberger–Lowes spectra of the secular variation at the Earth’s surface in 2014.3. The scale on the y axis is logarithmic. Solid blue line: the spectrum of the initial (non-regularized) model constructed from the Swarm data. Solid black, magenta and cyan lines: the spectra of the estimated secular variation, assuming values of the inflation factor β equal to 3.8, 95.7 and 2393.5, respectively. The dotted lines are the spectra of the difference between the initial model and the estimated secular variation (same color code). The light gray area is the one corresponding to harmonic degree n≤8, the IGRF truncation
The inflation factor β can be interpreted as a trade-off parameter that allows one to achieve a realistic fit to the data while also matching the coupled Earth dynamo statistics to an acceptable level. If the data errors were truly much smaller, of the level defined by Eq. 9, our candidate dynamo model would have to be dismissed, on the account of not being compatible with the observations. We find this scenario unlikely but cannot reject it on quantitative grounds. In order to reach a conclusion on this issue, a detailed analysis of the impact of unmodeled external field variations on the uncertainties affecting \(\mathbf {y}^{o}_{\text {sv}}\) should be undertaken in the near future; this is beyond the scope of the present study, which has to comply with the overall IGRF timing.
The steady flow assumption
Validation tests performed using geomagnetic field models spanning the last decade taught us that over a 5-year time window, a calculation using the full dynamics of the coupled Earth dynamo does not produce a better forecast than a linear extrapolation of the field. This is connected with the statistical, rather than dynamical, consistency of \((\widehat {\textbf {B}}_{\text {dyn}},\widehat {\textbf {u}}_{\text {dyn}},\widehat {C}_{\text {dyn}})\). A dynamical imbalance leads to a mispecification of the initial flow acceleration, \(\dot {{\mathbf u}}\). Since the secular acceleration \(\ddot {{\mathbf B}}\) is governed by
one readily sees that errors in the initial \(\dot {\mathbf {u}}\) will impact the first term on the right-hand side and degrade the accuracy of the secular acceleration, at least early on in the calculation. In the case of forecasts over periods larger than 5 years (for instance 30 years), we found (working over the last decades) that a dynamical calculation based on the coupled Earth dynamo model can outperform a linear extrapolation. However, over 5 years, this never occurs. This observation is connected with the one made by Christensen et al. (2012), who demonstrated that in numerical dynamo simulations, the \(\boldsymbol {\nabla } \times \left (\dot {\mathbf {u}} \times \mathbf {B} \right)\) term is responsible for the low-degree (n≤10) secular acceleration. Errors in this term can therefore have a large impact at the surface of the Earth. A conservative option for a 5-year forecast is to get rid of \(\dot {{\mathbf u}}\) and to assume that the flow is steady. Benefits from considering the fully dynamical situation are to be expected for forecasts horizons longer than the large-scale secular acceleration time scale, which is ∼10 year according to Christensen et al. (2012), that is twice the IGRF time scale.
In practice, getting rid of \(\dot {{\mathbf u}}\) implies taking a constant \(\widehat {\textbf {u}}_{\text {dyn}}\) to advance the three-dimensional induction equation forward in time, while taking diffusion into account. Table 4 shows the results of tests carried out over the 2005.0-2010.0 and 2009.0-2014.0 time windows, where we compare the quality of forecasts of four different strategies: the nocast (we assume that nothing changes), the linear extrapolation, the steady flow assumption, and the fully dynamical calculation. An update of the CHAOS-4 model (Olsen et al. 2014) including preliminary Swarm data, in particular version CHAOS-4plus_V2, is taken as the reference and also serves to define the initial condition for the integration of the coupled Earth dynamo in 2005.0 and 2009.0, following the methodology described at length above. This update is also used to specify the secular variation up to spherical harmonic degree 13 for the linear extrapolation at the start of each forecast (epochs 2005.0 or 2009.0). Inspection of the results listed in Table 4 prompted us to follow the conservative path and to resort to the steady flow assumption to propose our candidate. Note also that the differences between the linear prediction and the steady flow prediction are rather small, of order a few nT rms after 5 years.
Candidate model; uncertainties
Our candidate model has the following properties: an inflation factor β=95.7, the addition of the crustal covariance matrix C c during Step 1, and a forecast based on the steady flow assumption. Its coefficients are listed in Table 5, and the corresponding radial secular variations at the surface of the core and the surface of the Earth are shown in Fig. 5a and Fig. 5b, respectively.
In order to evaluate roughly the uncertainties that can be attached to this candidate, we consider other options: different values of β, the non-addition of C c , and fully dynamical calculations. We next take all the values found to define the uncertainty ranges, see the corresponding columns in Table 5. A quick inspection of the numbers shows that some large-scale coefficients do not appear on a strong footing, most notably \(\dot {g}_{4}^{1}\). This shows in particular in Fig. 6, where the Mauesberger–Lowes spectrum of the difference between each candidate model and the median candidate is plotted at the Earth’s surface. (For a thorough approach to evaluating the various candidates, the reader is referred to the systematic study by Thébault et al. (2015b) in this issue.) Our candidate appears on average within the envelope so defined, except precisely for degree 4. Our interpretation is that this comes from too strong an imprint of the prior (degree 4 is probably too damped).
Spectra of the difference between each candidate secular variation model and the median model, based on the eight candidates submitted to IGRF-12 (Thébault et al. 2015a, b, this issue). Magenta: the candidate presented in this study. Gray: the seven others
Conclusions
We have proposed a candidate secular variation model for the 12th release of the IGRF, whose design is new and rests on the injection of physical laws in the chain of production, in the form of multivariate statistics constructed from a free-run of the coupled Earth dynamo model. This chain is based entirely on in-house software. This candidate has been retained as a contributor to the secular variation component of IGRF-12. Its detailed assessment can be found in the study by Thébault et al. (2015b): suffice it to state here that the model is in conformity with the bulk of candidates, even though it is, to our knowledge, one of the two models which effectively evaluate the average secular variation by means of Eq. 14.
In 2020, the next generation of IGRF will allow us to examine how accurate our prediction has been, compared with the others. ‘Forecast-in-the-past’ experiments carried out over the last decades have already taught us that the 5-year IGRF lifetime is arguably too short a time scale for our approach to be highly beneficial: in part because the secular acceleration, whose low-degree component is controlled by the flow acceleration, has a time scale of 10 years (Christensen et al. 2012); in part because our technology can be improved.
This improvement can be sought on the numerical models themselves, who should ideally describe fast (interannual) core processes at work in the geomagnetic secular variation (e.g., Finlay et al. 2010a). This is not a trivial task. More within our reach are improvements on the inversion chain itself. First, its computational burden makes its actual truncation restricted to harmonic degree 30. Even though this is sufficient to take into account the unmodelled secular variation arising from the interaction of the small-scale magnetic field with the large-scale flow (Eymin and Hulot 2005), the robustness of the results reported here should nevertheless be established when the increase of compute power makes a higher truncation possible. Second, the sequential chain (Steps 1–3 in section “Initialization of the geodynamo state for 2014.3” above) is not entirely consistent, in the sense that the prior information supplied for Step i should contain the posterior information from Step i−1 (in the form of updated uncertainties on some components of the geodynamo state vector, and their Bayesian treatment). Current and future work includes improving on these aspects, along with testing the potential of the scheme to produce useful forecasts over multi-decadal periods.
Appendix: supplementary methodological information
The goal of this appendix is to provide the reader with supplementary information on the methodology used to combine the information coming from the coupled Earth dynamo model with the one coming from the initial field model. Recall that a comprehensive description of the inverse geodynamo modelling framework is given by Aubert (Aubert 2013, 2014). We will not duplicate this description here and will highlight instead some of the characteristics of the multivariate statistics of the coupled Earth dynamo contained in C p . As stressed in Section “Initialization of the geodynamo state for 2014.3” the combination of information is achieved by means of a Kalman filter
This step is made of several substeps.
Down-projection and renormalization of y\(^{o}_{\text {mf}}\) and C\(_{\mathbf {y}^{o}}^{\text {mf}}\)
In the numerical dynamo model, the toroidal and poloidal components of B dyn are discretized in the spherical shell by a set of complex-valued coefficients, \({B}^{t}_{kn m}\) and \({B}^{p}_{kn m}\), respectively; the k index refers to the radial level, which is comprised between 1 and 184, since the first 24 layers are used to discretize the solid inner core, and the remaining 160 layers are used to discretize the outer core. In addition, n and m are the spherical harmonic degree and order, respectively. Both n≤30 and m≤30 during Step 1, due to computational requirements.
Prior to applying the Kalman filter (whose details will be provided below), the information contained in the initial main field model \(\mathbf {y}^{o}_{\text {mf}}\) is cast in the numerical dynamo language: it is down projected at the core-mantle boundary and renormalized, since the dynamo representation uses a fully normalized spherical harmonic basis, as opposed to \(\mathbf {y}^{o}_{\text {mf}}\), which follows the Schmidt convention. In practice, each ‘observed’ poloidal coefficient \({B}^{po}_{n m}\) at the top of the core is obtained from the \({g_{n}^{m}}\) and \({h_{n}^{m}}\) of \(\mathbf {y}^{o}_{\text {mf}}\) following
in which i2=−1. This conversion can be described by the action of a rectangular, complex-valued, matrix Q such that
Likewise, the error covariance matrix \(\mathbf {C}_{\mathbf {y}^{o}}^{\text {mf}}\) (possibly augmented with C c ) is converted into a core-surface matrix R according to
where the dagger † implies conjugation and transposition.
For the sake of simplicity, let B knm be a vector which encapsulates the \({B}^{t}_{kn m}\) and \({B}^{p}_{kn m}\) coefficients necessary to describe the magnetic state of the core
With the resolution given above, B knm has a size of about 180,000. Only a modest part of B knm is observed, namely that corresponding to the \({B}^{po}_{n m}\), i.e., the top layer (the core surface), up to spherical harmonic degree 13 in our case. The restriction of B knm to its probed components can be formally represented by the action of a rectangular matrix H, of size 104 × 180,000. A predicted set of coefficients \({B}^{pf}_{n m}\) is then given by
In practice, H is rather sparse. It contains 1 entries only for those coefficients which are to be confronted with the \({B}^{po}_{n m}\) and 0 everywhere else. The action of H is therefore not implemented as a blind and naive matrix-vector product. In what follows, we will nevertheless find it useful to keep resorting to this formalism.
Statistics from the coupled Earth dynamo model
Strictly needed for Step 1 is the restriction of those statistics to the magnetic field B dyn, leaving aside the flow and buoyancy fields. We therefore restrict our attention here on the “magnetic” part of C p , hereafter denoted by C p B . As written above, C p is constructed from a integration of the coupled Earth dynamo model unconstrained by data. If N e ‘magnetic’ samples \(\mathbf {B}_{\textit {knm}}^{e}\), e=1,…,N e are extracted from this free run, we define the mean and covariances as follows
keeping in mind that N e =746 in this study (recall Section “Initialization of the geodynamo state for 2014.3”). Note that C p B does not have to be stored as such during the calculation, since (H C p B )† and H C p B H † are the sole matrices needed in practice (see below).
Magnetic Kalman filter
The estimate of the magnetic state is given by the Kalman filter formula
in which the Kalman gain matrix K combines the information emanating from the coupled Earth dynamo model and the initial field model. It writes
The (H C p B )† matrix is of particular importance, since it effectively connects what is observed or probed (the large-scale component of the poloidal field at the core surface) with the toroidal and poloidal fields in the core interior.
Figure 7 aims at illustrating the salient features of this matrix. In order to compute and represent the correlations, we normalize C p B by its diagonal elements (the variances) and represent the matrix of the moduli of the coefficients so obtained. The correlations represented here are between the poloidal field coefficients observed at the surface and the \({B}^{p}_{kn m}\) and \({B}^{t}_{kn m}\), at various depth levels, in Fig. 7a and Fig. 7b, respectively. These correlations are shown up to degree 10 only, in order to ease the visual inspection.
Magnetic correlations of the coupled Earth dynamo model. a The modulus of the variance-normalized magnetic covariance matrix, showing the correlation between the poloidal field coefficients at the core surface (y-axis) and the poloidal field coefficients at various depth levels (x-axis). Correlations are shown up to spherical harmonic degree 10. Coefficients are ordered according to a one-dimensional scheme where all admissible values of the degree n are grouped together for a given value of the order m, leading to iso-m blocks of decreasing size along the diagonal of the matrix. The two blue tracks have (n,m) x =(n,m) y =(1,0) (track 1) and (n,m) x =(3,2), (n,m) y =(2,1) (track 2). b Same as a, for the toroidal field coefficients at various depth levels. Note that correlations are undefined at the core surface, since the toroidal field vanishes there, by virtue of the insulating magnetic boundary condition. The two red tracks have (n,m) x =(3,1), (n,m) y =(2,1) (track 1) and (n,m) x =(4,2), (n,m) y =(5,2) (track 2). c Modulus of correlation along the tracks defined above. ICB and CMB stand for inner-core boundary and core-mantle boundary, respectively
For the poloidal coefficients, we note that the axial dipole coefficient is strongly correlated with its surface value throughout the depth of the core (blue track 1 in Fig. 7a, c). Other coefficients show weaker correlations (see the off-diagonal blue track 2 for instance). We also note that in the upper part of the core, substantial correlations are found along the diagonal, reflecting the effect of magnetic diffusion. All in all, these correlations result in the possibility of estimating the poloidal field inside the core, whose zonal component (dominated by the dipole) is shown in Fig. 2c.
The multivariate statistics contained in C p B also allows one to connect the toroidal field inside the core with the poloidal field at its surface. The relationship between these two is due to the interaction of the field with the flow. Strong correlations can be found as well throughout the core (see the red track 1, which peaks at about 0.6 near mid-depth, in Fig. 7c). Again, these correlations make it possible to produce a coherent estimate of the toroidal field inside the core, whose zonal component is shown in Fig. 2b.
Figure 7 shows in summary that noticeable correlations exist mostly within iso-m blocks, and that they are for the most part restricted to the large scales of the field. For the toroidal field, correlations within the m=1 block dominate; we interpret this as an indication of the imprint of the large-scale eccentric gyre of the coupled Earth dynamo (Aubert et al. 2013), which possesses strong m=0 and m=1 components, on the large-scale induction of the system.
Deep flow and buoyancy fields
The procedure followed to estimate u dyn and C dyn,
is similar to the one we just described for the internal magnetic field. Again, Aubert (2014) gives all the necessary details. We simply provide here the reader with the structure of the correlations which are used to connect the core-surface flow with the deep flow and buoyancy, if the numerical dynamo model is the coupled Earth dynamo model retained for this study. These correlations are shown in Fig. 8, whose logic is exactly the same as Fig. 7: The surface poloidal field is replaced by the surface toroidal flow, whose correlations with the deep toroidal flow and buoyancy are shown in Fig. 8b and Fig. 8a, respectively.
Flow and buoyancy correlations of the coupled Earth dynamo model. a The modulus of the variance-normalized hydrodynamic covariance matrix, showing the correlation between the toroidal flow coefficients at the core surface (y-axis) and the buoyancy field coefficients at various depth levels (x-axis). Correlations are shown up to spherical harmonic degree 10. Coefficients are ordered according to a one-dimensional scheme where all admissible values of the degree n are grouped together for a given value of the order m, leading to iso-m blocks of decreasing size along the diagonal of the matrix. The two blue tracks have (n,m) x =(1,1), (n,m) y =(2,1) (track 1) and (n,m) x =(7,7), (n,m) y =(10,7) (track 2). b Same as a, for the toroidal flow coefficients at various depth levels. Due to boundary conditions, the sole non-zero line at the inner-core boundary is the one corresponding to (n,m) x =(1,0). The two red tracks have (n,m) x =(n,m) y =(1,0) (track 1) and (n,m) x =(6,5), (n,m) y =(10,5) (track 2). c Modulus of correlation along the tracks defined above. ICB and CMB stand for inner-core boundary and core-mantle boundary, respectively
Columnar flow yields correlations concentrated within iso-m blocks in Fig. 8a, b, an imprint of the Coriolis force influence. The imposed, m=1, hemispheric buoyancy release at the inner-core boundary (ICB), at the origin of the eccentric gyre, causes long-range correlations such as the one exhibited by the blue track 1 in Fig. 8c. In addition, nonlinear interaction between the gyre and the flow causes rather strong, off-diagonal (m±1) correlations in Fig. 8b, in the upper part of the core. The red track 1 in Fig. 8c corresponds to a correlation coefficient crossing the zero-line in signed value at about two thirds of the core depth towards the ICB (recall that it is the modulus of the correlation that is represented in this figure), meaning that the large-scale zonal flow in the lowermost part of the core is anti-correlated with its counterpart in the upper part of the core. This is consistent with the dynamical features of the coupled Earth dynamo model: torques acting on the inner core tend to entrain it eastward (as well as the fluid surrounding it), whereas the upper part of the core drifts westward by virtue of angular momentum conservation.
References
Aubert, J (2013) Flow throughout the Earth’s core inverted from geomagnetic observations and numerical dynamo models. Geophys J Int 192(2): 537–556. doi:10.1093/gji/ggs051.
Aubert, J (2014) Earth’s core internal dynamics 1840–2010 imaged by inverse geodynamo modelling. Geophys J Int 197(3): 1321–1334. doi:10.1093/gji/ggu064.
Aubert, J, Fournier A (2011) Inferring internal properties of Earth’s core dynamics and their evolution from surface observations and a numerical geodynamo model. Nonlinear Process Geophys 18(5): 657–674. doi:10.5194/npg-18-657-201.
Aubert, J, Finlay CC, Fournier A (2013) Bottom-up control of geomagnetic secular variation by the Earth’s inner core. Nature 502: 219–223. doi:10.1038/nature12574.
Christensen, U, Wardinski I, Lesur V (2012) Timescales of geomagnetic secular acceleration in satellite field models and geodynamo models. Geophys J Int 190(1): 243–254. doi:10.1111/j.1365-246X.2012.05508.x.
Eymin, C, Hulot G (2005) On core surface flows inferred from satellite magnetic data. Physics of the Earth and Planetary Interiors 152: 200–220. doi:10.1016/j.pepi.2005.06.009.
European Space Agency (2015). https://earth.esa.int/web/guest/swarm/data-access/dataset-history.
Finlay, CC, Dumberry M, Chulliat A, Pais MA (2010a) Short timescale core dynamics: Theory and observations. Space Sci Rev 155(1–4): 177–218. doi:10.1007/s11214-010-9691-.
Finlay, CC, Maus S, Beggan CD, Bondar TN, Chambodut A, Chernova TA, Chulliat A, Golovkov VP, Hamilton B, Hamoudi M, Holme R, Hulot G, Kuang W, Langlais B, Lesur V, Lowes FJ, Lühr H, Macmillan S, Mandea M, McLean S, Manoj C, Menvielle M, Michaelis I, Olsen N, Rauberg J, Rother M, Sabaka TJ, Tangborn A, Tøffner-Clausen L, Thébault E, et al. (2010b) International Geomagnetic Reference Field: The Eleventh Generation. Geophys J Int 183(3): 1216–1230. doi:10.1111/j.1365-246X.2010.04804.x.
Fournier, A, Hulot G, Jault D, Kuang W, Tangborn A, Gillet N, Canet E, Aubert J, Lhuillier F (2010) An introduction to data assimilation and predictability in geomagnetism In: Space Science Reviews, 247–291. doi:10.1007/s11214-010-9669-4.
Fournier, A, Aubert J, Thébault E (2011) Inference on core surface flow from observations and 3-D dynamo modelling. Geophys J Int 186(1): 118–136. doi:10.1111/j.1365-246X.2011.05037.
Fournier, A, Nerger L, Aubert J (2013) An ensemble Kalman filter for the time-dependent analysis of the geomagnetic field. Geochem Geophys Geosyst 14: 4035–4043. doi:10.1002/ggge.20252. doi:10.1002/ggge.20252.
Friis-Christensen, E, Lühr H, Hulot G (2006) Swarm: A constellation to study the Earth’s magnetic field. Earth, Planets, and Space 58: 351–358.
Holme, R (2015) Large-scale flow in the core. In: Olson P Schubert G. (eds)Core Dynamics, 2nd edn. Treatise on Geophysics, 91–111.. Elsevier, Amsterdam. Chap. 4. doi:10.1016/B978-0-444-53802-4.00138-X.
Hulot, G, Lhuillier F, Aubert J (2010) Earth’s dynamo limit of predictability. Geophys Res Lett 37(L06305). doi:10.1029/2009GL041869.
Hulot, G, Olsen N, Sabaka TJ, Fournier A (2015) The present and future geomagnetic field. In: Kono M. Schubert G. (eds)Geomagnetism, 2nd edn. Treatise on Geophysics, 33–78.. Elsevier, Amsterdam. Chap. 2. doi:10.1016/B978-0-444-53802-4.00096-8.
Jackson, A, Finlay CC (2015) Geomagnetic secular variation and its application to the core. In: Kono M. Schubert G. (eds)Geomagnetism, 2nd edn. Treatise on Geophysics, 137–184.. Elsevier, Amsterdam. Chap. 5. doi:10.1016/B978-0-444-53802-4.00099-3.
Kuang, W, Wei Z, Holme R, Tangborn A (2010) Prediction of geomagnetic field with data assimilation: a candidate secular variation model for IGRF-11. Earth Planets Space 62: 775–785. doi:10.5047/eps.2010.07.008.
Lhuillier, F, Aubert J, Hulot G (2011) Earth’s dynamo limit of predictability controlled by magnetic dissipation. Geophys J Int 186: 492–508. doi:10.1111/j.1365-246X.2011.05081.x.
Mandea, M, Holme R, Pais A, Pinheiro K, Jackson A, Verbanac G (2010) Geomagnetic jerks: rapid core field variations and core dynamics. Space Sci Rev 155(1-4): 147–175. doi:10.1007/s11214-010-9663-x.
Maus, S, Weidelt P (2004) Separating the magnetospheric disturbance magnetic field into external and transient internal contributions using a 1D conductivity model of the Earth. Geophys Res Lett 31(12): 12614. doi:10.1029/2004GL020232.
National Space Institute, T.U.o.D. (2013) Swarm level 1b product definition. Technical Report 5.13, European Space Agency. https://earth.esa.int/documents/10174/1514862/Swarm_L1b_Product_Definition.
Olsen, N, Lühr H, Finlay CC, Sabaka TJ, Michaelis I, Rauberg J, Tøffner-Clausen L (2014) The CHAOS-4 geomagnetic field model. Geophys J Int 197(2): 815–827. doi:10.1093/gji/ggu033.
Olsen, N, Holme R, Hulot G, Sabaka T, Neubert T, Tøffner-Clausen L, Primdahl F, Jørgensen J, Léger JM, Barraclough D, Bloxham J, Cain J, Constable C, Golovkov V, Jackson A, Kotze P, Langlais B, Macmillan S, Mandea M, Merayo J, Newitt L, Purucker M, Risbo T, Stampe M, Thomson A, Voorhies C (2000) Ørsted initial field model. Geophys Res Lett 27(22): 3607–3610. doi:10.1029/2000GL011930.
Olsen, N, Lühr H, Sabaka TJ, Mandea M, Rother M, Tø ffner-Clausen L, Choi S (2006) CHAOS - A model of the Earth’s magnetic field derived from CHAMP, Ørsted, and SAC-C magnetic satellite data. Geophys J Int 166(1): 67–75. doi:10.1111/j.1365-246X.2006.02959.x.
Olsen, N, Friis-Christensen E, Floberghagen R, Alken P, Beggan CD, Chulliat A, Doornbos E, da Encarnaçao JT, Hamilton B, Hulot G, et al (2013) The Swarm satellite constellation application and research facility (SCARF) and Swarm data products. Earth, Planets Space 65(11): 1189–1200. doi:10.5047/eps.2013.07.001.
Park, J, Noja M, Stolle C, Luehr H (2013) The ionospheric bubble index deduced from magnetic field and plasma observations onboard Swarm. Earth, Planets Space 65(11): 1333–1344. doi:10.5047/eps.2013.08.005.
Roberts, PH, King EM (2013) On the genesis of the Earth’s magnetism. Reports Prog Phys 76(9): 096801. doi:10.1088/0034-4885/76/9/096801.
Talagrand, O (1997) Assimilation of observations, an introduction. J Meteorol Soc Jpn 75(1B): 191–209.
Tarantola, A, Valette B (1982) Generalized nonlinear inverse problems solved using the least squares criterion. Rev Geophys 20(2): 219–232. doi:10.1029/RG020i002p00219.
Thébault, E, Chulliat A, Maus S, Hulot G, Langlais B, Chambodut A, Menvielle M (2010) IGRF candidate models at times of rapid changes in core field acceleration. Earth Planets Space 62(10): 753–763. doi:10.5047/eps.2010.05.004.
Thébault, E, Finlay CC, Beggan C, Alken P, Aubert J, Barrois O, Bertrand F, Bondar T, Boness A, Brocco L, Canet E, Chambodut A, Chulliat A, Coisson P, Civet F, Du A, Fournier A, Fratter I, Gillet N, Hamilton B, Hamoudi M, Hulot G, Jager T, Kuang W, Lalanne X, Langlais B, Léger JM, Lesur V, Lowes FJ, Macmillan S, et al. (2015a) International geomagnetic reference field: the twelfth generation. Earth, Planets and Space 2015, 67: 79. doi:10.1186/s40623-015-0228-9, Published: 27 May 2015.
Thébault, E, Finlay CC, Alken P, Beggan C, Canet E, Chulliat A, Langlais B, Lesur V, Lowes FJ, Manoj C, Rother M, Schachtschneider R (2015b) Evaluation of candidate geomagnetic field models for IGRF-12. Earth, Planets and Space. in press.
Thébault, E, Vervelidou F (2015) A statistical spatial power spectrum of the Earth’s lithospheric magnetic field. Geophys J Int 201: 605–620. doi:10.1093/gji/ggu463.
Wessel, P, Smith WHF, Scharroo R, Luis J, Wobbe F (2013) Generic mapping tools: Improved version released. Eos, Trans Am Geophys Union 94(45): 409–410. doi:10.1002/2013EO450001.
Acknowledgements
We thank Ingo Wardinski and an anonymous referee for helpful comments which helped improve the manuscript. AF thanks Vincent Lesur and Gauthier Hulot for fruitful discussions on the Swarm mission. This work has been supported by the French “Agence Nationale de la Recherche” under the grant ANR-11-BS56-011 and by CNES. ESA is acknowledged for the provision of the Swarm data and for the principal investigator status granted following the Swarm Science and Validation call and selection. Numerical computations were partly performed on the S-CAPAD platform, IPGP, France (http://webpublix.ipgp.fr/rech/scp), and IDRIS HPC resources, under the allocations 2014-042122 and 2015-042122 made by GENCI. Figures were generated using the LATE X pstricks-add package and the generic mapping tools (Wessel et al. 2013); IPGP contribution number 3621.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
AF coordinated the study and wrote the manuscript. JA performed the inverse geodynamo modelling. ET designed the initial field model. All authors analyzed and discussed the results, commented on the manuscript, and approved its final version.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Fournier, A., Aubert, J. & Thébault, E. A candidate secular variation model for IGRF-12 based on Swarm data and inverse geodynamo modelling. Earth Planet Sp 67, 81 (2015). https://doi.org/10.1186/s40623-015-0245-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-015-0245-8