Correspondence/findings

Introduction

The development of real-time tsunami forecast and rapid tsunami warning systems is an important mission for science technology to mitigate tsunami disasters. The estimations of initial tsunami heights and the propagation effect are essential for tsunami forecasting. In recent years, ocean-bottom observation networks have been installed in deep oceans, and accurate tsunami forecasts have been realized by real-time tsunami data analysis (e.g., Wei et al. 2008; Tang et al. 2009). The real-time data directly estimate the initial tsunami height distribution as the tsunami source. It enables the more reliable prediction of tsunami than from the seismic analysis method where the tsunami source is set from the slip distribution estimated by the seismogram analysis with the assumptions of the subsurface homogeneous/inhomogeneous structure. However, Tsushima et al. (2012) pointed out that the slow tsunami propagation speed fundamentally limits the rapidness of the tsunami source estimation. They reported that it would take more than 20 min to stably estimate the source size even if the ocean-bottom stations are installed very near or inside the source area.

Seismogram analyses can contribute to a rapid tsunami forecast that complement a correct tsunami forecast based on tsunami analysis, because seismic waves propagate much faster (approximately 4,000 m/s) than tsunami (approximately 200 m/s). Gusman and Tanioka (2013) reported that the centroid moment tensor (CMT) solution can be determined by W phase inversion using 5 or 10 min waveform data from the P-wave arrival, and the initial tsunami height distribution from this solution can be used as the tsunami source. They show that the W phase solutions are reliable for use in tsunami modeling. The accuracy of tsunami simulation from a seismically estimated source needs to be understood. Also, it is important to enhance the performance of this method.

Toward these ends, this study focuses on the 2013 Santa Cruz Islands earthquake (Mw 8.0) tsunami propagating in the Coral Sea and Pacific Ocean. By setting an initial tsunami height distribution from simple faulting inferred from the CMT solution of the main shock, we simulate the tsunami propagation from the source to observation points. We investigate how well the simulation from the CMT solution can reproduce observed tsunami waveforms and how tsunami propagation modeling improves the reproduction of the tsunami waveforms.

The 2013 Santa Cruz Islands earthquake and tsunami

Around the Santa Cruz Islands, the Australian plate is subducting beneath the Pacific plate from the San Cristobal and New Hebrides trenches, although the Pacific plate subducted from the Vityaz trench before the Ontong Java plateau collided with the Australian plate about 10 Ma (e.g., Mann and Taira 2004). Such tectonic background produces complicated topographic features and controls tsunami propagation in this region. The Santa Cruz Islands earthquake (Mw 8.0) occurred at such a complicated convergent margin between the Australian and Pacific plates at 01:12 UTC 6 February 2013 (Figure 1). The hypocenter was located at latitude 10.738°S and longitude 165.138°E at a depth of 28.7 km, and the focal mechanism was thrust faulting with ENE-WSW compression (as reported by the U.S. Geological Survey). This event was an interplate earthquake on the subducted Australian plate judging from the focal mechanism. This earthquake excited a significant tsunami that hit the coast of the Solomon Islands and other countries and was observed at the ocean-bottom pressure gauges in the Coral Sea and Pacific Ocean. Lay et al. (2013) reported that the mainshock of this earthquake had two slip patches in the fault, identified by inverting teleseismic broadband P waves and the forward modeling of tsunami. The second slip occurred at a very shallow depth, near the trench, and the slip is larger than that for the slip patch near the hypocenter due to low rigidity. This earthquake, which is not characterized by a simple patch but by two patches of slip, would be a good example for evaluating the performance and the robustness of the tsunami forecast from a CMT solution.

Figure 1
figure 1

Index map of the study area. The red star indicates the epicenter of the 2013 Santa Cruz Islands earthquake (Mw 8.0). The focal mechanism of the mainshock is also shown. The DART stations used in this study are shown as red squares. The contours (every 0.5 m) in the right upper panel indicate initial tsunami height using tsunami simulations. Line A corresponds to Figure 5. AUS and PAC indicate the Australian and Pacific plates, respectively. Topography used is ETOPO2.

Full size image

Tsunami data

The National Oceanic and Atmospheric Administration (NOAA) employs the Deep-ocean Assessment and Reporting of Tsunamis (DART) real-time monitoring system to develop effective tsunami forecasting methods and tools (Titov et al. 2005; Tang et al. 2009). The bottom pressure data are continuously recorded at a sampling interval of at least 15 min. When a significant tsunami signal is expected to reach a gauge, 15-s or 1-min sampling data are provided.

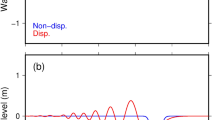
In this study, we analyzed 1-min sampling records of four DART stations located on the Coral Sea and Pacific Ocean floors around the epicenter. The distribution of the four stations is shown in Figure 1. The stations 55012 and 55023 are located on the Coral Sea bottom, and the stations 52406 and 51425 are located on the Pacific Ocean bottom. We show four waveforms calculated by subtracting tidal components from the original data and applying a 2-min low-pass filter (black lines in Figure 2). At the two stations in the Coral Sea (stations 55012 and 55023), the first peaks are not the maximum amplitude. At station 55012, the maximum amplitude appeared in the second phase approximately 15 min after the initial wave arrival. At station 55023, the maximum amplitude was observed in the third phase approximately 30 min after the initial tsunami. Both waveforms observed in the Coral Sea show the wave dispersion, with a shorter period wave following the long period wave. At the closest station 52406, which is located at approximately 600 km north of the source on the Pacific Ocean bottom, the initial tsunami arrived about 1 h after the earthquake origin time. The polarization of the initial wave was down, and the maximum height is approximately 0.05 m. At the furthest station 51425, which is located approximately 2,000 km east of the source, the initial tsunami arrived 2 h and 50 min after the origin time with the maximum height of approximately 0.02 m.

Figure 2
figure 2

Comparison of tsunami waveforms at four DART stations. Black curves indicate observed waveforms; red and blue curves indicate waveforms obtained by dispersive and linear long-wave models, respectively. The root-mean-squared residual between observation and synthetic waveforms in each gray rectangle are also shown. The observed waveforms are calculated by subtracting tidal components, and all waveforms have had a 2-min low-pass filter applied.

Full size image

Numerical simulations

We conducted numerical simulations based on the 2-D linear Boussinesq equation in a spherical coordinate system (e.g., Tanioka 1999). The governing equations used are as follows:

$$ \frac{\partial \eta }{\partial t}=-\frac{1}{R_0 \sin \theta}\frac{\partial M}{\partial \phi }-\frac{1}{R_0 \sin \theta}\frac{\partial }{\partial \theta}\left(N \sin \theta \right), $$
(1)
$$ \begin{array}{c}\hfill \frac{\partial M}{\partial t}+{g}_0h\frac{1}{R_0 \sin \theta}\frac{\partial \eta }{\partial \phi }=\frac{h^2}{3}\frac{\partial }{\partial t}\left\{\frac{1}{R_0 \sin \theta}\frac{\partial }{\partial \phi}\left[\frac{1}{R_0 \sin \theta}\frac{\partial M}{\partial \phi }+\frac{1}{R_0 \sin \theta}\frac{\partial }{\partial \theta}\left(N \sin \theta \right)\right]\right\}\hfill \\ {}\hfill \approx \frac{h^2}{3}\frac{\partial }{\partial t}\left\{\frac{1}{{\left({R}_0 \sin \theta \right)}^2}\frac{\partial^2M}{\partial {\phi}^2}+\frac{1}{{R_0}^2 \sin \theta}\frac{\partial^2N}{\partial \theta \partial \phi}\right\},\hfill \end{array} $$
(2)
$$ \begin{array}{c}\hfill \frac{\partial N}{\partial t}+{g}_0h\frac{1}{R_0}\frac{\partial \eta }{\partial \theta }=\frac{h^2}{3}\frac{\partial }{\partial t}\left\{\frac{1}{R_0}\frac{\partial }{\partial \theta}\left[\frac{1}{R_0 \sin \theta}\frac{\partial M}{\partial \phi }+\frac{1}{R_0 \sin \theta}\frac{\partial }{\partial \theta}\left(N \sin \theta \right)\right]\right\}\hfill \\ {}\hfill \approx \frac{h^2}{3}\frac{\partial }{\partial t}\left\{\frac{1}{R_0}\frac{\partial }{\partial \theta}\left[\frac{1}{R_0 \sin \theta}\frac{\partial M}{\partial \phi }+\frac{1}{R_0}\frac{\partial N}{\partial \theta}\right]\right\},\hfill \end{array} $$
(3)

where φ is the longitude, θ is the colatitude, R 0 is the Earth’s radius, g 0 is the gravity acceleration, η is the water height, h is the sea depth, and M and N are the flow rates in the φ and θ directions, respectively. The right-hand sides of (2) and (3) correspond to dispersive terms. If these terms are equal to zero, these equations represent the linear long-wave equations.

The simulation needs to assume the flow rates and tsunami height at the initial time. The initial flow rates should be zero for all space (Saito 2013). We calculated the initial tsunami height by setting the fault geometry under the assumption of a uniform slip on a single rectangular fault. We selected a fault plane of strike 309°, dip 17°, and rake 61° along subducting plate based on the USGS CMT solution. The length (L), width (W), and slip amount (D) of rectangular fault were inferred from moment magnitude using the scaling law, a relationship of L = 2 W and D/L = 5 × 10−5 (e.g., Scholz et al. 1986). The rigidity is assumed 30 GPa to calculate the seismic moment. We assumed the plane to be 119 km in length and 59 km in width and a uniform slip of 5.9 m corresponding to Mw 8.0. The depth of the center of the fault was assumed to be 15 km. Using these parameters, we calculated sea-bottom displacement using a static dislocation model (e.g., Okada 1985) and then the displacement was converted to the initial tsunami height, considering a spatial low-pass filtering effect due to the sea depth of 4 km (e.g., Kajiura 1963; Saito and Furumura 2009). The calculated initial tsunami height is shown in Figure 1. The bathymetry grid was 2 arcminutes (ETOPO2) and time step was 2 s. We assumed total reflection at the coastline. We numerically solved 5-h tsunami using the 2-D linear Boussinesq equation (Equations 1 to 3) with an implicit scheme (Saito et al. 2010) and also using the conventional linear long-wave equations for comparison.

Result and discussion

Tsunami waveform prediction from the CMT solution

Figure 2 shows a comparison between theoretical and observed waveforms, and Figure 3a shows the snapshots of tsunami propagation calculated by dispersive equations. We adjusted the tsunami origin time so as to make the fitting well in Figure 2 by delaying the tsunami origin time from the earthquake origin time by 90 s. Since the rupture duration was estimated as approximately 90 s (Lay et al. 2013), the delay introduced in Figure 2 can be interpreted as the rise time of the seismic slip. The theoretical dispersive model almost reproduces the observed tsunami features. The initial tsunami arrives about 1 h after the origin time at stations 52406 and 55012 and about 2 h after the origin time at station 55023 (Figures 2, 3a). Furthermore, the initial tsunami arrives about 3 h after the origin time at station 51425 (Figure 2). The polarities (positive or negative amplitude) of initial waves are also in good agreement with observation. For the maximum amplitude, our result is almost the same as observations at stations 55012 and 55023 in the Coral Sea but overestimated at stations 52406 and 51425 in the Pacific Ocean. Stations 52406 and 51425 are located across the island arc area from the source region. Since we do not consider the nonlinear bottom friction effects in our simulations, it may bring the overestimation at these stations. Saito et al. (2014) reported that the simulations including the effects attenuated the tsunami energy significantly and were able to reproduce the 2011 Tohoku-Oki earthquake tsunami records better than the simulations without these effects. The maximum amplitude is overestimated by about 100% at station 51425, but the difference between the observation and the calculation is only 0.03 m. They might mean that noise in the observed signals and numerical error in the model are large compared to the observations at small amplitudes (Tang et al. 2009). Those comparisons suggest that the tsunami prediction from a CMT solution would work suitably in this event even if the earthquake has a complicated source process represented by two patches of slip.

Figure 3
figure 3

Snapshots of tsunami propagation at the elapsed time of 60 and 120 min. (a) Dispersive model and (b) non-dispersive model. Red and blue areas indicate up and down tsunami phases, respectively. Gray stars indicate the epicenter of the main shock. Arrows indicate propagation of distinct dispersive tsunami.

Full size image

The simulation using a well-tuned earthquake source model and nonlinear tsunami propagation simulations would reproduce the tsunami waveform more correctly (Lay et al. 2013). This approach is certainly important for the purpose of precisely investigating the earthquake source process. On the other hand, for the purpose of rapid tsunami warning, the fine-tuning of the slip distribution model would be inappropriate because it would take considerable time to examine the waveforms carefully. Solving the nonlinear tsunami equations also costs computational time. If we consider the linear tsunami equations, however, we can save time by using the database of tsunami Green’s functions. The applicability to a rapid warning for the two-patch event shown above confirms that tsunami prediction using a CMT solution is a powerful candidate for a rapid warning system. Furthermore, in order to avoid a systematic overestimation/underestimation of tsunami height, it would be important to construct an appropriate scaling law to relate the moment magnitude and the tsunami source by analyzing the records of past tsunami events.

Improvement of the predictability by dispersive tsunami simulations

Most studies employ the linear long-wave equations for rapid tsunami prediction (e.g., Tsushima et al. 2012; Tang et al. 2009). The linear dispersive equations (Equations 1 to 3) can synthesize the waveforms as rapidly as the linear long-wave equations by using the Green’s function database. Hence, the linear dispersive equations are more appropriate for the tsunami prediction since they model the propagation more precisely across the deep ocean. Figure 2 illustrates an advantage of the dispersive equations in reproducing the observed waveforms. For this case study, the dispersive modeling reproduces observed waveforms better at stations 55012 and 55023 on the Coral Sea bottom than non-dispersive modeling. By introducing dispersive terms, the amplitude of the initial and second phases at station 55012 is significantly improved. At station 55023, the first phase is almost the same between the dispersive and non-dispersive models, while the second and the later phases have different waveforms showing a clear dispersion effect. The root-mean-squared (RMS) residual also decreases from 0.033 and 0.020 m to 0.030 and 0.008 m at stations 55012 and 55023, respectively. Figure 3a,b compares the snapshots calculated based on the dispersive and non-dispersive equations. The difference between them is clearly recognized in the Coral Sea, particularly the region east of station 55012 at the elapsed time of 60 min and the region between stations 55023 and 55012 at the elapsed time of 120 min (shown by arrows in Figure 3a).

Figure 4 compares the maximum tsunami amplitude distributions for non-dispersive and dispersive simulations. The distribution is quite different between the two models, in particular, the southwestern region from the source. By considering the dispersion effect, the area of the maximum amplitude with 0.4 m or more is decreased by approximately 34% from the non-dispersive model. This means that tsunami height is overestimated for the non-dispersive model in the deep sea. Figure 5 shows a maximum tsunami amplitude distribution through the 2013 epicenter and station 55012. The maximum amplitude by the dispersive model in the southwestern region (negative distance in Figure 5) is smaller than the amplitude by the non-dispersive model, and non-dispersive model overestimates the maximum amplitude in the region where the dispersion effect appears. The dispersion in the Coral Sea is due to the deep sea (sea depth approximately 4 km) in the range of 0 and −500 km in Figure 5.

Figure 4
figure 4

Distribution of the maximum tsunami amplitude. (a) Dispersive model and (b) non-dispersive model. Initial tsunami arrival times are also shown by white curves (every 1 h). The red stars indicate the epicenter of the 2013 event.

Full size image
Figure 5
figure 5

The cross-section of the maximum tsunami amplitude and bathymetry. The maximum tsunami amplitude (upper) and bathymetry (lower) are shown along a great circle (line A in Figure 1) through the 2013 epicenter (zero position) and station 55012. Red and black lines indicate dispersive and linear long-wave results, respectively. The maximum tsunami amplitude at station 55012 shown in Figure 2 is also plotted by a black dot.

Full size image

Conclusions

The present study has shown that the tsunami prediction from a CMT solution would work satisfactorily for the 2013 Santa Cruz Islands earthquake tsunami even though the earthquake source had been modeled as a complicated source in a past study. The tsunami simulations well explain the observed tsunami arrival times, maximum amplitudes, and polarities of initial wave observed at the deep ocean-bottom stations. The dispersive modeling significantly improved waveforms in the Coral Sea compared to conventional non-dispersive modeling, which prevents the overestimation of the maximum amplitude. The dispersive modeling decreases the area of maximum amplitude exceeding 0.4 m by 34% from the area calculated based on the non-dispersive modeling. Good performance for a complicated earthquake source confirms that the rapid tsunami calculation using a CMT solution is a powerful candidate for an early tsunami warning system.