Abstract
We determined the seismic attenuation structure of the Kumano Basin, a forearc basin in the central part of the Nankai subduction zone. Despite its importance for understanding the physical condition of the Earth's interior and seismic wave propagation processes, the attenuation factor Q has been poorly estimated in the crustal layers of the offshore areas of Nankai because severe attenuation occurring in the seafloor sediments prevents the reliable estimation of Q from conventional active source seismic surveys. In the present study, we derive Q values from the diminishing rate of the high-frequency contents of seismic energy during propagation through sub-seafloor layers. The records of vertical seismic profiling acquired at approximately 1,000 m below the seafloor, which have fewer effects from shallow attenuation, enabled us to elucidate depth variation of Q of P waves (Q P), the attenuation factor of P waves, down to approximately 8 km below the seafloor. Assuming that the frequency dependence of Q is small and using a previously obtained P-wave velocity structure model for the basin, we inverted the fall-off rate of the spectral ratios at various shot-receiver distances to obtain Q P in the three sub-bottom layers. The Q P values for the upper two layers with P-wave velocity (V P) < 2.7 km/s are 34 and 57. These values are almost identical to those obtained in the North Atlantic, suggesting the broad consistency of Q P within seafloor sediment. The basement layer (V P approximately 4 km/s) has a much higher Q P value of 349, which is comparable to the value estimated for crustal layers exposed onshore. This Q P value is higher than the value previously assumed in a simulation of strong ground motion associated with megathrust earthquakes along the Nankai margin. We interpret that the high Q P, low seismic attenuation in the basement layer reflects tectonic stability of the inner wedge of the accretionary margin. Our first estimates of Q P in the present study provide a strong basis for future studies of seismic structure and strong ground motion prediction.
Similar content being viewed by others
Correspondence/findings
Introduction
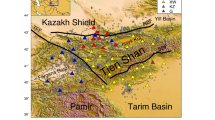
The Kumano Basin is a forearc basin along the Nankai subduction zone (Figure 1a). Beneath the basin, destructive earthquakes occur along the plate boundary (Ando, 1975). The 1944 Tonankai earthquake with a moment magnitude (Mw) of 8.1, which occurred beneath the basin, caused a devastating tsunami. The slip along a well-developed major out-of-sequence fault branching off of the décollement (megasplay fault) is considered to be responsible for the generation of the tsunami (e.g., Fukao et al. Fukao 1979; Park et al. 2002; Cummins and Kaneda 2000; Moore et al. 2007). Sporadic, very low-frequency earthquakes within the accretionary wedge reported by Ito and Obara (2006) indicate that the out-of-sequence fault is also active during the interseismic period of large megathrust events. The characteristics of the megasplay fault are important not only for understanding earthquake and tsunami generation but also for understanding the developmental history of the accretionary complex along the trough (e.g., Moore et al. 2007; Kimura et al. 2007; Strasser et al. 2009). Intensive seismic surveys have been made to characterize the sub-seafloor structure around the fault, such as the three-dimensional (3-D) geometry of the fault, the geometry of other active faults in the outer wedge or of the megathrust (e.g. Moore et al. 2007), and the detailed P-wave velocity (V P) distribution (Nakanishi et al. 2008; Park et al. 2010; Kamei et al. 2012). These detailed seismic structure models have contributed to a better understanding of the evolutionary processes of the accretionary prism and the fluid distribution, which plays an important role in controlling the frictional properties of the seismogenic faults (e.g., Bangs et al. 2009).
Map of the study area and seismic section. (a) The downhole vertical seismic array was deployed at site C0009. The shooting line of the VSP is shown in red. The star and contours denote the epicenter and the coseismic slip distribution of the 1944 Tonankai earthquake (Kikuchi et al. 2003). (b) Seismic profile across site C0009. Lithologic units defined by the Expedition 319 Scientists (2010) are also shown. Orange bar indicates the location of the vertical seismic array.
The seismic quality factor Q is a measure of the degree of attenuation of seismic wave energy and provides us with important physical information about the Earth's interior. Attenuation, which is inversely proportional to Q, is sensitive to factors such as the chemical composition, porosity, and permeability of the rock material, and it can be used to infer the distribution of pore fluid (e.g., Johnston et al. 1979; Toksöz et al. 1979; Winkler et al. 1979, Winkler and Nur 1982). A number of reports have indicated that active fault zones are characterized by high attenuation (low Q values) due mainly to high fracture density and/or the presence of abundant pore water (e.g., Rietbrock 2001; Bennington et al. 2008; Wang et al. 2012).
In megathrust seismogenic zones, which are mostly located in offshore areas, few studies of seismic attenuation structure have been conducted. Christeson et al. (2000) and Zhu et al. (2010) estimated Q of P waves (Q P) of the upper crust of the Costa Rican forearc and attributed the spatial variation of Q P to changes in the lithology or fracture density of the crust. The seismic attenuation structure of the offshore regions of Nankai is poorly known, with the exception of the very shallow portion of seafloor sediments. Matsushima (2005, 2006) studied seismic attenuation structure in methane-hydrate-bearing sediments, located at approximately 200 m depth beneath the seafloor, based on a downhole seismic experiment, but specific Q values were not determined conclusively. A thick cover of seafloor sediments with considerably low velocity and large attenuation (Ayres and Theilen 2001) makes it difficult for Q value determination through active seismic exploration, the most powerful tool for deriving crustal structure in the marine environment, to evaluate seismic attenuation precisely.
In 2009, we conducted a vertical seismic profile (VSP) using a vertical array of seismic sensors in a deep sub-seafloor borehole and a large volume airgun array during International Ocean Drilling Program (IODP) Expedition 319 in the Kumano Basin (Saffer et al. 2009). The seismic sensors were set at 908 to 1,137 mbsf (2,960 to 3,190 m below the sea surface) in the borehole drilled at site C0009 (Figure 1, Expedition 319 Scientists 2010). It is expected that reliable Q values of the sub-seafloor formation can be derived from an analysis of seismic waveform data, which are less affected by the strong attenuation of shallow seafloor sediments than those obtained by conventional ocean bottom or sea surface instruments. In this paper, we estimate the Q P structure of the Kumano Basin based on a spectral analysis of seismic data collected by the VSP and show for the first time the depth variation of seismic attenuation beneath the Nankai forearc.
Data and method for estimating Q P
The VSP experiment consisted of two sub-experiments with different objectives. One was a circular shooting VSP (CVSP) to evaluate seismic anisotropy and stress orientation in the sub-basin formation. The results of this experiment were reported by Tsuji et al. (2011). The other sub-experiment was a walk-away VSP (WVSP), in which a shooting vessel travels in a straight line, traversing the VSP site (Figure 1), to study the variation of seismic waveforms as a function of offset, i.e., shot-receiver distance. The Q P estimation presented here used the data obtained by the WVSP. The same data acquisition system was used in the CVSP and the WVSP, and its detailed description was provided by Tsuji et al. (2011). The location of the WVSP shot line (Figure 1) was set so that it overlapped with the survey line of a previous wide-angle seismic survey that used ocean bottom seismographs (Nakanishi et al. 2008). An airgun array of 128 L total volume was shot at a 60-m interval along the line.
We analyzed waveform data from the shots on the southeastern (trenchward) side of C0009 because the airgun array became unstable during operation along the northwestern part of the WVSP line. Figure 2 shows an example of common receiver gathers obtained by the WVSP. The records obtained by the vertical component sensor deployed at the deepest level of the seismic array, composed of 16 three-component sensors, are displayed with the reduction velocity of 4 km/s. The first arrivals were categorized into three groups, G1, G2, and G3, according to the difference in their apparent velocities. These groups correspond to the direct waves propagating downward through the basin sediment layers (L1 and L2), the diving waves traveling through the lower part of the sediment (L2), and the refracted waves in the high V P basement layer (L3), respectively (Figure 3). Later arrivals were also evident in the offset range from 12 to 18 km (megasplay fault, MSF) and are interpreted as wide-angle reflection arrivals from the megasplay fault plane. The phase interpretations given here are consistent with travel time calculations using the V P model derived from the previous seismic survey (Figure 3; Nakanishi et al. 2008).
Common shot gather obtained by WVSP. A reduction velocity of 4 km/s is used, and no filter is applied. Thin solid black lines mark bins for trace stacking. Trace groups G1, G2, and G3 correspond to down-going direct waves, diving waves through the lower part of the L2 layer, and refracted waves from L3. Clear later arrivals are interpreted as reflection arrivals from the megasplay fault (MSF).
Christeson et al. (2000) and Zhu et al. (2010) succeeded in estimating Q P by modeling the variation of signal amplitude with offset in their wide-angle seismic data. Amplitude variation, however, is dependent not only on attenuation but also on factors such as geometrical spreading and reflection/transmission across velocity discontinuities. Thus, it may be difficult to obtain reliable Q estimates from the amplitude data unless the spatial heterogeneity of the seismic velocity structure is small.
We estimated Q P by applying a spectral ratio method (e.g., Abercrombie 1997) to the vertical component seismograms with no discernible S waves. We modified the original method to process the WVSP data, in which we have to calculate spectral ratios of signals propagated along different ray paths (Additional file 1: Figure S1). A spectrum of a seismogram can be expressed as a convolution of 1) the instrumental response, 2) the source spectrum, 3) the site amplification factor, and 4) a factor associated with wave propagation through the media. We assume that the first three factors can be canceled by taking a ratio of the spectra of seismograms at a common receiving point. We explain the validity of these assumptions in Additional file 2: Supplemental material 1, Additional file 3: Figure S2 and Additional file 4: Figure S3.
Let A(f, x) and A(f, x 0) be the amplitude spectra of the seismic waveforms from shots at the two different offsets x and x 0. Then, the logarithm of the spectral ratio is expressed as follows:
where G(x, f) and G(x 0, f) are factors defined by the geometrical spreading and reflection/transmission coefficients along the ray paths. Under high-frequency approximation, the factors G are regarded as frequency independent. We consider that this approximation can be applied to our dataset because all the boundaries relevant to the present study have been distinctly defined as sharp interfaces by previous high-resolution seismic profiling (Park et al. 2002; Moore et al. 2007; Bangs et al. 2009). Under the assumption, the frequency dependence of the spectral ratio is characterized by a parameter t*, which is related to the seismic velocity v and the attenuation factor Q P along the ray path as follows:
Assuming that the spatial distribution of v is known, Q P can be estimated from t*, which is measured from the observed spectral ratio of the seismic survey.
Since the low signal-to-noise (S/N) ratio of the waveforms causes instability in the calculations of the spectral ratio, we used stacked seismic traces for the analysis. The observed common receiver gathers (Figure 2) were binned according to the offset distances, and the traces in each bin were stacked to yield a seismic trace representative of the corresponding bin. In the common receiver stacking, 10 neighboring traces of the G1 and G2 groups and 30 traces in the G3 and MSF groups (Figure 2) were stacked after the correction for the arrival time differences was made. We had to increase the number of stacked traces for G3 and MSF because the signal levels of these arrivals were much smaller than those of G1 and G2. By applying a time shift before trace stacking, the S/N ratio of the trace is effectively improved by the constructive superposition of the target signals and the destructive superposition of later arrival components with different apparent velocities. The later arrival components may be present in the time window for the spectrum calculation but may have different frequency characteristics from the target signals.
After the common receiver stacking, we formed common shot (bin point) gathers composed of 16 traces and stacked them (common shot stacking) to obtain the traces for the spectral analysis. One of the 16 sensors deployed did not work properly (Tsuji et al. 2011), so we excluded these data from the stacking process. The pre-stack time shifting based on the picked arrival times was also applied in this stacking. The stacked seismic traces are displayed in Figure 4. It is evident that the predominant period of seismic traces increases as the offset increases.
Stacked seismic traces. Traces in G2 are exaggerated by a factor of 10, and the G3 and MSF traces are exaggerated by a factor of 40. Red trace indicates the reference waveform (R) used for the calculation of spectral ratios. Vertical line indicates the picked arrival time of the first arrivals from refracted waves and the reflection arrival times from the reflected arrivals from the megasplay fault.
In the calculation of spectral ratio (1), a reference spectrum A(f, x 0) needs to be defined. It is desirable to choose a waveform with the highest quality as the reference, and we used the stacked trace from the ten records obtained in the offset range from 2.8 to 3.4 km, indicated as R in Figure 2 and the red trace in Figure 4. The reference signal corresponds to the down-going direct wave through shallow sedimentary layers. The length of the time window for the spectrum estimation was 0.512 s (256 data points of 2 msec sampled data) after the arrival times, and the spectra were smoothed by applying the Hanning window. The appropriateness of the used window length is briefly explained in Additional file 2: Supplemental material 2 and Additional file 5: Figure S4.
Figure 5 shows the spectral ratios as the functions of frequency from the stacked waveform records of the WVSP. For the first arrival signals of the G1 and G2 groups, it is evident that high-frequency contents decrease rapidly with the offset distance. However, no systematic variation with the offsets can be observed for the spectral ratios of the G3 and MSF groups. In the frequency ranges in which the spectral ratios are larger than the noise level, defined by the spectral ratio between the noise spectrum and the reference spectrum, the logarithms of spectral ratios exhibit almost constant decay slopes, meaning that the Δt* is relatively constant, independent of frequency. From this observation, we assume that Q P is independent of frequency in the following procedure of Q P estimation.
Spectral ratios of stacked seismic traces in the groups G1, G2, G3, and MSF. Colors indicate different offset values. Thick black curves in the G3 and MSF panels show spectral ratios calculated using the traces after stacking all the traces in the wave group. Lines with two arrowheads indicate the frequency ranges for the estimation of Δt*.
By assuming that Δt* is constant, it can be estimated by fitting the observed spectral ratios to Equation 1 with a linear least squares method within the frequency band where the ratio exceeds the noise level (shown by the two-headed arrows in Figure 5). We did not use the data in the frequency range f > 50 Hz, although signal levels are large enough for the traces in the G1 group. In this frequency range, the spectral ratios tend to have smaller fall-off rates than in the lower frequency band, but fluctuations of the ratios are too large to be examined for frequency dependence of Q.
We further assumed that Q P is constant within each layer of the V P model shown in Figure 3 in the Q P estimation. Under these assumptions, the parameter t* can be expressed as
where i is an index specifying the sub-bottom layers (i = 1, 3 corresponding to L1, L2, and L3, respectively, in Figure 3), Q P,i is the attenuation factor in the ith layer, and
is the travel time required for the corresponding signal observed at x to propagate in the ith layer. T i (x) was calculated by using ray tracing and the two-dimensional V P structure model (Figure 3). Using these relations, Q −1 P,i can be estimated by solving the following observation equations by a least squares method:
In the inversion, we applied a nonnegative least squares method (Lawson and Hanson 1995) because Q −1 P,i cannot take negative values. Note that the first and second integrals (summations) of the observation Equation 5 are evaluated along the ray path from the source at x and along that from the source at x 0, respectively.
Results and discussion
Figure 6 shows Δt* estimated from the observed spectral ratio as a function of offset distance. The estimated Δt* values are plotted at the midpoint of the span of the bins for the trace stacking (indicated by horizontal error bars). Vertical error bars represent estimation errors taking uncertainties in the spectrum estimation and in the least squares fitting into account. The observed Δt* values for the first arrivals in the offset range up to 10 km show clear monotonic increase with offset, as expected from Figures 4 and 5. Since the spectral ratios of the G3 and MSF groups do not show evidence for offset dependence, as explained above, we stacked all the traces within each group to obtain spectral ratios representative of these groups to make Δt* estimation more reliable.
Δt * as a function of offset (shot-receiver distance). Points with vertical and horizontal bars indicate the estimated Δt* from the spectral ratios shown in Figure 5. Horizontal bars indicate the range of offsets of stacked traces used to estimate the corresponding Δt*, and vertical bars indicate the uncertainties in Δt*. Solid circles indicate the Δt* values calculated by the best-fit Q P values shown in Table 1. Colored circles and squares are expected Δt* of the refracted waves from L3 and the reflected waves from the megasplay fault, respectively. Blue, red, and green symbols are for models with Q P = 100, Q P = 349, and Q P = 2,000 in L3, respectively.
The estimated Q P −1 (and Q P) values obtained by solving Equation 5 using the observed Δt* values are shown in Table 1 with their estimation errors. The Δt* values calculated from the Q P −1 structure are compared with the observed values in Figure 3. Although misfits are larger than the error of Δt* estimation for several data points, the misfits may be caused by small-scale spatial variation of Q P, and our model with three layers with constant Q P well explains the general pattern of offset dependence of the Δt*. Whereas the Q P −1 values in the top two layers, L1 and L2, are well constrained from a number of observed Δt* values, showing clear offset dependence, those in L3 are derived from the two observed Δt* values. One is from the stacked trace of the first arrivals from L3 and the other is from the reflection signals from the megathrust fault. In order to verify how well Q P is constrained from the observations, the offset dependence of Δt* was calculated by assuming three different Q P values in L3: 100, 349 (best-fit model), and 2,000 (Figure 6). In the calculation, Q P values in L1 and L2 were set to those of the best-fit solution.
The Δt* of the refracted waves from L3 and reflected waves from the megasplay fault (the bottom boundary of L3) show very small variation with offset distance, consistent with the observed behavior of the spectral ratio (Figure 5). On the other hand, the model with relatively low Q P in L3 predicts a substantial increase in Δt* with offset, and the expected value exceeds 0.05. These features clearly contradict the observed nature of the refracted waves from L3. Therefore, it is not probable that the Q P value in L3 is significantly lower than approximately 200, which is the lower limit from the estimation error of Q P −1 by the inversion.
It is notable that the Δt* values of the reflected waves from the megathrust fault are systematically smaller than those of the refracted waves from L3, despite their longer path lengths, when Q P in L3 is larger than the optimum value. This difference in Δt* reflects the difference in path lengths in the shallow sedimentary layers (L1 and L2) between the refracted waves and bottom reflections of L3. The total length of ray segments in the low Q P sedimentary layers is longer for the refracted wave than for the reflected wave due to the difference in the incidental angle of the ray paths in the layers (Figure 1b). In models with high Q P in L3, the amount of Δt* is much more dependent on the path length in the low Q P layers because the increase in Δt* due to the high Q P layer is relatively small.
The upper bound of the Q P in L3 is more difficult to assess than the lower bound. The Δt* of the L3 refraction signals are less sensitive to a change in Q P in L3 than those of the reflections from the megasplay fault, as demonstrated in Figure 6. The observed spectral ratios of the reflection arrivals from the megasplay fault are less stable, and the Δt* value estimated from the stacked trace contains larger uncertainty, mostly due to low S/N ratios of the reflection arrivals. This makes it difficult to exclude the model with Q P in L3 higher than the best-fit solution. The fall-off rate of the spectral ratio may not be substantially smaller than those in the offset range <6 km (Figure 5), and we regard that Q P is likely to be less than 2,000. Further discussion on the reliability of our Q P model is given in Additional file 2: Supplemental material 3, Additional file 6: Figure S5, and Additional file 7: Figure S6.
Here, we briefly discuss the effects of the frequency dependence of Q on the results. The frequency dependence is often expressed as Q(f) = Q 0 f α. Since it is difficult to constrain the constant α from our dataset, we tried to estimate Q 0 of the three layers by assuming α = 0.66, moderate frequency dependence, which is taken from the results of Yoshimoto et al. (1998). The estimated Q 0 values are 2.0, 3.3, and 44 for L1, L2, and L3, respectively. At the frequency f = 20 Hz, the center of the frequency band of the present WVSP data analysis, Q P is 14, 23, and 315, values somewhat smaller than the values assuming frequency-independent Q. However, misfit between the theoretical spectral ratio (1) and the observed ones increases by introducing the frequency dependent Q (accordingly, Δt* is frequency dependent), and we prefer the frequency-independent model (Additional file 8: Figure S7).
Interpretation
The estimated Q P values in the L1 and L2 layers are very close to those estimated by Grad et al. (2012) for seafloor sediments in the North Atlantic Ocean. They obtained Q P of 30 to 50 for the topmost layer with V P approximately 1.7 km/s and 40 to 50 for the underlying layer with V P approximately 2.2 km/s by modeling active seismic experiments using ocean bottom seismographs. From a laboratory experiment, Ayres and Thelen (2001) suggested that the attenuation of seismic waves of near-surface marine sediments is likely to be insensitive to changes in sediment physical properties. The similarity of the Q P values between the Kumano Basin and the North Atlantic, which are located in very different environments, supports their suggestion, and the estimated Q P values could be the universal values of marine sediments around the world.
Judging from the V P value, L3 is a more rigid basement than the top two layers. Nakanishi et al. (2008) interpreted the layer as Neogene-Quaternary accretionary prism. The Q P of the layer estimated in the present study is well within the range of the Q P values estimated for the crustal layers in various onshore regions compiled by Yoshimoto et al. (1998) in the frequency range 10 to 30 Hz. Since the Neogene-Quaternary accretionary prism pinches out near the coast, according to Nakanishi et al. (2008), layer L3 may not be identical to any onshore crustal layers in terms of lithology. Nevertheless, the layer has a Q P value as large as crustal layers exposed onshore. We interpret that the high Q P, low seismic attenuation in the basement layer reflects the tectonic stability of the inner wedge of the accretionary margin (Wang and Hu 2006). No major faults penetrating into the basement, which corresponds to the inner wedge, have been imaged beneath the Kumano Basin, whereas extensive development of out-of-sequence thrusts is observed in the outer wedge on the trenchward side of the megathrust fault (e.g., Park et al. 2002). According to detailed studies of the V P distribution in the region (e.g., Bangs et al. 2009; Park et al. 2010; Kamei et al. 2012), localized low-velocity anomalies related to the concentration of pore fluid were not identified in the basement of the basin, except in the hanging wall side of the megasplay fault.
The Q P values of the basement layer in the Kumano Basin are in contrast to those of the Costa Rica forearc. At this margin, the V P of the basement layer beneath the forearc area is approximately 4 km/s, almost equivalent to that of L3 in the Kumano Basin. Zhu et al. (2010) estimated the Q P of the layer as 50 to 150, a relatively low value. From the modeling of the offset dependence of the amplitudes of their airgun OBS data, they concluded that models with Q P > 200 are inconsistent with their data. They interpreted that extensive fracturing of the layer accounts for the low Q P. The difference in the attenuation structure may reflect a difference in the tectonic processes at the Nankai and Costa Rica subduction zones; the former is an accretionary margin whereas the latter is an erosive margin. This speculation should be reinforced by future studies of the attenuation structure in both subduction zones using various approaches, because the comparison of Q values derived by different methods is not straightforward.
The spatial distribution of Q in the crust has been drawing attention from seismologists, and a number of studies employing local earthquake tomography techniques to obtain the 3-D distribution of Q have been conducted. 3-D Q tomography is an effective tool for inferring the underground distribution of fracture density and the roles of fluids in the crust (e.g., Rietbrock 2001; Reyners et al. 2007; Bennington et al. 2008). Matsumoto et al. (2009) reported that a high Q P region corresponds to a large-slip fault patch where a large inland shallow earthquake occurred (the 2005 West off-Fukuoka earthquake, Mw 7.0), suggesting a correlation between the frictional strength along the fault and the seismic attenuation of the host rocks. A better understanding of the 3-D attenuation structure of the forearc region is required to fully characterize various features related to the formation and development of convergent margins and the generation of megathrust earthquakes. Extensive efforts are being made to build cabled seafloor systems for earthquake monitoring in the Nankai forearc (Kaneda 2012). High-quality seismic waveform data acquired by the system will be collected to illuminate the detailed spatial variation of seismic attenuation in the area. The first observation of the depth variation in Q P presented in the present study provides an important foundation for future studies.
The reliable estimation of Q in the forearc region is also important for the prediction of strong ground motion associated with giant megathrust earthquakes. Furumura et al. (2008) showed that long-period shaking with large amplitude develops during propagation in low-velocity layers. The strong and prolonged shaking of the long-period ground motions that could be generated by future great megathrust earthquakes along the Nankai Trough could cause serious damage to modern large-scale construction in the Tokyo region. Furumura et al. (2008) simulated the propagation process of seismic waveforms generated by an intraplate earthquake that occurred along the Kumano Basin (the 2006 SE Off-Kii Peninsula earthquake, Mw 7.4) assuming a realistic underground structure model that included the low-velocity forearc wedge as well as the subducting Philippine Sea plate slab. In the model, the forearc wedge was assumed to have lower Q P (90) than the value we estimated. Although their model reproduced the main features of the strong motion records of the moderate earthquake, models with observed Q values are required for the well-constrained prediction of ground motion. Small differences in simulated waveforms can result in significant differences in predicted ground motion for extraordinarily large megathrust earthquakes.
Conclusions
The Q P structure in the Kumano Basin, which is a forearc basin along the Nankai Trough located in the rupture area of the 1944 Tonankai earthquake (Mw 8.1), was derived from a long-offset walk-away vertical seismic experiment. The Q P values in the shallow basin sedimentary layers and the basement composed of the young accretionary prism were estimated by a spectral ratio method, utilizing the fall-off rate of high-frequency signals in seismic records. By assuming frequency-independent Q, the estimated Q P values were 34 and 57 for the top and second layers, respectively, (<2 km below seafloor) which are composed of unconsolidated sediment with small V P (<2.7 km/s). These values are almost identical to those derived from a wide-angle marine seismic exploration made in the North Atlantic, suggesting that the Q P values of seafloor sediment are likely to be uniform within broad areas of the ocean basins. The basement layer beneath the basin sediment has a much higher Q P value (349), which is comparable to the value estimated for the crustal layers exposed on land. Our result indicates the deeper part of the Nankai accretional complex is less attenuating than previously supposed. We interpret that the high Q P in the basement layer reflects the tectonic stability of the inner wedge of the accretionary margin. Although we could not resolve the spatial variation of seismic attenuation, which can be correlated to the distribution of fractures and fluid and to tectonic processes including megathrust earthquake generation, the first estimations of Q P by the present VSP provide a basis for future seismological studies, including those pertaining to seismic structure in the seismogenic zone and strong ground motion simulation.
References
Abercrombie RE. Near-surface attenuation and site effects from comparison of surface and deep borehole recordings. B Seismol Soc Am. 1997;87(3):731–44.
Ando M. Source mechanisms and tectonic significance of historical earthquakes along Nankai Trough, Japan. Tectonophysics. 1975;27(2):119–40. doi:10.1016/0040-1951(75)90102-X.
Ayres A, Theilen F. Preliminary laboratory investigations into the attenuation of compressional and shear waves on near-surface marine sediments. Geophys Prospect. 2001;49(1):120–7. doi:0.1046/J.1365-2478.2001.00243.X.
Bangs NLB, Moore GF, Gulick SPS, Pangborn EM, Tobin HJ, Kuramoto S, et al. Broad, weak regions of the Nankai Megathrust and implications for shallow coseismic slip. Earth Planet Sc Lett. 2009;284(1–2):44–9. doi:10.1016/J.Epsl.2009.04.026.
Bennington N, Thurber C, Roecker S. Three-dimensional seismic attenuation structure around the SAFOD site, Parkfield, California. B Seismol Soc Am. 2008;98(6):2934–47. doi:10.1785/0120080175.
Christeson GL, McIntosh KD, Shipley TH. Seismic attenuation in the Costa Rica margin wedge: amplitude modeling of ocean bottom hydrophone data. Earth Planet Sc Lett. 2000;179(2):391–405. doi:10.1016/S0012-821x(00)00118-7.
Cummins PR, Kaneda Y. Possible splay fault slip during the 1946 Nankai earthquake. Geophys Res Lett. 2000;27(17):2725–8. doi:10.1029/1999gl011139.
Expedition 319 Scientists (2010) Site C0009 in NanTroSEIZE Stage 2: NanTroSEIZE Riser/Riserless Observatory, Proc. Intergr. Ocean Drill. Program 319. doi:10.2204/iodp/proc/319.103.2010.
Fukao Y (1979) Tsunami earthquakes and subduction processes near deep-sea trenches. J Geophys Res 84(Nb5):2303–2314, doi:10.1029/Jb084ib05p02303.
Furumura T, Hayakawa T, Nakamura M, Koketsu K, Baba T. Development of long-period ground motions from the Nankai Trough, Japan, earthquakes: Observations and computer simulation of the 1944 Tonankai (Mw 8.1) and the 2004 SE Off-Kii Peninsula (Mw 7.4) earthquakes. Pure Appl Geophys. 2008;165(3–4):585–607. doi:10.1007/S00024-008-0318-8.
Grad M, Mjelde R, Czuba W, Guterch A, Grp IP. Elastic properties of seafloor sediments from the modelling of amplitudes of multiple water waves recorded on the seafloor off Bear Island, North Atlantic. Geophys Prospect. 2012;60(5):855–69. doi:10.1111/J.1365-2478.2011.01022.X.
Ito Y, Obara K (2006) Very low frequency earthquakes within accretionary prisms are very low stress-drop earthquakes. Geophys Res Lett 33 (9). doi:Artn L09302 doi:10.1029/2006gl025883.
Johnston DH, Toksoz MN, Timur A. Attenuation of seismic waves in dry and saturated rocks: II. Mechanisms Geophysics. 1979;44(4):691–711. doi:10.1190/1.1440970.
Kamei R, Pratt RG, Tsuji T. Waveform tomography imaging of a megasplay fault system in the seismogenic Nankai subduction zone. Earth Planet Sc Lett. 2012;317:343–53. doi:10.1016/J.Epsl.2011.10.042.
Kaneda Y (2012) Real-time monitoring on the megathrust seismogenic zones around the Nankai Trough, southwestern Japan — DONET and DONET2 development and data application. Abstract 2012 AGU Fall Meeting OS52A-02
Kikuchi M, Nakamura M, Yoshikawa K. Source rupture processes of the 1944 Tonankai earthquake and the 1945 Mikawa earthquake derived from low-gain seismograms. Earth Planets Space. 2003;55(4):159–72.
Kimura G, Kitamura Y, Hashimoto Y, Yamaguchi A, Shibata T, Ujiie K, et al. Transition of accretionary wedge structures around the up-dip limit of the seismogenic subduction zone. Earth Planet Sc Lett. 2007;255(3–4):471–84. doi:10.1016/J.Epsl.2007.01.005.
Lawson CL, Hanson RL. Solving least squares problems. Philadelphia: SIAM; 1995.
Matsumoto S, Uehira K, Watanabe A, Goto K, Iio Y, Hirata N, et al. High resolution Q-1 estimation based on extension of coda normalization method and its application to P-wave attenuation structure in the aftershock area of the 2005 West Off Fukuoka Prefecture Earthquake (M7.0). Geophys J Int. 2009;179(2):1039–54. doi:10.1111/J.1365-246x.2009.04313.X.
Matsushima J (2005) Attenuation measurements from sonic waveform logs in methane hydrate-bearing sediments at the Nankai Trough exploratory well off Tokai, central Japan. Geophys Res Lett 32 (3). L03306 doi:10.1021/2004gl021786.
Matsushima J (2006) Seismic wave attenuation in methane hydrate-bearing sediments: vertical seismic profiling data from the Nankai Trough exploratory well, offshore Tokai, central Japan. J Geophys Res-Sol Ea 111 (B10). B10101 doi:10.1029/2005jb004031.
Moore GF, Bangs NL, Taira A, Kuramoto S, Pangborn E, Tobin HJ. Three-dimensional splay fault geometry and implications for tsunami generation. Science. 2007;318(5853):1128–31. doi:10.1126/Science.1147195.
Nakanishi A, Kodaira S, Miura S, Ito A, Sato T, Park JO, Kido Y, Kaneda Y (2008) Detailed structural image around splay-fault branching in the Nankai subduction seismogenic zone: results from a high-density ocean bottom seismic survey. J Geophys Res-Sol Ea 113 (B3). B03105 doi:10.1029/2007jb004974.
Park JO, Tsuru T, Kodaira S, Cummins PR, Kaneda Y. Splay fault branching along the Nankai subduction zone. Science. 2002;297(5584):1157–60. doi:10.1126/Science.1074111.
Park JO, Fujie G, Wijerathne L, Hori T, Kodaira S, Fukao Y, et al. A low-velocity zone with weak reflectivity along the Nankai subduction zone. Geology. 2010;38(3):283–U119. doi:10.1130/G30205.1.
Reyners M, Eberhart-Phillips D, Stuart G. The role of fluids in lower-crustal earthquakes near continental rifts. Nature. 2007;446(7139):1075–8. doi:10.1038/Nature05743.
Rietbrock A. P wave attenuation structure in the fault area of the 1995 Kobe earthquake. J Geophys Res-Sol Ea. 2001;106(B3):4141–54. doi:10.1029/2000jb900234.
Saffer, D, McNeil L, Araki E, Byrne T, Eguchi N, Toczko, S, Takahashi, K, the Expedition 319 Scientists (2009) NanTroSEIZE stage 2: NantroSEIZE Riser/Riserless Observatory, Integr. Ocean Drill. Program Prelim. Rep. 319. doi:10.2204/iodp.pr.319.2009.
Strasser M, Moore GF, Kimura G, Kitamura Y, Kopf AJ, Lallemant S, et al. Origin and evolution of a splay fault in the Nankai accretionary wedge. Nat Geosci. 2009;2(9):648–52. doi:10.1038/Ngeo609.
Toksöz MN, Johnston DH, Timur A. Attenuation of seismic waves in dry and saturated rocks: I. Laboratory Measurements. Geophysics. 1979;44(4):681–90.
Tsuji T, Hino R, Sanada Y, Yamamoto K, Park JO, No T, Araki E, Bangs N, von Huene R, Moore G, Kinoshita M (2011) In situ stress state from walkaround VSP anisotropy in the Kumano Basin southeast of the Kii Peninsula, Japan. Geochem Geophy Geosy 12. Q0ad19 doi:10.1029/2011gc003583.
Wang KL, Hu Y (2006) Accretionary prisms in subduction earthquake cycles: the theory of dynamic Coulomb wedge. J Geophys Res-Sol Ea 111 (B6). B06410 doi:10.1029/2005jb004094.
Wang YJ, Lin YY, Lee MC, Ma KF. Fault zone Q values derived from Taiwan Chelungpu Fault borehole seismometers (TCDPBHS). Tectonophysics. 2012;578:76–86. doi:10.1016/J.Tecto.2011.12.027.
Winkler KW, Nur A. Seismic attenuation: effects of pore fluids and frictional sliding. Geophysics. 1982;47(1):1–15. doi:10.1190/1.1441276.
Winkler K, Nur A, Gladwin M. Friction and seismic attenuation in rocks. Nature. 1979;277(5697):528–31. doi:10.1038/277528a0.
Yoshimoto K, Sato H, Iio Y, Ito H, Ohminato T, Ohtake M. Frequency-dependent attenuation of high-frequency P and S waves in the upper crust in western Nagano, Japan. Pure Appl Geophys. 1998;153:489–502.
Zhu J, Kopp H, Papenberg C, Klaeschen D, Flueh ER, Planert L. Margin architecture and seismic attenuation in the central Costa Rican forearc. Mar Geol. 2010;276(1–4):30–41. doi:10.1016/J.Margeo.2010.07.004.
Acknowledgements
We thank the scientists and crew of IODP Expedition 319, especially the cochief scientists, D. Saffer, L. McNeill, and T. Byrne, and the staff scientists, S. Toczko, N. Eguchi, and K. Takahashi. The VSP data for this research were provided by IODP and IFREE/JAMSTEC. The seismic data processing was supported by SR2020 Corp. We are especially grateful to Dr. M. Karrenbach (SR2020) for the data processing. Dr. Ikuko Wada carefully read the manuscript and improved its scientific clarity. The careful reading of the manuscript and constructive comments by Dr. Ashi (editor) and three anonymous reviewers were very valuable. A part of this study was supported by Grant in Aid 24107701 (KANAME).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
RH carried out the spectral analysis of seismograms and the Q estimation and drafted the manuscript. TT interpreted the estimated Q in terms of rock physics. YS and EA contributed to the acquisition of the unique VSP data of the present study by developing a new system allowing long-offset shooting. NB, RvH, and MK participated in the data acquisition and processing. JOP and GM contributed the seismic data processing. The VSP was designed and conducted through detailed discussion among all the authors. All authors read and approved the final manuscript.
Additional files
Additional file 1: Figure S1.
Schematic view of shot-receiver geometry.
Additional file 2:
Supplementary materials 1 to 3. Supplementary material 1. Basis of spectral ratio method. Supplementary material 2. Data treatment. Supplementary material 3. Reliability of the Q P model.
Additional file 3: Figure S2.
Incident angle to the downhole sensor array as a function of offset. Incident angles of the first arrivals are calculated from the vertical slowness. The definition of the incident angle θ is shown in the inset. The rectangle shows the offset range for the amplitude spectra displayed in Additional file 4: Figure S3.
Additional file 4: Figure S3.
Amplitude spectra of WVSP records with different incident angles. Amplitude spectra are calculated from the seismic records obtained at the offset range of 5.8 to 6.4 km, shot by shot. Arrows show the frequency band for the Δt* estimation.
Additional file 5: Figure S4.
Spectral ratios calculated with different time window lengths. Blue: spectral ratios calculated from 128 data points (0.256 s length); red: 256 points (0.512 s); and green: 512 points (1.024 s). Lines with two arrowheads indicate the frequency ranges for the estimation of Δt*.
Additional file 6: Figure S5.
Normalized geometric spreading factors as a function of offset. Geometric spreading factors calculated from the V P model (shown in Figure 3) are represented by a solid circle and those estimated from the observed spectral ratios are shown as crosses with error bars.
Additional file 7: Figure S6.
Normalized amplitude as a function of offset. Crosses are maximum amplitudes within the time windows for the spectrum analysis, and solid circles are the amplitudes expected from the assumed V P model. Red symbols show amplitudes of refracted waves, and blue symbols show the reflection from the MSF.
Additional file 8: Figure S7.
Observed and theoretical spectral ratios. Black curves are the observed spectral ratio (same as those shown in Figure 5). Red and blue curves are the theoretical spectral ratios using the best-fit parameters assuming α = 0 (frequency-independent t*) and α = 0.66 (frequency-dependent t*), respectively.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hino, R., Tsuji, T., Bangs, N.L. et al. Q P structure of the accretionary wedge in the Kumano Basin, Nankai Trough, Japan, revealed by long-offset walk-away VSP. Earth Planet Sp 67, 7 (2015). https://doi.org/10.1186/s40623-014-0175-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40623-014-0175-x