Abstract
Triple Helix arrangements of bi- and trilateral relations can be considered as adaptive ecosystems. During the last decade, we have further developed a Triple Helix indicator of synergy as reduction of uncertainty in niches that can be shaped among three or more sets of relations. Reduction of uncertainty can be generated in correlations among distributions of relations, but this (next-order) effect can be considered as a feedback counterbalancing the uncertainty generated in the localized relations. We first explain the indicator and then review possible results when this indicator is applied to (i) co-author networks of academic, industrial, and governmental authors and (ii) synergies in the distributions of firms over geographical addresses, technological classes, and industrial-size classes for a number of nations. Co-variation is then considered as a measure of relationship. The balance between globalizing and localizing dynamics can be quantified. Too much synergy locally can also be considered as lock-in. Tendencies are different for the globalizing knowledge dynamics versus locally retaining wealth from knowledge in industrial innovations.
Similar content being viewed by others
1Multilingual abstracts
Please see Additional file 1 for translation of the abstract into the five official working languages of the United Nations and Portuguese.
2Background
Whereas a political economy is based on two organizing principles - the economy and politics - a knowledge-based economy is more complex to the extent that technological developments can be expected continuously to upset the equilibrium of the market. The third dynamic of organized novelty production has to be endogenized into a model of technological innovations (Nelson and Winter 1982; Storper 1997). Schumpeter (1939/1964, at p. 62) first defined innovation in relation to the two dynamics of factor substitutions along the production function and shifts of the production function towards the origin. Two dynamics can mutually shape each other and thus form a trajectory; a trajectory can lead to a competitive edge (Leydesdorff and Van den Besselaar 1998). Three dynamics, however, shape an adaptive ecosystem because the additional - third - degree of freedom allows for both globalization and localization (Ivanova and Leydesdorff, 2014a). A regime at the global level and potentially synergetic niches in local optima can then be expected (Dolfsma and Leydesdorff 2009). The system dynamics is adaptive to relations that are added or deleted because the resulting ‘ecosystem’ of communications remains in transition between local and global incentives (Etzkowitz and Leydesdorff 1998).
Under what conditions can a Triple Helix (TH) of university-industry-government (UIG) relations be considered as an ecosystem with synergy? Etzkowitz and Leydesdorff (1995, 2000) considered the synergy in a Triple Helix system as the result of an overlay of exchanges among perspectives on the bi- and trilateral relations. This overlay is constructed in terms of relations but can be expected to add another (hyper-cyclic) dynamic of shared meanings to the events (Leydesdorff 1994, pp. 186f.). Thus, one obtains a double-layered system: at the bottom, a network of exchange relations and a next layer in which these relations are appreciated from different perspectives. Next-order sharing of perspectives - that is, translations among codes of communication - can feedback on or feed-forward to the relations in the network.
As against a double helix, symmetry can be broken in a three- (or more-) dimensional system and the dynamics can therefore be positive or negative (Figure 1; Ivanova and Leydesdorff, 2014a and [b]). The virtuous and vicious circles among three (or more) dynamics contain the options of both globalization and localization at each moment of time. Thus, one is challenged for a balanced response that takes forward and backward loops in consideration.
In terms of the Triple Helix, localizations are needed, for example, in order to retain wealth in the (local) economy from global knowledge; but globalization of the perspectives is also needed in order to make a knowledge-based economy. In empirical cases, one can expect a trade-off between local organization (variation) versus global self-organization (‘beyond control’) in the selection environments of the relevant markets and sciences. In general, the three functional (sub-) dynamics in a Triple Helix can be specified at the system level as interactions among (i) scientific novelty production, (ii) economic wealth generation, and (iii) political control (Leydesdorff and Zawdie 2010). Carayannis and Campbell (2009 and 2010) proposed further extensions of the TH to a Quadruple or Quintuple Helix (cf. Bunders et al. 1999; Leydesdorff 2012).
This complex adaptive system is differentiated horizontally in terms of the three (or more) functional codes of the communication (economic, scientific, political) and vertically in terms of observable relations versus latent functions. The observable exchange relations in the network can be made the subject of network analysis. The relations, however, are differently distributed in terms of the structural components - universities, industries, and governments - and accordingly, what the relations mean can be different from each of these three perspectives.
The specification of how the codes operate as selection environments upon one another requires a systems perspective on the distributions of both relations and non-relations in terms of correlations. Specific relations can also be functionally equivalent. The correlations carry the latent functions that can operate synergetically to a varying extent. The synergy is an interaction effect among the distributions: do the functions fit? Other variants and development patterns are possible in niches (Bruckner et al. 1996; Kemp et al.1998; Schot and Geels 2007). In summary, this TH model of synergy becomes more abstract than a network model because a systems perspective is added that operates in terms of the functions of the relations.
2.1 Mutual information and mutual redundancy in three dimensions
The relative frequency distributions of the relations can be expected to contain uncertainty that can be specified using information theory (Shannon 1948; Theil 1972). Ulanowicz (1986; 1997) proposed to measure synergy as mutual information in bi- and trilateral relations when developing ascendency theory. Ascendency is the organizing power of the emerging next-order level in an ecosystem's trophic network: which combinations of food distributions enable a system to flourish? More recently, Ulanowicz (2009) suggested considering the loop in Figure 1 as potentially autocatalytic. Participation of a third party (or reagent) may enhance the relations between two of them to such an extent that the loop is reinforced by the mediation. In other words, the TH can then slip into another type of communication dynamics.
Can this indicator also be used for the specification of synergy in TH configurations (Ulanowicz, personal communication, October 6, 2001)? The mutual information in three dimensions (which is specified in the Appendix) follows analytically from Shannon's (1948) information theory (e.g., McGill 1954; Abramson 1963, at p. 129; Yeung 2008, at pp. 59f.) but has posed an anomaly within this theory because the results of the measurement can be positive or negative. In Shannon's theory information is defined as uncertainty and is necessarily generated as positive when the system operates (because of Shannon's intentional coupling of the information measure H to the second law of thermodynamics).a Negative information, however, would be a reduction of uncertainty as in a niche. Pockets of relatively less uncertainty are also assumed in Prigogine's (1980) theory of self-organizing systems when order emerges.
Why can a system of three reduce uncertainty? (Burt 1992; Simmel 1902; Tortoriello and Krackhardt 2010). In a system of three (or more) distributions, the correlation between two of them can be spurious upon the third (Sun and Negishi 2010). For example, when two parents answer the questions of a child consistently, uncertainty can be reduced. The answers of one parent inform the child in this case about the expected answers of the other because the two sources of variation are coordinated at a systems level (that is, the marriage as a latent construct). The child will not have direct access to this next-order sharing of expectations. Note that the consequent reduction of uncertainty cannot be attributed to specific agents but is generated in a configuration of relations. In the case of a divorce, for example, positive uncertainty among the answers may begin to prevail over the synergy measurable as negative uncertainty (that is, redundancy) in the configuration.
Similarly, in university-industry-government relations, a strong existing relation between two of the partners can make a difference for the third. The synergy indicator measures both positive and negative contributions to the uncertainty or, in other words, both the necessarily positive interaction information and the potentially negative correlational information. Krippendorff (2009a) showed that this summary measure cannot be considered as Shannon-type information; Shannon-type interaction information (IABC→AB:AC:BC; cf. Krippendorff 1980) can be defined differently. However, Krippendorff (2009b) added that interactions with next-order loops - such as overlays - ‘entail positive or negative redundancies, those without loops do not’ (at p. 676).
The overlay of TH relations provides additional loops of information processing to the interacting agents that may thus reduce uncertainty. Too much reduction of uncertainty, on the one side, may lead to insufficient stimulus to innovate. Too much uncertainty, on the other, may make new relations risky. The TH indicator of synergy indicates local reduction of uncertainty within a system (for example, a regional system of innovations) with a negative sign and opening up to globalization with a positive one. This choice of the signs is technical but makes the indicator consistent with Shannon's information theory (Leydesdorff 2010). Leydesdorff and Ivanova (2014) have shown that the indicator measures ‘mutual redundancy’, that is, the extent to which the same information is coded from two (or more) different perspectives.b The perspectives can also be considered as containing latent codes of communication that interact in the observable relations.
In summary, mutual redundancy in three or more dimensions enables us to indicate the configurations under study in terms of local integration, relations, and synergy versus global differentiation and opening. However, the indicator is not more than a formal instrument. One needs a research design for the appreciation of the results. In other words, interpretation of the results requires a discussion of a TH system in relation to its relevant selection environments (Meyer et al. 2014). As we shall see below in empirical cases, the synergy values can then serve as a heuristics by focusing our attention on intuitively unexpected possibilities.
Because all information measures are based on aggregation (using sigmas; see the Appendix), the synergy can also be decomposed in terms of the dimensions such as geographical regions or sectors such as medium-tech manufacturing and knowledge-intensive services. The indicator provides the option to test the assumptions of systemness such as in national or regional innovation ‘systems’. In recent studies, attempts were made to include institutions without first specifying their national boundaries (Choi, Yang, and Park 2014 forthcoming) and research domains (Khan and Park 2013). One can address these questions empirically: how much synergy is indicated regionally or nationally? Is there surplus between regions, nations, or sectors? Is this different for sectors in regions? The measurement results can be fully decomposed.
For example, when one considers the innovation systems of regions in Northern Italy such as Piedmont (OECD 2009) and Lombardy, the industry in the one region may fit more synergistically to the knowledge base of the other, but the political distribution of authority is regionalized (Beccatini et al. 2003; Cooke and Leydesdorff 2006). In such a configuration, the further development of university-industry-government relations in one of the regions might impede the trans-regional innovation system, but a trans-regional mechanism of political authority across Northern Italy is failing. One can thus indicate limitations on synergy generation and from this perspective provide a policy advice.
In the case of Norway, for example, Strand and Leydesdorff (2013) found that synergy among the three functions could be retrieved in relation to high- and medium-tech offshore activities on the west coast, whereas the traditional university centers (Oslo and Trondheim) have remained more distanced from TH models. In China, Leydesdorff and Zhou (2014) found synergy at the level of the 31 provinces by an order of magnitude more than at the lower level of 339 regional prefectures - with the exception of the four municipalities among them that are centrally administered as provinces (Beijing, Shanghai, Tianjin, and Chongqing). Thus, the knowledge-based economy of China seems not coordinated at the lowest regional level. Expanding the model of the four municipalities to other regions might enhance the knowledge-based pattern in the economy.
In Russia, Leydesdorff, Perevodchikov, and Uvarov, [in press] found that the knowledge-intensive services (KIS) - which are in Russia often related to state apparatuses - were synergetic at the local level but did not enhance globalization. In western countries, KIS is more ‘footloose’ (Vernon, 1979) and thus, a globalizer: when KIS is needed elsewhere, it travels. Similarly, Asian nations such as India and Indonesia show levels of synergy much higher than in China and western nations in a study of UIG co-authorship relations in scholarly publications (Ye et al. 2013). What may be synergetic from one (e.g., industrial) perspective may fail to be so from a perspective of regional government or university development.
2.2 Empirical studies
Using 1,432,401 corporate addresses provided on the CD-ROM version of the Science Citation Index 2000, Leydesdorff (2003) first explored the use of the indicator in terms of the address information in the bylines of these (725,354) records.c The addresses were distinguished as academic, industrial, and governmental using a dedicated routine (Park, Hong, and Leydesdorff 2005). How are UIG co-authorship relations distributed in relation to bilateral relations or single-sector attributions?
In this design, documents are the units of analysis. The corporate addresses to each individual document are scored on three variables: U, I, and G that can be zero or one. If U and I are both positive, this co-authorship counts as a UI relation, etc. For each set, one thus obtains aggregated values for all (seven) possible combinations (UIG, UI, UG, IG, U, I, and G). This design was later extended with international co-authorship relations as a fourth category in a Quadruple Helix model (Kwon et al. 2012; Leydesdorff and Sun 2009). One thus obtains three other possible synergies between university-government-foreign (UGF), UIF, and IGF, and also, the possibility to study the development of the Quadruple Helix of UIGF relations. Both the Korean and Japanese datasets allowed studying these indicators longitudinally (Figures 2 and 3, respectively). A similar design was also used for studies at the internet. The internet also contains documents, and one can count occurrences and co-occurrences of words like ‘university’, ‘industry’, or ‘government’ (Khan and Park 2011; Leydesdorff and Curran 2000; Park et al. 2005; Skoric 2014).
Synergy in TH co-authorship relations in Korea 1973-2005. Source: Park & Leydesdorff, 2010: 645; trend lines added.)
The mutual information in two, three, and four dimensions among Japanese articles. With a university, industrial and governmental address, and international co-authorships. Source: Leydesdorff & Sun (2009, at p. 783).
Figure 2 shows the result for the national TH system of publications with Korean addresses in the Science Citation Index (SCI). Several trend breaches are indicated. Under the dictatorship (until 1987), the increases in synergy in TH relations were initially slow. Democratization and civil liberty stimulated TH development in the period of transition. The 1990s witnessed a reversal of this trend; this reversal was reinforced by the increasing globalization (after, for example, the opening of China). Globalization can be expected to make local interactions among and between sectors less important than sector-specific ones because the latter can be more specialized. During the most recent years, the Korean publication system seems to stabilize again into a balance between local and global dynamics.
Using a similar design - with documents in the Science Citation Index as units of analysis - Leydesdorff and Sun (2009) found that the TH synergy in the Japanese set (TUIG) was −67.4 mbits in 1981 but declined to −1.2 mbits in 2004 (Figure 3). The decomposition shows that university-industry (TUI) relations declined during the entire period (1981-2004), but international co-authorship relations (TUF) steadily increased for university-based authors (Wagner, 2008). In other words, international collaboration is a long-term driver for these authors of scholarly articles more than integration with industry at the national level.
The Triple Helix of university, governmental, and non-Japanese authors (TUGF) gained in synergy since the first part of the 1990s, and this is reflected as a trend breach in the Quadruple Helix (TUIGF). In other words, international co-authorship has played a catalytic role in integrating national TH relations in Japan since the mid-1990s, whereas the national system of co-authorship relations tends to erode as a cultural trend (since the early 1980s). Thus, the effects of globalization are integrated in the Japanese case. A similar effect since the mid-1990s was found for Korea, but the composing three-dimensional subsystems of a Quadruple Helix of university-industry-government and foreign relations have been constructed differently in this country (Kwon et al. 2012, at p. 172).
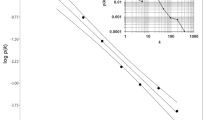
Figure 4 shows synergy values in the systems of co-authorship relations in a number of countries, including the G8, using data from SCI 2011 (Ye et al. 2013). (The results cannot directly be compared with the results of Figures 2 and 3 because of the differences in the data collection). Interestingly, Japan and Korea are positioned in Figure 4 at opposite ends. Japan is third after India and Indonesia in terms of national synergy, whereas in Korea, the system is globalized at the level of advanced western nations.
T UIG distribution for the various countries in 2011. Source: Ye et al., 2013, p. 2321.
One of the objectives of this last study was to consider the position of the Chinese Academy of Science (CAS) which is currently in transition from being a government agency towards being a university-type of institution. When CAS is counted as university, the synergy in the Chinese system is much less (−19.4 mbits) than in the case of counting CAS as governmental (−36.0 mbits). In the former case, China is placed among the most globalized countries (in this domain of publishing) such as Korea and Germany, whereas in the latter case, the Chinese system is far more nationally integrated (with a synergy value between Russia and the UK).
In summary, we have witnessed since the mid-1990s an unraveling of the Triple Helix in terms of co-authored publications under the pressure of globalization. Lawton-Smith and Leydesdorff, [in press] note that the Triple Helix model was proposed by Etzkowitz and Leydesdorff (1995) before this change in the system towards globalization became so prevalent. Internationalization was further reinforced by the competitive emphasis on university ranking since the introduction of the Shanghai rankings in 2004 (Shin et al. 2011). Patenting, for example, is no longer an incentive in leading universities (Leydesdorff and Meyer 2010 and 2013; cf. Etzkowitz 2013). Institutional incentives in academia have been increasingly focused on international publications and co-authorship relations during the last decade (Bornmann et al. 2014; Halffman and Leydesdorff 2010; Leydesdorff et al. 2014b).
2.3 Firms as units of analysis
Van der Panne and Dolfsma (2003) used micro-data of Dutch firms which were operationalized in terms of the TH dimensions (Storper 1997): (1) postal codes which indicate the region, etc., in the geographic dimension; (2) technological classifications (NACE codes of the OECD);d and (3) firm sizes indicating the economic dynamics (e.g., small- and medium-sized enterprises versus large corporations). Mutual information (co-variation) between each of the two distributions can be used as a relational measure so that synergy in three dimensions can be estimated. Synergy at the national level can then be disaggregated in terms of geographical levels (regions, provinces) or in the other two dimensions (sectors and size classes).
Leydesdorff, Van der Panne, and Dolfsma (2006) published the results of this analysis in a special issue of Research Policy dedicated to the Triple Helix. This new application of the indicator in the economic domain led to a series of studies at the national level. Leydesdorff and Fritsch's (2006) decomposition of Germany, for example, was published in the same issue. These two studies led to the conclusion that in the Netherlands additional synergy is indicated at the national level (on top of the sum of the regions and provinces), but in Germany, the States (Länder; e.g., Bavaria) of the Federal Republic are the most relevant level of integration. Using the data of 2004, however, the German Länder were still significantly different along the East-west divide, but at the next-lower (Nomenclature of Territorial Units for Statistics (NUTS)-2)e level of regions (Regierungsbezirke), the East-west divide was no longer dominant (Figure 5).
Mutual information in three dimensions (geography, technology, and organization; T GTO ) at the NUTS-2 level in Germany in 2004. Source: Leydesdorff & Fritsch, 2006, p. 1544.
Figure 5 shows the synergy at the NUTS-2 level of regions (Regierungsbezirke) in Germany. In terms of sectors, both studies indicated that medium-tech manufacturing is a crucial factor for generating synergy because of its relative embeddedness (Cohen and Levinthal 1990). High-tech manufacturing and knowledge-intensive services (KIS) can be less embedded and globalized or footloose (Vernon 1979). KIS tends to uncouple from local economies because access to an airport or train station is crucial. This uncoupling from the geographical locus is counter-acted when KIS is high-tech because of the need to maintain a laboratory or other specific installation (e.g., computer centers).
The synergy at the regional level was found in Germany around the major metropolitan centers in the western part of the country such as Munich, Hamburg, and Frankfurt but not in Berlin (cf. Fritsch and Graf 2011; Lengyel, Sebestyén, and Leydesdorff 2013). Thuringia, previously in the German Democratic Republic, however, is also high on synergy. This is a puzzling result which we only understood after further analysis of the Hungarian innovation system in similar terms. In this follow-up study of Hungary, but using a less complete dataset, Lengyel and Leydesdorff (2011) concluded that Hungary no longer provides surplus synergy at the national level to three regional subsystems that are differently integrated.
The most important subsystem in Hungary was found in the metropolitan area of Budapest and its environment. The western parts of the country were no longer integrated nationally but had successfully ‘accessed’ to relevant environments in Austria, Germany, and the remainder of the EU, whereas some eastern provinces had remained synergetic under the regime of the old (state-controlled) system. Although these conclusions were tentative, they could be supported by another reading of existing statistics. This disintegration of the national system followed during the 1990s after the demise of the Soviet Union, when the country first went into transition and then became an accession country to the EU. Given the dynamics of European unification, however, it was too late to construct a national system of innovations when Hungary became a free nation.
In a similar vein, Strand and Leydesdorff (2013) concluded on the basis of the full set of Norwegian firm data that the knowledge base of this national system was no longer primarily integrated in relation to the national universities, but driven by foreign investments in offshore industries in the western parts of the country. Internationalization and globalization in the latter two studies seemed thus core dimensions for understanding how the knowledge-based economy operates. These conclusions, however, made us turn to the Swedish innovation system as a baseline for comparison and validation (Leydesdorff and Strand 2013).
More than any other, the Swedish innovation system has been studied in detail, is documented statistically with great precision, and could thus provide us with a benchmark to test our Triple Helix methodology. Using the full set of data about 1,187,421 firms made available by Statistics Sweden (November 2011), the data was analyzed with a design similar to the previous studies. The Swedish case, however, allows us to specify an expectation.
In accordance with the expectation, three counties dominate the picture of the synergy within this nation (Figure 6) when decomposed in terms of regions: Stockholm (−3.49 mbits), Västre Gotalands län including Gothenberg (−2.91 mbits), and Skåne including Malmö and Lund (−2.31 mbits). Together, these three regions account for (8.71 / 17.95) 48.5% of the summed synergies of regions at the geographical scale of NUTS3. The between-region synergy at the national level is −4.61 mbits or 25.7%, so that the other 18 counties contribute (100 − 48.5 − 25.7) 25.8% to the national synergy.
Contributions to the reduction of uncertainty at the level of 21 Swedish counties. (Source: Leydesdorff & Strand, 2013, p. 1897).
All relevant distributions (of bi- and trilateral relations) are more skewed in Stockholm than in Gothenburg and Malmö. Most importantly, the synergy function ΔTGTO is far more negative for Stockholm. In summary, the different functions are more concentrated and the distributions operate more synergistically in the Stockholm region than around Gothenburg and Malmö/Lund. The other regions follow these three regions at a considerable distance (Etzkowitz and Klofsten 2005).
The final study which we wish to mention in this context is that of China. In this case, we used data downloaded (December 2012) from the Orbis™ database of Bureau van Dijk (available at https://orbis.bvdinfo.com). This data at the firm level is collected for commercial purposes; the official statistics of China are not available to the public. The results showed that most of the synergy in the Chinese innovation system is generated at the level of the 31 provinces: only 18.0% - that is, less than Sweden - was generated at the next level of the nation between the provinces.
Figure 7 shows an interesting finding of this study. At the next-lower level of the 339 prefectures, the four municipalities which are governed centrally as provinces stand out with together 33.0% of the total synergy at this level. This result came unexpectedly from our analysis but was immediately recognizable to our Chinese colleagues. The success of these four municipalities in constructing a knowledge-based economy regionally can perhaps be used as a role model for other regions.
3Conclusions
The operationalization of the TH as a measure of synergy in university-industry-government relations was pursued during the last decade using the mutual information in three (or more) dimensions as an indicator. This indicator was also automated as a routine available at http://www.leydesdorff.net/software/th4 that provides values for mutual information in two, three, and four dimensions of the data Leydesdorff et al. (2014a). Important advancements were made in understanding this indicator as a measure of redundancy (Krippendorff, 2009b; Leydesdorff and Ivanova 2014). Furthermore, the indicator has recently been applied to some complex social contexts: music festivals (Khan, Cho and Park 2012), socio-ideological divisions (Kim and Park 2012), social media-mediated innovation (Choi, Park and Park 2012), and presidential election campaigns (Park 2013).
When the results of using publications or firms as units of analysis, respectively, are compared, the different dynamics of globalization and localization become manifest. In the system of scientific publishing, the TH tends to unravel at the national level because of the increased priority of international publishing in academia. The competition is organized in terms of academic quality, and the nation has become less important as a frame of reference from this perspective (Wagner 2008). The dimension local-global seems the best candidate for a further extension of the model with a fourth helix, but one should take care that the sign has to be changed in order to calculate the mutual redundancy consistently in a Quadruple Helix model (see the Appendix; Leydesdorff and Ivanova 2014).
Whereas globalization prevails in the domain of scientific publishing, in the economy localization in terms of retaining wealth from knowledge can be expected to generate an opposite dynamics. Metropolitan areas can be expected to provide most synergy because they combine in a micro-cosmos the advantages of localization and globalization. Leydesdorff and Deakin (2011) used in this context the concept of ‘meta-stabilization’: as the large city can be expected to remain in transition between the local and global dimensions, it can reflect the global dynamics of a knowledge-based economy and become itself a localized center of attraction for preferential attachments.
Such cities do not have to be capital cities (e.g., London, Seoul) but can also be ‘smart cities’ such as Montreal, Munich, and perhaps Edinburgh as centers of concentration and mixing of functions (Deakin 2014). Furthermore, as in the Chinese case, a municipality or province with its own jurisdiction corresponding to a metropolitan area can similarly be a relevant unit of analysis (Shapiro et al. 2010; Shapiro and Park 2012). In these contexts, the local uncertainty may be reduced because sources of variation from the global level can be appreciated and thus, strengthen the local economy.
3.1 Normative implications
The Triple Helix indicator discussed in this study is a structural indicator which may inform policy-making by noting unexpected effects. More specifically, both process and outcome of policy programs can be quantitatively measured using the indicators. We mentioned a number of counter-intuitive results and made some policy recommendations in the various studies at the national level. For example, in the case of Norway, the integrative synergy in the areas on the west coast sheds a new light on the role of the traditional universities in Oslo and Trondheim in the innovation system of this country. However, it does not follow normatively from our study of Sweden whether innovation efforts should be directed towards spreading the knowledge-based economy beyond the three regions indicated as the most concentrated or that one should accept this division of labor as a condition for further policies. Structural indicators can only flag conditions that may require attention when making decisions.
Because these indicator values are structural, we are hesitant to suggest entrepreneurial action on the basis of these indicators Etzkowitz (2008). There is no optimal level to facilitate innovation because innovation is a micro-activity at the level of an individual enterprise, while our results are statistical. In other words, innovation is a form of action (hence, variation), whereas the TH indicator is about interactions among the relevant selection environments. An expectation can thus be specified about the selection environment. In one case, however, it may be considered as an advantage and in another, a disadvantage whether Triple Helix relations are synergetic or not. As noted, the dynamics for KIS and high- or medium-tech manufacturing are also very different.
An individual entrepreneur, for example, may be well advised to take advantage of the high levels of synergy in the four municipalities indicated in China (Figure 7), but as noted high levels of synergy may also indicate too much integration and potentially lock-in. Although not as apparent and convenient as traditional measures (e.g., Pearson r correlation value), TH evaluations will allow an organization or government to monitor past, ongoing, and possibly future process in a comparison to its role models or competitors (if their level of synergies can be calculated).
What the Triple Helix indicator provides is hopefully the awareness that systems cannot be considered as a priori integrated or synergetic at a specific level of systemness such as the nation (Lundvall 1988, 1992; Nelson 1993), the sector (Carlsson and Stankiewicz 1991), or a region (e.g., Braczyk et al. 1998; cf. Carlsson 2006). These are empirical questions which can be addressed and provided with informed answers. The added value of the national level, for example, can be specified such as in the cases of Germany and Hungary above; the added value of the international dimension may lead to further reflection about assumptions in national science and technology policies (Wagner 2008). Finally, we note that the model is abstract in the sense that one can use it for other variables than the three institutional ones central to the Triple Helix discussions about university-industry-government relations. In the case of Japanese and Korean publications, for example, we could extend with international co-authorship relations as another (fourth) dimension.
In summary, synergy in distributions of relations is not a precondition for innovation, since innovation is the result of specific relationships (e.g., between supply and demand) and realized by agency. After an innovation, furthermore, the systems dynamics may have changed. The conditions for innovation, however, can be informed by these indicators given the relevant sample choice (e.g., region, technology, size of the firm, etc.). An evolutionary perspective on TH arrangements can thus further be specified and operationalized (Ivanova and Leydesdorff 2014b and [c]).
4Endnotes
aThe communication of (Shannon-type) information necessarily adds uncertainty because Shannon (1948) defined information as probabilistic entropy: H = − ∑ i p i × log2p i . Probabilistic entropy is coupled to Gibbs' formula for thermodynamic entropy S = k B × H. In Gibbs' equation, k B is the Boltzmann constant that provides the dimensionality Joule/Kelvin to S, while H is dimensionless and can be measured in bits of information (or any other base for the logarithm) given a probability distribution (containing uncertainty). The second law of thermodynamics states that entropy increases with each operation, and Shannon-type information is therefore always positive (because k B is a constant).
bIn the case of three (or an uneven number of) dimensions, mutual redundancy is equal to mutual information, but in the case of an even number of dimensions, the sign has to be changed.
cThese addresses point to 725,354 records contained in this database on a total of 778,446 items. Only 3.7% of these records contain no address information. The total number of authors in this database is 3,060,436. Thus, on average, each record relates to four authors but at two addresses.
dNACE is an abbreviation of Nomenclature générale des Activités économiques dans les Communautés Européennes. The NACE code can be translated into the International Standard Industrial Classification (ISIC).
eNUTS is an abbreviation for Nomenclature des Unités Territoriales Statistiques (that is, Nomenclature of Territorial Units for Statistics). The NUTS classification is a hierarchical system for dividing up the economic territory of the EU.
Appendix
Mutual information in three (or more) dimensions - the Triple Helix indicator to be used here - is a signed information measure Yeung (2008), and therefore, not a Shannon information (Krippendorff, 2009a and [b]). However, this measure is derived in the context of information theory and follows from the Shannon formulas (e.g., Abramson, 1963; Ashby, 1964; McGill 1954). If the two bases are used for the logarithm, all values are in bits of information.
According to Shannon (1948), the uncertainty in the relative frequency distribution of a variable x () can be defined as . Shannon denotes this as probabilistic entropy, which is expressed in bits of information if the number two is used as the base for the logarithm. (When multiplied by the Boltzman constant k B , one obtains thermodynamic entropy and the corresponding dimensionality in Joule/Kelvin. Unlike thermodynamic entropy, probabilistic entropy is dimensionless and therefore, yet to be provided with meaning when a system of reference is specified).
Likewise, uncertainty in a two-dimensional probability distribution can be defined as . In the case of interaction between the two dimensions, the uncertainty is reduced with the mutual information or transmission , as follows: H XY = (H X + H Y ) − T XY . If the distributions are completely independent H XY = H X + H Y , and consequently, T XY = 0.
In the case of three potentially interacting dimensions (x, y, and z), mutual information can be derived (e.g., Abramson, 1963: 131 ff.) as
The interpretation is as follows: association information can be categorized broadly into correlation information and interaction information. The correlation information among the attributes of a dataset can be interpreted as the total amount of information shared between the attributes. The interaction information can be interpreted as multivariate dependencies among the attributes. A spurious correlation in a third attribute, for example, can reduce the uncertainty between the other two.
Compared with correlation, mutual information can be considered as a more parsimonious measure for the association. The multivariate extension to mutual information was first introduced by McGill (1954) as a generalization of Shannon's mutual information. The measure is similar to the analysis of variance, but uncertainty analysis remains more abstract and does not require assumptions about the metric properties of the variables (Garner and McGill 1956). Han (1980) further developed the concept; positive and negative interactions were also discussed by Tsujishita (1995), Jakulin (2005), and Yeung (2008): 59 ff.).
Since all terms in Equation 1 are composed by addition (using Σ; see Theil, 1972: 20 f.), mutual information in three dimensions can be decomposed into G groups as follows:
When one decomposes, for example, a country in terms of its regions (or provinces), T0 is between-region uncertainty or a measure of the dividedness among the regions; T G is the uncertainty at the geographical scale G; n G the number of firms at this geographical scale G; and N the total number of firms in the dataset. The values for T and T G can be calculated from the distributions (using Equation 1), when the values of N and n G are known. The normalized values of the contributions of regions to the national synergy and the between-group synergy (T0) can then be derived. T0 is equal to the difference between the T-value for the whole set minus the sum of the subsets.
Note that T0 can have positive or negative signs and can also be expressed as a percentage contribution to the total synergy for a system of reference (e.g., at the national level). A negative value of T0 indicates that the uncertainty at the next geographically aggregated level is reduced more than the sum of the parts, whereas a positive value indicates that the next level of integration does not add synergy to the system. Thus, one can test, for example, whether the national level adds to the systems integration more than the sum of the regional units. The relative contributions at each level can be specified after proper normalization for the number of firms.
The extension to more than three dimensions is straightforward, but one has to take care of sign changes between odd and even numbers of dimensions of mutual redudancy in order to remain consistent with Shannon's (1948) mathematical theory of communication (Leydesdorff and Ivanova, 2014). The online calculator at http://www.leydesdorff.net/software/th4 provides results in two, three, and four dimensions of the mutual information so that one can also test four-dimensional models (Bunders et al. 1999; Carayannis and Campbell 2009 and 2010; Leydesdorff and Sun 2009).
Additional file
References
Abramson N: Information Theory and Coding. 1963, McGraw-Hill, New York, etc
Ashby WR: Constraint analysis of many-dimensional relations. General Systems Yearbook. 1964, 9: 99-105.
Beccatini G, Bellandi M, Ottati GD, Sforzi F (2003) From industrial districts to local development: an itinerary of research. Edward Elgar, Cheltenham, UK; Northhampton, MA
Bornmann L, Wagner C, Leydesdorff L (2014) BRICS countries and scientific excellence: a bibliometric analysis of most frequently-cited papers. J\ Assoc Inform Sci Tech, in press
Braczyk H-J, Cooke P, Heidenreich M (eds) Regional innovation systems. 1998, University College London Press, London/ Bristol PA
Bruckner E, Ebeling W, Montaño MJ, Scharnhorst A: Nonlinear stochastic effects of substitution-an evolutionary approach. J Evol Econ. 1996, 6 (1): 1-30. 10.1007/BF01202370.
Bunders JFG, Broerse JEW, Zweekhorst MBM: The triple helix enriched with the user perspective: a view from Bangladesh. J Tech Tran. 1999, 24 (2): 235-246. 10.1023/A:1007811607384.
Burt RS: Structural holes: the social structure of competition. 1992, Harvard University Press, Cambridge, MA
Carayannis EG, Campbell DFJ: ‘Mode 3’ and ‘Quadruple Helix’: toward a 21st century fractal innovation ecosystem. Int J Tech Manag. 2009, 46 (3): 201-234. 10.1504/IJTM.2009.023374.
Carayannis EG, Campbell DFJ: Triple Helix, Quadruple Helix and Quintuple Helix and how do knowledge, innovation, and environment relate to each other?. Int J Soc Ecol Sustain Dev. 2010, 1 (1): 41-69. 10.4018/jsesd.2010010105.
Carlsson B: Internationalization of innovation systems: a survey of the literature. Res Pol. 2006, 35 (1): 56-67. 10.1016/j.respol.2005.08.003.
Carlsson B, Stankiewicz R: On the nature, function, and composition of technological systems. J Evol Econ. 1991, 1 (2): 93-118. 10.1007/BF01224915.
Choi S, Park J-Y, Park HW: Using social media data to explore communication processes within South Korean online innovation communities. Scientometrics. 2012, 90 (1): 43-56. 10.1007/s11192-011-0514-7.
Choi S, Yang JS, Park HW (2014) The triple helix and international collaboration in science. J Am Soc Inform Sci Techn, in press
Cohen WM, Levinthal DA: Absorptive capacity: a new perspective on learning and innovation. Adm Sci Q. 1990, 35 (1): 128-153. 10.2307/2393553.
Cooke P, Leydesdorff L: Regional development in the knowledge-based economy: the construction of advantages. J Tech Tran. 2006, 31 (1): 5-15. 10.1007/s10961-005-5009-3.
Smart cities: governing, modelling and analysing the transition. 2014, Routledge, Oxon, UK
Dolfsma W, Leydesdorff L: Lock-in and break-out from technological trajectories: modeling and policy implications. Technol Forecast Soc Change. 2009, 76 (7): 932-941. 10.1016/j.techfore.2009.02.004.
Etzkowitz H: The Triple Helix: university-industry-government innovation in action. 2008, Routledge, London
Etzkowitz H: Mistaking dawn for dusk: quantophrenia and the cult of numerology in technology transfer analysis. Scientometrics. 2013, 97 (3): 913-925. 10.1007/s11192-013-1007-7.
Etzkowitz H, Klofsten M: The innovating region: toward a theory of knowledge-based regional development. R D Manag. 2005, 35 (3): 243-255. 10.1111/j.1467-9310.2005.00387.x.
Etzkowitz H, Leydesdorff L: The Triple Helix-university-industry-government relations: a laboratory for knowledge-based economic development. EASST Rev. 1995, 14 (1): 14-19.
Etzkowitz H, Leydesdorff L: The endless transition: a ‘Triple Helix’ of university-industry-government relations, introduction to a theme issue. Minerva. 1998, 36 (3): 203-208. 10.1023/A:1004348123030.
Etzkowitz H, Leydesdorff L: The dynamics of innovation: from national systems and ‘Mode 2’ to a Triple Helix of university-industry-government relations. Res Pol. 2000, 29 (2): 109-123. 10.1016/S0048-7333(99)00055-4.
Fritsch M, Graf H: How sub-national conditions affect regional innovation systems: the case of the two Germanys. Papers Reg Sci. 2011, 90 (2): 331-353. 10.1111/j.1435-5957.2011.00364.x.
Garner WR, McGill WJ: The relation between information and variance analyses. Psychometrika. 1956, 21 (3): 219-228. 10.1007/BF02289132.
Halffman W, Leydesdorff L: Is inequality among universities increasing? Gini coefficients and the elusive rise of elite universities. Minerva. 2010, 48 (1): 55-72. 10.1007/s11024-010-9141-3.
Han TS: Multiple Mutual Information and Multiple Interactions in Frequency Data. Informaiton and Control. 1980, 46 (1): 26-45. 10.1016/S0019-9958(80)90478-7.
Ivanova IA, Leydesdorff L: Redundancy generation in university-industry-government relations: the Triple Helix modeled, measured, and simulated. Scientometrics. 2014, 99 (3): 927-948. 10.1007/s11192-014-1241-7. doi:10.1007/s11192-014-1241-7
Ivanova IA, Leydesdorff L: Rotational symmetry and the transformation of innovation systems in a Triple Helix of university–industry–government relations. Technol Forecast Soc Change. 2014b, 86: 143-156. 10.1016/j.techfore.2013.08.022. doi: 10.1016/j.techfore.2013.08.022
Ivanova IA, Leydesdorff L (20014c) Knowledge-generating efficiency in innovation systems: the relation between structural and temporal effects. Preprint available at , [http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2439165]
Jakulin A (2005) Machine learning based on attribute interactions. University of Ljubljana, Ljubljana, PhD Thesis. Available at , [http://stat.columbia.edu/~jakulin/Int/jakulin05phd.pdf]
Kemp R, Schot J, Hoogma R: Regime Shifts to Sustainability through Processes of Niche Formation. The Approach of Strategic Niche Management. Tech Anal Strat Manag. 1998, 10 (2): 175-195. 10.1080/09537329808524310.
Khan GF, Park HW: Measuring the triple helix on the web: longitudinal trends in the university-industry-government relationship in Korea. J Am Soc Inform Sci Tech. 2011, 62 (12): 2443-2455. 10.1002/asi.21595.
Khan G, Park H: International collaboration within electronic government research domain: a triple helix network analysis of collaboration at the regional, country, and institutional levels. Govern Inform Q. 2013, 30 (2): 182-193. 10.1016/j.giq.2012.09.003.
Khan GF, Cho SE, Park HW: A comparison of the Daegu and Edinburgh musical industries: a triple helix approach. Scientometrics. 2012, 90 (1): 85-99. 10.1007/s11192-011-0504-9.
Kim M, Park HW: Measuring twitter-based political participation and deliberation in the South Korean context by using social network and Triple Helix indicators. Scientometrics. 2012, 90 (1): 121-140. 10.1007/s11192-011-0508-5.
Krippendorff K: Q: an interpretation of the information theoretical Q-measures. Progress in cybernetics and systems research. Edited by: Trappl R, Klir GJ, Pichler F. 1980, Hemisphere, New York, 63-67.
Krippendorff K: W. Ross Ashby's information theory: a bit of history, some solutions to problems, and what we face today. Int J Gen Syst. 2009, 38 (2): 189-212. 10.1080/03081070802621846.
Krippendorff K: Information of interactions in complex systems. Int J Gen Syst. 2009, 38 (6): 669-680. 10.1080/03081070902993160.
Kwon KS, Park HW, So M, Leydesdorff L: Has Globalization strengthened South Korea's National Research System? National and International Dynamics of the Triple Helix of Scientific Co-authorship Relationships in South Korea. Scientometrics. 2012, 90 (1): 163-175. 10.1007/s11192-011-0512-9. doi:10.1007/s11192-011-0512-9
Lawton-Smith H, Leydesdorff L (in press) The Triple Helix in the context of global change: dynamics and challenges. Prometheus
Lengyel B, Leydesdorff L: Regional innovation systems in Hungary: the failing synergy at the national level. Regional Stud. 2011, 45 (5): 677-693. 10.1080/00343401003614274. doi:10.1080/00343401003614274
Lengyel B, Sebestyén T, Leydesdorff L (2013) Challenges for regional innovation policies in CEE countries: spatial concentration and foreign control of US patenting. Sc Publ Pol, Advance online publication doi:10.1093/scipol/sct087; arxiv.org/abs/1301.1757
Leydesdorff L: Epilogue. Besselaar Pvd (eds) Evolutionary economics and chaos theory: new directions for technology studies. Edited by: Leydesdorff L. 1994, Pinter, London/New York, 180-192.
Leydesdorff L: The mutual information of university-industry-government relations: an indicator of the Triple Helix dynamics. Scientometrics. 2003, 58 (2): 445-467. 10.1023/A:1026253130577.
Leydesdorff L: Redundancy in systems which entertain a model of themselves: interaction information and the self-organization of anticipation. Entropy. 2010, 12 (1): 63-79. 10.3390/e12010063. doi:10.3390/e12010063
Leydesdorff L: The Triple Helix, Quadruple Helix,…, and an N-tuple of Helices: explanatory models for analyzing the knowledge-based economy?. J Knowledge Econ. 2012, 3 (1): 25-35. 10.1007/s13132-011-0049-4. doi:10.1007/s13132-13011-10049-13134
Leydesdorff L, Curran M (2000) Mapping university-industry-government relations on the internet: an exploration of indicators for a knowledge-based economy. Cybermetrics 4(1), Paper 2 at < , [http://cybermetrics.cindoc.csic.es/articles/v4i1p2.html]
Leydesdorff L, Deakin M: The Triple Helix Model and the Meta-Stabilization of Urban Technologies in Smart Cities. J Urban Tech. 2011, 18 (2): 53-63. 10.1080/10630732.2011.601111.
Leydesdorff L, Fritsch M: Measuring the knowledge base of regional innovation systems in Germany in terms of a Triple Helix dynamics. Res Pol. 2006, 35 (10): 1538-1553. 10.1016/j.respol.2006.09.027.
Leydesdorff L, Ivanova IA: Mutual redundancies in inter-human communication systems: steps towards a calculus of processing meaning. J Assoc Inform Sci Tech. 2014, 65 (2): 386-399.
Leydesdorff L, Meyer M: The decline of university patenting and the end of the Bayh-Dole effect. Scientometrics. 2010, 83 (2): 355-362. 10.1007/s11192-009-0001-6.
Leydesdorff L, Meyer M: A reply to Etzkowitz' comments to Leydesdorff and Martin (2010): technology transfer and the end of the Bayh-Dole effect. Scientometrics. 2013, 97 (3): 927-934. 10.1007/s11192-013-0997-5. doi:10.1007/s11192-013-0997-5
Leydesdorff L, Strand Ø: The swedish system of innovation: regional synergies in a knowledge-based economy. J Am Soc Inform Sci Tech. 2013, 64 (9): 1890-1902. 10.1002/asi.22895. doi: 1810.1002/asi.22895
Leydesdorff L, Sun Y: National and international dimensions of the Triple Helix in Japan: university-industry-government versus international co-Authorship relations. J Am Soc Inform Sci Tech. 2009, 60 (4): 778-788. 10.1002/asi.20997.
Leydesdorff L, van den Besselaar P: Technological development and factor substitution in a non-linear model. J Soc Evol Syst. 1998, 21 (2): 173-192. 10.1016/S1061-7361(00)80004-1.
Leydesdorff L, Zawdie G: The Triple Helix Perspective of Innovation Systems. Tech Anal Strat Manag. 2010, 22 (7): 789-804. 10.1080/09537325.2010.511142.
Leydesdorff L, Zhou P: Measuring the knowledge-based economy of China in terms of synergy among technological, organizational, and geographic attributes of firms. Scientometrics. 2014, 98 (3): 1703-1719. 10.1007/s11192-013-1179-1. doi: 10.1007/s11192-013-1179-1
Leydesdorff L, Dolfsma W, Van der Panne G: Measuring the knowledge base of an economy in terms of Triple-Helix relations among ‘technology, organization, and territory’. Res Pol. 2006, 35 (2): 181-199. 10.1016/j.respol.2005.09.001.
Leydesdorff L, Park HW, Lengyel B: A Routine for Measuring Synergy in University-Industry-Government Relations: Mutual Information as a Triple-Helix and Quadruple-Helix Indicator. Scientometrics. 2014a, 99 (1): 27-35. 10.1007/s11192-013-1079-4. doi: 10.1007/s11192-013-1079-4
Leydesdorff L, Wagner CS, Bornmann L: The European Union, China, and the United States in the top-1% and top-10% layers of most-frequently cited publications: Competition and collaborations. Journal of Informetrics. 2014b, 8 (3): 606-617. 10.1016/j.joi.2014.05.002.
Leydesdorff L, Perevodchikov E, Uvarov A (in press) Measuring triple-helix synergy in the russian innovation systems at regional, provincial, and national levels. J Assoc Inform Sci Tech.
Lundvall B-Å: Innovation as an interactive process: from user-producer interaction to the national system of innovation. Technical Change and Economic Theory. Edited by: Dosi G, Freeman C, Nelson R, Silverberg G, Soete L. 1988, Pinter, London, 349-369.
National systems of innovation. 1992, Pinter, London
McGill WJ: Multivariate information transmission. Psychometrika. 1954, 19 (2): 97-116. 10.1007/BF02289159.
Meyer M, Grant K, Morlacchi P, Weckowska D: Triple Helix indicators as an emergent area of enquiry: a bibliometric perspective. Scientometrics. 2014, 99 (1): 151-174. 10.1007/s11192-013-1103-8.
Nelson RR (ed) National innovation systems: a comparative analysis. 1993, Oxford University Press, New York
Nelson RR, Winter SG: An evolutionary theory of economic change. Belknap Press of Harvard University Press. 1982, MA, Cambridge
OECD OECD reviews of regional innovation: Piedmont. 2009, Italy, OECD, Paris
Park HW: Mapping election campaigns through negative entropy: Triple and quadruple helix approach to South Korea’s 2012 presidential election. Scientometrics. 2014, 99 (1): 187-197. 10.1007/s11192-013-1122-5.
Park HW, Leydesdorff L: Longitudinal trends in networks of university-industry-government relations in South Korea: the role of programmatic incentives. Res Pol. 2010, 39 (5): 640-649. 10.1016/j.respol.2010.02.009.
Park HW, Hong HD, Leydesdorff L: A comparison of the knowledge-based innovation systems in the economies of South Korea and the Netherlands using Triple Helix indicators. Scientometrics. 2005, 65 (1): 3-27. 10.1007/s11192-005-0257-4.
Prigogine I: From being to becoming. Time and complexity in the physical sciences. 1980, Freeman, New York
Schot J, Geels FW: Niches in evolutionary theories of technical change. J Evol Econ. 2007, 17 (5): 605-622. 10.1007/s00191-007-0057-5.
Schumpeter J: Business Cycles: A Theoretical, Historical and Statistical Analysis of Capitalist Process. 1939/1964, McGraw-Hill, New York
Shannon CE: A mathematical theory of communication. Bell Syst Tech J. 1948, 27: 379-423. 10.1002/j.1538-7305.1948.tb01338.x. and 623–656
Shapiro MA, Park HW: Regional development in South Korea: accounting for research area in centrality and networks. Scientometrics. 2012, 90 (1): 271-287. 10.1007/s11192-011-0498-3.
Shapiro MA, So M, Woo Park H: Quantifying the national innovation system: inter-regional collaboration networks in South Korea. Tech Anal Strat Manag. 2010, 22 (7): 845-857. 10.1080/09537325.2010.511158.
Shin JC, Toutkoushian RK, Teichler U: University rankings: theoretical basis, methodology and impacts on global higher education. 2011, Springer, Dordrecht
Simmel G: The number of members as determining the sociological form of the group. I. Am J Sociol. 1902, 8 (1): 1-46. 10.1086/211115.
Skoric MK: The implications of big data for developing and transitional economies: Extending the Triple Helix?. Scientometrics. 2014, 99 (1): 175-186. 10.1007/s11192-013-1106-5.
Storper M: The Regional World - Territorial Development in a Global Economy. 1997, Guilford Press, New York
Strand Ø, Leydesdorff L: Where is synergy in the Norwegian innovation system indicated? Triple Helix relations among technology, organization, and geography. Technol Forecast Soc Change. 2013, 80 (3): 471-484. 10.1016/j.techfore.2012.08.010.
Sun Y, Negishi M: Measuring the relationships among university, industry and other sectors in Japan's national innovation system: a comparison of new approaches with mutual information indicators. Scientometrics. 2010, 82 (3): 677-685. 10.1007/s11192-010-0179-7.
Theil H: Statistical decomposition analysis. 1972, North-Holland, Amsterdam/ London
Tortoriello M, Krackhardt D: Activating cross-boundary knowledge: the role of Simmelian ties in the generation of innovations. Acad Manage J. 2010, 53 (1): 167-181. 10.5465/AMJ.2010.48037420.
Tsujishita T: On triple mutual information. Adv Appl Math. 1995, 16 (3): 269-274. 10.1006/aama.1995.1013.
Ulanowicz RE (1986) Growth and development: ecosystems phenomenology., toExcel, San Jose, etc.
Ulanowicz RE: Ecology. 1997, Columbia University Press, New York, The ascendent perspective
Ulanowicz RE: The dual nature of ecosystem dynamics. Ecol Model. 2009, 220 (16): 1886-1892. 10.1016/j.ecolmodel.2009.04.015.
Van der Panne G, Dolfsma W: The odd role of proximity in knowledge relations: high-tech in The Netherlands. Tijdschrift foor Economische en Sociale Geografie. 2003, 94 (4): 451-460.
Vernon R: The product cycle hypothesis in a new international environment. Oxf Bull Econ Stat. 1979, 41 (4): 255-267. 10.1111/j.1468-0084.1979.mp41004002.x.
Wagner CS: The New Invisible College. 2008, Brookings Press, Washington DC
Ye FY, Yu SS, Leydesdorff L: The Triple Helix of university-industry-government relations at the country level, and its dynamic evolution under the pressures of globalization. J Am Soc Inform Sci Tech. 2013, 64 (11): 2317-2325. 10.1002/asi.22931.
Yeung RW: Information theory and network coding. 2008, Springer, New York, NY
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The paper is co-authored. All authors read and approved the final manuscript.
Electronic supplementary material
40604_2014_4_MOESM1_ESM.pdf
Additional file 1: Multilingual abstracts in the five official working languages of the United Nations and Portuguese.(PDF 441 KB)
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Leydesdorff, L., Park, H.W. Can synergy in Triple Helix relations be quantified? A review of the development of the Triple Helix indicator. Triple Helix 1, 4 (2014). https://doi.org/10.1186/s40604-014-0004-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40604-014-0004-z