Abstract
There are several concepts in 2D Geometry that require understanding their application in the real practical world. However, in classrooms, such concepts are often taught without the analysis of the learners’ realization and interpretation of the existing concepts around them, in their surroundings. For this purpose, an Augmented Reality (AR) based module for the 7th and 8th grade syllabus has been designed to encourage the active participation of the learners in the classroom while learning the concept of Lines and Angles. It comprises three AR learning activities that enable the participants to recall, visualize, and identify the type of angle and then mark it by drawing on the augmented 3D house. Before conducting the main studies, a pilot study was conducted with 6 students of 8th grade. This helped in validating the data instruments, timing, and execution of the research study. The first study was conducted with 21 students of 8th grade where 12 participants performed the AR learning activities in dyads and 9 participants performed individually. Their perspectives, approaches, and motivation in performing the AR learning activities have been reported. Findings from the study showed that the majority i.e. 90.4% participants preferred to perform the AR learning activities in dyads than individually. Though the usability score was higher for the participants who performed the AR learning activities individually (M = 70.28) as compared to dyads (M = 65.23), there was no significant difference in the motivation scores between the participants of the two groups. In the second study, 28 students of 7th grade were divided into dyads and their behavior patterns of performing the AR learning activities have been reported. Using Lag Sequential Analysis, significant sequences were obtained based on the behaviors belonging to three categories of peer involvement, teacher prompts and AR interactions. It was found that the designed AR learning activities encouraged the participants to discuss the concepts with peers, enhanced their immersive experience as they together moved around and inside the house to find and identify the angles.
Similar content being viewed by others
Introduction
The 2D Geometry concepts like Lines and Angles are introduced at middle school level (6th to 8th grade) in a formal context. One of its major applications in the later years of Science, Technology, Engineering and Mathematics (STEM) education is the learning of basic Trigonometry concepts (Biber et al. 2013). Traditionally, teaching the Lines and Angles concepts consists of studying the meanings and diagrams of various angle forms (Bütüner and Filiz 2017). In classrooms, the instructor generally draws an angle on the blackboard, describing the calculations and orally explaining the concept and related properties that the students listen to, record the same in their notebooks and do some practical exercises (Ramdhani et al. 2017). In this procedure, the students like to learn such ideas by retaining the definitions and properties, which they will in general overlook in subsequent to writing examinations (Biber et al. 2013; Ramdhani et al. 2017). Consequently, they lack in understanding the utilization of lines and angles in a practical world (Ramdhani et al. 2017). There are textbooks that provide the instances of 3D objects, which possess a type of angle, in the form of 2D images. However, such examples tend to decrease with the increase in the intricacies of concepts (Bütüner and Filiz 2017). Thus, this makes it difficult for students to understand and observe the relationships, interactions, and imagination of working on angles (Biber et al. 2013). To improve on these dimensions, it is important to assist them in connecting the learned concepts to real-life examples and applications (Biber et al. 2013; Ramdhani et al. 2017). We have thus explored the use of an emerging technology called Augmented Reality (AR) to help the students relate to the examples from the surroundings by providing real-time instances and help explain the application of various types of angles to these examples. With the help of AR technology, one can see the computer-generated graphics being superimposed on the real-world in real-time, resulting in virtual and physical-world coexistence instantaneously (Azuma 1997). Along these lines, we have designed a few classroom-based learning activities in AR to help the students in applying the taught concepts through active and collaborative exploration of outside-class examples.
This article reports the design, implementation, and evaluation of an AR-based module designed on the topic of Lines and Angles for the 7th and 8th-grade syllabus. In Section 2, the related work on interactive and collaborative geometry, and the affordances of AR in Geometry have been discussed. Section 3 presents the design and implementation of the ScholAR’s module on Lines and Angles, highlighting the design of the AR interactions, design rationale and the pedagogy involved. Section 4 presents the methodology of the two studies that were conducted. The first study was a comparative study between those performing the AR learning activities in dyads and individually addressing the following two research questions (RQ):
RQ1: What are the perspectives of and approaches taken by the students in solving the AR learning activities when they perform it in dyads and individually?
RQ2: What motivated the dyads in performing the AR learning activities as compared to the individuals?
Based on the observations and results obtained from the first study, the second study was conducted with a new group of dyads, addressing the following research question:
RQ3: What is the learning behavior pattern of the participating dyads while performing the AR learning activities?
Section 5 and 6 present the result and discussion respectively of both the studies, reporting the analysis of the approaches, motivation and learning behavior of the participants to perform the AR learning activities. Section 7 presents the summary, concluding remarks, limitations of the studies and future work.
Related work
Learning interactive and collaborative geometry
One of the integral parts of Mathematics is Geometry, which further consists of 2D and 3D geometry. As students begin to develop the ability to logically think and grasp abstract concepts at around 11–15 years of age, this course is introduced and implemented at middle school (6th to 8th grade) level (Ojose 2008). Geometry may be used in numerous other fields of mathematics and helps in the study and interpretation of examples from the real world (Özerem 2012). Learning Geometry is not confined to only learning the definitions. The properties and theorems of 2D and 3D geometry should also be studied with a view to form geometric relationships while solving related problems (Narayana et al. 2016).
As the technology is blooming, it has given us an aid to the provision for visual presentations. To increase students’ attention to mathematical concepts and techniques, diverse modes of interactive geometry have been developed (Zbiek et al. 2007). The interactive geometry program aims to help students learn and explore geometric concepts by manipulating geometric objects such as dots, lines, circles, etc. (Koyuncu et al. 2015). One such software is GeoGebra that helps in exploring and learning the various mathematical representations of an object (Edwards and Jones 2006). There are more software that fall under the category of Dynamic Geometry Software (DGS) such as Cabri-Geometre (Straesser 2002) and SketchPad (McClintock et al. 2002), which facilitate in deeper exploration and analysis of geometric forms by means of dynamic manipulation (Jones 1998). A comparative study conducted earlier with GeoGebra software (Banu 2012) showed that it is difficult to do this kind of exploration for pen and pencil based learning. These interactions, however, are often limited to using a laptop with a keyboard and the mouse used as deceptive tools. Thus, the need is to explore other manipulatives that can be used to dynamically explore the 3D object properties.
Affordances of augmented reality in geometry
Augmented Reality (AR) technology tends to work as a manipulative in the education sector among various emerging technologies. It could provide an immersive and engaging experience to learners while maintaining the genuineness of the surrounding real environment (Squire and Klopfer 2007; Sarkar and Pillai 2019). Thus, its application in education is valuable for being able to provide the learners with rich contextual learning, where learners build their individual unique discovery path (Bujak et al. 2013). As during the skills training using AR, there are no real consequences taking place on making any mistakes, hence this technology can be worth gaining competence (Bujak et al. 2013). The learners are also able to interact with any educational content in a way similar to interacting with the physical world through the intuitive interactions of AR (Radu 2012). Several interactions tend to provide intuitive navigation such as the ability to move around a virtual object to see from different perspectives and being able to scale it by moving closer to or farther from the object (Isotani and de Oliveira Brandão 2008; Sarkar et al. 2019a). Also, the ability to manipulate by selecting and pointing at the virtual object tends to reduce the efforts of the learners to learn further than the acquired skills and knowledge (Isotani and de Oliveira Brandão 2008; Sarkar et al. 2018). Thus, the effort of finding and manipulating actual objects to learn abstract concepts can be taken care of by incorporating such physical movements in immersive AR platforms (Wilson 2002). Moreover, with the ubiquitous use of mobile phones and tablets, the research has been expanded to developing mobile AR platforms (Papagiannakis et al. 2008) as it can provide the opportunities for “ubiquitous knowledge construction” (Peng et al. 2009). Such affordances of AR have been explored in Geometry learning by manipulating 3D objects in AR (Kaufmann and Schmalstieg 2002), to enhance 3D thinking skills (İbili et al. 2020), spatial ability (Liao et al. 2015), mental rotation skills (Kaur et al. 2018), etc. All such explorations have been primarily done in 3D Geometry. There are very few studies on exploring the application of 2D Geometry using the AR platform, wherein one study, the 3D objects are developed from the drawn 2D shapes in AR (Banu 2012). There also exist studies that suggest the collaborative use of AR can help in improving visualization skills, critical thinking skills, problem-solving skills and communication of the participating students (Kaufmann and Schmalstieg 2002; Chen 2008; Dunleavy et al. 2009; Cai et al. 2019). While using the AR platform, collaboration is more effective with the learners when they get individual controls and personalized views for all the individuals working collaboratively in a group (Radu 2012; Cai et al. 2019).
In contrast to former studies, through the Lines and Angles module of ScholAR, we explore the application of 2D geometry on 3D virtual examples. Using this module, we expect that the AR learning activities will help middle school students in realizing the application of lines and angles in real-world objects and scenarios. Further, these activities when done in collaboration can motivate them towards the approaches of AR-based problem-solving.
Design and implementation
Design of ScholAR
To develop the Android-based Augmented Reality application, Unity software was used. The AR application ScholAR was made markerless using the Google ARCoreFootnote 1 SDK version 1.7.0. With the help of ARCore, the phone’s position as per the movement of the user was tracked and the lighting conditions of the surrounding real-environment could be estimated. The two essential components of ARCore in our application included plane detection and raycasting. The application starts by detecting the surrounding of the user and identifies a horizontal plane by placing a white-colored grid. The appearance of the grid works as an indication to superimpose the virtual 3D object on the screen in real-time. The further interactions based on the activities designed can then be performed which are explained below. The built-up android packages in Unity were then exported and deployed in Android-based (version 8.1.0) Samsung Galaxy S4 tablets.
Design of Augmented Reality (AR) interactions
In one of the studies (Sarkar et al., 2019b), a comparative analysis was done on three Augmented Reality Interaction Mediums (AIMs) using imagination, draw feature and tangible AR markers. Based on the context of use in this work, the draw feature as the AR interaction medium was considered to be explored in the design of this module of ScholAR. Along with the draw feature, the different combinations of finger taps were used in the design. Tapping and dragging with one finger enabled the learner to draw on the screen of the tablet. With two fingers tap, the 3D house would appear on the grid after scanning the surface. Also, the house could be scaled up by tapping closer on the identified grid on the horizontal plane and scaled down by tapping farther on the grid. The three fingers tap inside the house would erase all the content drawn on the screen. Tapping with three fingers outside the house would erase the house.
Design rationale
There exists several theoretical frameworks that provide direction towards the learning of geometrical reasoning needed to solve mathematical problems that involve visual phenomena (Jones 1998). One among them is the van Hiele Theory of Geometric Thinking (Crowley 1987). According to the theory of van Hiele, there are five levels of Geometric thinking for the students to learn Geometry. The students gain these levels with their experiences and are not dependent on their ages. Thus, different students can attain a level at different times/ages, characterized by increasing abstraction. These levels are as follows:
Level 0 - Visualization: In this level, the students gain the ability to recognize shapes and their names, compare and operate on them.
Level 1 - Analysis: The students at this level gain the ability to identify the characteristics of geometrical shapes by analyzing the relationships between the characteristics and properties of the shapes.
Level 2 - Informal Deduction/Abstraction: The students gain the ability to categorize and connect geometrical shapes as per their characteristics supported by arguments.
Level 3 - Formal Deduction: The students are able to make the deduction and to understand the theorem and their proof.
Level 4 - Rigor: The students are able to give correct geometrical proof and abstract deduction by comparing the different postulational systems.
In the design of ScholAR, we have targeted the first three levels which align with the syllabus of the middle school students based on their cognitive and thinking abilities at that age. They gradually attain each of the levels with the three progressive AR learning activities for this topic.
AR learning activities
The ScholAR’s module on the topic of Lines and Angles consisted of three AR learning activities based on the 7th-grade Indian state board syllabus. The key objective of the designed activities was to enable the learners to understand the application of the topic in the real-world scenes and objects. Moreover, Lines and Angles being a topic of Geometry, the attempt was to help the learners attain the first three levels of van Hiele Theory of Geometry Thinking (Crowley 1987), i.e. visualization, analysis, and informal deduction/abstraction. “The activities were targeted to be solved by recalling the definition of the type of angle, visualizing that angle by forming its mental image, then mapping that mental image of the recalled angle on to the 3D object and finally drawing on top of the identified angle” (Sarkar et al. 2019a). There were three activities designed on the sub-topics of Lines and Angles chapter:
- 1)
Activity 1 - Types of Angles
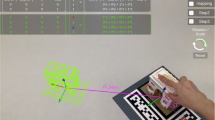
In this activity, the learning objective was that the participants will be able to identify and distinguish between acute, obtuse and right angles in their surrounding objects (Sarkar et al. 2019a). This activity required the participants to recall, visualize, identify and then mark three acute angles, three right angles, and three obtuse angles by moving around the augmented 3D house (Fig. 1). Level 0 of van Hiele’s theory of Geometric Thinking, i.e. Visualization was targeted through this activity. There were multiple possible solutions for each of the cases. Thus, the activity helped the students to get familiarised with the AR interface, the augmented 3D house, the interactions involved and the way to apply the learned concept.
- 2)
Activity 2 - Pairs of Angles
The learning objective of this activity was that the participants will be able to classify the different pairs of angles: complementary, supplementary, adjacent and linear pairs of angles in the examples of real-life objects (Sarkar et al. 2019a). This question had a unique answer, targeting level 1 of van Hiele’s theory. The contextualized question required the participants to find a wooden log on the right or left side of the 3D house (both were identical) for the carpenters to repair (Fig. 1). However, the condition was that the wooden log should be forming the common arm of an adjacent pair of angles. The pair of angles must also be forming a supplementary pair of angles, having one angle as acute.
- 3)
Activity 3 - Interior and Exterior Angles of a Triangle
The learning objective was that at the end of this activity, the students will be able to locate a polygon in their surroundings and practice calculating its sum of interior angles (Sarkar et al. 2019a). The more immersive experience was provided in this activity by letting the students go inside the 3D house and perform the activity. The activity was targeted at attaining level 2 of the van Hiele theory and was broken into smaller problems. In doing so, they were asked to go inside the 3D house and count the number of windows on the first floor of the 3D house. They were then asked to pick any of the windows and identify the type of polygon it is (Fig. 2). For the identified polygon, they had to draw the minimum number of triangles it formed. Then they had to calculate the sum of the interior angles of the window, by adding the sum of interior angles of every triangle drawn.
The overall framework of the Lines and Angles module of ScholAR is described in Fig. 3.
In the first study it was observed that beyond the cognitive difficulties, the participants faced certain issues with the AR interface and interactions. While drawing on the virtual 3D house, the marked lines were floating when the participants moved to the other side of the house. This made it difficult for them to show the facilitator(s) their final answers by overlaying the lines back on to the identified angles on the house. Moreover, the house would disappear on tapping with three fingers outside the house. Thus, certain amendments were done in the interactions for the next round of study. The lines drawn by the participants would snap on to the house to prevent the marked lines from floating on changing the perspective of the house while moving around. They could scale the 3D house the general way, i.e. by sliding two fingers closer and farther. Also, changes were done to prevent the augmented house from disappearing if the three fingers tap was done outside the detected plane of the house.
Methodology
Study 1
The objective of this study was to understand the perspectives and approaches taken by the students when they perform the AR learning activities individually or in dyads. In addition to that, it was required to know the motivating factor of the two groups in performing such activities. Thus, this study focused on the following research questions:
RQ1: What are the perspectives of and approaches taken by the students in solving the AR learning activities when they perform it in dyads and individually?
RQ2: What motivated the dyads in performing the AR learning activities as compared to the individuals?
Participants
This study was conducted with Indian sub-urban school students from a low-economic background. The school followed the blackboard teaching method with seldom use of the projector screens. Moreover, the school had only one section with a maximum of 30–40 students for each grade. It followed the state board syllabus. 27 students of 8th grade participated in the study through convenience sampling. Out of these 27 students, 6 students participated in the pilot study and the remaining 21 students participated in the main study. The topic of Lines and Angles for these participants was covered in their 7th grade. Hindi and English were the languages of instruction in their classroom as well as in our study. Before conducting the study, due consent was taken from the principal, teachers, participating students, and their parents. They were all informed about the study procedure and confidentiality of the data.
Pilot
The pilot study was conducted with 6 students from the same class. A protocol was designed to be followed during the study. Hence, through the pilot study, it was required to verify the delivery of instructions, timings, and steps for the overall execution of the protocol and the designed activities. Moreover, the data collection instruments to be used in the main study were also checked and refined accordingly.
Procedure
The two-groups pretest-posttest study was conducted in an empty classroom across 2 days in two slots per day of approximately 3 h each. A protocol was followed throughout to execute the task appropriately within the defined time duration of the study. Since the participants had studied the topic of Lines and Angles in the previous semester, around 6 months back, a revision session of 20 min was first conducted for them. It also helped us in ensuring that every student is aware of the topic and its related concepts while being a part of the study. The revision session was followed by a pretest of 20 min to evaluate their prior knowledge and understanding of the topic.
The students of a slot were then randomly distributed by picking chits, mentioning to perform the activities in dyads or individually. Overall 9 participants worked individually and 12 participants worked in dyads. After the distribution, an initial demo was shown to the participants to help them get acquainted with the interactions in the Lines and Angles module of ScholAR. The participants were then provided the tablets with the screen recorders on and asked to perform the three AR learning activities. Each of the three activities was initiated only when all the participants were able to solve the previous one. Their actions were video recorded throughout, where the cameras were placed at every corner of the room. Figure 4 shows the students performing the AR learning activities individually and in dyads. On completing the AR learning activities on the tablets, they were given a posttest paper of 20 min which was equivalent to the pretest. This was done to see if there was any improvement in their learning after using the AR application. The last phase of the study involved giving the participants questionnaires on the usability of the AR application and their motivation throughout the study. Both the questionnaires comprised questions to be answered in a 5-point Likert scale of Agreement, which took them around 20 min. Towards the end, each dyad and individually performing participant was interviewed with semi-structured questions.
Data sources and instruments
The aim of this study was to investigate the perspectives and approaches of the participants in solving the problems on the module of Lines and Angles of ScholAR. Multiple data sources and instruments were used in the study to answer the targeted research questions. The study was video recorded with the help of four cameras placed at every corner of the room. It helped in capturing the actions and interactions of the dyads while solving the AR learning activities. The interactions of each group with the AR interface on the tablet and the discussions while solving the AR learning activities were captured using the screen recorder. The equivalent pen and paper-based pre and posttest were conducted, comprising six questions assessing the first three levels of Bloom’s taxonomy (Sosniak 1994). One of the questions in the papers was similar to identifying angles as in the AR learning activities. This helped in evaluating if the participants were able to identify and mark angles in different real-life scenes shown to them.
The participants were also given questionnaires on usability developed from the System Usability Scale (SUS) questionnaire (Brooke 1996). This questionnaire consisted of 10 questions to be answered in a 5-point Likert scale of Agreement about their comfort and satisfaction in using the ScholAR application. Another questionnaire to measure the motivation in the study was given to the participants, developed from the Instructional Materials Motivation Survey (IMMS) (Song and Keller 2001). It comprised 36 questions to be answered in a 5-point Likert scale of Agreement on the motivation levels of the learners in the four dimensions of the ARCS (Attention, Relevance, Confidence, Satisfaction) model (Keller 1987). Among the 36 questions of IMMS, 12, 9, 9 and 6 items belonged to the scales measuring the attention, relevance, confidence, and satisfaction respectively. In order to reduce their cognitive load in answering 46 questions altogether, the participants were given five sheets, one after completing the previous one. There were 10 questions in the first four sheets and 6 questions in the last sheet. Answering the questionnaires was followed by a semi-structured interview for the dyads and individual participants. It captured the responses of the participants on their perceived preference for collaboration or individual work, their understanding of the concepts, areas of difficulties, challenges faced in using the intervention and suggestions if any.
Data analysis
In order to answer RQ1, video data and usability questionnaires were analyzed and thematic analysis was performed on the interview responses. RQ2 was analyzed by calculating the scores of the motivation questionnaire responses. There were 10 questions in the IMMS questionnaire which were reverse items. The lower scores given by the participants for these reverse items meant a high motivational score. The scores for these items were manually reversed before calculating the overall score.
Study 2
The objective of this study was to find the sequential behavior patterns of the dyads while performing the AR learning activities. This study focused on the following research question:
RQ3: What is the learning behavior pattern of the participating dyads while performing the AR learning activities?
This one-group pretest-posttest study was conducted in a rural school, where the students rarely used mobile phones on their own. The procedure of the entire study was the same as the earlier one. However, this study was conducted only with 14 dyads (N = 28) of 7th grade. Moreover, the students had recently covered the topic of Lines and Angles in their class, hence a quick revision of only 10 min was done by the teacher for these participants. The data sources and instruments in this study were also the same as the earlier study. However, the language of instruction and data instruments was as per the local language of the participants i.e. Marathi. To answer RQ3, the audio recordings from the tablet screen recordings were transcribed and translated to English. Based on the earlier study, we were able to generate certain codes that focused on the behaviors of the students while performing the AR learning activities. For all the three activities, Protocol Analysis (Ericsson and Simon 1984) of the tablet screen and video recordings of the participating groups were done. The codes, refined after the second study, have been classified into three categories: Peer Involvement, AR Interactions and Teacher Prompts also shown in Table 1.
To visualize the appearances of the behavioral sequences, lag sequential analysis (Bakeman and Gottman 1997) was performed. Two researchers coded the sequences of appearances of each dyad’s behaviors for every activity. The three activities generated 14 code strings in total, consisting of 2193 behavioral codes. The reliability coefficient came out to be 0.91% (Cohen’s kappa) between the two researchers generating the codes. The Z-scores of the sequences obtained were then calculated. The Z-scores of 1.96 or greater has been considered as it indicates a significant sequence (p < 0.05).
Results
Perspectives and approaches of students in solving AR learning activities
Thematic analysis was performed on the transcribed responses obtained from the semi-structured interviews. This helped in deriving key themes on the role of collaboration while performing the AR learning activities as shown in Table 2 (Sarkar et al. 2019a). Out of the 21 participants, only two participants preferred to perform the activities alone. One of them, who performed the activities individually, believed that a quarrel with the partner can arise while working together. They might have conflicts or be dominated by the other while marking the answers. The other participant belonging to the dyad group mentioned that the problems could be solved quickly on their own as they were taking time in discussing with the partner and explaining to each other before marking. Thus, the two participants felt that coordinating with the partners would have been difficult for them. The remaining 90.4% participants preferred performing the AR learning activities in dyads as it encouraged discussion with the partners. This further helped them in understanding the concepts better while they tried to explain the related concept to the partners, guided each other in taking quick actions and correcting mistakes. Moreover, they took alternate turns to solve the AR learning activities. They were reluctant to perform the activities individually as they perceived having difficulty in holding the tablet single-handedly, felt nervous and lacked confidence while marking the answers. Moreover, they perceived to have difficulty in understanding the questions, making it boring and like any other classroom activity while silently observing, thinking and marking the answers without any interaction. This would have also required more prompts or help from the facilitators. In this study, the prompts were provided by the facilitator(s) when the participants had difficulty in recalling the definitions or they would mark random lines and angles. The facilitators had to at times break down a question into smaller parts to help the participants respond by building upon the basic concept.
In terms of learnability, the dyads took 15, 20 and 5 min on average to solve activity 1,2 and 3 respectively. Whereas those performing individually took on an average, 17 and 25 min to solve activities 1 and 2 respectively. The latter group mostly tried to look into others’ tablet screens to find the answers or discuss the way to solve an activity. It was also observed that most of the participants had difficulty in recalling the definition or the property of a type of angle to be found and marked in an activity. Thus, in such a scenario, it required the facilitators to prompt with the definitions.
In terms of learning impact, the results from the pre and posttests were evaluated to analyze the effect of ScholAR’s module on Lines and Angles, on the participants’ learning. Table 3 gives the descriptive statistics derived from the normalized results of the pretest and posttest scores of those who participated in the study either by performing the AR learning activities individually or in dyads. It shows the means scores and standard deviation in the pre and posttest results for both the groups. The standard error obtained from the mean scores has been reflected on the bar chart as error bars in Fig. 5. The error bars represent the variability in the groups and test scores, giving a sense of whether or not a difference is significant.
Figure 5 represents the mean pretest and posttest scores of the participants who performed the AR learning activities either in dyads or individually along with the error bars. By looking at Fig. 5, it seemed that on comparing the overall performance of the dyads and those performing individually, there may be a significant difference between their performance. On observing the plotted pretest scores and the posttest scores, it seemed like the posttest scores may be significantly higher than the pretest scores. Also, it was interesting to investigate if there is a significant difference in the pretest and posttest scores of the dyads as there was slight overlap in the error bars. Similarly, as the overlap is quite a bit in the error bars, indicating that there is no significant difference in the pretest and posttest scores of those who performed the AR learning activities individually, it was required to statistically investigate the same.
To test the normality of the data, Shapiro-Wilk Test was done. At ɑ = 0.05, the statistical test on the scores of pretest (p = 0.832) and posttest (p = 0.912) for those who performed the AR learning activities individually indicated that the data was normally distributed. Similarly, at ɑ = 0.05, the statistical test on the scores of pretest (p = 0.661) and posttest (p = 0.085) for those who performed the AR learning activities in dyads indicated that the data was normally distributed. On attaining the normality, a paired sample t-test was done on the scores obtained from the pre and posttest results. At ɑ = 0.05 (t = − 0.34, p = 0.37), there was no significant difference in the pretest scores of the participants before performing the AR learning activities individually and in dyads. However, at ɑ = 0.05 (t = 2.21, p = 0.048), the dyads performed significantly higher after interacting with the AR-based module, which is indicated in Fig. 5. Moreover, at ɑ = 0.05 (t = 0.86, p = 0.41), there was no significant difference in the performance of the participants who solved the AR learning activities individually. This indicated that the peer discussion and correction of mistakes, as stated by the participants during the interview, might have led to the dyads understanding and performing better after performing the AR learning activities. Since the test scores have been evaluated for the pre and posttest results of the same participants belonging to either of the two groups (individuals and dyads), one-way ANOVA with repeated measures was calculated. This statistical test is used for the analysis of variance between two or more groups. The between-group ANOVA indicated no statistical difference (F(2,21) = 0.003, p = 0.956, ɑ = 0.05). As there was no significant difference between groups, ANOVA could not be followed by a post-hoc test to tell which means differ.
In terms of likeability, the participants had varied reasons for liking a particular AR learning activity. Activity 1 was liked the most by 1 participant who performed individually and 2 participants from the dyads. They found this activity to be basic and easiest as compared to the other two activities. Activity 2 was the most liked one for 2 participants who performed individually and 2 participants from the dyads, for being able to quickly solve this activity as compared to other participants. Activity 3 was liked the most by the remaining participants as this activity caused excitement in them while being able to go inside and come outside the house by physically moving back and forth. Moreover, they took the least time to solve this activity as it was broken into smaller problems which helped the participants solve them quickly. Moreover, the participants had by then got acquainted with the AR medium by performing two other activities viz. Activity 1 and Activity 2, which can be treated as their training and practice. For each of these activities, there were dislikes as well. The inability to recall the basic definition of an obtuse angle made it difficult for 1 participant from dyad and 2 participants performing individually to least like this activity. The similar difficulty in Activity 2, for not being able to recall the properties of supplementary pairs of angles, made it the least liked one for 5 participants who performed individually. Two participants from dyads and 1 performing individually least liked Activity 3 for not being able to recall the sum of interior angles of a triangle to be 180°.
In terms of the experience of using the AR technology on the tablets, the participants perceived to have been able to focus and concentrate while performing the AR activities that were based on the syllabus. They realized the affordances of AR by stating that moving around the 3D house as well as being able to go inside and come outside the house helped them in having an immersive and engaging experience which is otherwise not possible while seeing a 2D image of a 3D example in the textbooks. Moreover, they perceived that the ability to draw on the 3D house gave them the experience similar to drawing on a sheet, with a lesser effort to erase a mistake. Thus, the majority participants preferred learning using AR activities in place of their usual classroom teaching method that made them copy the taught concepts in their notebooks. They stated that the fun, interesting and active way of learning using the AR activities helped them to “watch, do and learn the concepts” themselves.
In terms of usability, the responses from the SUS questionnaire were evaluated to obtain the score for the designed ScholAR’s module on Lines and Angles. The average score of 68 is considered to be a standard score for a designed system. The overall SUS score for the designed AR module with three learning activities came out to be slightly less than the standard score i.e. 67.74. The SUS score for individually performing participants was 70.28, higher than the dyads who scored 65.83. This implies that in order to incorporate the perceived experience of the learners to collaboratively perform the AR learning activities, the system needs further improvements and amendments.
Motivation in performing the AR learning activities
The reliability of motivation questionnaire data was obtained using Cronbach alpha value (Wessa 2017). A Cronbach alpha value greater than or equal to 0.70 is considered to be an acceptable value and a value greater than or equal to 0.80 is considered to be a good value (Namdeo and Rout 2016). The overall Cronbach Alpha (N = 21 on 36 items) was found to be 0.91 indicating good reliability (Namdeo and Rout 2016). The Cronbach value for the items of the scale of Attention (0.71), Relevance (0.75), Confidence (0.70) and Satisfaction (0.88) indicated to be reliable.
The overall mean motivation score was 3.99 (N = 21), which was positive enough. The minimum and maximum overall mean motivation level scores were 2.58 and 4.64 respectively. The former score was that of a participant who performed the AR learning activities in dyad and the participant scoring the latter performed the AR learning activities individually. Different motivation score ranges were obtained on dividing the motivation level scores into low (< 3.00), medium (3.00–3.49), upper-medium (3.50–3.99) and high (4.00–5.00) ranges (Huang and Hew 2016). From the scores it could be observed that 47.2% (N = 10) fell in the range of having high motivation level scores. Similarly 47.2% (N = 10) also had upper-medium motivation level scores. No participant belonged to having a medium motivation level score. Whereas, only 4.76% (N = 1) belonged to having a low motivation level score.
Fig. 6 reflects the mean motivation level scores for all items from the four scales of the ARCS model. The highest motivation level score (M = 4.62) was that of Item 3 of Relevance scale i.e. “completing this study successfully was important to me”. The lowest motivation level score (M = 2.71) was of Item 3 of Confidence scale i.e. “After the revision at the beginning of the study, I felt confident that I knew what I was supposed to learn from this study” score. The mean motivation level score of Attention, Relevance, Confidence, and Satisfaction were 3.99, 4.05, 3.82 and 4.16 respectively. This indicated that the participants were quite satisfied with exploring the ScholAR’s module on Lines and Angles. However, as they were using the AR technology on a tablet for the first time, they might be under confident in using it.
The ones performing the AR learning activities individually had a slightly higher motivation level score (M = 4.07) as compared to the ones performing in dyads (M = 3.94). To check the statistical significance, the motivation level scores of the dyads and individuals were compared by conducting unpaired t-test. It seemed that there was no significant difference at ɑ = 0.05 (t = 0.69, p = 0.49) in the motivation level scores of the participants performing the AR learning activities in dyads and individually.
Learning behavior patterns in performing the AR learning activities
In the follow-up study, the participants were made to perform the activities in dyads. In order to understand their interaction patterns while performing the AR learning activities in dyads, lag sequential analysis (Bakeman and Gottman 1997) was used to identify the patterns based on the defined categories and related behavior (Table 1).
The significant sequences are shown in Fig. 7. In the shown diagram, the arrow indicates the direction of transfer for each sequence and the thickness represents the level of significance. These sequences can be read from anywhere as there is no starting point. The numerical value on each arrow represents the Z-score of the significant sequence. In total, 32 sequences with significant z-scores have been depicted in the diagram.
A bi-directional sequence between P7 ⇄ D1 and P7 ⇄ D3 indicates that the dyads discussed and tried to help each other to correctly draw the identified angles. However, on identifying the angles on the 3D house, one of the participants in the dyad would keep drawing until neat lines and angles for the final answers have been obtained, indicated by the bi-directional sequence between P8 ⇄ D4.
The two most significant sequences were M1 → P6 and M1 → P10 indicating that the participants were immersed in the AR experience of viewing the 3D house from all sides to find the answers. In doing so, the dominant behavior was both the participants moved together around the 3D house while holding the tablet.
The cyclic sequence of TP1 → S2 → P11 indicated that the participants required prompts from the teacher to scale the house using the feature of two-finger sliding on the screen, which was followed by one of the participants in the dyads asking the partner to hold the tablet while trying to scale the 3D house. Another cyclic sequence D2 → P5 → P3 was observed showing that if one of the participants in a dyad drew the wrong angle as the answer, the other partner would correct it and both would discuss where to mark the answer correctly. The third cyclic sequence of P9 → P1 → P2 indicated that in case of any discussion that was irrelevant to the study, the dyads would get back to understanding the problem and explain to each other the related concept.
P3 had the highest frequency of significant sequential relationships among the behaviors of peer involvement, including P10 → P3, P6 → P3, P5 → P3, P3 → D2, and P3 → D4. This described that the answers by a dyad were marked predominantly after peer discussion.
Discussion
The first research question was targeted towards identifying the perspectives and approaches of the participants while performing the AR learning activities individually or in dyads. From the findings of our study and the study by Chen 2008, it was seen that peer collaboration was the preferred mode for the participants to perform the AR learning activities on the tablets. The key reasons for such a preference included the ability to discuss the visualized and identified angles as the answers with the peer while clarifying the concept and reason for marking that on the virtual 3D house. In doing so, minimal teacher prompts are required and the tablet can be comfortably held with the partner’s assistance to confidently answer and mark the angles. Moreover, a positive learning impact of performing the AR learning activities in dyads got reflected in the pre-post test scores as compared to those performing individually. The dyads performed significantly higher at ɑ = 0.05 (t = 2.21, p = 0.048). The participants perceived to have been able to relate the posttest problems with the activities they performed using AR on the tablets, making it easier to solve as compared to the pretest problems. This finding was, however in contrast to the findings by Chen 2008, where the participants were not able to perform better while solving their designed AR learning activities in dyads. The participants also perceived that with the help of the AR learning activities, they were able to apply the learned concepts in a fun and engaging manner. This is otherwise not possible as they only jot down the concepts and related properties being taught by the teachers in the classrooms and solve a few related problems in their notebooks. Thus, as stated in earlier studies that with the AR lessons the students can gauge the learning and progress (Cai et al. 2019), the participants mentioned having realized the relevance of the immersive and interactive nature of AR. They regarded it as a means of watching the interactions in real-time and performing the activities themselves. This further helped them in concentrating and understanding the related concepts better. Studies have also revealed that students are able to retain content more with the help of AR mediums (Radu 2012). Similarly, the participants considered that repetition with the practical application helped them in understanding the concept better as compared to learning in the classroom in the traditional way.
In terms of AR interactions, the feature of manually rotating the house was disabled in our application in order to provide them the immersive experience of moving around the augmented 3D house. This was done as the learning experience tends to enhance through physical movement (Wilson 2002). One-third participants had difficulty in recalling the definition of an obtuse angle which took them time to identify and mark one. Also, they had difficulty in visualizing and marking the angles in the mirrored reference i.e. 0° to 360° in the clockwise direction. Thus, prompts from the facilitators were required at times when the participants faced difficulty in recalling the definition or properties of a certain type of angle. The facilitator had to break down the contextual problem in Activity 2 to smaller questions for the participants to easily visualize the required angles. The participants were most excited to solve Activity 3 as they could go inside the 3D house and explore the multiple floors in a way they would actually explore a real house. This activity took them the least time to solve as the problem was already broken into six smaller problems. Hence, this became the most like activity. The overall average usability score was slightly less than the standard score 68 for a system to be considered to have a good design. This implies that the system needs to be re-designed to tackle the conceptual and interaction difficulties that the students faced while using the current system.
It has been reported previously that learning Mathematics with AR enhances motivation (Estapa and Nadolny 2015). Hence, the second research question was aimed at evaluating the motivation levels of the participants belonging to the two groups, while performing the AR learning activities of ScholAR’s module on Lines and Angles. With the IMMS questionnaire, the motivation levels of the participants were measured in the four dimensions of ARCS (Attention, Relevance, Confidence, Satisfaction) model. The overall highest score was given to Item 3 of Relevance scale (M = 4.62). This indicated that the participants believed it was important for them to complete the AR learning activities as it would help them in applying the learned concepts in a way different from the usual way of learning in the classroom. On the contrary, Item 3 of the Confidence scale was given the least score (M = 2.71). This indicated that after the revision, the participants were not confident that they knew what they were supposed to learn from this study. The probable reason could be their difficulty in recalling the definitions of the different types of angles, which required the assistance of their partners or the facilitators. Beyond the difficulties, the overall motivation of the participants was positive enough (M = 3.99), indicating that the ScholAR’s module on Lines and Angles kept them motivated throughout to apply the learned concepts in an immersive and interactive manner.
Based on the findings from the first study, the second study was performed with only dyads, with minor changes to the design of the AR interactions. The third research question targeted towards identifying the sequences and learning behavior patterns of the participants while they performed the three AR learning activities. It was evident from the results that the participants discussed most on where to mark the angle on the 3D house. Thus P3 was the most predominant behavior among the peer involvement behaviors as it was involved in five significant sequences. In terms of the AR interactions, the participants in a dyad significantly moved together to change the side of the house (indicated by the significant sequence of M1 → P6) and moved forward or backward to scale the house. The other scaling feature by sliding the two fingers on the screen was not quite intuitive for the participants. Hence, they had to be often prompted by the teacher to scale the house by sliding the two fingers. This resulted in a significant cyclic sequence of TP1 → S2 → P11. The participants in a dyad also helped each other to mark the angles by correcting each other wherever needed. This was validated by three significant sequences of P7 ⇄ D1, P7 ⇄ D3 and the cyclic sequence of D2 → P5 → P3. Moreover, the participants explored the feature of AR by the ability to move around the house from all sides, which was indicated by the most significant sequence of M1 → P6 and M1 → P10. The significant sequences thus mentioned, were relatable to the perceived notions of the participants in the first study. Hence, the peer participation and immersive experience of AR as perceived by the participants in the first study could be validated through the significant sequences in the second study.
From the findings, it can be implied that the ScholAR’s module on Lines and Angles when used in collaboration by dyads, can be a worthy supplement to be used in the classrooms. This would further help in bringing active participation among the students while they would explore the practical applications of the learned concepts in real-time. The augmented 3D object can be a virtual example from the surrounding that can be superimposed and explored from all sides as is done with any real object. The teachers can then frame their own questions to find the ability of the students in identifying a type of angle in the augmented 3D object. However, there is a requirement to make changes in the design of the application for satisfactory use by the dyads, with minimal teacher prompts.
Conclusion
The article reports the results from two studies. The first study was a comparative one where participants performed the AR learning activities either individually (N = 9) or in dyads (N = 12). The aim of the study was to identify the perspectives of the participants belonging to the two groups, their ways of approaching the AR-based problems on Lines and Angles and motivation during the study. In doing so, two research questions were targeted. RQ1 focused on the perspectives and approaches of the participants while performing the AR learning activities. From the different data instruments, the findings implicated that 90.4% of total participants (N = 21) were motivated towards performing the AR learning activities in dyads rather than individually. They perceived that solving the AR-based problems on the tablets collaboratively in dyads would help them in understanding the concepts better through peer discussion and then confidently drawing the identified angles. In support of the perceived notion, the learning impact got reflected through their pre and posttest scores as the dyads performed significantly higher at ɑ = 0.05 (t = 2.21, p = 0.048). Moreover, the dyads took comparatively lesser time to solve the three AR learning activities. As along with the least time taken to solve the question that was put forth as multiple smaller problems, Activity 3 involved the ability and the immersive experience of going inside and coming outside the 3D house. Hence it was the most liked activity among the majority. However, in terms of usability, the participants performing individually were more satisfied with using the AR application. The probable implication is that the motivating factor for the former group might have been satisfactorily investing comparatively more time in solving the AR learning activities. While answering RQ2, it was seen that the mean motivation level score of the ones performing the AR learning activities individually (M = 4.07) was higher as compared to the dyads (M = 3.94). However, there was no statistical difference.
The follow-up study focused on answering RQ3 that derived the learning behavior patterns while performing the three AR learning activities in dyads (N = 28). This was done by using lag sequential analysis on the appearances of the behaviors coded under the categories of peer involvement, teacher prompts and AR interactions. It was observed that the participants significantly discussed the concepts and marked the angles after discussing them with their peers. Moreover, the immersive experience of moving around the 3D house as well as going inside and coming out of the house was the most significant behavior. The teacher prompts were majorly required for indicating to scale the 3D house by sliding the two fingers on the screen of the tablet.
The reported studies analyse the approaches of the participants who performed the designed AR learning activities either individually or in dyads. The studies were conducted with small sample sizes. This led to the limitation of having an in-depth analysis with larger sample size. Moreover, the lack of a control group might limit the conclusions of the studies reported here as it cannot confirm that the use of AR might be better than a traditional class. Hence, a control group with a comparable number of participants would have reflected upon the effectiveness of the AR medium as compared to the traditional mode of teaching in classrooms. Also, the pretest was conducted before using the AR medium, which might have affected the results of the pretest. Additionally, it is difficult to operationalize and fully measure the complex psychological construct of motivation using self-reported instruments. However, in the reported studies the motivation was measured by Instructional Materials Motivation Survey (IMMS) (Song and Keller 2001), by obtaining the reliability of motivation questionnaire using Cronbach alpha value (Wessa 2017).
Thus, in future studies, the sample size is required to be larger to have more concrete results and arguments. Moreover, the current system needs design amendments to incorporate the stated perspectives of collaboratively using it in dyads, the prompts with the related concepts and real-time feedback by the system for the answers drawn by the participants. This should further help in having significant results for the usability and motivation level scores while the dyads perform the AR learning activities. Furthermore, the AR learning activities will be designed for other topics in Mathematics based on the syllabus of 7th grade to begin with and gradually for other grades.
Availability of data and materials
The datasets generated and/or analyzed during the current study are not publicly available due to them containing information that could compromise research participant privacy/consent but are available from the corresponding author on reasonable request.
Abbreviations
- AR:
-
Augmented reality
- ARCS:
-
Attention, relevance, confidence, satisfaction
- IMMS:
-
Instructional materials motivation survey
- RQ:
-
Research question
- STEM:
-
Science, technology, engineering and mathematics
- SUS:
-
System usability scale
References
Azuma, R. T. (1997). A survey of augmented reality. Presence Teleoperators and Virtual Environments, 6(4), 355–385.
Bakeman, R., & Gottman, J. M. (1997). Observing interaction: An introduction to sequential analysis. United Kingdom: Cambridge university press.
Banu, S. M. (2012). Augmented reality system based on sketches for geometry education. In 2012 International Conference on E-Learning and E-Technologies in Education (ICEEE) (pp. 166–170). Lodz: IEEE. https://doi.org/10.1109/ICeLeTE.2012.6333384.
Biber, Ç., Tuna, A., & Korkmaz, S. (2013). The mistakes and the misconceptions of the eighth grade students on the subject of angles. European Journal of Science and Mathematics Education, 1(2), 50–59.
Brooke, J. (1996). SUS-A quick and dirty usability scale. Usability evaluation in industry, 189(194), 4–7.
Bujak, K. R., Radu, I., Catrambone, R., MacIntyre, B., Zheng, R., & Golubski, G. (2013). A psychological perspective on augmented reality in the mathematics classroom. Computers in Education, 68, 536–544.
Bütüner, S. Ö., & Filiz, M. (2017). Exploring high-achieving sixth grade students’ erroneous answers and misconceptions on the angle concept. International Journal of Mathematical Education in Science and Technology, 48(4), 533–554.
Cai, S., Liu, E., Yang, Y., & Liang, J. C. (2019). Tablet-based AR technology: Impacts on students’ conceptions and approaches to learning mathematics according to their self-efficacy. British Journal of Educational Technology, 50(1), 248–263.
Chen, Y. C. (2008). Peer learning in an AR-based learning environment. In 16th international conference on computers in education (pp. 291–295).
Crowley, M. L. (1987). The van Hiele model of the development of geometric thought. Learning and teaching geometry, K-12, 1–16.
Dunleavy, M., Dede, C., & Mitchell, R. (2009). Affordances and limitations of immersive participatory augmented reality simulations for teaching and learning. Journal of Science Education and Technology, 18(1), 7–22.
Edwards, J. A., & Jones, K. (2006). Linking geometry and algebra with GeoGebra. Mathematics Teacher, 194, 28–30.
Ericsson, K. A., & Simon, H. A. (1984). Protocol analysis: Verbal reports as data. Cambridge: The MIT press.
Estapa, A., & Nadolny, L. (2015). The effect of an augmented reality enhanced mathematics lesson on student achievement and motivation. Journal of STEM Education: Innovations and Research, 16(3), 40–48.
Huang, B., & Hew, K. F. T. (2016). Measuring learners’ motivation level in massive open online courses. International Journal of Information and Education Technology 6(10), 759–764. https://doi.org/10.7763/IJIET.2016.V6.788.
İbili, E., Çat, M., Resnyansky, D., Şahin, S., & Billinghurst, M. (2020). An assessment of geometry teaching supported with augmented reality teaching materials to enhance students’ 3D geometry thinking skills. International Journal of Mathematical Education in Science and Technology, 51(2), 224-246.
Isotani, S., & de Oliveira Brandão, L. (2008). An algorithm for automatic checking of exercises in a dynamic geometry system: iGeom. Computers in Education, 51(3), 1283–1303.
Jones, K. (1998). Theoretical frameworks for the learning of geometrical reasoning. Proceedings of the British Society for Research into Learning Mathematics, 18(1–2), 29–34.
Kaufmann, H., & Schmalstieg, D. (2002, July). Mathematics and geometry education with collaborative augmented reality. In ACM SIGGRAPH 2002 conference abstracts and applications (pp. 37–41).
Kaur, N., Pathan, R., Khwaja, U., Sarkar, P., Rathod, B., & Murthy, S. (2018). GeoSolvAR: Augmented reality based application for mental rotation. In 2018 IEEE Tenth International Conference on Technology for Education (T4E) (pp. 45–52). Chennai: IEEE. https://doi.org/10.1109/T4E.2018.00017.
Keller, J. M. (1987). Development and use of the ARCS model of instructional design. Journal of Instructional Development, 10(3), 2.
Koyuncu, I., Akyuz, D., & Cakiroglu, E. (2015). Investigating plane geometry problem-solving strategies of prospective mathematics teachers in technology and paper-and-pencil environments. International Journal of Science and Mathematics Education, 13(4), 837–862.
Liao, Y. T., Yu, C. H., & Wu, C. C. (2015). Learning geometry with augmented reality to enhance spatial ability. In 2015 international conference on learning and teaching in computing and engineering (pp. 221-222). Taipei: IEEE. https://doi.org/10.1109/LaTiCE.2015.40.
McClintock, E., Jiang, Z., & July, R. (2002). Students’ development of three-dimensional visualization in the Geometer's Sketchpad environment.
Namdeo, S. K., & Rout, S. D. (2016). Calculating and interpreting Cronbach’s alpha using Rosenberg assessment scale on paediatrician’s attitude and perception on self esteem. International Journal of Community Medicine and Public Health, 3(6), 1371–1374.
Narayana, S., Prasad, P., Lakshmi, T. G., & Murthy, S. (2016). Geometry via gestures: Learning 3D geometry using gestures. In 2016 IEEE Eighth International Conference on Technology for Education (T4E) (pp. 26–33). Mumbai: IEEE. https://doi.org/10.1109/T4E.2016.014.
Ojose, B. (2008). Applying Piaget's theory of cognitive development to mathematics instruction. Mathematical Education, 18(1), 26–30.
Özerem, A. (2012). Misconceptions in geometry and suggested solutions for seventh grade students. Procedia - Social and Behavioral Sciences, 55, 720–729.
Papagiannakis, G., Singh, G., & Magnenat-Thalmann, N. (2008). A survey of mobile and wireless technologies for augmented reality systems. Computer Animation and Virtual Worlds, 19(1), 3–22.
Peng, H., Su, Y. J., Chou, C., & Tsai, C. C. (2009). Ubiquitous knowledge construction: Mobile learning re-defined and a conceptual framework. Innovations in Education and Teaching International, 46(2), 171–183.
Radu, I. (2012). Why should my students use AR? A comparative review of the educational impacts of augmented-reality. In 2012 IEEE International Symposium on Mixed and Augmented Reality (ISMAR) (pp. 313-314). Atlanta: IEEE. https://doi.org/10.1109/ISMAR.2012.6402590.
Ramdhani, M. R., Usodo, B., & Subanti, S. (2017). Discovery learning with scientific approach on geometry. In Journal of Physics: Conference Series (Vol. 895, no. 1, p. 012033). IOP Publishing. http://dx.doi.org/10.1088/1742-6596/895/1/012033..
Sarkar, P., Kadam, K., & Pillai, J. S. (2019a). Collaborative approaches to problem-solving on lines and angles using augmented reality. In 2019 IEEE Tenth International Conference on Technology for Education (T4E) (pp. 193-200). Goa: IEEE. https://doi.org/10.1109/T4E.2019.00-24.
Sarkar, P., & Pillai, J. S. (2019). User expectations of augmented reality experience in indian school education. In Research into Design for a Connected World (pp. 745–755). Singapore: Springer.
Sarkar, P., Pillai, J. S., & Gupta, A. (2018). ScholAR: A collaborative learning experience for rural schools using augmented reality application. In 2018 IEEE Tenth International Conference on Technology for Education (T4E) (pp. 8-15). IEEE.
Sarkar, P., Sakhardande, P., Oza, U., & Pillai, J. S. (2019b). Study of augmented reality interaction mediums towards collaboratively solving open-ended problems. In International Conference on Computers in Education (pp. 472–477).
Song, S. H., & Keller, J. M. (2001). Effectiveness of motivationally adaptive computer-assisted instruction on the dynamic aspects of motivation. Educational Technology Research and Development, 49(2), 5.
Sosniak, L. A. (1994). In L. W. Anderson (Ed.), Bloom’s taxonomy. Chicago: Univ. Chicago press.
Squire, K., & Klopfer, E. (2007). Augmented reality simulations on handheld computers. The Journal of the Learning Sciences, 16(3), 371–413.
Straesser, R. (2002). Cabri-geometre: Does dynamic geometry software (DGS) change geometry and its teaching and learning? International Journal of Computers for Mathematical Learning, 6(3), 319–333.
Wessa, P. (2017). Cronbach alpha (v1. 0.5) in free statistics software (v1. 2.1). Office for Research Development and Education.
Wilson, M. (2002). Six views of embodied cognition. Psychonomic Bulletin & Review, 9(4), 625–636.
Zbiek, R. M., Heid, M. K., Blume, G. W., & Dick, T. P. (2007). Research on technology in mathematics education: A perspective of constructs. Second handbook of research on mathematics teaching and learning, 2, 1169–1207.
Acknowledgments
We are thankful to the school principals, teachers, students and their parents for giving us the consent and their valuable time to conduct the studies. Special mention of Mr. Pankaj Parekh from Anandacare Trust for connecting us to the rural school. Thanks to Amarnath Murugan for technical assistance and development. We are also grateful to the volunteers from IIT Bombay - Amal Dev, Madhuri S., Angela Simon, Shraddha Dhodi and Suraj Kendre.
Funding
This work is supported by TATA Centre for Technology and Design, IIT Bombay (No. DO/2018-TATA001–127).
Author information
Authors and Affiliations
Contributions
The first author contributed to system design, study design, and data analysis. The first and second authors conducted the studies. The second and third authors provided supervision of the research. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
IIT Bombay Institute Ethic Committee (No. IITB-IEC/2019/019) approved the research proposal submitted.
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sarkar, P., Kadam, K. & Pillai, J.S. Learners' approaches, motivation and patterns of problem-solving on lines and angles in geometry using augmented reality. Smart Learn. Environ. 7, 17 (2020). https://doi.org/10.1186/s40561-020-00124-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40561-020-00124-9