Abstract
Continuous high-resolution gravimetry is increasingly used to monitor mass distribution changes in volcanic, hydrothermal or other complex geosystems. To quantify the often small target signals, gravity contributions from, e.g. atmospheric mass changes, global and local hydrology should be accounted for. We set up three iGrav superconducting gravity meters for continuous monitoring of the Þeistareykir geothermal field in North Island. Additionally, we installed a set of hydrometeorological sensors at each station for continuous observation of local pressure changes, soil moisture, snow and vertical surface displacement. We show that the contribution of these environmental parameters to the gravity signal does not exceed 10 µGal (1 µGal = 10–8 m s−2), mainly resulting from vertical displacement and snow accumulation. The seasonal gravity contributions (global atmosphere, local and global hydrology) are in the order of ± 2 µGal at each station. Using the environmental observations together with standard gravity corrections for instrumental drift and tidal effects, we comprehensively reduced the iGrav time-series. The gravity residuals were compared to groundwater level changes and geothermal mass flow rates (extraction and injection) of the Þeistareykir power plant. The direct response of the groundwater levels and a time-delayed response of the gravity signal to changes in extraction and injection suggest that the geothermal system is subject to a partially confined aquifer. Our observations indicate that a sustainable “equilibrium” state of the reservoir is reached at extraction flow rates below 240 kg s−1 and injection flow rates below 160 kg s−1. For a first-order approximation of the gravity contributions from extracted and injected masses, we applied a simplified forward gravity model. Comparison to the observed gravity signals suggest that most of the reinjected fluid is drained off through the nearby fracture system.
Similar content being viewed by others
Introduction
Many geoscientific studies make use of continuous terrestrial gravity measurements to estimate subsurface mass changes associated with, for example, groundwater flow (Watlet et al. 2020), volcanic activity (Jousset et al. 2000; Carbone et al. 2019) or exploitation of geothermal reservoirs (Portier et al. 2018). Additional gravity effects from environmental phenomena, like Earth tides, atmospheric pressure changes, rain and snowfall superimpose onto the target signals of the gravity time-series and have not been always considered, making interpretation inaccurate when gravity variations are small. The amplitudes of the environmental contribution in the recorded gravity signals range from a few hundred nGal (e.g. sea level rise) to several hundreds of µGal (e.g. large volcanic eruptions) and vary from seconds to years (Boy and Hinderer 2006; Damiani 2014). Mikolaj et al. (2019) pointed out the need to account for gravity contributions from atmospheric mass displacement, large-scale hydrology and nontidal ocean loading when performing local geophysical applications of terrestrial gravity measurements. They quantified the uncertainties of these corrections to be in the order of a few µGal, depending on the locations and the time scale of the mass variations of interest. Gitlein et al. (2013) modelled the combined gravity contributions of local and global atmospheric mass changes and applied them for reduction of superconducting gravity data, which improved the residuals by about 15% compared to the standard air pressure reduction with an admittance of −0.3 µGal hPa−1. Voigt et al. (2021) used a superconducting gravity meter for hydrological monitoring of Mount Zugspitze and identified the snowpack as the primary contributor to seasonal water storage variations, with a snow-gravimetric footprint (i.e. snow related gravity contributions > 10–4 µGal) of up to 4 km distance around the gravity meter. In addition to environmental gravity contributions, artefacts of the gravity meter like instrumental drift or self-noise may decrease the accuracy of the target signal (Crossley et al. 2004; Rosat and Hinderer 2018). With respect to long-term drift rates, Schäfer et al. (2020) showed the impact of transporting a superconducting gravimeter. Therefore, an accurate estimation and reduction of instrumental drift and environmental contributions is essential before we can interpret the gravity residuals accurately with respect to a specific geophysical phenomenon.
With the aim of estimating subsurface mass changes associated with geothermal exploitation (geothermal fluid extraction and reinjection), we set up a network of three continuously recording and remotely operated iGrav superconducting gravity meters, together with GNSS stations and hydrometeorological sensors (humidity sensors, snow gauges, pressure sensors, temperature sensors, etc.) at Þeistareykir, a geothermal field in North Iceland. This region is part of the North Volcanic Zone and is located close to the Husavik fault (Gudmundsson et al. 1993) and the Krafla Caldera (Ármannsson et al. 1987). Surface deformation and seismic activity associated to the mid-oceanic ridge have been monitored in Iceland for over 50 years (Sturkell et al. 2006). Surface explorations at Þeistareykir in the 1970s and 1980s suggested beneficial reservoir temperatures (< 280 °C), which was confirmed after exploration well drilling between 2002 and 2012 (Óskarsson 2015). We started our observations in December 2017 shortly after a new geothermal power plant (with 90 MWe total capacity) started operation in Þeistareykir. Figure 1 shows the location of the three superconducting gravity (SCG) stations. The east station (SCGE, iGrav032) is positioned in the vicinity of the geothermal extraction wells and the west station (SCGW, iGrav006) is located close to the reinjection wells. In June 2019, we started continuous measurements with iGrav015 at the central station (SCGC), in the transient area between geothermal extraction and injection. Schäfer et al. (2020) provide further details about the gravity station setup and the continuous observation chronology. Gravity observations are subject to various environmental contributions (e.g. rain, snow and soil humidity). Therefore, we deployed a series of instruments for measuring environmental parameters, which contribute to the total recorded gravity signal. Over more than three years, we acquired a unique data set of high-resolution gravity and environmental time-series. We developed and applied an approach to reduce all environmental effects that may hide the geothermal mass changes.
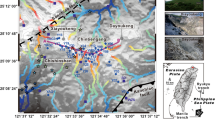
Location of the three continuous gravity stations (red stars) at Þeistareykir geothermal field in North Iceland; the east station (SCGE, iGrav032) is positioned in the vicinity of the geothermal extraction wells (well pads marked by red circles, orange lines show subsurface well paths), the west station (SCGW, iGrav006) is positioned in the vicinity of the reinjection well pad (green square) close to the Tjarnarás fault (yellow dashed line), the central station (SCGC, iGrav015) is positioned between the extraction and injection zones; groundwater level monitoring wells (GWL, blue triangles)
Methods for quantifying the gravity contributions
In this work, we assess the contributions of different geophysical phenomena to the observed gravity signals, based on observations and models. Equation 1 shows the gravity contributions examined in our study:
These include gravitational effects induced by solid Earth and ocean tides Δgtide, local atmospheric mass changes Δgatm, polar motion Δgpm, global atmosphere, large-scale hydrology and nontidal ocean loading Δgglob, local hydrology in terms of soil moisture changes Δghydr, snow Δgsnow, vertical surface displacement Δh with the vertical gravity gradient δg/δh and geothermal mass changes Δggeoth. The “Error” in Eq. 1 consists of further gravity contributions like magma-induced mass changes from volcanic activity that are neglected in this study. For interpretation of geothermal-related mass changes, we identified and reduced the interfering gravity effects that superimpose onto the target signal. To assess the contribution of the local environmental parameters in the gravity records, we analysed the continuous hydrometeorological measurements from remotely operated multiparameter stations (ROMPS; Schöne et al. 2013) at each site. Fig. 11 in the Appendix shows top view sketches of the ROMPS sensors and gravity containers for the three gravity stations. In the following subsections, we describe details of the instruments, the methods and the models for these individual gravity contributions, and we show the environmental signals recorded at Þeistareykir. In addition to the environmental parameters from Eq. 1, we also give a summary about the contribution and correction of instrumental drift.
Earth tides, local pressure effects, polar motion and instrumental drift
The largest gravity signal results from the solid Earth and ocean tides and is estimated by tidal modelling (Agnew 2015). Besides the tidal parameters, we also estimated the barometric admittance factor for each station to be later used for the local pressure residual of the total atmospheric effect (see “Global gravity contributions” below). Both, local tidal models and barometric admittance factors were computed for each gravity station at Þeistareykir using the ETERNA 3.4 package (Wenzel 1996). Results of the tidal analyses are given in the Appendix (chap. A1, A2 and A3). Due to the small distance of less than 2 km between the gravity stations, no significant changes of the tidal parameters were observed; with the main tidal waves varying by less than 1% in amplitude factors and less than 1 degree in phase. Therefore, we applied one uniform model for all three stations comprising the modelling results of SCGW and theoretical long period tidal parameters from solid Earth and ocean tides models (chap. A4, Appendix). The polar motion effect is provided as Earth orientation parameter file by the International Earth Rotation and References Systems Service (IERS; https://hpiers.obspm.fr/eoppc/eop/eopc04/, Accessed 05 November 2021). We used the TSoft package (Van Camp and Vauterin 2005) for computation of the associated gravity contributions. Detailed explanation of these standard corrections is given in Schäfer et al. (2020).
We examined and corrected the individual drift behaviour of the instruments by comparison to absolute gravity measurements (Hinderer et al. 2015). For this, we performed absolute gravity campaigns (with FG5#206) at each station once every year and adjusted the continuous time-series to the absolute values. Figure 12 in the Appendix shows the drift corrections for the iGrav time-series between December 2017 and October 2020. The uncertainties of the FG5#206 measurements at the three gravity stations (in summers 2018, 2019 and 2020) range between ± 0.9 µGal and ± 2.0 µGal. Initial exponential drift of a few days is removed for iGrav006. Schäfer et al. (2020) showed an overall reduction of drift rates for iGrav015 and iGrav032 suggesting that these two instruments may have exponential drift components with slowly decreasing magnitudes. This could be a reason for the strong initial gravity decrease of iGrav032 (−12 µGal after 40 days). However, for the long-term drift rates linear adjustments could be determined for all three iGravs (+ 6.1 µGal yr−1 for iGrav006, + 5.2 µGal yr−1 for iGrav015 and −53.9 µGal yr−1 for iGrav032) within the uncertainties of the FG5#206 measurements.
Global gravity contributions
In order to determine the contribution of global atmospheric mass variations in the gravity signal, we used the Atmacs model (Klügel and Wziontek 2009). Besides the correction of the atmospheric effect by Atmacs, we additionally calculated the local pressure residuals and applied the remove–restore method suggested by the Atmacs service (http://atmacs.bkg.bund.de/docs/computation.php, Accessed 05 November 2021), using Atmacs model pressure and the locally recorded pressure at each station. The large-scale hydrological effects on gravity by continental water storage variations were considered by using the simulated soil moisture and snow water equivalent (SWE) of the land surface model NOAHv21 of the GLDAS model (Rodell et al. 2004). In addition, we computed nontidal ocean loading with the OMCTv06 model (Dobslaw et al. 2017). The simulated storage and mass variations from both models were converted to gravity effects using the mGlobe toolbox (Mikolaj et al. 2016).
Local hydrology
At each station we recorded the variations of soil water content with in situ soil moisture sensors. The sensors are arranged at different depths within soil profiles and at different distances to the gravity meter pillar (Table 1). From the soil moisture time-series of all three gravity stations, we calculated the mean water content variations and their associated standard deviation at the four measurement depths (10 cm, 30 cm, 50 cm, 80 cm) and assigned those to the respective soil layers (0–20 cm, 20–40 cm, 40–65 cm, 65–95 cm). Assuming that the temporal variability of soil moisture decreases linearly with depth, we used the observed depth-dependence of the standard deviation to extrapolate at which depth it becomes zero, i.e. the threshold at which depth temporal variations of soil water content can be expected to vanish (Fig. 13, Appendix). The soil moisture variations of the deepest observation depth at 80 cm were accordingly extrapolated to this threshold depth (here 1.8 m, see Fig. 13, Appendix).
The calculated soil water content variations at the different depths, expressed in millimetre water equivalent were used as input variable to model the local hydrological gravity effects. Further, we included local digital elevation models (DEM) to account for topographic characteristics (i.e. relative height changes of the soil layers with regard to the gravity sensor). The hydro-gravitational modelling (HyGra) is based on the method of Leirião et al. (2009) and was adapted to gravimetric observatory buildings by Reich et al. (2019). HyGra is a spatially distributed model that enables the setup of a nested component grid (grid containing smaller grids of refined cell discretisation) with adjustable radii around the gravity station. We chose a small lateral discretisation (of 0.1 m) for the model cells closest to the gravity sensor (radius of 50 m) and larger model cells with increasing distance (1 m cells for 50 to 300 m radius and 10 m cells for 300 to 3000 m radius), and a vertical discretisation (cell height) of 0.1 m for every cell. The gravity sensor height above the ground surface of the DEM is 1.0 m. For the volume of the field container and the subsurface column below the container, no (hydrological) mass changes were assumed because the building shields the natural underground from direct infiltration of rain or snowmelt (“umbrella effect”, Creutzfeldt et al., 2008).
Snow
To determine the mass changes of the snow cover around the monitoring stations in the course of snowfall and snowmelt, we continuously measured (every 15 min) the SWE, i.e. the amount of water that is stored in the snow cover in solid and liquid state by two snow monitoring instruments at SCGE (Fig. 2). We used a snow scale to determine the SWE by weighing the column of snow that is on top of a pressure pillow of 6.72 m2 in size. Additionally, we used a snow pack analyser system (Sommer Messtechnik) equipped with strap sensors that measure (with an electro-magnetic approach) the specific volume contents of ice, water and air within the snow cover, from which the snow density is calculated. Snow depth is derived from travel time measurement of the pulse between an ultrasonic sensor and the snow surface. Snow density and snow depth are then used to calculate the SWE. We used the mean SWE of the time-series of both measuring systems (snow scale and snow pack analyser) as input to calculate the gravity effect of snow with the HyGra model. It should be noted that the calculation of the snow gravity effect considered the actual thickness of the snow cover relative to the gravity meter sensor height, so that both positive and negative gravity contributions may occur, depending on whether parts of the snow cover are below or above the sensor, respectively. Piling up of snow on top of the gravity container was minimal because of the windy conditions at the sites, as confirmed by daily photos of automatic cameras (see Fig. 11 Appendix) deployed at each station. Also, based on the camera observations, no snow mass accumulation was observed within the first 2 m around the container due to snow drift by wind. Thus, the snow mass in the near field of the gravity meter was neglected when computing the gravity effect of the snow cover.
Vertical surface displacement
We used GNSS data observed at each gravity station at Þeistareykir to estimate the vertical surface displacement. The GNSS processing was performed using GFZ’s EPOS.P8 software based on a classical network approach while introducing satellite orbits, clock corrections, and Earth rotation parameters from GFZ repro3 solution (Männel et al. 2020, 2021). According to the current IERS Conventions 2010 (Petit and Luzum 2010) nontidal surface loading was not corrected.
To account for the contribution of the observed height changes to gravity, we used the free-air vertical gravity gradient (FAG) measured by a Scintrex CG5 gravity meter (Portier et al. 2020). This method (Hunt et al. 2002) was realised by gravity measurements with a tripod (at different heights above the concrete pillar) at each of the three gravity stations (Fig. 15, Appendix). We observed −319 µGal m−1 for SCGW (iGrav006), −330 µGal m−1 for SCGC (iGrav015) and −307 µGal m−1 for SCGE (iGrav032).
Gravity contributions and geothermal signals
Local environmental observations at Þeistarykir
Figure 3 displays the measured environmental parameters for the 3-year study period at the Þeistareykir site. Table 2 gives the minimum and maximum values, and standard deviations for each parameter. The time-series show daily values, representing the smallest common time interval of the obtained data. Figure 3a shows the relative soil water content variations at different depths averaged from all soil moisture measurements at the three Þeistareykir gravity stations. The short- and long-term soil water content variations are similar in their overall dynamics in all depth layers, but their amplitudes decrease with depth. We observe largest soil water content variations at 10 cm depth with a standard deviation of 1.45 Vol% and decreasing variations with increasing depth (SD of 1.10 Vol% at 80 cm depth, see also Figure 13, Appendix).
Environmental observations at Þeistareykir between November 2017 and October 2020, including a soil water content variations at different depths, averaged from soil moisture measurements at the three Þeistareykir gravity stations, b snow water equivalent observed from snow pack analyser and snow scale at SCGE, and c vertical surface displacement observed from continuous GNSS measurements at the three gravity stations and linear approximations; data gaps in the GNSS records (Dec. 2017 to May 2018 for SCGW, Feb. 2019 to June 2019 and Oct. 2019 to Feb. 2020 for SCGC) are due to receiver malfunctions
The results of the snow measurements are shown in Fig. 3b. The SWE time-series from the snow pack analyser (black line) and the snow scale (red line) show simultaneous responses to snow mass accumulation during the three winter periods. However, there is a large difference in amplitude between the two monitoring systems, with signals more than ten times larger for the snow pack analyser than for the snow scale. This can partly be explained by the different positions of the two instruments at SCGE (Fig. 14, Appendix). As a result of different wind exposure, the snow cover can be expected to be different at the two installation sites. This is also confirmed by time-lapse photos taken by the automatic cameras at the site. Snow conditions at SCGE in the course of one year are shown in Figure 16 in the Appendix. The differences between the two time-series could also be due to systematic measurement errors of the devices. The snow scale is known to underestimate SWE because of the internal cohesion of the snowpack, i.e. the formation of snow or ice bridges between the snow pack on top of the scale and the surrounding snow cover (e.g. Grossi et al. 2017). On the other hand, the lowest monitoring strap of the snow pack analyser used here for deriving SWE may tend to overestimate SWE because of the more compacted, denser snow pack at this depth, compared to the lower density snow in upper parts of the snow cover. To model the gravity effect of the snow mass, we used mean SWE values (blue line) from the two measuring systems.
In Fig. 3c, we show vertical surface displacement observed from GNSS monitoring at the three gravity stations at Þeistareykir (blue, green and red dots). The periodical variations of approximately ± 5 mm per 3 months are caused by nontidal loading. For calculation of the vertical velocities, we applied a linear fit on the 3-year GNSS data (coloured lines in Fig. 3c). This revealed a significant subsidence of −11.1 mm year−1 for SCGW (blue line) and small trends of −1.5 and −0.3 mm year−1 for SCGC and SCGE (green and red lines). These values coincide with InSAR observations from the Iceland GeoSurvey (ÍSOR), which show increased subsidence rates of −7 to −8 mm year−1 in the injection zone (SCGW) between summer 2018 and 2019 (Drouin et al. 2020). For the subsequent gravity reductions, we only used the contributions from the vertical velocities (linear trends) of the GNSS data.
Environmental gravity reductions
Figure 4 shows the gravity contributions from global models (for the entire study area) and the observed environmental parameters (from Fig. 3) expressed in µGal for each of the three gravity stations at Þeistareykir. Table 3 gives the minimum, maximum and standard deviation for each parameter. Among the global gravity contributions (Fig. 4a), the atmospheric effect (green line) shows the largest gravity contribution of more than 2 µGal. The gravity contributions modelled for global hydrology (red line) are dominated by a seasonal component, whereas the gravity signal of nontidal ocean loading (blue line) is of higher frequency. Both components have a minor effect on the reduction of the local gravity residuals. We expect mean uncertainties of 0.38 µGal for global hydrology and 0.17 µGal for nontidal ocean loading, based on the uncertainty assessment of Mikolaj et al. (2019). The total effect (black line) of these large-scale contributions to the local gravity observations has a seasonal amplitude of up to 4 µGal peak-to-peak and a standard deviation of about 1 µGal (Fig. 4a, Table 3).
From all environmental contributions vertical surface displacement at SCGW (−11.1 mm year−1; see also Fig. 3) causes the largest gravity effect of up to 10 µGal over the entire observation period (Fig. 4d). Global gravity contributions and variations in soil water content only exhibit a very small contribution to the gravity variations observed by all three iGravs. For the reduction of snow, the gravity effect for SCGE and SCGC are larger than for SCGW, visible between December 2019 and May 2020 (Fig. 4c). This can be explained by the different topography surrounding the three gravity stations, considered as input parameter for the snow effect modelling. At SCGW with several little hills around it, a larger amount of snow cover is located at elevations higher than the gravity sensor of iGrav006. This creates a partly negative gravity effect and reduces the net gravity reduction of snow mass changes for SCGW.
Gravity residuals
In Fig. 5, we compare the time-series of gravity residuals of iGrav006, iGrav015 and iGrav032, before and after the combined environmental reductions of global effects, soil water content, snow water equivalent and vertical surface displacement. The initial residuals (before the aforementioned environmental reductions were applied) have been derived by reducing Earth and ocean tides, polar motion, local pressure and instrumental drift, as well as removing spikes and offsets (caused by earthquakes and other disturbances) from the original gravity time-series (Schäfer et al. 2020). Reductions of the individual environmental gravity contributions for each iGrav are shown in Figures 17, 18, 19 in the Appendix.
Gravity residuals of the three iGravs at Þeistareykir before and after the combined reduction of environmental effects including global effects, soil water content variations, snow water equivalent and vertical surface displacement (see Figs 17, 18, 19 in the Appendix for individual environmental contributions)
From linear regression of the reduced time-series, depicted by dashed lines in Fig. 6, we determined a gravity increase of 2.2 µGal year−1 for SCGW (iGrav006) and a gravity decrease of −9.0 µGal year−1 for SCGE (iGrav032). Figure 6 also shows the gravity differences between the iGrav residuals after reduction of the environmental contributions. The gravity differences of two instruments exhibit an additional reduction of variability and amplitudes, i.e. they are smoother than the iGrav residuals themselves. This is because gravity changes that similarly appear at two stations cancel out to some extent in the differences. The remaining gravity variations can be attributed to effects that are locally different at the two stations and have not been reduced by the applied reduction models. Assuming that the local and large-scale gravity contributions as described above are precisely evaluated based on the in situ observations and the standard models, these remaining variations can be mainly attributed to geothermal mass changes (Δggeoth in Eq. 1), induced by mass extraction in the vicinity of SCGE (iGrav032) and reinjection of effluent water close to SCGW (iGrav006). For iGrav015, the gravity signal is more similar to iGrav032 than to iGrav006, which is clearly visible in the lower residual amplitudes of the differences between iGrav032 and iGrav015 (red line) compared to the differences between iGrav006 and iGrav015 (orange line). This suggests that SCGC receives a larger contribution to the gravity signal from mass extraction (depth ~ 2 km) rather than from mass reinjection (depth ~ 400 m).
Gravity residuals and differences between iGrav006, iGrav015 and iGrav032 after reduction of global effects, soil water content variations and vertical surface displacement; dotted sections of gravity residuals show possible effects of snow melting between May and July 2020, which are excluded for the linear approximations for iGrav006 and iGrav032 (black, dashed lines)
One particular phenomenon is the large gravity increase of about 10 µGal between May and July 2020, which is most pronounced in the signal from iGrav006. We assume this is due to local accumulation of snowmelt water (see also higher values of soil water content for that time; Fig. 4b) which drains off more easily at the other stations. At SCGW there is a small nearby lake, which may contribute to this pronounced water storage increase for a period of several weeks. This anomaly (dotted sections in iGrav residuals in Fig. 6) was excluded for the linear approximations of iGrav006 and iGrav032.
Geothermal signals
We investigate the subsurface mass changes that are primarily caused by geothermal fluid extraction and reinjection activities at the Þeistareykir power plant. For this purpose, we compare the gravity residual time-series (from Fig. 6) with relative groundwater levels (GWL) and geothermal flow rates at Þeistareykir. The latter two were supplied as local monitoring data by the power plant operator (Landsvirkjun). The locations of the GWL monitoring wells and the injection well pad are depicted in Fig. 1. As shown in Fig. 7, during the initial period, when injection flow is increased to just below 120 kg s−1 (May 2017 until January 2018), only a slight increase of GWL of about 2 m occurs. After January 2018, when injection flow is increased above 180 kg s−1, GWL increases at a higher rate and by about 6 m until July 2018. For the subsequent periods of reduced geothermal flow rates (start of extraction and injection declines indicated by dashed arrows in Fig. 7), we notice an immediate descending response in the GWLs followed by a rebound when the flow rates are increased again. The direct response in the GWLs during periods of high extraction and injection flow rates suggests that the subsurface hydrology consists of pressure controlled systems. When the injection flow rates are reduced below 160 kg s−1, pressure reduces instantaneously indicating that the reinjection system is open with a natural westward outflow in the order of the same amount towards the GWL monitoring wells. We observe similar effects for the gravity time-series, like the long-term increasing trend in the differences (iGrav006–iGrav032) and short-term gravity responses (decrease in the differences and increase in the iGrav015 and iGrav032 residuals; marked by A, B, C and D in Fig. 7) after reduced geothermal flow rates in March to April 2019 and July to September 2019. However, the gravity responses show time delays of several days up to weeks in comparison to the injection rates and GWL changes. For iGrav006 these responses are missing (or barely visible) in the gravity residuals. Although GWL observation wells are missing in the eastern (extraction) area of the geothermal field, these observations are indicating a boundary between the injection and extraction areas that can be assumed between SCGW and SCGC (s. below).
Comparison of iGrav residuals and gravity differences between iGrav006 and iGrav032 with relative groundwater levels (GWL 2, 7 and 8) and with geothermal extraction and injection flow rates of the Þeistareykir power plant from July 2017 until October 2020; dashed arrows mark the beginning of periods with reduced geothermal flow rates and capital letters mark possible response in the gravity residuals and differences (A, B, C and D; with same colour as the corresponding gravity time-series)
Geothermal interpretation
Implications from gravity, groundwater and geothermal observations
Following temporary reduction in extraction and injection rates, the GWL data show a direct response, indicating that the reinjection aquifer is confined at high injection rates (above 180 kg s−1) and that the observed response is relative to pressure change in the aquifer. The delayed responses in the gravity data indicate that groundwater is moving with different time constants in the extraction and injection areas, possibly due to pressure-induced changes in permeability. These time delays may also be attributed to a season-dependent natural recharge in the area of the extraction wells, resulting from, e.g. rainfall or snowmelt events that recharge the groundwater system at larger distances from the monitoring site, e.g. on the surrounding volcano ridges, and that are thus not registered by the local hydrometeorological sensors at the gravity stations. In May 2020, injection and extraction were more permanently reduced, and the response of the gravity meters is also delayed. In addition, the gravity difference (iGrav006–iGrav032) is not raising any more, suggesting that the mass difference may have become stationary between extraction and recharge, and injection and outflow. This could indicate that the system may have attained “equilibrium/steady-state” conditions.
The gravity responses from iGrav015 and iGrav032 (marked by A, B, C and D in Fig. 7) are missing (or barely visible) in the iGrav006 residuals. This suggests that reinjected fluids cause a much lower gravity contribution, compared to extraction although the injection depth is much shallower than for extraction, which is another indication for an (to some extend) open injection aquifer. The varying gravity responses between SCGW and SCGE/SCGC additionally indicate, that there is a boundary between the reinjection area in the west and the extraction area in the east. The location of this boundary may be indicated by the surface appearance of the Tjarnarás fault (see Fig. 1). In order to understand and quantify those data, one should model the hydraulic features and adjust hydraulic parameters such as hydraulic diffusivity and consider other influences, such as the temperature and density of the fluid injected, and the detailed geology of the reservoir, as known from exploration drilling at Þeistareykir (Kewiy 2013; Óskarsson 2015; Gudjónsdóttir 2018).
In a first-order approximation, from the GWL data observation, it seems that the “equilibrium/steady-state” conditions for the injection aquifer may be reached when injection rate is around 140 kg s−1 after about 3 years of power plant operation. Above that injection value, the pressure in the aquifer increases. This indicates that the aquifer is a partly open system with additional storage capacities for the reinjected fluids. Correlation between changes in reinjection and GWL changes west of the Tjarnarás fault system (yellow dashed line in Fig. 1) suggest that there is good pressure connection in the western compartment of the Þeistareykir geothermal reservoir. When injection rates are very low, the aquifer system tends to return to the initial state, prior the start of reinjection. The data after June 2020, when power production was reduced by approximately 30% and extraction rates are in the order of 220 kg s−1 (and ~ 140 kg s−1 injection) suggests “steady-state conditions” for such operation modus after about 3 years of operation. This hypothesis is also supported by the gravity observations in Fig. 7: the difference between the gravity variations at SCGW and SCGE that was continuously increasing changes slope and remains more or less constant for the time interval observed after extraction decrease (June 2020).
Our continuous gravity monitoring results were also used in a hybrid gravity study including measurements of the three iGravs and a Scintrex CG5 gravity meter at Þeistareykir (Portier et al. 2021). The study with both gravity meter types confirms our observation of long-term gravity decrease at the extraction zone and minor gravity changes at the injection zone.
Newtonian gravity model of extracted and injected geothermal fluids
Using production data from Landsvirkjun (extracted geothermal fluid and injected water), we can compute the total mass extracted during the period from 2018 to 2020 (3 years, Fig. 8). This allows us to estimate a first order of magnitude of the expected gravity signal. The following modelling approach is based on the studies from Jousset et al. (2000).
As first estimation of the expected gravity signal, we computed separately the contributions of extracted and injected masses, assuming that there is only one well which extracts (or injects) the total mass (~ 2.3 1010 kg) between starting and end point. As we are in volcanic terrain, we assume that masses are extracted from and injected to a single layer at the bottom depth of the wells below surface, ~ 2000 m for extraction and ~ 400 m for injection. We assume the thickness of the layer to be 20 m, with porosity of 10%. When mass is extracted (or injected) the affected volume is supposed to be confined in the layer, and we assume that the influence is isotropic. Therefore, the affected area of the model has a cylindrical shape. Equation 2 and Table 4 show the results for such configuration. The final radius of the cylinder is less than 2000 m. For the extraction (depth 2000 m), the amplitude of the gravity signal above the cylinder is of the order of −20 to −30 μGal at the surface. For the injection (depth 400 m), the amplitude of the gravity is about +60 to +70 μGal. The net gravity should then increase, by about 30 to 50 μGal:
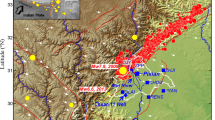
As a further attempt to describe more accurately the gravity changes and follow temporal evolution, we computed the daily mass transfer contribution of each well (extraction and injection) for each gravity station (SCGW, SCGC and SCGE). Assuming that each well affects a cylindrical area surrounding the feed zone location at depth, we computed the attraction due to mass extraction and injection for each gravity station with time (1 value per day). Figure 9 shows the locations of the iGravs and the feed zones for each well. Figure 10 shows the results of the continuous gravity model for each gravity station. The largest gravity contributions result from the injection wells (near SCGW) because the injection depth is closer to the surface than for extraction.
Gravity modelled for the three gravity stations considering masses extracted/injected from all wells. Although the mass balance is close to zero in the modelling, gravity increases as the injected mass is located closer to the surface, explaining that the modelled total contribution is positive at all three locations
The orders of magnitude found from both computations are larger than the observed gravity amplitudes. In particular, for injection, those results suggest that most of the injected fluid is transported away through the Tjarnarás fault system, leaving the geothermal area or returning into the deep reservoir. More detailed computations are required to better understand the influence of the heterogeneous reservoir parameters and to conclude on recharge processes and long-term behaviour of the geothermal field.
Conclusions
We deployed and maintained a network of multiparameter stations including three iGravs superconducting gravity meters for more than 3 years at the Þeistareykir geothermal field in North Iceland. This allows us to monitor and detect mass changes associated with environmental and geothermal phenomena. The continuous gravity records were reduced from environmental contributions by means of accurate measurements and modelling of global effects, hydrology, snow and vertical surface displacement. The amplitudes of the environmental contributions never exceeded 10 µGal (except tides). Residuals were interpreted in terms of groundwater level changes and redistribution of geothermal fluids. The analysis of the continuous observation data revealed:
-
Gravity increase of 2.2 µGal year−1 at the site above injection (as expected due to the injected water mass).
-
Gravity decrease of −9.0 µGal year−1 at the site above the extraction of mass.
-
Direct correlation between groundwater levels/pressures and injection flow rates, which indicates that the reinjection system is subject to a confined aquifer.
-
Delayed responses in the gravity signals only above the extraction zone, indicating that there is a reservoir boundary between the reinjection and the extraction areas.
-
The observed responses in groundwater levels and gravity indicate that the hydraulic response of the hydrothermal system is mainly governed by a partially filled aquifer up to injection flow rates of 140 kg s−1 for which the system may have reached steady-state conditions between extraction, natural recharge, injection and outflow. Above this value, the injection system is over-pressurised.
-
Comparison to a simplistic gravity model of the extracted and injected water masses shows larger amplitudes than the observed gravity signals at the injection zone, which indicates a quick fracture-favoured run-off of the reinjected fluids. However, due to the very heterogeneous underground, refined computations are required to fully understand the complex mass transport processes within the geothermal system.
This study demonstrates that a network of multiple gravity stations is useful for monitoring geothermal reservoirs and for determining steady-state injection and extraction conditions. In addition, it shows that observations of environmental parameters are fundamental to obtain accurate estimations of geothermal signals in volcanic environments. This study may also be useful for understanding gravity changes occurring at active volcanoes, where the effects of environmental parameters must be accurately evaluated, in order to understand volcano-related mass changes.
Availability of data and materials
The datasets analysed during this study are available from the corresponding author on reasonable request. A persistent web link in the GFZ repository will be implemented after embargo dates of the follow-up project in 2024.
Change history
20 December 2022
A Correction to this paper has been published: https://doi.org/10.1186/s40517-022-00237-z
Abbreviations
- DEM:
-
Digital elevation model
- FAG:
-
Free-air vertical gravity gradient
- GNSS:
-
Global Navigation Satellite System
- GWL:
-
Groundwater level
- HyGra:
-
Hydro-gravitational modelling
- IERS:
-
International Earth Rotation and References Systems Service
- SCGC:
-
Superconducting Gravity Station, Central Position
- SCGE:
-
Superconducting Gravity Station, Eastern Position
- SCGW:
-
Superconducting Gravity Station, Western Position
- ROMPS:
-
Remotely operated multiparameter stations
- SWE:
-
Snow water equivalent
References
Agnew DC. Earth tides, in Treatise on Geophysics. 2nd ed, vol. 3: Geodesy, pp. 151–178. In: Herring T. Schubert G, editor-in-chief, Elsevier. 2015. https://doi.org/10.1016/b978-0-444-53802-4.00058-0.
Ármannsson H, Gudmundsson Á, Steingrímsson BS. Exploration and development of the Krafla geothermal area. Jökull. 1987;37:13–30. https://www.researchgate.net/profile/Asgrimur-Gudmundsson/publication/284698694_Exploration_and_development_of_the_Krafla_geothermal_area/links/56e9697208ae47bc651c716e/Exploration-and-development-of-the-Krafla-geothermal-area.pdf. Accessed 05 Nov 2021.
Boy JP, Hinderer J. Study of the seasonal gravity signal in superconducting gravimeter data. J Geodyn. 2006;41(1):227–33. https://doi.org/10.1016/j.jog.2005.08.035.
Carbone D, Cannavò F, Greco F, Reineman R, Warburton RJ. The benefits of using a network of superconducting gravimeters to monitor and study active volcanoes. J Geophys Res Solid Earth. 2019;124(4):4035–50. https://doi.org/10.1029/2018JB017204.
Creutzfeldt B, Güntner A, Klügel T, Wziontek H. Simulating the influence of water storage changes on the superconducting gravimeter of the Geodetic Observatory Wettzell, Germany. Geophysics. 2008;73(6):WA95–104. https://doi.org/10.1190/1.2992508.
Crossley D, Hinderer J, Boy JP. Regional gravity variations in Europe from superconducting gravimeters. J Geodyn. 2004;38(3–5):325–42. https://doi.org/10.1016/j.jog.2004.07.014.
Damiani TM. Dynamic effects in gravimetry: an assessment of the current state of knowledge. NOAA-National Geodetic Survey, 1315 East-West Hwy, SSMC3, Silver Spring, MD 20910, G51B-0362; 2014. https://ftp.ngs.noaa.gov/web/science_edu/presentations_archive/files/damiani_agu_2014_36x65.pdf. Accessed 05 Nov 2021.
Dobslaw H, Bergmann-Wolf I, Dill R, Poropat L, Thomas M, Dahle C, Flechtner F. A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06. Geophys J Int. 2017;211(1):263–9. https://doi.org/10.1093/gji/ggx302.
Drouin V, Sigmundsson F, Li S. Ground deformation at the Theistareykir volcanic system, Iceland 535 following onset of geothermal utilization. Proceedings World Geothermal Congress, Reykjavik, Iceland; 2020.
Gitlein O, Timmen L, Müller J. Modeling of atmospheric gravity effects for high-precision observations. Int J Geosci. 2013;4(4):663–71. https://doi.org/10.15488/1531.
Grossi G, Lendvai A, Peretti G, Ranzi R. Snow precipitation measured by gauges: systematic error estimation and data series correction in the central Italian Alps. Water. 2017;9(7):461. https://doi.org/10.3390/w9070461.
Gudjónsdóttir SR, St. Ásgeirsdóttir R, Sigurgeirsson MÁ, Gudmundsson Á. Drilling of nine high temperature wells in the Þeistareykir geothermal field, NE-Iceland, 2016–2017. Overview of the project, geology of the area and interpretation of the lithology and alteration of the sub-surface strata. In EGU General Assembly Conference Abstracts. 2018;1369.
Gudmundsson A, Brynjolfsson S, Jonsson MT. Structural analysis of a transform fault-rift zone junction in North Iceland. Tectonophysics. 1993;220(1–4):205–21. https://doi.org/10.1016/0040-1951(93)90232-9.
Hinderer J, Crossley D, Warburton RJ. Superconducting gravimetry, in Treatise on Geophysics, 2nd ed, vol 3: Geodesy, pp. 66–122. In: Herring T, Schubert G, editor-in-chief, Elsevier. 2015. https://doi.org/10.1016/B978-0-444-53802-4.00062-2.
Hunt T, Sugihara M, Sato T, Takemura T. Measurement and use of the vertical gravity gradient in correcting repeat microgravity measurements for the effects of ground subsidence in geothermal systems. Geothermics. 2002;31(5):525–43. https://doi.org/10.1016/S0375-6505(02)00010-X.
Jousset P, Dwipa S, Beauducel F, Duquesnoy T, Diament M. Temporal gravity at Merapi (Java, Indonesia) during the 1993–1995 crisis: an insight into the dynamical behaviour of volcanoes. J Volcanol Geotherm Res. 2000;100:289–320. https://doi.org/10.1016/S0377-0273(00)00141-4.
Kewiy WR. Injection and production well testing in the geothermal fields of southern Hengill and Reykjanes, SW-Iceland and Theistareykir, N-Iceland. Geothermal Training in Iceland. 2013;747–768. http://os.is/gogn/unu-gtp-report/UNU-GTP-2013-31.pdf. Accessed 05 Nov 2021.
Klügel T, Wziontek H. Correcting gravimeters and tiltmeters for atmospheric mass attraction using operational weather models. J Geodyn. 2009;48(3–5):204–10. https://doi.org/10.1016/j.jog.2009.09.010.
Leirião S, He X, Christiansen L, Andersen OB, Bauer-Gottwein P. Calculation of the temporal gravity variation from spatially variable water storage change in soils and aquifers. J Hydrol. 2009;365(3–4):302–9. https://doi.org/10.1016/j.jhydrol.2008.11.040.
Männel B, Brandt A, Bradke M, Sakic P, Brack A, Nischan T. Status of IGS reprocessing activities at GFZ. In International Association of Geodesy Symposia. Springer; 2020. https://doi.org/10.1007/1345_2020_98.
Männel B, Brandt A, Bradke M, Sakic P, Brack A, Nischan T. GFZ repro3 product series for the International GNSS Service (IGS). GFZ Data Services. 2021. https://doi.org/10.5880/GFZ.1.1.2021.001.
Mikolaj M, Meurers B, Güntner A. Modelling of global mass effects in hydrology, atmosphere and oceans on surface gravity. Comput Geosci. 2016;93:12–20. https://doi.org/10.1016/j.cageo.2016.04.014.
Mikolaj M, Reich M, Güntner A. Resolving geophysical signals by terrestrial gravimetry: a time domain assessment of the correction-induced uncertainty. J Geophys Res Solid Earth. 2019;124(2):2153–65. https://doi.org/10.1029/2018JB016682.
Óskarsson F. Exploration and development of a conceptual model for the Theistareykir geothermal field, NE-Iceland. Short Course VII on Surface Exploration for Geothermal Resources”, organized by UNU-GTP and LaGeo, in Santa Tecla and Ahuachapán, El Salvador. 2015. www.os.is/gogn/unu-gtp-sc/UNU-GTP-SC-23-0502A.pdf. Accessed 05 Nov 2021.
Petit G, Luzum B. IERS conventions (2010). Bureau International des Poids et mesures sevres (france); 2010. https://apps.dtic.mil/sti/citations/ADA535671. Accessed 05 Nov 2021.
Portier N, Hinderer J, Riccardi U, Ferhat G, Calvo M, Abdelfettah Y, Heimlich C, Bernard J-D. Hybrid gravimetry monitoring of Soultz-sous-Forêts and Rittershoffen geothermal sites (Alsace, France). Geothermics. 2018;76:201–19. https://doi.org/10.1016/j.geothermics.2018.07.008.
Portier N, Hinderer J, Drouin V, Sigmundsson F, Schäfer F, Jousset P, Erbas K, Magnusson I, Hersir GP, Águstsson K, De Zeeuw Van Dalfsen E, Guðmundsson Á, Bernard J-D. Time-lapse Micro-gravity Monitoring of the Theistareykir and Krafla Geothermal Reservoirs (Iceland). Proceedings World Geothermal Congress, Reykjavik, Iceland; 2020.
Portier N, Forster F, Hinderer J, Erbas K, Jousset P, Drouin V, Li S, Sigmundsson F, Magnússon I, Hersir GP, Ágústsson K, Guðmundsson Á, Júlíusson E, Hjartasson H, Bernard J-D. Hybrid microgravity monitoring of the Theistareykir geothermal reservoir (North Iceland). Pure and Applied Geophysics; 2021. submitted.
Reich M, Mikolaj M, Blume T, Güntner A. Reducing gravity data for the influence of water storage variations beneath observatory buildings. Geophysics. 2019. https://doi.org/10.1190/geo2018-0301.1.
Rodell M, Houser PR, Jambor U, Gottschalck J, Mitchell K, Meng CJ, Toll D. The global land data assimilation system. Bull Am Meteor Soc. 2004;85(3):381–94. https://doi.org/10.1175/BAMS-85-3-381.
Rosat S, Hinderer J. Limits of detection of gravimetric signals on earth. Sci Rep. 2018;8(1):15324. https://doi.org/10.1038/s41598-018-33717-z.
Schäfer F, Jousset P, Güntner A, Erbas K, Hinderer J, Rosat S, Voigt C, Schöne T, Warburton RJ. Performance of three iGrav superconducting gravity meters before and after transport to remote monitoring sites. Geophys J Int. 2020;223(2):959–72. https://doi.org/10.1093/gji/ggaa359.
Schöne T, Zech C, Unger-Shayesteh K, Rudenko V, Thoss H, Wetzel H-U, Gafurov A, Illigner J, Zubovich A. A new permanent multi-parameter monitoring network in Central Asian high mountains—from measurements to data bases. Geosci Instrum Method Data Syst. 2013;2:97–111. https://doi.org/10.5194/gi-2-97-2013.
Sturkell E, Einarsson P, Sigmundsson F, Geirsson H, Olafsson H, Pedersen R, Van Dalfsen ZE, Linde AT, Sacks SI, Stefánsson R. Volcano geodesy and magma dynamics in Iceland. J Volcanol Geotherm Res. 2006;150(1–3):14–34. https://doi.org/10.1016/j.jvolgeores.2005.07.010.
Van Camp M, Vauterin P. Tsoft: graphical and interactive software for the analysis of time series and Earth tides. Comput Geosci. 2005;31(5):631–40. https://doi.org/10.1016/j.cageo.2004.11.015.
Voigt C, Schulz K, Koch F, Wetzel K-F, Timmen L, Rehm T, Pflug H, Stolarczuk N, Förste C, Flechtner F. Introduction of a superconducting gravimeter as novel hydrological sensor for the alpine research catchment zugspitze. 2021. Hydrol Earth Syst Sci Discuss. https://doi.org/10.5194/hess-25-5047-2021.
Watlet A, Van Camp M, Francis O, Poulain A, Rochez G, Hallet V, Quinif Y, Kaufmann O. Gravity monitoring of underground flash flood events to study their impact on groundwater recharge and the distribution of karst voids. Water Resour Res. 2020. https://doi.org/10.1029/2019WR026673.
Wenzel HG. The Nanogal software: Earth tide data processing package ETERNA3.30, Bull. Inform. Marees Terrestres. 1996;124:9425–9439. http://www.eas.slu.edu/GGP/ETERNA34/MANUAL/ETERNA33.HTM. Accessed 05 Nov 2021.
Acknowledgements
We gratefully acknowledge Anette Kærgaard Mortensen and her colleagues from Landsvirkjun the National Power Company of Iceland for the friendly collaboration, supportive provision of borehole monitoring data and for providing the necessary facilities and infrastructure at the Þeistareykir geothermal field. Many thanks to GWR Instruments, Inc. for their ongoing assistance during operation and maintenance of the iGrav superconducting gravity meters. We also thank Tilo Schöne, Nico Stolarczuk, Julia Illigner and Cornelia Zech for installation and maintenance of the remotely operated multiparameter stations at Þeistareykir.
Funding
Open Access funding enabled and organized by Projekt DEAL. Funding for this project was provided by the German Federal Ministry for Education and Research (BMBF, Grant: 03G0858A), the Helmholtz Centre Potsdam—GFZ German Research Centre for Geosciences and Landsvirkjun.
Author information
Authors and Affiliations
Contributions
FF: corresponding author, writing the manuscript, field work, data acquisition, formal analysis, methodology, visualisation, validation. AG: methodology, conceptualisation, writing the manuscript, supervision. PJ: field work, conceptualisation, gravity modelling, writing the manuscript, supervision. MR: field work, methodology. BM: methodology, visualisation, writing the manuscript. JH: field work, methodology. KE: field work, data acquisition, project administration, writing the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Results of ETERNA 3.4 tidal analysis for iGrav006 (SCGW)

Appendix 2: Results of ETERNA 3.4 tidal analysis for iGrav015 (SCGC)

Appendix 3: Results of ETERNA 3.4 tidal analysis for iGrav032 (SCGE)

Appendix 4: Theoretical models used for long period tides (SCGW)

See Figures 11, 12, 13, 14, 15, 16, 17, 18, 19.
Instrumental drift correction for the three iGravs at Þeistareykir by comparison to FG5#206 absolute measurements in summers 2018, 2019 and 2020 (red dots with error bars); drift corrected iGrav residuals shown with dark shaded colours (dark blue, dark green and purple); enlarged section shows initial exponential drift that was removed in iGrav006 residuals
Variation of soil water content with depth below surface; black squares show standard deviation of mean soil water content at different depths from all gravity stations, red stars mark mean SD for each depth layer, linear fit of SD mean values (red dashed line) reveals depth of zero soil water content variation at y0 = 1.82 m
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Forster, F., Güntner, A., Jousset, P. et al. Environmental and anthropogenic gravity contributions at the Þeistareykir geothermal field, North Iceland. Geotherm Energy 9, 26 (2021). https://doi.org/10.1186/s40517-021-00208-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40517-021-00208-w