Abstract
Mechanical damage in oil paintings on canvas show up as cracks and loss of original paint. Several parameters can contribute to this type of degradation. These paintings have a complex layered structure, typically composed of minimum four or more hygroscopic materials, each of which has different (non-linear) material properties and geometrical complexities. The mechanical degradation of canvas paintings occurs because each of these materials have diverse responses under fluctuating environmental conditions, especially temperature and relative humidity (RH). By examining the geometrical complexities and the non-linear material properties, this paper presents an investigation of three degradation phenomena under desiccation: (1) bulging formation around the corners, (2) crack formation in glue and ground layers, and (3) plastic deformation in the ground and oil paint layers.
This on-going investigation provides further insights into the global and local stress distribution in typically constructed oil canvas paintings. This includes finite element method (FEM) and extended-FEM (XFEM) computer models at various scales, under desiccation from the initial RH of 90%, and 50–10%. The models consist of four to five different materials, namely lead white oil paint, red iron oxide oil paint, rabbit skin glue, linen canvas, and a spruce stretcher. The models were constructed using several combinations of materials to conduct parametric studies on the effects of glue shrinkage in paintings due to desiccation, and changing the mechanical properties of the ground layers. The relevant geometrical and mechanical properties with respect to the stress relaxation conditions are discussed in detail.
The simulation results of the full-scale models show that the shrinkage of glue lowers the level of induced tension stresses in the paint layers in the central area of the painting due to the inward bowing of the stretcher. The inward deformation of the stretcher can be 4.5 times as large in a painting with a glue layer as in one without. This indicates the difficulty in forming cracks near the center of paintings purely by desiccation; however, in close-up cross-section model, cracks of 20 μm in length could still be observed in the ground exposed to an extreme RH change of 90% to 10%.
The analysis of cross-section models with the full geometrical complexity for the corners showed that multiple cracks are likely to form in ground and paint layers in the corners when desiccated by 40%; RH 50–10%. Furthermore, in extreme cases with stiffer ground/paint such as zinc white, cracks can form from smaller drop in RH; RH 50% to 35%. Such cracks are form in the ground layers, and therefore, are not initially visible as they are positioned below the uncracked paint layer. This result can be the possible explanation for cracks in the ground, which are initially invisible with the naked eye, but can be revealed with X-radiographs.
The results support the hypothesis that fluctuations in relative humidity can cause hidden cracks in the lower layers, which can eventually propagate further into the upper-lying paint layers of paintings. The cracks typically form when the desiccation reaches a 40% drop, but in cases of brittle materials the drop causing cracks can be lower. The actual RH drop causing cracks depends on the specific material composition.
Similar content being viewed by others
Introduction
Cracks in decorative layers of oil canvas paintings are a common defect, which can accumulate due to processes or historic events such as changes in relative humidity, temperature, chemical evolution of painting components, excessive stretching and impact due to handling. Cracks may compromise the artistic value by changing the visual appearance, but in some cases, cracks are also considered proof of antiquity and authenticity. However, it is certain that cracks and permanent deformations are signs of deterioration, and thus may indicate the need for additional care to prevent permanent loss of artistic quality and authentic material. Therefore, the various aspects of crack formation and propagation have been studied as described in the following.
Various aspects of crack formation and propagation have been studied by scientists and conservators. Attempts to classify and characterize cracks have been made by Stout [1] and Bucklow [2]. Bucklow showed that the crack patterns were era-specific, as well as related to the geographic location and the painting traditions including materials and their application. Such observations indicated that material characteristics and application techniques have direct impact on crack patterns in paintings.
There exists common observations in oil canvas paintings, that cracks are often formed in the area, which is not buffered by the wooden stretcher [3]. Until present, it is understood that the larger temperature and RH fluctuations related to the interaction of the air and the walls behind the painting, are the main causes of the cracks in the unprotected area of the paintings [4,5,6]. The environmental changes cause various expansion or contraction of materials in paintings based on their different mechanical properties that in turn cause uneven strain developments, which may lead to crack formations. This understanding is also consistent with the past investigations, which discussed the crack formations based on the shrinkage in canvas and glue [7,8,9,10].
The distinction between drying and brittle cracks due to changes in environmental conditions were investigated by Keck [11] which is still frequently referenced in present time. Giorgiutti-Dauphine and Pauchard [12] found that the spacing in ageing cracks depends on thickness of the paint layer and the mechanical properties of paint, and substrates; which was confirmed by Flores [13]. The systematic work of Mecklenburg et al. [14] who determined material properties for hundreds of materials used in heritage objects, indicated that, any environmental variations generating strains lower than 0.5%, can be considered safe for oil paints (except brittle or weak paints like zinc oxide and titanium white), and 0.2% for animal glue based grounds. Using the typical methods of structural engineering disciplines Mecklenburg proposed that ± 8% RH centered at 50% RH would be safe for most artefacts. Fundamental work of Mecklenburg was refined by other researchers further broadening the RH range for most object in museums collections. The most recent summary of current state-of-the-art and consensus of the experts on environmentally induced degradation mechanism is presented in the Chapter 24 ‘Museums, Archives, Galleries and Libraries’ of the American Society of Heating, Refrigerating and Air-Conditioning Engineers (ASHRAE handbook [15]). The main conclusions presented in the chapter is that, most of the objects found in collections tolerate fluctuations of at least ± 10% RH, whereas fluctuations beyond 20% RH cause rapidly increasing risk of fracture. The safe range for objects that have ‘acclimatised’ to the environment within which they have been preserved for a long time is determined by the largest past RH fluctuations. It is commonly accepted that, there is an extremely low risk of physical damage beyond what is already accumulated in the past, assuming that fluctuations do not go beyond the historic climate [16]. In spite of undisputable progress in elucidating object response to environmental variations, there is significant gap in understanding of crack pattern formation and structural behaviour of canvas paintings, one of the most valuable and significant part of most collections worldwide. This understanding is particularly relevant in times of increasing tendency to manage environment in museums and historical houses in more responsible manner, particularly in terms of reducing energy consumption and carbon emission.
Despite the numerous studies carried out there are still issues that need further investigation such as permanent deformation (for example, out-of-plane bulging around corners of paintings) and overlying cracks. Permanent deformation has been used as a criterion to determine allowable range of RH variations in the past [14], yet local deformations are almost inevitable. Also, it is not clear whether permanent deformations in paintings have direct connection to the critical degradation conditions in the later life. On the other hand, any formed cracks, regardless of their initial sizes bear a greater risk of developing into critical degradations such as the eventual loss of paints. Therefore, the prevention, or even slowing down crack formation in paintings is considered as great importance in conservation.
In 1990s, Mecklenburg et al. [17] demonstrated the use of computational (numerical) method to analyse the environmentally incurred stresses in painting, and predicted the locations and directions of the tension cracks, which correlated well with the observations from real paintings. They applied finite element method (FEM) to understand the levels, and characteristic distributions of stresses in oil canvas painting due to changes in temperature and RH. In FEM modelling the object is reproduced digitally and divided into smaller sections. For each section the computer calculates forces and deformation resulting from a stimulus such as change in T or RH. This technique provides valuable insight into parameters governing the development of damage. Mecklenburg’s studies showed stress concentrations near the corners of paintings, and also the change of stress directions across the different parts of the painting; which closely matched the crack patterns observed in historical paintings [18]. Mecklenburg’s computational degradation model further clarified the effect of changes in temperature and RH on the internal stress in the restrained materials [19]. In 1999, de Willigen published his work in computational analysis of oil canvas painting, in which he showed results that were comparable to Mecklenburg’s [20]. The earlier computational models of Mecklenburg and de Willigen include paint, glue and canvas layers. Each layer was geometrically defined as a flat rectilinear sheet which was in full contact with the adjacent layer(s). The model was restrained on the circumferential edges of the canvas; however, in reflection of the real canvas painting structure, the restrained edge boundary condition can be replaced to better mimic the real condition. For example, the inclusion of a wooden stretcher as part of the model can change the resultant variables in the paint layer by including a realistic geometrical deformation of the stretcher bars.
Present scope of investigation
The results from the earlier models showed the effective application of FEM in understanding crack formation, propagation, and later development in canvas paintings. Since computational models in general are mere abstractions of the detailed reality, they must be accepted as approximated solutions. Therefore, results from computational analysis should be verified experimentally.
For the extreme model sizes, the required computational facilities may not be readily available. Hence, many investigations often take the route of developing mathematically valid but highly abstract computational models at first, and gradually increase the complexity closer to reality. The current investigation is based on the same basis of understanding, and it starts by adopting the theoretically valid degradation models for oil paintings on canvas, and further attempts to increase the level of precision by introducing further geometrical and material complexities.
It can be observed from several paintings, which have been exposed to the comparable environmental conditions, that the crack patterns and sizes can vary significantly [21]. One may argue that the current conditions of paintings cannot be discussed without the thorough review of both environmental and physical history of specific objects. Such historical record is, however, rarely complete, for example, for a 200-year-old painting; and arguably, it only takes one incident such as a sudden drop in RH or a poor handling of the painting during transportation to cause significant cracks. Conservators may further argue that the different geometrical and material specifications between the paintings can also incur varying magnitudes of degradations. Indeed, the review of historical paintings can reveal that the range of material compositions and geometrical specifications such as the size of stretcher and the thickness of different layers can be widespread, which can be the reason behind the varying crack patterns. For these reasons, it is always difficult to provide a sharp and definite explanation for the local cracks on a specific painting based on the studied mechanisms, which were initially derived from parametrically generalized models. Consequently, this paper presents a more focused investigation with specific sets of materials in their different compositions.
Oil paintings on canvas with different material compositions
This paper presents an investigation, which focuses on compositions of four specific material layers: Canvas layer, glue/size layer, ground layer and paint layer. They are considered the basic layers in oil paintings on canvas. In some paintings the glue layer can be absent, but the majority in the western painting tradition are composed with these layers. The specific materials occupying the layers can vary. However, earth pigments were typically used extensively in grounds in the 17th to eighteenth century, while lead white mixed with fillers, such as chalk or barium sulphate was widely used as ground material in the nineteenth century [22], as well as in the twentieth century to some degree [23]. Moreover, the common observation is, that paintings containing earth pigments in the ground exhibit more conservation issues and are in worse state of the preservation comparing to other types of grounds. The materials and the types of layer compositions investigated in this study are summarised in Table 1. They represent a simplified version of the tendency described above, where either an earth colour or a lead white based oil ground was used as the structurally significant ground layer applied on the (sized) canvas. Mechanically, these represent a strong and a weak ground. The presence of glue sizing cannot always be assumed and a case without glue is incorporated to investigate the significance of this layer. The glue layer is important since this layer is mechanically dominant due to its stiffness and strength in the lower RH region and can therefore affect crack initiation in a painting structure.
The material definitions used in the analysis were dependent on two environmental parameters: relative humidity and temperature. However, the research interest limits the material definitions to be functions of RH only, and the temperature is assumed to be constant at 25 °C. The material definitions of the applied materials, such as paint, ground and glue were derived based on the full-relaxation stress state which correlates better to the incurred stresses when the paintings are exposed to slow environmental variations, reflecting for example the effect of natural seasonal change in uncontrolled indoor climate.
With respect to RH, the paint samples took about 48 h to reach full equilibrium with the environment, but took 7–10 days to full stress relaxation. The corresponding material tests were carried out at the Smithsonian Institution, in which 20–21-year-old flake white safflower oil specimen was given the sufficient time to fully relax between strain increments. The results were compared with the results from rapid tests with only 30 s strain interval. The comparison showed that, the material behaved significantly different under full-relaxation condition; when the specimen were given the consistent time to relax between the strain intervals, the measured modulus and the ultimate stress were only 14% and 20% of when strained with only 30 s interval, respectively. Glues took much longer to reach fully relaxed state at the minimum of 160–200 days depending on the thickness [24], and the current study considered the glue at 7 to 10 days relaxation state (Fig. 1).
Glue is the most responsive material among the three materials in the desiccation model with the largest moisture expansion (, αG = 2.6E-4) and the elastic modulus. The effective elastic modulus can be calculated from the equations (Eq. 1, 2, 3) allowing for the reconstruction of the restrained tests at Smithsonian Institution.
where RHi is initial relative humidity value, RH is the relative humidity at the point of interest, and µ is the offset coefficient for RHi, which can be calculated from below:
For RHi > 71,
For RHi < 71,
Figure 1 shows the comparison of test results and FEM results of desiccation induced stress in glue samples. The computational analysis was run in Abaqus (Dassault Systèmes, 2018), and the comparison shows that the FEM results are very accurate in predicting stresses in restrained materials under desiccation.
The material definitions introduced in this investigation are given in Table 2 which are based on fully relaxed stress conditions. The Poisson’s ratios of the materials were kept constant at 0.3. For canvas, elastic modulus of 35 MPa and moisture expansion coefficient of 1.0E-4 are used [20, 24].
Effect of strain rate on the material property
Characteristics of wooden stretcher
The structural constraint in a canvas painting is provided by the stretcher. The distributions of displacements in paintings are related to aspect dimension ratios of the stretchers. The typical dimensional ratios of the stretchers commonly used from 18th Century [31, 33] and onwards are used in current study. Pernety’s ratio of 1:1.2 is confirmed by a study of 38 Danish Golden age paintings [32] (Andersen 2013), thus the canvas size in the current study is set to 762 by 635 mm (30 in. × 25 in.).
Pine and Spruce is the commonly known types of stretchers, and the following material properties of Scots Pine were adopted for the current models (Table 3; the subscription number indicate the transverse strain direction and the stressed direction of the material, while 1, 2 and 3 represents directions in x, y and z-axis, respectively).
The moisture induced deformation of different timber species in conservation has been investigated in the past. However, the understanding about the response time varies [26, 27]. The amount of shrinkage in the wooden stretcher over time affects the induced stress in paint layers and stress in paint layer under desiccation is greater when the shrinkage of the stretcher is minimal. Therefore, in the consideration of worst-case scenario, the wood shrinkage is assumed negligible at the time of the other layers reached the equilibrium state.
Computational models for global and local behaviours of oil canvas painting
Geometrical definitions
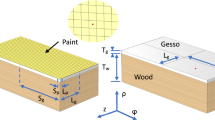
Models in two different scales were constructed; global scale and local scale. In the global scale models (global model), the full-size painting (762 mm by 635 mm) was digitally reconstructed in three-dimension, and the local scale models (local model) are two-dimensional cross-section models, which were constructed based on an image of an actual painting.
Two types of global model were tested initially. The first type has paint and ground layers with constant thickness (C-Type), while the thicknesses were varied for the second type (V-type) (Fig. 2). The constant thicknesses of C-Type model are the average of empirically measured values from 37 paint cross sections at the Royal Danish Academy, Institute of Conservation (see Valbjørn Nielsen et al., forthcoming), and the measured values of paint ranged between 0.012 mm to 0.5 mm, and 0.0069–0.4 mm for the ground. The computational model for the V-Type was constructed with randomly generated thickness within the given ranges for each layer at 200 grid points, which were spaced at equal distances. As the result of such geometrical refinement, the mesh was also refined with the approximate element size of 3 mm, which is similar to the maximum element size (5 mm) defined from the mesh independent study of constant thickness model.
Figure 3 shows the induced maximum principal stress (MPS) in painting models of the different thickness types. The painting models had material layer composition 1, which were exposed to RH change from 50 to 10%. In the figure, Type-V has up to 38% more stress than Type-C model. It is to note that, despite the thickness of C-Type is the average value of V-Type, the average of the undulating MPS values in V-Type is not the same, but greater than Type-C. Such result is often seen from analysis of thin structures; when geometrical imperfection is introduced to numerically perfect geometry, the stress level can increase by multiple factors. Similarly, the simulation result indicates that the impact of geometrical undulation (can be understood as introducing the realistic geometrical imperfection to the ‘ideal’ constant thickness model) on the stress development in the paint layer is actually greater than using ideally flat model with the corresponding thickness. Furthermore, the thickness in the model was varied only every 3 mm, and in reality, the thickness can vary as small as every 1 mm. Thus, it is expected that the stress variation can be greater in the real painting.
The immediate advantages of modelling in local scale in addition to the global scale is, firstly, that the analysis can be based on the models with the realistic geometrical definitions and secondly, that the interactions between different material layers can be closely observed for the possible crack formations. For the realistic geometrical definitions, the cross-section model was reconstructed based on the cross-section image of an actual painting (Fig. 4).
As discussed in the earlier section (Table 1), the glue layer is omitted in the study of composition type 2; the above figure is only the depiction of the models when all material layers are present. In the model with glue layer omitted, the void was replaced with ground layer.
Computation scheme for desiccation strain in the finite element analysis
The RH induced strains are calculated based on the assigned moisture expansion coefficients of materials (Table 2), and calculation used the following equation:
where \({\alpha }_{f}\) is the material’s moisture expansion coefficient, which is a function of the field variable, \({f}_{\beta } or {f}_{\beta }^{I}\), which in this case is the prescribed relative humidity at different steps. \(\left({f}_{n}-{f}_{n}^{0}\right)\) refers to the change in RH at the current RH step, \({f}_{n}\) with respect to the reference RH value, at which the strain is assumed to be zero.
Therefore, the induced stress is eventually calculated from the equation below:
where [ɛ] is the total strain and [D] is the material stiffness matrix.
Boundary condition
The global models have been restrained in Z-axis translation at the four corners of the stretcher, while all the models have one more translation constraint in X and Y-axes at the centre point (Fig. 5). These nodal constraints were only applied to prevent the unwanted out-of-frame distortions of the entire model due to unbalanced forces, and do not have impact on the shrinkage behaviours of the elements.
The displacement boundary conditions are applied to the outer edges of the section model as shown in Fig. 6, where the horizontal displacements are applied. The different magnitudes of the displacements were obtained from simulations of the global models.
Numerical analysis of local crack formations
In the analysis of full oil canvas painting under RH changes, the specific moments and locations of crack formations have not been discussed in depth. For FEM, the simulations of crack propagation are time-consuming process since the crack paths must be followed and the mesh refinement around the crack-tips must be updated every step increment. Therefore, the current investigation adopts the framework of extended finite element method (XFEM) to approximate and understand the underlying mechanisms of crack initiation and propagation in the local scale. As the name implies, XFEM can be understood as extending the existing FEM through additions of the enrichment functions, which typically consist of discontinuous basis functions to standard polynomial functions, and also the near-tip asymptotic functions for the singularity around the crack tip.
However, the current crack propagation simulations were executed, in which traction-separation laws based cohesive segments damage modelling, which can follow crack developments in the element based on the calculated criteria, thus the near-tip asymptotic singularity functions (the right most term in Eq. 6) can be omitted [28]. The main reason behind the choice of cohesive segments method was, that the method better suits the intention of the study to examine crack initiation at any possible location, and the propagation of the initiated cracks are not dependent on predefined paths nor element boundaries [28]
where \({N}_{i}\) is the shape function associated to node i, \({u}_{i}\) is nodal displacement vector at node i, \({a}_{i}\) is enriched degrees of freedom, and \(H(x)\) is the Heaviside function as given below:
where \(x\) is an integration point in the element, \({x}^{*}\) is the point on the crack closest to \(x\), and \(n\) is the unit outward normal to the crack at \({x}^{*}\). The initiation of crack occurs when the provided maximum principal stress is reached. For the propagation, the damage evolution model based on energy is used, where the energy value is calculated from the empirical data.
It is often promoted that XFEM does not require extensive mesh refinements as seen in FEM for fracture analysis. However, preliminary studies showed the effect of mesh size on the results from XFEM, especially for the location of first crack formation and the length of crack propagation. The mesh independency study confirmed, that the time of first crack formation could be comparable, while the exact locations and the size of the cracks can differ with the element sizes; mainly due to the fact that the traction–separation cohesive behaviour makes the cracks run across the full size of the elements when the failure criteria is met. The mesh independence study showed that the models with the maximum element size below 0.005 mm didn’t show further stress discrepancies at the measured locations.
Results and discussions
Impact of glue in oil canvas paintings
Figure 7 shows the maximum principal stress (MPS) distribution in the paint layer when the models have been desiccated from 50 to 10% RH and Fig. 8 shows the stress plots along the diagonal path (Fig. 3). The most notable difference is the decrease of MPS of Composition 1 (C1) with glue layer towards the centre of the painting, while Composition 2 (C2) without glue layer stress level remains rather consistent along the path. The MPS of C1 near the corner are only slightly higher than the maximum stress observed in C2 (Fig. 8) which shifted at about 350 mm (0.7 of the path length) from the center of the painting. The stress reduction in the central region of C1 is from the shrinkage of glue, which pulls in the supporting stretcher. Figure 9 shows the deflections of the stretcher of C1 in the vertical axis. The inward deflections of the stretcher due to the shrinkage of the glue can be about 4.5 times greater than C2. Such deformation of stretcher reduces the development of tension stresses in the paint layer. The shrinkage effect of glue on the stress level in the paint layer is diminishing towards the corners due to the high corner stiffness of stretcher that prevents the inward deflections.
MPS plot in paint layer along the straight path from center to corner of the painting as shown in Fig. 7: C1 with glue layer and C2 without glue layer under desiccation of RH 50% to 10%
Vertical Displacement (U2) Plot: the maximum inward displacements are distributed around the middle of the longer stretchers (left) and the longer stretcher pulled inward eccentrically causing lateral torsional buckling, which is shown in the cross-section plot; the deformation is exaggerated by 5 times for the purpose of visualisation (right)
The impact of glue shrinkage on paint layer is affected by the stiffness of ground layer in between. The comparison of the strain distribution between C1 and Composition 3 (C3) shows that having stiffer material as ground layer reduced both compression and tension in the centre and corner regions, respectively.
Weaker ground vs stronger ground
The simulation results of the section models showed that the micro cracks are likely to initiate in the ground, and when the glue layer is present (C1 and C3). The glue layers were cracked in both cases of C1 and C3 with the local stresses reaching above 60 MPa. In case of C1 with weaker ground layer, the crack near the hill of the canvas cuts through almost the entire depth of the ground layer, where it is the thinnest (Fig. 10). The crack remained in the ground layer at the end of the first desiccation cycle, and remained hidden under the paint layers. However, in respect of the aging properties of materials, the crack in the ground layer will eventually propagate into the paint layers through the future desiccation cycles. It is still intriguing to see that, within such thinly bound structure of the total thickness around 0.5 mm, the crack initiation can be layer specific. Cracks that exist only in the ground layer are also observed in real paintings ) [30] (Fig. 11).
The result again emphasizes the relevance of adopting the realistic geometrical parameters in the analysis. A ground layer crack was also observed near the hill of canvas in case of C3, however, the crack in the stronger ground layer was still minor with the length around 5 μm. Therefore, the stronger ground layer can better resist crack formation than the weaker ground. The same result of only minor crack initiation in C3 was also observed in case of C2, which means the paintings with the glue have higher risk of crack formation in the weak ground layer than the ones without.
As indicated before, it is more difficult to generate cracks in the centre of the painting than near the corners. Not significant cracks are expected in C3 (with glue layer) when desiccated from RH 70–10%. Only very small cracks in the glue layer were observed, likely from its small thickness in combination with high stiffness, which attracts greater share of the load. Notable cracks (lengths around 34 μm) were found in the ground layer under 64% desiccation from 90%.
Observations from real painting
A pair of images of a real painting were used to compare cracks in different layers. The infrared image showed cracks at the top of the ground layer and in the paint layers, while the X-radiograph image showed cracks down into the ground layer. The comparison of the images (Fig. 11) show that majority of the cracks exist in both paint and ground layers, while also revealed the cracks, which only exist in the ground layers. It is not clear whether the ground cracks were formed during earlier desiccation cycles, or later formed ground cracks.
Summary and conclusions
The current paper presents an investigation, in which the possible crack formation among different compositions of material layers was explored. The specific materials for different layers were discussed in this investigation; these include lead white and red iron oxide as either the paint or the ground layer and rabbit skin glue for the glue layer. The investigation used the FEM and XFEM, and both full-size and detailed Sect. (1.89 mm width) models were constructed for the analysis.
The edge boundary condition, which fully-restrained the displacements of the canvas in the previous research, was replaced with the modelled wooden stretcher. The simulation results showed that the geometrical deformation of the stretcher was a result of the shrinkage of the glue, which reduced the tension stress in the centre of painting. The deformation was about 4.5 times greater than the case without the glue.
The simulation results of the section models representing the corner regions confirmed that; (1) the glue layer is sensitive to crack formation; it can crack with a 36% drop in RH, (2) the weaker ground can experience cracks, which cut through its entire depth (estimated crack length of 70 μm) from a 48% drop in RH, (3) applying the stronger ground layer (lead white) can delay the crack initiation.
It is more difficult to form cracks in the centre region of the painting under pure desiccation, and the change in RH should be as large as from 90 to 10% to generate any notable cracks in the area. The results that show the difficulty of creating cracks in the centre of the painting suggests that there are other reasons for cracks in paintings than could be simulated here. The findings of cracks which develop in weak grounds is in line with what is seen in real paintings investigated.
The current study was developed with 15- to 20-year-old material data, therefore, any older paintings are likely to expect cracks from smaller RH changes in the expectation that, the materials become more brittle [29], and ultimate strain reduces exponentially with age.
The specific range of RH that initiated the crack is highly dependent on the specific material characteristic used in this investigation, and the time of occurrence and size of the crack can vary according to the different material characteristics adopted for the models. Furthermore, the mechanical properties of the materials mentioned in the current investigation are time dependent, as well as the strain-rate dependent. Therefore, different cases of aged oil canvas paintings with various materials and layer compositions under different rate of environmental changes are under investigation.
Availability of data and materials
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Stout GL. A trial index of laminal disruption. J Am Inst Conserv. 1977;17(1):17–26.
Bucklow S. The description of craquelure patterns. Stud Conserv. 1997;42:129.
Roche A. Influence du type de chassis sur le vieillissement mecanique d’une peinture sur toile. Stud Conserv. 1993;38(1):17–24.
Padfield T, et al. Back protection of canvas paintings. Heritage Science. 2020;8(1):96.
Mecklenburg MF. Micro Climates and Moisture Induced Damage to Paintings. in Conference on Micro Climates in Museum. 2007. Copenhagen.
Erhardt D, Tumosa CS, Mecklenburg MF. Applying science to the question of museum climate. in Conference on Micro Climates in Museum. 2007. Copenhagen.
S Rehbein, M Huisgen, Modellversuche zu Grundierungstechniken der Leinwandgemälde im 19. Jahrhundert, in Das 19. Jahrhundert und die Restaurierung: Beiträge zur Malerei, Maltechnik und Konservierung H. Althöfer, Editor. 1987, Callwey. p. 255–260.
Bilson T. Canvas Shrinkage: A Preliminary Investigation into the Response of a Woven Structure. in ICOM Committee for Conservation, 11th Triennial Meeting. 1996. Edinburgh.
Andersen CK, et al. The industrialisation of canvas production in Denmark and its implications for the preservation of Danish nineteenth century paintings. in Incredible Industri : Preserving the evidence of industrial society. 2009. Copenhagen
Karpowicz A. In-plane deformations of films of size on paintings in the glass transition region. Stud Conserv. 1989;34(2):67–74.
Keck S. Mechanical alteration of the paint film. Stud Conserv. 1969;14(1):9–30.
Giorgiutti-Dauphiné F, Pauchard L. Painting cracks: a way to investigate the pictorial matter. J Appl Phys. 2016;120(6): 065107.
Flores JC. Mean-field crack networks on desiccated films and their applications: girl with a pearl earring. Soft Matter. 2017;13(7):1352–6.
Mecklenburg MF. Determining the Acceptable Ranges of Relative Humidity And Temperature in Museums and Galleries: Part 1, Structural Response to Relative Humidity. 2007.
ASHRAE handbook: heating, ventilating, and air-conditioning applications: Chapter 24 museums, galleries, archives, and libraries. 2019: American Society of Heating, Refrigerating and Air-Conditioning Engineers.
Michalski S. The power of history in the analysis of collection vulnerabilities. in ICOM Committee for Conservation 17th Triennial Meeting. Melbourne. 2014.
Mecklenburg MF, Tumosa CS. Mechanical Behavior of Paintings Subjected to Changes in Temperature and Relative Humidity. in Art in Transit: Studies in the Transport of Paintings. Washington D.C. 1991
Mecklenburg MF, McCormick-Goodhart M, Tumosa CS. Investigation into the deterioration of paintings, and photographs using computerized modeling of stress development. J Am Inst Conserv. 1994;33(2):153–70.
Mecklenburg MF, Tumosa CS, McCormick-Goodhart MH. A general model relating externally applied forces to environmentally induced stresses in materials. MRS Proc. 1995;352:285.
de Willigen P. A mathematical study on craquelure and other mechanical damage in paintings. Delft: Delft University Press; 1999.
Vila A, et al. Picasso 1917: An insight into the effects of ground and canvas in the failure mechanisms in four artworks. In conservation of modern oil paintings. Amsterdam: Springer; 2020.
Witlox M, Carlyle L. A perfect ground is the very soul of the art’ (Kingston 1835): ground recipes for oil painting, 1600–1900. In ICOM Committee for conservation 14th triennial meeting the Hague 12–16 September 2005. Hague: James & James/Earthscan; 2005.
van Driel BA, et al. The white of the 20th century: an explorative survey into Dutch modern art collections. Herit Sci. 2018;6(1):16.
Mecklenburg MF, Tumosa CS, Mecklenburg MF. Mechanical behavior of paintings subjected to changes in temperature and relative humidity in Art In Transit: studies in the transport of paintings. London: National Gallery of Art; 1991. p. 173–216.
Mirianon F, Fortino S, Toratti T. A method to model wood by using ABAQUS finite element software. Part 2. application to dowel type connections. Espoo: VTT Publications; 2008.
Rachwal B, et al. Response of wood supports in panel paintings subjected to changing climate conditions. Strain An Int J Exp Mech. 2012;48(5):366–74.
Stevens WC. Rates of change in the dimensions and moisture contents of wooden panels resulting from changes in the ambient air conditions. Stud Conserv. 1961;6(1):21–5.
Dassault Systèmes Simulia Corp. Abaqus Theory Guide. 2018.
Mecklenburg MF, Tumosa CS, Erhardt D. The changing mechanical properties of aging oil paints. In Materials Research Society Symposium. Warrendale: Materials Research Society; 2005.
Scharff M, Andersen CK, Filtenborg T. Canvas-related micro-cracks in Danish 19th century paintings. in ICOM-CC Triennial Conference in Beijing: Transcending Boundaries: Integrated Approaches to Conservation, 2021. Beijing.
Filtenborg T, Andersen CK. Canvas supports and grounds in paintings by C.W. Eckersberg. Paper presented at Technology & Practice: Studying the European Visual Arts 1800-1850 – Paintings, Sculpture, Interiors and art on Paper, 2016. Copenhagen.
Andersen CK. Lined canvas paintings. Mechanical properties and structural response to fluctuating relative humidity, exemplified by the collection of Danish Golden Age paintings at Statens Museum for Kunst (SMK). PhD Thesis, KADK Royal Danish Academy of Fine Arts, Schools for Architecture, Design and Conservation, School of Conservation. 2013
Pernety AJ. Dictionnaire portatif de Peinture, Sculpture et Gravure: avec un traité pratique des différentes manières de peindre, chez Bauche. 1757.
Acknowledgements
Not applicable.
Funding
This research was funded by the European Union’s Horizon 2020 research and innovation program under grant agreement No. 814624. Łukasz Bratasz’s work was financed by also the Polish National Agency for Academic Exchange, project Polish Returns [grant PPN/PPO/2018/1/00004/U/00001].
Author information
Authors and Affiliations
Contributions
DS-HL: conception development and design of work, analysis, and interpretation of data and drafted the work. N-SK: analysis, and interpretation of data. MS: conception development, and design of work, revision of work. AV. N: interpretation of data, revision of work. MM: conception development, and design of work, interpretation of data, revision of work. LF-L: conception development, revision of work. LB: conception development, revision of work. CK. A: conception development, and design of work, revision of work. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Lee, D.SH., Kim, NS., Scharff, M. et al. Numerical modelling of mechanical degradation of canvas paintings under desiccation. Herit Sci 10, 130 (2022). https://doi.org/10.1186/s40494-022-00763-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40494-022-00763-w