Modelling between tree and longitudinal variation in green density within <Emphasis Type="Italic">Pinus radiata</Emphasis>: implications for estimation of MOE by acoustic methods

Michael S. Watt; Guillermo Trincado

doi:10.1186/s40490-014-0016-5

New Zealand Journal of Forestry Science

December 2014, 44:16 | Cite as

Modelling between tree and longitudinal variation in green density within Pinus radiata: implications for estimation of MOE by acoustic methods

Authors
Authors and affiliations

Michael S. Watt
Guillermo Trincado

Open Access

Research article

First Online: 06 September 2014

1.7k Downloads
1 Citations

Abstract

Background

Instruments based on resonance are widely used in the forest industry to predict modulus of elasticity (MOE) and segregate logs of varying quality for different end uses for fast growing softwoods such as Pinus radiata D. Don. Predictions of MOE, made using resonance instruments, often assume a constant green density, ρ_g, of 1,000 kg m^–3. However, little research has been done to test the robustness of this assumption. The objective of this research was to describe changes in predictive precision of MOE as ρ_g is increasingly well characterised.

Methods

Longitudinal measurements of velocity, V, and ρ_g taken from eighty 17-year old unthinned P. radiata trees growing at two sites in Chile were used to calculate MOE. Predictions of MOE were then made by substituting measurements of ρ_g for values predicted by the following models (i) Model 1 - assuming a constant ρ_g of 1,000 kg m⁻³, (ii) Model 2 - using the mean tree ρ_g of 914 kg m⁻³, (iii) Model 3 - using a model with fixed effects to account for the mean longitudinal variation in ρ_g, (iv) Model 4 - inclusion of previous terms and random effects to account for tree level variation and (v) Model 5 - inclusion of previous effects (in model 4) and a random quadratic term. Differences in MOE determined from measurements of ρ_g and the five predictions of ρ_g were expressed as both a percentage difference, (D) and an absolute percentage difference (D_a) to assess precision and bias.

Results

At the tree level, values for mean D and D_a (in brackets) were −9.9 (10.4)%, −0.459 (5.49)%, −0.262 (4.15)%, −0.045 (0.232)% and −0.0406 (0.189)%, for Models 1, 2, 3, 4 and 5, respectively. At the log level, considerable longitudinal bias in D was evident for Model 1 where over-prediction of MOE was greatest between relative heights of >0.1–0.4, with D reaching maximum values of −33.8% between relative heights of >0.1–0.2.

Conclusion

Assuming constant ρ_g can result in substantial error in estimates of MOE using acoustic instruments particularly when predictions are made at the log level. The mixed effects modelling approach described here demonstrates a useful method for characterising variation in ρ_g allowing more accurate estimates of MOE to be made using acoustic methods.

Keywords

Green density Longitudinal variation Pinus radiata Radiata pine

Background

Modulus of elasticity (MOE) is a measure of the resistance of wood to deformation under an applied load, and it is a useful indicator of corewood quality in the widely grown plantation softwood Pinus radiata D. Don. Modulus of elasticity is used as a threshold criterion in machine stress-grading of structural timber and is also a key property for determining quality of laminated veneer timber. Plantation-grown Pinus radiata has a relatively poor MOE (Moore [2012]) when compared with other internationally traded structural timber species.

Instruments that use sound or stress waves to estimate velocity and MOE have been widely adopted as they are simple, compact and easy to operate. Although the use of sound to measure MOE has been researched for over 50 years (Schultz [1969]), it is only recently that the method has seen widespread application (Dowse and Wessels [2013]; Wang et al. [2007]). The two types of tools available are resonance tools for use on logs and time of flight tools (TOF) that are suitable for use on both standing trees and logs. Tools based on TOF are generally considered to be less accurate than resonance tools (Andrews [2000], [2002]).

Resonance tools are routinely used within the forest industry. Considerable research has been undertaken with these instruments to characterise variation in MOE at a range of scales. These instruments are also widely used by the forest industry during harvesting operations to segregate logs. Resonance tools can be used to screen logs and divert those below the structural-grade threshold to other applications avoiding the expense of processing wood that will not meet final specifications (Tsehaye et al. [2000]; Matheson et al. [2002]).

Despite the widespread use of resonance methods, there are errors associated with this type of methodology. One of the potentially largest sources of error is the assumption of a constant green density, ρ_g, when predicting MOE from velocity. Green density is used in combination with velocity (V), determined from resonance, to predict MOE using the following equation:

MOE = V^{2} ρ_{g}

Open image in new window

(1)

Typically values for ρ_g of 1,000 kg m⁻³ are assumed and variation in MOE using this assumption have been widely described among sites and among trees (Watt et al. [2009]; Lasserre et al. [2004]).

Although constant values for ρ_g are often assumed, ρ_g is highly dependent on the ratio of heartwood to sapwood within a tree. In P. radiata, sapwood is close to saturation and typically values for ρ_g are 1,100 kg m⁻³ (Loe and Mackney [1953]; Cown [1999]) while heartwood has a moisture content just above the fibre saturation point and low ρ_g that is typically about 600 kg m⁻³ (Cown [1999]). The ratio of heartwood to sapwood has been found to be affected primarily by tree age and height and to a lesser extent by site and thinning (Cown et al. [1991]; Kininmonth [1991]; Wilkes [1991]; Cown [1974]). In mature P. radiata ρ_g is often lower than 1,000 kg m⁻³ because the percentage of heartwood increases with tree age (Chan et al. [2012]). Indeed, whole-stem values as low as 798 kg m⁻³ have been found in 36-year-old trees (Chan et al. [2012]). Although variation in ρ_g has been studied (Chan et al. [2012]; Cown and McConchie [1982]), little research has fully partitioned and modelled variation in ρ_g among sites, among trees and/or within trees, or investigated the impact of this variation on estimates of MOE.

In this study longitudinal measurements of velocity and ρ_g obtained from P. radiata growing at two contrasting sites were used to calculate MOE. Predictions of MOE were then made by substituting measurements of ρ_g for values predicted by five different models. These models ranged in complexity from the simplest which assumed constant ρ_g of 1,000 kg m⁻³ through to the most complex which was a mixed-effects model that included fixed and random effects to determine ρ_g. Differences between measured MOE and that predicted by the five models was determined to quantify the magnitude of errors that occur as ρ_g is increasingly well characterised. Finally, a methodology is described for accurately predicting longitudinal variation in ρ_g for a single tree from measurements obtained from that tree at a given height.

Methods

Study sites

Data for this research were obtained from two sites spanning a climatic range located at Santa Lucia (latitude 37° 12 41, longitude 71° 48′ 31″) and Santa Isabel (latitude 37° 24 45, longitude 72° 15′ 29″) in the Bio region (region VIII) of Chile. Santa Lucia is located in the Andean foothills at an elevation of 727 m. It has a relatively low mean annual temperature (10.9°C) and high mean annual rainfall (2,022 mm year⁻¹). In contrast, Santa Isabel is located at a lower elevation (170 m) in the Central Valley and has higher mean annual temperature (12.9°C) and lower mean annual rainfall (1,166 mm year⁻¹) than Santa Lucia. The soil types underlying the sites were volcanic ash and sandy, respectively, for Santa Isabel and Santa Lucia.

Plant material, treatments and stand history

Plant material at both sites were drawn from a half-sib family named Colicheu produced through the breeding programme of the Chilean company Forestal Mininco. Seedlings and one-year-old cuttings were used as treatments at both sites.

For each treatment, a permanent sample plot (PSP) of 630 m² (30 m × 21 m) was established in which there were six rows of 15 plants. At both sites, the initial planting density was 1,428 trees ha⁻¹ (2 × 3.5 m) and the PSPs were not thinned or pruned prior to the measurements.

Measurements

Measurements were made during September 2012 on 17-year-old trees that were planted in 1995. A total of 40 sample trees at each site (20 per plant material treatment) were selected for measurement. These represented all diameter classes. Malformed trees (including leaning trees or those with forked trunks or with large branches) were not selected.

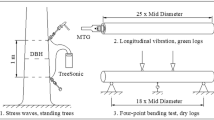
Following the felling of each tree, measurements of height and diameter at breast height (DBH) were taken. Stem slenderness was determined from these measurements as height/DBH. Each tree was cut into 3-m long sections until a diameter of 10 cm was reached. All branches were removed. Discs that were 30-mm thick were taken at the top and base of each section. Green density, ρ_g, (kg m⁻³) was determined on each sample disc following a standard protocol (ASTM D2395) from the following equation,

ρ_{g} = \frac{W_{g}}{V_{g}}

Open image in new window

(2)

where W_g is green weight (kg), and V_g is green volume (m³) determined using the immersion method. All values of ρ_g reported in this paper use values of ρ_g averaged over the log from measurements made at the top and base.

Velocity was determined for each log without removing bark using a resonance tool (Hitman HM200, Fibre-Gen). Velocity (V) was determined from sample length (l) and the resonant frequency (f) as V = 2 fl.

Description of the modelling approach

Longitudinal measurements of velocity and ρ_g were used to calculate MOE from Equation (1). Although these calculated values were not direct measurements of MOE, as they were determined from V and ρ_g, they will be referred to hereafter as measured MOE for clarity. Predictions of MOE were then made by substituting measurements of ρ_g for values predicted by the following models (i) Model 1 - assuming a constant ρ_g of 1,000 kg m⁻³, (ii) Model 2 - using the mean ρ_g across all trees of 914 kg m⁻³, (iii) Model 3 - using a model with only fixed effects to account for the mean longitudinal variation in ρ_g, (iv) Model 4 - using a model with the previous fixed effects and random effects to account for variation in intercepts for ρ_g between trees and (v) Model 5 - using a model with the previous effects (in Model 4) and a random quadratic term to account for differences in the longitudinal pattern of variation in ρ_g among trees. A summary of the terms included within each model is given in Table 1.

Table 1

Form of the five models developed to predict green density, where relht is the relative height

Model no.	Terms included in the model
	Constants	Fixed effects	Random effects
1	ρ_g = 1,000 kg m⁻³	−	−
2	ρ_g = 914 kg m⁻³	−	−
3	−	a + b relht + c relht² + d relht³	−
4	−	a + b relht + c relht² + d relht³	Intercept
5	−	a + b relht + c relht² + d relht³	Intercept, relht, relht²

Model development

Using SAS (SAS Institute Inc. [2008]) a random-coefficients mixed-effects model was used to characterise variation in ρ_g at the log level for Models 3, 4 and 5. Mixed effects models can include both fixed and random effects. An effect is termed fixed if the levels in the study include all possible levels of the factor, or at least the levels about which inference is to be made. In contrast, a factor is considered random if its levels plausibly represent a larger population with a probability distribution. Only fixed effects (relative height) were used for predictions of ρ_g made by Model 3 while fixed effects and the random intercept were included for Model 4 (Table 1). The full random-coefficients model (Model 5) included fixed effects and random effects for both the intercept and quadratic terms (Table 1).

Relative height, which was defined as the ratio of the measurement or prediction height to the total tree height, was used as a predictive variable within the model rather than actual measurement height. This was because the Akaike Information criterion, which measures the relative quality of a statistical model (Littell et al. [2006]), was lower (4673.4 vs. 4725.6) for the final model with the relative height term included. The fixed-effects part of the model included relative height as a third-order polynomial. Neither site nor treatment, nor the interaction of these two terms with any of the terms in the relative height equation, was significant at P = 0.05. Random effects included the intercept (P < 0.001), relative height (P < 0.001) and the square of relative height (P < 0.001). A full description of Model 5 is given in the next section of the methods.

Predictions of ρ_g against relative height using only the fixed effects in the model are shown as the black line while predictions of ρ_g using all random effects for individual trees (Model 5) are shown as the blue lines in Figure 1. Predictions of longitudinal variation in ρ_g for individual trees were markedly offset from the mean value. These results supported the significance of different intercepts for different trees but followed a similar longitudinal pattern to that of the mean, for most trees, although there were exceptions (Figure 1).

Figure 1
**Predictions of green density using Model 5 plotted against relative height.** Black line: mean relationship between relative height and green density, predicted from the fixed effects; blue lines: tree-level estimates (predicted using both fixed- and random effects).

Analyses

Differences between measured values (y_m) and predictions (y_p) of ρ_g and MOE using the five models were expressed at the mean tree level (by averaging across logs) and log level. These differences were expressed as both a percentage difference, D (D = ((y_m-y_p)/y_m) ⋅ 100) and an absolute percentage difference, D_a (D_a = |D|). For a given model, both D and |D| were identical between ρ_g and MOE . Consequently results showing these differences from the measured values can be interpreted to represent either wood property. The distribution and mean values for D and D_a were examined for each model to respectively assess model bias and precision. The relationship between relative height and both D and D_a was also examined to determine within tree bias and precision for the five models.

Calibration of Model to predict longitudinal variation in ρ_g from a single disc

The methodology by which the most complete and accurate model (Model 5) can be used to predict longitudinal variation in ρ_g from measurements obtained from a single disc is demonstrated below. Use of the linear mixed-effects model described in Model 5 permitted the estimation of a mean response (population-specific) or a calibrated response (cluster-specific) for a new tree (Verbeke and Molenberghs [2000]). A mean response can be obtained using only the fixed-effect components of Model 5, where the vector of random effects u_k for a new k th individual is assumed to have expected value E(u_k) = 0. In contrast, a calibrated response can be obtained when auxiliary information is available allowing for prediction of random parameter components. In this case, auxiliary information corresponds to a measure or prediction of ρ_g at a given stem height for a new tree. Using this information, the vector of random parameters can be predicted using an approximate Bayes estimator of u_k (Vonesh and Chinchilli [1997]; Rencher [2000]).

{\hat{u}}_{k} ≅ D {\hat{Z}}_{k}^{'} W_{k} {\hat{e}}_{k},

Open image in new window

(3)

where

W_{k} = {[{\hat{Z}}_{k} D {\hat{Z}}_{k}^{'} + R_{k}]}^{- 1}

Open image in new window

and the error vector

{\hat{e}}_{k} = y_{k} - f (A_{k} β, x_{k})

Open image in new window

. The design matrix

{\hat{Z}}_{k}

Open image in new window

and the variance-covariance matrix for the random-effects D and residuals R_k are defined for Model 5 as:

{\hat{Z}}_{k} = [\begin{array}{c} 1 & x_{k 1} & x_{k 1}^{2} \\ . & . & . \\ 1 & x_{k n_{k}} & x_{k n_{k}}^{2} \end{array}], D = (\begin{array}{c} Var (u_{0}) & Cov (u_{0}, u_{1}) & Cov (u_{0}, u_{2}) \\ Cov (u_{0}, u_{1}) & Var (u_{1}) & Cov (u_{1}, u_{2}) \\ Cov (u_{0}, u_{2}) & Cov (u_{1}, u_{2}) & Var (u_{2}) \end{array})

Open image in new window

(4)

and

R_{k} = Var [e_{k}] = σ^{2} I_{n_{k}}

Open image in new window

, where

I_{n_{k}}

Open image in new window

is an identity matrix of dimension (n_k x n_k) and n_k is the number of observations used for calibration. Under this structure, random errors are assumed to be uncorrelated and have constant variance (σ²).

Longitudinal predictions of ρ_g can be made from Model 5 using ρ_g data obtained from a single disc. As an example, ρ_g measured at breast height (1.3 m) for a randomly selected sample tree in the dataset was 985.08 kg m⁻³. The relative height of the disc was 0.041 (disc height of 1.3 m divided by the total tree height of 31.6 m). Thus, the difference between the observed value and the estimated mean-response value from Model 5 is determined from the fixed effects component of the model as:

{\hat{e}}_{k} = 985.08 - (959.06 - 942.14 \cdot 0.041 + 2865.78 \cdot 0 {.041}^{2} - 2063.88 \cdot {0.041}^{3}) = 60.07 kg m^{- 3}

Open image in new window

(5)

The design matrix

{\hat{Z}}_{k}

Open image in new window

and the variance-covariance matrices for the random coefficients and error estimated for Model 5 are determined as,

{\hat{Z}}_{k} = (\begin{array}{c} 1 & 0.041 & {0.041}^{2} \end{array}), D = (\begin{array}{c} 1860.36 & - 3679.95 & 3279.74 \\ - 3679.65 & 52716.0 & - 67668.0 \\ 3279.74 & - 67668.0 & 91975.0 \end{array}) and R_{k} = 430.06

Open image in new window

(6)

Now, replacing the matrices in Equation 3 gives the following predictions for the random parameters of this specific tree: u_0k = 49.5454, u_1k = −49.9722 and u_2k = 18.8294 and the calibrated parameters for the model are given below in Equations 7, 8 and 9:

{\hat{β}}_{0 k} = 959.06 + 49.5454 = 1008.6054

Open image in new window

(7)

{\hat{β}}_{1 k} = - 942.14 - 49.9722 = - 989.1122

Open image in new window

(8)

{\hat{β}}_{2 k} = 2865.78 + 18.8294 = 2884.6094

Open image in new window

(9)

Thus, the calibrated model for the sample tree is

{\hat{β}}_{kj} = 1008.6054 - 989.1122 x_{ij} + 2884.6094 x_{ij}^{2} - 2063.88 x_{ij}^{3}

Open image in new window

(10)

The accuracy of this prediction is assessed by comparing the predicted longitudinal pattern to that obtained through measurements.

Results

Variation in tree dimensions

Tree diameter ranged from 18.5 to 40.1 cm (average 27.6 cm) and was not significantly affected by either the main or interactive effects of treatment and site (Table 2). The total tree height of cuttings at Santa Lucia was significantly greater than for the other three site × treatment combinations, but no other significant differences in height were noted among treatments (Table 2). Tree height ranged from 20.4 − 35.5 m (average 28.0 m). Neither the main nor interactive effects of site and treatment influenced stem slenderness which ranged from 82.0–129 (average 103) (Table 2).

Table 2

Treatment and site variation in stem dimensions and wood properties determined from 20 trees per treatment per site

Variable¹	Santa Lucia		Santa Isabel		Analysis of variance²
	Seedlings	Cuttings	Seedlings	Cuttings	Treatment (T)	Site (S)	T × S
Dimensions
DBH (cm)	26.4 (11.2)	30.2 (10.7)	26.8 (8.17)	26.9 (9.58)	3.73^ns	2.00^ns	3.40^ns
Height (m)	27.5 (7.93)b	30.3 (6.19)a	27.6 (3.93)b	26.5 (4.71)b	2.00^ns	9.41**	11.0**
Slenderness	106 (2.76)	102 (2.54)	104 (2.46)	100 (2.65)	2.46^ns	0.38^ns	0.00^ns
Wood properties
Green dens. (kg m⁻³)	919 (12.0)	910 (8.07)	923 (6.77)	902 (10.3)	2.50^ns	0.05^ns	0.39^ns
Velocity (km s⁻¹)	2.96 (0.0228)	2.89 (0.0267)	2.95 (0.0290)	2.95 (0.0242)	1.71^ns	1.08^ns	1.55^ns
MOE (GPa)	8.07 (0.180)b	7.62 (0.146)a	8.03 (0.138)ab	7.85 (0.136)ab	4.37*	0.39^ns	0.75^ns

Values shown include the tree-level mean followed by the standard error in brackets¹ For variables where there was a significant effect, means followed by different letters significantly vary at P = 0.05.

² F-values are shown followed by the P category, where asterisks **, *denote respective significance at P = 0.01 and 0.05; ^nsis not significant at P = 0.05.

Table 3

Variation in green density and modulus of elasticity (determined using values of green density) with relative height determined from 80 trees at the two sites

Relative	Wood property
height class	Green density (kg m⁻³)		Modulus of elasticity (GPa)
	Mean (s.e.)¹	Range	Mean (s.e.)¹	Range
0-0.1	922 (5.1)	777 − 1037	6.76 (0.09)	4.74 − 8.24
>0.1-0.2	861 (5.4)	748 − 990	8.27 (0.11)	5.94 − 10.19
>0.2-0.3	883 (5.3)	774 − 1004	8.57 (0.12)	5.77 − 11.52
>0.3-0.4	905 (6.1)	752 − 1027	8.41 (0.11)	6.57 − 11.86
>0.4-0.5	928 (5.6)	790 − 1039	8.15 (0.11)	5.64 − 10.79
>0.5-0.6	959 (6.4)	837 − 1066	7.91 (0.11)	6.08 − 10.08
>0.6-0.7	995 (6.7)	891 − 1085	7.36 (0.11)	6.02 − 8.48
>0.7-0.8	1006 (8.9)	943 − 1049	6.83 (0.17)	5.69 − 8.26
Mean²	914 (4.8)	792 − 1018	7.89 (0.08)	6.29 − 9.83

¹Values shown are the mean followed by the standard error (in brackets) and the range from 80 trees.

²Mean tree values shown were determined as the average of all logs within the tree.

Variation in green density and MOE

Neither site, treatment nor their interaction significantly affected tree level values of ρ_g (Table 2). At the tree level, ρ_g ranged from 792−1,018 kg m⁻³ with a mean value of 914 kg m⁻³ (Table 2). Within-tree variation in green density was also large and showed a complex pattern when plotted against relative height (Figure 2a). Green density declined rapidly from mean values of 922 kg m⁻³ at relative heights of 0 − 0.1 reaching mean minima of 861 kg m⁻³ at relative heights of >0.1 − 0.2 before increasing slowly to mean maxima of 1,006 kg m⁻³ at relative heights of >0.7−0.8 (Figure 2a, Table 3).

Figure 2
**Relationship between relative height of a log and (a) green density and (b) MOE predicted using measurements of green density for logs from 80 trees.**

At the tree level, there were marginally significant (P = 0.04, Table 2) treatment differences in MOE. Although mean values for seedlings exceeded those of cuttings by 4% (least square means of 8.05 vs. 7.73 GPa), these differences were only significant at Santa Lucia (8.07 vs. 7.62 GPa). Neither site nor the interaction of site and treatment significantly affected MOE (Table 2).

At the tree level, MOE ranged from 6.29–9.83 GPa (average 7.89 GPa, Table 3). The within-tree pattern in MOE was the opposite to that of ρ_g (Figure 2b). Modulus of elasticity increased from mean minimum values of 6.76 GPa at relative heights of 0 – 0.1 reaching highest values at relative heights between >0.1 – 0.4, with a mean maximum of 8.57 GPa reached at relative heights of >0.2 – 0.3 (Table 3). Values of MOE declined at relative heights above 0.4 with a mean value of 6.83 GPa at relative heights ranging from >0.7 – 0.8 (Figure 2b, Table 3).

Variation in green density and MOE from actual values for the five models tested

Tree-level variation

Estimates of ρ_g and MOE, at the tree level were considerably biased using Model 1. Using an assumed ρ_g of 1,000 kg m⁻³ resulted in over-prediction of both ρ_g and MOE for all but two of the 80 trees (Figure 3a). Mean D was −9.9% with range of −26.6 to 1.6% (Figure 3a) while mean D_a was 10.4% with range of 3.78 to 26.6% (Figure 3b) for both properties.

Figure 3
Variation in the (a) percentage difference and (b) percentage absolute difference in both green density and modulus of elasticity (values are identical between properties) for predictions made from the five models tested. The boundary of the box closest to zero indicates the 25^th percentile, a line within the box marks the median, and the boundary of the box farthest from zero indicates the 75^th percentile. Error bars above and below the box indicate the 90^th and 10^th percentiles, beyond which outliers are shown.

Use of Model 2 to predict ρ_g improved both bias and precision at the tree level for both wood properties. Mean D was −0.459% with range of −15.7 to 10.1% (Figure 3a) while mean D_a was 5.59%, with range of 2.00 to 15.7% (Figure 3b). Little reduction in precision was achieved at the tree level using Model 3, for which mean D was −0.262% with range of −15.2 to 9.74% (Figure 3a) while mean D_a was 4.15%, with range of 0.968 to 15.2%.

Accounting for tree-level variation in the intercept (Model 4) and variation in the longitudinal pattern (Model 5) for ρ_g resulted in marked improvements over Models 1, 2 and 3 for both properties at the tree level. Precision and bias was very similar between Models 4 and 5, and Model 5 was the least biased and most precise of all models tested. For Model 5, the mean D was −0.0406%, with range of −1.27 to 0.477% (Figure 3a) while mean D_a was 0.189% with range of 0.0088 to 1.27% (Figure 3b).

Within-tree variation

Using Model 1, over-prediction of MOE was most marked in the lower half of the stem reaching maximum over-prediction between relative heights of >0.1–0.2 (Figures 4a,f). Maximum D_a was 33.8% between these relative heights (Figure 4f) while mean D_a was 16.5% for both properties (Figure 5a).

Figure 4
Relationships between relative height and the difference (left hand panels) and percentage difference (right hand panels) for MOE predicted using Model 1 (a, f), 2 (b, g) 3 (c, h), 4 (d, i) or 5 (e, j).

Figure 5
**Relationships between relative height and (a) absolute percentage difference (** D_a) in both wood properties (values are identical between properties), (b) modulus of elasticity and (c) green density for Model 1 (red open squares), 2 (blue filled triangles), 3 (cyan filled diamonds), 4 (black open triangles) and 5 (pink filled circles). Also shown in panels **(b)** and **(c)** are measured values of MOE and green density (green filled circles connected by green lines).

In addition to over-predicting measured values, the assumption of 1,000 kg m⁻³ for ρ_g also resulted in prediction errors in the longitudinal pattern in MOE. For Model 1, there was a sharp increase in predicted MOE with relative height that declined markedly after relative heights of >0.1–0.3 were reached (Figure 5b). In contrast, measured MOE increased more slowly with relative height, with highest values found across a broader range of relative heights from >0.1–0.4 (Figure 5b). The largest difference between measured values of MOE and that predicted by Model 1 occurred at the highest values of MOE at relative heights of between >0.1–0.4 (Figure 5b).

Predictions using Model 2 also resulted in over-prediction at low relative heights and under-predictions at high relative heights, in both ρ_g (Figure 5c) and MOE (Figures 4b,g, 5b). This bias was highest between relative heights of >0.1 – 0.2, >0.6 – 0.7 and >0.7 – 0.8 where values for mean D_a were, respectively, 6.97, 8.21 and 9.07% (Figure 5a). The largest values of D_a (22.2%) occurred at relative heights ranging from >0.1 – 0.2 (Figure 4g).

Estimates of MOE using predictions of ρ_g from Model 3 were relatively unbiased and precise (Figures 4c,h). Predictions from Model 3 closely followed measured changes in ρ_g (Figure 5c) and MOE (Figure 5b) across the relative height range. Consequently, across the relative height range, there was little bias in either D (Figure 4h) or D_a (Figure 5a).

Inclusion of random effects to account for tree-level influences on ρ_g resulted in substantial gains in precision over the other three models. Estimates using either Model 4 or Model 5 resulted in little apparent bias when predictions were plotted against relative height for either ρ_g (Figure 5c) or MOE (Figures 4d,e,i,j, 5b). Across the range in relative heights, mean D_a was 2.11% for Model 4 and 1.44% for Model 5.

Calibration of predictions made using Model 5

Longitudinal variation in green density for a single sample tree was determined using either the mean response or the calibrated response for Model 5. Both these results are presented in Figure 6 along with measured values. Clearly, the calibrated response accurately represents longitudinal variation in ρ_g (Figure 6) and represents a substantial improvement in precision over mean-response predictions from Model 5 (which included fixed effects only).

Figure 6
**Relationship between relative height and measured green density (open black circles) for a tree randomly selected from the dataset.** Longitudinal variation in green density generated from a single measured disc of green density (at a relative height of 0.014) using Model 5 (red squares) and predictions of green density using Model 5 containing only fixed effects (blue triangles) are also shown.

Discussion

This study shows that assuming a constant value of ρ_g can result in substantial errors in estimates of MOE using acoustic instruments. Differences from the assumed value of ρ_g for the site, and significant variation in ρ_g among and within trees were three sources of variation in ρ_g found to substantially affect predictions of MOE. The modelling approach described here demonstrates a useful method for characterising variation in ρ_g so that more accurate estimates of MOE can be made using acoustic methods.

Assuming a constant ρ_g of 1,000 kg m⁻³ is likely to result not only in poor precision but also biased estimates of MOE. Site values of ρ_g were considerably lower than 1,000 kg m⁻³ so assuming this value resulted in consistent over-prediction of both ρ_g and MOE at the tree level. Previous research has shown that there is an increasing proportion of heartwood as P. radiata matures (Chan et al. [2012]). Consequently, recorded values of whole stem ρ_g in mature stands are often lower than 1,000 kg m⁻³, as demonstrated in the present study and in previous research (Waghorn et al. [2007]; Chan et al. [2012]; Cown and McConchie [1982]).

Assuming a constant ρ_g of 1,000 kg m⁻³ also resulted in poor prediction of longitudinal variation in MOE. Measured ρ_g exhibited significant longitudinal variation that was consistent with previously observed longitudinal patterns (Chan et al. [2012]; Cown and McConchie [1982]). As ρ_g was lowest between relative heights of >0.1 – 0.4, results show MOE to be markedly over predicted for the lower half of the tree when a ρ_g of 1,000 kg m⁻³ was assumed. In addition to over-predicting values of MOE, this assumption also resulted in erroneous prediction of the longitudinal pattern in MOE. The highest values for MOE were reached over a broader range of tree heights (relative heights of >0.1 – 0.3) than the more peaked pattern described using a constant ρ_g of 1,000 kg m⁻³.

At the tree level, assumption of a site mean value for ρ_g (Model 2) resulted in a significant precision gain over the model that assumed ρ_g of 1,000 kg m⁻³ (Model 1). This assumption effectively removed bias at the tree level and reduced the mean absolute error from 10.4% to 5.59%. Despite these improvements, there was still considerable error at the tree level that was attributable to among-tree variation in ρ_g. Predictions using Model 2 also showed considerable within-tree bias that was attributable to the large longitudinal variation in ρ_g not captured by site mean level values in ρ_g.

Although the site mean value of ρ_g was markedly lower than 1,000 kg m⁻³, neither site nor treatment significantly affected values of ρ_g. The lack of a significant site effect on ρ_g in this study is likely to be attributable to the low number of sites sampled. Previous research has shown significant site variation in ρ_g and also that ρ_g is lowest in P. radiata stands growing in drier areas (Chan et al. [2012]). For trees growing under drought conditions, whole stem values for 36-year-old trees as low as 798 kg m⁻³ have been recorded (Chan et al. [2012]). Further research is needed to develop models that can characterise variation in site level ρ_g across gradients in age and environment.

At the tree level, modest gains in predicting MOE were made by accounting for the longitudinal pattern in density. As the longitudinal pattern was relatively similar between trees, this did remove the within-tree bias that was evident in log-level predictions. The longitudinal variation in ρ_g reported here is consistent with previous research within mature P. radiata stems (Chan et al. [2012]; Cown and McConchie [1982]). These authors also found a decline from the tree base to about one-third tree height, above which height values for ρ_g increased reaching maxima within the top third of the tree. Although this pattern remains the same regardless of tree age, the values for the longitudinal minima decline as trees age. A study within New Zealand across a range of stand ages found minimum ρ_g at ca. 30% of total tree height, with values for ρ_g ranging from ca. 985 kg m³ at stand age 12 to ca. 770 kg m⁻³ at stand age 52 (Cown and McConchie [1982]).

The marked between tree variation in ρ_g was well accounted for by addition of random terms to the model. Addition of random effects to Models 4 and 5 substantially improved predictions of ρ_g compared with the model with fixed effects only (Model 3). The parameter D_a declined by over an order of magnitude from 4.15% for Model 3 to 0.231% for Model 4 and 0.189% for Model 5. Most of the variation among trees was accounted for by addition of a random term allowing for different intercepts in the longitudinal pattern (Model 4). Although gains were significant, addition of a random term that allowed for variation in the longitudinal shape did not greatly improve D_a. The relative importance of shape and intercept is visually evident through inspection of Figure 1 which shows a wide range in different intercepts between trees but somewhat less variation in the shape.

Clearly, use of a mixed-effects model that includes random terms to account for tree level variation, such as Model 5, provides the most accurate means of modelling longitudinal variation in ρ_g and MOE between sites and trees. A methodology for parameterising such a model from measurements of ρ_g at a single height has been demonstrated. This procedure could considerably reduce the sampling effort required to characterise longitudinal variation in ρ_g. Further research should explore whether easier-to-obtain, non-destructive measurements (such as increment cores) could be used to parameterise this type of model.

Conclusion

Results from this study show that marked over-prediction of ρ_g and MOE occurred when constant ρ_g values of 1,000 kg m⁻³ were assumed. At the log level the most accurate predictions of ρ_g were obtained using a mixed-effects model that included fixed effects to account for mean longitudinal variation in ρ_g and random effects to account for deviations in this longitudinal variation between trees. Using this mixed effects model, log level D_a for ρ_g and MOE averaged 0.189%. Further research should extend this approach to a broader range of sites and treatments and use mixed effects models to characterise variation in ρ_g as a function of tree height, stand age and treatment and site related factors, such as climate.

Authors' contributions

MSW was the primary author and undertook most analyses. GT was a secondary author, was instrumental in study design and planning of methodologies and undertook analyses related to model calibration. Both authors read and approved the final manuscript.

Notes

Acknowledgements

Financial support from Fondo Nacional de Desarrollo Científico y Tecnológico (FONDECYT) Grant No. 1120433 is gratefully acknowledged. The authors also thank to Forestal Mininco for providing the necessary data and facilities for performing this research.

Supplementary material

40490_2014_16_MOESM1_ESM.gif (17 kb)

Authors’ original file for figure 1

40490_2014_16_MOESM2_ESM.gif (14 kb)

Authors’ original file for figure 2

40490_2014_16_MOESM3_ESM.gif (15 kb)

Authors’ original file for figure 3

40490_2014_16_MOESM4_ESM.gif (73 kb)

Authors’ original file for figure 4

40490_2014_16_MOESM5_ESM.gif (12 kb)

Authors’ original file for figure 5

40490_2014_16_MOESM6_ESM.gif (5 kb)

Authors’ original file for figure 6

References

Andrews M: Where we are With Sonics? In Workshop 2000. Capturing the Benefits of Forestry Research: Putting Ideas to Work. Wood technology research centre. University of Canterbury, New Zealand; 2000:pp. 57–61.Google Scholar
Andrews M: Wood quality measurement – son et lumiere. New Zealand Journal of Forestry 2002, 47: 19–21.Google Scholar
Chan JM, Walker JCF, Raymond CA: Green density and moisture content of radiata pine in the Hume region of New South Wales. Australian Forestry 2012,75(1):31–42. 10.1080/00049158.2012.10676383CrossRefGoogle Scholar
Cown DJ: Comparison of the effects of two thinning regimes on some wood properties of radiata pine. New Zealand Journal of Forestry Science 1974, 4: 540–551.Google Scholar
Cown DJ: New Zealand Pine and Douglas-fir: Suitability for Processing. Forest Research Bulletin 216. Forest Research, Rotorua New Zealand; 1999.Google Scholar
Cown DJ, McConchie DL: Rotation age and silvicultural effects on wood properties of four stands of Pinus radiata . New Zealand Journal of Forestry Science 1982, 12: 71–85.Google Scholar
Cown DJ, McConchie DL, Young GD: Radiata Pine Wood Properties Survey. FRI Bulletin No. 50, Rotorua, New Zealand; 1991.Google Scholar
Dowse GP, Wessels CB: The structural grading of young South African grown Pinus patula sawn timber. Southern Forests 2013, 75: 7–17. 10.2989/20702620.2012.743768CrossRefGoogle Scholar
Kininmonth JA: Wood/Water Relationships. In Properties and Uses of New Zealand Radiata Pine. Volume 1-Wood Properties. Edited by: Kininmonth JA, Whitehouse LJ. Ministry of Forestry, Forest Research Institute, Rotorua; 1991:7.1–7.23.Google Scholar
Lasserre JP, Mason EG, Watt MS: The influence of initial stocking on corewood stiffness in a clonal experiment of 11 year old Pinus radiata D. Don. New Zealand Journal of Forestry 2004, 49: 18–23.Google Scholar
Littell RC, Milliken GA, Stroup WW, Wolfinger RD, Schabenberger O: SAS for Mixed Models. SAS Institute Inc., Cary, NC; 2006.Google Scholar
Loe JA, Mackney AW: Effect of age on density and moisture content of New Zealand Pinus radiata . Appita 1953, 7: 183–191.Google Scholar
Matheson AC, Dickson RL, Spenser DJ, Joe B, Ilic J: Acoustic segregation of Pinus radiata logs according to stiffness. Annals of Forest Science 2002, 59: 471–477. 10.1051/forest:2002031CrossRefGoogle Scholar
Moore J: Growing fit-for-purpose structural timber. What is the target and how do we get there? New Zealand Journal of Forestry 2012, 57: 17–24.Google Scholar
Rencher AC: Linear Models in Statistics. John Wiley and Sons Inc, New York; 2000.Google Scholar
SAS/STAT 9.2 User's Guide. SAS Institute Inc., Cary NC; 2008.Google Scholar
Schultz TJ: Acoustical properties of wood: a critique of the literature and a survey of practical applications. Forest Products Journal 1969,19(2):21–29.Google Scholar
Tsehaye A, Buchanan AH, Walker JCF: Sorting of logs using acoustics. Wood Science and Technology 2000,34(4):337–344. 10.1007/s002260000048CrossRefGoogle Scholar
Verbeke G, Molenberghs G: Linear Mixed Models for Longitudinal Data. Springer, New York; 2000.Google Scholar
Vonesh EF, Chinchilli VM: Linear and Nonlinear Models for the Analysis of Repeated Measurements. Marcel Dekker, New York; 1997.Google Scholar
Waghorn MJ, Mason EG, Watt MS: Influence of initial stand density and genotype on longitudinal variation in modulus of elasticity for 17-year-old Pinus radiata . Forest Ecology and Management 2007,252(1–3):67–72. 10.1016/j.foreco.2007.06.019CrossRefGoogle Scholar
Wang X, Carter P, Ross RJ, Brashaw BK: Acoustic assessment of wood quality of raw forest materials – a path to increased profitability. Forests Product Journal 2007, 57: 6–14.Google Scholar
Watt MS, Clinton PC, Parfitt RL, Ross C, Coker G: Modelling the influence of site and weed competition on juvenile modulus of elasticity in Pinus radiata across broad environmental gradients. Forest Ecology and Management 2009,258(7):1479–1488. 10.1016/j.foreco.2009.07.003CrossRefGoogle Scholar
Wilkes J: Heartwood development and its relationship to growth in Pinus radiata . Wood Science and Technology 1991, 25: 85–90. 10.1007/BF00226808CrossRefGoogle Scholar

Copyright information

Authors and Affiliations

Michael S. Watt
- 1
Email author
Guillermo Trincado
- 2

1.ScionChristchurchNew Zealand
2.Facultad de Ciencias Forestales y Recursos NaturalesUniversidad Austral de ChileValdiviaChile

Modelling between tree and longitudinal variation in green density within Pinus radiata: implications for estimation of MOE by acoustic methods