Introduction

The shortest path problem is widely applied to network optimization and has been studied by a lot of researchers. Classical shortest path problems focus on networks with deterministic arc weights (lengths), and Dijkstra [1], Bellman [2], and Dreyfus [3] have proposed some efficient algorithms which are still referenced widely now. However, due to the failure, maintenance, and other uncertain factors, arc weights are usually non-deterministic in a busy transportation network. In view of this fact, some researchers introduced probability theory into the shortest path problem and used probability distributions to describe the existing indeterminacy, such as Frank [4], Loui [5], Mirchandani [6], Yang et al. [7], and Yang and Zhou [8]. However, this method is typically imprecise when we are lack of a priori data information with respect to networks. With this concern, Dubois and Prade [9] first introduced a fuzzy shortest path problem. In the fuzzy set theory, the decision can be estimated by experts based on their experiences and professional judgments. Some other routing optimization with fuzzy information can be referred to Ji et al. [10], Hernandes et al. [11], and Yang et al. [12].

However, both probability theory and fuzzy set theory may lead to counterintuitive results [13]. In this case, uncertainty theory was founded to rationally deal with belief degrees, which enlightened a new approach to describe non-deterministic phenomena. Up to now, the uncertainty theory has been applied to many classical optimization problems, such as solid transportation problem [14], project scheduling problem [15], maximum flow problem [16], optimal assignment problem [17], uncertain graph [18], etc. As for the shortest path problem, Liu [19] introduced three concepts of uncertain path according to different decision criteria, including the expected shortest path, α-shortest path, and the most shortest path. He formulated three types of uncertain programming models and converted them into deterministic optimization ones. Gao [20] studied the uncertainty distribution of the shortest path length and proposed an effective method to find the α-shortest path and the most shortest path in an uncertain network. He pointed out that there existed an equivalence relation between the α-shortest path in an uncertain network and the shortest path in a corresponding deterministic network. Moreover, an effective algorithm was proposed to find the α-shortest path and the most shortest path. Zhou et al. [21] discussed the inverse shortest path problem on the graph with uncertain edge weights. This problem was formulated as an uncertain programming and was reformulated into a deterministic programming model.

Multi-modal transportation refers to a trip consisting of two or more means of transport to guide the passengers reach their destinations. The multi-modal shortest path problem is a significant generalization of the traditional shortest path problem, and it has been extensively investigated by a lot of researchers. Lozano and Storchi [22] found the shortest viable path in a multi-modal network using label correcting techniques. They defined the viable path as a path whose sequence of modes is feasible with respect to a set of constraints. Ma [23] presented an A ∗ label setting algorithm to solve a constrained shortest path problem in a multi-modal network. In this work, each link is characterized with a vector of resource consumption besides the travel time. Ambrosino and Sciomachen [24] proposed an approach for computing shortest routes in multi-modal networks with objectives of minimizing the overall time, cost, and users’ discomfort. Liu et al. [25] designed an improved exact algorithm for a multi-criteria multi-modal shortest path problem with both arriving time window and transfer delaying. Galvez-Fernandez et al. [26] introduced a transfer graph approach, which was believed to better abstract the distributed nature of real transport information sources, to calculate the best paths in multi-modal networks. Yamani et al. [27] presented a fuzzy shortest path algorithm in multi-modal transportation networks, which concerned about not only the path cost but also the path time which consisted of travel time and delays.

Indeed, due to the complexity of the real-world situations, it is in general difficult to explicitly determine travel time or travel costs in a large-scale multi-modal network. What is more, it is also complicated when we consider the transfer time and costs from one mode to another. Thus, investigating the multi-modal shortest path problem in the indeterministic environment becomes a significant and challenging issue for the practical applications. We here note that finding the shortest path in a multi-modal network has been studied in various forms such as static [22], dynamic [26,28], stochastic [29,30], fuzzy [27], constrained [23], and multi-criteria [24,25,31,32]. However, to the best of our knowledge, few studies have been considered in the uncertain environment within the framework of uncertain programming.

This paper aims to investigate the multi-modal shortest path problem, in which both travel time and travel costs are regarded as uncertain variables. Specifically, the travel time includes travel time on the travel arcs and transfer time spent on the mode change. The travel costs consist of cost on each arc and the fixed cost. We intend to formulate a chance-constrained programming model with two objectives minimizing the travel time and travel cost simultaneously. The results of this research will provide a fundamental framework for investigating the shortest path problems with both multi-modes and uncertainty characteristics.

The remainder of this paper is organized as follows. Section ‘Preliminaries’ introduces some basic concepts and properties of uncertainty theory used throughout this paper. Section ‘Model formulations’ makes a description of the problem and formulates a chance-constrained programming model with two objectives. In Section ‘Crisp equivalent of the model’, we demonstrate how to convert the model into its crisp equivalent. In Section ‘Numerical experiments’, some experiments are given to illustrate the performance of the proposed model. Finally, some conclusions are made in Section ‘Conclusions’.

Preliminaries

As this research will investigate the problem of interest within the framework of uncertainty theory, we next first introduce some basic knowledge in this field for the completeness of this paper. Uncertainty theory was proposed by Liu [13], and it provided an axiomatic system to handle the imprecise information. Some foundational definitions and results in uncertainty theory are introduced below.

Definition 2.1.

[13] Let Γ be a nonempty set, and L be a σ-algebra over Γ. Each element Λ in L is called a measurable set. Then, the triplet (Γ,L,M) is called an uncertainty space if the uncertain measure M satisfies the following axioms: Axiom 1. (Normality Axiom) M{Γ}=1 for the universal set Γ. Axiom 2. (Duality Axiom) M{Λ}+M{Λ c}=1 for any event Λ. Axiom 3. (Subadditivity Axiom) For every countable sequence of events Λ 1,Λ 2,⋯, we have

$$M\left\{\bigcup_{i=1}^{\infty}\Lambda_{i}\right\}\leq \sum_{i=1}^{\infty}M\left\{\Lambda_{i}\right\}. $$

Based on the uncertainty space, a formal definition of the uncertain variable will be introduced for better describing the uncertainties mathematically.

Definition 2.2.

[13] An uncertain variable is a measurable function ξ from an uncertainty space (Γ,L,M) to the set of real numbers such that {ξ∈B} is an event for any Borel set B.

Definition 2.3.

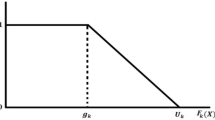
[13] The uncertainty distribution Φ of an uncertain variable ξ is defined by:

$$\Phi(x)=M\{\xi\leq x\} $$

for any real number x.

Theorem 2.1.

([33], Measure Inversion Theorem) Let ξ be an uncertain variable with continuous uncertainty distribution Φ. Then for any real number x, we have:

$$ M\{\xi \leq x\}= \Phi(x), M\{\xi> x\}=1-\Phi(x). $$
((1))

Definition 2.4.

[33] Let ξ be an uncertain variable with regular uncertainty distribution Φ(x). Then, the inverse function Φ −1(α) is called the inverse uncertainty distribution of ξ.

Definition 2.5.

[13] The uncertain variables ξ 1,ξ 2,⋯,ξ n are said to be independent if:

$$M\left\{\bigcap_{i=1}^{n}\{\xi_{i}\in B_{i}\}\right\}=\bigwedge_{i=1}^{n} M\left\{\xi_{i}\in B_{i}\right\} $$

for any Borel set B 1,B 2,⋯,B n of real numbers.

There are some kinds of special uncertain variables namely the linear uncertain variable, the zigzag uncertain variable, the normal uncertain variable and the lognormal uncertain variable. As an example, the following will describe corresponding properties of the zigzag uncertain variable.

Definition 2.6.

[13] An uncertain variable ξ is called zigzag if it has a zigzag uncertainty distribution

$$\begin{array}{@{}rcl@{}} \Phi(x)=\left\{\begin{array}{cc}0, & \text{if} \ x\leq a, \\ (x-a)/2(b-a), & \text{if} \ a\leq x\leq b, \\ (x+c-2b)/2(c-b), & \text{if} \ b\leq x\leq c,\\ 1, & \text{if} \ x\geq c. \end{array} \right. \end{array} $$
((2))

denoted by Z(a,b,c), where a,b, and c are real numbers with a<b< c.

Theorem 2.2.

[13] Assume that ξ 1 and ξ 2 are independent zigzag uncertain variables Z(a 1,b 1,c 1) and Z(a 2,b 2,c 2), respectively. Then, the sum ξ 1+ξ 2 is also a zigzag uncertain variable Z(a 1+a 2,b 1+b 2,c 1+c 2), i.e.,

$$ Z(a_{1},b_{1},c_{1})+Z(a_{2},b_{2},c_{2})=Z(a_{1}+a_{2},b_{1}+b_{2},c_{1}+c_{2}). $$
((3))

The product of a zigzag uncertain variable Z(a,b,c) and a scalar number k>0 is also a zigzag uncertain variable Z(k a,k b,k c), i.e.,

$$ k\cdot Z(a,b,c)=Z(ka,kb,kc). $$
((4))

To characterize the structural features of an uncertain variable, the concepts of critical values, including optimistic value and pessimistic value, are formally defined as follows.

Definition 2.7.

[13] Let ξ be an uncertain variable.

  1. (1)

    The optimistic value of ξ is defined by:

    $$\begin{array}{@{}rcl@{}} \xi_{\sup}(\alpha)=\sup\{r|M\{\xi\geq r\}\geq \alpha\}, \alpha\in (0,1], \end{array} $$
    ((5))
  2. (2)

    The pessimistic value of ξ is defined by:

    $$\begin{array}{@{}rcl@{}} \xi_{\inf}(\alpha)=\inf\{r|M\{\xi\leq r\}\geq \alpha\}, \alpha\in (0,1]. \end{array} $$
    ((6))

Model formulations

Consider a multi-modal network G=(V,E,M), in which V is the set of nodes and E is the set of arcs. M represents the transport modes set that consists of three different modes, namely, private, metro, and bus. Each arc is denoted by an ordered node pair (i,j,k) to indicate connections between the adjacent nodes of mode k. The whole network thus can be divided into three subnetworks as the private network, metro network, and bus network correspondingly. It should be noted that multi-modal network is characterized by weights on both nodes and arcs. Weights on arcs are generally used to represent the travel time or travel cost spent on some kind of vehicle. Besides, weights should be added on the transfer nodes if a mode change happens. The weights on the transfer nodes may indicate the transfer time or transfer cost when a passenger transfers from one mode to another. For the simplicity of our model, we shall divide a transfer node into different nodes according to the number of modes at this node. Additionally, dummy arcs will be added between these newly created nodes to indicate a modal transfer. Take a small network shown in Figure 1 as an example. Obviously, there exist three modes at node a. Therefore, we divide a into three different nodes as a, b, and c with modes private, metro, and bus, respectively, and three dummy arcs should be added to the network in order to represent the mode change between different subnetworks. In this case, the three subnetworks can be connected by the given transfer arcs. Then, we can give weights to the transfer arcs to indicate the transfer time or costs. For convenience of modeling formulation, the transfer will be treated as a special kind of mode, namely, the transfer mode. Thus, four modes are included in the mode set M, which is denoted as M={p,b,m,t}.

Figure 1
figure 1

Schematic diagram of multi-modal network.(a) Physical network. (b) Transfer network.

Full size image

There are various measures to evaluate a multi-modal path, while in this paper, we are concerned with the total travel time and travel costs. In a multi-modal network, the total travel time mainly includes in-vehicle time within a certain subnetwork and transfer time when there is a transfer. Generally, a transfer between different modes needs the traveler to walk to the stop (or station) of the following mode, then he/she may have to wait for the bus or train coming. After getting on the vehicle, more time may be spent for waiting for the vehicle to depart the stop. In summary, the transfer time consists of the passenger’s walking time, waiting time, and the vehicle’s stopping time. To make the problem easy to be dealt with, we consider the transfer time as a whole. Let ξ ijk represent time spent on arc (i,j,k) with a specific mode k. Therefore, it is the in-vehicle travel time when k denotes the private mode, the bus mode, or the metro mode. While when k means a transfer mode, ξ ijk is actually the transfer time. Define a decision variable x ijk : x ijk =1 denotes arc (i,j,k) is selected by the path, and x ijk =0 otherwise. Then, the total travel time of a multi-modal path can be expressed as follows:

$$ f_{1}=\sum_{(i,j,k)\in E} x_{ijk} \xi_{ijk}. $$
((7))

In addition, we need a flow balance constraint to generate the feasible path, which is given as below. (In this constraint, O and D represent the origin node and destination node of the network, respectively).

$$ \sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}= \left\{\begin{array}{ll} {~1,}&\text{\textit{i=O}},\\ {-1,}&\text{\textit{i=D}},\\ {~0,}&\rm{otherwise}. \end{array}\right. $$
((8))

It is no doubt that minimizing the total travel time cannot meet all the demands of the travelers. Each mode has its own monetary cost, and sometimes, it may be contrary to the travel time. For instance, the private mode is faster than the bus mode, but it has much higher monetary cost as well. With this concern, the travel costs also need to be considered in the model. In this paper, we take two types of costs into consideration: costs on travel arcs and the fixed cost. Denote c ijk to represent the travel cost on arc (i,j,k), where k∈M∖{t}. The fixed cost represents the ticket price of the public modes. It always happens along with the occurrence of the transfer. For example, when a passenger transfers from the bus subnetwork to the metro subnetwork, he/she then needs to pay for the fixed cost to the metro subnetwork. Therefore, if any arc (i,j,k) of a certain mode k is selected by a path, the fixed cost will occur. To depict this relationship, we introduce another decision variable y k as:

$$\begin{array}{@{}rcl@{}} y_{k}=\left\{\begin{aligned} 1,& \text{ if } x_{ijk}=1, \text{ for a certain } (i,j,k)\in E, \text{ and }k\in M\backslash \{t\},\\ 0,& \text{ otherwise.} \end{aligned}\right. \end{array} $$
((9))

Obviously, y k =1 indicates the fixed cost happens, and 0 otherwise. Let d k denote the fixed cost when a certain arc of mode k(k∈M∖{t}) is taken by a path. Then, we can easily get the total travel costs as:

$$ f_{2}=\sum_{(i,j,k)\in E} x_{ijk} c_{ijk}+ \sum_{k\in M\backslash\{t\}} y_{k} d_{k}. $$
((10))

Indeed, travelers would pay more attention to the times of transfer, and most travelers would not like to transfer too many times. So, it is rational to limit the number of the modes adopted by a path. Then, we have the following constraint to ensure that the number of modal transfers is not greater than N.

$$ \sum_{k\in M\backslash\{t\}}y_{k}\leq N. $$
((11))

For the convenience of formulating the model, we would like to summarize the above notations in Table 1.

Table 1 Notations used in formulations
Full size table

In this paper, we intend to formulate a bi-objective integer programming model to minimize both the travel time and travel costs. Different decision criteria have been used to evaluate the shortest path problem under uncertain environment. One of the widely used criteria is the critical value. Uncertain programming using the critical value is called the chance-constrained programming. Enlightened by this, we shall formulate a chance-constrained programming model, which is shown as follows:

In the above model, α and β are predetermined confidence levels. The objective function implies optimizing the total travel time and total travel cost. Constraints (12) and (13) mean that the total travel time and travel cost will be less than \(\overline {f_{1}}\) and \(\overline {f_{2}}\) with confidence levels α and β, respectively. Constraints (14), (15), and (16) ensure that a feasible path can be generated in the network. Constraint (17) implies the total transfer times will not exceed the given limit N. It is noted that the travel time and travel cost on arcs are imprecise due to the complexity of the actual network. Hence, the corresponding variables like ξ ijk ,c ijk , and d k are treated as uncertain variables.

Crisp equivalent of the model

It is easy to know that if the involved uncertain variables are complex, the model may be difficult to be dealt with. So it is necessary for us to transform the model into its crisp equivalent. In this section, we shall introduce how the model can be transformed into a deterministic form.

Theorem 4.1.

[33] Let ξ and η be two independent uncertain variables. The corresponding optimistic values and pessimistic values are ξ sup(α) and ξ inf(α), η sup(α) and η inf(α), respectively. Then, we have:

  1. (I)

    (ξ+η)sup(α)=ξ sup(α)+η sup(α),

  2. (II)

    (ξ+η)inf(α)=ξ inf(α)+η inf(α).

Theorem 4.2.

[33] Let ξ be an independent uncertain variable, k be a scalar number with k>0. Then, we have:

  1. (I)

    (k ξ)sup(α)=k·ξ sup(α),

  2. (II)

    (k ξ)inf(α)=k·ξ inf(α).

Theorem 4.3.

Let ξ and η be two independent uncertain variables, k 1 and k 2 are scalar numbers with k 1>0,k 2>0. Then we have:

  1. (I)

    (k 1 ξ+k 2 η)sup(α)=k 1·ξ sup(α)+k 2·η sup(α),

  2. (II)

    (k 1 ξ+k 2 η)inf(α)=k 1·ξ inf(α)+k 2·η inf(α).

It is worth noting that the critical value of an uncertain variable is associated with the uncertainty distribution according to the Measure Inversion Theorem. Just for completeness, two theorems will be cited to illustrate this point.

Theorem 4.4.

[34] Suppose that ξ is an uncertain variable with continuous uncertainty distribution Φ(x) when 0<Φ(x)<1, and g(x,ξ)=h(x)−ξ, α is a confidence level in (0,1). Then, we have M{g(x,ξ)≤0}≥α if and only if h(x)≤f ξ (α), where f ξ (α)=Φ −1(1−α).

Theorem 4.5.

[34] Suppose that ξ is a continuous uncertain variable with increasing uncertainty distribution Φ(x) when 0<Φ(x)<1, g(x,ξ)=h(x)−ξ and α is a confidence level in (0,1). Then, M{g(x,ξ)≥0}≥α if and only if h(x)≥f ξ (α), where f ξ (α)=Φ −1(α).

Based on the aforementioned theorems, we can easily deduce the following conclusions:

Theorem 4.6.

Let ξ be a continuous uncertain variable. The proposed critical value can also be expressed as:

$$\begin{array}{@{}rcl@{}} \xi_{\sup}(\alpha)=\sup\left\{r|r \leq \Phi_{\xi}^{-1}(1-\alpha)\right\}=\Phi_{\xi}^{-1}(1-\alpha), \alpha\in (0,1], \end{array} $$
((19))
$$\begin{array}{@{}rcl@{}} \xi_{\inf}(\alpha)=\inf\left\{r|r\geq \Phi_{\xi}^{-1}(\alpha)\right\}=\Phi_{\xi}^{-1}(\alpha), \alpha\in (0,1]. \end{array} $$
((20))

With the aid of relevant theorems given above, the following theorem intends to show the equivalent model.

Theorem 4.7.

In the established chance-constrained programming model, we assume that ξ ijk , c ijk , and d k are all independent continuous uncertain variables. The equivalent model is as follows:

$$\begin{array}{@{}rcl@{}} \left\{\begin{aligned} &\min~\displaystyle\left\{\sum\limits_{(i,j,k)\in E} x_{ijk}\cdot\Phi^{-1}_{\xi_{ijk}}(\alpha),\sum\limits_{(i,j,k)\in E} x_{ijk}\cdot\Phi^{-1}_{c_{ijk}}(\beta)+\sum\limits_{k\in M\backslash\{t\}} y_{k}\cdot \Phi^{-1}_{d_{k}}(\beta)\right\}\\ &s. t. ~~(14)\sim (18).\\ \end{aligned} \right. \end{array} $$
((21))

Proof.

In the model, the two objective functions are to minimize \(\overline {f_{1}},\overline {f_{2}}\) with the constraint conditions:

$$M\displaystyle\left\{\sum_{(i,j,k)\in E} x_{ijk} \xi_{ijk}\leq \overline{f_{1}}\right\}\geq \alpha,~~M\displaystyle\left\{\sum_{(i,j,k)\in E} x_{ijk} c_{ijk}+ \sum_{k\in M\backslash\{t\}} y_{k} d_{k} \leq \overline{f_{2}}\right\} \geq \beta. $$

That is to say we need obtain the minimum values of \(\overline {f_{1}},\overline {f_{2}}\) which meet the above conditions, i.e.,

$${\small{\begin{aligned} {}\inf\left\{\overline{f_{1}}~|M\!\left\{\sum_{(i,j,k)\in E}\! x_{ijk} \xi_{ijk}\leq \overline{f_{1}}\right\}\!\geq\! \alpha\!\right\},~\inf\left\{\overline{f_{2}}~|M\left\{\sum_{(i,j,k)\in E\!} x_{ijk} c_{ijk}+\! \sum_{k\in M\backslash\{t\}}\!y_{k} d_{k} \leq \overline{f_{2}}\right\}\!\geq\! \beta\!\right\}. \end{aligned}}} $$

According to the definition of pessimistic value, it means that \(\overline {f_{1}}, \overline {f_{2}}\) are the pessimistic values. By utilizing the properties of addition and multiplication, the constraints can be rewritten as the form of pessimistic values in the objective functions, expressed as follows:

$$\sum\limits_{(i,j,k)\in E} x_{ijk}\cdot(\xi_{ijk})_{\inf}(\alpha),~\sum\limits_{(i,j,k)\in E} x_{ijk}\cdot(c_{ijk})_{\inf}(\beta)+\sum\limits_{k\in M\backslash\{t\}} y_{k}\cdot(d_{k})_{\inf}(\beta). $$

Based on Equation 20, the pessimistic value of an uncertain variable is the inverse function with respect to α. Hence, we can easily obtain the equivalent model. The proof is thus completed.

Remark.

In the shortest path problem, the optimal objectives are related to the confidence levels α,β, i.e., if the confidence levels satisfy α 1<α 2 and β 1<β 2, then the corresponding optimal objectives satisfy: \(\min ~\overline {f}_{1}<\min ~\overline {f}_{1}'\) and \(\min ~\overline {f}_{2}<\min ~\overline {f}_{2}'\), because the uncertainty distributions of uncertain variables are monotone nondecreasing functions. Here, \(\overline {f}_{1}\), \(\overline {f}_{1}'\), \(\overline {f}_{2}\), and \(\overline {f}_{2}'\) indicate the optimal objective values with α=α 1, α=α 2, β=β 1, and β=β 2.

Corollary 4.1.

Especially, suppose that ξ ijk , c ijk , and d k are all independent zigzag uncertain variables with \(\xi _{\textit {ijk}}\sim \left (\xi _{\textit {ijk}}^{1}, \xi _{\textit {ijk}}^{2}, \xi _{\textit {ijk}}^{3}\right)\), \(c_{\textit {ijk}}\sim \left (c_{\textit {ijk}}^{1}, c_{\textit {ijk}}^{2}, c_{\textit {ijk}}^{3}\right)\), and \(d_{k}\sim \left ({d_{k}^{1}}, {d_{k}^{2}}, {d_{k}^{3}}\right)\), respectively. Then, according to Theorem 4.7, we have the following crisp equivalent of the above model.

$$\begin{array}{@{}rcl@{}} \left\{\begin{aligned} &\min ~~g_{1}(x),~g_{2}(x,y) \\ &\ s.t.~~(14)\sim(18).\\ \end{aligned} \right. \end{array} $$
((22))

where

$$ g_{1}(x,y)= \left\{ \begin{array}{ll} (1-2\alpha)\sum\limits_{(i,j,k)\in E}\xi_{ijk}^{1} x_{ijk}+2\alpha \sum\limits_{(i,j,k)\in E} \xi_{ijk}^{2} x_{ijk},& \textrm{if \ \(\alpha\leq0.5\)}\\ (2-2\alpha)\sum\limits_{(i,j,k)\in E} \xi_{ijk}^{2} x_{ijk}+(2\alpha-1) \sum\limits_{(i,j,k)\in E}\xi_{ijk}^{3} x_{ijk},& \textrm{if \ \(\alpha>0.5\)}\\ \end{array} \right. $$
((23))

and

$$ g_{2}(x,y)= \left\{ \begin{array}{ll} (1-2\beta)r_{1}(x,y)+2\beta r_{2}(x,y),& \textrm{if \ \(\beta\leq0.5\)}\\ (2-2\beta)r_{2}(x,y)+(2\beta-1) r_{3}(x,y),& \textrm{if \ \(\beta>0.5\)}\\ \end{array} \right. $$
((24))
$$r_{1}(x,y)= \sum_{(i,j,k)\in E} c_{ijk}^{1} x_{ijk}+\sum_{k\in M\backslash\{t\}}{d_{k}^{1}}y_{k} $$
$$ r_{2}(x,y)=\sum_{(i,j,k)\in E} c_{ijk}^{2} x_{ijk}+\sum_{k\in M\backslash\{t\}}{d_{k}^{2}}y_{k} $$
((25))
$$r_{3}(x,y)=\sum_{(i,j,k)\in E} c_{ijk}^{3} x_{ijk}+\sum_{k\in M\backslash\{t\}}{d_{k}^{3}}y_{k} $$

Numerical experiments

In this section, we give a multi-modal network which consists of 47 nodes and 87 arcs, as shown in Figure 2, to illustrate the proposed model. There exist four modes in the network, namely, private (mode 1), bus (mode 2), metro (mode 3), and transfer (mode 4) as we have mentioned in Section ‘Model formulations’. In a real-world situation, the private mode will be adopted only at the origin node. That is to say, one would not enter the private mode from other modes. So, it just generates fixed cost when entering into the bus subnetwork and the metro subnetwork from other modes, which follow d 2∼Z(2,3,5) and d 3∼Z(3,5,9), respectively. For the convenience of calculations, we assume that all weights on arcs are zigzag uncertain variables; the time and costs on travel arcs and time on transfer arcs are illustrated in Tables 2 and 3, respectively.

Figure 2
figure 2

Multi-modal transportation network.

Full size image
Table 2 Time and costs on travel arcs of the multi-modal network
Full size table
Table 3 Transfer time on transfer arcs of the multi-modal network
Full size table

Before starting the experiments, we first need to transform our bi-objective model into a single-objective one. In literature, there were a variety of methods to handle the multi-objective programming problems, such as the linear weighting method, ideal point method, layered method, min-max method, etc. In this paper, we prefer to adopt a constraint-based method, which chooses one objective as the main objective function while the other objectives are transformed into constraints within the given thresholds. As for the problem of interest, the total cost will be treated as the main goal that needs to be optimized. To produce a single-objective model, we firstly solve the model with single-objective function g 1(x), given as follows.

$$\begin{array}{@{}rcl@{}} \left\{\begin{aligned} &\min g_{1}(x) \\ &s. t.\\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=1, \ i=O, \\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=0, \ i\neq O, D, \\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=-1, \ i=D, \\ &\hspace*{15pt}\sum_{k\in M\backslash\{t\}}y_{k}\leq N \\ &\hspace*{15pt}\boldsymbol{x}_{ijk}, y_{k}\in \{0,1\}, \forall (i,j,k)\in E, k\in M\backslash\{t\}\\ \end{aligned} \right. \end{array} $$
((26))

Assume that we obtain the optimal objective value \(\overline {g_{1}}(x')\). Then, \(\overline {g_{1}}(x')\) with a threshold value δ will be regarded as upper limit to g 1(x), which forms a new constraint to the model. In this case, the initial model can be transformed into the following single objective model.

$$\begin{array}{@{}rcl@{}} \left\{\begin{aligned} &\min g_{2}(x,y) \\ &s. t.\\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=1, \ i=O, \\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=0, \ i\neq O, D, \\ &\hspace*{15pt}\sum_{(i,j,k) \in E} x_{ijk}- \sum_{(j,i,k) \in E} x_{jik}=-1, \ i=D, \\ &\hspace*{15pt}\sum_{k\in M\backslash\{t\}}y_{k}\leq N \\ &\hspace*{15pt}\boldsymbol{x}_{ijk}, y_{k}\in \{0,1\}, \forall (i,j,k)\in E, k\in M\backslash\{t\}\\ &\hspace*{15pt}g_{1}(x)\leq {\overline{g_{1}}(x')}+\delta\\ \end{aligned} \right. \end{array} $$
((27))

With this method, the LINGO optimization software is employed to generate the shortest path from origin node 0 to destination node 46 in the multi-modal network. It is noted that α, β and δ are three parameters which will influence the optimal objective values. To capture the corresponding relations between the parameters and the objective functions, we shall implement two sets of experiments as follows:

(1) Optimal solutions with different α and β: As the optimal solution is closely related to parameters α and β, we firstly use different critical values to produce the shortest paths, with the fixed parameter δ=5. The results are listed in Table 4, in which the confidence levels in critical values are set as 0.6, 0.7, 0.8, 0.9, and 1.0, respectively. Figure 3 shows the variation tendency of the optimal objectives with respect to different α and β values. Obviously, both the objective values of g 1(x) and g 2(x,y) are increasing with respect to the relevant parameters when δ is fixed. This conclusion just coincides with the Remark.

Figure 3
figure 3

Objective values with different α and β (δ=5).

Full size image
Table 4 Optimal solutions with different α and β ( δ=5 )
Full size table

(2) Optimal solutions with different δ: The second set of experiments focus on the other index δ. Table 5 illustrates the relationship between the optimal objectives and different δ values, in which α and β are all set as 0.9. When we depict the results in Figure 4, we can find that the optimal objectives will not change any more when δ is set to be not less than 7; moreover, the optimal objective value of g 2(x,y) is decreasing with respect to the increase of δ, while g 1(x) varies with an opposite tendency. When the objective value of g 2(x,y) reaches 47.2, which is the optimal objective when g 2(x,y) is treated as the single objective, the figure will not change any more.

Figure 4
figure 4

Objective values with different δ (α=0.9, β=0.9).

Full size image
Table 5 Optimal solutions with different δ ( α=0.9 , β=0.9 )
Full size table

Conclusions

Uncertainty theory is a branch of mathematics to study the characteristics of nondeterministic phenomenon. In this paper, we applied uncertainty theory to investigating the multi-modal shortest path problem in which the arc time and arc costs are represented by uncertain variables. Considering two objectives, which are to minimize the total travel time and travel costs, we formulated a chance-constrained programming model for the problem of interest. For handling convenience, the model was then transformed into its deterministic crisp equivalent. Additionally, the bi-objective model was simplified into a single objective model by converting one objective function into a new constraint with the given threshold. Finally, the results of the numerical experiments deriving from the LINGO software demonstrated the performance of the proposed approaches. Actually, multi-modal shortest path problems have been widely solved by the label-setting algorithm [35], label-correcting algorithm [25], and genetic algorithm [36,37], which can also be considered in our further studies.