Introduction

Solid elements with low-order interpolations are generally recommended in structural mechanics because they can be used efficiently in nonlinear applications since they have a more robust performance in the distorted configurations. However, in many cases, especially in bending dominated problems, standard brick elements show severe stiffening effects known as locking problems [1, 2]. Several methods have been proposed over years in order to overcome these locking phenomena. For example, the enhanced assumed strain (EAS) have been used in geometrically nonlinear version [3,4,5] where the strain field can be enriched in order to improve the element’s performance under certain conditions. 3D solid elements with rotational degrees of freedom are also proposed with different discrete approximations like the method of the mixed interpolations of tensorial components [6] for the brick element of Wils on and Ibrahimbegovic [2]. The Space Fiber Rotation concept (SFR) [7] and the shift of the mid-side displacement DOFs of the classical 20-node hexahedral element into corner nodal translations and rotations are proposed by Yunu and al. [8].

In this paper, we propose the method of incompatible modes for constructing enhanced strain approximation as the most viable approach for improving the performance of low order elements. A very important choice pertains to large strain measures, which allows to separate large displacements and large rotations. We illustrate the proposed approach on an 8-node displacement-based hexahedron, including both usual displacement degrees of freedom and rotation degrees of freedom that are independently interpolated. We recapitulate the variational formulation including the incompatible displacement modes for 3D finite displacement elasticity problems, along with the fine details of the numerical implementation.

Given the goal of using this element in dynamics, we introduce the inertial effects in the variational formulation in order to handle dynamic analysis. It is important to state that the proposed formulation is shown to be more efficient than others formulations using floating frames. In fact, it is set in a fixed frame that allows to eliminate the Coriolis effects and lead to a simple quadratic form of the kinetic energy. This results with a mass matrix with constant components and consequently simplifies the time-integration computational phase.

The proposed enhanced solid element is compatible with shell finite elements [9] as well as beam elements [10]. This offers an efficient performance for modeling linear and nonlinear dynamic behavior of complex structures. The rotational degrees of freedom are presented by orthogonal tensor, as an intrinsic representation of large rotations.

The outline of the paper is as follows. In “Standard variational formulations for statics” section we present the variational formulations for the continuum with independent rotation fields in geometrically nonlinear theory. Then, we discuss the regularized form of the variational formulations, with some details of numerical implementation in “Modified variational formulations for statics and its discrete approximation” section. We extend to dynamics analysis in “Variational formulations for dynamics” section. The solution procedures are developed to obtain the corresponding solutions in “Newmark implicit time-stepping scheme” section. Several numerical simulations dealing with static and dynamic problems are presented in “Numerical examples” section. Some closing remarks are given in “Closing remarks” section.

Standard variational formulations for statics

In this section we discuss the variational formulations for the continuum with independent rotation field in geometrically nonlinear theory. The starting point in our considerations can be provided by the classical potential energy principle. It is a function of the finite displacement field \(\mathbf u \), writing as a sum of the strain energy and the potential energy of external forces

$$\begin{aligned} \varPi (\mathbf{u }) = \int _\mathbf{V } \ W ( {\mathbf{H }} ({\mathbf{u }}) ) ~d\mathbf V - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } ~d\mathbf V \end{aligned}$$
(1)

where \(W ( \mathbf{H } (\mathbf{u }) )\) is a stored energy given as a function of the chosen Biot’s finite strain measure and \(\mathbf u \) is the finite displacement field. The second integral represents the external work for the Dirichlet boundary value problem.

The finite strain measure \(\mathbf{H }\), often called Biot strain [11], can be the most explicitly defined via the polar decomposition theorem (e.g., see [12], p. 14). Namely, if the deformation is a vector field \({\varvec{\varphi }}\), which is, without loss of generality for our purposes, specified with respect to the Euclidean coordinate system with the base vectors \(\mathbf{e }_i\), i.e. if

$$\begin{aligned} \mathbf{x }^{\varphi } = \varvec{\varphi }( \mathbf{x }); \ \mathbf{x } = x_i \mathbf{e }_i; \ \varvec{\varphi }= \varphi _i \mathbf{e }_i \end{aligned}$$
(2)

then, the deformation gradient can be written as

$$\begin{aligned} \mathbf{F } = {\nabla } \varvec{\varphi }; \ \mathbf{F } = {\partial \varphi _i \over \partial x_j } \mathbf{e }_i \otimes \mathbf{e }_j \end{aligned}$$
(3)

where \(' \otimes '\) denotes the tensor product.

Introducing the displacement vector field: \(\mathbf{u } = {\varvec{\varphi }} (\mathbf{x }) - \mathbf{x }\), the deformation gradient can be rewritten in terms of the displacement gradient \({\nabla } \mathbf{u }\) as

$$\begin{aligned} \mathbf{F } = {\nabla } {\varvec{\varphi }} = \mathbf{I } + \nabla \mathbf{u }; \quad \nabla \mathbf{u } = {\partial u_i \over \partial x_j } \mathbf{e }_i \otimes \mathbf{e }_j; \quad \mathbf{I } = \delta _{ij} \mathbf{e }_i \otimes \mathbf{e }_j \end{aligned}$$
(4)

The polar decomposition theorem [13] states that the deformation gradient can be factored in a unique way into \(\mathbf F =\mathbf R {} \mathbf U \) where \(\mathbf U \) is the right stretch tensor describing deformation, while \(\mathbf{R }\) is the orthogonal rotation tensor. Then, the Biot strain tensor, defined with: \(\mathbf{H } = \mathbf{U } - \mathbf{I }\), is used to rewrite the polar decomposition theorem

$$\begin{aligned} \mathbf{I } + \nabla \mathbf{u } =\mathbf{R } (\mathbf{H }+\mathbf I ) \end{aligned}$$
(5)

By eliminating the rotation field in (5) via orthogonality of \(\mathbf{R }\), we get a functional relationship between \(\mathbf{H }\) and \(\mathbf{u }\)

$$\begin{aligned} \mathbf{H } + {1 \over 2} \mathbf{H }^2 = \frac{1}{2}( \nabla \mathbf{u } + ( \nabla \mathbf{u })^T + (\nabla \mathbf{u })^T \ \nabla \mathbf{u }) \ \end{aligned}$$
(6)

which is needed in (1).

The relation in (6) is quite complex given geometrically nonlinear nature of the problem. Thus, we can choose much simpler formulation if the Biot strain is included in the functional (1).

Hence, we want that the polar decomposition in (5) be recovered as the Euler Lagrange equation of a new variational formulation rather than having it as a subsidiary condition of the variational formulation in (1). The Lagrange multiplier procedure can be used to impose that condition in the form

$$\begin{aligned} PF = \int _\mathbf{V } \mathbf{P }{:} \ [ ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{R } ( \mathbf{I } + \mathbf{H } ) ] \ d\mathbf V \ \end{aligned}$$
(7)

\(\mathbf{P }\) is the non-symmetric Piola–Kirchhoff stress, which plays the role of the Lagrange multiplier [14].

The weak form of the polar decomposition in (7) can be added to the variational formulation in (1)

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{R } , \mathbf{P } , \mathbf{H } ) = \int _\mathbf{V } \ \{ W ( \mathbf{H } ) - \mathbf{P } \cdot [ ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{R } ( \mathbf{I } + \mathbf{H } ) ] \} ~d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } ~d\mathbf V \end{aligned}$$
(8)

The formulation we propose, considers Biot strain and stress measures. The Biot stress tensor is obtained by the pull-back of the first Piola–Kirchhoff stress \(\mathbf{P }\), by using the rotation part \(\mathbf{R }\) of the deformation gradient: \(\mathbf{T } = \mathbf{R }^T \mathbf{P }\). The variational formulation in (8) can be written as

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{R } , \mathbf{T } , \mathbf{H } ) = \int _\mathbf{V } \ \{ W ( \mathbf{H } ) - \mathbf{T } \cdot \ \mathbf{H } + \mathbf{T } \cdot \ [ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{I } ) ] \} ~d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } ~d\mathbf V \end{aligned}$$
(9)

The Euler–Lagrange equations associated with the principle in (9) can be obtained by taking the directional derivative in the direction of virtual displacements \(\delta \mathbf{u }\), virtual rotations \(\delta \mathbf{R }\), virtual stresses \(\delta \mathbf{T }\) and virtual strains \(\delta \mathbf{H }\). We thus obtain: linear momentum balance, angular momentum balance, definition of strains \(\mathbf{H }\) and rotations \(\mathbf{R }\) and constitutive equations

$$\begin{aligned} \begin{aligned}&(i)~~div ( \mathbf{R } \mathbf{T } ) + \mathbf{f } = \mathbf{0 }\\&(ii)~~ \mathbf{R } \mathbf{T } ( \mathbf{I } + \nabla \mathbf{u } )^T = ( \mathbf{I } + \nabla \mathbf{u } ) ( \mathbf{R } \mathbf{T } )^T\\&(iii)~~\mathbf{H } = symm [ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{I } ];~~ skew \, [ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) ] = \mathbf{0 } \\&(iv)~~symm \mathbf{T } = { \partial W ( \mathbf{H } ) \over \partial \mathbf{H } } = \mathbf C {} \mathbf H ;~~symm \mathbf{T } = {1 \over 2} ( \mathbf{T } + \mathbf{T }^T ) \end{aligned} \end{aligned}$$
(10)

We use the Legendre transform to introduce the complementary energy \(\varSigma ( symm \mathbf{T } )\)

$$\begin{aligned} - \mathbf{H } \cdot \ symm \mathbf{T } + W ( \mathbf{H } ) = - \varSigma ( symm \mathbf{T } ) \end{aligned}$$
(11)

By introducing the result in (11) into the variational formulation in (9), we can eliminate the strain field \(\mathbf{H }\) to get the three-field variational formulation

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{R } , \mathbf{T } ) = \int \mathbf{V } \ \left\{ - \varSigma ( symm \mathbf{T } ) + \mathbf{T } \cdot \ \left[ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{I } \right] \right\} \ d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } \ d\mathbf{V } \end{aligned}$$
(12)

The Euler–Lagrange equations in (10) remain preserved, apart from constitutive equations, which connects directly the stresses with the displacements and rotations

$$\begin{aligned} { \partial \varSigma ( symm \mathbf{T } ) \over \partial \, symm\mathbf{T } } = symm [ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) - \mathbf{I } ];~~ skew \, [ \mathbf{R }^T ( \mathbf{I } + \nabla \mathbf{u } ) ] = \mathbf{0 } \end{aligned}$$
(13)

Modified variational formulations for statics and its discrete approximation

Enhanced displacement gradient

In seeking to improve performance of the discrete approximation, we consider the incompatible modes method to reparameterize the assumed displacement gradient field in terms of additive decomposition of ‘compatible’ \(\nabla \mathbf{u } \) and enhanced (‘incompatible’) part \(\mathbf d \). In particular, we assume the enhanced displacement gradient given as

$$\begin{aligned} \mathbf D = \nabla \mathbf{u }+\mathbf{d } \end{aligned}$$
(14)

The condition above can be included in the variational principle in (12) via Lagrange multiplier procedure to get

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{d } ,\mathbf{R } , \mathbf{T },\mathbf P )= & {} \int _\mathbf{V } \ \left\{ - \varSigma ( symm \mathbf{T } ) + \mathbf{T } \cdot \ \left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] \right. \nonumber \\&\left. -\,\mathbf P \cdot \mathbf{d }\right\} \ d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } \ d\mathbf{V } \end{aligned}$$
(15)

where \(\mathbf P \) is the first Piola–Kirchoff stress tensor, conjugate with the enhanced displacement gradient \(\mathbf d \).

Note that in the variational principle in (15) it is sufficient that the enhanced displacement gradient belongs only to the space of square-integrable functions in the domain \(\mathbf V \) denoted \(L^{2}(\mathbf V )\). Thus, the enhanced displacement gradient in the finite element approximation can be discontinuous over an element boundaries (‘incompatible’). We note in passing that the strong form and the Euler–Lagrange equation will not change, since

$$\begin{aligned} \int _\mathbf{V } \delta \mathbf P \cdot \mathbf{d } \ d\mathbf{V } = 0 ;~\mathbf{d } = 0 \end{aligned}$$
(16)

Regularized variational formulations

We assume that the complementary energy potential can be constructed as a quadratic form in terms of stress

$$\begin{aligned} \varSigma ( symm \mathbf{T } ) = {1 \over 2} symm \mathbf{T } \cdot { \mathbf C }^{-1} symm \mathbf{T } \end{aligned}$$
(17)

where \(\mathbf C \) is the elasticity tensor defined by its standard form [13].

Hence, the variational principle in (15) becomes

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{d } ,\mathbf{R } , \mathbf{T },\mathbf P )= & {} \int _\mathbf{V } \ \left\{ -{1 \over 2} symm \mathbf{T } \cdot { \mathbf C }^{-1} symm \mathbf{T } \right. \nonumber \\&\left. + \, \mathbf{T } \cdot \ \left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] -\mathbf P \cdot \mathbf{d }\right\} \ d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } \ d\mathbf{V } \end{aligned}$$
(18)

The variational principle needs to be regularized in order to preserve stability. In geometrically linear theory, Hughes and Brezzi proposed a regularized form of the variational principle [14] in order to be able to use any convenient discrete approximation. The corresponding generalization of their proposal for the present geometrically nonlinear case can be written as

$$\begin{aligned} \varPi _{\gamma } ( \mathbf{u } , \mathbf{d } ,\mathbf{R } , \mathbf{T },\mathbf P ) = \varPi ( \mathbf{u } , \mathbf{d } ,\mathbf{R } , \mathbf{T },\mathbf P ) - \int _\mathbf{V } {1 \over 2} skew\mathbf{T } \cdot {\gamma }^{-1} skew\mathbf{T } \ d\mathbf{V } \end{aligned}$$
(19)

where \(\gamma \) is a regularization parameter. An optimal value of \(\gamma \), \(\gamma \) \(= \mu \), was identified in geometrically linear cases [14].

The regularized form of the variational principle preserves the Euler–Lagrange equations (10) and (13), while producing an additional Euler–Lagrange equation which is given as

$$\begin{aligned} skew\mathbf{T } = \gamma ~ skew[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } ]\ \end{aligned}$$
(20)

By means of Eq. (20), the regularized variational principle can be obtained featuring only the kinematics variables being able to reduce to a minimum the number of unknown fields.

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{d } ,\mathbf{R } , \mathbf{T },\mathbf P )= & {} \int _\mathbf{V } \left\{ \ {1 \over 2} symm\left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] \cdot \mathbf{C } symm \left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] \right. \nonumber \\&+ \, {1 \over 2}skew \left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] \cdot \gamma skew \left[ \mathbf{R }^T ( \mathbf{I } + \mathbf{D } ) - \mathbf{I } \right] \nonumber \\&\left. -\,\mathbf P \cdot \mathbf{d }\right\} \ d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } \ d\mathbf{V } \end{aligned}$$
(21)

Variational equations in compact notation

For computational efficiency, we will further switch to the matrix notation. The variational principle in (21) can be restated as

$$\begin{aligned} \varPi ( \mathbf{u } , \mathbf{d } , \mathbf{R }, \mathbf{p } )= & {} \int _\mathbf{V } \left\{ \ {1 \over 2}\mathbf{e } ( \mathbf{u } , \mathbf{R }, \mathbf{d } ) \cdot \mathbf{C } \mathbf{e } ( \mathbf{u } , \mathbf{R }, \mathbf{d } ) \right. \nonumber \\&\left. + \, {1 \over 2}{\varvec{\omega }} ( \mathbf{u }, \mathbf{R }, \mathbf{d } ) \cdot \gamma {\varvec{\omega }} ( \mathbf{u } , \mathbf{R }, \mathbf{d } ) -\mathbf{p }^T \mathbf{d } \right\} \ d\mathbf{V } - \int _\mathbf{V } \mathbf{u } \cdot \mathbf{f } \ d\mathbf{V } \end{aligned}$$
(22)

where the symmetric part of the Biot strain measure is mapped into a 6-dimensional vector

$$\begin{aligned} \mathbf e (\mathbf u ,\mathbf R ,\mathbf d ) = \varvec{\varLambda }(\mathbf R )(\mathbf y (\mathbf u )+\mathbf d )-{\varvec{1}} \end{aligned}$$
(23)

while the shew-symmetric part is mapped into a 3-dimensional vector

$$\begin{aligned} \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d ) = \varvec{\varXi } (\mathbf R )(\mathbf y (\mathbf u )+\mathbf d ) \end{aligned}$$
(24)

Here we used the following compact notation

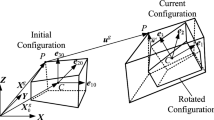
$$\begin{aligned} \begin{array}{ll} \mathbf{R } = \left[ \mathbf{r }_1 , \mathbf{r }_2 , \mathbf{r }_3 \right] {;} \quad \left[ \mathbf I + \nabla \mathbf u \right] = \left[ \mathbf y _{1}(\mathbf u ),\mathbf y _{2}(\mathbf u ),\mathbf y _{3}(\mathbf u )\right] {;} \quad \ \mathbf{d ^{T}} =\left[ \mathbf{d _{1}^{T}}\mathbf{d _{2}^{T}}\mathbf{d _{3}^{T}}\right] \\ \\ \varvec{\varLambda }(\mathbf R )=\begin{bmatrix} \mathbf r _{1}^{T}&{}0^{T}&{}0^{T} \\ 0^{T}&{}\mathbf r _{2}^{T}&{}0^{T}\\ 0^{T}&{}0^{T}&{}\mathbf r _{3}^{T}\\ \mathbf r _{2}^{T}&{}\mathbf r _{3}^{T}&{}0^{T}\\ 0^{T}&{}\mathbf r _{3}^{T}&{}\mathbf r _{1}^{T}\\ \mathbf r _{3}^{T}&{}0^{T}&{}\mathbf r _{2}^{T}\\ \end{bmatrix}{;}\ \quad \varvec{\varXi } (\mathbf R )=\begin{bmatrix} \mathbf r _{2}^{T}&{}-\mathbf r _{1}^{T}&{}0^{T} \\ 0^{T}&{}\mathbf r _{3}^{T}&{}-\mathbf r _{2}^{T}\\ -\mathbf r _{3}^{T}&{}0^{T}&{}\mathbf r _{1}^{T}\\ \end{bmatrix}{;} \ \quad \mathbf y (\mathbf u )=\begin{pmatrix} \mathbf y _{1}(\mathbf u )\\ \mathbf y _{2}(\mathbf u )\\ \mathbf y _{3}(\mathbf u )\\ \end{pmatrix}{;} \ \quad {\varvec{1}}=\begin{pmatrix} 1\\ 1\\ 1\\ 0\\ 0\\ 0\\ \end{pmatrix} \end{array} \end{aligned}$$
(25)

The perturbed configuration is defined by \(\mathbf u _{\epsilon }=\mathbf u +\epsilon \delta \mathbf u \) and \(\mathbf R _{\epsilon }=exp(\epsilon \delta \mathbf W )\mathbf R \) with \(\delta \mathbf u \) as the virtual displacement and \(\delta \mathbf W \) as the infinitesimal skew-symmetric tensor of virtual rotation where

$$\begin{aligned} \delta \mathbf W =\delta \mathbf R {} \mathbf R ,~\delta \mathbf W {} \mathbf b =\delta \mathbf w \times \mathbf b ,~\forall ~\mathbf b \in \mathbb {R}^{3} \end{aligned}$$
(26)

We note the key difference in dealing with large displacements (vector) and large rotations (tensor) in this kind of computation (e.g. see [15] for more elaborate presentations). This allows to write the variation of strain measures

$$\begin{aligned} \begin{array}{cc} \delta \mathbf e (\mathbf u ,\mathbf R ,\mathbf d )=\varvec{\varLambda }(\mathbf R )(\mathbf y (\delta \mathbf u )+\left[ \mathbf Y (\mathbf u )+\widetilde{\mathbf{D }}\right] \delta \mathbf w )\\ \\ \delta \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d )=\varvec{\varXi } (\mathbf R )(\mathbf y (\delta \mathbf u )+\left[ \mathbf Y (\mathbf u )+\widetilde{\mathbf{D }}\right] \delta \mathbf w ) \end{array} \end{aligned}$$
(27)

where \(\mathbf Y (\mathbf u )\) and \(\widetilde{\mathbf{D }}\) are defined as follows

$$\begin{aligned} \mathbf Y (\mathbf u )=\begin{bmatrix} \varUpsilon (\mathbf y _{1}(\mathbf u ))\\ \varUpsilon (\mathbf y _{2}(\mathbf u ))\\ \varUpsilon (\mathbf y _{3}(\mathbf u ))\\ \end{bmatrix}{;} \quad \widetilde{\mathbf{D }}=\begin{bmatrix} \varUpsilon (\mathbf d _{1})\\ \varUpsilon (\mathbf d _{2})\\ \varUpsilon (\mathbf d _{3})\\ \end{bmatrix}{;} \quad \varUpsilon (\mathbf v )=\begin{bmatrix} 0&v_{3}&-v_{2} \\ -v_{3}&0&v_{1}\\ v_{2}&-v_{1}&0\\ \end{bmatrix} \end{aligned}$$
(28)

We further simplify the writing with virtual displacement and virtual rotation vectors grouped together in \(\delta \mathbf a ^T =\left\langle \delta \mathbf u ^T,\delta \mathbf w ^T\right\rangle \). The variational equations (principle of virtual work) that follow from (22) are obtained by the directional derivative in the direction of virtual displacement and virtual rotation \(\delta \mathbf a \), virtual enhanced displacement gradient \(\delta \mathbf d \) and virtual stresses \(\delta \mathbf p \).

$$\begin{aligned} \begin{aligned} \delta \mathbf a \cdot \mathbf r (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } \lbrace \delta \mathbf e \cdot \mathbf C \mathbf e (\mathbf u ,\mathbf R ,\mathbf d )+\delta \varvec{\omega }\cdot \gamma \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d )\rbrace \\&-\int _\mathbf{V }\delta \mathbf u .\mathbf f ~d\mathbf V =0 \\ \delta \mathbf{d }\cdot \mathbf h (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } \lbrace \delta \mathbf d \cdot \varvec{\varLambda }^{T}(\mathbf R )\mathbf C \mathbf e (\mathbf u ,\mathbf R ,\mathbf d )\\&+\delta \mathbf d \cdot \varvec{\varXi }^{T}(\mathbf R )\gamma \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d ) - {\delta \mathbf{d }}^T \mathbf p \rbrace d\mathbf V =0\\ \delta \mathbf{p }\cdot \mathbf g (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } \lbrace \delta \mathbf{p }^T \mathbf d \rbrace d\mathbf V =0 \end{aligned} \end{aligned}$$
(29)

Finite element incompatible mode interpolations

We deal here with the discrete problem, defined with the finite element approximations. The displacement and rotation fields are approximated by using the standard isoparametric interpolations for three-dimensional solid elements with 8 nodes

$$\begin{aligned} \mathbf u (\underline{\mathbf{x }}) = \sum _{I=1}^{8} N_{I}(\underline{\mathbf{x }}) \mathbf u _{I} \equiv \mathbf N {} \mathbf u ^{e} , \quad \mathbf w (\underline{\mathbf{x }}) = \sum _{I=1}^{8} N_{I}(\underline{\mathbf{x }}) \mathbf w _{I} \equiv \mathbf N \mathbf w ^{e} \end{aligned}$$
(30)

where \(N_{I}\) are the standard shape functions while \(\mathbf u _{I}\) and \(\mathbf w _{I}\) are the corresponding nodal values.

The virtual displacements \(\delta \mathbf u \) and virtual rotations \(\delta \mathbf w \) are approximated in the same manner

$$\begin{aligned} \begin{aligned} \delta \mathbf u (\underline{\mathbf{x }})&= \sum _{I=1}^{8} N_{I}(\underline{\mathbf{x }})\delta \mathbf u _{I}, \quad \delta \mathbf w (\underline{\mathbf{x }})&= \sum _{I=1}^{8} N_{I} (\underline{\mathbf{x }})\delta \mathbf w _{I}\\ \end{aligned} \end{aligned}$$
(31)

With these interpolations, the displacement gradient of the virtual displacement field can be written as

$$\begin{aligned} \mathbf y (\delta \mathbf u )=\sum _{I=1}^{8} \mathbf B _{I} \delta \mathbf u _{I},~~~\mathbf B _{I}=\begin{bmatrix} \frac{\partial {N_{I}}}{\partial {x_{1}}}{} \mathbf I _{3}\\ \\ \frac{\partial {N_{I}}}{\partial {x_{2}}}{} \mathbf I _{3}\\ \\ \frac{\partial {N_{I}}}{\partial {x_{3}}}{} \mathbf I _{3}\\ \end{bmatrix} \end{aligned}$$
(32)

The interpolation of the enhanced displacement gradient is constructed by using derivatives of the incompatible displacement \(\varvec{\alpha }\) [2]

$$\begin{aligned} \mathbf d = \sum _{J=1}^{N_{im}} \hat{\mathbf{G }}_{J}(\underline{\mathbf{x }})\varvec{\alpha }_{J}\equiv \hat{\mathbf{G }}(\underline{\mathbf{x }})\varvec{\alpha }^{e},~\hat{\mathbf{G }}=\left[ \hat{\mathbf{G }}_{1},\hat{\mathbf{G }}_{2},\hat{\mathbf{G }}_{3} \right] ,~~~\hat{\mathbf{G }}_{I}=\begin{bmatrix} \frac{\partial {M_{I}}}{\partial {x_{1}}}{} \mathbf I _{3}\\ \\ \frac{\partial {M_{I}}}{\partial {x_{2}}}{} \mathbf I _{3}\\ \\ \frac{\partial {M_{I}}}{\partial {x_{3}}}{} \mathbf I _{3}\\ \end{bmatrix} \end{aligned}$$
(33)

where \(M_{1}=(1-\xi ^{2})\), \(M_{2}=(1-\eta ^{2})\) and \(M_{3}=(1-\zeta ^{2})\) are chosen as quadratic polynomials. This choice is made to enhance the bending dominated performance [2].

The proposed interpolation should be modified to ensure that the incompatible modes are not active for constant stress, which guarantees the convergence of the incompatible mode method in the spirit of the patch test [16]; we impose:

$$\begin{aligned} \int _\mathbf{V }\hat{\mathbf{G }} d\mathbf V =0 \end{aligned}$$
(34)

which will in turn eliminate the variable \(\mathbf p \) from the variational equations. For a given interpolation \(\hat{\mathbf{G }}\), we can always construct the modified interpolation enforcing (34) as shown in [17] .

$$\begin{aligned} \hat{\mathbf{G }}_{m}=\hat{\mathbf{G }}- \frac{1}{\mathbf{V }}\int _{\mathbf{V }}\hat{\mathbf{G }} d\mathbf V =0 \end{aligned}$$
(35)

Such modified incompatible mode interpolation will in turn eliminate the variable \(\mathbf p \) from the variational equations. We should thus compute the stress tensor as follows

$$\begin{aligned} \mathbf s =\varvec{\varLambda }^{T}{} \mathbf C \mathbf e (\mathbf u ,\mathbf R ,\mathbf d )+ \varvec{\varXi }^{T}\gamma \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d ) \end{aligned}$$
(36)

which further reduces the variational equations in (29) to a set of equilibrium equations, which can be written as

$$\begin{aligned} \mathbf r (\mathbf u ,\mathbf R ,\mathbf d )&= \int _\mathbf{V }\hat{\mathbf{B }}^{T} \mathbf s \,d\mathbf V -\int _\mathbf{V }{} \mathbf N ^{T} \mathbf f \,d\mathbf V =0 \nonumber \\ \mathbf h (\mathbf u ,\mathbf R ,\mathbf d )&=\int _\mathbf{V }\hat{\mathbf{G }}^{T}{} \mathbf s \,d\mathbf V =0 \end{aligned}$$
(37)

where

$$\begin{aligned} \begin{array} {ll} \hat{\mathbf{B }}=\left[ \mathbf B ,\hat{\mathbf{Y }}\right] , \quad \mathbf B =\left[ \mathbf B _{1},\mathbf B _{2},\ldots ,\mathbf B _{8}\right] \\ \\ \hat{\mathbf{Y }}=\left[ N_{1} \left[ \mathbf Y (\mathbf u )+\widetilde{\mathbf{D }}\right] ,N_{2}\left[ \mathbf Y (\mathbf u )+\widetilde{\mathbf{D }}\right] ,\ldots ,N_{8}\left[ \mathbf Y (\mathbf u )+\widetilde{\mathbf{D }}\right] \right] \end{array} \end{aligned}$$
(38)

One possibility to solve the non-linear system in (37) is to linearize the complete system, as presented in [18] for a two-dimensional case. In present 3D case, the linearization leads to more complexity and involves the use of the secondary storage. Note however that the system size is not increased thanks to using the operator split method, which is presented in detail in Appendix I.

Variational formulations for dynamics

The equations of motion for the transient problem is based upon the variational formulations, by appealing to the Hamilton principle. In fact, the only new term with respect to the variational formulations in statics concerns the directional derivative of the kinetic energy, written as

$$\begin{aligned} \mathbf Q (\mathbf u (\underline{\mathbf{x }},t))=\int _\mathbf{V }\frac{1}{2}~\dot{\mathbf{u }}(\underline{\mathbf{x }},t) \cdot \rho ~\dot{\mathbf{u }}(\underline{\mathbf{x }},t)~d\mathbf V \end{aligned}$$
(39)

The kinetic energy in (39) is chosen as quadratic form only in terms of displacement fields. The independent rotation field is not involved, for it only serves to introduce the Biot strain measures. Thus, the variational equations in dynamics are written as modified form of these in (29) assuming for inertial effects

$$\begin{aligned} \begin{aligned} \delta \mathbf a \cdot \mathbf r (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } {\delta \mathbf u } \cdot \rho \ddot{\mathbf{u }}~d\mathbf V + \int _\mathbf{V } \lbrace \delta \mathbf e \cdot \mathbf C \mathbf e (\mathbf u ,\mathbf R ,\mathbf d ) \\&+\delta \varvec{\omega }\cdot \gamma \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d )\rbrace -\int _\mathbf{V }\delta \mathbf u .\mathbf f ~d\mathbf V =0 \\ \delta \mathbf{d }\cdot \mathbf h (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } \lbrace \delta \mathbf d \cdot \varvec{\varLambda }^{T}(\mathbf R )\mathbf C \mathbf e (\mathbf u ,\mathbf R ,\mathbf d )\\&+\delta \mathbf d \cdot \varvec{\varXi }^{T}(\mathbf R )\gamma \varvec{\omega }(\mathbf u ,\mathbf R ,\mathbf d ) - {\delta \mathbf{d }}^T \mathbf p \rbrace d\mathbf V =0\\ \delta \mathbf{p }\cdot \mathbf g (\mathbf u ,\mathbf R ,\mathbf d ,\mathbf p ):=&\int _\mathbf{V } \lbrace \delta \mathbf{p }^T \mathbf d \rbrace d\mathbf V =0 \end{aligned} \end{aligned}$$
(40)

In dynamics, displacement and rotation fields are functions of both space and time. We use the separation of variables approach in order to construct the finite element approximations of displacements and rotations

$$\begin{aligned} \mathbf u (\underline{\mathbf{x }},t) = \sum _{I=1}^{8} N_{I}(\underline{\mathbf{x }}) \mathbf u _{I}(t);~\mathbf w (\underline{\mathbf{x }},t) = \sum _{I=1}^{8} N_{I}(\underline{\mathbf{x }}) \mathbf w _{I}(t);~ \mathbf d (\underline{\mathbf{x }},t)= \sum _{J=1}^{N_{im}} \hat{\mathbf{G }}_{J}(\underline{\mathbf{x }})\varvec{\alpha }_{J}(t) \end{aligned}$$
(41)

The variational equations in (40) can now be rewritten as

$$\begin{aligned} \mathbf r (\mathbf u ,\mathbf R ,\mathbf d )=&\int _\mathbf{V }\rho \mathbf N ^{T} \ddot{\mathbf{u }}~d\mathbf V + \int _\mathbf{V }\hat{\mathbf{B }}^{T} \mathbf s \,d\mathbf V -\int _\mathbf{V }{} \mathbf N ^{T} \mathbf f ~d\mathbf V =0 \nonumber \\ \mathbf h (\mathbf u ,\mathbf R ,\mathbf d )=&\int _\mathbf{V }\hat{\mathbf{G }}^{T} \mathbf s \,d\mathbf V =0 \end{aligned}$$
(42)

with the accelerations field \(\ddot{\mathbf{u }}\) interpolated in the same way as the compatible displacements field. It is easy to see that the mass matrix will have constant entries and take the following form

$$\begin{aligned} \mathbf M =\int _\mathbf{V }\begin{bmatrix} \mathbf N ^{T}\rho \mathbf N&\mathbf 0 \\ \mathbf 0&\mathbf 0 \end{bmatrix}~d\mathbf V \end{aligned}$$
(43)

We note that the zero masses associated to angular accelerations \(\ddot{\mathbf{w }}\) can prove troublesome and affect computation stability in dynamic problems. In order to illustrate that clearly, we consider the linearized form of equations of motion in (42)\(_{(1)}\) for free vibration case: \(\mathbf U exp(i~~\overline{\omega } t)\) and \(\mathbf W exp(i~~\overline{\omega } t)\), which leads to

$$\begin{aligned} \frac{1}{{\overline{\omega }}^2}\begin{bmatrix} \mathbf K _{11}&\mathbf K _{12}\\ \mathbf K _{21}&\mathbf K _{22} \end{bmatrix} \begin{bmatrix} \mathbf U \\ \mathbf W \end{bmatrix} =\begin{bmatrix} \mathbf M _\mathbf{u }&\mathbf 0 \\ \mathbf 0&\mathbf 0 \end{bmatrix} \begin{bmatrix} \mathbf{U }\\ \mathbf{W }\end{bmatrix} \end{aligned}$$
(44)

This clearly shows by choosing: \(\mathbf U =0\), \(\mathbf W \ne 0\) that the presence of zero terms in the mass matrix would require infinite frequencies, which is the ultimate case of stiff equations [19] with all difficulties that will impose.

The simplest way to overcome this deficiency is by using the penalty method and introducing the mass matrix contribution of the rotational degrees of freedom through a kind of regularization. This contribution is assigned to be equal to the ones coming from translational degrees of freedom, multiplied by a regularization parameter \(\eta \) which varies from 0 and 1. Finally, the regularized mass matrix can be written as

$$\begin{aligned} \mathbf M _\mathbf{r }=\int _\mathbf{V }\begin{bmatrix} \mathbf N ^{T}\rho \mathbf N&\mathbf 0 \\ \mathbf 0&\eta \mathbf N ^{T}\rho \mathbf N \end{bmatrix}~d\mathbf V \end{aligned}$$
(45)

Newmark implicit time-stepping scheme

For nonlinear problems, the evolution of state variables is obtained by step-by-step integration schemes. To that end, the time interval of interest is partitioned into a number of time steps (\(0\prec t_{1} \prec t_{2} \prec \cdots \prec t_{n} \prec t_{n+1}\prec \cdots \prec T\)). At a typical time \(t_{n}\), the values of \(\mathbf u _{n}\) and \(\mathbf R _{n}\) are known. The corresponding values at time \(t_{n+1}\) are computed in each step independently for single-step schemes, such as Newmark. For displacement vector we have sample additive updates

$$\begin{aligned} \mathbf u _{n+1}^{(i+1)}=\mathbf u _{n+1}^{(i)}+\varDelta \mathbf u _{n+1}^{(i)} \end{aligned}$$
(46)

where \(\varDelta \mathbf u _{n+1}^{(i)}\) is the incremental displacement at each iteration (i). The rotation update is somewhat more involved in that we have to choose between various possibilities of parameters for rotation representation (e.g. see [15]). If the spatial representation is used, we can carry out the rotation update as

$$\begin{aligned} \mathbf R _{n+1}^{(i+1)}= \widetilde{\varvec{\varLambda }}\left( \varvec{\theta }_{n}^{(i)}+\varDelta \varvec{\theta }_{n+1}^{(i)}\right) \mathbf R _{n} \end{aligned}$$
(47)

where \(\varDelta \varvec{\theta }_{n+1}^{(i)}\) is the incremental rotation vector at each iteration (i) and \(\widetilde{ \varvec{\varLambda }}(\bullet )\) corresponds to a direct representation of the orthogonal rotation tensor via the rotation vector.

The intrinsic representation of the finite rotations by an orthogonal tensor can be reduced to a set of four quaternion parameters. The rotational update can be written as

$$\begin{aligned} \mathbf R _{n+1}^{(i+1)}=\left( 2q_{(n+1)\textit{0}}^{(i+1)2}-1\right) \mathbf I _{3}+2q_{\textit{0}(n+1)}^{(i+1)}\left[ \mathbf q ^{(i+1)}_{n+1}\times \mathbf I _{3}\right] +2\mathbf q ^{(i+1)}_{n+1}\otimes \mathbf q ^{(i+1)}_{n+1} \end{aligned}$$
(48)

where

$$\begin{aligned} \begin{aligned} q_{\textit{0}(n+1)}^{(i+1)}&= q_{\textit{w0}(n+1)}^{(i)}~q_{\textit{0}(n+1)}^{(i)}-\mathbf q _{\textit{w}(n+1)}^{(i)}. \mathbf q _{n+1}^{(i)}\\ \mathbf q _{n+1}^{(i+1)}&= q_{\textit{w0}(n+1)}^{(i)}{} \mathbf q _{n+1}^{(i)}+q_{\textit{0}(n+1)}^{(i)}.\mathbf q _{\textit{w}(n+1)}^{(i)}+\mathbf q _{\textit{w}(n+1)}^{(i)}\times \mathbf q _{n+1}^{(i)}\\ \end{aligned} \end{aligned}$$
(49)

The quaternion parameters of the iterative rotation parameter of the orthogonal tensor \(\{q_{\textit{w0}(n+1)}^{(i)},\mathbf q _{\textit{w}(n+1)}^{(i)}\}\) above are given by

$$\begin{aligned} \begin{aligned} \left\{ q_{\textit{w0}(n+1)}^{(i)},\mathbf q _{\textit{w}(n+1)}^{(i)}\right\}&=\left\{ \cos \left( \frac{\varDelta \textit{w}^{(i)}_{n+1}}{2}\right) ,\frac{sin\left( \frac{\varDelta \textit{w}^{(i)}_{n+1}}{2}\right) }{\varDelta \textit{w}^{(i)}_{n+1}}{} \mathbf w ^{(i)}_{n+1}\right\} \\ \varDelta \textit{w}^{(i)}_{n+1}&=\left( \varDelta \mathbf w ^{(i)}_{n+1}.\varDelta \mathbf w ^{(i)}_{n+1}\right) ^{\frac{1}{2}} \end{aligned} \end{aligned}$$
(50)

where \(\varDelta \mathbf w _{n+1}\) is the axial vector of incremental rotation. Note that \(\varDelta \mathbf w _{n+1}\) and \(\varDelta \varvec{\theta }_{n+1}\) are interconnected

$$\begin{aligned} \varDelta \mathbf w _{n+1}= \tilde{\mathbf{T }} (\varvec{\theta }_{n+1})\varDelta \varvec{\theta }_{n+1} \end{aligned}$$
(51)

where

$$\begin{aligned} \tilde{\mathbf{T }} (\varvec{\theta }):=\frac{sin \theta }{\theta }{} \mathbf I +\frac{1- cos \theta }{\theta ^{2}}\varvec{\varTheta }+\frac{\theta - sin \theta }{\theta ^{3}} \varvec{\theta } \times \varvec{\theta } \end{aligned}$$

The scalar \(\theta \) is the euclidean norm of \(\varvec{\theta }\) and the tensor \(\varvec{\varTheta }\) is the shew-symmetric matrix associated to \(\varvec{\theta }\).

In dynamics, besides computation of displacements and rotations, one also needs to provide the values of velocities and accelerations at each time step. In what follows, the Newmark time integration scheme is used. The linear velocity and acceleration are advanced from time \(t_{n}\) to \(t_{n+1}\) by using the standard Newmark approximations

$$\begin{aligned} \begin{aligned} \dot{\mathbf{u }}_{n+1}&=\dot{\mathbf{u }}_{n}+\varDelta t((1-\gamma )\ddot{\mathbf{u }}_{n}+\gamma \ddot{\mathbf{u }}_{n+1}) \\ \ddot{\mathbf{u }}_{n+1}&= \frac{1}{\beta \varDelta t^{2}}(\mathbf u _{n+1}-\mathbf u _{n})-\frac{1}{\beta \varDelta t}\dot{\mathbf{u }}_{n}-\frac{0.5-\beta }{\beta }\ddot{\mathbf{u }}_{n} \end{aligned} \end{aligned}$$
(52)

where \(\varDelta t\) is the time step while \(\beta \) and \(\gamma \) are the Newmark coefficients.

The Newmark implementation for finite rotations is a bit more laborious [20]. Here, we follow previous works on 3D beams [15] with an extension of the standard Newmark algorithm valid only for so-called spatial incremental rotation vector \(\varvec{\theta }_{n+1}\). We assume that the angular velocity and acceleration, respectively \(\dot{\mathbf{w }}_{n+1}=\dot{\mathbf{w }}(t_{n+1})\) and \(\ddot{\mathbf{w }}_{n+1}=\ddot{\mathbf{w }}(t_{n+1})\), can be provided by the Newmark approximations for finite rotations

$$\begin{aligned} \begin{aligned} \dot{\mathbf{w }}_{n+1}&= \widetilde{ \varvec{\varLambda }}(\varvec{\theta }_{n+1})\left[ \frac{\gamma }{\beta {\varDelta t}}\varDelta \varvec{\theta }_{n+1}+ \tilde{\varvec{\omega }}_{n+1}\right] \\ \ddot{\mathbf{w }}_{n+1}&= \widetilde{ \varvec{\varLambda }}(\varvec{\theta }_{n+1})\left[ \frac{1}{\beta {\varDelta t}^{2}}\varDelta \varvec{\theta }_{n+1}+ \tilde{\varvec{\alpha }}_{n+1}\right] \end{aligned} \end{aligned}$$
(53)

where \(\tilde{\varvec{\omega }}_{n+1} \) and \(\tilde{\varvec{\alpha }}_{n+1}\) are given by

$$\begin{aligned} \begin{aligned} \tilde{\varvec{\omega }}_{n+1}&= \frac{\beta -\gamma }{\beta }\dot{\mathbf{w }}_{n} +\frac{\beta -0.5\gamma }{\beta } \varDelta t \ddot{\mathbf{w }}_{n}\\ \tilde{\varvec{\alpha }}_{n+1}&=- \frac{1}{\beta \varDelta t}\dot{\mathbf{w }}_{n}- \frac{0.5-\beta }{\beta } \ddot{\mathbf{w }}_{n} \end{aligned} \end{aligned}$$
(54)

From the proposed form of the Newmark approximations for both displacements and rotations, we can compute the linearization of velocities and accelerations, providing corresponding iterative updates. First, we can write for displacements

$$\begin{aligned} \begin{aligned} \dot{\mathbf{u }}_{n+1}^{(i+1)}&=\dot{\mathbf{u }}_{n+1}^{(i)}+ \frac{\gamma }{\beta \varDelta t}\varDelta \mathbf u _{n+1}^{(i)}\\ \ddot{\mathbf{u }}_{n+1}^{(i+1)}&=\ddot{\mathbf{u }}_{n+1}^{(i)}+ \frac{1}{\beta \varDelta t^{2}}\varDelta \mathbf u _{n+1}^{(i)} \end{aligned} \end{aligned}$$
(55)

Similarly, angular velocity and acceleration iterative updates are obtained using the iterative incremental rotation vector

$$\begin{aligned} \begin{aligned} \dot{\mathbf{w }}_{n+1}^{(i+1)}&= \dot{\mathbf{w }}_{n+1}^{(i)}+ \frac{\gamma }{\beta {\varDelta t}} \widetilde{ \varvec{\varLambda }}( \varvec{\theta }_{n+1}^{(i)})\varDelta \varvec{\theta }_{n+1}^{(i)}\\ \ddot{\mathbf{w }}_{n+1}^{(i+1)}&= \ddot{\mathbf{w }}_{n+1}^{(i)}+ \frac{1}{\beta {\varDelta t^{2}}} \widetilde{ \varvec{\varLambda }}( \varvec{\theta }_{n+1}^{(i)})\varDelta \varvec{\theta }_{n+1}^{(i)}\\ \end{aligned} \end{aligned}$$
(56)

where \(\widetilde{ \varvec{\varLambda }}(\bullet ) \) is given by the exponential mapping formula of Rodrigues [15], written as

$$\begin{aligned} \widetilde{ \varvec{\varLambda }}(\varvec{\theta })= \cos \theta \mathbf I +\frac{\sin \theta }{\theta }\varvec{\varTheta }+\frac{1-\cos \theta }{\theta ^{2}} \varvec{\theta } \times \varvec{\theta } \end{aligned}$$

By exploiting the relationship presented in (51), angular velocity and acceleration updates become

$$\begin{aligned} \begin{aligned} \dot{\mathbf{w }}_{n+1}^{(i+1)}&= \dot{\mathbf{w }}_{n+1}^{(i)}+ \frac{\gamma }{\beta {\varDelta t}} \mathbf T ^{-T}\left( \varvec{\theta }_{n+1}^{(i)}\right) \varDelta \mathbf w _{n+1}^{(i)}\\ \ddot{\mathbf{w }}_{n+1}^{(i+1)}&= \ddot{\mathbf{w }}_{n+1}^{(i)}+ \frac{1}{\beta {\varDelta t^{2}}} \mathbf T ^{-T}\left( \varvec{\theta }_{n+1}^{(i)}\right) \varDelta \mathbf w _{n+1}^{(i)}\\ \end{aligned} \end{aligned}$$
(57)

where we use the result in [15], \(\mathbf T ^{-T}(\bullet )=\widetilde{ \varvec{\varLambda }}(\bullet ) \tilde{\mathbf{T }}^{-1}(\bullet )\).

It is interesting to note that the rotation updates in terms of incremental rotation vector can be easily computed thanks to the additive procedure of updates, \(\varvec{\theta }_{n+1}^{(i+1)}=\varvec{\theta }_{n+1}^{(i)}+\varDelta \varvec{\theta }_{n+1}^{(i)}\). Moreover, velocity and acceleration updates in (55) and (57) have formally the same structure for both linear and angular configurations which is the main advantage of the proposed Newmark algorithm for finite rotation.

The linearized form of the equations of motion in dynamics is given as

$$\begin{aligned} \frac{1}{\beta \varDelta t^{2}} \mathbf M \begin{bmatrix} \varDelta \mathbf u _{n+1}^{(i+1)}\\ \tilde{\mathbf{T }}^{-T}\left( \varvec{\theta }_{n+1}^{(i+1)}\right) \varDelta \mathbf w _{n+1}^{(i+1)}\\ \end{bmatrix}+\mathbf K \begin{bmatrix} \varDelta \mathbf u _{n+1}^{(i+1)}\\ \varDelta \mathbf w _{n+1}^{(i+1)}\\ \end{bmatrix}+\mathbf F ^{T}\varDelta \tilde{\varvec{\alpha }}_{n+1}^{(i+1)}=-\overline{\mathbf{R }} \end{aligned}$$
(58)

where

$$\begin{aligned} \overline{\mathbf{R }}=\mathbf r +\frac{1}{\beta \varDelta t^{2}} \mathbf{M }\begin{bmatrix} \varDelta \mathbf{u }_{n+1}^{(i+1)}\\ \tilde{\mathbf{T }}^{-T}\left( {\varvec{\theta }}_{n+1}^{(i+1)}\right) \varDelta \mathbf{w }_{n+1}^{(i+1)}\\ \end{bmatrix}+\hbar \end{aligned}$$
(59)
$$\begin{aligned} \hbar =\mathbf M \Bigg (\frac{1}{\beta \varDelta t^{2}}\begin{bmatrix} \mathbf{u }_{n} \\ 0\\ \end{bmatrix}+\frac{1}{\beta \varDelta t}\begin{bmatrix} \dot{\mathbf{u }}_{n}\\ \tilde{\mathbf{T }}^{-T}({\varvec{\theta }}_{n+1})\dot{\mathbf{w }}_{n+1}\\ \end{bmatrix}+\frac{0.5-\beta }{\beta }\begin{bmatrix} \ddot{\mathbf{u }_{n}}\\ \tilde{\mathbf{T }}^{-T}({\varvec{\theta }}_{n+1})\ddot{\mathbf{w }}_{n+1}\\ \end{bmatrix}\Bigg ) \end{aligned}$$

Numerical examples

Several numerical examples are presented in order to demonstrate a very satisfying performance of the enhanced 3D solid element proposed herein. The presented simulation results concern both static and dynamic problems. All the computations are performed with a research version of the computer program FEAP, written by Prof. R.L. Taylor at UC Berkeley [16].

Short cantilever beam in large compressive deformation: static problem

The first example presents a comparison between the proposed solid element and a standard solid element, which employs the Green–Lagrange strain measure. A single finite element cantilever beam is subjected to large compression, by imposing the displacement at one end while keeping the other end fixed (see Fig. 1). The material properties are selected as: \(\mathbf E =2000\) N/m\(^2\) and \(\mu =0\). The imposed displacement (\(\mathbf u _{x}=-0.99\)) is increased in 10 equal increments until practically reaching maximum possible compressive strains.

Fig. 1
figure 1

Short cantilever beam in large compressive deformation; stress as function of stretch: a Green–Lagrange strain measures, b Biot strain measures

Full size image

The plots of the xx-component of the PiolaKirchhoff stress as function of stretch are presented in Fig. 1 for both models. We can easily see that the zero stress value accompanying maximum compressive strain for the Saint-Venant–Kirchhoff material cannot be justified for any real material. In fact, a large compression must logically be accompanied by a large value of stress which is shown, moreover, by the results of the proposed model.

The deficiency in representing very large compressive strains by the standard solid element is due to the loss of convexity of the strain energy. However, this drawback of violating poly-convexity conditions is easily repaired by the proposed element. For this, it is useless to compare the proposed element to others solid element, which employ Green Lagrange deformations measures.

Large deflection of a cantilever: static problem

In this second validation example, we consider the cantilever beam of Fig. 2 clamped at one end and loaded, at the another, with four equal concentrated moments which add to the total value of \(m=0.01\pi \) Nm. The beam is modeled with \(10 \times 1 \times 1\) enhanced 3D elements.

The exact rotation angle \(\theta \) can be computed with the classical Euler formula based upon the classical beam theory [10]: \(\theta = m/{EI}\). For the given value of the moment, geometric and material proprieties the reference solution of the deformed shape is a semi circle.

Fig. 2
figure 2

A cantilever beam subjected to an end moment modeled with regular mesh \(10 \times 1 \times 1\) and his deformed shape

Full size image

The deformed shape is presented in Fig. 2, showing an excellent agreement with the reference shape. The loading is applied in a single load step, and the solution is obtained after 7 iterations, with a satisfying rate of convergence (see Table 1).

Table 1 Convergence rates for the cantilever
Full size table

Circular arch under single load: static instability problem

The next example shows the efficient use of the proposed enhanced 3D solid element to solve a geometric instability problem, first solved by 3D beam. We consider a circular arch, hinged at one end and clamped at another, under a vertical point load in the middle. The selected properties of the arch are given in Fig. 3a. The numerical solution is obtained by a mesh having thirty 8-node enhanced elements.

Fig. 3
figure 3

Finite element mesh of a clamped-hinged circular arch: a initial shape, b deformed shape

Full size image

The computation is performed with a time step \(\varDelta t = 0.01\) s and needs only 5 iterations to converge. The corresponding result is also computed with the same number of 2-node beam elements (see [10]). In Fig. 4, the load/displacement curves for both approximations are given, indicating a very good agreement for two curves obtained with the different finite element models.

Fig. 4
figure 4

Force-display diagram

Full size image

Beam distortion by a solid plate: static problem

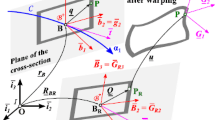
In order to show the compatibility of the proposed element with beam element, we propose the following example. We consider a straight beam of length \(l=4\) m, aligned with the z-axis. The finite element model of the beam consists of five 3D geometrically exact beam elements. The mechanical properties of the beam are chosen as: \({EA}=100\) N, \({GA}=50\) N and \({EI}=159\) Nm\(^2\). The finite element model employs 6 two-node beam elements. The lower end of the beam is fixed, while a square plate is attached at the other end in the center c as shown in Fig. 5. The plate is composed of four proposed solid elements with \({E}=5000\) N/m\(^2\) and \(\nu =0\). The beam is subjected to a torque through the external forces applied to the four corners of the plate. The direction of forces is given in Fig. 5. The total moment at point c, provided by the forces \({F}_{i=1,4}\) is calculated as \({M}_{\tau }=4a\times {F}\). The angle of twist can be found by using the following formula

$$\begin{aligned} \theta = \frac{{M}_{\tau }~l}{{G}{I}} \end{aligned}$$

where G is the shear modulus. For the chosen characteristics (\({F}_{i=1,4}=3.9\) N), the value of the angle of twist is \(\varPi /4\). The computation is performed in 10 increments of \(\varDelta t = 0.1\) s. The numerical solution corresponds perfectly to the analytical solution: the rotation \(\theta _{6}\) at node c is equal to \(0.78541\approx \varPi /4\).

Fig. 5
figure 5

Beam distortion by a solid plate

Full size image

Free vibration analysis: dynamic problem

For the dynamics part, the first example is proposed for free vibration analysis. For a cantilever beam fixed at one end, we are concerned with the identification of natural frequencies and mode shapes. This beam is modeled with \(10 \times 1 \times 1\) enhanced 3D elements (Fig. 6).

Fig. 6
figure 6

10 elements mesh for the cantilever beam fixed at one end

Full size image
Table 2 Natural frequencies of the first ten modes for the cantilever beam
Full size table

Table 2 gives the natural frequencies of the first ten modes, sorted in increasing order for both enhanced solid element and standard beam element. The results reveal that solid element detects mode shapes of distortion which are unseen by the beam element. We can also see that the natural frequency values of both elements correspond well to each other. Duplicated frequencies are justified by the fact that each bending mode in y direction has a similar bending mode in z direction.

Fig. 7
figure 7

Mode shapes of the cantilever beam obtained with the proposed solid element

Full size image

The mode shapes obtained with mesh of elements are presented in Fig. 7. Compared to the standard beam element, the proposed element is capable of taking into account sectional changes as showing in the mode shapes 3 and 6. In order to captive that in the case of beam, one needs higher order geometrically-exact beam models [21, 22], incorporating in-plane cross sectional changes and out-plane warping by adding supplementary degrees of freedom. Here, the difficulty lies in the choice of distortion and warping functions which depend on the geometry of the structures and the need for a post-treatment to get the final results and sketch out the deformed shapes. However, with the proposed solid element, the result could be obtained directly for any shape.

Cantilever beam subjected to end shear force: dynamic problem

In the second version of the same test, we keep all the data the same as in the first version, except that we change the loading proprieties. First, the beam is subjected to four vertical forces at the free end. Each force has a weak amplitude (\(f=0.001\) N) in order to assimilate linear behavior and a sinusoidal time variation with the frequency \(\omega =3.12413236\times 10^{-1}\) rad/s, which is the first natural frequency in the initial configuration.

Fig. 8
figure 8

Vertical displacement in the free end of the cantilever beam under force: resonance

Full size image
Fig. 9
figure 9

Free-end displacement component in the direction of the applied force

Full size image
Fig. 10
figure 10

Free-end displacement component in the direction of the applied force over a large time interval

Full size image

The vertical displacement under force applied at the free end is presented in Fig. 8. The resonance condition is satisfied and the dynamic response presents rapidly increasing as expected.

We have proposed two alternatives to define the mass matrix. In order to compare these possibilities, we examine the bending problem of a cantilever beam under four concentrated forces applied at its free ends. The proprieties of the beam are maintained as before (Fig. 6). At each node, the applied force is a triangular pulse, linearly increasing for \(0 \le t \le 1\) to attain the maximum value \(\mathbf F =0.5\) N, then decreasing for \(1 \le t \le 3\) to \(-\mathbf F \) and finally increasing again for \(3 \le t \le 4\) to return to 0 at \(t=6\). The computations are carried out with the time step \(\varDelta t=0.1\) s. Time histories for the free end displacement components for the different configurations are given in Fig. 9. We note that the amplitude of vibration is of the same order as the total sum of the applied forces.The obtained results show a good agreement between the geometrically exact beam and 3D enhanced solid elements. The beam reference response is very close to the response of the 3D solid, with somewhat greater accuracy in the case of the incomplete mass matrix (neglecting the rotation inertia) regarding the dominant response frequencies.

Despite better accuracy of computed response, the presence of a zero matrix block associated with rotation degrees of freedom is the source of major difficulty in the computational treatment of such problem over a very long interval of time. In order to illustrate this, we increase the amplitude of the loading to \(\mathbf F =2\) N and we perform the computation of the fields of displacement over a longer interval in time. The time step is selected as \(\varDelta t=0.1\) for both configurations. The dynamic response for displacement at the free end is plotted in Fig. 10. First, we note high oscillations in the computed displacement which are obtained by the Newmark scheme. Moreover, the configuration using the standard mass matrix can no longer converge for time exceeding \(\mathbf T =81.3\). However, with a regularized mass matrix, the residual remains sufficiently small to ensure the convergence for substantially longer period.

Adding terms in the mass matrix associated to the rotational degrees of freedom ensures a satisfying performance of the proposed element in computations over very long time interval. However, this implies additional computation operations corresponding to the angular accelerations.

Large scale wind turbine: dynamic problem

For the last example, we consider a dynamic analysis for a model of wind turbine with flexible blades. We choose to make simpler blade design, since our first objective is to check the efficiency of the proposed approach to handle numerically the structure behavior under large overall motion without getting into too much details of shape optimal design.

Fig. 11
figure 11

Wind turbine model example

Full size image

The turbine consists of three blades with a length of 50 m. Each blade is modeled with the proposed enhanced 3D solid. The revolute joint, providing connectivity between blades, is defined with two rigid bodies [23]. The interaction between flexible and rigid components doesn’t need any special requirements given that the rotational degrees of freedom appear in the rigid body formulation for the large displacement in a non-linear form [23]. The tower, which is 85 meters tall and with circular cross section, is modeled with geometrically exact beam [24] (see Fig. 11). The wind turbine blades are subjected to a uniform distributed load using follower pressure approach (see Appendix II). The blades facets where the loading is applied are defined with 4 nodes two-dimensional elements that belong to the boundaries of the three-dimensional 8 nodes brick elements of the blades. We choose an amplitude of the follower pressure \(p=360\) N/m\(^{2}\), equivalent to an average wind speed 60 km/h (see Appendix II for special treatment of follower pressure loads). The pressure function \(\overline{p}\) is presented in Fig. 11.

The chosen material and geometric characteristics are presented in Fig. 11. The computations are carried out with the constant time step \(\varDelta t=0.2\). The number of iterations per step doesn’t exceed 20, showing rather robust convergence with regard to multi-finite elements used in the same structure.

The proposed element describes properly the rotational motion of the wind turbine. For a long time period, we start observing a large deformation related to a combined bending and twisting motion which causes premature damage of the turbine. This demonstrates the usefulness of the proposed solid element with respect to the geometrically exact beam element for this kind of modeling. Namely, beam formulation is based on the rigid cross-section assumption, which can not captive such damage phenomena.

The tower is submitted to large bending, involving harmful effect on the wind turbine stability which may be even more pronounced for large scale structures in offshore environments. In order to overcome this problem, we introduce pre-stressed cables connecting the wind tower to the support (see Fig. 12). The finite element approach for computing cable structure undergoing large displacement is coded for non linear analysis, based on the previous work [25].

Fig. 12
figure 12

Cables effect on the bending of the tower: geometry of structure

Full size image

The cross-section area of the cable used here is \(A=0.018\) m\(^{2}\) and the mass density is \(\rho =0.1\) kg/m\(^{3}\). The undeformed cable configuration is straight line, with an initial pre-tension stress \(\mathbf S _{0}=800\) N/m\(^{2}\). The Saint Venant material model is adopted \(E=2\times 10^{7}\) N/m\(^{2}\). We increase the pressure amplitude to 900.

The time histories of the horizontal displacement at the top of the tower for both configurations, with or without cables, are plotted in Fig. 13. We note that tower’s deflection is reduced, on average, by half when cables are added. Hence, the proposed solution combines robustness and low weight to improve the stability of the wind turbine without increasing costs.

Fig. 13
figure 13

Cables effect on the bending of the tower: horizontal displacement of the free end tower

Full size image

Closing remarks

In this paper, we have discussed the regularized variational formulation for 3D solid element with the incompatible mode method to analyze geometrically nonlinear problems in statics and dynamics. The statics formulation is follow up of our previous works limited only to 2D statics [18, 26]. The main novelty is the generalization of the formulation as well as the finite element implementation to framework of 3D nonlinear dynamic problems.

In particular, the mass matrix is defined from a simple quadratic form of the kinetic energy as opposed to the co-rotational formulation and the floating frame formulation used by the others authors. Moreover, a regularized form of the mass matrix is proposed in order to ensure high computational performance without adding complexity. It is important that the regularized mass matrix ensures a good performance by being able to avoid infinite frequencies, and thus facilitating the convergence of the Newmark implicit scheme. Further gain in computational efficiency, which is worth to note, is brought about by the operator split methodology reducing the computation of the the final value of the incompatible mode parameters to a single iteration.

It is interesting to note that the proposed elements with rotational degrees of freedom can be easily combined with geometrically exact beam models and can also be efficient in the nonlinear dynamic analysis of thick plates and shells [9]. This enables a smooth transition between solid and structural elements. Moreover, they are constructed to allow in plane cross-sectional changes as well as out of plane cross-sectional warping.

In order to reduce the impact of zero masses associated to the rotational degrees of freedom, besides of a simple regularization of the mass matrix, another alternative seems more relevant by controlling the dissipation of high frequency modes contribution as proposed for beam case in [19, 27] .