Abstract
Background
Due to their Arctic habitat and elusive nature, little is known about the narwhal (Monodon monoceros) and its foraging behaviour. Understanding its ability to catch prey is essential for understanding its ecological role, but also to assess its ability to withstand climate changes and anthropogenic activities. Narwhals produce echolocation clicks and buzzing sounds as part of their foraging behaviour and these can be used as indicators of prey capture attempts. However, acoustic data are expensive to store on the tagging devices and require complicated post-processing. The main goal of this paper is to predict prey capture attempts directly from acceleration and depth data. The aim is to apply broadly used statistical models with interpretable parameters. The ultimate goal is to be able to estimate prey consumption without the more demanding acoustic data.
Results
We predict narwhal buzzing activity using mixed-effects logistic regression models with 83 features extracted from acceleration and depth data as explanatory variables. The features encompass both instantaneous values as well as delayed values to capture behavioural patterns lasting several seconds. The data correlations were not strong enough to predict the exact timing of the buzzes, but were reliably able to detect buzzes within a few seconds. Most of the of the buzz predictions were within 2 s of an observed buzz (68%), increasing to 94% within 30 s. Conversely, 46% of the observed buzzes were within 2 s of a predicted buzz, increasing to 82% within 30 s. Additionally, the model performed well, although with a tendency towards underestimation of the number of buzzes per dive. In total, we predicted 17, 557 buzzes versus 25, 543 observed across data from 10 narwhals. Classifying foraging and non-foraging dives yielded a precision of 86% and a recall of 91%.
Conclusion
We conclude that narwhal foraging estimation through acceleration and depth data is a valid alternative or supplement to buzz recordings, even when using somewhat simple statistical methods, such as logistic regression. The methods in this paper can be extended to foraging detection in similar marine species and can aid instrument development.
Similar content being viewed by others
Background
The narwhal (Monodon monoceros) is a marine mammal belonging to the Monodontidae family. They are medium-sized whales known for their long characteristic tusk present predominantly in males. A physically mature male will on average grow to be 4.6 ms long and a mass of 1650 kg, while the smaller female on average grows to 4 ms in length and a mass of approximately 900 kg [1]. The narwhal lives year-round in the Arctic waters around Greenland, Canada and Russia with a global population estimated at approximately 170,000 specimens [2] resulting in a categorization of “least concern” in the International Union for Conservation of Nature red list of threatened species [3].
The narwhal and the beluga whale are the sole members of the Monodontidae family: they are toothed whales but lack functioning teeth for prey capture. Instead, both species utilize presumably suction feeding. In similar marine mammals, such as harbour seals, porpoises and sperm whales, the animals shows strong jerking motions in acceleration when surging forward capturing a prey [4,5,6]. We hypothesize that suction feeding, in comparison to raptorial feeding, is more likely to involve less vigorous movements and therefore might be harder to detect. Jerking motions do, however, seem to be present during pinniped suction feeding, albeit at a shorter duration and less amplitude compared to raptorial feeding [4].
When foraging for food, the narwhal dives to depths below 500 m, where it mainly preys on polar cod, Greenland halibut and squid [7]. It is among the deepest diving cetaceans and has been observed to dive deeper than 1800 m [8]. As light is scarce, the narwhal orients itself and explores the environment using echolocation. The vocalizations emitted during foraging largely consist of short clicking sounds and longer buzzes [9]. In other marine mammals, echolocation is used for overall orientation, while the buzzes are used for continuously visualizing prey up to the moment of striking [5, 6]. We hypothesize the same holds for narwhals.
The narwhal’s foraging behaviour is of great interest, both from a biological perspective to understand the ecological role of the narwhal, but also to assess the robustness of the species to the ongoing environmental changes in the Arctic. The narwhal is highly specialized to its Arctic habitat with strong site fidelity and low long-term genetic diversity [10]. This indicates that the narwhal may be unsuited to adapt to the ongoing climate changes. Furthermore, as the sea-ice coverage decreases, human activities in the Arctic are likely to increase. Recent studies have shown anthropogenic activities to have a greater effect on narwhal behaviour than previously anticipated with sound exposure effects on narwhal foraging being detected at very low sound exposure levels below background noise [11, 12].
Because of their deep diving behaviour in an ice-covered habitat, narwhal foraging is difficult or impossible to monitor directly. Instead, foraging is estimated using acoustic recordings of narwhal buzzes obtained from animal-borne instruments under the assumption that a buzz corresponds to a prey catch attempt. However, obtaining acoustic data with recordings of narwhal sound production is a demanding process as acoustic data are expensive to store. Additionally, buzzes have to be verified by specialized experts listening to the recordings. The purpose of this paper is therefore to investigate whether buzzing (and therein foraging behaviour) can be accurately estimated using statistical models and recordings of only acceleration and depth, as these are more easily measured and have previously proven to be useful for estimating marine mammal behaviour [7, 13, 14]. As foraging behaviour is our primary focus, we are mainly concerned with identifying approximate forage times and dives, as well as the proportional number of prey capture attempts, whereas exact timing of buzzes are of minor interest.
Modelling of narwhal buzzing using accelerometer and depth data was already attempted using U-Net convolutional networks, logistic regression and random forest in [15], by using the presence of a buzz as the response variable. Here, the U-Net vastly outperformed the two latter models. However, the U-Net has the disadvantages of being complex, computationally demanding and nontransparent in its prediction process. In this paper, we investigate whether further improvements on the simpler logistic regression model through the inclusion of random effects, additional features, autoregressive effects and non-linear inclusions amongst other things, might present a valid choice for detecting narwhal foraging. As a further simplification, we do this with a response variable of buzz startup sampled at 1 Hz instead of buzzing presence sampled at 10 Hz, as registering the duration of a buzz is significantly more demanding and less precise than the approximate start. This is done using two approaches. One where 10 models are trained, each on data with one whale left out and performance is evaluated on the left-out whale. This should help assess if results are overconfident when evaluating on previously observed narwhals, compared to new specimens. Another approach is a single model fitted and evaluated on 80% of the data from all narwhals and evaluated on the left-out 20%. Data are split chronologically to preserve the temporal structures in the data.
Methods
Narwhal tagging and data sampling
Data consist of measurements from 10 narwhals previously analysed in [9, 12]. The narwhals were captured in Scoresby Sound fjord in cooperation with local Inuit hunters after which they were equipped with Acousonde acoustic and orientation tags (www.acousonde.com) and thereafter released. The tags were attached to the rear half side of the dorsal ridge with suction cups and reinforced with a magnesium corrodible link and 1 mm nylon threads going through the top of the dorsal ridge in order to extend the recording period. As the link corrodes, the tag detaches and can be retrieved. For six of the data series, the tag was placed on the right side of the dorsal ridge (2016MM1, 2016MM3, 2017MM1, 2017MM3, 2018MM2 and 2018MM3), while the remaining had their tag placed on the left side (2014MM6, 2018MM1, 2018MM4, 2018MM5, 2018MM6). The narwhals were also equipped with location tags. These were attached as backbags using methods described in [16]. The backpack tags were mounted on the back of the whale with either two or three 8 mm sterilized nylon pins secured with washers and bolts on each end. The transmitters were programmed to collect an unrestricted number of positions through August and September. Three different types of location tags were used: 1) SPLASH tag from Wildlife Computers, Redmond, WA (2014MM6); 2) Argos CTD tag from SMRU (Sea Mammal Research Unit, St Andrews, UK) (2016MM1) and 3) SPLASH tag with Fastloc GPS option from Wildlife Computers (the rest of the whales). The Wildlife Computer tags have an accuracy of \(\le\) 100 m, whereas Argos tag accuracy ranges between 250 m and 1500 m. For the modelling process in this study, only the Acousonde tag data were used. The narwhals were captured in four different years in August. First four digits of the i.d. indicate year of capture. Out of the ten narwhals, eight were males (2016MM1, 2017MM1, 2017MM3, 2018MM1, 2018MM2, 2018MM4, 2018MM5, 2018MM6) and two were females (2014MM3, 2016MM6). 2017MM3 and 2018MM3 refer to the same narwhal, which was tagged both in 2017 and 2018 (see Table 1).
To avoid any irregular behaviour connected to capture and tagging, data before the first registered echolocation event were discarded [9]. This results in a data series for each narwhal (or two in the case of 2017MM3) ranging between one and six days approximately (Fig. 1). Additionally, 2014MM6 and 2016MM3 had their data cut a few hours short as the tags filled to capacity and stopped recording acoustics. An overview of each narwhal’s trajectory during this period can be seen in Fig. 2.
Depth timeline for each tagged whale. Buzzing times are indicated by black dots. Dashed lines indicate midnight. Red lines indicate the initiation of echolocation. The blue line for 2014MM6 and 2016MM3 indicates where Acousonde were filled to capacity and acoustic data were no longer recorded. The data prior to the red lines and after the blue lines were discarded for the analysis
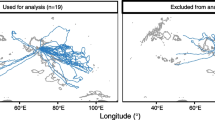
Narwhals were equipped with GPS tags (blue) and Acousonde behavioural tags (orange) (A) inside Scoresby Sound fjord in East Greenland (B). The panels show the GPS tracks (average position/hour) for each narwhal during the included data period, separated by tagging year. 2018MM3 refers to the second tagging period for narwhal 2017MM3. Tagging site, Hjørnedal, is marked with a star. Data points from 2014MM6 and 2016MM1 are less accurate and more sparse (20016MM1 more so than 2014MM6) as these were equipped with different location tags. For 2018 data the observation count has been reduced to one position per hour to reduce overlap
The depth recordings were measured in metres and originally sampled at 10 Hz, but averaged to 1 Hz. Information loss should be minimal as depth does not change significantly on a momentary basis. The depth measurements were corrected for drifting using recursive smoothing filters as described in [17].
Acceleration was measured along three axes X, Y and Z at 100 Hz. Positive samples along the X-axis correspond to the animal pointing up, while positive samples along Y and Z correspond to pointing left and being upside down, respectively. Narwhals are prone to rolling and swimming upside down [16].
Lastly, data also included the date and time of day as well as a binary variable indicating if a startup of a buzz was detected in a given second or not. Buzz initiations were obtained using a custom-written Matlab buzz detection algorithm tuned to miss a minimal number of buzzes, after which the buzzes were manually verified by a specialized analyst. The algorithm and verification process is described in greater detail in [9]. Buzz initiation was used as the response variable in the model.
Diving phase and RMS jerks
A dive was defined as a period during which the narwhal was at 10 m or deeper below surface level, and at some point reaches depths of at least 20 m. Dives are partitioned into four phases. [7, 18]. The surface phase is when the narwhal is not in the process of diving, staying at depths less than 10 m. The bottom phase is when the narwhal is at \(75\%\) or lower than the maximum depth of the dive. For transition periods between surface and bottom, we define the phases descending and ascending. If a narwhal returns to the bottom level before reaching the surface, we define the phase in between to be ascending. We may therefore observe a phasing of \(bottom\rightarrow ascending\rightarrow bottom\), while \(bottom\rightarrow descending\rightarrow bottom\) per definition cannot occur. When estimating narwhal foraging, the diving state is important as buzzes occur most frequently at the bottom of a dive (Fig. 1) [7].
Similar studies on harbour seals, harbour porpoises and sperm whales found clear acceleration peaks—jerks—around the time of prey capture [4,5,6]. A jerk is defined as the difference between consecutive observations of any of the three acceleration measurements [4]. An RMS jerk was then calculated by first taking the euclidean norm of the three-dimensional jerk measurements and then calculating the root-mean-square over 200 ms corresponding to 20 norm jerk observations [4].
In contrast to the aforementioned species, the narwhal has no teeth in its jaws, indicating that raptorial feeding is unlikely. Jerking motions are therefore likely to be less powerful. [15] found that big RMS jerks above different thresholds were not sufficiently correlated with buzzing to allow for buzz detection. However, [4] found that RMS jerks were also indicative of foraging with suction feeding in Harbour seals. We therefore still expect RMS jerks to have some predictive power and include them as features.
Feature extraction
We extracted a series of features from the acceleration data based on [19], where human activities were recognized using accelerometer data from a pocketed cellphone. Average peak frequency was left out as narwhal movements, in comparison, are characterized by smaller fluctuations and are less cyclical compared to human movements. Local peaks, therefore, yielded poor predictive results. Distance between minimum and maximum observation was also excluded as it was highly correlated with the standard deviation. We additionally included the effects of RMS jerks as we expect more rapid short-interval movements in narwhal foraging as opposed to, for instance, a human running. The feature extraction process was largely inspired by [15].
The features are:
-
Corrected depth, time of day in hours and diving phase (surface, descending, bottom and ascending) (3 features).
-
Mean, standard deviation and root-mean-square within a given second for each of the three accelerometer measurements \(A_{X}, A_{Y}\) and \(A_{Z}\) (9 features).
-
Standard deviation and root-mean-square of the magnitude of acceleration defined by \(A_{m}=\sqrt{A_{X}^{2}+A_{Y}^{2}+A_{Z}^{2}}\) (2 features).
-
Correlations between the three acceleration observations in a given second (\(\text {Corr}_{XY}\), \(\text {Corr}_{XZ}\) and \(\text {Corr}_{JK}\)) (3 features).
-
Mean and standard deviation of RMS jerk measurements (2 features).
Since data only included the time of buzz onsets and buzzes often last for several seconds [9], any potential acceleration patterns were likely to be present after the onset of a buzz. Therefore, we included 4 future values of all features (except the first three, i.e. depth, time of day and dive phase) to ’backcast’ if a buzz was initiated the moment before. Four future values were selected based on results on narwhal buzz duration where [9] found the upper quartile of narwhal buzz duration to be approximately 4 s or less (one out of six narwhals has upper quartile duration of 4.1 s. Rest is below 4 s). The mean acceleration in X, Y and Z were found to be highly correlated with their future observations. To avoid potential issues with collinearity, we instead include the change in mean for the future values.
In order to account for variation in the behaviour of individual narwhals, we used mixed-effect models allowing narwhal i.d. to be included as a random effect on the intercept. For the narwhal with two tagging periods we use i.d. 2017MM3 for both data series. In total, we have the listed 19 features of which 16 have 4 future observations included as well. This results in a model with one random effect and 83 fixed-effects features.
Mixed-effects logistic regression implementation
To test the model predictions, we divided the data following two approaches. The first approach splits the data chronologically for each narwhal into \(80\%\) training and \(20\%\) test data. Training data were used for fitting the model and finding appropriate probability prediction cutoff, while test data were used for evaluating the performance of the model. When fitting and evaluating on the same set of narwhals, we risk overestimating performance as every whale has been previously observed by the model. In practice, we are unlikely to tag the same narwhal more than once. To minimize overconfidence, we renamed the narwhals used in the test set such that the model treats the data as being from not previously observed narwhals. The second approach involves leaving one narwhal out for test set and fitting to the remainder. The split is repeated with each whale used as test set, meaning the entirety of our data set serves as both test and training set. This method ensures that we do not overestimate performance by training and testing on the same individual. However, evaluation across 10 models is less transparent and parameter values and importance is likely to vary between the different models, compared to fitting and evaluating a single model fit across all individuals.
The mixed-effects logistic regression model was implemented using the glmer function from the lme4 R-package (version 1.1.29) [20] with option family = binomial. The response was the 0-1 variable of absence or presence of a buzz initiation, and explanatory variables were the features listed in the previous section. Following [7, 9], we modelled depth with a natural cubic spline with three degrees of freedom using the ns function from the splines package (version 4.1.2) [21]. Degrees of freedom were kept constant to avoid overfitting. Time of day was included with a periodic B-spline with 3 degrees of freedom and boundary knots in 0-24, such that the spline is connected at the change of day. This was implemented using the pbs function from the pbs-package (version 1.1) [22].
All features were included as additive effects. Predictions of the model are given as estimated probabilities \({\hat{p}}(x_t)\) of a buzz at each time point with features \(x_t\). We then predict a buzz at time t if the predicted probability is larger than some cutoff value \(p_0\).
Dealing with imbalanced data
Since data are imbalanced (the response \(Y_t=1\), initiation of a buzz at time t, is much less frequent than \(Y_t=0\), only \(1.08\%\) of observations are positive buzz observations) and we are more interested in correctly predicting a buzz \(Y_t=1\) than a non-buzz \(Y_t=0\), we use a different cutoff value than the usual \(p_0 = 0.5\). To select \(p_0\), we used fivefold cross-validation on a grid of cutoff values between 0.05 and 0.5 with increments of 0.01. As error measure, we used the Dice loss [23] function defined by
Here, \(y_{i}\) and \(\hat{y}_{i}\), \(i = 1, \ldots , n\), denote the ith observed and predicted response values within a given fold, respectively. Dice loss was chosen as it is designed for classification problems with imbalanced data. To prevent too many positive predictions, the loss increases when the total sum of positive predictions increases, and only the correct predictions lead to a zero loss.
Cross-validation folds were split chronologically for each whale in the same vein as the training and test set partitioning. These splits respect the time structure of the data, but might yield poor results for narwhals with shorter tagging periods as a potential break from foraging can result in a fold with little to no buzzing. Therefore, we also tried cross-validation with folds partitioned randomly for comparison. We evaluated both cases using Dice loss. For the chronological split, we also defined an adjusted version of Dice loss in the equation below:
Logistic regression and ordinary dice loss have the disadvantage of not accounting for the temporal structures in the data. A positive prediction increases the loss, unless it lines up with the exact second of the observed onset. This is regardless of the prediction potentially being only a few seconds off. The adjusted dice loss is designed to partially correct for this by also reducing loss if a positive prediction falls within 1 s of a positive observation. Adjusted dice loss with 2-s and 3-s lags were also considered, but yielded same conclusion. The adjusted Dice loss was not attempted on the randomly assigned folds as neighbouring data points might belong to different folds.
When fitting on imbalanced data, one should be aware of the one-in-ten rule of thumb [24], which states that there should be at least 10 minority class observations for each included feature. In each training fold, we had at least 14227 recorded buzzes indicating that our model meets the one-in-ten rule, even with a few non-linear features that use several degrees of freedom.
Likelihood approximation
In generalized linear mixed modelling, the marginal density of the response Y is too complex to be evaluated in closed form. The log-likelihood is instead estimated and maximized using numerical methods. In glmer this is done using a Gauss–Hermite approximation with parameter nAGQ denoting the number of points per axis in which the approximation is evaluated. The standard setting is \(\texttt {nAGQ}=1\) corresponding to a Laplace approximation. However, for the given number of features and data points, this setting proved too computationally demanding. Instead, \(\texttt {nAGQ}=0\) was used, where fixed effects are estimated in the Penalized Iteratively Reweighted Least Squares step (PIRLS) when estimating the random effects conditioned on the response [20]. This means that the fixed-effect coefficients are fitted much quicker, but the deviance at the fit may be higher than if we had included the fixed effects in the non-linear optimization of the Laplace approximation. This method was chosen as it yielded better results than excluding random effects altogether or decreasing the number of fixed-effect features down to where the running times were manageable. For this data set it took \(\approx 12\) min on a Lenovo ThinkPad T490, whereas it had still not converged after 3 days when using the option \(\texttt {nAGQ}=1\). We also attempted using other software packages such as glmmTMB (version 1.1.5) [25], but with the same results regarding running times.
Quasi-poisson model
For comparison purposes we also tried to fit the number of buzzes per dive to a quasi-poisson model, using features related to the depth, duration shape of the dive. This should help assess if the inclusion of acceleration data is significant when aggregating buzz activity per dive instead of on a momentary basis. The quasi-poisson model uses number of buzzes per dive as response and maximum corrected depth, seconds spent at the bottom phase and proportion of dive spent at bottom phase as features.
Results
Prediction cutoff
In Fig. 3, the results of the cross-validation are shown for the different cutoff values \(p_0\). The Dice loss was overall marginally lower on the randomly assigned folds than on the chronological splits, but they both yield an optimum of 0.09. Using the adjusted Dice loss gives a slight edge to a cutoff value of 0.10, but the difference is minimal. Adjusted Dice loss with two and three seconds delay was also attempted, leading to the same optimum (results not shown). Based on these results a cutoff value of \(p_0=0.10\) was chosen. The low threshold is likely a result of the model being unable to detect the exact second of some buzzes, resulting in the probability being spread across several seconds. Therefore, we end up with a few seconds of medium-high probability instead of one second with probability above 0.5.
Average Dice loss from fivefold cross-validation for different prediction cutoff values. Optimal value is between \(0.09-0.10\) (large dots). Black line: Dice loss on chronologically split folds, eq. (1). Blue line: Dice loss on randomly split folds, eq. (1). Red line: adjusted Dice loss on chronologically split folds, eq. (2)
Buzz detection
Movement patterns correlated with foraging are expected to be prevalent up to or after an observed buzz. Therefore, estimated buzz probabilities are likely to be above the threshold in a time window around the true buzzes. Thus, classifying buzzes using cutoff values will result in one true buzz yielding several buzz predictions at the seconds in the window. As a result, the buzzing frequency is likely to be overestimated. Furthermore, a buzz tends to inhibit initiation of a new buzz in the first couple of seconds, but thereafter excite new buzzes [26]. To correct for this, we counted consecutive positive predictions as one buzz and placed the startup in the observation at the highest probability (Fig. 4). A marginal number of consecutive buzzes are present in the data, but not enough to have any significant effects on the results. Additionally, buzzes interlinked by breaks shorter than a second are likely to be tied to the same prey capture attempt.
We assessed the precision and recall of the model predictions. Precision is defined as the number of true positives over the number of positive predictions (i.e. the proportion of estimated buzzes that are true buzzes), while recall is the number of true positives over the number of positive observations (i.e. the proportion of buzzes that are correctly identified):
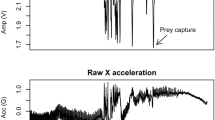
One-minute representative extract of buzz probability predictions from 2016MM1 bottom dive data (lower panel), visualizing how highest point probability above threshold results in buzz prediction (blue dots) and how these align with observed buzzes (red dots). Three-dimensional acceleration and RMS jerks are also shown to indicate how these interact with the buzz activity
To allow for slightly time-shifted predictions, we defined extended versions of precision and recall as functions of the distance k in seconds to the nearest observed or predicted buzz:
Together, these indicated how much of the buzzing activity is recognized by the model as well as how reliable the model predictions are. The results based on the test set predictions for \(k = 0,1,\ldots ,30\) are plotted in Fig. 5.
Precision/proportion of predicted test set buzzes that are within 0-30 s of an observed buzz (left) and recall/proportion of observed buzzes which are within 0-30 s of a predicted buzz (right). Results are shown both for model trained on 80% of data across all narwhals and models trained by leaving one whale out
For the leave-one-out approach, the precision was 0.309 and the recall was 0.213 (\(k=0\)). Of the predicted buzzes, 68% were at most 2 s from an observed buzz. Furthermore, \(46\%\) of the observed buzzes fell in a 2-s window of a positive prediction. For 30-s intervals, the numbers increase to 94% of predicted buzzes and 82% observed buzzes. This implies that the vast majority of predicted buzzes correspond to true buzzes, however, some buzzes are missed. In the "Detection analysis" section, we investigate whether the undetected \(54\%\) (2-s window) and \(18\%\) (30-s window) of observed buzzes differ from the detected buzzes in a systematic way. A limit of 30-s was chosen to asses if a buzz was detected within the same foraging event, while 2-s intervals indicate if the individual buzz was detected.
The results for the chronological split of data gave similar results for recall with slightly better precision. For \(k=0\), the precision was 0.323 and the recall was 0.208. For 2-s intervals this increases to precision 0.729 and recall 0.457, while for 30-s intervals the precision was 0.967 and the recall was 0.826. This can also be derived from Fig. 5 where the precision is a few percent above the leave-one-out curve after the initial seconds, while the recall is essentially the same. Predicting on the training data yielded a slightly higher precision of 0.339 and recall of 0.251. This is fairly unsurprising as testing on the training data tends to overestimate performance. \(71\%\) and \(94\%\) of predictions fell in a 2- and 30-s window of a prediction, respectively. \(51\%\) and \(86\%\) of observed buzzes were within 2 and 30 s of a prediction.
Detection analysis
In Table 3, we list the distribution of time elapsed between buzzes in the detected and undetected groups. Results are shown for the leave-one-out analysis only as both approaches gave similar results. For the 30-s intervals the average and third quartile both have twice as much time between undetected buzzes, than that of the detected, thus indicating that undetected buzzes showed tendency towards being more “solitary” buzzes. However, the model was able to detect some truly solitary buzzes (the max among the detected buzzes was 4851 s, which is more than an hour and thus is a single observed buzz in a dive). Due to the high maximum values caused by dives with only one buzz occurrence, the distribution is skewed, and the median is therefore more informative of the typical time distance than the mean. For 2-s intervals, the distribution is more similar between undetected and detected buzzes.
Results across the 10 models trained by leaving one whale out were best for 2016MM1 and 2018MM5 and worst for 2018MM1 and 2018MM2 (Table 2). Performance varies a lot depending on the narwhal with \(\approx 80\%\) of buzzes for 2016MM1 being detected within 2-s intervals, whereas 2018MM1 barely reaches \(50\%\) detection rate in 30-s intervals.
For the model fitted on all whales, performance was best for 2016MM1, 2017MM3 and 2018MM4, and worst for 2016MM3 and 2018MM1 (Table 4). In the extreme cases, the model was \(\frac{15.22}{0.30}\approx 51\) times more likely to detect a buzz in a 2-s interval for 2016MM1 than for 2018MM1. Compared to the leave-one-out approach, results seem noticeably better for 2014MM6, 2017MM3 and 2018MM4 and noticeably worse for 2016MM3, 2018MM1, 2018MM5 and 2018MM6. Potential causes for this are considered in the "Discussion" section.
Buzz frequency per dive
To assess the ecological role of the narwhal, it is of interest to estimate the quantity of dives that are dedicated to foraging. Inspired by [15], we compared the observed number of buzzes per dive with the predicted amount in Fig. 6. We likewise assessed how well the model could distinguish between non-foraging versus foraging dives, i.e. dives with or without buzzes. Overall, we predicted 17,557 buzzes versus 25,432 observed across the 10 leave-one-out splits, meaning the buzz quantity was underestimated. When classifying dives, our model had a precision of 0.860 and a recall of 0.909. Further details on the dive classification results are shown in Table 5. Among the misclassified forage dives 72 of the 85 dives belonged to 2016MM6 of which most were shallow dives of depths under 50 m and with a marginal number of buzzes. This behaviour pattern was mostly unique to 2016MM6 and not prevalent among the other narwhals. For the 80-20 split the results were similar regarding underestimation yielding 3, 869 predicted buzzes versus 6, 001 observed. Results for classifying dives were noticeably better with a precision of 0.947 and recall of 0.939. The quasi-poisson model predictions were greatly underestimated with a maximum of 4 predicted buzzes in any given dive. Results did not improve when excluding non-forage dives from the training and test data.
Predicted versus observed number of buzzes per dive on test set for leave-one-out split (left) and chronological split (right). The line is the identity and thus, the closer the points fall to this line, the better the predictions. Point size indicates number of observations. There are more buzzes and dives in the left plots because the leave-one-out split has larger test set and smaller training set than the chronological split. Top row shows results for the main model, while bottom row shows results for the quasi-poisson model
Discussion
The models performed poorly when trying to detect the exact timing of a buzz initiation. However, a significant proportion of the predictions were only off by a few seconds (Fig. 5). We found that \(\approx { 68\%}\) of the buzz predictions were within 2 s of an observed buzz and \(\approx { 94\%}\) within 30 s. When the model predicts a buzz it is therefore highly likely that buzzing is taking place within 30 s of the given time. Obviously, buzz detection within larger intervals will always improve the accuracy, but there is a noticeable jump in accuracy, especially in the first seconds of both precision and recall (Fig. 5). The observed buzzes are largely in close proximity to predicted buzzes, but a bit less so, with \(\approx { 46\%}\) and \(\approx { 82\%}\) falling within 2 and 30 s windows of a prediction, respectively. The curve for recall does not seem to have converged within the 30-s interval. However, we deem buzzes more than 30 s from a prediction to be too inaccurate to be considered detected.
The purpose of this study was not to predict the exact timing of narwhal buzzes, but rather if a prey capture attempt has a corresponding positive model prediction. This is indeed the case: most buzz predictions fall in a short interval of a true observation, although \(\approx 18\%\) of buzzes remained undetected, even when considering 30-s intervals. It is apparent that the detected buzzes were more clustered and therefore more likely to overlap with a prediction (Table 3). Most buzzes were, however, spaced out with 5+ seconds in between and the results were still fairly good when allowing predictions to be off by only 4 s (Fig. 5). The majority of observations should, therefore, have a corresponding prediction and vice versa. The estimated number of buzzes per dive seems to follow similar trends to the true buzzes, although with noticeable levels of underestimation (Fig. 6).
Another reason for the undetected buzzes could be differences in behavioural patterns compared with the detected buzzes (such as less strong jerk motions or shallow depths). The undetected buzzes were associated with slightly lower acceleration activity on average, but no other features were found to have obvious distributional changes (results not shown). Alternatively, the prediction performance varied significantly between individuals. Overall performance was good for 2016MM1, 2016MM3, 2017MM1, 2018MM5 and 2018MM6, decent for 2014MM6, 2017MM3 and 2018MMM4 and poorest for 2018MM1 and 2018MM2. The narwhals, on which the model performed worst, have in general fewer and more spread-out buzzes, which might explain why they were harder to detect. Variations in tag placement could be a reason behind the large gaps in performance, but comparing the narwhal’s tag placement side with their detection rate does not indicate any strong correlations as both left- and right-side tagged whales are in the best and worst performing groups.
Comparing the leave-one-out approach to the chronological split showed varying results (Table 2 and Table 3). Somewhat surprisingly, some narwhals performed better when not previously observed. Comparing the chronological and individual-based test sets showed that, for most narwhals, a higher detection rate seems to correspond to a lower median buzz distance, which seems like a probable explanation for the better performance. For 2014MM6 and 2017MM3, we saw a significant increase in quality despite having a high number of buzzes and similar median buzz distance in both test data splits. In contrast, 2016MM1 saw only marginal improvement while also having a large number of observed buzzes in each test set. Overall, the results are worse on the individual-based split. However, the effects vary a lot depending on the individual narwhal. Overall, fitting and evaluating on the same narwhals seem to have less of an impact than the variations in test and training set.
The estimations of buzz frequency per dive are centred around the ground truth with a tendency towards underestimation, especially among dives with a higher number of buzzes (Fig. 6). It should be noted that dive duration has not been corrected for in this figure and longer dives contain more buzzes all things equal. For the dives with more than approximately 50 buzzes we underestimate the number of buzzes in all dives, indicating that we perform worst on the dives with highest buzzing rate. The majority of dives with zero buzzes were, however, correctly identified (Table 5). Results for the main model were vastly better than for the quasi-poisson model on both data splits (Fig. 6). This is despite that fact that the quasi-poisson model is fitted to aggregated results per dive, whereas the main model only considers buzzes on a moment-to-moment basis. This seem to indicate that acceleration and jerk motions diving patterns alone are not sufficient for estimating buzzing activity and that the inclusion of acceleration and jerk data greatly enhances the predictions.
Comparing the results to those of [15], our model performs significantly better than the logistic regression and random forest model. Comparing the results of the U-net implementation, our implementation seems at the very least competitive if not better. The predictions of the U-net model tend towards overestimating the number of buzzes per dive whereas our model underestimates. The precision of the U-net is initially higher at around \(\approx 0.62\) vs our 0.31. However, within the 5-s interval our precision increases to around 0.80, where the U-net is fairly stagnant at around 0.7. The random forest and logistic regression methods of [15] seem both significantly less precise in a 5-s interval and also less accurate when estimating buzz frequency per dive.
When classifying foraging and non-foraging dives, the model performed well. Dive depth had a strong determining effect as the correctly classified non-foraging dives are significantly more shallow than the rest (Table 5 ). This is backed by [7], where dives below 300 ms were found to predominantly be related to foraging. Thus, a rough classification of foraging dives is probably possible solely based on the dive depth and shape. However, shallow dives (less than 40 m deep) are present in all classification groups (Table 5). Results were significantly better on the 80-20 data split than the leave-one-out approach. A determining factor was 2016MM4 as this whale showed a larger tendency towards very shallow forage dives, most of which were included in the training set of the 80-20 approach. It is unknown if this is unusual or part of variable behaviour. It is, therefore, hard to determine which data split has the most realistic precision and recall. The shallow dives occurred at areas also visited by other narwhals. Hunting ground does, therefore, not seem to be the determining factor.
Data limitations
The narwhals included in this paper were all tagged around the fjords of Scoresby Sound for a week or less in August. Data might not be representative of overall narwhal behaviour and should therefore preferably be compared to similar data. The narwhals inhabit Scoresby Sound fjord for most of the summer, but spent winters off-shore [8] where they dive deeper and eat more [27]. The difference in depth and hunting ground indicate that the narwhal hunt other prey during winter, which could yield different jerk signals than seen in the summer data. However, the model can be refitted on winter data if available.
When used for foraging detection, accelerometer estimations are less precise and transparent than buzz recordings, since specific motion patterns are unlikely to be as indicative as a specific and recognizable buzz sound. Additionally, if the environment of the narwhal changes drastically, it might also affect the model’s performance. External factors expected to affect foraging might also affect movement patterns. If, for example, the narwhal becomes more stressed it might show more sporadic movement patterns which could be mistaken for foraging patterns. However, judging by data initially following release it seems that escape dives, in general, are not sufficiently deep to be mistaken for foraging dives. This was also observed under a controlled noise exposure study [11, 12]. This indicates that narwhal behaviour, at least during some stressful situations, is clearly distinct from foraging behaviour.
Conclusion
We provide an alternative or supplement to acoustic recordings when detecting narwhal foraging attempts in the form of statistical estimation using accelerometer data. Model predictions were not accurate enough to estimate the exact timing of a buzz, but were in general only off by a few seconds. 46% of observed buzzes were in 2-s windows of a prediction, increasing to 82% in 30-s windows, although performance varied depending on the narwhal. Additionally, we found the model estimates of buzz frequency per dive and dive classification to be accurate, although underestimating the number of buzzes, especially in dives with high buzz activity.
Comparing the results to [15], the methods are competitive to the U-Net convolutional network, despite the simpler model choices and data sampling. Comparing the results to the logistic regression model, we see significant improvements in our implementation. Additionally, we conclude that considering only the startup of narwhal buzzes seems to yield adequate results for modelling narwhal foraging, as long as effects of future acceleration features are accounted for. Lastly, we reason that the methods discussed in this paper can be repeated for detecting foraging activity of other marine mammals. Our results offer new avenues for animal-borne tag development demonstrating a new and valuable usage for depth and acceleration data. By integrating on-board processing of these data into long-duration tagging applications, information on foraging activity could be relaid via satellite links from the entire deployment period. The narwhal and the closely related beluga (Delphinapterus leucas), are the only toothed whale species inhabiting the Arctic year-round. Due to its habitat, there are still major knowledge gaps regarding their behaviour and habitat use during winter. In addition, the Arctic is changing rapidly with increasing sea temperature, decreasing ice-coverage and increasing anthropogenic disturbance. A tag that could estimate the amount of buzzes in a given dive or even just detect buzzes and recognize a dive as a foraging dive, would yield critical knowledge on narwhal behaviour during migration and at the wintering grounds. Additionally, it may allow identification of critical foraging habitats during winter when most of the foraging is thought to occur. This has not only high biological significance, but would also improve the management of the species. Finally, this type of data would allow us to assess narwhal resilience in the changing Arctic and their responses to anthropogenic disturbance outside their fjord habitats during summer. Data collected in the future would allow to determine any spatiotemporal shifts in foraging.
Data availability
Code and data are available from https://erda.ku.dk/archives/97bbc5b5b837b8afaf6dfaacb112b112/published-archive.html.
Change history
18 April 2023
A Correction to this paper has been published: https://doi.org/10.1186/s40317-023-00330-5
References
Garde E, Tervo OM, Sinding M-HS, Nielsen NH, Cornett C, Heide-Jørgensen MP. Biological parameters in a declining population of narwhals (monodon monoceros) in scoresby sound, Southeast greenland. Arctic Sci. 2022;8(2):329–48. https://doi.org/10.1139/as-2021-0009.
NAMMCO Group. Report of the NAMMCO global review of monodontids. Hillerod: North Atlantic Marine Mammal Commission; 2018.
Lowry L, Laidre K, Reeves R. Monodon monoceros. IUCN Red List Threat Species. 2017;2017: e. T13704A50367651.
Ydesen KS, Wisniewska DM, Hansen JD, Beedholm K, Johnson M, Madsen PT. What a jerk: prey engulfment revealed by high-rate, super-cranial accelerometry on a harbour seal (Phoca vitulina). J Exp Biol. 2014;217(13):2239–43. https://doi.org/10.1242/jeb.100016.
Wisniewska D, Johnson M, Teilmann J, Rojano-Doñate L, Shearer J, Sveegaard S, Miller L, Siebert U, Madsen P. Ultra-high foraging rates of harbor porpoises make them vulnerable to anthropogenic disturbance. Curr Biol. 2016;26(11):1441–6. https://doi.org/10.1016/j.cub.2016.03.069.
Fais A, Johnson M, Wilson M, Aguilar Soto N, Madsen PT. Sperm whale predator-prey interactions involve chasing and buzzing, but no acoustic stunning. Sci Rep. 2016;6(1):28562. https://doi.org/10.1038/srep28562.
Tervo OM, Ditlevsen S, Ngô MC, Nielsen NH, Blackwell SB, Williams TM, Heide-Jørgensen MP. Hunting by the stroke: how foraging drives diving behavior and locomotion of East-Greenland Narwhals (Monodon monoceros). Front Marine Sci. 2021. https://doi.org/10.3389/fmars.2020.596469.
Heide-Jørgensen M, Nielsen N, Hansen R, Schmidt H, Blackwell S, Jørgensen O. The predictable narwhal: satellite tracking shows behavioural similarities between isolated subpopulations. J Zool. 2015;297:54–65.
Blackwell SB, Tervo OM, Conrad AS, Sinding MHS, Hansen RG, Ditlevsen S, Heide-Jørgensen MP. Spatial and temporal patterns of sound production in East Greenland narwhals. PLoS ONE. 2018;13(6):0198295. https://doi.org/10.1371/journal.pone.0198295.
Westbury MV, Petersen B, Garde E, Heide-Jørgensen MP, Lorenzen ED. Narwhal genome reveals long-term low genetic diversity despite current large abundance size. iScience. 2019;15:592–9. https://doi.org/10.1016/j.isci.2019.03.023.
Heide-Jørgensen MP, Blackwell SB, Tervo OM, Samson AL, Garde E, Hansen RG, Ngo MC, Conrad AS, Trinhammer P, Schmidt HC, Sinding M-HS, Williams TM, Ditlevsen S. Behavioral response study on seismic airgun and vessel exposures in narwhals. Front Marine Sci. 2021. https://doi.org/10.3389/fmars.2021.658173.
Tervo OM, Blackwell SB, Ditlevsen S, Conrad AS, Samson AL, Garde E, Hansen RG, Mads Peter H-J. Narwhals react to ship noise and airgun pulses embedded in background noise. Biol Lett. 2021;17(11):20210220. https://doi.org/10.1098/rsbl.2021.0220.
Leos-Barajas V, Photopoulou T, Langrock R, Patterson TA, Watanabe YY, Murgatroyd M, Papastamatiou YP. Analysis of animal accelerometer data using hidden markov models. Methods Ecol Evol. 2017;8(2):161–73. https://doi.org/10.1111/2041-210X.12657.
Williams TM, Blackwell SB, Richter B, Sinding M-HS, Heide-Jorgensen MP. Paradoxical escape responses by narwhals (Monodon monoceros). Science. 2017;358(6368):1329. https://doi.org/10.1126/science.aao2740.
Ngô MC, Selvan R, Tervo O, Heide-Jørgensen MP, Ditlevsen S. Detection of foraging behavior from accelerometer data using U-Net type convolutional networks. Ecol Inform. 2021;62: 101275. https://doi.org/10.1016/j.ecoinf.2021.101275.
Dietz R, Shapiro AD, Bakhtiari M, Orr J, Tyack PL, Richard P, Eskesen IG, Marshall G. Upside-down swimming behaviour of free-ranging narwhals. BMC Ecol. 2007;7(1):14. https://doi.org/10.1186/1472-6785-7-14.
Luque SP, Fried R. Recursive filtering for zero offset correction of diving depth time series with GNU R package diveMove. PLoS ONE. 2011;6(1):15850. https://doi.org/10.1371/journal.pone.0015850.
Hooker SK, Baird RW. Diving and ranging behaviour of odontocetes: a methodological review and critique. Mamm Rev. 2001;31(1):81–105. https://doi.org/10.1046/j.1365-2907.2001.00080.x.
Bayat A, Pomplun M, Tran DA. A Study on Human Activity Recognition Using Accelerometer Data from Smartphones. In: The 9th International Conference on Future Networks and Communications (FNC’14)/The 11th International Conference on Mobile Systems and Pervasive Computing (MobiSPC’14)/Affiliated Workshops 2014;34:450–457. https://doi.org/10.1016/j.procs.2014.07.009
Bates D, Mächler M, Bolker B, Walker S. Fitting linear mixed-effects models using lme4. J Statist Softw. 2015;67(1):1–48. https://doi.org/10.18637/jss.v067.i01.
R Core Team. R: a language and environment for statistical computing. R foundation for statistical computing. Vienna: R Foundation for Statistical Computing; 2021.
Wang S. Pbs: Periodic B Splines. 2013. R package version 1.1. https://CRAN.R-project.org/package=pbs
Milletari F, Navab N, Ahmadi S-A. V-Net: Fully Convolutional Neural Networks for Volumetric Medical Image Segmentation. arXiv 2016. arxiv:1606.04797
Peduzzi P, Concato J, Kemper E, Holford TR, Feinstein AR. A simulation study of the number of events per variable in logistic regression analysis. J Clin Epidemiol. 1996;49(12):1373–9. https://doi.org/10.1016/s0895-4356(96)00236-3.
Brooks ME, Kristensen K, van Benthem KJ, Magnusson A, Berg CW, Nielsen A, Skaug HJ, Maechler M, Bolker BM. glmmTMB balances speed and flexibility among packages for zero-inflated generalized linear mixed modeling. R J. 2017;9(2):378–400. https://doi.org/10.32614/RJ-2017-066.
Søltoft-Jensen A, Heide-Jørgensen MP, Ditlevsen S. Modelling the sound production of narwhals using a point process framework with memory effects. Ann Appl Stat. 2020;14(4):2037–52. https://doi.org/10.1214/20-AOAS1379.
Laidre KL, Heide-Jørgensen MP. Winter feeding intensity of Narwhals (Monodon monoceros). Marine Mamm Sci. 2005;21(1):45–57. https://doi.org/10.1111/j.1748-7692.2005.tb01207.x.
Acknowledgements
The team in Hjørnedal is thanked for their invaluable assistance in data collection. A special thanks to S. Blackwell and A. Conrad for the analysis of buzzing data. This study is part of the Northeast Greenland Environmental Study Program which is a collaboration between DCE-Danish Centre for Environment and Energy at Aarhus University, the Greenland Institute of Natural Resources, and the Environmental Agency for Mineral Resource Activities of the Government of Greenland. Permission for capturing, handling, and tagging of narwhals was provided by the Government of Greenland (Case ID 2010±035453, document number 429 926). The project was reviewed and approved by the IACUC of the University of Copenhagen (17 June 2015). Access and permits to use land facilities in Scoresby Sound were provided by the Government of Greenland. No protected species were sampled.
Funding
The research was financially supported by the Novo Nordisk foundation NNF20OC0062958 and Independent Research Fund Denmark | Natural Sciences 9040-00215B. Instruments were paid by the Carlsberg Foundation CF14-0169 and Danish Cooperation for the Environment in the Arctic (DANCEA) 2013_01_0289. Additionally, this study is part of the Northeast Greenland Environmental Study Program which is a collaboration between DCE—Danish Centre for Environment and Energy at Aarhus University, the Greenland Institute of Natural Resources, and the Environmental Agency for Mineral Resource Activities of the Government of Greenland. Field work was paid through this program.
Author information
Authors and Affiliations
Contributions
SD and OMT conceived the study; FHJ and SD designed the methodology; OMT and MPHJ collected the data; FHJ and OMT analysed the data; FHJ led the writing of the manuscript; SD and MPHJ provided funding. All authors contributed critically to the drafts and gave final approval for publication. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
The narwhal study was reviewed and approved by the Institutional Animal Care and Use Committee of the University of Copenhagen (17 June 2015). Permission for capturing, handling, and tagging of narwhals was provided by the Government of Greenland (Case ID 2010 ± 035453, document number 429 926).
Consent for publication
Not applicable
Competing interests
The authors declare no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original online version of this article was revised: The error in the co-author name had been corrected.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. The Creative Commons Public Domain Dedication waiver (http://creativecommons.org/publicdomain/zero/1.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the data.
About this article
Cite this article
Jensen, F.H., Tervo, O.M., Heide-Jørgensen, M.P. et al. Detecting narwhal foraging behaviour from accelerometer and depth data using mixed-effects logistic regression. Anim Biotelemetry 11, 14 (2023). https://doi.org/10.1186/s40317-023-00325-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40317-023-00325-2