Abstract
Additive manufacturing (AM), widely known as 3D printing, is a direct digital manufacturing process, where a component can be produced layer by layer from 3D digital data with no or minimal use of machining, molding, or casting. AM has developed rapidly in the last 10 years and has demonstrated significant potential in cost reduction of performance-critical components. This can be realized through improved design freedom, reduced material waste, and reduced post processing steps. Modeling AM processes not only provides important insight in competing physical phenomena that lead to final material properties and product quality but also provides the means to exploit the design space towards functional products and materials. The length- and timescales required to model AM processes and to predict the final workpiece characteristics are very challenging. Models must span length scales resolving powder particle diameters, the build chamber dimensions, and several hundreds or thousands of meters of heat source trajectories. Depending on the scan speed, the heat source interaction time with feedstock can be as short as a few microseconds, whereas the build time can span several hours or days depending on the size of the workpiece and the AM process used. Models also have to deal with multiple physical aspects such as heat transfer and phase changes as well as the evolution of the material properties and residual stresses throughout the build time. The modeling task is therefore a multi-scale, multi-physics endeavor calling for a complex interaction of multiple algorithms. This paper discusses models required to span the scope of AM processes with a particular focus towards predicting as-built material characteristics and residual stresses of the final build. Verification and validation examples are presented, the over-spanning goal is to provide an overview of currently available modeling tools and how they can contribute to maturing additive manufacturing.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Review
Introduction
Metal additive manufacturing (AM) utilizes several processes such as powder bed processes (ALM/SLM/DMLS/DMLM), blown powder (DLMD/LMD/EMD/LENS) and wire feed processes (WAAM). Whereas the processes vary widely in their details, the common denominator for all ad4ditive-manufacturing processes is the ability to nearly “net-shape” manufacture complex products:
-
1.
Powder bed process: Thin layers (micrometers) of metal particles are spread on a processing table. A laser or an electron beam melts the metallic powder in certain areas of the powder bed. These areas then solidify to become a section of the final build. An additional powder layer is then added, and the process is repeated. At the end of the build process, the un-melted powder is removed to reveal the workpiece created. Housholder’s patent, dated 1981, is very similar to today’s powder bed machines [1].
-
2.
Blown powder process is based on providing the powder feedstock through a nozzle focused to the area being built. The nozzle used is often coaxial, where the heat source (laser or electron beam) is focused through the center of the nozzle to the substrate. The powder is carried by a shield gas through an outer concentric ring and is directed to the general area, where the heat source is applied. The nozzle is mounted on a multi-axis robot that moves as the workpiece is being created [2].
-
3.
Wire feed systems are based on systems that are very similar to traditional welding, where a heat source is used to melt a wire adding material in regions to be built. The heat source might be an arc discharge, laser, or an electron beam. The wire-feeding system is mounted on a multi-axis robot that moves as the workpiece is being created. First reports on this technology date as far back as 1926 [3].
The design freedom offered by the AM processes is not yet fully utilized because current design standards and procedures are aimed at harnessing the strengths and limitations of traditional manufacturing routes. A new design paradigm taking advantage of AM’s unique possibility to design functional products is enabled via physics-based modeling and optimization. Topology optimization is based on assessing functional requirements, such as operation loads, and constraints to obtain a design that fulfils product specifications. In due course of the optimization calculations, certain assumptions are made about the material properties such as material strength, porosity, or residual stresses accumulated during the build process [4].
A very large amount of experimental research suggests that material properties are dependent on feedstock characteristics and process parameters [5–8]. Choren et al. attempted to gather correlations describing Young’s modulus and porosities for additive-manufacturing processes as a foundation for designers and process engineers. Their conclusion was that predictive equations do not exist yet [9]. Given the large number of process parameters [10] and their complex interactions, extensive trial and error research is needed to ensure the faultless production of CAD models via AM.
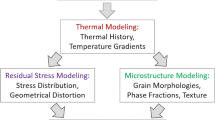
Physics-based modeling has the potential to shed light into how competing process parameters interact providing the basis for process optimization. Models can predict the as-built properties and eventually support rapid qualification of topologically optimized functional components. Length- and timescale considerations make it necessary to split models into micro-, meso-, and macroscale models [11–13]—Fig. 1.
-
1.
Micromodels address the heat source feedstock interaction, the heat absorption, and the phase changes in a domain comparable in size to the melt pool and the heat-affected zone. The micromodels provide information about the melt pool size, the thermal cycle, and about the material consolidation quality and enable the identification of the most suitable process window.
-
2.
Macromodels utilize the determined melt pool dimensions and the thermal cycle to calculate the as-built residual stresses in models comparable in size to the workpiece being manufactured. The feedstock details and thermodynamic phase change are not resolved. The evolution of the metallurgical phases and the corresponding evolution of material properties are accounted for as the thermal history of the workpiece is calculated (see mesoscale below). Clamping conditions as well as deposition strategies are prescribed as boundary conditions to predict residual stresses and the final workpiece shape.
-
3.
Mesoscale models are dedicated to the calculation and provision of composition- and temperature-dependent metallurgical properties describing the thermo-mechanical behavior of the material. This information is provided to micro- and macromodels as required during their respective calculations. Models resolving the evolution of grains and microstructures belong to the micromodeling category but can be coupled to both micro- and macromodels.
The following sections discuss algorithmic details and options for each of the model scales introduced briefly above. The final goal is to establish predictive tools as components of an integrated computational materials engineering platform (ICME) ensuring successful delivery of additive-manufacturing assessment tools. Computational module verification and validation examples are provided. The arrangement of sections is by length scale rather than by additive-manufacturing process. The justification lies in the assumption that the physics governing the behavior of any of the processes considered is identical. The relative weight of phenomena considered may vary from one process to the other, but the fundamental equations should capture these weights either via corresponding boundary conditions or user intervention. The paper is then concluded by assessing the current state of ICME for AM and an outlook on future challenges yet to be addressed.
Micromodeling
Micromodels resolve the melt pool physics including heat source interaction with the feedstock and substrate, heat transfer, phase change, and surface tension forces as well as the effect of thermal gradients leading to Marangoni forces.
The models are based on computational fluid dynamics algorithms to solve the Navier-Stokes equations [14–17]. The momentum equations are extended using source terms to account for gravitational body forces, recoil pressure, and surface tension. The energy equation accounting for conduction (diffusion term) and convection is complemented with source terms accounting for the latent heat released or required during solidification/melting and evaporation/condensation as well as radiation (Eqs. (1)–(5)).
Mass conservation
where ρ is the fluid mixture density, t is time, and \( \overrightarrow{v} \) is the mass-averaged velocity vector.
Momentum conservation
where p is the hydrodynamic pressure, τ the deviatoric shear stress tensor—calculated using the mixture-effective dynamic viscosity, C is a large constant, f L is the liquid fraction, σ the surface tension, κ the surface curvature, \( \overrightarrow{n} \) the surface normal, T the temperature, p R is the recoil pressure, and \( \overrightarrow{g} \) the gravity vector. The third term on the right-hand side describes momentum losses in the mushy zone, which is considered to be a porous medium. The fourth term represents the surface tension forces at the molten material surface and the Marangoni effects resulting from temperature-dependent surface tension.
Energy conservation
where h is the total enthalpy and λ is the mixture thermal conductivity. h i is the specific enthalpy of species i, \( {\overrightarrow{j}}_i \) is the species mass flux, and L f and L v are the latent heat of fusion and evaporation, respectively. f L and f v are the liquid and vapor fraction, respectively. Further source terms S R representing radiation are needed for the energy equation. They will be addressed further below when discussing the particularities of the different AM processes. The pressure gradient term is important when considering the trapped gases in consolidated material. The viscous dissipation term is negligible for the AM process.
Species conservation
where Y i is the species mass fraction. In the build chamber, vapor emitted during the build process is tracked using the species conservation equation to provide information on whether the gases are correctly extracted or whether they obscure the heat source. Species conservation could also be used to track alloy elements in the evaporating melt pool and the solid substrate; results from such an implementation have not been published yet.
The above equations are complimented by a scalar equation to track the free surface of the molten metal. The scalar is usually chosen to be a fluid volume fraction of one of the material states, such as that of the liquid state (volume of fluid—VOF):
where α L is the liquid volume fraction and m L, m V are the liquid and vapor mass sources due to phase change, respectively. The common formulation of free-surface tracking algorithms supports tracking of one or two material states, such as liquid and gas [18–20]. Vogel et al. and N’Dri et al. extended the formulation to support three material states: solid, liquid, and gas/vapor [12, 13].
Two numerical approaches are pursued to solve conservation Eqs. (1)–(5): Lattice Boltzmann methods [21, 22] and finite-volume algorithms [23–25].
Power bed micromodeling
Using equivalent properties for the powder layer enables quick simulations and analysis of how different parameters interact to predict the melt pool characteristics and to determine the thermal history of the deposited material, Dai and Shaw pursued such models assuming powder layer thicknesses of 0.5 mm [26]. The powder conductivity was calculated as a function of bed packing density using a correlation proposed by Sih and Barlow [27]. The laser energy was modeled as an isothermal heat source applied on the surface being processed. Residual stresses were calculated using the thermal histories obtained. Fischer et al. investigated the thermal behavior of the powder estimating the irradiance penetration depth and loose powder conductivity [28]. Roberts et al. utilized absorption estimates to model the material thermal history using temperature-dependent powder properties in an element birth and death model [29]. N’Dri et al. assessed the reliability of equivalent powder property models by performing an uncertainty quantification study. They showed that the results are very sensitive to the accuracy of absorption and loose powder conductivity [13]. In spite of the efficiency of these models, their reliance on accurate equivalent property approximations render them non-predictive.
Results obtained from resolved particle models do not depend on powder property correlations. Instead, the resolution of the powder particles enables the prediction of radiation absorption and penetration depth as well as the overall powder conductivity change as the powder starts to melt [13, 19].
Figure 2 shows a powder bed consisting of uniform spherical particles arranged in a BCC structure. The nickel super alloy powder has an unconsolidated powder layer thickness of approximately 50 μm, and the particles’ diameter is 22 μm. The laser power is 197 W, and the scan speed is 1 m/s. The amount of heat absorbed is determined via the radiation model [30]. At the beginning of the process, the temperature of the upper particles is close to the evaporation temperature. As more liquid is generated, it flows between solid particles via capillary forces. Once it reaches the baseplate, a direct bridge between the hot surface and the base material is established decreasing the overall melt temperature slightly. The surface waviness is due to the powder bed shape and Rayleigh flows. The heat does not diffuse sidewards due to the limited contact areas between loose powder particles. Gas between the powder particles (not shown in this sequence) is modeled and interacts with the molten material.
Resolved powder model: temperature on melt pool surface [13]
Attar et al. [19, 31] have pursued resolved powder bed models using Lattice Boltzmann methods. In their model, the gas phase was not accounted for, limiting the ability to capture the effect of gas entrapment in consolidated material. King et al. [20] pursued a finite-volume/finite-element implementation that also neglects the gas phase. The importance of gas modeling and how it relates to the prediction of consolidated material density is discussed in more detail below.
Very little validation studies have been reported due to the extreme harsh conditions under which microprocesses occur. N’Dri et al. compared track widths predicted by their micromodels with those measured (Fig. 3). The numerical study accounted for two adjacent tracks. The width of one track was found to be 95 μm. The corresponding built specimen showed track widths of 97 μm. Experimental efforts are underway to record melt pool evolution and measure the temperatures. New experimental insights will enable quantitative validation of the micromodels.
Comparison of numerically predicted track width with experimental measurement [13]
The powder bed packing density and the distribution of particles is expected to be a first-order parameter affecting the material behavior and the process evolution. Attar and Körner et al. used rain models [32] to obtain randomly arranged particle distributions. They also removed single particles from the powder bed to manipulate the overall packing density [19, 33]. King et al. used Gaussian distribution of the particles when distributing them in a numerical powder bed [20]. A more precise approach taking the dynamics of the powder-spreading process into account is based on discrete element models [34].
Figure 4 shows a comparison between the powder particle distribution as predicted by a rain model and as a result of modeling the coating process. It can be readily seen that for the same particle size distribution and the same amount of particles placed on the processing table there is a significant difference in the powder bed characteristics, especially the resulting packing density. Whereas the rain model predicts an almost uniform packing density of approximately 50 %, the model taking the coating process into account shows a packing density as high as 68 % with large deviations depending on how the particles lock and obscure a certain region during the coating process. At one particular point, the coating model predicts a minimum packing density of 36 %.
It is therefore considered important to resolve the coating process using a discrete element method (DEM). DEM is a Lagrangian tracking algorithm where each individual particle is resolved and tracked throughout the simulation time. The powder size distribution is discretized into size bins. The volume fraction distribution of all bins corresponds to that of the real powder. The powder particles are assumed to be spherical. Mechanical properties (elasticity and damping coefficients) are defined to calculate forces acting on each powder particle; up to 10 different materials can be accounted for. A sufficiently large number of particles are tracked to enable reliable statistical analysis of the results. The coating arm is assumed to be a rigid body the velocity of which is described as a boundary condition. Once the particles are created, the coating arm is set into motion spreading the particles onto the processing table [35].
Figure 5 shows the evolution of the calculated powder packing density for multiple layers. Here, the powder size distribution ranges from 10 to 70 μm in diameter. Several layers of powder are spread one after the other. The processing table displacement is 25 μm per layer. In between layers, the powder bed is not processed by a heat source; the results are therefore representative for a region where the heat source is not active. It can be seen that very low packing densities of approximately 20 % with large deviations are predicted for the first few layers. These results are expected to be representative for powder beds on solidified sections of the build. This is attributed to the interaction between large particles and the small gap between the coating arm and the processing table. The large particles block the gap limiting the process ability to deposit the powder in a uniform manner.
After several layers of loose powder particles, more space is available for larger particles that packing densities of up to 50 % with low deviations are predicted.
Radiation plays an important role in the heating of powder particles. McVey et al. deduced an equation for the absorbed energy assuming that all the incident energy is absorbed by the powder layer. Reflectance measurements were performed for multiple powders and different lasers to determine the absorbed energy as a function of powder layer thickness. The attenuation coefficient required for the deduced equation was provided for the measurements performed [36]. Boley et al. performed ray-tracing calculation on idealized as well as random powder beds obtained from rain models [37]. It is most interesting to note that the amount of absorbed energy is dependent on the powder distribution on the processing table. A high packing density powder layer was also studied yielding very high absorption.
For micromodels, radiation source terms are added to the energy equation (Eq. (3)—last term on the right-hand side). N’Dri et al. [13] and Mindt et al. [38] used a finite-volume formulation for the discrete ordinate radiation model [30]. The model was extended to track the position of a molten surface. Figure 6 shows the temperatures predicted by the micromodel for a nickel-based alloy, 200 W and 1 m/s scan speed. The peak temperature when allowing for evaporation is predicted to be approximately 2200 K. The rapid evaporation gives rise to a recoil pressure that contributes to large local forces acting on the free surface [17]. Qiu et al. showed that the recoil pressure is a possible explanation for the sparks observed during powder bed processes [39]. Manual-distribution powder beds have been studied numerically indicating ejection velocities of up to 15 m/s.
Figure 7 shows the consolidated material structure for the melt pool of Fig. 6 (transparent melt pool surface). The spheres remaining in the molten track depict the surface of gas bubbles entrapped in the melt. Many of the bubbles are able to leave the liquid during the preliminary stages of the melt process. Nevertheless, at the time point of this image, material on the left side of the image is solidifying capturing some gas bubbles that will not escape.
A recent validation study is summarized in Fig. 8 where the predicted material structure and porosity is compared with micrographs for multiple operating conditions [40]. It can be seen that slower scan speeds generally lead to high material densities. Higher energy densities are generally needed for larger hatch spacing and thick powder layers.
Comparison of predicted porosity with micrographs for different processing parameters [40]
Figure 9 compares the surface roughness for two build scenarios: The upper image corresponds to a case where the energy density is low leading to variations in surface height of up to 60 μm at the edge of the processed hatch and 25 μm around the center of the studied domain. In comparison, the lower image shows the resulting roughness at a higher energy density, where the increased fluidity of the melt and the high surface tension lead to balling of the melt and roughness values in the order of 110 μm. Further studies are needed to identify correlations between energy density and surface roughness.
Whereas results presented in Figs. 2, 3, 4, 5, 6, 7, 8, and 9 are representative for powder bed machines using a continuous laser active along a line as used in hatching or island scanning strategies, Fig. 10 shows a sequence of melt pool images for a machine utilizing a modulated laser. The laser “jumps” from one point to the other remaining stationary during an exposure time to melt the powder bed. The upper row shows the top view of the melt pool evolution, which gives the impression of a continuous melt pool and is not much different to that of a continuous laser moving along a straight trajectory. The lower row shows the melt pool shape of the corresponding points in time as seen from below the substrate surface. It can be seen that the laser modulation and the exposure time leads to singular deep melt pools. As the melt pools grow in diameter during the exposure time, they join into one solid build, which is what is seen in the top view. The depth of the joined melt pools compares to that obtained using a continuous laser; the additional deep conical melt pools might imply additional anchorage for the new layer to the previous layers.
Blown powder micromodeling
In order for micromodels to resolve the melt pool of blown powder processes, the feed nozzle and powder particle trajectories must be resolved in detail. The gas flow is resolved using Eulerian Eqs. (1)–(5). The powder flow through the nozzle is calculated using Lagrangian tracking [41]. As the particles might cross the laser in their trajectory, they may cause laser scatter and attenuation. The Lagrangian equations are coupled with the Eulerian equation system via source terms in continuity, momentum, and energy equations.
The equation of motion for the powder particles can be written as follows:
where m P is the particle mass; \( \overrightarrow{v} \) is the particle velocity; C D is the drag coefficient; ρ and \( \overrightarrow{V} \) are the density and velocity of the surrounding gas, respectively; and A P is the particle frontal area. For a spherical particle, A P = πd 2/4 where d is the particle diameter. The gravity vector is represented by \( \overrightarrow{g} \). S m is a mass source to represent the nozzle inlet for example.
The particle drag coefficient, C D, is a function of the local Reynolds number, which is evaluated as follows:
where μ is the dynamic viscosity of the gas. The simplest drag relationship is C D = Re/24; further extensions to this correlation are needed for drag in turbulent flows.
The particle locations are determined from the velocities by numerically integrating the velocity-defining equation:
where \( \overrightarrow{r} \) is the particle position vector. Assuming that particles heated and melted by the laser do not undergo significant change in size nor do they evaporate, the particle energy equation is written as follows:
where T P is the particle temperature; C P − P is the particle specific heat; and λ and T g are the thermal conductivity and temperature of the gas, respectively. The Nusselt number Nu is obtained from the Ranz-Marshall correlation [42], m pm is the particle molten mass, and ΔH m is the melting latent heat. S R is a source term describing the energy absorbed by the particles as they traverse the laser:
where I is the laser intensity, η P is the particle absorption coefficient, σ is the Stephan-Boltzmann constant, ϵ P is the particle emissivity, and T ∞ is the far field temperature. The first term in the right-hand side describes the particle heating due to the laser energy absorbed, and the second term describes the energy loss due to radiation. The second term in Eq. (10) is added as a “volumetric” source term to the radiation model:
with the boundary condition
where G is irradiance, β = η + σ S is the spectral extinction factor, σ S. is the scattering coefficient, \( \overrightarrow{n} \) is the boundary normal vector, and ϵ is the emissivity of the boundary surface. The laser attenuation is calculated by assessing the particle front surface area in a computational cell between the laser source and the substrate.
where I att the laser intensity after crossing a cloud of particles, N P is the number of particles in a given cell, and A cell is the cell face area.
When particles reach the substrate or the melt pool, they undergo a filtering process based on the thermodynamic state of collision partners. If the particles or the substrate are partially molten, then the particles are eliminated from the Lagrangian system and added as a mass source to the Eulerian representation of the melt pool. If both the substrate and the particles are still solid, then the particles bounce off the surface based on a restitution coefficient and the tracking algorithm continues to account for their travel throughout the computational domain. Table 1 summarizes the combinations considered when deciding what is to happen when a particle collides with the substrate or the melt pool.
Multiple parameters of blown powder processes were studied in an isolated manner [43–46]. Ibarra-Medina performed detailed nozzle analysis showing the particle distribution for different distances between the nozzle opening and the substrate (Fig. 11) and validating the particle heat up during their trajectories towards the substrate [47]. Figure 11 shows how the particle jet shape changes at the substrate with distance. At the design focal distance, the jet shows an optimal concentration of particles where the heat source is active. Moving the substrate closer to or away from the nozzle mouth leads to ring or cross-distributions, respectively, that affects the final melt bead deposited and the overall powder-capturing efficiency of the process. Figure 12 shows the influence of carrier and shield gas flow rates on the powder distribution at the design substrate–nozzle distance. As the gas flow rates increase, the spot size increases, which might be desired to achieve wider beads. Increasing the gas flow rates further leads to increased number of particles reflecting from the substrate surface (right-most image). These particles are not captured in the melt pool and decrease the particle overall process capture efficiency.
Coaxial nozzle geometry and grid (upper left), particle trajectories and velocity magnitude (upper right) and particle jet cross section at different distances from the nozzle mouth [47]
Particle jet diameter and particles losses change with feed gas flow: Left: with the lowest shield gas flow rate shows highest jet concentration and least amount of loss. Middle: average flow rate with slightly higher particle loss rate. Right: highest shield gas flow rate leads to much larger jet diameter and significant increase in particles loss
Beads are deposited with overlaps to ensure a dense build and to avoid large variations in bead height. Figure 13 compares numerically predicted stainless steel bead shapes. The powder flow rate is 0.28 g/s, laser power is 730 W, and the nozzle head scan speed is 10 mm/s [12, 47]. Numerical results for different overlap percentages are compared with experimental profiles showing very good agreement.
Bead shape validation for different track overlaps [47]
Process scanning/mapping
High-fidelity micromodels are generally computationally intensive. In spite of the demonstrated accuracy in predicting porosities and providing input to residual stress models discussed below, it is desirable to pursue much quicker tools that might be founded on simplifying assumptions or empirical correlations to pre-scan the process window decreasing the computational cost required to characterize the powder and the machine combination being used.
Kamath et al. performed a full fractional design of experiments using the Eagar-Tsai model to determine the melt pool dimensions for powder bed process and stainless steel specimens [48]. The analysis allowed the identification of the significant process parameters affecting the melt pool width and depth: scan speed and laser power. The process window was further refined via single track and pillar experiments to obtain high-density builds.
Körner et al. considered several dimensionless numbers to characterize powder bed processes [31]. They were able to identify an optimal scan speed that would balance the amount of energy input with the diffusion through the powder layer. Megahed extended this model assessing the build density by comparing the global energy density with micrographs and corresponding porosity measurements. The model was further extended to include an assessment of the build rate as a function of scan speed, laser diameter, and powder layer thickness. The input to the algebraic equations includes the machine capabilities and defines the bounds of an optimization problem with two cost functions: maximize density and maximize build rate. Figure 14 shows an example result of the optimization scheme showing that the build rate is inversely proportional to the density. Following the build rate curve in clockwise direction indicates an increase in build rate. At the same time, the build porosity decreases until it is no longer acceptable, indicated by the red triangle. The threshold of acceptable porosities is arbitrarily chosen based on product quality requirements. Corresponding micrographs show the build quality for some of the build parameters assessed. By choosing a certain porosity to be acceptable, the process parameters delivering the highest possible build rate can be determined from the corresponding parameter curves. It is interesting to note that the processing table displacement and heat source scanning speed also show an inversely proportional relationship. A large displacement requires a reduction of the scan speed to ensure high densities. The dimensionless analysis was very efficient in providing guidance to choose process parameters enabling production of dense material at a high build rate. Micromodels were used to confirm the results.
Weerasinghe and Steen created process maps based on blown powder experimental data [49]. Beuth and Klingbeil utilized normalized dimensions and process parameters to numerically create process maps for thin bodies using blown powder processes [50]. The procedure has since been extended for large bodies and corner effects as well as powder bed processes.
It is, however, important to remember that the speed of these pre-screening tools comes at the cost of lower physics fidelity. It is mandatory to verify and confirm the reliability of these tools for the materials and process parameters under consideration [9].
Macromodeling
Macromodels are dedicated to the modeling of the whole workpiece predicting residual stresses and distortions during and after the build process. Stresses and strains are mainly induced by thermal loads. The effects of phase changes on thermo-mechanical properties can be neglected as a first approach. The large amount of heat supplied to the part at the upper build layers is transferred to the rest of the workpiece by conduction resulting in a global thermal expansion of the product. During both stages of solidification and cooling, the plastic strains caused by the thermal expansion and by the constraints of clamping devices will lead to residual stresses. After clamp release, the workpiece reaches its final shape.
Whereas the physics governing micromodels depend significantly on the process details, macromodels are mainly driven by thermal loads (or the thermal cycle). This enables a simplification of the physics models allowing a coarser discretization and finally facilitating the computation of complete industrial workpieces. Finite-element methods based on a Lagrangian formulation are usually used for macromodeling [51–54]. Whereas the validity of Eulerian approaches for welding is limited, the high scan speed of AM sources reduces the impact of the free-edge effects on the final results. Ding et al. demonstrated that a steady-state Eulerian thermal analysis of wire arc additive manufacturing (WAAM) was less computationally costly with a gain of 80 % in speed as compared to a Lagrangian framework [55]. Nevertheless, difficulties adapting Eulerian methods to complex geometries are a limitation of this approach.
The additive-manufacturing macroscale simulation can be divided into two main stages: the heat transfer analysis and the mechanical analysis. They are computed separately, presenting a one-way coupling of the thermo-mechanical computation. The transient temperature field is stored at every time step and is then applied as a thermal load in the quasi-static thermo-mechanical analysis [56–58]. As shown in Fig. 15, during the deposition of a layer on a T-Wall using blown powder process, the thermal distributions computed at the initial, intermediate, and final states are used as input data for computing the intermediate and final stress states. The thermal model remains geometrically fixed during the whole thermal analysis whereas the mechanical model distorts as the calculations progress in time. Such an approach is permissible in the case of a relatively small structure deformation [58]. The successive computations are repeated as many times as melt beads need to be deposited to create the workpiece.
Thermo-metallurgical analysis
Energy equation
The thermal analysis is both non-linear and transient. The non-linearity originates from the temperature dependence of the material properties, while the transience originates from the time variation of thermal boundary conditions (i.e., imposed temperature or heat flux).
The energy equation discussed above (Eq. (3)) is reduced to a pure diffusion equation as shown in Eq. (14) with corresponding sources and boundary conditions simplifying the overall thermal analysis.
with ρ, h, λ, T, Q V representing the density, the enthalpy, the conductivity, the temperature, and the volumetric heat source, respectively. q S corresponds to the heat flux or Neumann condition applied on the surface (of normal \( \overrightarrow{n} \)) of the computational domain. The latent heat of fusion effect on the thermal distribution is taken into account by defining an equivalent specific heat C P − eq which increases significantly at the fusion point. Enthalpy and specific heat are linked by the equation
where f L, C P, L f are the liquid fraction, the specific heat, and the latent heat, respectively. An equivalent specific heat can be pre-processed using the equation
Equation (14) can be reformulated to provide the material temperature directly:
Equation (17) is solved for the whole domain composed of first-order elements. An implicit temporal discretization and a quasi-Newton method are usually used for solving the non-linear problem [58, 59]. A symmetrical direct method may be applied for the linear system resolution [60]. The time step is adjusted automatically according to convergence criteria.
Metallurgical phase transformations and material properties
The thermal model can be coupled with metallurgical phase calculations, becoming a thermo-metallurgical model. The temperature and the material transformation properties are provided as input data to compute the metallurgical transformations at Gaussian points. Papadakis et al. used the metallurgical transformations model implemented in Sysweld [61] to reproduce Johnson-Mehl-Avrami-type kinetics [62] to obtain the evolution of each phase with time and the corresponding temperature distribution [58]. Transformation phase laws are defined for both heating and cooling stages and they are material/alloy dependent. The scarcity of thermo-metallurgical properties in the literature often obliges researchers to disregard the phase dependency of the thermal properties. Conductivity, density, and specific heat are temperature dependent and are assumed constant above 800 °C for most materials (IN718 [58], Ti-6Al-4V [63]) or are obtained from a library such as JMatPro® for the metallurgical composition (X4CrNiCuNb 16-4 hardening stainless steel [64] or 316L stainless steel [54]).
Metal deposition modeling
Depending on the finite-element framework chosen (Eulerian or Lagrangian), the representation of metal deposition is different—these methods were developed and matured for weld modeling. When the transient thermo-mechanical simulations are carried out within an Eulerian approach, interface-tracking methods such as volume of fluid or level set are used. Desmaison et al. developed a full transient thermo-mechanical model for multi-pass hybrid welding [65], a process easily comparable to wire feed additive manufacturing. In spite of advanced numerical tools (adaptive remeshing, Hamilton-Jacobi resolution algorithm among others), the finest of inherent numerical parameters make the approach too complex for the modeling of large and complex AM. In comparison, the Lagrangian framework enables easy handling of an activation/deactivation element technique, named differently by the authors according to the FE codes used: activation element method with Sysweld® [58] or MSC Marc® [64], element birth technique with Abaqus® [55], and quiet or inactive element method with Cubic® [56]. All these methods can be classified into two categories, the “quiet” and the “inactive” element methods [59].
The “quiet” element method is based on the initial existence of all the elements in the model. The properties of “quiet” elements differ from those of “active” elements—scaling factors are multiplied to the conductivity and the specific heat. The “inactive” element method removes elements representing metal to be deposited from the computation up to their activation. Michaleris compared both these techniques in terms of accuracy and computational time [59] for thermal analysis only. He concluded his work by proposing a hybrid “quiet”/“inactive” element method where elements of the current deposited layer would be switched to “quiet” and the ones of further layer depositions switched to “inactive.” Whatever the method chosen, accuracy of the thermal and residual stress distributions is fulfilled and computational time is saved. It is moreover possible to increase the gain of CPU time saving by implementing an adaptive coarsening method [51, 63].
Thermal boundary conditions
Thermal boundary conditions account for both the heat source modeling and heat transfer within and from the workpiece. As macroscale thermal models do not reflect all the physics of the process, equivalent heat sources are defined according to the AM process considered. Martukanitz et al. modeled a laser employed for powder bed fusion as a spot whereas a laser used for direct metal deposition was represented as a defocused beam. Similarly, electron beams are characterized by a Gaussian distributed source [51]. Hence, a very common approach is the definition of a Gaussian or Goldak [66] heat source scaled by an appropriate absorption efficiency factor η representing process optical losses [26, 29, 56, 67–69]. In spite of the much simpler energy equation considered (compare Eqs. (3) and (17)), the computational effort tracking the heat source trajectory throughout the build can be significant. Analytical solutions are suggested as an efficient alternative for simple geometries [70, 71].
King et al. defined the thermal cycle using the Gusarov thermal profile [72] to perform coupled thermo-mechanical analysis. In spite of the fact that the Gusarov model is limited to a scan speed of 0.1–0.2 m/s, the residual stresses obtained are in the order of several hundred megapascals and compare well with experimental observations [20].
The moving heat source and workpiece geometric complexities are best addressed using adaptive locally refined grids. Fine accurate resolution is defined around the heat source while coarser grids are used elsewhere retaining the overall computational effort within reasonable limits (Fig. 16). The fine grid (local) resolves the heat source and exchange accurately. The coarse grids (global) distribute the energy in the build geometry prior to performing the thermo-mechanical analysis. Hence, the numerical evaluation of the residual stress is faster [52–54, 64].
Other authors decomposed the thermal analysis of the whole process into two or three models of ascending scales (heat source, hatch, and macroscales). Literature refers to these model length scales as micro-, meso-, and macromodels. These names were not adopted in this paper because the length scale names are used here to represent different levels of physics fidelity. Keller et al. developed two transient thermal models for selective laser melting (SLM) modeling: the first one in order to calibrate the heat input modeled as a Goldak heat source and the second one for consideration of the trajectory of the laser spot (the Goldak source is replaced by the estimated energy distribution in a cubic element) [54, 64]. The same strategy is followed by Li et al. The authors defined a heat source scale model to extract a thermal load from a laser Gaussian source heating the powder. This thermal load is then applied on a mesoscale hatch layer for a transient thermo-mechanical analysis [52]. A macroscale model can also be used for lumping methodology when several layers are numerically deposited at the same time [12, 13, 53].
All scales used in the thermal model do not include all the physics related to the process. Uncertainty quantification studies indicated that the results are very sensitive to the input parameters, such as homogenized powder properties and heat source description [13]. Vogel et al. [12] and N’Dri et al. [13] obtained the input thermal cycle from micromodel results for both blown powder and powder bed processes. A tool has been developed to extract the thermal history from micromodels and to define an equivalent heat source (e.g., Goldak volumetric or Gaussian surface sources). The boundary condition utilized to describe the heat source in the macromodel might be a Dirichlet (temperature history) or a Neumann (heat flux history) boundary condition. Corresponding spatial and temporal interpolation is necessary because of the difference in micro- and macromodel grids. This approach is the most accurate description of energy input—as it accounts for the process details and the predicted material porosity. It does, however, require a sufficiently fine mesh to resolve thermal gradients around the melt pool. Time step sizes must also fit with the element size and the heat source scanning velocity. As the build simulation progresses (and the model size increases), the high resolution should be reduced by applying equivalent (averaged) thermal cycles for larger deposits. Average thermal cycles are extracted at the middle cross section of the deposited material. They are then used in subsequent time steps to accelerate the computation. By applying the averaged thermal cycles, whole layers can be processed in one time step. This “lumping” methodology was validated for bars and plate workpieces [13].
The main heat transfer mechanisms from the workpiece to the surrounding environment are radiation and convection. The radiation is applied to all free surfaces, including those of the newly deposited material, and used the Stefan-Boltzmann law:
Where q R is a Neumann condition part of the term q S in the energy Eq. (17), ϵ the emissivity, σ the Stefan-Boltzmann constant, and T S and T ∞ are the surface temperature and the far field temperature. The emissivity value will depend both on the process and the material and can be characterized both experimentally and numerically [56].
In welding process modeling, heat transfer via convection plays an insignificant role, since the material deposition volume is small in comparison to the volume of the existing part: heat transfer is driven by conduction inside the bulk material while the effect of the shielding gas flow is negligible. For AM, convection cannot be neglected. Excluding electron beam processes that take place in a vacuum environment, the volume of deposited material can exceed the initial volume of the build and the effects of the surrounding environment on the heat exchange must be taken into account. Shield gas and in the case of blown powder processes the powder carrier gas are utilized in the process chamber to extract vapors that might contaminate the optical components and to deliver the feedstock. The gas flow characteristics can lead to significant flow velocities across the workpiece. The convection heat loss,
is added to q S in Eq. (17), where h is the heat transfer coefficient. Its value will depend on many factors such as surface orientation, existence, or absence of forced convection, surface roughness, and solid and gas properties [57, 59]. In powder bed processes, heat transfer from the workpiece sides is limited by the low powder conductivity. Sih and Barlow quantified powder conductivity for high temperatures reporting values ranging from 0.2 to 0.6 W/m2K for Al2O3 [27]. Instead of defining the measured equivalent powder conductivity directly, it is possible to reduce the solid powder conductivity by applying a reduction factor (around 1/100) to the bulk material conductivity as in [64]. This approach is very similar to the one used in active/quiet element modeling as described in [59].
The surface of the workpiece will be affected by the shield gas flow. Heigl et al. used heat transfer coefficients ranging from 10 to 25 W/m2K for blown powder processes. The variation is dependent on the distance from the nozzle [57]. Michaleris used 10 W/m2K for free surfaces and 210 W/m2K in the vicinity of the nozzle [73]. The heat transfer rates are lower for powder bed processes; heat transfer to unprocessed powder is often assumed to be negligible, and the convection heat transfer coefficient at the top surface is taken to be 0.005 W/m2K [64] or 50 W/m2K [54, 58, 74].
Mechanical analysis
The mechanical analysis may be considered as weakly coupled to the thermo-metallurgical analysis since it is only thermal history dependent [56]. The temperature and the phase proportions of the previous analysis are only needed to compute the thermal expansion in the whole domain and to define the thermo-mechanical properties. The mesh still remains the same, and the elements are also of the same order. Moreover, the model is set up in the Lagrangian framework, which is more convenient for distortion modeling of large parts.
The mechanical analysis is also non-linear (because of the non-linearity of the material behavior) but considered as a quasi-static incremental analysis [56, 57, 63]. The governing stress equation can be expressed as [63, 75] follows:
where σ is the stress tensor associated to the material behavior law and \( {\overrightarrow{f}}_{\mathrm{int}} \) is the internal forces. Considering an elasto-plastic behavior for the material, strain and stress tensors are linked by the equation
where C is the fourth-order material stiffness tensor and the total strain tensor ϵ is decomposed into three components: the elastic strain ϵ e, the plastic strain ϵ p, and the thermal strain ϵ th:
with
where E, ν are the Young’s modulus and Poisson’s coefficient, respectively; g(σ Y) is a function associated to the material behavior; σ Y is the yield stress; and α, θ, θ 0 are the thermal expansion coefficient, the nodal temperature, and the initial temperature, respectively. The presence of the thermal strain tensor in the Eq. (22) ensures correct distortion calculation during the material deposition (melting) stage as well as the thermal shrinkage during the global cooling of the workpiece. For a pure plastic behavior with isotropic strain hardening [56, 57, 63], the plastic strain ϵ p is computed by enforcing the von Mises yield criterion and the Prandtl-Reuss flow rule:
where f is the yield function, σ VM is von Mises’ stress
and \( {\overset{.}{\epsilon}}^q \) the equivalent plastic strain rate and a the flow vector. If a kinematic strain hardening is also taken into account, the von Mises yield criterion is replaced by the Prager linear kinematic strain-hardening model:
\( {\sigma}_{ij}^{\prime } \) and \( {\chi}_{ij}^{\prime } \) are the components i, j of the deviator stress and kinematic tensors, respectively, with
where p is the strain-hardening slope p = ∂σ VM/∂ϵ q. The mechanical properties as α, σ Y, and E are temperature dependent. If the yield stress σ Y(T) is independent of the equivalent plastic strain ϵ q, the behavior is pure plastic, while it is isotropic strain hardening if σ Y(T, ϵ q) and kinematic strain hardening if p(T) is defined. The Poisson’s ratio is always constant.
Annealing effects
The annealing effects are not considered in shrinkage models. They should to be considered since the previously deposited layers are subsequently re-melted and reheated during the new layer deposition. Above a certain relaxation temperature T relax each strain component of Eq. (22) is reset to zero. The relaxation temperature has been studied for Ti-6Al-4V electron beam additive manufacturing by Denlinger et al. [56]. By comparing numerical and experimental data, the authors found that the relaxation temperature needs to be adapted for AM process modeling in order to not overestimate the residual stresses and distortions.
Figure 17 shows the residual stress distribution in a wall created using Ti-6Al-4V and the blown powder process. The numerical results are compared with those obtained using neutron diffraction along the geometric center line [76] showing good agreement confirming the thermal-mechanical properties, the mechanical model, and the stress relaxation calculations.
Mechanical boundary conditions
Only nodal constraints are taken into account. All the nodes of the substrate lower surface are usually rigidly constrained [54, 58, 64], but some spring constraints may be applied to model the elasticity of the clamps [63]. The final distortion of the AM workpiece is obtained once the domain is fully cooled and the clamps are released. An additional step is needed to simulate the removal of the support or the removal of the baseplate from the final product [58, 64]. This operation is often modeled by applying an additional thermal load to the lower layers of the workpiece or by deactivating the baseplate elements.
Applied plastic strain method
In welding process modeling, the concept of applied plastic inherent strain has originally been proposed by Ueda et al. [77]. It has then been largely used in order to reduce the computational time of the mechanical analysis in welding distortion prediction [73, 78, 79].
The principle steps can be summarized as follows [78]:
-
1.
High-resolution model of the transient thermo-mechanical analysis—this is usually performed on a smaller specimen of the workpiece.
-
2.
Calculation of the plastic strain tensor components and the equivalent plastic strain once the whole domain has cooled down to the ambient temperature.
-
3.
Transfer of the plastic strains obtained on the high-resolution model to the complete workpiece.
-
4.
Elastic computation with the macromodel to estimate the final distortions.
The main advantage of this method is the drastic reduction of computational time required for the mechanical analysis. Only a linear elastic solution is required for each time step. This method is not compatible with the local/global approach (see the “Thermal boundary conditions” section) since a very fine and accurate model is needed to determine the plastic strains. A thermal load applied on a coarse mesh would not be sufficient for this approach. Consequently, large modeling efforts have to be accounted for during the initial transient thermo-mechanical analysis and for developing an efficient field transfer tool. Moreover, it is compulsory to wait for the complete cooling of the domain before extracting the plastic strains; otherwise, the results will be inaccurate.
Since this technique has been largely validated for welding modeling [73], it has been adopted for AM and powder bed processes [52, 54, 64]. Keller et al. applied this method for the modeling of a cantilever build process and could analyze the effects of the laser scan strategy on the final distortions of the workpiece. Numerical results are in good agreements with the experiment. They also discuss a new accelerated mechanical simulation based on the assumption that thermal strains only affect the topmost layer allowing a reduction of distortion prediction computational effort to a few hours. Most of the efforts are made to obtain the thermal field [54, 80].
Figure 18 shows a comparison of the numerically calculated final plate distortion with experimental measurements. The plates are produced using powder bed process. IN718+ is processed using a 200-W laser and scan speed 1 m/s, and all layers are processed using the same hatching trajectory. Two deposition strategies were studied: In the first approach, each layer is rotated relative to the previous one by 90o; in the second, each layer is rotated by 67o. The numerical results are accurate within 3 % [13].
Plate validation case demonstrating the ability of macromodels to capture the influence powder bed deposition strategy [13]
Thermodynamics and properties
The metrics required to assess metallurgical properties are process peak temperature, heating, and cooling rates. Figure 19 shows a typical thermal history for powder bed processes as predicted by the micromodel. The cooling rate reaches 1.5 million degrees per second and is in agreement with thermographic images and temperature histories reported by Lane et al. [81]. The cooling rate is much higher than those measured for the traditional manufacturing process. Most sited literature focuses on experimental characterization of phase distributions and grain structures. For example, Murr et al. compare the microstructures of laser and electron beam systems. The difference in cooling rates was found to lead to directional differences in grain structures of some of the materials tested. They did not necessarily correlate to measured hardness [6]. Körner et al. coupled 2D grain growth models with micromodels [82]. The numerical results demonstrated the effect of hatching on the resulting microstructure of Ti-6Al-4V. The implications of the cooling rates were not discussed.
The cooling rate in blown powder processes, typically in the order of 104 K/m, is much lower than that in powder beds. Vogel et al. [12] utilized Leblond model and Koistinen-Marburger equation to determine phase proportions of M2 high-speed steel at the end of blown powder processes. The results were validated using XRD measurements. Mokadem et al. utilized the cellular automata finite element (CAFE) [83] to calculate the microstructure of Ti-6Al-4V deposited via a transverse blown powder stream [84]. The results of Figs. 17 and 18 provide implicit validation of thermo-mechanical data for Ti-6Al-4V (blown powder) and IN718+ (powder bed tuned properties), respectively.
Modeling readiness for real-life AM
The readiness of a technology for industrial use is best measured by the Technology Readiness Level (TRL) (Fig. 20). The TRL scale was originally developed by NASA in the 1980s and has since been implemented and modified for multiple applications and technologies including the assessment of software solutions [85, 86]. ICME verification and validation procedures are also standardized to achieve high TRL levels [87].
TRL levels for hardware and software [86]
As discussed above, micromodels have been validated to predict porosities and melt pool dimensions reliably for different materials, different AM processes and different commercial machines. The models have not yet been used on a sufficiently wide scale to claim wide industrial use. A simplified assessment would place micromodels at TRL 4 to 5. Macromodels have been demonstrated based on bulk material properties that originate from available databases. The majority of the studies reported in the literature calibrate the thermal cycle or strains via experiments. Geometries studied are usually laboratory demonstrators, and limited focus was placed on physics-based design of deposition strategy and of support structures. The macromodel TRL is generally estimated to be around 3 to 4, where the lower readiness level corresponds to powder bed processes and higher values correspond to blown powder and wire feed systems.
In order for AM modeling to be deployed in an industrial environment, TRL 6 and beyond must be achieved via coupling of the different length scales and physics into an integrated computational materials engineering (ICME) platform (Fig. 21). Design for additive manufacturing is achieved using physics-based modeling—topology optimization [88–90]—and is therefore an integral component of ICME. The common practice of separating functional requirements from manufacturing constraints (e.g., minimum wall thickness or overall component size) is certainly not desirable and is one example of the many couplings yet to be supported by ICME.
Material databases play a central role in ICME. Additively manufactured material properties and manufacturing constraints are process specific—see, for example, fatigue performance of additively manufactured Ti-6Al-4V [91]. Figure 21 postulates that two schema will be used: One describes the material properties and the other gathers process data. The required strong link between these databases implies the possibility of unifying them into one system such as that proposed by [92].
The databases will gather information from multiple sources: Experimental characterization of material properties is an obvious source that is currently state of the art. Atomistic models can be used to characterize feedstocks and to set targets for properties to be achieved during the manufacturing process. Micromodels can be used to characterize the processes and process finger prints for different geometric features, scanning strategies, and intentionally inserted defects (e.g., powder contamination) in order to provide a better understanding of process implications and eventually to enable knowledge based in-process monitoring and control.
The optimized design, the material, and the process data all contribute to macromodels and the accurate prediction of as-built distortion and residual stresses. The large-scale models might communicate thermal boundary conditions back to the lower scale models, but the main goal is to compare the final geometry shape and characteristics with acceptance criteria. If the distortion, for example, is too high, an alternative build direction or scan strategy would require a repetition of the macromodeling process. If, however, the distortions during the build are too high, then process parameters or even the material choice might be revised requiring a repetition of the topology optimization step.
Managing uncertainty is important when comparing the product compliance with acceptance criteria and for downstream decisions such as certification or supplier qualification. The uncertainty of material properties, feedstock tolerances, and process variability has to be propagated throughout the systems and linked to the final result. More tools might be also considered for integration, for example, to calculate projected production cost. AM ICME results can then be uploaded to the enterprise and production management systems as required by the institution’s business process.
This paper focused on micro- and macromodels only. Coupling approaches to increase macromodel independence from experimental calibration were suggested. Vogel et al. [12] and N’Dri et al. [13] reported research towards integrating micro- and macromodels with uncertainty quantification. Körner et al. attempted coupling micromodels with grain growth simulations [82]. Allaire et al. demonstrated how casting constraints can be accounted for to obtain topological optimized designs that fulfil both functional and manufacturing requirements [93]. The DARPA Open Manufacturing program demonstrated a framework integrating modeling tools with in-process monitoring sensors towards rapid qualification of AM processes (Peralta AD, Enright M, Megahed M, Gong J, Roybal M, Craig J (2016) Towards rapid qualification of powder bed laser additively manufactured parts. IMMI. Under Review).
In spite of significant progress developing and validating AM modeling tools, integrating tools into an ICME platform as suggested in Fig. 21 is yet to be demonstrated.
Conclusions
Modeling additive-manufacturing processes is a very challenging enterprise. The large differences in length- and timescales necessitate a subdivision of spatial and temporal resolutions into micro-, meso-, and macroscale models. The names chosen in this compilation also distinguish large differences in the physics considered in each of the model categories. Micromodels resolve fine details of heat source feedstock interaction and how the melt pool evolves requiring the highest physics fidelity. Results obtained are homogenized or projected to macromodels to predict the overall build characteristics including residual stresses and distortions. Mesoscale models describing the material properties are queried by other models to obtain the required information about material behavior.
The same micromodeling tools were used to compare the performance of both continuous and modulated laser behaviors of different powder bed machines as well as blown powder processes. Materials studied include SS316L, IN718+, and Ti-6Al-4V. The verification and validation examples presented demonstrate the generality of the algorithms described and the ability to capture the thermal cycle and porosity defects. This information can be utilized to characterize process parameters towards better identification of the optimal process window. Macromodels were also applied to a wide range of processes and materials. Validation was presented for successful builds. The tools utilized in our studies demonstrated the ability to capture the influence of deposition strategy on the final build distortion accurately.
Nevertheless, multiple topics of interest to designers and process engineers such as predicting the required compensation of build shrinkage and optimization of deposition strategy are yet to be addressed. The optimization schemes and physics behind these tasks are generally known; the challenge remains mainly related to the computational effort involved. When performing parameter studies, large amounts of data are generated that users are not only confronted by the input/output effort involved but also by the need to analyze large amounts of information. Management of big data—also in combination with uncertainty quantification and optimization studies—is a major task, where solutions are yet to be established. Standardization of databases as well as modeling information should facilitate the later reference of data available.
As ICME components mature, integration effort increases in importance. The need for standardized benchmarks and reference results will be mandatory to qualify and certify additive-manufacturing ICME tools. Parallel to improving robustness and computational performance, it is expected that future research and development will be focused on establishing suitable modeling standards and benchmarks.
References
Housholder RF (1981) Molding process. US Patent 4,247,508
Ciraud PA (1972) Process and device for the manufacture of any objects desired from any meltable material. FRG Patent 2263777
Baker (1926) The use of an electric arc as a heat source to generate 3D objects depositing molten metal in superimposed layers
Allaire G (1992) Homogenization and two-scale convergence. SIAM J Math Anal 23(6):1482–1518
Dinda GP, Dasgupta AK, Mazumder J (2009) Laser aided direct metal deposition of Inconel 625 superalloy: microstructural evolution and thermal stability. Mater Sci Eng A 509:98–104. doi:https://doi.org/10.1016/j.msea.2009.01.009
Murr LE, Martinez E, Amato KN, Gaytan SM, Hernandez J, Ramirez DA et al (2012) Fabrication of metal and alloy components by additive manufacturing: examples of 3D materials science. Journal of Materials Research and Technology 1:42–54. doi:https://doi.org/10.1016/S2238-7854(12)70009-1
Li J, Wang HM, Tang HB (2012) Effect of heat treatment on microstructure and mechanical properties of laser melting deposited Ni-Base superalloy Rene’41. Mater Sci Eng A 505:97–102. doi:https://doi.org/10.1016/j.msea.2012.04.037
Bi G, Sun CN, Chen HC, Ng FL, Ma CK (2014) Microstructure and tensile properties of superalloy IN100 fabricated by micro-laser aided additive manufacturing. Mater Des 60:401–408. doi:https://doi.org/10.1016/j.matdes.2014.04.020
Choren JA, Heinrich SM, Silver-Thorn MB (2013) Young’s modulus and volume porosity relationships for additive manufacturing applications. J Mater Sci 48:5103–5112. doi:https://doi.org/10.1007/s10853-013-7237-5
Yadroitsev I (2009) Selective laser melting: direct manufacturing of 3D-objects by selective laser melting of metal powders. LAP Lambert Academic Publishing, Saarbrücken, Germany.
Chernigovski S, Doynov N, Kotsev T (2006) Simulation thermomechanischer Vorgänge bein Laserstrahlschweissen unter Berücksichtigung transienter Einflüsse im Nahtbereich. AIF-Forschungsvorhaben Report No.: 13687 BG/1.
Vogel M, Khan M, Ibarra-Medina J, Pinkerton A, N’Dri N, Megahed M (2013) A coupled approach to weld pool, phase and residual stress modeling of laser direct metal deposition (LDMD) processes. In: 2nd World Congress on Integrated Computational Materials Engineering, Salt Lake City, USA. John Wiley & Sons Inc. p 231–236.
N’Dri N, Mindt HW, Shula B, Megahed M, Peralta A, Kantzos P, et al. (2015) Supplemental Proceedings. DMLS process modeling & validation. TMS 2015 144th Annual Meeting & Exhibition, Orlando, USA. In: Proceedings. John Wiley & Sons Inc. p 389–396.
Bird RB, Stewart WE, Lightfoot EN (1960) Transport phenomena. New York: John Wiley & Sons. p 780.
Ansorge R, Sonar T (1998) Mathematical models of fluid mechanics., Wiley-VCH Verlag GmbH & Co KGaA
Fuerschbach PW, Norris JT, He X, DebRoy T (2003) Understanding metal vaporization from laser welding. Sandia National Laboratories Report No.: SAND2003-3490
Bäuerle D (2011) Laser processing and chemistry. Springer Verlag.
Hirt CW, Nichols BD (1981) Volume of fluid (VOF) method for the dynamics of free boundaries. J Comput Phys 39:201–225
Attar E (2011) Simulation der selektiven Elektronenstrahlschmelzprozesse. PhD Thesis University of Erlangen-Nuremberg.
King WE, Anderson AT, Ferencz RM, Hodge NE, Kamath C, Khairallah SA et al (2015) Laser powder bed fusion additive manufacturing of metals; physics, computational, and materials challenges. Applied Physics Reviews 2:041304. doi:https://doi.org/10.1063/1.4937809
He X, Luo LS (1997) A priori derivation of the lattice Boltzmann equation. Phys Rev E 55(6):R6333–R6336
Chen S, Doolen DG (1998) Lattice Boltzmann method for fluid flows. Annu Rev Fluid Mech 30:329–364
Patankan SV (1980) Numerical heat transfer and fluid flow. McGraw-Hill, New York
Ferziger JH, Peric M. (2008) Numerische Strömungsmechanik. : Springer-Verlag
Peric M, Kessler R, Scheurer G (1988) Comparison of finite-volume numerical methods with staggered and collocated grids. Computers and Fluids 16(4):389–403
Dai K, Shaw L (2004) Thermal and mechanical finite element modeling of laser forming from metal and ceramic powders. Acta Mater 52:69–80. doi:https://doi.org/10.1016/j.actamat.2003.08.028
Sih SS, Barlow JW (1994) Measurement and prediction of the thermal conductivity of powders at high temperature. 5th Annual SFF Symposium Austin, In: The University of Texas p 321–329.
Fischer P, Romano V, Weber HP, Karapatis NP, Boillat E, Glardon R (2003) Sintering of commercially pure titanium powder with a Nd:YAG laser source. Acta Mater 51:1651–1662. doi:https://doi.org/10.1016/S1359-6454(02)00567-0
Roberts IA, Wang CJ, Esterlein R, Stanford M, Mynors DJ (2009) A three dimensional finite element analysis of the temperature field during laser melting of metal powders in additive layer manufacturing. International Journal of Machine Tools & Manufacture 49:916–923. doi:https://doi.org/10.1016/j.ijmachtools.2009.07.004
Vaidya N (1998) Multi-dimensional simulation of radiation using an unstructured finite volume method. 36th Aerospace Sciences Meetingand Exhibition, Reno. In: AIAA 98-0857
Körner C, Bauereiß A, Attar E (2013) Fundamental consolidation mechanisms during selective beam melting of powders. Modeling Simul Mater Sci Eng 21(085011):18. doi:https://doi.org/10.1088/0965-0393/21/8/85011
Meakin P, Jullien R (1987) Restructuring effects in the rain model for random deposition. J Physique 48:1651–1662
Attar CKE, Heinl P (2011) Mesoscopic simulation of selective beam melting processes. J Mater Process Technol 211:978–987. doi:https://doi.org/10.1016/j.matprotec.2010.12.016
Cundall PA, Strack OD (1979) A discrete numerical model for granular assemblies. Geotechnique 29(1):47–65
Mindt HW, Megahed M, Lavery NP, Homes MA, Brown SG (2016) Powder bed layer characteristics - the overseen first order process input. 145th TMS Annual Meeting & Exhibition, Nashville, USA
McVey RW, Melnychuk RM, Todd JA, Martukanitz RP (2007) Absorption of laser radiation in a porous powder layer. Journal Laser Applications 19(4):214–224
Boley CD, Khairallah SA, Rubenchik MA (2015) Calculation of laser absorption by metal powders in additive manufacturing. Appl Opt 54(9):2477–2482. doi:https://doi.org/10.1364/AO.54.002477
Mindt HW, Megahed M, Perlata A, Neumann J (2015) DMLM models - numerical assessment of porosity. 22nd ISABE Conference, Oct. 25–30, Phoenix, AZ., USA.
Qiu C, Panwisawas C, Ward M, Basoalto HC, Brooks JW, Attallah MM (2015) On the role of melt flow into the surface structure and porosity development during selective laser melting. Acta Mater 96:72–79. doi:https://doi.org/10.1016/j.actamat.2015.06.004
H-W M, Megahed M, Shula B, Peralta A, Neumann J (2016) Powder bed models – numerical assessment of as-built quality. AIAA Science and Technology Forum and Exposition, San Diego. In: AIAA 2016-1657
Crowe CT, Sommerfeld M, Tsuji Y (1998) In: Taylor F (ed) Multiphase flows with droplets and particles. CRC Press LLC, Boca Raton
Ranz WE, Marshall WR (1952) Evaporation from drops. Chemical Engineering Prog 48(3):141–148
Lin J (1999) Concentration mode of the powder stream in coaxial laser cladding. Opt Laser Technol 31(3):251–257
Liu CY, Lin J (2003) Thermal processes of a powder particle in coaxial laser cladding. Optics and Laser Technilogy 35(2):81–86
Pinkerton A, Li L (2005) Multiple-layer laser deposition of steel components using gas- und water-atomised powders: the difference and the mechanisms leading to them. Appl Surf Sci 247(1-4):175–181
Pinkerton AJ (2007) An analytical model of beam attenuation and powder heating during coaxial laser direct metal deposition. J. of Physics D: Appl. Phys. 40(23) doi:https://doi.org/10.1088/0022-3727/40/23/012
Ibarra-Medina J (2012) Development and application of a CFD model of laser metal deposition. PhD. Thesis University of Manchester, United Kingdom.
C. Kamath BEDGFGWEKAS (2013) Density of additive-manufactured, 316L SS parts using laser powder-bed fusion at powers up to 400 W. LLNL-TR-648000 Lawrence Livermore National Laboratory.
Weerasinghe VM, Steen WM (1987) Laser cladding with blown powder. Metall Construction. (10):581-585.
Beuth J, Klingbeil N (2001) The role of process variable in laser-based direct metal solid freeform fabrication. Journal of Materials. (9):36-39
Martukanitz R, Michaleris P, Palmer T, DebRoy T, Liu ZK, Otis R et al (2014) Toward an integrated computational system for describing the additive manufacturing process for metallic materials. Additive Manufacturing 1:52–63
Li C, Fu CH, Guo YB, Fang FZ (2015) Fast prediction and validation of part distortion in selective laser melting. Procedia Manufacturing 1:355–65. doi:https://doi.org/10.1016/j.promfg.2015.09.042.
Papadakis L, Loizou A, Risse J, Schrage J (2014) Numerical computation of component shape distortion manufactured by selective laser melting. Procedia CIRP 18:90–95
Keller N, Ploshikhin V (2014) New method for fast predictions of residual stress and distortion of AM parts. Solid Freeform Fabrication Symposium, Austin, Texas
Ding J, Colegrove P, Mehnen J, Ganguly S, Sequeira Almeida PM, Wang F et al (2011) Thermo-mechanical analysis of wire and arc additive layer manufacturing process on large multi-layer parts. Comput Mater Sci 50(12):3315–3322
Denlinger ER, Heigel JC, Michaleris P (2014) Residual stress and distortion modeling of electron beam direct manufacturing Ti-6Al-4V. J Eng Manuf 1:1–11
Heigel JC, Michaleris P, Reutzel EW (2015) Thermo-mechanical model development and validation of directed energy deposition additive manufacturing of Ti-6Al-4V. Additive Manufacturing 5:9–19
Papadakis L, Loizou A, Risse J, Bremen S, Schrage J (2014) A computational reduction model for appraising structural effects in selective laser melting manufacturing. Virtual and Physical Prototyping 9(1):17–25
Michaleris P (2014) Modeling metal deposition in heat transfer analyses of additive manufacturing processes. Finite Elem Anal Des 86:51–60
ESI-Group (2015) Systus reference analysis manual
ESI-Group (2015) Sysweld user manual
Johnson AW, Mehl F (1939) Reaction kinetics in processes of nucleation and growth. Transactions of the Metallurgical Society 135(1):416–442
Denlinger ER, Irwin J, Michaleris P (2014) Thermomechanical modeling of additive manufacturing large parts. J Manuf Sci Eng 136:1–8
Neugebauer F, Keller N, Ploshikhin V, Feuerhahn F, Köhler H (2014) Multi scale FEM simulation for distortion calculation in additive manufacturing of hardening stainless steel. International Workshop on Thermal Forming and Welding Distortion, Bremen, Germany
Desmaison O, Bellet M, Guillemot G (2014) A level set approach for the simulation of the multipass hybrid laser/GMA welding process. Comput Mater Sci 91:240–250
Goldak J, Chakravarti A, Bibby M (1984) A new finite element model for welding heat sources. Metall Trans B 15(2):299–305
Hussein A, Hao L, Yan C, Everson R (2013) Finite element simulation of the temperature and stress fields in single layers built without support in selective laser melting. Mater Des 52:638–647. doi:https://doi.org/10.1016/j.matdes.2013.05.070
Wang L, Felicelli S, Gooroochurn Y, Wang PT, Horstemeyer MF (2008) Optimization of the LENS® process for steady molten pool size. Materials Science and Engineering A. 148–156. doi:https://doi.org/10.1016/j.msea.2007.04.119.
Niebling F, Otto A, Geiger M (2002) Analyzing the DMLS-process by a macroscopic FE-model. University of Texas, Austin
Fachinotti VD, Cardona A (2008) Semi-analytical solution of the thermal field induced by a moving double-ellipsoidal welding heat source in a semi-infinite body. Mecanica Computacional XXVII:1519–1530
Akbari M, Sinton D, Barami M (2009) Moving heat source in a half space: effect of source geometry. ASME, San Francisco
Gusarov AV, Yadroitsev I, Bertrand P, Smurov I (2009) Model of radiation and heat transfer in laser-powder interaction zone at selective laser melting. Journal of Heat Transfer. 131 doi:https://doi.org/10.1115/1.3109245
Michaleris P (2011) Modeling welding residual stress and distortion: current and future research trends. Sci Technol Weld Join 16(4):363–368
Papadakis L, Branner G, Schober A, Richter KH, Uihlein T (2012) Numerical modeling of heat effects during thermal manufacturing of aero engine components. World Congress on Engineering
Bellet M, Thomas BG (2007) Solidification Macroprocesses. Materials Processing Handbook. CRC Press. ᅟ
Szost BA, Terzi S, Martina F, Boisselier D, Prytuliak A, Pirling T, et al. A comparative study of additive manufacturing techniques: residual stress and microstructural analysis of CLAD and WAAM printed Ti-6Al-4V components. Material Science and Engineering A. (Under Review)
Ueda Y, Fukuda K, Nakatcho K, Endo S (1975) A new measuring method of residual stresses with the aid of finite element method and reliability of estimated values. Journal of the Society of Naval Architects of Japan 138:499–507
Zhang L, Michaleris P, Marugabandhu P (2007) Evaluation of applied plastic strain methods for welding distortion prediction. J Manuf Sci Eng 129(6):1000–1010
Jung GH, Tsai CL (2004) Plasticity-based distortion analysis for fillet welded thin-plate T-joints. Weld J 83(6):177–187
Keller N, Ploshikhin V (2014) Fast numerical predictions of residual stress and distortion of AM parts. 1st International Symposium on Material Science and Technology of Additive Manufacturing, Bremen, Germany.
Lane B, Moylan S, Whitenton E, Donmez A, Falvey D, Ma L (2015) Thermographic and FE simulation of the DMLS Process at NIST. AMC Winter Meeting, Knoxville
Körner C, Bauereiß A, Osmanlic F, Klassen A, Markl M, Rai A (2014) Simulation of selective beam melting on the powder scale: mechanisms and process strategies. Materials Science and Technology of Additive Manufacturing - ISEMP/Airbus, Bremen, Germany
Gandin CA, Rappaz M (1994) A coupled finite element - cellular automaton model for the prediction of dendritic grain structures in solidification processes. Acta Metall 42:2233–2246
Mokadem S, Bezencon C, Hauert A, Jacot A, Kurz W (2007) Laser repair of superalloy single crystals with varying substrate orientations. Metallurgical and Materials Transactions. 38A doi:https://doi.org/10.1007/s11661-007-9172-z
(2007) R.L. Clay, S.J. Marburger, M.S. Shneider, T.G. Trucano. SAND2007-0570 Sandia National Laboratories.
Nolte WL, Kennedy BC, Dziegiel RJ (2003) Technology readiness level calculator., NDIA Systems Engineering Conference
Cowles B, Backman D, Dutton R (2012) Verification and validation of ICME methods and models for aerospace applications. IMMI 1:2
G A (1992) Homogenization and two-scale convergence. SIAM Journal on Mathematical Analysis. 23(6):1482-1518
Bendsoe MP, Kikuchi N (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224
Haslinger J, Kocvara M, Leugering G, Stingl M (2010) Multidisciplinary free material optimization. SIAM J Appl Math 70(7):2709–2728
Li P, Warner DH, Fatemi A, Phan N (2016) On the fatigue performance of additively manufactured Ti-6Al-4V to enable rapid qualification for aerospace applications. AIAA Sci-Tech, 57th AIAA Structure, Structural Dynamics and Materials Conference, San Diego. In: AIAA 2016-1656
Mies D, Marsden W, Dryer S, Warde S (2016) Data-driven certification of additively manufactured parts. AIAA Sci-Tech, 57th AIAA Structure, Structural Dynamics and Materials Conference, San Diego. In: AIAA 2016-1658
Allaire G, Jouver F, Michailidis G (2013) Casting constraints in structural optimization via a level-set method. 10th World Congress on structural and multidisciplinary optimization, Orlando, Florida.
Acknowledgements
The authors acknowledge the financial support of collaborative programs, each focused on a certain aspect of the additive-manufacturing modeling challenges. In particular, the co-funding of the European Commission 7th Framework Program AMAZE and the DARPA Open Manufacturing program, USA, are greatly appreciated.
The authors would like to thank Prof. Stephen Brown and Dr. Marc Holmes, University of Swansea, for their help with the coating models. Thanks are also due to Dr. Paul Dionne for his contributions on grid overlay method as well as project partners and collaborators for the ongoing discussions, support, and motivation.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
All authors are employees of ESI Group, a software vendor dedicated to engineering software development. The results presented in this work are that of the team involved in additive-manufacturing research effort. References to literature and results of other research teams are made neutrally to gain a better understanding of the modeling algorithms and the implications for real-life applications.
Authors’ contributions
All authors contributed to the contribution of this article. MM, HWM, and NN are mainly involved in the development of micromodeling capabilities. HZD and OD performed all macromodeling work. MM leads the research and development effort. All authors read and approved the final manuscript
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://doi.org/creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Megahed, M., Mindt, HW., N’Dri, N. et al. Metal additive-manufacturing process and residual stress modeling. Integr Mater Manuf Innov 5, 61–93 (2016). https://doi.org/10.1186/s40192-016-0047-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1186/s40192-016-0047-2