Abstract
Symmetric and asymmetric tilt grain boundaries in Cu and Al were generated using molecular statics energy minimization in a classical molecular dynamics code with in-plane grain boundary translations and an atom deletion criterion. The following dataset (NIST repository, http://hdl.handle.net/11256/358) contains atomic coordinates for minimum energy grain boundaries in three-dimensional periodic simulation cells, facilitating their use in future simulations. This grain boundary dataset is used to show the relative transferability of grain boundary structures from one face-centered cubic system to another; in general, there is good agreement in terms of grain boundary energies (R2 > 0.99). Some potential applications and uses of this tilt grain boundary dataset in nanomechanics and materials science are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Data Description
Introduction
The bulk properties of polycrystalline materials are heavily influenced by atomic details associated with the crystallography of the grains and the structure of grain boundaries [1]. While one route to achieving an improvement to the properties of polycrystalline materials is to engineer the texture of the material, another route that is being increasingly explored is to engineer the distribution of special grain boundaries in the polycrystal. This latter technique is motivated by the fact that different atomic structures at the grain boundary often lead to different properties or responses. Hence, the notion of “grain boundary engineering” [2] has evolved to increase the number density of grain boundaries with beneficial properties, while reducing the number density of boundaries that have detrimental properties. It can also refer to compromise trade-offs of distributions to achieve competing property sets. In practice, grain boundary (GB) engineering has largely referred to increasing the number of low-Σ boundaries [3], e.g., increasing the number of coherent twin boundaries [4], which have properties that differ significantly from general high-angle grain boundaries. As computational techniques have improved, more researchers are turning to atomistic studies to quantify the influence of grain boundary structure on properties and collective responses at higher length and time scales. Many of the early studies (e.g., [5, 6]) focused on understanding the grain boundary structure and energy. However, recent studies have expanded to address grain boundary sliding [7–10], migration and bulk dislocation slip transfer [11–13], grain boundary fracture [14–16] or spall [17–20], grain boundary segregation [21–23], phase transformations [24], grain boundary mobility [25, 26], etc. In many cases, grain boundary structures have to be recreated in order to assess properties, and it is unclear whether the minimum energy structure was used or a higher energy metastable structure; hence, openly publishing grain boundary datasets in materials repositories can aid in providing a common starting configuration for these studies.
The objective of this data descriptor article is to provide and describe datasets for minimum energy (<100>, <110>, <111>) symmetric and (Σ3, Σ5, Σ9, Σ11, Σ13) asymmetric tilt grain boundaries in Cu and Al [27], which have been previously used to explore structure-energy relationships [28–31] as well as dislocation nucleation at the grain boundary [32–37]. The grain boundary datasets for Al and Cu can support future studies of structure-property relations, as well as providing data to support multiscale models of various types [38].
Simulation methods
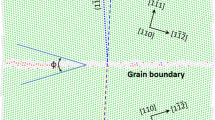
The macroscopic grain boundary geometry is defined using five degrees of freedom (DOF) that fully describe the crystallographic orientation of one grain relative to the other (3 DOF) and the orientation of the boundary relative to one of the grains, i.e., the grain boundary plane (2 DOF). On a microscopic level, the translation between the two adjoining crystal lattices requires three additional DOF. Atomistic simulations are used to explore how the grain boundary DOF affect the structure and properties of particular grain boundaries.
A few terms are often used to describe the crystallography of grain boundaries: sigma values (Σ), tilt versus twist, symmetric versus asymmetric boundaries, crystallographic directions for GB tilt/twist classification (e.g., <100>, <110>, <111>), and specification of grain boundary planes. First, the Σ value is often used in conjunction with the coincident site lattice (CSL) model, which simply states that at certain orientations between two interpenetrating lattices there are a number of positions where the atoms are in coincidence. Boundaries with a large fraction of coincident sites may have properties different from more general grain boundaries with a much lower number of coincident points. In this context, the Σ value refers to the reciprocal of the density of coincident sites, i.e., a Σ3 boundary has 1/3 of the atoms in coincident sites, the Σ13 has 1/13, and so on. Tilt and twist boundaries arise from both crystal lattices having a shared lattice vector; in tilt boundaries, this lattice vector is contained within the grain boundary plane, and in twist boundaries, this lattice vector is orthogonal to the grain boundary plane. For most general grain boundaries, they are a combination of both tilt and twist. For pure tilt boundaries, they can be separated into symmetric and asymmetric boundaries based on their relationship to the grain boundary plane, i.e., the crystallographic directions of symmetric tilt boundaries are mirrored about the grain boundary plane. In terms of specifying lattice directions in this work, the tilt direction is often specified as <100> or <110> or <111>, which specifies a family of crystallographically identical directions (i.e., <110> can refer to [110], [101], [011], etc.). In the same manner, a family of planes can be referred to by {210}, for example, where this can denote the planes (210), (120), (012), etc. Therefore, for tilt boundaries, a lattice direction is often given to denote the shared tilt axis (e.g., <110>) and either one (symmetric) or two (asymmetric) planes are given to fully characterize the grain boundary crystallography. For further information on the crystallography of grain boundaries and the coincident site lattice, the reader is referred to books such as by Randle [39].
The datasets for Al and Cu tilt grain boundaries [27] are generated using a computational cell with three-dimensional (3-D) periodic boundary conditions, which results in two grains and two grain boundaries. The crystal lattices for the two grains are created such that periodicity in all directions is maintained through the simulation cell boundaries. In the case of the direction perpendicular to the grain boundary plane, this periodic distance is selected to ensure that the two grain boundaries are identical in structure. The size of the computational cell is large enough to eliminate any interaction between the two grain boundaries while attempting to minimize the number of atoms in the cell. The two grain boundaries are separated by similar distances in terms of lattice units—a minimum distance of 12.0 nm in Cu and ~13.4 nm in Al, corresponding to the simulated minimum energy lattice constants a0 = 3.615 Å and a0 = 4.032 Å with the present Cu and Al interatomic potentials, respectively. The minimum periodic distance is used for the orthogonal directions parallel to the grain boundary plane. This effectively minimizes the number of atoms required without affecting the 0 K grain boundary structure or energy. For calculating properties, replication in these dimensions may be required to ensure that simulation cell size effects are not affecting the results (e.g., suppressing dislocations on certain {111} systems).
The included scriptsFootnote 1 for the 15 May 2015 version of the classical molecular dynamics code LAMMPS (Large-scale Atomic/Molecular Massively Parallel Simulator) [40] serve as an example of a brute force method for obtaining the local and global “minimum energy” grain boundary structures for a particular set of macroscopic DOF. Because of different translations of the grains with respect to each other and different densities of atoms at the interface, a single set of macroscopic DOF can produce a multitude of different grain boundary structures and energies. In practice, the minimum energy structure (from this distribution of different structures) correlates well with high-resolution TEM images of interface structures [34, 41]. There are multiple steps for obtaining the minimum energy structure: grain boundary initialization, rigid body translation, atom deletion criterion, and conjugate gradient energy minimization.
The grain boundary initialization step involves selecting the crystallographic orientations of the two lattices, defining the interatomic potential, calculating the lattice constant and periodic distances, defining the simulation cell bounds, and building the atom positions within the two grains. Next, the rigid body translation of one lattice with respect to the other is used to sample different starting configurations, thus improving the probability that a “global” minimum energy structure is obtained following energy minimization. In these datasets, a grid of translations was defined to sample the in-plane translations uniformly (minimum of four translations in the tilt direction and eight translations in the grain boundary period direction). Since atoms in the two lattices are built up to the GB plane, an atom deletion criterion—i.e., if atom a from lattice A is within a certain distance of atom b in lattice B, then delete atom a—is used to remove atoms that may physically lie too close to each other. Note that this criterion removes atoms identically at both grain boundaries. In these datasets, the atom deletion criterion uses distances between 0.275a0 and 0.700a0 in increments of 0.005a0 at each in-plane translation (for face-centered cubic (fcc), i.e., nearest neighbor distance is \( \sqrt{2{a}_0} \)). Here, successive atom deletion criteria that do not reduce the number of atoms reproduce a previously examined structure and thus are ignored to improve computational efficiency. It should be noted that for asymmetric grain boundaries, the decision to delete an atom from lattice A or lattice B will give different starting configurations, so the number of configurations is doubled (e.g., 86 distances/starting configurations for symmetric GBs, 172 distances for asymmetric GBs). After the initial configuration is generated, energy minimization is used to obtain the final structure for a particular combination of the grain boundary crystallography, in-plane translations, and atom deletion distance. In this case, the nonlinear conjugate gradient algorithm employed the Polak-Ribiere formula and the secant method for calculating the new search direction (i.e., for atom movement) and the appropriate step size (magnitude of movement), respectively. The conjugate gradient algorithm terminates when the residual of the potential energy (i.e., the force vector) falls below a predefined value. Since there are no fixed regions of atoms in the computational cell, the crystal lattices can translate as appropriate and grain boundary atoms can move to obtain the final minimum energy structure. Further details can be found in Ref. [29].
In the present datasets, embedded atom method (EAM) potentials for Cu [42] and Al [43] were used to generate the minimum energy grain boundaries. These potentials were experimentally fit to give the correct physical properties for Cu and Al, including the equilibrium lattice parameter, the cohesive energy, three elastic constants, and the vacancy formation energy, to name a few. The calculated stacking fault energies (SFE) for these potentials are consistent with experimental data and ab initio calculations. The stable SFE determines the width of dislocation dissociation within both the lattice and the grain boundary. While these potentials were deemed valid for generating grain boundary structures and energies, it should be checked that their properties are suitable for capturing other grain boundary properties or responses.
As an indication of the validity of the methods and potentials, the computed grain boundary energies are in good agreement with experimental energy curves for <110> symmetric tilt grain boundaries [44] and for Σ3 asymmetric grain boundaries [45, 46]. For instance, Fig. 1 compares the computed grain boundary energiesFootnote 2, which have been normalized by the {110} surface energy, to experimentally measured energies. The grain boundary structures generated are also in good agreement with prior simulated grain boundary structures for low- and high-SFE materials [47, 48] as well as experimentally observed structures using high-resolution transmission electron microscopy [41, 49], which includes the observation of the 9R phase in low-SFE fcc metals [50–52], as shown in Fig. 2.
Simulated and experimental grain boundary energy divided by the surface energy as a function of inclination angle for Σ3 ATGBs in Cu. The experimental values are measured by the thermal grooving technique [46]. The present dataset contains the simulated Σ3 ATGB structures. The lower energy (asterisks) Σ3 structures have 100 nm between grain boundaries to aid in capturing the extended dissociation of partial dislocations to create the 9R phase
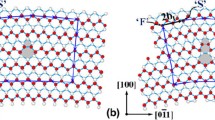
Comparison of calculated Σ3 Φ = 81.95° ATGB structure with the 9R phase in Cu with experimental HRTEM image of the 9R phase in Ag [50]. a Interface structure with structural units outlined, (b) simulated image using atom positions from (a), and (c) HRTEM image of Ernst and coworkers [50]. The white lines correspond to the {111} planes in the adjoining crystals and at the interface. Panel (c) reprinted from [50] with permission; © 1992 The American Physical Society
Dataset description
The following dataset [27] contains 174 symmetric and asymmetric tilt grain boundaries in both Al and Cu (total of 348 grain boundaries) along with the corresponding interatomic potentials mentioned previouslyFootnote 3. In this dataset, there are 68 symmetric tilt grain boundaries (STGBs), which include 29 <100> STGBs, 32 <110> STGBs, and 7 <111> STGBs. The remaining 106 grain boundaries in the dataset are asymmetric tilt grain boundaries (ATGBs), which include 26 Σ3 ATGBs, 16 Σ5 ATGBs, 27 Σ9 ATGBs, 27 Σ11 ATGBs, and 10 Σ13 ATGBs. In the dataset, the coordinates of the simulation cell and atoms for Al and Cu are provided in a LAMMPS data file format and can be accessed using the “read_data” command within a LAMMPS input file. The data file names are in the following format: lammps.#1.#2_#3.dat where argument #1 is the element type (Cu or Al), argument #2 is the system (e.g., stgb001 for <100> STGBs or sigma3 for Σ3 ATGBs), and argument #3 is a reference number that is sequentially numbered in order of increasing misorientation angle from a vector describing the GB plane (1, 2, 3, etc.). The reference number (argument #3) is used to identify the different GBs in the associated text file (info.#4.txt, where argument #4 corresponds to the aforementioned argument #2), which contains the minimum information required to specify the orientations of the surrounding two crystal lattices (the lattice vector describing the GB plane, i.e., x1, y1, z1 for lattice 1 and x2, y2, z2 for lattice 2), the computed grain boundary energies, and the sigma values for the symmetric tilt grain boundaries. Table 1 shows an example of the information within this text file for Σ3 asymmetric tilt grain boundaries. First, the misorientation angle is with reference to the <110>{112} STGB (first boundary); if the reference is the <110>{111} STGB (the 26th boundary), then all misorientation angles θ would be 90°-θ. Also, x1, y1, z1 and x2, y2, z2 refer to the grain boundary planes of lattices 1 and 2, respectively, in this dataset. Since the tilt direction is also known for the symmetric and asymmetric systems, the three orthogonal lattice vectors describing the complete lattice orientation can be calculated. For asymmetric tilt grain boundaries, both planes are necessary to completely describe the grain boundary, i.e., the Σ3 (110)/(114) ATGB.
In the ATGB systems, it should be noted that the two STGBs that bracket the asymmetric boundaries are also included. These are actually duplicates of grain boundaries in the STGB systems, and the text file “duplicate_boundaries.txt” identifies the duplicate boundary file names. These duplicate boundaries were retained to enable easy identification with the corresponding ATGBs. Therefore, there are 164 unique tilt grain boundaries in this dataset, with a fine sampling of low CSL ATGBs in the <100> and <110> tilt systems.
Figures 3 and 4 illustrate the grain boundary energies in different systems as a function of misorientation (inclination) angle for STGBs (ATGBs) in Al and Cu. Figure 3 follows the well-known grain boundary energy curves in <100> and <110> STGBs, where major energy cusps are the Σ3{111} (i.e., coherent twin) and Σ11{113} STGBs and minor cusps appear for the Σ5{310} STGB. The low-Σ boundaries (Σ ≤ 13) are identified, and there are two STGBs for each Σ value, i.e., the Σ3{111}θ = 109.47° and the Σ3{112}θ = 70.53° boundaries in the <110> STGB system.
Grain boundary energy as a function of misorientation angle for <100> and <110> STGBs in (a) Al and (b) Cu. The low-Σ boundaries are identified in each tilt system. The misorientation angle is defined as the (symmetric) rotation of the adjoining lattices from the reference plane (i.e., 0°), which is a {001} plane for both STGB systems. A few lower energy boundaries (circled asterisk, >1 mJ m−2) are also plotted based on the transferability analysis
Grain boundary energy as a function of inclination angle for (a, b) <100> and (c, d) <110> ATGBs in (a, c) Al and (b, d) Cu. The inclination angle is defined from a reference plane from one of the low-Σ STGBs (0°): Σ5{310} and Σ13{510} for <100> tilt boundaries and Σ3{111}, Σ9{114}, and Σ11{113} for <110> tilt boundaries. Some lower energy boundaries (circled asterisk, >1 mJ m−2) are also plotted based on the transferability analysis
For each of these low-Σ STGBs, the grain boundary plane can be rotated about the tilt direction to break the crystal symmetry and create an ATGB in that Σ systemFootnote 4. This rotation is termed the inclination angle. Figure 4 shows the change in grain boundary energy for low-Σ systems in the <100> and <110> tilt systems as a function of inclination angle for Cu and Al. At 90° in ATGBs with a <110> tilt axis (and 45° for <100> tilt axis), the grain boundary reaches the other STGB in that Σ system. The dataset includes all STGBs and ATGBs in Figs. 3 and 4.
Transferability
As a measure of transferability, the tilt grain boundaries in the dataset [27] are also tested to assess their utility in generating tilt grain boundary datasets for other fcc materialsFootnote 5. For example, consider transforming the Cu dataset to a new Al dataset, which can then be compared to the Al grain boundaries obtained through a large number of different starting configurations (>1000). For each grain boundary in the Cu dataset, both the simulation cell and the atom coordinates are affinely displaced according to the ratio of the minimum energy lattice constants for the two interatomic potentials (aAl/aCu = 4.050 Å/3.615 Å = 1.1204); this correctly scales the simulation cell to ensure the correct bulk lattice constant for Al. Then, the conjugate gradient minimization routine is used to obtain the minimum energy structure at the grain boundary. This converted (Cu→Al) grain boundary dataset can then be directly compared to the energies obtained in the original Al dataset from the large number of in-plane translations and atom deletion.
The results are plotted in Fig. 5a for Al grain boundaries and in Fig. 5b for Cu grain boundaries. In general, the grain boundary energies agree well in Al (R2 = 0.9868) and agree even better in Cu (R2 = 0.9971). Figure 5 also highlights that not all grain boundaries agree in terms of energy, with some boundaries lying both above and below the 45° perfect correlation line. Interestingly, some of the converted grain boundaries exhibited lower grain boundary energies than the initial dataset (shown in red). This most likely stems from the fact that the in-plane translations were more coarsely sampled as the in-plane periodic distances increased, i.e., the more complex boundaries (higher Σ value resulting in larger grain boundary area) tended to have this issue. Hence, the initial dataset includes data files for the lower energy grain boundary structures (in red) along with the original grain boundary structures. This results in an even greater agreement for Al and Cu (R2 = 0.9918 and R2 = 0.9974, respectively), indicating that these datasets can be adequate predictors for minimum energy structures (and energies) in other fcc systems.
Plot of grain boundary energies in (a) Al and (b) Cu for all grain boundaries in this dataset. The grain boundary energies for the minimum energy structures are on the (horizontal) x-axis while grain boundary energies from the transferred cases (Cu to Al and vice versa) are plotted on the (vertical) y-axis
Several converted grain boundary energies, shown in Fig. 5, are substantially higher than those from the original dataset (by as much as 25 %). Because Cu has a much lower SFE than Al, the grain boundary structures are not expected to directly match when scaled by the lattice constant, i.e., partial dislocations in low-SFE materials will dissociate much more readily than in high-SFE materials, which tend to form more compact full dislocations. Hence, variation in grain boundary energy between the two fcc materials when transferred to a new system is perhaps expected.
Once one grain boundary dataset is transferred to a new system, other relationships between different fcc materials can be examined using the same structure. For instance, the grain boundary energies can be compared for two materials, as shown in Fig. 6. In the analysis that follows, the grain boundary energies in Cu are 1.78–2.03 times those in Al, depending on whether or not an intercept is applied to the linear model. It is hypothesized that the intercept value is a consequence of a large number of Σ3 ATGBs at the lower end of the energy distribution and is related to the SFE, i.e., the Σ3 coherent twin has a lower energy in Cu than in Al (22 versus 75 mJ m−2, respectively). Indeed, other studies have explored understanding the relationship between grain boundary energies using the ratio of a number of different element properties [53], including stable SFE, the C44 elastic constant, and the Voigt average shear modulus μ.
Potential applications of this dataset
The present dataset [27] can be applied in various ways. First, it can serve as a reference set of tilt grain boundaries for exploring grain boundary properties as a function of grain boundary character. For example, this grain boundary set was first applied to the problem of dislocation nucleation in symmetric and asymmetric tilt grain boundaries [32, 33, 35], of which an example input script is includedFootnote 6, but could easily be extended to any number of nanomechanical or materials science studies, atomistic or continuum in nature, including but not limited to the following:
-
1.
Dislocation nucleation in unexplored asymmetric tilt grain boundary systems (Σ5, Σ9, Σ11, Σ13), similar to the previous study on Σ3 boundaries [33]
-
2.
Grain boundary shear, shuffling, and sliding [7–10, 54–58] or dislocation interactions [11–13, 59–61]
- 3.
-
4.
Connecting grain boundary degrees of freedom or structure with energy [31, 62] and connecting grain boundary structure to experiments [63–65]
-
5.
New techniques for examining grain boundary structure [66–69]
-
6.
Fracture, fracture mechanisms [14, 15], and spall in grain boundaries [17–20]
-
7.
Grain boundary structural mechanisms, including dissociation and faceting [70]
-
8.
Interaction, diffusion, and precipitation of solutes [21, 22] and impurities [71, 72]
- 9.
Second, this dataset can serve as a starting point for exploring grain boundaries in other fcc systems (i.e., transferability). This transferability to minimum energy structures in other fcc systems can allow for exploring properties in other fcc systems based on a standard grain boundary representation as a starting point.
Third, this dataset can serve as a starting point for modification to explore metastable grain boundary states or even to obtain lower energy boundaries, if the global minimum energy boundary was not attained. For instance, by removing atoms at the boundary, different metastable (higher energy) or perhaps even lower boundaries could be obtained to understand how sensitive the grain boundary properties of a single grain boundary are to changes in grain boundary structure and energy, e.g., for examining inelastic deformation in metastable boundaries [77] or the potential multiplicity of grain boundary structures [78, 79]. This includes the incorporation of additional elements as solutes or segregants.
Last, the structures and energies within this dataset can be used as reference data to compare results of more efficient computational techniques for obtaining minimum energy structures in fcc systems. As researchers explore methods to probe grain boundary DOF, more efficient techniques are required to efficiently probe this space. The dataset here utilized a brute force method with translations and atom deletion criteria; certainly, there are likely more efficient but perhaps more approximate methods to obtain minimum energy structures at a fraction of the computational cost.
Availability and Requirements of Software Used
The 15 May 2015 version of the classical molecular dynamics code LAMMPS [40] was used in the following work. LAMMPS is distributed as an open source code under the terms of the GPL. LAMMPS is distributed by Sandia National Laboratories, a US Department of Energy laboratory, at http://lammps.sandia.gov/. All input scripts and datafiles associated with the dataset are tested on the aforementioned version of LAMMPS.
Availability of Supporting Data
The dataset is openly distributed through the NIST Material Measurement Laboratory data repository server at https://materialsdata.nist.gov/. Within this repository, the dataset [27] supporting the results of this article is available in the NIST Computational File Repository, Atomistic Simulations, at http://hdl.handle.net/11256/358.
Notes
In the directory “Grain Boundary Generation” of the dataset [27].
Some of the 9R structures were computed with a larger spacing between the two grain boundaries and are included in the directory “lammps15May2015_Cu_9R” of the dataset [27].
In the directories “lammps15May2015_Al” and “lammps15May2015_Cu” of the dataset [27].
Since only the grain boundary plane is rotated, the rotation matrix describing the misorientation between the two crystal lattices does not change; hence, the Σ value is the same for these ATGBs.
The LAMMPS input script for this transferability is included in the Al and Cu grain boundary directories in the dataset [27].
In the directory “Grain Boundary Property” of the dataset k, which can be modified for different properties.
References
Mishin Y, Asta M, Li J (2010) Atomistic modeling of interfaces and their impact on microstructure and properties. Acta Mater 58:1117–51
Watanabe T (1984) An Approach to Grain-Boundary Design for Strong and Ductile Polycrystals. Res Mech 11:47–84
Watanabe T (1994) The Impact of Grain-Boundary-Character-Distribution on Fracture in Polycrystals. Mater Sci Eng A 176:39–49
Randle V (1999) Mechanism of twinning-induced grain boundary engineering in low stacking-fault energy materials. Acta Mater 47:4187–96
Sutton AP, Vitek V (1983) On the Structure of Tilt Grain-Boundaries in Cubic Metals: 1. Symmetrical Tilt Boundaries. Philos T R Soc A 309:1–68
Wolf D (1990) Structure-Energy Correlation for Grain-Boundaries in Fcc Metals: 3. Symmetrical Tilt Boundaries. Acta Metall Mater 38:781–90
Warner DH, Molinari JF. Effect of normal loading on grain boundary migration and sliding in copper. Model Simul Mater Sc. 2008;16:075007. Doi:10.1088/0965-0393/16/7/075007
Sansoz F, Molinari JF (2005) Mechanical behavior of Sigma tilt grain boundaries in nanoscale Cu and Al: A quasicontinuum study. Acta Mater 53:1931–44
Fensin SJ, Asta M, Hoagland RG (2012) Temperature dependence of the structure and shear response of a Sigma 11 asymmetric tilt grain boundary in copper from molecular-dynamics. Philos Mag 92:4320–33
Peron-Luhrs V, Sansoz F, Noels L (2014) Quasicontinuum study of the shear behavior of defective tilt grain boundaries in Cu. Acta Mater 64:419–28
de Koning M, Kurtz RJ, Bulatov VV, Henager CH, Hoagland RG, Cai W et al (2003) Modeling of dislocation-grain boundary interactions in FCC metals. J Nucl Mater 323:281–9
Dewald M, Curtin WA. Multiscale modeling of dislocation/grain-boundary interactions: III. 60 degrees dislocations impinging on Sigma 3, Sigma 9 and Sigma 11 tilt boundaries in Al. Model Simul Mater Sc. 2011;19:055002. Doi:10.1088/0965-0393/19/5/055002
Spearot DE, Sangid MD (2014) Insights on slip transmission at grain boundaries from atomistic simulations. Curr Opin Solid St M 18:188–95
Adlakha I, Bhatia MA, Tschopp MA, Solanki KN (2014) Atomic scale investigation of grain boundary structure role on intergranular deformation in aluminium. Philos Mag 94:3445–66
Adlakha I, Tschopp MA, Solanki KN (2014) The role of grain boundary structure and crystal orientation on crack growth asymmetry in aluminum. Mat Sci Eng A 618:345–54
Cui CB, Beom HG (2014) Molecular statics simulations of intergranular fracture along Sigma 11 tilt grain boundaries in copper bicrystals. J Mater Sci 49:8355–64
Luo SN, Germann TC, Tonks DL, An Q. Shock wave loading and spallation of copper bicrystals with asymmetric Sigma 3 <110> tilt grain boundaries. J Appl Phys. 2010;108:093526. Doi:10.1063/1.3506707
Han WZ, An Q, Luo SN, Germann TC, Tonks DL, Goddard WA. Deformation and spallation of shocked Cu bicrystals with Sigma 3 coherent and symmetric incoherent twin boundaries. Phys Rev B. 2012;85:024107. Doi:10.1103/Physrevb.85.024107
Fensin SJ, Valone SM, Cerreta EK, Escobedo-Diaz JP, Gray GT, Kang K, et al. Effect of grain boundary structure on plastic deformation during shock compression using molecular dynamics. Model Simul Mater Sc. 2013;21:015011. Doi:10.1088/0965-0393/21/1/015011
Fensin SJ, Escobedo-Diaz JP, Brandl C, Cerreta EK, Gray GT, Germann TC et al (2014) Effect of loading direction on grain boundary failure under shock loading. Acta Mater 64:113–22
Tschopp MA, Gao F, Solanki KN. Binding of HenV clusters to alpha-Fe grain boundaries. J Appl Phys. 2014;115:233501. Doi:10.1063/1.4883357
Tschopp MA, Gao F, Yang L, Solanki KN. Binding energetics of substitutional and interstitial helium and di-helium defects with grain boundary structure in alpha-Fe. J Appl Phys. 2014;115:033503. Doi:10.1063/1.4861719
Rajagopalan M, Tschopp MA, Solanki KN (2014) Grain Boundary Segregation of Interstitial and Substitutional Impurity Atoms in Alpha-Iron. JOM 66:129–38
Frolov T, Olmsted DL, Asta M, Mishin Y. Structural phase transformations in metallic grain boundaries. Nat Commun. 2013;4:1899. Doi:10.1038/Ncomms2919
Olmsted DL, Holm EA, Foiles SM (2009) Survey of computed grain boundary properties in face-centered cubic metals-II: Grain boundary mobility. Acta Mater 57:3704–13
Janssens KGF, Olmsted D, Holm EA, Foiles SM, Plimpton SJ, Derlet PM (2006) Computing the mobility of grain boundaries. Nat Mater 5:124–7
Tschopp MA, Coleman SP, McDowell DL. Al-Cu Symmetric/Asymmetric Tilt Grain Boundary Dataset. NIST Computational File Repository, 2015, http://hdl.handle.net/11256/358
Tschopp MA, McDowell DL (2007) Structural unit and faceting description of Sigma 3 asymmetric tilt grain boundaries. J Mater Sci 42:7806–11
Tschopp MA, McDowell DL (2007) Structures and energies of Sigma 3 asymmetric tilt grain boundaries in copper and aluminium. Philos Mag 87:3147–73
Tschopp MA, McDowell DL (2007) Asymmetric tilt grain boundary structure and energy in copper and aluminium. Philos Mag 87:3871–92
van Beers PRM, Kouznetsova VG, Geers MGD, Tschopp MA, McDowell DL (2015) A multiscale model of grain boundary structure and energy: From atomistics to a continuum description. Acta Mater 82:513–29
Tschopp MA, McDowell DL (2008) Grain boundary dislocation sources in nanocrystalline copper. Scr Mater 58:299–302
Tschopp MA, McDowell DL (2008) Dislocation nucleation in Sigma 3 asymmetric tilt grain boundaries. Int J Plast 24:191–217
Tschopp MA, Spearot DE, McDowell DL. Chapter 82 - Influence of Grain Boundary Structure on Dislocation Nucleation in FCC Metals. In: Hirth JP, editor. Dislocations in Solids: Elsevier; 2008. p. 43–139.
Tschopp MA, Tucker GJ, McDowell DL (2008) Atomistic simulations of tension-compression asymmetry in dislocation nucleation for copper grain boundaries. Comput Mater Sci 44:351–62
Tschopp MA, Tucker GJ, McDowell DL (2007) Structure and free volume of <110> symmetric tilt grain boundaries with the E structural unit. Acta Mater 55:3959–69
Tucker GJ, Tschopp MA, McDowell DL (2010) Evolution of structure and free volume in symmetric tilt grain boundaries during dislocation nucleation. Acta Mater 58:6464–73
The Minerals, Metals & Materials Society (TMS), Modeling Across Scales: A Roadmapping Study for Connecting Materials Models and Simulations Across Length and Time Scales (Warrendale, PA 15086: TMS, 2015), http://www.tms.org/multiscalestudy/
Randle V (1996) The Role of the Coincidence Site Lattice in Grain Boundary Engineering: Institute of Materials
Plimpton S (1995) Fast Parallel Algorithms for Short-Range Molecular-Dynamics. J Comput Phys 117:1–19
Rittner JD, Seidman DN, Merkle KL (1996) Grain-boundary dissociation by the emission of stacking faults. Phys Rev B 53:R4241–4
Mishin Y, Mehl MJ, Papaconstantopoulos DA, Voter AF, Kress JD. Structural stability and lattice defects in copper: Ab initio, tight-binding, and embedded-atom calculations. Phys Rev B. 2001;63.
Mishin Y, Farkas D, Mehl MJ, Papaconstantopoulos DA (1999) Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. Phys Rev B 59:3393–407
Hasson G, Herbeuva I, Boos JY, Biscondi M, Goux C (1972) Theoretical and Experimental Determinations of Grain-Boundary Structures and Energies - Correlation with Various Experimental Results. Surf Sci 31:115
Ernst F, Finnis MW, Koch A, Schmidt C, Straumal B, Gust W (1996) Structure and energy of twin boundaries in copper. Zeitschrift Fur Metallkunde 87:911–22
Wolf U, Ernst F, Muschik T, Finnis MW, Fischmeister HF (1992) The Influence of Grain-Boundary Inclination on the Structure and Energy of Sigma=3 Grain-Boundaries in Copper. Philosophical Magazine A 66:991–1016
Rittner JD, Seidman DN (1996) <110> symmetric tilt grain-boundary structures in fcc metals with low stacking-fault energies. Phys Rev B 54:6999–7015
Spearot DE, Tschopp MA, Jacob KI, McDowell DL (2007) Tensile strength of <100> and <110> tilt bicrystal copper interfaces. Acta Mater 55:705–14
Medlin DL, Mills MJ, Stobbs WM, Daw MS, Cosandey F (1993) Hrtem Observations of a Sigma=3 (112) Bicrystal Boundary in Aluminum. Atomic-Scale Imaging of Surface and Interfaces (MRS Symposium Proceedings, Volume 295). Materials Research Society, Pittsburgh, PA, pp 91–6
Ernst F, Finnis MW, Hofmann D, Muschik T, Schonberger U, Wolf U et al (1992) Theoretical Prediction and Direct Observation of the 9r Structure in Ag. Phys Rev Lett 69:620–3
Hofmann D, Finnis MW (1994) Theoretical and Experimental-Analysis of near Sigma-3 (211) Boundaries in Silver. Acta Metallurgica Et Materialia 42:3555–67
Campbell GH, Chan DK, Medlin DL, Angelo JE, Carter CB (1996) Dynamic observation of the FCC to 9R shear transformation in a copper Sigma=3 incoherent twin boundary. Scr Mater 35:837–42
Holm EA, Olmsted DL, Foiles SM (2010) Comparing grain boundary energies in face-centered cubic metals: Al, Au, Cu and Ni. Scripta Materialia 63:905–8
Warner DH, Molinari JF (2008) Deformation by grain boundary hinge-like behavior. Mater Lett 62:57–60
Sansoz F, Molinari JF (2004) Incidence of atom shuffling on the shear and decohesion behavior of a symmetric tilt grain boundary in copper. Scr Mater 50:1283–8
Cahn JW, Mishin Y (2009) Recrystallization initiated by low-temperature grain boundary motion coupled to stress. Int J Mater Res 100:510–5
Cahn JW, Mishin Y, Suzuki A (2006) Coupling grain boundary motion to shear deformation. Acta Mater 54:4953–75
Wan L, Li J. Shear responses of [110]-tilt {115}/{111} asymmetric tilt grain boundaries in fcc metals by atomistic simulations. Model Simul Mater Sc. 2013;21:055013. Doi:10.1088/0965-0393/21/5/055013
de Koning M, Miller R, Bulatov VV, Abraham FF (2002) Modelling grain-boundary resistance in intergranular dislocation slip transmission. Philos Mag A 82:2511–27
Dewald MP, Curtin WA (2007) Multiscale modelling of dislocation/grain-boundary interactions: I. Edge dislocations impinging on Sigma 11 (113) tilt boundary in Al. Model Simul Mater Sc 15:S193–215
Dewald MP, Curtin WA (2007) Multiscale modelling of dislocation/grain boundary interactions. II. Screw dislocations impinging on tilt boundaries in Al. Philos Mag 87:4615–41
Bulatov VV, Reed BW, Kumar M (2014) Grain boundary energy function for fcc metals. Acta Mater 65:161–75
Marquis EA, Medlin DL (2005) Structural duality of 1/3 <111> twin-boundary disconnections. Phil Mag Lett 85:387–94
Medlin DL, Campbell GH, Carter CB (1998) Stacking defects in the 9R phase at an incoherent twin boundary in copper. Acta Mater 46:5135–42
Medlin DL, Carter CB, Angelo JE, Mills MJ (1997) Climb and glide of a/3<111> dislocations in an aluminium Sigma=3 boundary. Philosophical Magazine A 75:733–47
Coleman SP, Sichani MM, Spearot DE (2014) A Computational Algorithm to Produce Virtual X-ray and Electron Diffraction Patterns from Atomistic Simulations. JOM 66:408–16
Coleman SP, Spearot DE (2015) Atomistic simulation and virtual diffraction characterization of homophase and heterophase alumina interfaces. Acta Mater 82:403–13
Coleman SP, Spearot DE, Capolungo L. Virtual diffraction analysis of Ni [010] symmetric tilt grain boundaries. Model Simul Mater Sc. 2013;21:055020. Doi:10.1088/0965-0393/21/5/055020
Coleman S, Tschopp M, Weinberger C, Spearot D (2015) Bridging atomistic simulations and experiments via virtual diffraction: understanding homophase grain boundary and heterophase interface structures. J Mater Sci. doi:10.1007/s10853-015-9087-9
Brown JA, Mishin Y. Dissociation and faceting of asymmetrical tilt grain boundaries: Molecular dynamics simulations of copper. Phys Rev B. 2007;76:134118. Doi:10.1103/Physrevb.76.134118
Han WZ, Demkowicz MJ, Fu EG, Wang YQ, Misra A (2012) Effect of grain boundary character on sink efficiency. Acta Mater 60:6341–51
Rajagopalan M, Bhatia MA, Tschopp MA, Srolovitz DJ, Solanki KN (2014) Atomic-scale analysis of liquid-gallium embrittlement of aluminum grain boundaries. Acta Mater 73:312–25
Suzuki A, Mishin Y (2003) Atomistic modeling of point defects and diffusion in copper grain boundaries. Interface Sci 11:131–48
Tschopp MA, Solanki KN, Gao F, Sun X, Khaleel MA, Horstemeyer MF. Probing grain boundary sink strength at the nanoscale: Energetics and length scales of vacancy and interstitial absorption by grain boundaries in alpha-Fe. Phys Rev B. 2012;85:064108. Doi:10.1103/Physrevb.85.064108
Bai XM, Voter AF, Hoagland RG, Nastasi M, Uberuaga BP (2010) Efficient Annealing of Radiation Damage Near Grain Boundaries via Interstitial Emission. Science 327:1631–4
Bai XM, Vernon LJ, Hoagland RG, Voter AF, Nastasi M, Uberuaga BP. Role of atomic structure on grain boundary-defect interactions in Cu. Phys Rev B. 2012;85.
Tucker GJ, McDowell DL (2011) Non-equilibrium grain boundary structure and inelastic deformation using atomistic simulations. Int J Plasticity 27:841–57
Vitek V, Sutton AP, Wang GJ, Schwartz D (1983) On the Multiplicity of Structures of Grain-Boundaries. Scripta Metall Mater 17:183–9
Wang GJ, Sutton AP, Vitek V (1984) A Computer-Simulation Study of (001) and (111) Tilt Boundaries - the Multiplicity of Structures. Acta Metall 32:1093–104
Acknowledgements
MT and SC would like to acknowledge the US Army Research Laboratory for funding this work. DLM is grateful for the support of the National Science Foundation (CMMI-1232878) and the Carter N. Paden, Jr. Distinguished Chair in Metals Processing.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing Interests
The authors declare that they have no competing interests.
Authors' contributions
MT, SC, and DM conceived the idea for the manuscript, compiled the dataset, and wrote/edited the manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Tschopp, M.A., Coleman, S.P. & McDowell, D.L. Symmetric and asymmetric tilt grain boundary structure and energy in Cu and Al (and transferability to other fcc metals). Integr Mater Manuf Innov 4, 176–189 (2015). https://doi.org/10.1186/s40192-015-0040-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1186/s40192-015-0040-1