Background

Honeycombs are ordered cellular materials with prismatic cells. The cells of the honeycomb can assume a variety of cross-sectional shapes, including hexagonal, kagome, square, triangular, and mixed triangular and square [1, 2]. Relative to other low-density materials, such as stochastic foams, honeycombs provide very high levels of compressive strength and energy absorption, and those characteristics are linked directly to cell shape and density [2].

The high levels of energy absorption in honeycomb materials can be explained by their characteristic stress-strain response [1]. As illustrated in Fig. 1, honeycombs comprised of elastic-plastic materials typically exhibit a linear elastic region in which cell walls either bend or axially compress in response to in-plane compression. Beyond a critical stress level, the cell walls collapse via elastic buckling (at very low relative densities) or plastic buckling. A region of plateau stress is then observed as the cell walls collapse row by row. Finally, when void space is eliminated by cell wall collapse, the structure densifies and stiffness rapidly increases to approach that of the material in the cell walls.

Fig. 1
figure 1

Mechanical behavior of honeycombs [1, 2]

Full size image

The superior energy absorption capabilities of honeycombs are highly dependent on the relatively flat, extended region of plateau stress in Fig. 1. Once a critical plateau stress is reached, honeycombs absorb very large amounts of energy at the plateau stress level without exposing an underlying structure to additional compressive stress unless the energy imparted to the honeycomb is large enough to cause densification. One disadvantage to utilizing honeycombs for energy absorption applications is that energy absorption in the plateau regime requires plastic buckling, which means that the honeycombs must be replaced after a single use. While it is possible to achieve a plateau stress region with recoverable, elastic buckling for very low density structures (cf. [3]), such cellular structures cannot be fabricated with typical manufacturing methods and also demonstrate very low initial stiffness and plateau stress.

Recent work has shown that negative stiffness honeycombs also provide high levels of initial stiffness, compressive strength, and energy absorption; however, these new cellular structures are unique in that they provide those capabilities in a recoverable way, such that the materials can be subjected to repeated cycles of compressive loading and unloading [4, 5]. A representative negative stiffness honeycomb is illustrated in Fig. 2. Like regular honeycombs, negative stiffness honeycombs consist of an ordered configuration of prismatic cells. Unlike regular honeycombs, the cells are designed to provide recoverable energy absorption. Recoverable energy absorption is enabled by constructing each unit cell from curved beams that exhibit force-displacement behavior similar to that of bistable or snap-through structures [6, 7].

Fig. 2
figure 2

Negative stiffness honeycomb (left) and negative stiffness unit cell (right)

Full size image

As shown in Fig. 3, each curved beam (Fig. 4) is known to exhibit a region of positive stiffness deformation when subjected to a transverse (vertical) load [8]. This positive stiffness behavior is followed by a region of negative stiffness deformation as it transitions from one first-mode-buckled shape to another. The maximum positive force supported by the beam is called the force threshold. The existence of negative stiffness behavior is governed by Q, the ratio of apex height, h, of the beam to its in-plane thickness, t. As established by Qiu et al. [8], a single curved beam exhibits negative stiffness behavior for a wide range of ratios greater than approximately 1.3 and transitions to bistable behavior at ratios greater than 2.31. The double beams utilized in the honeycomb in Fig. 2 transition to bistable behavior at much higher ratios.

Fig. 3
figure 3

Normalized force versus normalized displacement for a single curved beam

Full size image
Fig. 4
figure 4

Shape function and dimensions for a single curved beam

Full size image

While it has been known for some time that properly constrained curved beams exhibit the behavior illustrated in Fig. 3, the authors of this publication have recently designed a negative stiffness honeycomb structure to leverage this behavior for energy absorption [4, 5]. All of the features in the negative stiffness honeycomb structure shown in Fig. 2 have a specific purpose. The double concentric beams are utilized to constrain the beams to transition from one first-mode-buckled shape to another via the third buckling mode, rather than the second mode, which is known to significantly reduce the force threshold of the beam and the magnitude of its negative stiffness. The flat, horizontal walls constrain the horizontal expansion of the unit cell upon application of in-plane compression, thereby enabling snap-through-like behavior. Chamfers near the intersection of the horizontal and vertical walls help prevent twisting of the cell walls during loading.

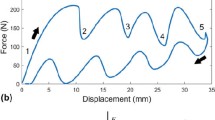
When subjected to in-plane compressive loading, a negative stiffness honeycomb exhibits the force-displacement behavior illustrated in Fig. 5 [4, 5]. The force-displacement behavior in Fig. 5 is obtained by compression testing the negative stiffness honeycomb illustrated in Fig. 2 with the dimensions shown in Fig. 6 on a universal testing machine [4, 5]. As shown in Fig. 5, the negative stiffness honeycomb exhibits a region of positive initial stiffness approaching its force threshold, at which point the first row of curved beams begins to buckle, resulting in a region of negative stiffness. Rows of curved beams buckle sequentially, resulting in each of the negative stiffness regions in Fig. 5. Together, the negative stiffness regions create an extended region of relatively constant force, similar to the plateau stress exhibited by regular honeycombs. When all beams have buckled, the load is shunted to the contacting pillars on the sides of the honeycomb, resulting in a region of high positive stiffness similar to the densification exhibited by regular honeycombs. The magnitude of the force threshold is proportional to the number of columns of cells, and the length of the plateau region is proportional to the number of rows of cells. When the negative stiffness honeycomb is unloaded, it returns to its original configuration, following the unloading path in Fig. 5. The area within the hysteresis curve represents the net energy absorbed by the negative stiffness honeycomb over the complete cycle.

Fig. 5
figure 5

Experimental force-displacement relationship for a nylon 11 prototype of the honeycomb in Fig. 2. The prototype was fabricated with selective laser sintering with dimensions h = 5.08 mm, l = 50.8 mm, t = 1.27 mm, and overall height of 90.2 mm, as illustrated in Fig. 6. Adopted from [4, 5]

Full size image
Fig. 6
figure 6

Experimentally tested honeycomb cell dimensions (mm) and overall honeycomb dimensions. Adopted from [4, 5]

Full size image

The properties of a negative stiffness honeycomb can be tailored by adjusting the dimensions of the unit cells. Assuming that the characteristic cell size is fixed, regular honeycombs offer a single degree of design freedom––density or the thickness of the cell walls––such that adjusting the density results in unique values of plateau stress, initial stiffness, and energy absorption per cell. Similarly, assuming that the characteristic cell length, l, is fixed, negative stiffness honeycombs offer two degrees of design freedom––the apex height and in-plane thickness of the beams––such that it is possible to achieve a particular relative density with cells of various geometries, each of which offers different levels of stress threshold, initial stiffness, and energy absorption. This paper describes the analysis and design of negative stiffness honeycombs for energy absorption applications and outlines the types of design trade-offs that can be achieved.

Methods

Modeling the energy absorption properties of negative stiffness honeycombs begins with the force-displacement behavior of a single curved beam. According to Qiu et al. [8], the transverse displacement of the center of a curved beam is related to the transverse force applied to the center of the beam as follows:

$$ F=\frac{3{\pi}^4{Q}^2}{2}\Delta \left(\Delta -\frac{3}{2}+\sqrt{\frac{1}{4}-\frac{4}{3{Q}^2}}\right)\left(\Delta -\frac{3}{2}-\sqrt{\frac{1}{4}-\frac{4}{3{Q}^2}}\right) $$
(1)

where F and ∆ represent normalized force and normalized displacement, respectively. Those terms are related to applied transverse force, f, and transverse displacement, d, as follows:

$$ F=\frac{f{l}^3}{E_{\mathrm{s}}Ih}, $$
(2)
$$ \Delta = \frac{d}{h} $$
(3)

In those expressions, Es is the modulus of elasticity of the cell wall material and I is the area moment of inertia of the cell wall. The moment of inertia term I accounts for the out-of-plane depth, b, of the beam, assuming a rectangular cross section. Therefore, the relations derived in Equations 1, 2, and 3 are valid for a beam with arbitrary out-of-plane depth, provided it is uniformly loaded throughout its depth. Transverse displacement is measured as illustrated in Fig. 4 for a beam with its undeformed shape defined as follows:

$$ w(x)=\frac{h}{2}\left[1- \cos \left(2\pi \frac{x}{l}\right)\right] $$
(4)

Equation 1 predicts the resulting force-displacement behavior illustrated in Fig. 3 and can be used for any curved beam geometry as long as the beam is constrained to avoid second-mode buckling when it transitions from one first-mode-buckled shape to another.

The force threshold is defined by the peak of the force-displacement curve in Fig. 3. The force threshold can be calculated by taking the partial derivative of Eq. 1 with respect to normalized displacement, setting the partial derivative equal to zero, solving for the normalized displacements, and substituting into Eq. 1. For a beam with a Q of 2.31, the force threshold, Fth, occurs at a normalized displacement, ∆th, of 0.5 and a normalized force, F, of 389.

The normalized force threshold can then be expressed as a stress threshold, σth, for comparison with the critical stress level of a regular honeycomb, σpl, illustrated in Fig. 1. The stress threshold is found to be

$$ {\sigma}_{\mathrm{th}}=\frac{F_{\mathrm{th}}{E}_{\mathrm{s}}Ih}{b{l}^4}=\frac{F_{\mathrm{th}}{E}_{\mathrm{s}}h{t}^3}{12{l}^4}, $$
(5)

where b is the out-of-plane depth of the cell. Normalizing by the modulus of elasticity of the cell wall material yields the specific stress threshold:

$$ \frac{\sigma_{\mathrm{th}}}{E_{\mathrm{s}}}=\frac{F_{\mathrm{th}}h{t}^3}{12{l}^4} $$
(6)

The specific stress threshold can also be described as the specific elastic buckling strength of a single beam in the negative stiffness honeycomb. For regular honeycombs with relative densities greater than or less than the critical density defined by Hayes et al. [2], the specific elastic buckling strength can be compared to the specific plastic buckling strength or specific elastic buckling strength, respectively, of a regular honeycomb. For a hexagonal honeycomb, for example, the critical relative density is 3.46 %, above which the hexagonal honeycomb collapses due to plastic buckling at a specific plastic buckling strength defined as follows [2]:

$$ \frac{\sigma_{\mathrm{pl}}}{\sigma_{\mathrm{ys}}}=0.5{\rho}^2, $$
(7)

where σys and ρ represent the yield strength of the cell wall material and the relative density of the hexagonal honeycomb, respectively.

The specific initial stiffness of the curved beam, E0/Es, can be calculated by evaluating the partial derivative of Eq. 1 with respect to normalized displacement and then substituting Eqs. 2 and 3 as follows:

$$ \frac{\partial F}{\partial \Delta}\Big|{}_{\Delta =0}=\frac{3{\pi}^4{Q}^2}{2}\left(2-\frac{4}{3{Q}^2}\right), $$
(8)
$$ \frac{E_0}{E_{\mathrm{s}}}=\left(\frac{1}{E_s}\right)\frac{\partial f}{\partial d}=\frac{h{t}^3}{12{l}^4}\left(\frac{3{\pi}^4{Q}^2}{2}\right)\left(2-\frac{4}{3{Q}^2}\right). $$
(9)

The specific initial stiffness can be compared to the specific elastic stiffness of a regular honeycomb, although the specific initial stiffness of the negative stiffness honeycomb is valid only at the origin and decreases gradually as the stress threshold is approached, as shown in Figs. 3 and 5. In contrast, regular honeycombs typically exhibit nearly linear elastic stiffness prior to the critical buckling stress.

Finally, the maximum strain in the individual beam elements during snap-through deflection is calculated by Qiu et al. [8] as follows:

$$ {\varepsilon}_{\max }=2{\pi}^2\frac{th}{l^2} $$
(10)

Plastic deformation of the cell wall material occurs when εmax exceeds the yield strain or elongation at yield of the material. Thicker, shorter beams with larger apex heights undergo greater strains and risk exceeding the yield strength of the material. Maximum strain serves as a geometric constraint on the relative dimensions of the curved beams.

Equations 1 through 9 are valid for a single curved beam, but the unit cell in Fig. 2 incorporates two concentric curved beams. To represent double curved beams, the specific stress threshold in Eq. 6 and the specific stiffness in Eq. 9 must be doubled. The honeycomb in Fig. 2 is created by combining multiple rows and columns of concentric curved beams. The force threshold of the honeycomb is calculated by multiplying the force threshold of a single set of double beams by the number of columns of double beams, while the overall displacement is calculated by multiplying the displacement of a single set of double beams––equivalent to double the apex height, h––by the number of rows of double beams. As with a regular honeycomb, the specific stress threshold and specific stiffness of the honeycomb are equivalent to that of a single set of double beams.

The analytical relationships are verified by comparison with finite element analysis (FEA). A single curved beam with dimensions identical to those of Fig. 6 (i.e., a beam length, l, of 50.8 mm; an apex height, h, of 5.08 mm; thickness, t, of 1.27 mm; and depth, b, of 12.7 mm) was subjected to quasi-static displacement loading in ABAQUS. A finite element mesh of hexahedral elements was created by first creating a two-dimensional mesh of the front face of the honeycomb and then extruding the mesh through its depth, b. The solver used for the simulation was ABAQUS/Explicit with nonlinear geometry enabled. FEA simulations were also performed on a structure consisting of a double beam, a structure with two rows of double beams, and a structure with two columns of double beams. In each simulation, the horizontal displacements of the ends of the structures were constrained to prevent lateral expansion of the structures. The predicted force thresholds obtained from these simulations are summarized in Table 1. The predicted force thresholds match the assumptions in this section precisely. Specifically, the force threshold of a double beam is exactly two times that of a single beam, and the force threshold is proportional to the number of columns of double beams. Additionally, the force threshold of the double beam, two-column structure agrees very closely with the experimentally observed force threshold of approximately 210 N in Fig. 5.

Table 1 FEA prediction of force thresholds of various beam elements
Full size table

Results and discussion

The analytical relationships in Eqs. 1 through 10 can be used to design negative stiffness honeycombs for applications that require combinations of lightweight stiffness and energy absorption. Regular honeycombs are typically designed by adjusting relative density, which defines the ratio of cell wall thickness to characteristic length, and thereby defines the mechanical properties of the honeycomb, including specific stiffness and strength. Negative stiffness honeycombs offer an additional degree of design freedom. In addition to specifying the thickness of the cell wall, t, and the characteristic length of the cell, l, designers may vary the apex height, h, of the curved beams, such that various ratios of cell dimensions provide equivalent relative densities. As a result, honeycombs of equivalent relative densities can be tailored geometrically to provide different combinations of stress threshold and energy absorption. The phenomenon is similar to the functional grading of regular honeycombs to achieve Pareto sets of trade-offs between thermal and structural performance [9, 10], for example, but the focus here is on structural energy absorption.

Figure 7 illustrates the trade-offs between stress threshold, relative density, and compaction energy for representative negative stiffness honeycombs. The results are compared to the behavior of regular hexagonal honeycombs. Compaction energy estimates for hexagonal honeycombs assume that the plateau stress in Fig. 1 is defined by the plastic buckling strength in Equation 7 and that densification occurs when opposing cell walls contact one another. Compaction energy estimates for negative stiffness honeycombs assume that the plateau stress for each curved beam is defined by the stress threshold in Eq. 5 and that densification occurs when the total transverse displacement, d, of each curved beam equals twice its apex height, h, which is equivalent to a normalized displacement, ∆, of 2. The characteristic length of the unit cells used to generate the curves in Fig. 7 was fixed at 3 cm while the out-of-plane depth was fixed at 1 cm. Clearly, the characteristic length in a negative stiffness cell is a contributing factor to the cell behavior. However, in order to make an unambiguous comparison to regular honeycombs and ensure that they are being compared on the same platform, the length of the beams are fixed in this study. For the purposes of this analysis, the negative stiffness unit cell is defined as two concentric curved beams. The material is specified as a nylon 11 with modulus of elasticity and yield strength of 1400 and 47 MPa, respectively [11]. In Fig. 7, negative stiffness honeycomb contours are generated by maximizing the compaction energy for a fixed relative density and stress threshold, subject to a constraint on the maximum strain, εmax, in Eq. 10. The maximum strain cannot exceed the elongation at yield of the cell wall material, which is assumed to be 20 % for nylon 11 [12]. The maximum strain constraint determines the boundary of the negative stiffness contours in Fig. 7.

Fig. 7
figure 7

Compaction energy per unit cell versus relative density

Full size image

For the range of relative densities plotted in Fig. 7, the compaction energy of regular hexagonal honeycombs increases with relative density. This trend is expected because the hexagonal honeycomb’s plateau stress increases quadratically with the relative density of the material, although this trend is counteracted somewhat by the decrease in distance between opposing cell walls in a denser hexagonal honeycomb. In contrast, for the range of relative densities plotted in Fig. 7, the compaction energy of negative stiffness honeycombs tends to increase with decreasing relative density, and the effect is more pronounced for negative stiffness honeycombs with higher stress thresholds. A particular stress threshold can typically be achieved by relatively thick curved beams with relatively short apex heights or by relatively thin curved beams with relatively tall apex heights. The latter geometry affords more travel and therefore greater compaction energy for beams of equivalent stress threshold with less relative density. These trends illustrate that the mechanism used for energy absorption in negative stiffness honeycombs—buckling in a snap-through-like fashion—leads to a much richer set of trade-offs than those of regular honeycombs. As shown in Fig. 7, for relatively large stress thresholds and low relative densities, the negative stiffness honeycomb provides greater compaction energy than the regular hexagonal honeycomb of equivalent relative density. This advantage diminishes as relative density increases because the hexagonal honeycomb’s increasing plastic buckling strength leads to increasing compaction energy while the negative stiffness honeycomb’s increasing density leads to diminishing apex heights, less travel and a shorter plateau region, and ultimately a lower compaction energy. It is important to note that the characteristic length of the unit cells used to generate the curves in Fig. 7 was fixed at 3 cm while the out-of-plane depth was fixed at 1 cm. Adjusting those values would affect the magnitude of the compaction energy, but the trends observed in Fig. 7 would not change.

Regardless of the relative levels of compaction energy exhibited in Fig. 7, it is important to note that the compaction energy absorbed by the regular hexagonal honeycombs is not recoverable by virtue of the underlying plastic deformation that leads to energy absorption. The negative stiffness honeycombs, in contrast, are designed to return to their initial configurations upon removal of external loading. Indeed, preliminary physical experimental results shown in Fig. 5 indicate that the negative stiffness honeycombs are fully recoverable. Net energy absorbed by a negative stiffness honeycomb depends on the area encompassed by the hysteresis curve in Fig. 5 with the extent of hysteresis influenced by the viscoelastic behavior of the cell wall material among other factors. The presence of hysteresis indicates that the analytical predictions in Fig. 7 most likely overestimate experimentally measured magnitudes of net energy absorbed by a negative stiffness honeycomb. Comparisons are documented in previous research by the authors [4, 5].

Conclusions

Mechanical energy absorption properties of negative stiffness honeycomb materials have been examined. In contrast to regular honeycombs, which rely on plastic buckling for in-plane mechanical energy absorption, negative stiffness honeycombs rely on tailored elastic buckling phenomena. As a result, they are capable of absorbing large amounts of mechanical energy and returning to their original configuration. Due to their unique energy absorption mechanism, negative stiffness honeycombs offer a multi-dimensional design space for achieving the desired capacity for energy absorption. Specifically, two parameters of the cell geometry, apex height and in-plane thickness, can be altered to achieve the desired performance. This design freedom allows the force threshold to be designed independently of relative density, which is in direct contrast to traditional honeycombs. Negative stiffness honeycombs have been shown to have comparable levels of compaction energy per unit cell as hexagonal honeycombs but only for low relative densities that permit relatively large transverse displacements of curved beams with large apex heights.

This newly introduced honeycomb material offers many opportunities for future work. An initial experimental validation of the behavior of these materials has been conducted by the authors [4, 5], but additional experimentation should be carried out to verify the compaction energy per unit cell predicted in Fig. 7. Additional experimental efforts need to be focused on comparing the predictions in this paper with experimental performance for a wide range of strain rates. Finally, this experimental and theoretical knowledge can be merged to design energy-absorbing materials that achieve new combinations of performance. By adjusting the geometry of the unit cell and the population of unit cells in a negative stiffness honeycomb, for example, it is possible to independently tailor the density, force threshold, and energy absorption capabilities. Potential applications include bumpers, orthotics, and personal protective devices such as helmets.