RETRACTED ARTICLE: Do offenders avoid offending near home? A systematic review of the buffer zone hypothesis

Abstract

Background

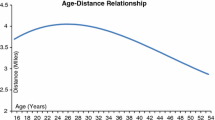
There is general agreement that the frequency of crime decreases with the distance from the offender’s home. By way of exception to this distance decay pattern, the buffer zone hypothesis states that offenders avoid offending very close to home. The purpose of the present study was to assess the validity of this hypothesis.

Methods

We conducted a systematic literature review of 4 bibliographic databases, in which we identified 108 studies on criminal distance decay, from which we selected 33 studies that include sufficient information to assess the existence of the buffer zone. Based on the full text of the research articles, we created a measure indicating whether the study supported or rejected the hypothesis and a measure summarizing the relative quality of the evidence as either weak-medium or strong.

Results

Of the 33 studies, 22 rejected the buffer zone hypothesis and 11 supported it. Across the whole sample, the methodological rigor of the studies was limited, but unrelated to whether the buffer zone hypothesis was supported or rejected.

Conclusions

Based on the available evidence the buffer zone hypothesis has gained limited support. We conclude by making recommendations on how to report data on the home-crime distance and suggesting a testing methodology for future research.

Background

A comprehensive body of literature has documented criminal distance decay, the empirical phenomenon that the frequency of crime decreases with the distance from the offender’s home (e.g., Wiles and Costello 2000; Levine and Lee 2013). Distance decay has also been observed in commuting, shopping, recreation trips and other types of human mobility that are studied in geography, economics, an urban planning (e.g., Lenormand et al. 2016; Martínez and Viegas 2013).

Some studies on criminal distance decay, however, have suggested that offenders generally do not offend in the immediate vicinity of their homes. In the first empirical study of the home-crime distance, e.g., Turner (1969) found that index offenses were less likely to be perpetrated within a block of juvenile offenders’ homes. This area of reduced criminal activity has been labeled the buffer zone. A buffer zone may exist because offenders avoid offending near home for fear of being recognized, but could also result from a lack of criminal opportunities near their homes (O’Leary 2011; Rengert et al. 1999; Rossmo 2000).

Whereas the existence of a buffer zone is often either tentatively hypothesized or routinely assumed, empirical findings appear to be mixed. To the best of our knowledge, there is no assessment of the buffer zone hypothesis that systematically collects, evaluates and summarizes the available evidence in the empirical literature.

There are two reasons why is it important to test the buffer zone hypothesis. The first reason is theoretical. The buffer zone hypothesis challenges the general principle of distance decay that applies to most human activities. The hypothesis suggests that, unlike many other activities, offending does not follow a monotonically decreasing distance decay function. The second reason is practical. The buffer zone hypothesis is implemented in some software tools for geographic offender profiling, a technique that has been developed to help the police prioritize suspects of serious crimes. In particular, the Rigel software (Rossmo 2000) is based on a model that assumes the existence of a buffer zone.¹ Whether the buffer zone hypothesis is rejected or confirmed is thus relevant for software aimed to help the police track down offenders.

The purpose of the present study was to investigate the validity of the buffer zone hypothesis. To that end, we conducted a systematic literature review of published empirical studies that include information on the distribution of home-crime distances.

Theoretical background

There is overwhelming empirical evidence for the distance decay hypothesis, i.e. the hypothesis that the frequency of crime monotonically decreases with the distance between the offender’s home and the crime location (Hammond and Youngs 2011; Santtila et al. 2007; Canter and Hammond 2006; Wiles and Costello 2000; Levine and Lee 2013; Bernasco et al. 2013; Gill et al. 2019; Rossmo 2000). Distance decay is usually explained by the principle of least effort: The effort an offender must spend on moving to a target is a monotonically increasing function of distance. Therefore, a location closer to home is more attractive than a location further away.

The buffer zone hypothesis proposes an exception to the distance decay pattern. It has found its way in the literature through its formulation by Brantingham and Brantingham (1981) who write “While criminals know more of the area close to home and are more likely to locate a target easily, they are also more likely to be known and increase their risks close to home. One would expect that there would be an area right around the home base where offenses would become less likely”, a hypothesis they support by referring to the block-length range of decreased involvement in index crimes by juveniles reported by Turner (1969). Interviews with offenders have shown that most of them are concerned about being seen by witnesses before, during, and after offending (Cromwell et al. 1991; Wright and Decker 1994).

Two explanations have been suggested for the existence of a buffer zone. Both explanations suggest a countervailing force to the principle of least effort. The first explanation states that offenders avoid offending near home to reduce the likelihood of being recognized by victims or witnesses. The other explanation suggests that criminal opportunities increase exponentially with distance, so that the additional cost of traveling another kilometer may be offset by the increase of crime opportunities (Rengert et al. 1999; O’Leary 2011).² The latter explanation is challenged, however, by the fact that crime location choice studies, in which distance effects are estimated while accounting for criminal opportunities, have consistently reported a monotonically decreasing function of distance, without any study reporting a buffer zone effect (Ruiter 2017).³ A complicating factor is that both mechanisms, anonymity and target availability, might not be mutually exclusive. They could operate simultaneously and both give rise to buffer zones that do not necessarily have the same length. Moreover, their role might depend on other factors, such as the type of crime or situational conditions such as lighting.

Whereas distance decay appears to be a robust phenomenon supported by a large body of empirical evidence, the evidence supporting the buffer zone hypothesis seems to be scarce and mixed. The theoretical relevance of the hypothesis and its practical significance for geographic offender profiling motivate a systematic study of its validity.

Data and methods

Database selection, article search and article selection

Guidelines for systematic reviews typically recommend that multiple bibliographic and research databases be searched (e.g., Bown and Sutton 2010; Møller and Myles 2016). To optimize the selection of databases, we tested the presence of twelve relevant articles in each of sixteen bibliographic databases. Based on the results, four bibliographic databases were selected: PsycINFO, Criminal Justice Abstracts, Web of Science, and Scopus. For details of the procedures, see Appendix 1.

The search for relevant articles was based on a combination of terms referring to both distance and crime either in the title, the abstract or the keywords. To make sure that articles only referring to specific crime types were included, a set of specific crimes (arson, burglary, homicide, rape, robbery, theft) were included as well. As the distance term is very general, it had to also appear together with one of the terms “home”, “residence”, “decay”, or “journey”. After removing duplicates, 707 articles were eligible to enter the next stage. For details on the search strategy, see Appendix 2. Appendix 3 provides an example search syntax.

In the next phase, based on the contents of the abstracts, the 707 articles were judged by the second author on whether they fulfilled each of the following five criteria: (1) It was written in English language,⁴ (2) It was published in a peer reviewed scientific journal, or it was a PhD Thesis ,⁵ (3) It was related to crime, (4) It included empirical research findings, and (5) It included findings on home-offense distance. Based on his judgements, 172 studies fulfilled all five criteria enumerated above, and thus entered the next stage of the selection procedure. An analysis of inter-rater reliability based on a subset of 100 abstracts judged independently by both authors demonstrated an acceptable level of inter-rater agreement. See Appendix 4 for details.

During the next phase, the full text of the remaining 172 publications was read and coded by the second author with the aim of assessing whether the results of the study addressed the buffer zone hypothesis. Another 64 of the 172 publications were removed at this stage because they did not fulfil five criteria mentioned in the preceding paragraph.⁶ Of the remaining 108 articles, the 33 articles were selected that (1) analyzed distances measured with less than 200 m error margins (excluding, for example, articles reporting distances based on neighborhood or census tract centroids) (2) analyzed the distribution of the home-crime distance (excluding articles that only reported means or medians), and (3) drew a (negative or a positive) conclusion on the existence of a buffer zone, or included information detailed enough to allow the coder to draw a conclusion on the buffer zone.⁷

Quantification of study characteristics and findings

The characteristics of the studies that were coded included the authors’ names, the year of publication, the country where data had been collected, the sample size,⁸ and the distance measurement method (Euclidian, Manhattan, or both). If the reviewed article was not explicit on the distance measurement method, we assumed that Euclidian distance was used. We also coded the types of crimes analyzed in the reviewed studies. Because many studies included multiple types of crime and because crime types are not necessarily mutually exclusive (e.g. ‘property crime’ is a category involving a subset of burglary, larceny, vehicle theft and other appropriative crimes), the inclusion of each type of crime was coded separately.

The main findings regarding the buffer zone of the 33 studies were quantified in a dichotomous outcome measure, indicating whether the reported evidence for a buffer zone was either positive (buffer zone hypothesis confirmed) or negative (buffer zone hypothesis rejected). In addition, we assessed the strength of this conclusion as either ‘weak-medium’ or ‘strong’. The judgement was based on the size and representativeness of the sample and on methods of inference. Conclusions based on more representative and larger samples were judged as being stronger, as were conclusions based on regression analysis that accounted for confounding factors, as opposed to descriptive methods like cross-tabulations, histograms or density plots. These elements were not quantitatively scored and weighted, but were weighted heuristically.

Results

Study characteristics

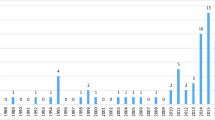
Table 1 presents the key attributes of the 33 included studies. The large majority of studies appeared during the past two decades, 60 percent between 2005 and 2014.

Table 1 Key characteristics of studies

About two-thirds of the reviewed studies were conducted in the United States, the United Kingdom or Canada, Australia, New Zealand. All other studies were from a variety of countries, each of which was the origin of 1 or 2 studies. Three out of every four studies used Euclidian distance measures, the others used Manhattan distance measures or both Euclidian and Manhattan distances. Street network measures (in which the shortest of quickest travel distance over an actual street network is calculated) were not used. The reported studies displayed a wide range of sample sizes, ranging from 30 to 750,000. The distribution was strongly positively skewed with a mean of 23,948 and a median of 228. Without two outliers with sample sizes above 100,000, the mean was 1259 and the median 221.

Table 2 lists the offense types being analyzed in the 33 reviewed studies. Generally, most types of offenses are represented, although the more serious violent offenses (homicide, rape, robbery) appear to be overrepresented compared to their incidence in crime figures. More than half of the reviewed studies included burglary as one of the crimes of interest.

Table 2 Offense types in 33 studies analyzed

Main findings on the buffer zone

The question that this systematic review attempts to answer is whether the available empirical evidence is sufficient to either confirm or refute the existence of a buffer zone: an area of reduced criminal activity around the home of the offender. In the original version of this hypothesis, the buffer is believed to exist because for fear of being recognized by local residents, offenders actively avoid offending in the proximity of their homes.

Of the 33 included studies, one-third provided evidence supporting the buffer zone hypothesis, while two-third (22) did not. In sum, support for the buffer zone hypothesis appears limited. The outcomes were unrelated to the assessed methodological qualities of the study(as based on sample size, representativeness and analytic rigor), as for both the ‘support’ and the ‘reject’ outcomes exactly 63.6 percent of the studies (14 and 7 respectively) the methodological quality was judged as ‘strong’ (as opposed to ‘weak-medium’).

Using cross-tabulations we explored whether support for buffer zone hypothesis was related to the variables in Table 1 (time period, country, distance measure and sample size). or Table 2 (crime type). This was not the case.⁹

Discussion

Conclusion

The purpose of the present study was to assess the buffer zone hypothesis, which is the hypothesis that in contradiction to the well-established distance decay pattern, offenders avoid offending very close to home. The hypothesis was assessed by conducting a systematic review of the empirical literature. The literature search and selection resulted in 33 published studies that were reviewed to assess whether their findings supported or rejected the hypothesis, and to assess the quality of the evidence.

Our findings suggest that the empirical evidence regarding the buffer zone hypothesis is generally weak and therefore inconclusive. It does not provide much support for the buffer zone hypothesis. Of the 33 studies, only 11 confirmed the hypothesis while 22 rejected it. The strength of the evidence did not differentiate between confirmation and rejection. Admittedly, a limitation of our own analysis is that due to the heterogeneity of the data and methods of the reviewed studies, to aggregate study results we had to resort to a dichotomous ‘support-reject’ outcome measure, instead of using a more sophisticated assessment method that would be able to preserve some of the statistical properties of the reviewed studies (e.g. samples sizes or effect sizes), as is common in meta-analysis.

Weighting the evidence we could possibly collect in this systematic review, we conclude that the buffer zone hypothesis should not be accepted as an empirical fact until alternative evidence becomes available that supports it. The theoretical consequence is that the general distance decay principle appears to be sufficient to describe the home-crime distance. The practical consequence is that in criminal investigations, in particular geographic offender profiling, the application of the buffer zone hypothesis may need to be reconsidered. Whether hard-coded in computer geographic profiling algorithms or used informally as a rule of thumb, the assumption that offenders avoid committing crimes nearby their homes appears not based on sufficient empirical evidence. It may lead to an under-prioritization of the area in the immediate vicinity of the offender’s home, and may therefore be counterproductive.

This claim is most easily appreciated if we consider a stylized example where only a single crime is committed on a street by an unknown resident. The geographic profiling task is to find the most likely home of the offender. If we assume that a general distance decay function without a buffer zone represents the ground truth (as is suggested tentatively by our findings), than the likelihood distribution along the street is unimodal, with the most likely offender home being the residence nearest to the crime location. However, any geographic offender profiling tool that assumes a buffer function greater than zero, will create a bimodal likelihood distribution along a street, and the most prioritized homes will be located X meters left and right from the crime location (where X is the radius of the buffer zone). In this case, correctly assuming the absence of a buffer zone (i.e. X = 0) could improve the accuracy and detection speed would be improved by dropping the buffer zone assumption.

In the remainder of this section, we discuss two issues relevant to future assessments of the buffer zone hypothesis. We first address problems that hinder the assessment of reported findings on the home-crime distance, and make recommendations to help mitigate these problems. Next, observing a lack of methodological and statistical rigor in the empirical literature, we discuss how future researchers could go about rigorously testing the hypothesis.

Judging empirical evidence from the literature

For a variety of reasons, finding evidence in the literature on the buffer zone hypothesis is complicated. The first issue is that the buffer zone hypothesis is not the key issue of most studies that contain relevant home-crime distance data to test the hypothesis. For example, many studies utilize home-crime distance data to compare the mean length of the journey-to-crime between different types of offenders of different types of crime. These studies usually only report measures of central tendency and dispersion (e.g. mean and standard deviation) rather than the full distribution of the home-crime distance. For an assessment of the buffer zone hypothesis, an analysis of the complete distribution of the home-crime distance is required.

A second issue is that not all studies that contain information on the full distribution of the home-crime distance, mention the buffer zone hypothesis in the abstract, the list of keywords or even in the text of the manuscript text. Systematic reviews may easily miss relevant studies because they crucially depend on keywords and abstracts. Observing this limitation, in the present research we also included search terms like ‘distance decay’ and included studies that appeared to include a measure of the home-crime distance. We recommend that all published future studies explicitly analyzing or reporting the full home-crime distance, list ‘buffer zone’ among their keywords.

Judging findings in the literature is further complicated by the fact that confirmation of the buffer zone hypothesis, or tentative support for it, may be a methodological artefact. Both rounding and kernel density smoothing of distance measures are data transformations that may create the appearance of a buffer zone even if the underlying data are generated by a flat or monotonically decreasing distance function. Both artefacts are caused by the distribution of distance being left-truncated at zero.¹⁰ For example, in a study of home-crime distances in commercial robberies in The Netherlands (van Koppen and Jansen 1998), the authors present a distance decay graph based on distances rounded to whole kilometers. The shape is suggestive of a buffer zone, but this might just as well merely be an artefact of rounding distances to kilometers. Presenting histograms constructed from equally sized bins (distance classes) prevents this potential methodological artefact. Kernel density estimates have been used to smoothen the observed distribution of discrete frequencies (e.g., Laukkanen and Santtila 2006; Santtila et al. 2007, 2008) but are saddled with the same issue: the estimates are biased downwards near zero, creating the false visual impression of a buffer zone. Future studies aiming for testing the buffer zone hypothesis, or other issues that require measurement of small distances, should be careful to prevent bias through rounding or smoothing operations on the distance measure.

The methodology of testing the buffer zone hypothesis

Existing research on the buffer zone hypothesis seems to lack a standard for determining the existence or non-existence of a buffer zone. In addition, most inferences made about the buffer zone lack statistical rigor. Together, these conclusions call for an methodological and statistical strategy that can yield stronger conclusions.

A lack of standards applies to the question of the size of the buffer zone: how large can it be? A plausible buffer zone size depends on the presumed underlying mechanism. If the presumed mechanism underlying the buffer zone is the offender’s fear of being recognized by local residents, it seems that any buffer zone detected should be within a range of up to 500 m (i.e. an area of .79 km²) in dense urban areas and up to 1000 m (i.e. an area of 3.13 km²) in more rural areas. At larger distances fear of recognition by local residents seems implausible. If, however, the presumed underlying mechanism is availability of suitable targets, deciding on an appropriate threshold value is more complicated, as it will depend on the type of crime under consideration and on the spatial density of potential targets. Because targets may not be available nearby the offender’s home, a minimum home-crime distance of several kilometers might be a natural condition for some types of crime, such as a commercial robbery (Laukkanen 2007), but not for other types, such as personal (street) robbery. Research investigating the buffer zone hypothesis should consider target availability and distinguish between crime types that vary in target density, in whether they are premediated or opportunistic and whether they are confrontational or non-confrontational.

Another reason for separating specific type of crime is that the risk of recognition by witnesses may be elevated near the offender’s home, but is strongly decreased once the crime takes place inside the offender’s home. Although our findings did not suggest differences between studies that exclusively included homicides or rapes (crimes are often committed at home) and other studies, the distinction between crimes that can and that cannot be committed at home is potentially relevant for evaluating the buffer zone hypothesis.

An interesting alternative to defining a given distance threshold for all offenders in the sample is to assume that the size of the buffer zone varies across offenders. Some offenders may thus avoid offending within the street block they live in, while others may avoid offending in their home neighborhood. To assess the existence of a buffer zone, this assumption requires either data on serial offenders (i.e. multiple home-crime distances for committed by the same offender) or a predefined measure of the size of the individual buffer zone.

An example of the former option is a study included in the present research (Warren et al. 1998), in which the authors studied home-crime distances of serial rapists and standardized the distances per offender before aggregation.¹¹ While variation in the size or shape of the buffer zone across offenders is a plausible possibility, and a potentially important aspect of geographic profiling, unconstrained estimation does not do justice to the two theoretical reasons for the existence of a buffer: avoidance of the area near home to prevent recognition, and lack of opportunities near home. As argued above, both theoretical arguments require that buffer zones should be reasonably small (below 500–1000 m around the offender’s home), except maybe for situations where criminal opportunities are extremely sparse.

An example of the latter option (using a predefined measure of buffer zone size) is provided by Bichler et al. (2011), who suggest that individual-specific buffer zones of juvenile offenders might be quantified by measuring the distance traveled to offenders’ primary hangout locations (i.e., locations other than their homes where they meet and socialize with their peers). In their study, juvenile offenders’ primary hangout locations were situated at .5 miles (0.8 km) from their homes on average, but did vary within the sample.

An additional issue that may complicate the assessment of the buffer zone hypothesis concerns not the size but the geometrical shape of the hypothesized buffer zone. It has been demonstrated that offenders’ journeys to crime are typically not in a random direction but display a consistent directional bias (Costanzo et al. 1996; Frank et al. 2012; Van Daele and Bernasco 2012). In line with these findings, we might expect that if a buffer zone exists, it may not extend from the offender’s home equally far in all directions, but be ellipse-shaped or have an irregular shape that indicates a preference for certain directions or specific destinations. To systematically address this possibility, measuring home-crime distances alone is not sufficient, and the directional angles should be included as well.

Statistical rigor is an important prerequisite for testing the buffer zone hypothesis. Many authors, in particular those who mention the possibility of a buffer zone only in passing, base their conclusions exclusively on the visual inspection of either a histogram or kernel density estimates of observed distances. In these cases, considerations of sample size and other aspects of statistical power are ignored, and the risk of unjustly rejecting the implicit null hypothesis (of no buffer zone) is quite likely.

A rigorous and conclusive evaluation of the buffer zone hypothesis therefore requires, in addition to reliably measured distances, a sufficient sample size and an appropriate statistical analysis. An important observation is that that any type of regression analysis in which the home-crime distance is the dependent variable, cannot be an appropriate test of the buffer zone hypothesis. This is because the buffer zone hypothesis is essentially a hypothesis that concerns the functional form of the distance decay curve (O’Leary 2011), and any type of linear or non-linear regression model assumes a certain distributional form of the dependent variable, conditional on the covariates. In linear regression, for example, the dependent variable is assumed to be conditionally normally distributed, and in Poisson regression it is assumed to conditionally follow a Poisson distribution. Because the shape of the distribution cannot be tested by assuming it, the home-crime distance cannot be a dependent variable in a regression analysis that aims to test the buffer zone hypothesis.

To test hypotheses on the functional form of a distance distribution, including the buffer zone hypothesis, the distance variable should be an independent variable and its probability or frequency should be the dependent variable. This approach is exemplified by the ‘journey-to-crime estimation’ module that has been included the CrimeStat software since version 2 (Levine 2002, 2015), and by the analyses of Canter and Hammond (2006) and Hammond and Youngs (2011). In order to assess which parametric function (e.g. linear, normal, lognormal, logarithmic, (truncated) negative exponential or quadratic) best describes the empirical distance decay of the home-crime distance, they regressed crime frequencies on the home-crime distance.

To test the existence of a buffer zone, we recommend estimating a regression model with a piecewise-constant distance function, as this approach makes few assumptions on the form of the distance decay function, but allows the analyst to specify buffer zone threshold. For example, if it is hypothesized that a buffer zone of 200 m describes the target selection of the offender sample, one could define dichotomous (dummy) variables that indicate the ranges 0–200 m, 200–400 m, 400–600 m, …, and subsequently regress the frequency on this set of dichotomous variables. To decide whether the data support the buffer zone hypothesis, the analyst might test whether the parameter indicating the 200–400 m range is larger than the parameter indicating the buffer zone range (0–200 m) and also larger than the parameter indicating the 400–600 m distance range. This approach allows a flexible buffer zone distance threshold, and makes no specific assumption on the form of the distance decay function (other than that it is constant within each 200 m range).

Based on these recommendations, future research on the buffer zone hypothesis might become more rigorous and yield stronger conclusions, and also become more standardized and therefore useful for future systematic reviews or even meta-analyses.

Appendices

Appendix 1: Selection of bibliographic databases

Based on our pre-existing knowledge of the literature, we constructed a list of twelve studies that we considered potentially relevant to the buffer zone hypothesis.¹² For each of these 12 studies we checked whether they were included in the following sixteen bibliographic databases: Criminal Justice Abstracts, Heinonline, JSTOR, PsychINFO, RuQuest, SAGE, Sciencedirect, Scopus, SocINDEX, Sociological Abstracts, Social Sciences Database, Violence & Abuse Abstracts, War & Terrorism Collection, Web of Science, Westlaw UK, and Women’s Studies International. The results of this query are presented in Table 3, which excludes the databases in which none of the twelve article were found. The four bibliographic databases that contained more than 6 of the 12 articles were selected for the next step of the systematic literature review. These were PsycINFO (8 of 12 found), Criminal Justice Abstracts (8 of 12 found), Web of Science (10 of 12 found) and Scopus (12 of 12 found).

Table 3 Bibliographic databases in which at least one of twelve selected articles was abstracted

Appendix 2: Article search in bibliographic databases

The four selected databases were searched between October 4–11, 2018, and the search term resulted in 218 potentially relevant studies in Web of Science, 251 in Scopus, 48 in Criminal Justice Abstracts, and 192 in PsychINFO. Of these 734, detailed comparisons proved 27 to be duplicates that had not been automatically recognized as duplicates due to minor differences in the records. After removing these duplicates, 707 studies were selected for the next phase (see Table 4).

Table 4 Number of studies selected based on keyword searches in titles, abstract and keywords fields of four bibliographic databases

Appendix 3: Example search terms (PsychInfo)

• 1. (“Buffer zone*” AND crime)

• 2. (“Distance*” Decay AND crime)

• 3. (“Journey to crime*” AND crime)

• 4. ((“Buffer zone” AND homicide) or (“distance decay” AND homicide) or (“Journey-to-crime” AND homicide)).

• 5. ((“Buffer zone” AND rape) OR (“distance decay” AND rape) OR (“Journey-to-crime” AND rape)).

• 6. ((“Buffer zone” AND burglary) OR (“distance decay” AND burglary) OR (“Journey-to-crime” AND burglary) OR (“Buffer zone” AND robbery) OR (“distance decay” AND robbery) OR (“Journey-to-crime” AND robbery) OR (“Buffer zone” AND arson) OR (“distance decay” AND arson) OR (“Journey-to-crime” AND arson) OR (“Buffer zone” AND theft) OR (“distance decay” AND theft) OR (“Journey-to-crime” AND theft)).af.

• 7. ((distance AND crime AND home) OR (distance AND crime AND residence) OR (distance AND homicide AND home) OR (distance AND homicide AND residence) OR (distance AND rape AND home) OR (distance AND rape AND residence) OR (distance AND burglary AND home) OR (distance AND burglary AND residence) OR (distance AND robbery AND home) OR (distance AND robbery AND residence) OR (distance AND arson AND home) OR (distance AND arson AND residence)).ab.

Appendix 4: Inter-rater reliability of abstract-based article selection

Based on the contents of abstracts, we assessed whether the 707 articles (1) were written in English, (2) were peer reviewed, (3) were related to crime (4) were based on empirical research and (5) included findings on the home-offense distance. To assess the reliability of the overall judgment whether all five criteria were met, a random sample of 100 of the 707 publication records was independently judged by the first author on the same criteria. Cohen’s Kappa κ, a measure of inter-rater reliability, was .56. According to widely accepted rules of thumb (Landis and Koch 1977), a value of .56 indicates a’moderate’ (0.41–0.60) strength of inter-rater agreement, and is quite close to the 0.61–0.80 range that is rated as ‘substantial’. Given this acceptable level of inter-rater agreement, we decided that the judgement of the second author was decisive.

In many studies, inter-rater reliability assessment is used as a tool to improve the quality of the coding. Based on the established differences between the coders, instructions are changed with the aim of the increasing the inter-rater reliability. We did not follow this approach because it would dictate that after a first round of instruction improvements we would have to conduct another inter-rater reliability analysis to assess whether instruction improvements had actually been successful in raising the inter-rater reliability. As the available resources did not allow this, we decided to do the reliability check as a post hoc test and ascertain that the result was good enough to proceed with the analysis.