Abstract
In this study, a modified Artificial Neural Network (ANN) and Support Vector Regression (SVR) with three different optimization algorithms (Genetic, Salp Swarm and Grasshopper) were used to establish an accurate and easy-to-use module to predict the lateral pressure exerted by fresh concrete on formwork based on three main inputs, namely mix proportions (cement content, w/c, coarse aggregates, fine aggregates and admixture agent), casting rate, and height of specimens. The data have been obtained from 30 previously piloted experimental studies (resulted 113 samples). Achieved results for the model including all the input data provide the most excellent prediction of the exerted lateral pressure. Additionally, having different magnitudes of powder volume, aggregate volume and fluid content in the mix exposes different rising and descending in the lateral pressure outcomes. The results indicate that each model has its own advantages and disadvantages; however, the root mean square error values of the SVR models are lower than that of the ANN model. Additionally, the proposed models have been validated and all of them can accurately predict the lateral pressure of fresh concrete on the panel of the formwork.
Similar content being viewed by others
1 Introduction
Generally, conventional concrete has an exerted pressure on formwork at an early stage of casting. Specifically, self-compacting concrete (SCC) type is a novel type of concrete that has the ability to flow quickly without any effort. This type of concrete has high exerted lateral pressure on the formwork because of its high flowability. It can fill the formwork and compact under its own weight which eliminates the shaking and vibration process through vibrator. This also reduces noise pollution and labour work in the field. Furthermore, SCC increases the potential of construction productivity, reduces the total cost of the structure, provides a sustainable environment, and improves the quality of the structures (Almeida Filho et al., 2010). In general, there are many studies on the performance of SCC, such as mechanical strength (Roussel & Cussigh, 2008), durability (Tabatabaeian et al., 2017) as well as cost and life cycle assessment (Margallo et al., 2015). Development of SCC was undertaken by authors Okamura (1997) and Okamura and Ozawa (1996) in Japan. Despite having abundant research on the benefits of SCC, related to its performance and flow of SCC since its first developments in the late 1980s in Japan, there are many limitations and a lack of results regarding the expected lateral pressure exertion on the different types of formwork (Shakor & Gowripalan, 2020).
SCC is highly subject to changes in material behaviour and characterization (Kurda et al., 2022); therefore, it is necessary to have a suitable quality control. One way to overcome this is by controlling the fresh properties of concrete that directly affect its lateral pressure on the formwork. To ensure adequate fresh properties, it is necessary to have a suitable SCC mix. These are also substantial investigations of lateral pressure properties in the fresh SCC, hardened properties, and durability (Brito & Kurda, 2021; Koehler, 2007). Since a number of parameters affect the performance of concrete and its lateral pressure on the formwork (Gowripalan et al., 2021), it is necessary to use machine learning on the SCC and conventional concrete as well (Shakor & Pimplikar, 2011). Having limited data on the SCC lateral pressure causes difficulty in simulating and predicting lateral pressure on formwork by machine learning; therefore, studies on lateral pressure of conventional concrete have been included in the data collection.
Machine learning techniques such as Artificial Neural Network (ANN) and Support Vector Regression (SVR) have been used to predict concrete properties in the past two decades (Ahmadi et al., 2020; Alam & Al Riyami, 2018; Farooq et al., 2020; Kandiri & Fotouhi, 2021; Kandiri et al., 2020; Lizarazo-Marriaga et al., 2020; Mohammed et al., 2021; Ramezani et al., 2020; Velay-Lizancos et al., 2018; Vickers, 2017; Yu et al., 2020). For instance, Golafshani et al. (2020) modified ANN with a multi-objective grey wolf optimizer and used that to forecast the compressive strength of high-performance and normal concrete (Golafshani et al., 2020). The study of Kandiri et al. (2021) used three different optimization algorithms to modify ANN and used those models to predict the compressive strength of recycled aggregate concrete (Kandiri et al., 2021). In another study, Jahangir and Eidgahee (2021) used a hybrid artificial bee colony algorithm-ANN to evaluate the bond strength of fibre-reinforced polymers-concrete. In addition, Ahmed et al. predicted 7 and 28 days of flexural strength of normal concrete using SVR (Jahangir & Eidgahee, 2021).
Nevertheless, the performance of SVR and ANN significantly depends on the selection of training set data and features. These data are not only used for SCC, but also applicable for three-dimensional printed concrete as shown in the study (Izadgoshasb et al., 2021). The number of hidden layers and their nodes for ANN, and the values of the penalty coefficient, error limit, and the slack variable for SVR determine the models’ performance. However, the challenge is in the fact that it is needed to determine these parameters in the first step, and they are not changeable during the process. Therefore, in this study, the Genetic Algorithm (GA), Salp Swarm Algorithm (SSA), and Grasshopper Optimization Algorithm (GOA) are used to develop a systematic approach to achieve the optimum structures and increase the accuracy of the models as much as possible.
2 Research Significance
SCC has many advantages in terms of fresh state, but it may generate high lateral pressure on the formwork that has not been studied in detail. Thus, this research aims to provide an approach to estimate the maximum lateral pressure of concrete (conventional and self-compacting concrete). Guessing the behaviour of Bingham fluid (e.g. concrete) would be interesting which is part of input and output data to produce the right models and closest approach to the resulted outcome. Concrete at the hardened stage might be easier to predict considering the complexities of the mixed components of concrete at the early ages. Predicting the lateral pressure of fresh concrete is highly important and considered a great outcome to know its lateral pressure before pouring. On the other hand, there are not enough studies on predicting the lateral pressure of concrete on the formwork and there are no investigations particularly on the machine learning modelling to predict the lateral pressure of fresh concrete on the formwork. The predicting models could be precise for engineering application predictions and it could eliminate the need for extensive further laboratory in situ testing (Vickers, 2017), and it will be advantageous for the design of the formwork.
3 Methodology
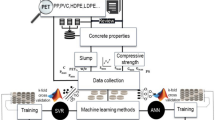
As shown in the flowchart (Fig. 1), this study was made to estimate the lateral presser exerted by fresh concrete on the formwork, namely by using modified ANN and SVR. For that purpose, data from 30 previous studies (113 experimental data) were collected (Appendix 1). As input data, (i) mix composition such as cement, coarse aggregates, fine aggregates, water and admixture contents was considered as well as (ii) dimensions of casted specimen and (iii) casting rate of concrete (Sect. 3.1).
Two most accurate algorithms were considered to establish the required model based on the collected data, namely SVM (Sect. 3.2) and ANN (Sect. 3.3). However, accurate mathematical methods cannot solve optimization problems. Hence, to find the optimum answer possible at a convenient time, heuristic and metaheuristic algorithms are used. For that purpose, GA, SSA and GOA are used (Sect. 3.4) in order to modify the SVM and ANN models. The modification process of the two algorithms are shown in Sect. 3.5.
3.1 Materials and Data Collection
The experimental dataset consists of 113 data extracted from 30 previous studies, which is tested to provide models from both types of concrete. This study counted different factors in its approaches, for example, the height effect of the casted specimens, the casting rate (placement rate) of casting the concrete, the constant gravitational unit, the ratio of water to cement, the quantity of cement, coarse aggregate, fine aggregate, and admixtures. Fig. 2 illustrates histograms of the inputs and the output of the models. Moreover, Table 1 represents the statistical parameters of the inputs and the output.
These factors assist in evaluating and predicting the lateral pressure of the fresh concrete on the formwork using each model as statistical evaluation parameters. These would be also beneficial for the construction industry to identify and predict the value of the pressure before the casting process. Table 3 (Appendix 1) represents the results of earlier studies on exerted lateral pressure of concrete, mix design, casting rate, slump and height of casting.
Based on the available data in Table 3 (Appendix 1), the data could be entered and applied into algorithm modelling for machine learning. The selected algorithms have been chosen and attempted for the process and the most suited are opted for the application.
3.1.1 Mix Composition of Concrete
Concrete mix design uses various methods to mix and various systems to cure them. Most of the concrete mixes are considered to be evaluated through visual inspection (Day, 2006). According to the earlier studies by Alyamac and Ince (2009), the concrete mix design could be combined their expression of fresh and hardened into one graph in terms of compressive strength. These could be presented in a nomogram diagram; see Fig. 3.
However, as Fig. 3 shows that the w/c ratio directly affects the compressive strength, with increasing w/c ratio is decreasing the compressive strength. On the other hand, the increase in the w/c ratio increased the workability and lateral pressure on the formwork as a result. Therefore, it should be considered that the lateral pressure highly depends on the percentage of water content in the mix design.
In the collection of data shown in Appendix 1, the w/c ratio is between 0.3 to 0.9. It is quite obvious that the maximum water content in the mix design of concrete is usually 0.6–0.7 of cement ratio. However, sometimes the w/c ratio may be changed in the construction site in order to achieve a certain workability. This kind of changes must not be allowed. In other words, the output of this study can be recommended only for concrete mixes made with w/c of 0.3–0.9. The most common mix design ratio also for concrete proportion is the 1:2:4 mix ratio which represents the cement ratio 1 to fine aggregate ratio 2 and the coarse aggregate 4. However, other mix designs could be observed in the matrix of concrete mixes, such as 1:1.25:2.25, and 1:2.25:3.75.
3.1.2 Fresh Properties of Concrete
Concrete at early ages, called fresh-state concrete, behaves as a Bingham fluid. This fluid is quite different from water which is called Newtonian fluid. Bingham fluid is commenced with a yield stress point (YP) which is basically the starting point of the concrete rheology. Concrete materials behave as a thixotropic material with a dilatant property (shear thickening) (Feys et al., 2009). Fig. 4 shows the comparison between Bingham fluid and Newtonian fluid.
Shear thickening materials are such materials that the viscosity increases with increasing of the shear rate. Generally, it has a resistance to the applied rate when it applies. However, these could be beneficial for concrete to reduce its lateral pressure at a later stage.
Regarding the formwork and instalment of the formwork panel, on the construction site; it is required to provide a high amount of bracing to prevent any collapse due to huge pressure on the lateral side of the formwork. However, this extreme pressure on the formwork will increase when the height of the casting structural member increases due to the gravitational unit and height rate. Fig. 5 displays certain details on the normal formwork that should be considered during casting and bracing it properly before casting.
Sometimes the formwork and handling procedure would be so costly as to exceed the total cost of concrete implementation by 40% (Haron et al., 2005; Lloret et al., 2015; Shakor & Gowripalan, 2020). Therefore, considering to have a better implementation of casting concrete and to not lose the formwork and the proper amount of concrete, it is better to understand and study more on exerted lateral pressure modelling to mitigate the risk of losing the cost of implementation and prevent the risk of injury at the field.
However, according to the theoretical calculations, the lateral pressure of concrete on formwork depended on height which is related to the rate of the gravitational unit. Moreover, the density of materials relatively depends on the mass of the materials. Therefore, according to the law of hydrostatic pressure, the maximum pressure could be expressed as below Eq. (1) (Merriam, 1992):
where P is pressure, ρ is density, g is gravity and H is the height of the concrete.
According to Puente et al. (2010), the lateral pressure of fresh concrete on the formwork is theoretically expressed as (Eq. 2):
where P is lateral pressure, λc is the relationship between horizontal and vertical pressure, γ is the concrete weight and H is the height of the concrete.
However, Rodin (1952) explained that the maximum pressure Pmax could be found when the concrete mix is 1:2:4 with a slump of 150 mm and temperature is about 21 °C and density is assumed to be about 2400 kg/m3 (Eqs. 3, 4):
where Hm is the height which the maximum lateral pressure occurred which is considered to be (m), Pmax is the maximum lateral pressure of the concrete on the formwork in (kPa) and R is the casting rate of the concrete (m/h). These dataset and earlier information on the concrete pressure and different mix designs would be beneficial to create a model to predict the lateral pressure of the concrete on the formwork and find the maximum pressure on the formwork panel.
Therefore, usually expect the lateral pressure of concrete should be one of the following expectation for the concrete. This is based on the materials mix, density, temperature and slump. Fig. 6 displays all types of lateral pressure of concrete on formwork. However, Rodin (1952) proposed that the formwork should be designed for full hydrostatic pressure considering the density of concrete.
Lateral pressure exerted on formwork at different points (Puente et al., 2010).
3.2 Support Vector Regression
Support vector machine (SVM) is an AI-based method that is used for classification and regression analysis using hyperplane classifiers. The best hyperplane can minimize the risk of classification by maximizing the distance between the two classes, where the support vectors lie (Sun et al., 2019). A linear regression hyperplane equation is defined as Eq. (5) by mapping the input data into a higher-dimensional feature space with linearly separable output data:
where W is a multi-dimensional vector determining the orientation of the hyperplane, and b is the bias term.
Support vector regression (SVR) is a machine learning method, which was proposed in 1992 (Boser et al., 1992). It has been used to solve non-linear classification, regression, and prediction problems recently (Ahmad et al., 2020; Suykens & Vandewalle, 1999; Vapnik, 2013). The following equation represents the SVR’s objective function (Eq. 6):
where C is the penalty coefficient, \(\upvarepsilon\) is the error limit, \({\delta }_{i}\) is the slack variable above the sample observation point and \({{\delta }^{^{\prime}}}_{i}\) is the slack variable under the sample observation point. Slack variables are defined in Eq. (7):
where \({t}_{i}\) is the ith target value of the model and \({y}_{i}\) is the ith predicted value of the model.
The optimization problem in Eq. (8) is solved by its dual formulation more easily by introducing Lagrange multipliers, described as follows:
where L is the Lagrangian function; \({\eta }_{i}^{+}\), \({\eta }_{i}^{-}\), \({\alpha }_{i}^{+}\), and \({\alpha }_{i}^{-}\) are positive Lagrangian multipliers.
This method is developed for linear classification; therefore, to solve non-linear classification kernel functions are defined (Brereton & Lloyd, 2010). Any function which is symmetric, positive and semi-definite (Mercer’s condition) qualifies to be a kernel function (Pan et al., 2009). However, the most used one is the Gaussian radial basis function (RBF). The description of the function is defined in Eq. (9) (Smola & Schölkopf, 2004; Vapnik et al., 1997):.
where \(\sigma\) is the width of the RBF.
After using a proper kernel function at last, the basic equation describing the modelling of the data is shown in Eq. (10):
The biggest challenge in this algorithm is to find the optimum C, \(\varepsilon\), and \(\sigma\). The accuracy of an SVR closely depends on these values. In this study, the position of a salp and a grasshopper and chromosome of an individual has three parts. The first part is dedicated to the C parameter, the second part is for the \(\varepsilon\), and the third part is allocated to the \(\sigma\).
3.3 Artificial Neural Networks
Artificial Neural Network (ANN) is developed inspired by the human brain. If an ANN has enough inputs to learn, it can solve new problems. Multi-layer feed-forward back-propagation perceptron (MLFFBPP) is a kind of ANN in which there are an input layer and an output layer. Between these layers, there can be one or more layers called hidden layers (Kandiri & Fotouhi, 2021; Shakor & Pimplikar, 2011). There are several neurons (nodes) in each layer connected to the next layer’s nodes with weighted links (Farooq et al., 2020; Lizarazo-Marriaga et al., 2020). In MLFFBPP, the flow of the information is from the input to the output layer. Then, weights of the network are modified in the back-propagation phase (Cybenko, 1989). ANNs use a learning algorithm to modify their weights such as Bayesian regularization and Levenberg–Marquardt, which is used in this study because of its better performance (Golafshani & Behnood, 2018). Moreover, each node in the hidden layer includes an activation function such as tangent sigmoid and hyperbolic tangent sigmoid that is used in the current paper.
Each neuron in the hidden layers receives weighted inputs from the previous layer’s nodes and after summing them enter them in the activation function. The neurons in the output layer do the same without activation function, and input layer nodes just receive input parameters from data records. An example of an ANN with one hidden layer, two inputs, three nodes in the hidden layer and one output is illustrated in Fig. 7.
3.4 Optimization Algorithms
Accurate mathematical methods cannot solve optimization problems. Hence, to find the optimum answer possible at a convenient time, heuristic and metaheuristic algorithms are used. The most popular algorithms are the ones that are developed inspired by nature (Behnood & Golafshani, 2018; Kandiri et al., 2020). Most of these algorithms consist of two parts: exploration and exploitation. The possible solutions that are far from each other are investigated in the exploration phase, then, in the exploitation phase, the close possible solutions are studied. In fact, algorithms need the exploration phase to avoid local optimums. GA, SSA, and GOA are three of them.
3.4.1 Genetic Algorithm
A genetic algorithm is a metaheuristic algorithm to solve optimization problems proposed by John Holland (1992). This nature-inspired algorithm uses Darwin’s evolutionary theory. GA saves the data set in genes and each pattern of the dataset is recorded in an individual’s gene. As mentioned before, every metaheuristic algorithm includes the exploration and exploitation phase, and GA uses mutation and crossover for these purposes, respectively. A number of individuals equal to the number of the initial population are going to survive based on their fitness function. In other words, the algorithm calculates the fitness function for each individual, and individuals who are fitter have a better chance to survive. In this study, a roulette wheel is used to choose the survivors. This algorithm has been used to train an ANN in a number of previous studies (Chandwani et al., 2015; Sahoo & Mahapatra, 2018; Shahnewaz & Alam, 2020; Shahnewaz et al., 2020; Yan et al., 2017; Yuan et al., 2014).
3.4.2 Salp Swarm Algorithm
Salps, which look like jellyfishes, belong to the Salpidae group, with a body shape like a transparent barrel (Mirjalili et al., 2017). To coordinate rapidly for finding food, they usually create a chain. SSA is inspired by salps’ swarm intelligence. There is a leader in the chain that stands at the front of the chain, and the rest of the group are followers. The exploration phase is the leader responsibility and the exploitation phase is handled by the followers.
The position of each salp is defined in an n-dimension search space where n is the number of decision variables in the optimization problem. The following equation updates the leader position (Eqs. 11–13):
where \({\mathrm{LB}}_{{r}}\) is the lower bound in the rth dimension, \({\mathrm{UB}}_{{r}}\) is the upper bound in the rth dimension, \({\mathrm{FP}}_{{j}}\) is the position of the food, \({{P}}_{{r}}^{{i}}\) is rth dimension of the leader position, \({{c}}_{1}\) balances exploration and exploitation phases; \({{c}}_{2}\) and \({{c}}_{3}\) are random numbers in [0,1]. \({{c}}_{1}\) is calculated as follows:
where \(T\) is the maximum number of iterations and \(t\) represents the current iteration. The position of the followers are calculated as follows:
where \({{P}}_{{r}}^{{i}}\) is position of the ith salp in the rth dimension. Now, it is possible to simulate the salp swarm. Fig. 8 illustrates the pseudocode of SSA. This algorithm has been used to train an ANN in a number of previous studies (Kandiri & Fotouhi, 2021; Kandiri et al., 2020; Kang et al., 2019).
3.4.3 Grasshopper Optimization Algorithm
Although grasshoppers are observed individually in nature, they live in a huge swarm, and this behaviour is found in both nymph and adulthood (Rogers et al., 2003; Simpson et al., 1999). In their adulthood phase, they move in the long-range while their steps are small in their nymph phase. In fact, the big steps are for exploration and the small steps are for exploitation. Each grasshopper search agents have a position (\({X}_{j}\)) made of n-dimensions, which is defined in Eqs. (14 and 15):
where \({S}_{j}\), \({G}_{j}\), and \({W}_{j}\) are social interaction, gravity force, and wind advection on the jth search agent. \({c}_{1}\), \({c}_{2}\), and \({c}_{3}\) are random numbers between zero and one to make random behaviour. The following equation discusses the social interaction (\({S}_{r}\)):
where drm is the distance between the rth and the mth grasshopper, calculated as \({{d}}_{{rm}} = |{{x}}_{{m}}-{{x}}_{{r}}|\), \(\widehat{{{d}}_{\mathrm{rm}}}\) is a unit vector from the rth to the mth grasshopper as computed as \(\widehat{{{d}}_{\mathrm{rm}}}= \frac{{{x}}_{{m}}-{{x}}_{{r}}}{{{d}}_{\mathrm{rm}}}\), and s is a function to describe the social forces’ strength represented in Eq. (16):
where \(\mathrm{ia}\) and \(\mathrm{lc}\) are the intensity of attraction and the attractive length scale, respectively. Based on the distance between two grasshoppers, they apply force on each other. This force could be absorption for far grasshoppers and repulsion for close grasshoppers. However, there is an exact value of distance, in which grasshoppers apply no force on each other, which is called comfort zone. \({G}_{i}\) and \({W}_{i}\) are calculated in Eqs. (17 and 18):
where \({g}\) and \(\widehat{{{e}}_{{g}}}\) are the constant of gravity and a unity vector towards the earth’s centre, respectively, and \({u}\) and \(\widehat{{{e}}_{{w}}}\) are the constant of gravity drift and a unity vector in the wind’s direction, respectively. A modified version of the is represented as follows (Eq. 19):
where ubd and lb are the upper bound and the lower bound in the dth dimension, respectively, \(\widehat{{T}_{d}}\) is the dth dimension of the target position, m is a decreasing coefficient to shrink the comfort zone. In the first iteration, the rate of exploration is higher than that in the final iterations. Therefore, m should decrease as the algorithm get close to its end. The m parameter is calculated in Eq. (20):
where IT is the number of maximum iterations and mmax and mmin are 1 and 0.00001, respectively. Fig. 9 shows the different steps of the GOA.
3.5 Proposed Models
This section defines that how the proposed models are developed and how the optimization algorithms are combined by ANN and SVR.
3.5.1 Modified ANN
The performance of an ANN is affected by its architecture; in fact, obtaining the optimum number of hidden layers and their nodes is the biggest challenge in building a network. In the present paper, three different optimization methods are used to develop ANNs with the optimum architectures and reliable performances. The position of a search agent and the gene of an individual are divided into two parts. As shown in Fig. 10, the upper part is allocated to the existence of a hidden layer, and the lower part is allocated to the number of nodes in the hidden layers. Each cell of the upper part can take a value of either 0 or 1. If the nth cell has the value of 1, the network includes the nth hidden layer, and if it has the value of 0, the networks do not include the mentioned hidden layer. Regarding the lower part, the mth cell indicates that the related hidden layer includes how many nodes.
These three models have almost the same process as their original algorithms, but instead of a fitness function they use and ANN with the obtained architecture to calculate the fitness of each individual or search agent, and their errors are computed by root mean square error (RMSE) (Eq. 21):
3.5.2 Modified SVR
Finding the best values for the penalty coefficient (C), the error limit (\(\upvarepsilon\)), and the slack variable (\(\delta\)) are really important in the SVR method; in fact, the performance of an SVR is dependent on those parameters. To address this challenge in this paper, the gene of an individual and the position of a search agent are made with three cells. Each cell is allocated to one of the parameters. Therefore, the optimization algorithms can optimize the SVR performance and reduce its error as much as possible. The method that used in this section is similar to the method that used in Sect. 3.4.1.
4 Results and Discussion
4.1 Normalization
In the first step, before entering the inputs into the model, it is needed to normalize them because of the difference in the scales of inputs. In this study, the following equation is used (Eq. 22):
where \(a\) is an input value, \({a}_{\rm min}\), \({a}_{\rm max}\), and \({a}_{n}\) are minimum, maximum, and normal values of the a, respectively.
4.2 Comparison of the Models’ Performances
After running the models, three ANNs and two SVRs are made. The architecture of ANNGOA, ANNSSA, and ANNGA are 9–7–4–1, 9–15–1, and 9–13–10–5–1, respectively. The weighted links and biases of these ANNs are represented in Appendix 2. In other words, ANNSSA has the simplest architecture with 15 nodes in its only hidden layer, ANNGOA has the second simplest architecture with seven and five nodes in its first and second hidden layer, respectively, and ANNGA has the most complex one with three hidden layers including 13, 10, and 5 nodes in them, respectively. Moreover, the error limits, penalty coefficients, and the slack variables of SVRGOA are 5, 0.267, and 1 while these parameters of SVRSSA are 5, 0.237, and 1, respectively. These two SVRs are working almost the same. Fig. 11 demonstrates the errors of the models for the dataset.
In this study, to compare the performances of the proposed models, in addition to RMSE, mean absolute percentage error (MAPE—Eq. 23), correlation coefficient (R—Eq. 24), mean absolute error (MAE—Eq. 25), scatter index (SI—Eq. 26), and mean absolute bias error (MBE—Eq. 27) are used:
where \(\overline{M }\) is the mean value of measured results, and other parameters are explained in the previous section. MBE indicates that the model overestimates (MBE > 0) or underestimates (MBE < 0). SI determines that the performance of the model is “excellent” (0 ≤ SI < 0.1), “good” (0.1 ≤ SI < 0.2), “fair” (0.2 ≤ SI < 0.3), or “poor” (0.3 ≤ SI). Table 2 represents these indicators for the models.
According to Table 2, SVRSSA has the lowest MAE followed by ANNGA while SVRGOA is following that closely, and ANNGOA and ANNSSA have the second-highest and highest MAE, respectively. Based on MBE, ANNGOA overestimates the output while other models underestimate that. According to RMSE, SVRGOA, SVRSSA, and ANNGOA, are the first to third-best models, respectively, so that their distances are so low, and finally, ANNSSA and ANNGA are the worst and the second-worst ones, respectively. With regard to MAPE, SVRSSA has the best performance by far, SVRGOA has the second-best performance followed by ANNGA closely, and ANNGOA and ANNSSA are the fourth and fifth models. SI indicates that all of the models have fair performances. Finally, all models have a correlation coefficient of 0.98. Fig. 12 illustrates the predicted values against the experimental values for the models in which it can be seen that the scatter around the baseline for all models is almost the same. Furthermore, Fig. 13 compares the RMSE, MAE, and MAPE of the models in a radar chart in which, it can be seen that SVRSSA has the lowest RMSE, MAE, and MAPE values among all models.
4.3 Validation with Mathematical Modelling
Mathematical modelling is always a decent method to predict the different characteristics of concrete. Hence, a study by Lange et al. (2008) used mathematical modelling to predict the maximum lateral pressure of concrete while the casting, this is expressed in Eq. (28):
where Co is the initial pressure and time-dependent variable, and a is used to fit the function of pressure decay, while α is a time-dependent variable used to fit the function to the pressure decay. Therefore, according to this formula most changes are in the density, casting rate and initial pressure. In addition, if the results in Fig. 8 are checked, most of the results are located between 50 to 70 kPa. This indicated that most of the height of the formwork is not more than 3 m cast at the same. However, there are still some values that can be seen as over 100 kPa.
Another study by Ovarlez and Roussel (2006) expressed the lateral pressure for rectangular and circular formwork can be obtained using Eqs. (29) and (30), respectively:
where r is the formwork radius, K2 is the ratio of lateral to vertical pressure and Athix is a flocculation coefficient of concrete. Based on these formulae show there are no differences between shape geometry. Their equations show clearly the height of the formwork has a major influence in an increase or decrease the lateral pressure exertion on the formwork. Nevertheless, there are not many differences in the shape of the formwork for casting; therefore, it could not also see obvious differences. As a comparison with machine learning, these equations could be quite matched with all five models (ANNSSA, ANNGOA, ANNGA, SVRSSA, SVRGOA).
In machine learning, all five models (ANNSSA, ANNGOA, ANNGA, SVRSSA, SVRGOA) yield excellent result values for R (coefficient of correlation) which recorded approximately 0.98 value for all models. This outcome is identical to use any of them as a prediction model for measuring lateral pressure of fresh concrete on the panel of the formwork.
5 Conclusion
Lateral pressure exertion from fresh concrete on the formwork panel creates uncertainty for industries while casting concrete. This is due to high pressure, particularly when the casting rate increases. Therefore, this study collected the various samples around the world to analyse and train in data learning. These machine learning applications would be useful to investigate and predict the lateral pressure of concrete before casting and pouring into the formwork. So briefly the outcomes of this investigation can be listed as follows:
-
Following ACI 347-04 Guide to Formwork for Concrete, it can be said that the lateral pressure exerted concrete in the real-world application did not record a value above 200 kPa. However, this mostly depends on the height of casting, casting rate, the constant value of gravity and the density of the materials; therefore, it could be expected to increase with increasing these parameters.
-
Generally, SVR-based models have better performances compared to ANN-based models, although all models have the same correlation coefficient approximately.
-
Based on MAE, MBE, and MAPE, SVRSSA is the most accurate model followed by SVRGOA closely. Nevertheless, SVRGOA has lower RMSE compared to SVRSSA.
-
All machine-learning-based models have a high correlation coefficient, which indicates the great correlation between experimental and predicted lateral pressure. Therefore, all of them can be used to estimate the lateral pressure of concrete.
-
Even ANNSSA which is the least accurate model has an acceptable performance with the RMSE value of 7.24 and MAE value of 4.08.
Availability of data and materials
The data and materials are included in this manuscript.
References
Ahmad, M. S., et al. (2020). A novel support vector regression (SVR) model for the prediction of splice strength of the unconfined beam specimens. Construction and Building Materials, 248, 118475.
Ahmadi, M., et al. (2020). New empirical approach for determining nominal shear capacity of steel fiber reinforced concrete beams. Construction and Building Materials, 234, 117293.
Alam, M. A., & Al Riyami, K. (2018). Shear strengthening of reinforced concrete beam using natural fibre reinforced polymer laminates. Construction and Building Materials, 162, 683–696.
Almeida Filho, F., et al. (2010). Hardened properties of self-compacting concrete—a statistical approach. Construction and Building Materials, 24(9), 1608–1615.
Alyamaç, K. E., & Ince, R. (2009). A preliminary concrete mix design for SCC with marble powders. Construction and Building Materials, 23(3), 1201–1210.
Behnood, A., & Golafshani, E. M. (2018). Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. Journal of Cleaner Production, 202, 54–64.
Boser, B.E., Guyon, I.M., & Vapnik, V.N. (1992). A training algorithm for optimal margin classifiers. in Proceedings of the fifth annual workshop on Computational learning theory.
Brereton, R. G., & Lloyd, G. R. (2010). Support vector machines for classification and regression. The Analyst, 135(2), 230–267.
Chandwani, V., Agrawal, V., & Nagar, R. (2015). Modeling slump of ready mix concrete using genetic algorithms assisted training of Artificial Neural Networks. Expert Systems with Applications, 42(2), 885–893.
Cybenko, G. (1989). Approximation by superpositions of a sigmoidal function. Mathematics of Control, Signals and Systems, 2(4), 303–314.
Day, K. W. (2006). Advice to specifiers. Concrete Mix Design, Quality Control and Specification (pp. 21–27). CRC Press.
de Brito, J., & Kurda, R. (2021). The past and future of sustainable concrete: A critical review and new strategies on cement-based materials. Journal of Cleaner Production, 281, 123558.
Farooq, F., et al. (2020). A comparative study of random forest and genetic engineering programming for the prediction of compressive strength of high strength concrete (HSC). Applied Sciences, 10(20), 7330.
Feys, D., Verhoeven, R., & De Schutter, G. (2009). Why is fresh self-compacting concrete shear thickening? Cement and Concrete Research, 39(6), 510–523.
Golafshani, E. M., & Behnood, A. (2018). Application of soft computing methods for predicting the elastic modulus of recycled aggregate concrete. Journal of Cleaner Production, 176, 1163–1176.
Golafshani, E. M., Behnood, A., & Arashpour, M. (2020). Predicting the compressive strength of normal and high-performance concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Construction and Building Materials, 232, 117266.
Gowripalan, N., Shakor, P., & Rocker, P. (2021). Pressure exerted on formwork by self-compacting concrete at early ages: A review. Case Studies in Construction Materials, 15, e00642.
Haron, N. A., et al. (2005). Building cost comparison between conventional and formwork system: A case study of four-storey school buildings in Malaysia. American Journal of Applied Sciences, 2(4), 819–823.
Holland, J. H. (1992). Adaptation in natural and artificial systems: an introductory analysis with applications to biology, control, and artificial intelligence. USA: MIT Press.
Izadgoshasb, H., et al. (2021). Predicting compressive strength of 3D printed mortar in structural members using machine learning. Applied Sciences, 11(22), 10826.
Jahangir, H., & Eidgahee, D. R. (2021). A new and robust hybrid artificial bee colony algorithm—ANN model for FRP-concrete bond strength evaluation. Composite Structures, 257, 113160.
Kandiri, A., & Fotouhi, F. (2021). Prediction of the module of elasticity of green concretes containing ground granulated blast furnace slag using hybridized multi-objective ANN and Salp swarm algorithm. Journal of Construction Materials, 2, 2–2.
Kandiri, A., Golafshani, E. M., & Behnood, A. (2020). Estimation of the compressive strength of concretes containing ground granulated blast furnace slag using hybridized multi-objective ANN and salp swarm algorithm. Construction and Building Materials, 248, 118676.
Kandiri, A., Sartipi, F., & Kioumarsi, M. (2021). Predicting compressive strength of concrete containing recycled aggregate using modified ANN with different optimization algorithms. Applied Sciences, 11(2), 485.
Kang, F., Li, J., & Dai, J. (2019). Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms. Advances in Engineering Software, 131, 60–76.
Koehler, E.P. (2007). Aggregates in self-consolidating concrete.
Kurda, R., et al. (2022). Mix design of concrete: Advanced particle packing model by developing and combining multiple frameworks. Construction and Building Materials, 320, 126218.
Lange DA, et al. (2008). Modeling formwork pressure of SCC, in Proceedings of the 3rd North American conference on the design and use of self-consolidating concrete. Chicago, USA.
Lizarazo-Marriaga, J., et al. (2020). Probabilistic modeling to predict fly-ash concrete corrosion initiation. Journal of Building Engineering, 30, 101296.
Lloret, E., et al. (2015). Complex concrete structures: Merging existing casting techniques with digital fabrication. Computer-Aided Design, 60, 40–49.
Margallo, M., et al. (2015). Life cycle assessment of technologies for partial dealcoholisation of wines. Sustainable Production and Consumption, 2, 29–39.
Merriam, J. (1992). Atmospheric pressure and gravity. Geophysical Journal International, 109(3), 488–500.
Mirjalili, S., et al. (2017). Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Advances in Engineering Software, 114, 163–191.
Mohammed, A., et al. (2021). Soft computing techniques: Systematic multiscale models to predict the compressive strength of HVFA concrete based on mix proportions and curing times. Journal of Building Engineering, 33, 101851.
Monteiro, P. J., Helene, P. R., & Kang, S. (1993). Designing concrete mixtures for strength, elastic modulus and fracture energy. Materials and Structures, 26(8), 443–452.
Okamura, H. (1997). Self-compacting high-performance concrete. Concrete International, 19(7), 50–54.
Okamura, H., & Ozawa, K. (1996). Self-compacting high performance concrete. Structural Engineering International, 6(4), 269–270.
Ovarlez, G., & Roussel, N. (2006). A physical model for the prediction of lateral stress exerted by self-compacting concrete on formwork. Materials and Structures, 39(2), 269–279.
Pan, Y., et al. (2009). A novel QSPR model for prediction of lower flammability limits of organic compounds based on support vector machine. Journal of Hazardous Materials, 168(2–3), 962–969.
Puente, I., Santilli, A., & Lopez, A. (2010). Lateral pressure over formwork on large dimension concrete blocks. Engineering Structures, 32(1), 195–206.
Ramezani, M., Kim, Y. H., & Sun, Z. (2020). Probabilistic model for flexural strength of carbon nanotube reinforced cement-based materials. Composite Structures, 253, 112748.
Rodin, S. (1952). Pressure of concrete on formwork. Proceedings of the Institution of Civil Engineers, 1(6), 709–746.
Rogers, S. M., et al. (2003). Mechanosensory-induced behavioural gregarization in the desert locust Schistocerca gregaria. Journal of Experimental Biology, 206(22), 3991–4002.
Roussel, N., & Cussigh, F. (2008). Distinct-layer casting of SCC: The mechanical consequences of thixotropy. Cement and Concrete Research, 38(5), 624–632.
Sahoo, S., & Mahapatra, T. R. (2018). ANN modeling to study strength loss of fly ash concrete against long term sulphate attack. Materials Today: Proceedings, 5(11), 24595–24604.
Shahnewaz, M., Rteil, A., Alam, M.S. (2020). Shear strength of reinforced concrete deep beams–a review with improved model by genetic algorithm and reliability analysis. in Structures. Amsterdam: Elsevier.
Shahnewaz, M., & Alam, M. S. (2020). Genetic algorithm for predicting shear strength of steel fiber reinforced concrete beam with parameter identification and sensitivity analysis. Journal of Building Engineering, 29, 101205.
Shakor, P.N., & Pimplikar, S. (2011). Glass fibre reinforced concrete use in construction. International Journal of Technology and Engineering System. 2(2).
Shakor, P., & Gowripalan, N., Pressure Exerted on Formwork and Early Age Shrinkage of Self-Compacting Concrete. Concrete in Australia, 2020.
Simpson, S. J., McCaffery, A. R., & Hägele, B. F. (1999). A behavioural analysis of phase change in the desert locust. Biological Reviews, 74(4), 461–480.
Smola, A. J., & Schölkopf, B. (2004). A tutorial on support vector regression. Statistics and Computing, 14(3), 199–222.
Sun, J., et al. (2019). Prediction of permeability and unconfined compressive strength of pervious concrete using evolved support vector regression. Construction and Building Materials, 207, 440–449.
Suykens, J. A., & Vandewalle, J. (1999). Least squares support vector machine classifiers. Neural Processing Letters, 9(3), 293–300.
Tabatabaeian, M., et al. (2017). Experimental investigation on effects of hybrid fibers on rheological, mechanical, and durability properties of high-strength SCC. Construction and Building Materials, 147, 497–509.
Vapnik, V., S.E. Golowich, & A. Smola. (1997). Support vector method for function approximation, regression estimation, and signal processing. Advances in Neural Information Processing Systems, 281–287.
Vapnik, V. (2013). The nature of statistical learning theory. Springer science & business media.
Velay-Lizancos, M., et al. (2018). Concrete with fine and coarse recycled aggregates: E-modulus evolution, compressive strength and non-destructive testing at early ages. Construction and Building Materials, 193, 323–331.
Vickers, N. J. (2017). Animal communication: When i’m calling you, will you answer too? Current Biology, 27(14), R713–R715.
Yan, F., et al. (2017). Evaluation and prediction of bond strength of GFRP-bar reinforced concrete using artificial neural network optimized with genetic algorithm. Composite Structures, 161, 441–452.
Yu, B., Tang, R.-K., & Li, B. (2020). Probabilistic bond strength model for reinforcement bar in concrete. Probabilistic Engineering Mechanics, 61, 103079.
Yuan, Z., Wang, L.-N., & Ji, X. (2014). Prediction of concrete compressive strength: Research on hybrid models genetic based algorithms and ANFIS. Advances in Engineering Software, 67, 156–163.
Acknowledgements
The authors would like to thank the tremendous support from the Future University in Egypt, specifically Professor Ahmed Farouk Deifalla.
Funding
No funding was received.
Author information
Authors and Affiliations
Contributions
All authors contributed equally in this paper. PS and AK wrote the first draft of the paper. RK and AFD revised the paper completely with detailed comments and improvement. All authors read and approved the final manuscript.
Authors’ information
Amirreza Kandiri, PhD Candidate, University College Dublin. Pshtiwan Shakor, Lecturer, Sulaimani Polytechnic University/ Tishk International University. Rawaz Kurda, Lecturer, Erbil Polytechnic University/ Nawroz University. Ahmed Farouk Deifalla, Professor, Future University.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
No ethical approvals were needed in this experimental study.
Consent for publication
Not applicable.
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Journal information: ISSN 1976-0485 / eISSN 2234-1315
Appendices
Appendix 1
See Table 3
Appendix 2
1.1 Biases and Weights of the ANNSSA Model
1.2 Biases and Weights of the ANNGOA Model
1.3 Biases and Weights of the ANNGA Model
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kandiri, A., Shakor, P., Kurda, R. et al. Modified Artificial Neural Networks and Support Vector Regression to Predict Lateral Pressure Exerted by Fresh Concrete on Formwork. Int J Concr Struct Mater 16, 64 (2022). https://doi.org/10.1186/s40069-022-00554-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40069-022-00554-4