Abstract
Temperature variability may have direct and indirect impacts on the environments of the Accra and Kumasi Metropolises in Ghana. This study analysed temperature and trends in temperature in both cities using in-situ measurements from one meteorological station in both cities from 1986 to 2015. The temperature indices were computed using the RClimdex package from the Expert Team on Climate Change Detection Monitoring Indices (ETCCDMI). The temperature time series was pre-whitened before the Mann–Kendall trend and Sen’s slope estimator analysis were applied. Initial analysis revealed minimal variation in temperature in both cities. The results from the analysed temperature indices revealed an increase in warm days and a general rise in the minimum temperature compared to maximum temperatures. Mann Kendall and Sen’s slope revealed significant trends in the annual and seasonal (dry and wet seasons) in minimum temperature in both cities. These might lead to an increased rate of heat-stressed diseases and an overall rise in urban warming in both cities. The analysis of temperature, indices and trends provided comprehensive insights into the temperature of Accra and Kumasi. The results highlight the essence of evaluating temperature indices and trends in light of Climate Change concerns. It is recommended that urban green and blue spaces should be incorporated into land use plans as these policy directions can aid regulate the temperature in both cities.
Similar content being viewed by others
Introduction
Globally, temperature is considered an important variable within the climate system and it is chosen as one of the standard variables for analysis (Kajtar et al. 2021; Ragatoa et al. 2018). Temperature variability may lead to a rise in the frequency, magnitude and seasonality of extreme events which are likely to happen in the future (van der Wiel and Bintanja 2021).
Temperature indices are essential indicators used for monitoring and detecting variability (Qaisrani et al. 2021). Various groups of indices have been invented using percentiles and thresholds. The most popular and utilized is the group of indices of the Expert Team on Climate Change Detection and Indices (ETCCDI), sponsored by the Commission for Climatology of the World Meteorological Organization (WMO), the Joint Commission for Oceanography and Marine Meteorology (JCOMM) and by the Climate Variability and Predictability (CLIVAR) project (Faye and Akinsanola 2022). Temperature viability studies have been done at the global level (Hansen et al. 2021), national level using Ghana and at the local level using the city of Abuja in Nigeria and Shenyang in China (Mahmoud 2016; Yang et al. 2021).
Karaburun et al. (2011) investigated the evolution of mean, minimum and maximum temperatures in the monthly, seasonal and annual temperatures in Istanbul utilising the Mann–Kendall test and revealed positive trends in annual averages and average maximum temperature at both 95% and 99% significance. Larbi et al. (2018) investigated trends in annual temperature extremes using the Vea Catchment (one of the sub-catchments within the white Volta basin) in Ghana from 1985 to 2016 using quality-controlled weather station data. The non-parametric Mann–Kendall test and Sen’s slope estimator were utilised to detect trends in temperature. A general warming trend was observed over the Vea Catchment. The work of Gadedjisso-Tossou and Adjegan (2021) investigated trends in monthly and annual minimum and maximum temperature from 1977 to 2012 utilising the Mann–Kendall test and Sen’s slope to evaluate the significance of selected cereal crops utilising multiple regression analyses. The results from the regression analyses revealed non-linear yield responses to alterations in temperature. It was however concluded that temperature variability affected the productivity of the cereal crops negatively.
According to Oduro et al. (2022), the temperature of Ghana increased by about 1.0 °C between 1960 and 2000. Ghana has a mean annual temperature ranging from 24 °C to 30 °C (Asante and Amuakwa-Mensah 2015). Temperature has been increasing more rapidly in the Northern than Southern parts of Ghana (Minia 2008). The mean annual air temperature increased by 0.9 °C between 1960 and 2001 along the coast of Ghana. The maximum temperature increased by 2.5 °C whilst the minimum temperature also rose by 2.2 °C during the same period (Dontwi et al. 2008). Subaar et al. (2018) analysed the daily mean air temperature from 1990 to 2009 in Wa, Upper West Region, Ghana. The study revealed a rise in annual mean temperature of 0.4 ℃. Klutse et al. (2020) predicted temperature and its probable consequences on smallholder farming systems in the Northern Regions of Ghana. The analysed temperature data from 1961 to 2000 indicated that the average annual temperature across Ghana increased by 1.0 ℃ (Klutse et al. 2014).
Temperatures will increase by 1.1–1.3 °C for southern Ghana and up to 1.4 °C for Northern Ghana by 2030 (Läderach, 2011). The mean annual temperature will rise progressively by 2050 by 1.7–2.1 °C in southern Ghana and up to 2.5 °C in the northern parts of Ghana. There have been rising temperatures in different study locations in Ghana due to climate change (Adusu et al. 2022; Asare-Nuamah and Botchway 2019; Kabo-Bah et al. 2016).
Ghana has experienced the impacts of temperature variability with an increase of 1.0 °C in temperature from 1960 to 2000 (Oduro et al. 2022). The pressing issues about the consequences of temperature variability include but are not limited to: The agricultural sector, which consists of mainly small-scale farmers who have the least resources to invest in and are vulnerable to the potential impacts of temperature variability. Estimates of the cost of environmental degradation in 2006 indicated a loss of 10% of Gross Domestic Products (GDP) yearly. This is attributed to the unsustainable management of lands and forests (MESTI 2013). The impacts are land degradation, deforestation and biodiversity loss but deforestation stood out within the Ghanaian Landscape (Kumeh et al. 2022; Kyere-Boateng and Marek 2021).
A handful of works to determine trends in temperature in Ghana exist in the literature. Most of them were done at national and regional levels (Baffour-Ata et al. 2021; Boansi et al. 2017; Dankwa et al. 2021; Issahaku et al. 2016). Adu-Prah et al. (2019) used trajectory and time series analysis of temperature anomalies across the agroecological zones of Ghana. The study revealed that the local temperature increased for the study period from 0.5 ℃ to 1.0 ℃. Asare-Nuamah and Botchway, (2019) utilised temperature data from 1989 to 2015 to ascertain the characteristics and trends in temperatures across the agroecological zones in Ghana. Oduro et al. (2022) investigated seasonal and annual trends from 1901 to 2018 in Ghana. The findings revealed that there has been a significant rise in both the annual and seasonal temperatures of minimum and maximum temperatures whilst mean temperature recorded a steady increment over the study period. Finally, Asamoah and Ansah-Mensah (2020) investigated the temporal variations in temperature in Bawku, Upper East Region of Ghana from 1976 to 2015. The mean temperature revealed a significant increase. In addition, it was observed that day and night temperatures increased during the study period (Asamoah and Ansah-Mensah 2020).
Although temperature has been analysed throughout Ghana in seminal works (e.g. Abbam et al. 2018; Asamoah and Ansah-Mensah 2020; Issahaku et al. 2016), limited attention has been given to the analysis of temperature time series, temperature indices and temperature trends in Accra and Kumasi. Both cities are the most urbanised centres in Ghana and led to the transformation of green areas into urban/built-up areas (Addae and Oppelt 2019; Frimpong and Molkenthin 2021; Ghana Statistical Service (GSS) 2014a, b). This research, therefore, chose these two cities due to the high levels of land use land cover changes. The research seeks to fill this knowledge gap by analysing the maximum and minimum temperatures, indices and trends (seasonal and annual) of both cities. In this research, the dry seasons were made up of the months; November, December, January, February and March. On the other hand, the wet season consisted of the months; April, May, June, July, August, September and October as also used in the work of (Amoah et al. 2016).
Material and methods
Case study cities (Accra and Kumasi)
Accra acts simultaneously as the capital of the Greater Accra Region and Ghana. The capital is in the south-eastern portion of the coast of the Gulf of Guinea. Geographically, Accra is bounded on the north by latitude 5.41° N, on the south by the Gulf of Guinea, on the east by longitude 0.30° E and on the west by longitude 0.17° W (Ghana Statistical Service (GSS) 2014a, 2014b) (Fig. 1). The Accra Metropolitan Assembly consists of the Ablekuma, Ayawaso, Kpeshie, Okaikoi and Osu Klottey administrative boundaries (Ghana Statistical Service (GSS), 2014a) with a population of 2,066,275 and it is the most populated city in Ghana (Ghana Statistical Service (GSS) 2021).
Kumasi, the capital of the Ashanti Region is found between Latitude 6.35° N and 6.40° S and Longitude 1.30° W and 1.35° E. It is about 270 km north of Accra (Ghana Statistical Service (GSS) 2014a, b) (Fig. 1). The Kumasi Metropolitan Assembly was made up of the Asawase, Asokore-Mampong, Asokwa, Bantama, Kwadaso, Manhyia, Nhyiaeso, Oforikrom, Suame, Subin and Tafo (Ghana Statistical Service (GSS) 2014a, b) with a population of 1,823,316 and it is the second most populated city in Ghana (Ghana Statistical Service (GSS) 2021).
Dataset utilised
Temperature datasets comprising daily values of minimum and maximum temperature spanning from 1st January 1986 to 31st December 2015 were used for this retrospective study. The study period was chosen as it spanned 30 years and the complete dataset was readily available for both cities.
The dataset was obtained from the Ghana Meteorological Agency (GMA) stations (Kotoka International Airport weather station in Accra and the Kumasi weather station). It was made up of daily maximum and minimum temperatures.
Methods
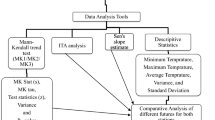
Initial data analysis
Preliminary analysis was run for the temperature dataset. Time plots were constructed for daily maximum and minimum temperature. This provided a general overview and insights into the distribution of the data.
Temperature indices
Daily values of maximum and minimum temperature datasets from 1986 to 2015, were used to calculate five temperature indices as recommended by the Joint CCl/CLIVAR/JCOMM Expert Team (ET) on Climate Change Detection and Indices (Frich et al. 2002) (Table 1).
The indices not calculated were rainfall indices. The other temperature indices were not applicable in the study areas since both cities are situated in the tropics, such as the number of frost days, summer days, ice days, and tropical nights (Parsons et al. 2022; WMO 2021). Data quality checks were done to identify missing values, outliers, and days when the minimum temperature was greater than the maximum temperature. Finally, the input file of the adjusted daily maximum temperature and daily minimum temperature was used to calculate the temperature indices (Table 1). The RClimdex was used for the computation of temperature indices and trends in the temperature dataset. Initially, it was employed to check the quality of the data. RClimdex provided insights into extreme variations in temperature (Zhang and Yang 2004).
Trend analysis methods
Non-parametric methods were used to detect significant trends in the temperature time series. Since the temperature data was not normally distributed, the Mann–Kendall and Sen's slope estimator were used to detect trends and the slopes respectively.
Serial Correlation (seasonal and annual)
The serial correlation was removed from the temperature data to pre-whiten the dataset before using the Mann–Kendall test (von Storch and Navarra 1999). The study incorporated this suggestion before utilising the Mann–Kendall test and Sen's slope estimator.
The possible statistically significant trends in the temperature data (x1, x2, …, xn) were assessed utilising the following procedures:
1. The lag-1 serial correlation coefficient (r1) was computed. The lag-1 serial correlation coefficient of sample data xi was computed using the equation below (Kendall and Stuart 1961).
where E(xi) is the average of the sample data and n is the sample size.
2. If the computed r1 was not significant at the 5% level, then the Mann–Kendall test and Sen's slope estimator were applied to the original values of the time series.
3. If the computed r1 was significant, before applying the Mann–Kendall test and Sen's slope estimator, the ‘pre-whitened’ time series might be acquired as (x2 − r1 x1, x3 − r1 x2, …, xn − r1 xn−1).
The critical value of r1 for a given significance level depended on whether the test was one-tailed or two-tailed. The alternative hypothesis for the one-tailed hypothesis was usually that the true r1 is greater than zero, whereas the alternative hypothesis for the two-tailed test was that the true r1 is different from zero, with no indication of whether it was positive or negative. According to (Anderson 1942), the probability limits of an independent series for r1 were computed as;
where n was the sample size.
Both one-tailed and two-tailed tests were employed since there was reason to suspect both positive and negative autocorrelation was present in the temperature dataset.
Mann–Kendall trend test
The Mann–Kendall test statistic S (Kendall 1955; Mann 1945) was computed as;
where,
n = the total number of data points.
xi and xj = data values in time series i and j (j > i), respectively and sgn(xj − xi) is the sign function:
The variance was computed as;
where,
n = the number of data points,
m = the number of tied groups and ti denotes the number of ties to the extent i. A tied group is a set of sample data having the same value.
In the case, where the sample size, n > 10, the standard normal test statistic ZS was computed using the equation;
Positive values of ZS indicated increasing trends while negative ZS values showed decreasing trends.
Sen's slope estimator
Sen (1968) devised the non-parametric method for the estimation of the slope of a trend in the sample of N pairs of data:
where, Xj and Xk = the data values at times j and k (j > k), respectively.
If there is only one datum in each period, then \({\text{N }} = \frac{{n\left( {n{-}{ 1}} \right)}}{2}\). where n = number of periods.
If there are multiple observations in one or more time periods, then \({\text{N < }}\frac{{n\left( {n{-}{ 1}} \right)}}{2}\). where n = total number of observations.
The N values of Qi are ranked from the least to the highest and the median slope or Sen’s slope estimator was calculated as
The Qmed sign reflects the data trend, while its value indicates the steepness of the trend. To determine whether the median slope is statistically different from zero, the computation of the confidence interval of Qmed at a specific probability is done.
The confidence interval about the time slope was calculated as:
where Var(S) is defined in Eq. 8.14 and Z1−α/2 is obtained from the standard normal distribution table.
In this study, the confidence interval was computed at a significance level of α = 0.05.
The positive values indicated an increasing trend whilst negative values denoted a decreasing trend in the time series of analysed temperature.
The XLSTAT was utilised to compute trends (Mann Kendall and Sen’s slope) in the temperature data. The XLSTAT is an add-in tool in Excel (Addinsoft 2019).
Results
Annual plots of temperature for both cities
Both cities exhibited fairly constant steadiness in temperature throughout the study period. Mean values overlapped. Nonetheless, it was apparent that Kumasi slightly yielded higher mean values for maximum temperature. The values ranged from 30.9 °C (1996) to 32.2 °C (2010) compared to values for Accra that ranged from 29.6 °C to 32 °C that occurred in 2003 and 1998 respectively.
Generally, Accra received higher values for minimum temperature compared to Kumasi. Likewise, maximum temperature and steadiness were observed throughout the study period. The values for Accra ranged between 23.7 °C (1988 and 1992) and 25 °C (2010). On the other hand, values for Kumasi were between 21.5 °C (1986) and 22.8 °C (1998). Interestingly, there was an increase in the measured average maximum and minimum temperature of both cities in 1987, 1998 and 2010 (Fig. 2). There was also a sudden drop in the years 2003 and 2012 for the maximum and minimum temperature, respectively for Accra.
Analysis of temperature indices
A. Cold days—percentage of days when the maximum temperature was less than the 10th percentile
Accra had a decline in values from 1986 to 1987. A few fluctuations followed until it dropped significantly in 1995. Again, there was a rise with variations till it peaked in 2001. A sudden decrease followed by fluctuations that led to its bottoming out in 2011. A sudden rise was observed and afterwards, fluctuations in values occurred that led to a decline in the last year.
Just like Accra, Kumasi also experienced a decline from 1986 to 1987. It dropped drastically, followed by steady variations before its lowest value in 2015. The results were significant in both cities (Fig. 2).
B. Cold nights—percentage of days when minimum temperature was less than the 10th percentile
It was observed that there was a sudden decline from 1986 to 1987 in Accra. However, it rose afterwards, which was followed by fluctuations. These fluctuations continued until 2012. Then, steady values were yielded in 2014, followed by a drop in the last year of the study. Then, it suddenly dropped in the subsequent years till 2015 (Fig. 2).
In Kumasi, there was also a drastic decrease from 1986 to 1987, and it rose until 1989. Fluctuations followed before the year 2000 when the highest value was measured. There was a sudden drop in the subsequent year. Steady fluctuations followed this until 2015. This index was significant in both cities (Fig. 2).
C. Warm days—percentage of days when the maximum temperature was greater than the 90th percentile
In Accra, the percentage of the number of days fluctuated for this index from 1986 to 1990, with a slight decrease in the ensuing year. However, there were fluctuations before 1996. A sudden rise was seen up till 1998. Moreover, it was followed by a drop in the number of warm days in 2001. After that, values began rising again with few fluctuations before 2011. Finally, there was a steady rise before 2015 (Fig. 2).
Kumasi experienced steadiness from 1986 to 1988. This was followed by a rise into 1990. After that, the gradual decline in percentages followed until it bottomed out in 1993. However, it was noticed that sharp fluctuations abruptly followed gradual fluctuations in percentages before they peaked in 2010. There was a sudden decline in 2011, and a rise was observed, afterwards by a steady increase until 2014. Finally, a gradual decrease was noticed in 2015. The index was significant in both cities (Fig. 2).
D. Warm nights—percentage of days when minimum temperature was greater than the 90th percentile
Generally, it was observed that the number of warm nights revealed a constant rise throughout the study period. There was a rise from 1986 to 1987 for Accra. The values exhibited steady fluctuations before the year 1999. However, from 1999, values rose into 2005. It was observed that percentages dropped before the year 2012, fluctuations followed into 2014 and a sharp rise was noticed in 2015 (Fig. 2).
In Kumasi, there were no initial recordings (i.e. no values were measured) before 1993. There were a sudden rise and few fluctuations till 2006. Sharp fluctuations followed this until 2014. Interestingly, the percentage for 2014 remained unchanged in 2015. The index was significant in both cities (Fig. 2).
E. Diurnal temperature range (DTR)—monthly mean difference between maximum temperature and minimum temperature °C)
Similar patterns were observed for both cities, but Kumasi recorded higher DTR values compared to Accra.
The monthly mean difference between the maximum and minimum temperatures revealed a gradual decrease from 1986 to 1988 in Accra. However, this was followed by fluctuations which generally depicted a downward trend throughout the study period (Fig. 2).
Similarly, in Kumasi, there was a decrease in values from 1986 to 1987. This was followed by a lot of steady fluctuations with a decreasing trend but remained stable for the last three years. The diurnal temperature range was significant in both cities (Fig. 2).
Trends in temperature indices (1986–2015)
The calculated temperature indices revealed positive trends per year in both cities. The percentile-based indices for temperature produced 0.08 (Kumasi) and 0.06 (Accra) for cold days (Table 2). Cold nights revealed 0.09 for Accra and 0.10 (Kumasi) while warm days produced 0.13 for Accra and 0.06 for Kumasi. However, the warm nights yielded positive trends of 0.11 (Accra) and 0.13 (Kumasi).
The annual monthly maximum value of daily maximum temperature and annual monthly maximum value of daily minimum temperature yielded 0.01 °C. On the other hand, the monthly minimum value of daily maximum temperature and monthly minimum value of daily minimum temperature produced 0.02 °C for Accra. In the case of Kumasi, the annual monthly maximum value of the daily maximum temperature and the monthly minimum value of the daily minimum temperature was 0.02 °C. The monthly maximum temperature value of daily minimum temperature and monthly minimum value of daily maximum temperature recorded 0.01 °C. Finally, the DTR produced 0.01 for both cities (Table 2).
Serial correlation (seasonal and annual)
The serial correlation coefficients were positive. The strongest serial correlation was obtained for maximum temperature. The lag 1 series produced lower values for both dry and wet seasons for rainfall. The lag 1 in this research referred to the relationship between a present temperature value and its preceding value. On the other hand, the annuals recorded a higher correlation value than seasonal variability except for the annual minimum temperature for Kumasi. Generally, Kumasi yielded a better serial correlation coefficient than Accra. Maximum temperature yielded a higher serial correlation coefficient for all except for the dry season for the maximum temperature of Accra. Minimum temperature yielded moderate values for the serial correlation coefficient for all seasons and annuals for both cities (Table 3).
Mann Kendall and Sen’s slope
The Mann Kendall and Sen’s slope provided insights into the trends with their statistical significance. The Mann–Kendall test and Sen’s slope estimator were applied to the original values of the series because the calculated serial correlation coefficient was not significant at a confidence level of 95%.
The maximum temperature had trends in the dry season of Accra, the wet season and the annual of Kumasi. Minimum temperature revealed trends for both seasons and annuals for both cities (Table 4).
The magnitude of change i.e. Sen’s slope revealed that the wet season of the minimum temperature for Accra was 0.191 which was the highest. The least was revealed at the annual maximum temperature of Kumasi throughout the study period (Table 4).
Discussions
Annual plots of temperature for both cities
Temperature variations were minimal in both cities due to the local climate. The temperature did not substantially differ since the cities are 250 km apart and this attributed to the less variation in temperature as the highest correlation was revealed for (maximum and minimum temperature Amoako and Boamah, 2015; Dickson et al. 1988). The increase in the measured average maximum and minimum temperatures for 1987, 1998 and 2010 could be due to inherent characteristics present in the temperature dataset. The sudden decrease in the maximum and minimum temperature for Accra could be considered, an outlier for the entire temperature dataset (Peterson et al. 1998).
This preliminary analysis stands to serve as a basis for the analysis of temperature in both cities and will serve as a rudimentary source of information for other researchers for future studies.
Temperature indices
It was generally observed that there were decreasing trends in the cold nights compared to increasing trends in the warm nights. These results agreed with the works of (Klein Tank et al. 2006; New et al. 2006; You et al. 2011). There were fluctuations in both the cold days and warm days. However, the bottoming of cold days might be due to inherent characteristics present in the temperature dataset (Peterson et al. 1998). Minimal increasing trends were obtained in DTR. This could be attributed to the increase in the minimum temperatures in the three decades of study as found in the work of (Easterling et al. 1997). This outcome attests to the increased urban warming experienced in both cities.
The monthly mean difference between the maximum and minimum temperature showed significant positive trends in both cities. The decrease in the DTR may be an indicator of urban warming in both cities. This was similar to the findings of (Easterling et al. 1997), where DTR increased significantly. Earlier works have revealed that the minimum temperature has increased faster than the maximum temperature globally (Alexander et al. 2006) and locally in the Greater Accra Region of Ghana (Wemegah et al. 2020).
The significance of increasing warm days in both cities reaffirmed the impacts of temperature changes. The rise in warm days might have led to discomfort amongst the populace and increased cooling systems in houses and vehicles in both cities. This outcome corroborates the outcome of Mahmoud (2016) that used Abuja, Nigeria as a test site.
Warm nights have increased in both cities agreeing with earlier works (Wang et al. 2020; Yeh et al. 2021). It has made people who cannot afford the cooling systems in their homes sleep on the compounds of their homes, especially when there is no supply of electricity.
Previous researches have established the nexus between temperature variability and human health. This study agrees with Chan et al. (2012) that increasing warm days and warm nights may affect the health of the aged, especially it could lead to respiratory disorders. It is also asserted that malaria increases with extreme temperatures (Nelson and Agbey 2005). Danuour et al. (2010) revealed a positive correlation between maximum temperature and the incidence of malaria. In the case of infants, heat rashes develop on their skins (Basagaña et al. 2011; Xu et al. 2012). This is very discomforting for babies (Basagaña et al. 2011; Xu et al. 2012). The findings in this research suggest that there could be an impact of heat influx on the populace in both cities. The findings agreed with the earlier studies of (Alexander et al. 2006; Volodin and Yurova 2013) that indicated that urban warming was caused by rises in warm extremes.
Therefore, the consequences of increasing warm days and nights and reducing the cold days and nights may lead to increased heat-stressed diseases associated with the lungs and skins of humans in both cities. Health practitioners, especially those in the field of dermatology and pulmonology, may benefit from this outcome by educating their patients on the effects rising temperature may have on them and could also design mitigation measures to help guard their patients against the harsh extremes of temperature in both cities. The analysis using the temperature indices provided in-depth comprehension of the meteorological variables (Iyakaremye et al. 2021).
Trends in temperature (indices, seasonal and annual)
The trends identified a higher rise in the number of warm days and warm nights in both cities compared to the number of cold days and cold nights which were similar to the findings of Huong and Pathirana (2013). The annual monthly maximum value of daily minimum temperature, the annual monthly maximum value of daily minimum temperature and the diurnal temperature range produced the same values for both cities in Table 2. This confirms that there is less variation in temperature as similar trends were found in this research as found in previous literature (Amoako and Boamah 2015; Dickson et al. 1988). The higher variation in the annual monthly minimum value of daily maximum temperatures of Accra compared to Kumasi may be attributed to the higher number of warm days in Accra compared to Kumasi.
The increasing trends in temperature as found in this research are consistent with previously published works in different geographical locations in Ghana that revealed increasing temperature (Kabo-Bah et al. 2016; Nkrumah et al. 2014). There was an increase in temperature in both the maximum and minimum temperatures in both cities and it was in line with the results in the works of (Gocic and Trajkovic 2013; Oduro et al. 2022), where increasing trends were identified in both the annual and seasonal maximum and minimum air temperature time series analysis. There were increasing trends in annual maximum temperature ranging between 0.5 °C/year to 0.7 °C/year at the Negotin weather station. However, the annual minimum temperature ranged between 0.3 °C/year to 0.4 °C/year (Gocic and Trajkovic 2013). This was higher than the values obtained in this research. This higher variation may be due to the differences in the biophysical factors at the different geographical locations. In addition, the research of Mahmoud (2016) revealed that Abuja has witnessed a minimum increase of 8 °C from 1986 to 2014 (i.e. 0.28 °C/year) whilst the annual average temperature has also increased by 0.83 °C while the annual average maximum temperature also increased by 1.6 °C during the 32 years of study in Istanbul (Karaburun et al. 2011). The works of (Karaburun et al. 2011; Mahmoud 2016) recorded higher changes in the temperature as compared to this research. The results in the work also agree with the research of (MESTI 2013) which indicated the temperature of Ghana had increased by about 1.0 °C between 1960 and 2000. Again, it collaborates with the works of Dontwi et al. (2008) that the maximum temperature rose by 2.2 °C from 1960 to 2001 and Adu-Prah et al. (2019) also concluded that was a rise in temperature between 0.5 °C to 1.0 °C from 1981 to 2009 in Ghana, although the values produced in Table 2 were lower. It is therefore evident that there are increasing trends even though the values differ amongst the various researches, especially in Ghana. The differences could be attributed to the different ranges of temperature data utilised and the extent of coverage in terms of physical/administrative borders.
It was interesting that for maximum temperature; the dry, wet and annual of lag 1 serial correlation coefficient produced higher values in Kumasi compared to Accra whilst the reverse was found for minimum temperature. This may be linked to the lower range of recorded values for maximum temperature in Kumasi and the lower range of values for minimum temperature in Kumasi.
The Mann Kendall and Sen`s slope tests revealed no trends in the maximum temperature in the wet season and annual assessment of Accra but a significant trend was detected in the dry season. The reverse was found in Kumasi as no trend was found in the dry season of Kumasi. However, trends were detected in the wet and annual of Kumasi. The wet, dry and annual for minimum temperatures had trends, meaning the results were significant in both cities. This may explain the fact that the minimum temperature has been rising in both cities and it agrees with earlier works that minimum temperatures are rising higher as compared to maximum temperature (Alexander et al. 2006; Stone and Weaver 2002).
Urbanisation has led to the transformation of green areas (agricultural and forestlands) in both cities have attributed to urban temperature changes (Frimpong and Molkenthin 2021; Owusu 2018). The urban population have also increased and has necessitated the need for more housing units and other infrastructure in both cities (Frimpong and Molkenthin 2021).
Increasing trends in both seasonal and annual temperature could lead to consequences such as dry spells and droughts. This has an enormous negative impact on food security, gross domestic products and agriculture (MESTI 2013). Aside from the effects of temperature changes on the agricultural sector, it may also lead to the loss of arable lands, forestlands, biodiversity, sensitive habitats and the drying up of water bodies. The rising temperature could also reduce surface and groundwater resources. Policymakers may use this outcome as a springboard for developing information for the needed populace to reduce vulnerabilities to extreme temperature variations and also aid in the planning of the mitigation actions needed to avert the continuous increases in temperature.
Research conclusions and future guidelines
The historical temperature data (1986–2015) analysis using temperature indices revealed alterations in the temperature variables. This enabled an in-depth comprehension of trends in temperature. The temperature indices analysed revealed that minimum air temperature has been altered significantly with positive trends in both cities. Besides, it was confirmed in the increasing number of warm days and nights and a significant reduction in cold days and nights in both cities. The trends revealed increasing warm days and nights and a reduction in the number of cold days and nights. The increasing warming trends may also be indicative of urban warming in both cities.
The seasonal trend analysis also revealed a warming trend in temperature. Except for the wet and annual of Accra and the dry season of Kumasi (no trend), varying trends were observed for (dry, wet and annual) of minimum temperatures for both cities. However, the maximum temperature of both cities had trends in the dry seasons for Accra and the wet and annual for Kumasi.
The temperature indices and the seasonal trend analysis revealed increasing trends and served as a valuable means of communicating the impacts of temperature variability.
The research utilised a meteorological dataset for the analysis of temperature in both cities. Nevertheless, it provided a foundation for future temperature studies. The research, therefore, suggests the following guidelines.
Temperature analysis can make use of other sources of temperature data, such as global gridded products. For instance, data from the Climate Research Unit from the University of East Anglia and the MODIS climate modelling grid could be used for an in-depth analysis of the long-term temperature. The resolution may be 0.5° by 0.5° or 0.25° by 0.25°. There are merits to using gridding products over in-situ measurements of temperature (see Donat et al. 2013; Frich et al. 2002). Again, the focus of this research was not on temperature prediction. The data mining technique, k-Nearest Neighbour (see Jan et al. 2008; King et al. 2015) can be utilised for the prediction of temperature. The forecasting of temperature will provide more insights for environmental managers and planners in Ghana.
Both cities had only one meteorological station and this might have affected the temperature variability. This led to flaws in data measurement. There should be the establishment of additional weather stations in both cities such that, there could be sharing of tools, resources and information. There could be the establishment of an online portal to catalogue the activities of recording weather station parameters from all the synoptic stations located in both cities. This enables climate variables to be recorded from synoptic weather data into the portal. The activities of recording the weather parameters in the cities will become more visible and will enhance data exchange. It may also include materials that would describe workflows to upscale monitoring schemes.
The increase in vegetated areas is the most applied mitigation measure adopted for the regulation of temperature (Kikegawa et al. 2006). Again, urban blue spaces can aid in the provision of ecosystems and support transportation activities in cities (Coutts et al. 2012; Völker et al. 2013) and these strategies should be adopted in both cities.
The key findings in this research will serve as baseline information for other scientists, end-users and policymakers regarding the analysis of temperature variability in both cities.
Availability of data and materials
Derived data supporting the findings of this study are available from the corresponding author (BFF) on request.
References
Abbam T, Johnson FA, Dash J, Padmadas SS (2018) Spatiotemporal variations in rainfall and temperature in Ghana over the twentieth century, 1900–2014. Earth and Space Science 5(4):120–132. https://doi.org/10.1002/2017EA000327
Addae B, Oppelt N (2019) Land-use/land-cover change analysis and urban growth modelling in the greater Accra Metropolitan Area (GAMA), Ghana. Urban Science 3(1):26. https://doi.org/10.3390/urbansci3010026
Addinsoft (2019) XLSTAT statistical and data analysis solution. https://www.xlstat.com/en/
Adu-Prah S, Appiah-Opoku S, Aboagye D (2019) Spatiotemporal evidence of recent climate variability in Ghana. Afr Geogr Rev 38(2):172–190. https://doi.org/10.1080/19376812.2017.1404923
Adusu D, Anaafo D, Abugre S, Addaney M (2022) Experiential Knowledge of urbanites on climatic changes in the Sunyani municipality, Ghana. J Urban Aff 00(00):1–17. https://doi.org/10.1080/07352166.2022.2044836
Alexander LV, Zhang X, Peterson TC, Caesar J, Gleason B, Klein Tank AMG, Haylock M, Collins D, Trewin B, Rahimzadeh F, Tagipour A, Rupa Kumar K, Revadekar J, Griffiths G, Vincent L, Stephenson DB, Burn J, Aguilar E, Brunet M et al (2006) Global observed changes in daily climate extremes of temperature and precipitation. J Geophys Res Atmos 111(5):1–22. https://doi.org/10.1029/2005JD006290
Amoah ID, Abubakari A, Stenström TA, Abaidoo RC, Seidu R (2016) Contribution of wastewater irrigation to soil transmitted helminths infection among vegetable farmers in Kumasi, Ghana. PLoS Negl Trop Dis 10(12):1–12. https://doi.org/10.1371/journal.pntd.0005161
Amoako C, Boamah EF (2015) The three-dimensional causes of flooding in Accra, Ghana. Int J Urban Sustain Dev 7(1):109–129. https://doi.org/10.1080/19463138.2014.984720
Anderson RL (1942) Distribution of the serial correlation coefficient. Ann Math Stat 13(1): 1–13. http://www.jstor.org/stable/2236157
Asamoah Y, Ansah-Mensah K (2020) Temporal description of annual temperature and rainfall in the Bawku Area of Ghana. Adv Meteorol. https://doi.org/10.1155/2020/3402178
Asante FA, Amuakwa-Mensah F (2015) Climate change and variability in Ghana: stocktaking. Climate 3(1):78–99. https://doi.org/10.3390/cli3010078
Asare-Nuamah P, Botchway E (2019) Understanding climate variability and change: analysis of temperature and rainfall across agroecological zones in Ghana. Heliyon 5(10):e02654. https://doi.org/10.1016/j.heliyon.2019.e02654
Baffour-Ata F, Antwi-Agyei P, Nkiaka E (2021) Climate variability, land cover changes and livelihoods of communities on the fringes of bobiri forest reserve, Ghana. Forests 12(3):1–24. https://doi.org/10.3390/f12030278
Basagaña X, Sartini C, Barrera-Gómez J, Dadvand P, Cunillera J, Ostro B, Sunyer J, Medina-Ramón M (2011) Heat waves and cause-specific mortality at all ages. Epidemiology 22(6):765–772. https://doi.org/10.1097/EDE.0b013e31823031c5
Boansi D, Tambo JA, Müller M (2017) Analysis of farmers’ adaptation to weather extremes in West African Sudan Savanna. Weather Clim Extremes 16(October 2016):1–13. https://doi.org/10.1016/j.wace.2017.03.001
Chan JCW, Beckers P, Spanhove T, Borre JV (2012) An evaluation of ensemble classifiers for mapping Natura 2000 heathland in Belgium using spaceborne angular hyperspectral (CHRIS/Proba) imagery. Int J Appl Earth Obs Geoinf 18(1):13–22. https://doi.org/10.1016/j.jag.2012.01.002
Coutts AM, Tapper NJ, Beringer J, Loughnan M, Demuzere M (2012) Watering our cities: the capacity for Water Sensitive Urban Design to support urban cooling and improve human thermal comfort in the Australian context. Prog Phys Geogr Earth Environ 37(1):2–28. https://doi.org/10.1177/0309133312461032
Dankwa P, Cudjoe E, Amuah EEY, Kazapoe RW, Agyemang EP (2021) Analyzing and forecasting rainfall patterns in the Manga-Bawku area, northeastern Ghana: possible implication of climate change. Environ Challenges 5(July):100354. https://doi.org/10.1016/j.envc.2021.100354
Danuour SK, Tay SC, Annor T, Forkuo EK, Bosompem K, Antwi V (2010) The impact of climate variability on malaria incidence and prevalence in the forest zone of Ghana-a case study at two (2) hospitals located within the Kumasi Metropolitan area of the Ashanti Region of Ghana. In: ICID+18 2nd international conference: climate; sustainability and development in semi-arid regions, August 16–20, 2010.
Dickson KB, Benneh G, Essah RR (1988) A new geography of Ghana, vol 34, Longman London.
Donat MG, Alexander LV, Yang H, Durre I, Vose R, Dunn RJH, Willett KM, Aguilar E, Brunet M, Caesar J, Hewitson B, Jack C, Klein Tank AMG, Kruger AC, Marengo J, Peterson TC, Renom M, Oria Rojas C, Rusticucci M et al (2013) Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J Geophys Res Atmos 118(5):2098–2118. https://doi.org/10.1002/jgrd.50150
Dontwi J, Dontwi IK, Buabeng SN (2008) Climate change impacts on fisheries production. In: Allotey J, Mensah L eds. Ghana climate change impacts, vulnerability and adaptation assessments, under the Netherlands climate assistance programme: Environmental Protection Agency, vol 101319, pp 14–73.
Easterling DR, Horton B, Jones PD, Peterson TC, Karl TR, Parker DE, Salinger MJ, Razuvayev V, Plummer N, Jamason P, Folland CK (1997) Maximum and minimum temperature trends for the globe. Science 277(5324):364–367. https://doi.org/10.1126/science.277.5324.364
Faye A, Akinsanola AA (2022) Evaluation of extreme precipitation indices over West Africa in CMIP6 models. Clim Dyn 58(3–4):925–939. https://doi.org/10.1007/s00382-021-05942-2
Frich P, Alexander LV, Della-Marta P, Gleason B, Haylock M, Tank Klein AMG, Peterson T (2002) Observed coherent changes in climatic extremes during the second half of the twentieth century. Climate Res 19(3):193–212. https://doi.org/10.3354/cr019193
Frimpong BF, Molkenthin F (2021) Tracking urban expansion using random forests for the classification of landsat imagery (1986–2015) and predicting urban/built-up areas for 2025: a study of the kumasi metropolis, Ghana. Land. https://doi.org/10.3390/land10010044
Gadedjisso-tossou A, Adjegan KII (2021) Rainfall and temperature trend analysis by Mann–Kendall test and significance for rainfed cereal yields in. Science 3(17):1–20
Ghana Statistical Service (GSS) (2014a) Accra Metropolitan. In: Ghana statistical service. https://new-ndpc-static1.s3.amazonaws.com/CACHES/PUBLICATIONS/2016/06/06/AMA.pdf
Ghana Statistical Service (GSS) (2014b) Urbanisation. 2010 population & Housing Census Report.
Ghana Statistical Service (GSS) (2021) Ghana 2021 population and housing census.
Gocic M, Trajkovic S (2013) Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Global Planet Change 100:172–182. https://doi.org/10.1016/j.gloplacha.2012.10.014
Huong HTL, Pathirana A (2013) Urbanization and climate change impacts on future urban flooding in Can Tho city, Vietnam. Hydrol Earth Syst Sci 17(1):379–394. https://doi.org/10.5194/hess-17-379-2013
Issahaku AR, Campion BB, Edziyie R (2016) Rainfall and temperature changes and variability in the Upper East Region of Ghana. Earth Space Sci 3(8):284–294. https://doi.org/10.1002/2016EA000161
Iyakaremye V, Zeng G, Yang X, Zhang G, Ullah I, Gahigi A, Vuguziga F, Asfaw TG, Ayugi B (2021) Increased high-temperature extremes and associated population exposure in Africa by the mid-21st century. Sci Total Environ 790:148162. https://doi.org/10.1016/j.scitotenv.2021.148162
Jan Z, Abrar M, Bashir S, Mirza AM (2008) Seasonal to inter-annual climate prediction using data mining KNN technique. Commun Comput Inf Sci 20 CCIS(April):40–51. https://doi.org/10.1007/978-3-540-89853-5_7
Kabo-Bah AT, Diji CJ, Nokoe K, Mulugetta Y, Obeng-Ofori D, Akpoti K (2016) Multiyear rainfall and temperature trends in the Volta River basin and their potential impact on hydropower generation in Ghana. Climate. https://doi.org/10.3390/cli4040049
Kajtar JB, Santoso A, Collins M, Taschetto AS, England MH, Frankcombe LM (2021) CMIP5 intermodel relationships in the baseline southern ocean climate system and with future projections. Earth’s Future 9(6):1–21. https://doi.org/10.1029/2020EF001873
Karaburun A, Demirci A, Kara F (2011) Analysis of spatially distributed annual, seasonal and monthly temperatures in Istanbul from 1975 to 2006. World Appl Sci J 12(10):1662–1675
Kendall MG, Stuart A (1961) The advanced theory of statistics. Technometrics 5(4):525–528. https://doi.org/10.1080/00401706.1963.10490133
Kendall MG (1955) Rank correlation methods.
Kikegawa Y, Genchi Y, Kondo H, Hanaki K (2006) Impacts of city-block-scale countermeasures against urban heat-island phenomena upon a building’s energy-consumption for air-conditioning. Appl Energy 83(6):649–668. https://doi.org/10.1016/j.apenergy.2005.06.001
King LM, Mcleod AI, Simonovic SP (2015) Improved weather generator algorithm for multisite simulation of precipitation and temperature. J Am Water Resour Assoc 51(5):1305–1320. https://doi.org/10.1111/1752-1688.12307
Klein Tank AMG, Peterson TC, Quadir DA, Dorji S, Zou X, Tang H, Santhosh K, Joshi UR, Jaswal AK, Kolli RK, Sikder AB, Deshpande NR, Revadekar JV, Yeleuova K, Vandasheva S, Faleyeva M, Gomboluudev P, Budhathoki KP, Hussain A et al (2006) Changes in daily temperature and precipitation extremes in central and south Asia. J Geophys Res Atmos 111(16):1–8. https://doi.org/10.1029/2005JD006316
Klutse NAB, Aboagye-Antwi F, Owusu K, Ntiamoa-Baidu Y (2014) Assessment of patterns of climate variables and malaria cases in two ecological zones of Ghana. Open J Ecol 04(12):764–775. https://doi.org/10.4236/oje.2014.412065
Klutse NAB, Owusu K, Boafo YA (2020) Projected temperature increases over northern Ghana. SN Appl Sci 2(8):1–14. https://doi.org/10.1007/s42452-020-3095-3
Kumeh EM, Bieling C, Birner R (2022) Food-security corridors: a crucial but missing link in tackling deforestation in Southwestern Ghana. Land Use Policy 112(November 2021):105862. https://doi.org/10.1016/j.landusepol.2021.105862
Kyere-Boateng R, Marek MV (2021) Analysis of the social-ecological causes of deforestation and forest degradation in ghana: application of the dpsir framework. Forests 12(4):1–29. https://doi.org/10.3390/f12040409
Läderach, D. P. (2011). Predicting the impact of climate change on the cocoa- growing regions in Ghana and Cote d ’ Ivoire. International Center for Tropical Agriculture (CIAT), pp 1–26.
Larbi I, Hountondji FCC, Annor T, Agyare WA, Gathenya JM, Amuzu J (2018) Spatio-temporal trend analysis of rainfall and temperature extremes in the Vea catchment, Ghana. Climate 6(4):1–17. https://doi.org/10.3390/cli6040087
Hansen et al. (2021). Global temperature in 2020. 2021(January), 1–6. https://mailchi.mp/caa/global-temperature-in-2020?e=670df34344
Mahmoud MI (2016) Integrating geoinformation and socioeconomic data for assessing urban land-use vulnerability to potential climate-change impacts of Abuja. May, pp 1–256.
Mann HB (1945) Nonparametric tests against trend. Econometrica 13(3):245–259. https://doi.org/10.2307/1907187
MESTI (2013) Ghana National Climate Change Policy.
Minia Z (2008) Climate change scenario development. W. K. Agyemang-Bonsu, editor. Ghana climate change impacts, vulnerability and adaptation assessments. Environmental Protection Agency, Accra, Ghana. Climate change and vulnerability. https://doi.org/10.4324/9781315067179
Nelson W, Agbey SND (2005) Linkages between poverty and climate change: adaptation for livelihood of the poor in Ghana. Technical Paper, 71.
New M, Hewitson B, Stephenson DB, Tsiga A, Kruger A, Manhique A, Gomez B, Coelho CAS, Masisi DN, Kululanga E, Mbambalala E, Adesina F, Saleh H, Kanyanga J, Adosi J, Bulane L, Fortunata L, Mdoka ML, Lajoie R (2006) Evidence of trends in daily climate extremes over southern and west Africa. J Geophys Res Atmos 111(14):1–11. https://doi.org/10.1029/2005JD006289
Nkrumah F, Klutse NAB, Adukpo DC, Owusu K, Quagraine KA, Owusu A, Gutowski W (2014) Rainfall variability over Ghana: model versus rain gauge observation. Int J Geosci 05(07):673–683. https://doi.org/10.4236/ijg.2014.57060
Oduro C, Shuoben B, Ayugi B, Beibei L, Babaousmail H, Sarfo I, Ullah S, Ngoma H (2022) Observed and Coupled Model Intercomparison Project 6 multimodel simulated changes in near-surface temperature properties over Ghana during the 20th century. Int J Climatol 42(7):3681–3701. https://doi.org/10.1002/joc.7439
Oduro C, Ayugi B, Asare-nuamah P (n.d.). Changes in near-surface temperature in Ghana , West Africa and the links with climatic factors.
Owusu AB (2018) An assessment of urban vegetation abundance in Accra Metropolitan Area, Ghana: a geospatial approach. J Environ Geogr 11(1–2):37–44. https://doi.org/10.2478/jengeo-2018-0005
Parsons D, Stern D, Ndanguza D, Sylla MB (2022) Evaluation of satellite-based air temperature estimates at eight diverse sites in Africa. Climate. https://doi.org/10.3390/cli10070098
Peterson TC, Vose RS (1998) Global Historical Climatology Network (GHCN) (DSI9100). 1179(18): 1169–1179.
Qaisrani ZN, Nuthammachot N, Techato K (2021) Drought monitoring based on standardized precipitation index and standardized precipitation evapotranspiration index in the arid zone of Balochistan province, Pakistan. Arabian J Geosci. https://doi.org/10.1007/s12517-020-06302-w
Ragatoa DS, Ogunjobi KO, Okhimamhe AA, Francis SD, Adet L (2018) A trend analysis of temperature in selected stations in nigeria using three different approaches. Oalib 05(02):1–17. https://doi.org/10.4236/oalib.1104371
Sen PK (1968) Estimates of the regression coefficient based on Kendall’s Tau. J Am Stat Assoc 63(324):1379–1389. https://doi.org/10.1080/01621459.1968.10480934
Stone DA, Weaver AJ (2002) Daily maximum and minimum temperature trends in a climate model. Geophys Res Lett 29(9): 70-1-70-74. https://doi.org/10.1029/2001gl014556
von Storch H, Navarra A (1999) Analysis of climate variability. Applications of statistical techniques. J Atmos Solar-Terr Phys 59(2):263–264. https://doi.org/10.1016/s1364-6826(97)87052-6
Subaar C, Apori N, Fletcher JJ, Galyuon R, Edusei G, Adayira VW (2018) Time series analysis for prediction of meteorological data from Wa, Upper West Region of Ghana. J Climatol Weather Forecast. https://doi.org/10.4172/2332-2594.1000237
van der Wiel K, Bintanja R (2021) Contribution of climatic changes in mean and variability to monthly temperature and precipitation extremes. Commun Earth Environ 2(1):1–11. https://doi.org/10.1038/s43247-020-00077-4
Völker S, Baumeister H, Classen T, Hornberg C, Kistemann T (2013) Evidence for the temperature-mitigating capacity of urban blue space—a health geographic perspective. Erdkunde 67(4):355–371. https://doi.org/10.3112/erdkunde.2013.04.05
Volodin EM, Yurova AY (2013) Summer temperature standard deviation, skewness and strong positive temperature anomalies in the present day climate and under global warming conditions. Clim Dyn 40(5–6):1387–1398. https://doi.org/10.1007/s00382-012-1447-4
Wang J, Chen Y, Tett SFB, Yan Z, Zhai P, Feng J, Xia J (2020) Anthropogenically-driven increases in the risks of summertime compound hot extremes. Nat Commun. https://doi.org/10.1038/s41467-019-14233-8
Wemegah CS, Yamba EI, Aryee JNA, Sam F, Amekudzi LK (2020) Assessment of urban heat island warming in the greater accra region. Sci Afr 8:e00426. https://doi.org/10.1016/j.sciaf.2020.e00426
WMO (2021) Guidelines on surface station data quality control and quality assurance for climate applications 2021 (Issue 1269).
Xu Z, Etzel RA, Su H, Huang C, Guo Y, Tong S (2012) Impact of ambient temperature on children’s health: a systematic review. Environ Res 117:120–131. https://doi.org/10.1016/j.envres.2012.07.002
Yang J, Ren J, Sun D, Xiao X, Xia JC, Jin C, Li X (2021) Understanding land surface temperature impact factors based on local climate zones. Sustain Cities Soc 69(November 2020):102818. https://doi.org/10.1016/j.scs.2021.102818
Yeh SW, Lee EH, Min SK, Lee YH, Park IH, Hong JS (2021) Contrasting factors on the trends in hot days and warm nights over Northern Hemisphere land during summer. Weather Clim Extremes 34:100389. https://doi.org/10.1016/j.wace.2021.100389
You Q, Kang S, Aguilar E, Pepin N, Flugel WA, Yan Y, Xu Y, Zhang Y, Huang J (2011) Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim Dyn 36(11–12):2399–2417. https://doi.org/10.1007/s00382-009-0735-0
Zhang X, Yang F (2004) RClimDex (1.0) user manual, pp1–23.
Acknowledgements
The authors are grateful to the Ghana Meteorological Agency for the temperature dataset for Accra. We are also grateful to the EuroAquae family and the Department of Hydrology for their support.
Funding
Open Access funding enabled and organized by Projekt DEAL. B.F.F. is thankful to the Katholischer Akademischer Ausländer—Dienst (KAAD) for the scholarship support for his PhD studies which gave birth to this research.
Author information
Authors and Affiliations
Contributions
BFF and FM conceptualised the research and the applied methods; BFF curated the data, did the formal analysis, utilised the software and wrote the initial draft; FM provided the resources and supervised the research; All authors aided in the administration of the project, read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Frimpong, B.F., Koranteng, A. & Molkenthin, F. Analysis of temperature variability utilising Mann–Kendall and Sen's slope estimator tests in the Accra and Kumasi Metropolises in Ghana. Environ Syst Res 11, 24 (2022). https://doi.org/10.1186/s40068-022-00269-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40068-022-00269-1