Abstract
Background
Discovering causality in environmental systems is challenging because frequently controlled experiments or numerical simulations are difficult. Algorithms to learn directed acyclic graphs from system data are powerful, but they often result in too many possible causal structures that cannot be properly evaluated.
Results
An approach to this problem proposed here is to initially restrict the system to a target variable with its two major drivers. Subsequently, testable causal structures are obtained from rules to infer directed acyclic graphs and expert knowledge. The proposed approach, which is essentially based on correlation and regression, was applied to understand drivers of a toxic algal bloom in the Odra River in summer 2022. Through this application, useful insight on the interplay between river flow and salt inputs that likely caused the algal bloom was obtained.
Conclusions
The Odra River example demonstrated that carefully applied correlation and regression techniques together with expert knowledge can help to discover reliable casual structures in environmental systems.
Similar content being viewed by others
Background
When searching for causal relationships in environmental systems, multiple direct and indirect causes can usually explain an observed phenomenon (Stow and Borsuk 2003). To illuminate causal relations among observed system variables—if controlled experiments are infeasible and numerical simulations are too complicated—often spatial and temporal associations of empirical data were investigated via correlation and regression techniques (Runge et al. 2019a). However, significant statistical associations only sometimes represent direct causal relationships, as e.g. both an indirect relationship via a mediating variable (Pearl and Makenzie 2019, p. 302ff) and a common cause can make two observations statistically dependent (Pearl and Makenzie 2019, p. 69ff). Cause and effect, the precise direction of the influence (positive or negative effect), and the strength of a directed effect often remain unclear if conventional correlation and regression analysis is applied (Ombadi et al. 2020). Complex methodologies were therefore developed with which—if all relevant drivers of an effect were observed (Runge et al. 2019a)—causal relationships in environmental systems may be discovered (Runge et al. 2019b). These causal relations are typically expressed as directed acyclic graphs (DAG). DAG are ‘dot-and-arrow’ pictures (Pearl and Makenzie 2019, p. 7) relating system variables (‘dots’) using directed arcs (‘arrows’). Directed arcs represent causal links pointing from a ‘parent’ representing a cause to a ‘child’ representing an effect (Jensen and Nielsen 2007, p. 26). Feedback loops, e.g. A causes B and B causes A, are not allowed for a DAG because with these loops, cause and effect cannot be distinguished anymore. Hence, DAG are different to equations in the way that for the latter the direction of a relationship does not matter (e.g. A equals B is the same as B equals A). For inference of DAG, there are a few methods available such as the Peter-Clark (PC) algorithm (Spirtes and Glymour 1991) with its extensions like PCMCI (Runge et al. 2019b). In practical applications of these methods, however, already a few variables (say > 3) result in too many possible causal structures, which are difficult to evaluate from a technical point of view (see e.g. Alameddine et al. 2011). If the number of variables examined is equal to three, possible causal structures are still complex enough but at the same time they can still be evaluated in detail. For a reliable detection and quantification of causal structures, therefore the problem of causal discovery among multiple observations in environmental systems may be first reduced to the target variable and its most important two controlling variables. Driving variables could be selected using suitable methods such as classification and regression trees (CART, Breiman et al. 1984) in advance of the actual detection of a causal structure. Here, I hypothesised that causal structures can be determined if the system analysis is reducible to only three variables, i.e. one target with two driving variables. In this case, possible causal structures and the various assumptions of the analyses are still testable. Assuming both X1 and X2 as direct or indirect driving variables of a target variable Y (where X1, X2 and Y could represent either temporally or spatially correlated data), the following five causal structures are conceivable:
-
a.
X1 controls X2 and X2 in turn controls Y (X1 → X2 → Y),
-
b.
X2 controls X1 and X1 in turn controls Y (X2 → X1 → Y),
-
c.
Both X2 and X1 control Y directly (X1 → Y ← X2),
-
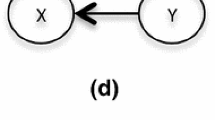
d.
X1 controls Y both directly and indirectly via X2 (X1 → X2 → Y and X1 → Y), and
-
e.
X2 controls Y both directly and indirectly via X1 (X2 → X1 → Y and X2 → Y).
In this article, correlation and regression techniques are combined and for the first time applied in this composition for finding causal structures in environmental systems. Specifically, the following techniques were combined: CART and random forests (Breiman 2001) to find two key drivers of a target variable, the inference of DAG from linear marginal and partial correlations (Jensen and Nielsen 2007, p. 320ff) and linear regression to further test and refine DAG. The approach is demonstrated using measured time series from the Odra River in eastern Germany. The aim of this analysis of time series, besides demonstrating the proposed approach, was to better understand causes of a toxic algal bloom in the Odra River in August 2022 (German Environment Agency 2022). In previous studies, a bloom of the toxic brackish water algae Prymnesium parvum was identified as likely cause of a massive fish kill observed in the Odra River (European Commission 2023), but processes leading to the algal bloom remained less understood.
Methods
Overview of the proposed approach to find causal relationships
A schematic overview on the proposed approach is given in Fig. 1. The approach involves three steps. For each step, statistical techniques as well as expert knowledge are applied.
Schematic overview of the approach to find causal structures in an environmental system. ‘Y’ is a target variable, whereas ‘X1’ and ‘X2’ represent drivers of Y. ‘?’ are variables, directed arcs or effect sizes that need to be determined using the approach presented in this paper. Further explanations of the different steps are given in the text
In a first step, two driving variables of a given target variable along with the associated time lags (if observed variables are time series) are identified from a set of preselected drivers using CART or random forests. Expert knowledge may be used to preselect measured variables as potential drivers. Data analysis with CART and random forests neither requires a specific distribution of potential drivers nor a particular form of relationship between the investigated variables. Therefore, raw data may be used to find driving variables of the untransformed target variable. Random forests can be used instead of CART as the former technique overcomes the problem of relatively unstable decision trees that are generated if the data set is slightly changed. CART and random forests can both be understood as non-linear regression methods. However, as subsequent steps of the approach are based on linear methods and if time series are analysed, time lags identified using CART and random forests may be modified via linear cross-correlations.
In a second step, possible causal structures are obtained based on rules to infer DAG using linear marginal and partial correlations among the three variables coming out of the first step of the analysis. DAG may be inferred from correlation coefficients using tests for statistical independence of system variables, i.e. ‘rules to infer DAG’ (Jensen and Nielsen 2007, p. 230ff). Briefly, starting with a fully connected graph with undirected arcs between all system variables, arcs are removed if two variables are ‘d-separated’. Two variables are d-separated if they are statistically independent, either marginally or conditional on a third variable or a set of variables. For remaining undirected arcs, v-structures (e.g. both A and B cause C, i.e. A → C ← B) are first directed if suitable statistical dependencies between system variables were found, and subsequently the remaining undirected arcs are randomly directed but creation of new v-structures or cyclic structures is avoided.
In a third step, possible causal structures (DAG) from step two are further tested via linear regression, with which effect sizes for possible DAG are quantified. A DAG can be expressed as a set of linear equations (but an equation has many possible DAG), with coefficients representing the strength (effect sizes) of causal links between ‘parent’ and ‘child’ variables (Spirtes et al. 1993, p. 14ff). Coefficients of those linear equations can be estimated using linear regression.
Both steps two and three involve expert knowledge as well as practical considerations to evaluate possible causal structures. As those two steps rely on a quantification of correlation and regression coefficients including their significance, means and variances of time series may be stabilised over time by suitable variable transformations and trend corrections. Transformations may also be applied to make relations between system variables more linear. If time series (correlation) or residuals of modelled time series (regression) are autocorrelated, conventionally determined confidence intervals of coefficients are too narrow (Selle and Hannah 2010). To compute reliable confidence intervals for correlation and regression coefficients in the context of time series analyses, block bootstrapping (Mudelsee 2013, p. 61ff) is applied. Appropriately quantified confidence intervals help to obtain reliable causal structures as well as effect sizes.
Study area and dataset used to demonstrate the proposed approach
To apply the proposed approach, I analysed a dataset of the Odra River in the context of a fish kill in August 2022. The Odra River, which discharges into the Baltic Sea, has a total length of 855 km and a basin area of about 120,000 km2 with 86% in Poland and minor basin fractions in Germany and the Czech Republic (Fig. 2, Wiederhold et al. 2023). Population of the basin is about 16 × 106 habitants, approximately 50% of the basin area is used as cropland (European Commission 2023). A major tributary of the Odra River is the Warta River, which drains almost half of the total basin area, and discharges at Odra-km 618 into the main river (Fig. 2). Annual precipitation amounts to 1000–1400 mm in the upper basin, but the major fraction of the basin only receives 500–600 mm per year. During the last two decades, the Odra River had elevated annual average concentrations of total phosphorus of > 0.1 mg/L at nearly all monitoring sites; and steadily increasing electrical conductivities of about 17 µS/cm per year were observed in the lower reach of the Odra River, where also water temperatures increased significantly. In Poland, saline waters are regularly discharged from coal and copper mining in Silesia (Fig. 2, Wiederhold et al. 2023).
Map of the study area for demonstrating the proposed approach with geographic features and monitoring sites mentioned in the text. Inset in the lower left corner of the map shows approximate location of the study area within Europe. Inset in the upper right corner of the map shows a photograph (picture taken by the author) of the Odra riverscape between Eisenhüttenstadt and Frankfurt
In the context of kills of fish and other aquatic organisms along a major river section in August 2022 (European Commission 2023), hourly average chlorophyll-a concentrations attributed to diatoms (AL), electrical conductivities (EC), river flows (Q), water temperatures, pH values, dissolved oxygen and nitrate concentrations were analysed from 26 July to 19 August 2022 for the Odra River in Frankfurt (Odra-km 885). Fish kills in the Odra River, likely caused by a bloom of the toxic brackish water algae Prymnesium parvum (European Commission 2023), were first observed at Frankfurt on 9 August 2022. After 19 August, abundances of Prymnesium parvum at Frankfurt fell below a critical value of 20 × 106 cells/L, which is relevant for fish kills (German Environment Agency 2022). As a measure for the abundance of Prymnesium parvum, chlorophyll-a concentrations—obtained from a spectral fluorometer with an integrated differentiation of algae classes (BBE Moldänke GmbH)—were used. According to the manufacturer of the spectral fluorometer, the toxic algae Prymnesium parvum falls into the diatom class in terms of its absorption and hence chlorophyll-a concentrations attributed to diatoms were used as target variable AL. Hourly average time series on water levels at Frankfurt, Q at Hohensaaten-Finow and Q at Eisenhüttenstadt as well as EC at Hohenwutzen were used to generate time series of Q and EC at Frankfurt (Fig. 2, see Additional file 1 for details). Water quality data were provided by the Landesamt für Umwelt Brandenburg (dl-de/by-2-0, www.govdata.de/dl-de/by-2-0) and were measured according to the German Surface Waters Ordinance (Oberflächengewässerverordnung 2016). Water levels and Q were provided by the Bundesanstalt für Gewässerkunde (https://www.pegelonline.wsv.de). Original time series had temporal resolutions in the order of minutes but were aggregated to hourly averages. Data gaps for individual hours were filled in by linear interpolation.
In a synopsis of time series at Frankfurt (Fig. 3), one can see a small discharge event, which started approximately at t = 160 h (1 August). Note that the peak discharge of the event was still less than the mean annual low flow of about 120 m3/s. Time series of EC seem to follow the hydrograph with a time delay. This time delay could either be (i) the result of a Q source located downstream of an EC source or; (ii) a result of both sources coming from the same location or even; and (iii) a source of Q upstream EC. For cases (ii) and (iii), Q changes (wave speed) need to travel faster down the river than EC changes (flow velocity), which is normally observed (Glover and Johnson 1974). Slightly increasing EC at the beginning of the analysis period was associated with decreasing Q. Generally, time series of AL and EC were similar. A sudden increase as well as a decrease in AL were both associated with a threshold of about EC = 2,000 µS/cm. Also shown in Fig. 3 are hourly averaged pH values, dissolved oxygen and nitrate-N concentrations. With their diurnal variations and the step change at about t = 300 h, these water quality variables probably indicated the magnitude of algal photosynthesis, which simultaneously consumed nitrate, increased pH and produced oxygen. As pH, oxygen and nitrate concentrations were effects rather than causes of AL, these variables were excluded from the analysis of causes of AL. Water temperatures showed diurnal variations and there was a slight temperature decrease during the Q event.
Hourly time series for Frankfurt used to apply the proposed approach to find causal relationships. ‘River flow’ was calculated based on water levels measured at Frankfurt and river flows observed in Eisenhüttenstadt (see Additional files for details). ‘Chlorophyll-a’ are concentrations attributed to diatoms from a spectral fluorometer with an integrated differentiation of algae classes
Results
First step of the approach: identification of two driving variables of a target variable and the associated time lags using CART, random forests and linear cross-correlation
CART was applied to find two key variables driving observed levels of AL during the algal bloom episode in summer 2022. EC, water temperatures, and Q (Alameddine et al. 2011) were preselected to potentially explain AL. Note that nutrient concentrations (nitrogen, phosphorous, silicon and iron) and pH may also be relevant (Yin et al. 2021). While nitrate concentrations and pH were predominantly interpreted as consequences rather than causes of changing AL (Fig. 3), phosphorus, silicon and iron concentrations were unavailable, but these nutrients likely behaved similarly to nitrate. For CART, time series of potential drivers were shifted forwards in time up to 100 h because AL could lag behind its drivers; and these time lags resulted in 3 variables × 101 time lags = 303 explanatory variables. For the application of CART, firstly a maximum tree was generated, which was subsequently pruned back to the size of an optimal tree using a tenfold cross-validation (Venables and Ripley 2003, p. 251ff). Little improvements were observed beyond a tree size (number of end nodes) of three (Fig. 4a) and therefore an optimal tree with two decision nodes was selected (Fig. 4b). Decision nodes were based on EC and Q with time lags of 95 h and 80 h, respectively. Note that there were several time lags with similar or even the same importance coming out of CART. A time lag of 50 h associated with the first split based on EC had the same importance as the time lag of 95 h displayed in Fig. 4b. In contrast to EC, the most important five time lags for Q (in the second split) were all between 78 and 82 h. Consistently, both higher EC and Q implied larger AL (Fig. 4b). According to the CART analysis, water temperatures had a minor effect on AL. EC was more important for explaining AL than Q; this can be seen in the optimal tree from the vertical distances between decision and end nodes, which are scaled according to the cross-validated variance of AL explained by the split (Fig. 4b).
Selected results from first step of the approach. a Result of CART: ‘size of tree’, i.e. the number of its end nodes versus ‘X-val Relative Error’, which is equal to unity minus the cross-validated proportion of explained variance of AL (chlorophyll-a concentrations attributed to diatoms). Complexity parameter ‘cp’ is part of CART and is associated with a certain number of end nodes (Breiman et al. 1984). Vertical bars represent one standard deviation of ‘X-val Relative Error’. b Result of CART: optimum sized tree with three end nodes (squares) and the number of hours (n) assigned to each end node. Ovals represent decision nodes with decisions based on the driving variables electrical conductivity (EC) and river flow (Q) with time lags of 95 h and 80 h, respectively. c Result of linear cross-correlations: time lags (h) versus coefficients of correlation for time series of AL and EC. Red line indicates a time lag of 45 h, which was the maximum correlation coefficient. d Linear cross-correlations: time lags (h) versus coefficients of correlation for time series of AL and Q. Red line indicates a time lag of 81 h, which was the maximum correlation coefficient
An additional assessment of controlling variables using random forests confirmed Q and EC as most important drivers but time lags were 100 h for Q and 12 h for EC (see Additional file 2: Data set and Additional file 3: R-script). Random forests are based on many regression trees, with every tree generated from subset of the observations and each split within each tree created by a random subset of variables (Grömping 2009). Random forests supplement CART results because drivers may be more reliably selected by random forests but—at the same time—the interpretability of a single decision tree (Fig. 4b) is lost. Time lags obtained from CART and random forests were modified based on linear cross-correlations between AL and its drivers Q and EC. Maximum coefficients were computed at time lags of 45 h (EC) and 81 h (Q) (Fig. 4c and d).
As a result of this first step of the approach, EC and Q with time lags of 45 h and 81 h, respectively, were selected as controlling variables of AL. Apart from the system variables involved (EC, Q and AL) in the causal structure, the actual DAG as well as effect sizes remained unclear from the first step of the analysis. Here, steps two and three of the approach brought clarity.
Second step of the approach: detecting causal structures using linear correlation coefficients with bootstrapped confidence intervals and expert knowledge
In a second step, all possible linear marginal and partial correlation coefficients among AL, Q and EC were calculated to obtain plausible causal structures between the variables according to rules for inferring DAG (Jensen and Nielsen 2007, p. 320ff). The variable AL was LN-transformed for the correlation and later regression analyses, as this transformation made variances of the periods before and during the algal bloom more similar (compare Figs. 3 and 5). As measured values for AL and EC steadily increased over the study period (Fig. 3), a linear trend was subtracted from both time series of LN(AL) and EC, which stabilised their means over time. Time series for Q did not show a clear linear trend and thus Q remained uncorrected. The linearly increasing trend for both LN(AL) and EC as opposed to Q probably resulted from the fact that the former two time series did not reach their background values by the end of study period (Fig. 3) and thus these trends were likely unrelated to any causal relationships. Before conducting the correlation and regression analyses, one could also remove other components from the time series, such as non-linear trends or diurnal cycles, which are presumably unrelated to the causal structure under investigation. In the present analysis, however, there were no pronounced diurnal cycles for AL, EC and Q (as opposed to pH, water temperature, nitrate and dissolved oxygen, Fig. 3). Furthermore, non-linear trends, such as those that can be calculated via generalised additive modelling (Hastie and Tibshirani 1990), were not factored out because they likely reflected the sought-after causal relationships. In general, trends in the data should not be removed if they were caused by the interplay of the investigated system variables.
Time series used in step two of the analysis. a Unlagged time series of chlorophyll-a concentrations attributed to diatoms (LN(ALt)de), which was LN-transformed and then detrended by subtracting a linear trend (and hence subscript de). b Time series of electrical conductivities with a time lag of 45 h (ECt-45,de), which were linearly detrended. c Time series of discharges with a time lag of 81 h (Qt-81). Note that time series were shortened in the beginning compared to unlagged data presented in Fig. 3
For the analyses of linear correlation, I obtained ρQ;EC = 0.727, ρQ;LN(AL) = 0.652, and ρEC;LN(AL) = 0.774, where ρQ;EC, e.g. represents the marginal coefficient of linear correlation between lagged Q, and lagged and detrended EC. Note that sub-subscripts of correlation coefficients (for detrended and lagged time series) were suppressed. From the three marginal correlation coefficients, another three partial correlation coefficients were calculated:
and
where ρQ;EC;LN(AL), e.g. measures the correlation between EC and Q with the influence of LN(AL) removed. Note that the coefficient ρQ;LN(AL);EC = 0.206 was less than half of the other two partial coefficients. To obtain confidence intervals for correlation coefficients, block bootstrapping (Mudelsee 2013, p. 73ff) with a block size of 18 h was applied because partial autocorrelations were significant up to a time lag of 6 h (see Additional file 2: Data set and Additional file 3: R-script). Overlapping blocks of all three variables were drawn. Block bootstrapping yielded the following 95% confidence intervals: ρQ;EC = [0.631…0.893], ρQ;LN(AL) = [0.509…0.794], ρEC;LN(AL) = [0.624…0.856], ρQ;EC;LN(AL) = [0.348…0.779], ρQ;LN(AL);EC = [− 0.188…0.471], and ρEC;LN(AL);Q = [0.184…0.735]. Thus, the coefficient ρQ;LN(AL);EC appeared statistically insignificant. Consequently, Q and LN(AL) may be considered stochastically independent if the influence of EC was removed and hence AL and Q are ‘d-separated’. According to the rules for inferring DAG and starting with a fully connected but undirected graph, because of d-separation due to ρQ;LN(AL);EC = 0, a direct (still undirected) arc between Q and AL was removed. This removed arc resulted in possible causal structures with an arrangement of EC between Q and AL: i.e. (i) Q → EC → AL, (ii) Q ← EC ← AL or (iii) Q ← EC → AL. Given the time lags for Q → AL (81 h) and for EC → AL (45 h), option (i) maintained a plausible temporal sequence of cause and effect. The second option (ii) was impractical, as AL remained unexplained. The last option (iii) was implausible, because this would require changing EC to alter Q. Additionally, with option (iii) there would be only one driver of AL, i.e. EC → AL, which contradicted results from the first step of the analysis (that there were two direct or indirect drivers of AL). Since it remained uncertain if ρQ;LN(AL);EC was really insignificant (even bootstrapping of correlation coefficients is imperfect), I further hypothesised a direct causal link between Q and AL, which was investigated again in the third step of the analysis. Note that a new v-structure is created by the direct link EC → AL, which is to be avoided by rules to infer DAG. However, starting from the plausible causal structure Q → EC → AL (reasoning see above), an additional directed arc must necessarily point from Q to AL, because otherwise a cyclic structure would result, where cause and effect are arbitrarily interchangeable (this would not be a DAG anymore). The result of the second step of the causal analysis was therefore the possible causal structures: (i) Q → EC → AL or (ii) Q → EC → AL and Q → AL.
Final step of the approach: refining the causal structure via a quantification of effect sizes using linear regression coefficients with bootstrapped confidence intervals
In a third step, a linear regression was performed to quantify the effect sizes of the DAG Q → EC → AL and Q → AL (from the second step), and to further test this causal structure. One can best determine the effect sizes using linear regression if the variables are z-standardised, i.e. variables are normalised to a mean of zero and a standard deviation of unity. With z-standardisation, regression coefficients can be interpreted as changes of the detrended and transformed target variable AL if (detrended) driving variables are increased by one standard deviation. Hence, z-standardisation of variables makes regression coefficients comparable for different drivers. For the structure Q → EC → AL and Q → AL, there are three effects acting on AL (see also ‘mediation analysis’ as explained, e.g. by de Heus 2012): (i) the direct effect of Q on AL; (ii) an effect of EC on AL and (iii) the indirect effect of Q via EC on AL. Effects (i) and (ii) represent all causal links pointing directly to AL; and these were quantified using a linear regression explaining the ‘child’ variable AL from its ‘parent’ variables Q and EC:
where AL, Q and EC are lagged, detrended (subscript de) and z-standardised (subscript z) time series; k1 = 0 (because of z-standardisation), a and b are coefficients of the linear regression model, and εLN(AL) are model residuals (sub-subscripts are suppressed for simplicity). I obtained a = 0.19 and b = 0.636; and these coefficients represented the direct effect Q → AL (coefficient a) and an effect of EC → AL (coefficient b). While the direction of the relationship for b was plausible (positive effect: higher salinity lead to higher concentrations of the brackish algae), a positive relationship between Q and AL was less comprehensible. Higher Q would rather lead to lower AL due to reduced residence times of water in a given river section as well as greater turbidity and thus less light penetration (Alameddine et al. 2011). Coefficient b cannot be interpreted directly as an effect size for EC → AL, but it is used to determine the indirect effect Q → EC → AL. For a comparison of the direct effect of EC on AL and an indirect effect via changes in Q, a variance-based approach may be suitable (de Heus 2012), which will be explained below.
A direct effect Q → EC was obtained via a regression explaining EC from its only parent Q:
where c = 0.727 represents the size of the direct effect Q → EC; k2 is another coefficient that is zero due to z-standardisation; and εEC are model residuals (where sub-subscripts are suppressed for simplicity). Because of z-standardisation, it follows that c = ρQ;EC = 0.727. The size of the indirect effect Q → EC → AL was:
The total effect size of Q on AL was:
i.e. the sum of a direct (a = 0.19) and an indirect effect (d = 0.462). The total effect e = 0.652 was equivalent to the marginal correlation between Qt-81 and LN(ALt)de, i.e. ρQ;LN(AL) = e = 0.652, because of the z-standardisation. Thus, the direct effect Q → AL was only about one-third of the indirect effect of Q → EC → AL. A confidence interval for the size of the direct effect Q → AL was quantified using block bootstrapping because model residuals of the regression (4) were autocorrelated. For bootstrapping, blocks of 18 h were resampled from model residuals. Bootstrapping observations were constructed using blockwise drawn residuals plus the initially fitted LN(ALt)de,z values; and regression coefficients were 5,000 times fitted to bootstrapping observations (Selle and Hannah 2010). The 95% confidence interval for a was [− 0.104…0.488]. Consequently, the strength of Q → AL may be negligible. If the direct effect of Q on AL can be neglected, a causal structure Q → EC → AL would result as most plausible and reliable structure.
The structure Q → EC → AL can be further illuminated using a variance-based interpretation (de Heus 2012). Because of ρEC;LN(AL)2 = 0.599, 59.9% of the total variance of LN(ALt)de was explained by ECt-45,de. This explained variance can be decomposed using the semipartial correlation ρ LN(AL);(EC;Q), which is the correlation between LN(ALt)de and ECt-45,de after the influence of Qt-81 is computed out of ECt-45,de. The semipartial correlation was:
Thus, 19.1% of the variance of LN(ALt)de is explained by ECt-45,de alone because ρLN(AL);(EC;Q)2 = 0.191 is a variance-based measure of EC → AL. This leaves a residual effect of ρEC;LN(AL)2—ρ LN(AL);(EC;Q)2 = 0.599—0.191 = 0.408, which represents a variance-based measure of Q → EC → AL. Thus, it can be calculated that the effect of EC on AL via Q dominates over the effect of EC on AL (without changes in Q).
Discussion
Technical aspects of the proposed approach to find reliable causal structures
If—in the second step of the approach—ρEC;LN(AL);Q was insignificant and all other five correlation coefficients were unequal to zero, the further procedure would be similar to one demonstrated in the Results sections—only that possible and practical causal structures (i) EC → Q → AL as well as (ii) EC → Q → AL plus EC → AL needed to be evaluated based on linear regression and expert knowledge. For a causal ‘v-structure’ EC → AL ← Q, it would be required that ρQ;EC = 0 and all other five marginal and partial correlations unequal to zero. For this v-structure, effect sizes can be quantified using regression Eq. (4), where a and b are then direct effects of Q on AL and EC on AL, respectively; and there would be no indirect effects. Given that—based on results from the first step of the analysis—the identified two drivers control a given target variable, either directly or indirectly, and if there are no unobserved additional drivers, cases mentioned in Results sections and in this paragraph cover likely outcomes of the statistical analyses and the associated five conceivable causal structures listed in the introduction.
If—in the first step of the approach—an optimum sized tree with more than two driving variables was obtained, these could be simply reduced to the two most important ones. An alternative, arguably better, option may be a principal component analysis of all potential drivers with a selection of two principal components as linear combinations of the investigated explanatory variables. In case of a principal component analysis, CART and random forests would be unnecessary but time lags may still be relevant, which can be obtained using an analysis of linear cross-correlation between principal component scores and the target variable. If controlling variables were reduced via a principal component analysis, the causal structure and effect sizes between the target variable (TV) and the two principal component scores (PC) would be examined. In this case, only a v-structure may be found (PC1 → TV ← PC2), since PC1 and PC2 should be stochastically independent.
If—in practical applications of the approach—there were no two major drivers but many equally important non-linear drivers, one could try to capture them using two principal components as mentioned above. In the second step, relations between principal component scores and target variables may be linearised using suitable transformations. If there are more than two statistically independent drivers, principal component analysis would not work. Furthermore, the proposed approach only works if major drivers were measured and included in the first step of the analysis. If they were not included, one may end up with causal structures involving minor drivers, or even non-causal or indirect relationships—if the variables included as drivers in the second and third step of the analysis were just driven by the same missing variables. Therefore, expert knowledge remains the key for causal discovery and the analysis can only assist experts to obtain reliable causal relationships.
Plausibility of the identified causal structure for Odra river application
In the three steps of the outlined approach, the causal model Q → EC → AL crystallised, with Q → EC and EC → AL acting with 36 h and 45 h time lags, respectively. The causal model indicates that increasing EC were a consequence of a discharge event, which in turn triggered an algal bloom. This causal model is plausible; and this will be explained in the following two paragraphs.
The identified causal structure implies that an EC increase was caused by a flow event, and this inference will be illuminated in the following paragraph. Regular discharges of highly mineralised mine groundwaters from both Upper Silesia (primarily from active and abandoned coal mines) and from Lower Silesia (primarily from copper mines) are known for the Odra River (Fig. 2, Wiederhold et al. 2023). To explore the option that both Q and EC at Frankfurt increased due to these mine water discharges, a salt mass of M = 52,586 t of total dissolved solids (TDS) injected into the Odra River during the episode and the volume of the flow event of V = 18,201,388 m3 were estimated from time series of Q and EC in Frankfurt (Fig. 3 and Additional file 1: Table S1). With an estimated input period of 13.8 d (Additional file 1: Table S1), salt inputs of 3,811 t TDS/d during the episode were calculated, which—according to previously published salt inputs from Silesia—had a plausible order of magnitude (Additional file 1: Table S1). In contrast, calculated concentrations of M/V = 2,889 g TDS/m3 appeared uncharacteristically low for mine discharges and would be characteristic of low mineralised groundwaters from shallow depths (Rogoż et al. 1987). Therefore, the Q event likely originated from rainfall in the Odra River basin upstream of Frankfurt rather than from discharges of mine groundwaters. The Q event lasted from 1 to 18 August and reached its peak discharge on 7 August (Fig. 3). With a maximum travel time of water of 8 d from the headwaters to Frankfurt (using a distance of 585 km and a conservative estimate of wave speed of 3 km/h, Dehmel 1992, p. 13), rainfall in the Odra River basin from 24 July onwards was relevant for the calculated event volume V = 18,201,388 m3 (Additional file 1: Table S1). During the relevant period, most rain fell on 30 July in the Odra River basin upstream of Frankfurt (basin area of about 53,000 km2) with a computed area averaged precipitation of 20.7 mm (Cornes et al. 2018, data available at http://www.ecad.eu, Additional file 1: Fig. S2b) and hence the area averaged runoff coefficient was probably only 1–2% for the event with its presumably dry antecedent moisture conditions. Significant rainfall occurred on 30 July both in the upper and the central basin (Additional file 1: Fig. S2b). It can be inferred that mine waters from Silesia, that were likely discharged between 27 July and 9 August (see Additional file 1: Table S1), were at least partly diluted by a concurrent Q event. As in upper basin of the Odra River significant rain fell already on 26 July with local rainfalls of more than 12 mm/d (Additional file 1: Fig. S2a), increasing river flows likely trigged the decision to discharge saline groundwaters in Silesia. Consequently, salt inputs appeared as an effect of the observed flow event in the causal model Q → EC → AL. It can only be speculated if salt inputs would have happened without the observed Q event. Certainly, salinities in the Odra River would have been worse in August 2022 with salt inputs alone and without those dilutions from catchment runoff.
Based on the identified causal model Q → EC → AL, a small natural discharge event caused anthropogenic salt inputs increasing EC, which in turn—probably at a threshold of about 2,000 µS/cm—triggered an algal bloom. When EC dropped below the aforementioned threshold, the algal bloom ceased (Fig. 3). It is discussed now whether such a threshold is plausible. Based on observed chlorophyll-a concentrations attributed to diatoms, a median exponential growth rate of about 0.6 1/d was determined between t = 280 h (beginning of growth) and t = 375 h (maximum of AL). Similar growth rates were observed in laboratory experiments with Prymnesium parvum (Baker et al. 2009; Yin et al. 2021) at water temperatures of 23 °C and at EC of about 2000 µS/cm, which were the conditions in the Odra River at Frankfurt during the algal bloom event. The threshold of EC = 2,000 µS/cm was reached in Frankfurt at the beginning of increasing AL at about t = 280 h. Water temperatures during the algal bloom fluctuated around 23 °C (Fig. 3). However, because AL responded to EC with a delay, the threshold was likely lower than 2000 µS/cm. In a publication of the European Commission (2023) it was concluded that the risk for an algal bloom of Prymnesium parvum would increase already with EC > 1500 µS/cm. So, it seems likely that exceedance of an EC threshold between 1500 and 2000 µS/cm triggered algal bloom in the Odra River. Furthermore, satellite imagery shows elevated chlorophyll levels moving downstream from a suspected source area in Upper Silesia from the beginning of August 2022 (European Commission 2023). I therefore conclude that an increase of EC brought the algal bloom in the Odra River and this likely caused the fish kill. The latter point was not subject of this analysis but reported previously (European Commission 2023).
Conclusions
An approach to find causal relationships from a set of environmental variables was proposed and applied for time series of water quality during the toxic algal bloom in summer 2022 in the Odra River, Germany. For the proposed approach, firstly the two most important drivers of an observed target variable including their time lags are identified. Subsequently, the most reliable and plausible causal structure from a set of statistically possible structures is determined. The approach is based on established correlation and regression techniques, which are compiled in a novel composition. For the exemplary application, specific circumstances of salt inputs to the Odra River as likely cause of the toxic algal bloom in summer 2022 were illuminated. More generally, it was demonstrated that carefully conducted and hypothesis-driven regression und correlation analyses can help to detect causal structures and to quantify causal relationships.
Change history
05 March 2024
A Correction to this paper has been published: https://doi.org/10.1186/s13717-024-00500-0
Abbreviations
- DAG:
-
Directed acyclic graph
- CART:
-
Classification and regression trees
- AL:
-
Chlorophyll-a concentrations attributed to diatoms
- Q:
-
River flow
- EC:
-
Electrical conductivity
References
Alameddine I, Cha JK, Reckhow KH (2011) An evaluation of automated structure learning with Bayesian networks: an application to estuarine chlorophyll dynamics. Environ Model Softw 26(2):163–172. https://doi.org/10.1016/j.envsoft.2010.08.007
Baker JW, Grover JP, Ramachandrannair R, Black C, Valenti TW, Brooks JBW, Roelkec DL (2009) Growth at the edge of the niche: an experimental study of the harmful alga Prymnesium parvum. Limnol Oceanogr 54(5):1679–1687. https://doi.org/10.4319/lo.2009.54.5.1679
Breiman L (2001) Random forests. Mach Learn 45:5–32. https://doi.org/10.1023/A:1010933404324
Breimann L, Friedmann JH, Olshen RA, Stone CJ (1984) Classification and regression trees. Wadsworth, Belmont
Cornes R, van der Schrier G, van den Besselaar EJM, Jones PD (2018) An ensemble version of the E-OBS temperature and precipitation datasets. J Geophys Res Atmos 123:9391–9409. https://doi.org/10.1029/2017JD028200
De Heus P (2012) R squared effect-size measures and overlap between direct and indirect effect in mediation analysis. Behav Res Methods 44:213–221. https://doi.org/10.3758/s13428-011-0141-5
Dehmel H (1992) Analyse und Auswertung des vorhandenen Datenmaterials zur Bewertung der Wasserbeschaffenheit der Oder. Umweltbundesamt, Berlin
European Commission (2023) An EU analysis of the ecological disaster in the Oder River of 2022: lessons learned and research-based recommendations to avoid future ecological damage in EU rivers, a joint analysis from DG ENV, JRC and the EEA. Publications Office of the European Union, Luxembourg city. https://doi.org/10.2760/067386
German Environment Agency (2022) Fish die-off in the Oder River, August 2022—Status report as of 30 September 2022. https://www.bmuv.de/en/download/status-report-on-fish-die-off-in-the-oder-river. Accessed on 1 July 2023
Glover BJ, Johnson P (1974) Variations in the natural chemical concentration of river water during flood flows, and the lag effect. J Hydrol 22:303–316. https://doi.org/10.1016/0022-1694(74)90083-3
Grömping U (2009) Variable importance assessment in regression: linear regression versus random forest. Am Stat 63(4):308–319. https://doi.org/10.1198/tast.2009.08199
Hastie TJ, Tibshirani RJ (1990) Generalized additive models. Chapman and Hall, London
Jensen FV, Nielsen TD (2007) Bayesian networks and decision graphs, 2nd edn. Springer, New York
Mudelsee M (2013) Climate time series analysis: classical statistical and bootstrap methods, 2nd edn. Springer, New York
Oberflächengewässerverordnung (2016) Verordnung zum Schutz der Oberflächengewässer. BGBl. I Nr. 28 vom 23.06.2016 S. 1373
Ombadi M, Nguyen P, Sorooshian S, Hsu K (2020) Evaluation of methods for causal discovery in hydrometeorological systems. Water Resour Res 56:e2020WR027251. https://doi.org/10.1029/2020WR02725
Pearl J, Makanzie D (2019) The Book of why: the new science of cause and effect. Penguin Books, Westminster
Rogoż M, Rózkowski A, Wilk Z (1987) Hydrogeological problems in the upper silesian coal basin: hydrogeology of coal basins. In: Proceedings of the International mine water association symposium “hydrogeology of coal basins”, Katowice: 1987
Runge J, Bathiany S, Bollt E, Camps-Valls G, Coumou D, Deyle E, Glymour C, Kretschmer M, Mahecha MD, Muñoz-Marí J, Van Nes EH, Peters J, Quax R, Reichstein M, Scheffer M, Schölkopf B, Spirtes P, Sugihara G, Sun J, Zhang K, Zscheischler J (2019a) Inferring causation from time series in Earth system sciences. Nat Commun 10:2553. https://doi.org/10.1038/s41467-019-10105-3
Runge J, Nowack P, Kretschmer M, Flaxman S, Sejdinovic D (2019b) Detecting and quantifying causal associations in large nonlinear time series datasets. Sci Adv 5:eaau4996. https://doi.org/10.1126/sciadv.aau4996
Selle B, Hannah M (2010) A bootstrap approach to assess parameter uncertainty in simple catchment models. Environ Model Softw 25:919–926. https://doi.org/10.1016/j.envsoft.2010.03.005
Spirtes P, Glymour C (1991) An algorithm for fast recovery of sparse causal graphs. Soc Sci Comput Rev 9:62–72. https://doi.org/10.1177/089443939100900106
Spirtes P, Glymour C, Scheines R (1993) Causation, prediction, and search. Springer, New York
Stow CA, Borsuk ME (2003) Enhancing causal assessment of estuarine fishkills using graphical models. Ecosystems 6:11–19. https://doi.org/10.1007/PL00021508
Venables WN, Ripley BD (2003) Modern applied statistics with S, 4th edn. Springer, New York
Wiederhold J, Buchinger S, Düster L, Fischer H, Hahn J, Helms M, Hermes N, Jewell K, Kleinteich J, Krenek S, Löffler D, Mora D, Rademacher S, Schlüsener M, Schütze K, Wahrendorf DS, Wick A, Ternes T (2023) Untersuchungen zum Fischsterben in der Oder im August 2022. Bundesanstalt Für Gewässerkunde, Koblenz. https://doi.org/10.5675/BfG-2143
Yin J, Sun X, Zhao R, Qiu X, Eeswaran R (2021) Application of uniform design to evaluate the different conditions on the growth of algae Prymnesium parvum. Sci Rep 11:12672. https://doi.org/10.1038/s41598-021-92214-y
Acknowledgements
I would like to thank Michael Schmook (Landesamt für Umwelt Brandenburg) for providing water quality data of the Odra River and expertise regarding the use of chlorophyll-a concentrations obtained from a spectral fluorometer with integrated algae class differentiation (BBE Moldänke GmbH). Wilfried Wiechmann (Bundesanstalt für Gewässerkunde) provided time series of water levels and discharges for the Odra River. I acknowledge the E-OBS dataset from the EU-FP6 project UERRA (http://www.uerra.eu) and the data providers in the ECA&D project (https://www.ecad.eu). Alexander Blume helped with the spatial analysis of the E-OBS data. Marc Schwientek provided valuable suggestions at various stages of this work. Two anonymous reviewers significantly improved the presentation of this research through their critical suggestions.
Funding
Open Access funding enabled and organized by Projekt DEAL. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Contributions
Not applicable.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The author declares that he has no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article was revised: Caused by a typesetting error, four spare brackets were mistakenly added to Equations 1 and 2. This error has been corrected.
Supplementary Information
Additional file 1.
(i) Additional details on the data set from the Odra River, (ii) Figs. S1 and S2 and (iii) Table S1.
Additional file 2.
Full data set to reproduce the analysis presented in this paper.
Additional file 3.
R-Script to reproduce the analysis presented in this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Selle, B. An approach for finding causal relations in environmental systems: with an application to understand drivers of a toxic algal bloom. Ecol Process 13, 8 (2024). https://doi.org/10.1186/s13717-023-00482-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13717-023-00482-5