Introduction

With the increasing advancement of information technology and 6G, there has been a rapid increase in the number of intelligent terminals and emerging Artificial Intelligence (AI) applications [1]. By 2025, it is estimated that the number of global intelligent terminal devices will exceed 25 billion and will continue to grow rapidly in the following decades [2]. Moreover, computing-intensive AI applications such as ultra-high-definition video streaming analysis, intelligent driving, augmented reality, and facial recognition are developing swiftly, leading to a massive demand for computing-intensive tasks from devices [3, 4]. However, due to the limited battery capacity and computational resources of these devices, it becomes challenging or even impossible to process all the tasks generated by these AI applications locally [5].

Mobile Cloud Computing has large task processing capabilities. By offloading AI tasks to the cloud, it can effectively reduce the processing burden on end-user devices [6]. However, the distance between end-user devices and cloud computing infrastructure, along with network capacity constraints, may lead to significant transmission delays and energy consumption [7]. Furthermore, offloading a large amount of data to the cloud could cause network overload and congestion. Mobile Edge Computing (MEC), as an emerging computing paradigm, provides a powerful way to solve this problem [8]. By moving cloud computing resources and services closer to the AI data generation and processing location, MEC can bring numerous benefits to users, such as reducing service latency, decreasing network congestion, and improving service quality [9].

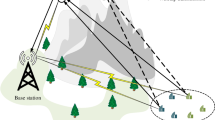
The base stations of traditional MEC deployed on cellular networks are typically fixed to the ground and immovable [10]. However, for some remote regions like oceans, wilderness, and deserts, ground-based MEC networks struggle to provide coverage [11]. Airborne devices with extensive coverage and strong computing capabilities have become a research hotspot for overcoming the limitations of ground-based MEC. High Altitude Platforms (HAPs) with their large coverage area and computing capacities, can serve as airborne base stations providing services to Ground Devices (GDs), thus becoming an important research problem [12]. HAPs have advantages such as low transmission delay, robust computing capability, wide service area, and prolonged endurance [13]. Additionally, HAPs can be flexibly deployed according to specific circumstances, offering better MEC services to GDs. Consequently, the issue of computation offloading in MEC systems supported by HAP is gaining extensive attention [13].

In this manuscript, we study the online dynamic computation offloading and the allocation of resources among multiple users within the HAP-assisted MEC framework. The aim is to optimize energy efficiency alongside maintaining system stability. The control variables for decision-making are: 1) GD’s local CPU cycle frequency, 2) the size of computation tasks offloaded by GDs, and 3) the computational resources allocated by the HAP. Based on stochastic optimization techniques, an online approach is proposed to tackle these challenges. The proposed Energy Efficient Dynamic Offloading (EEDO) algorithm is designed to adaptively make the computation offloading and resource allocation decisions. Extensive experiments including both parameter analysis and comparison experiments validate EEDO’s efficacy. The main contributions of this study are as follows:

  1. 1

    We study the task offloading and resource allocation problem in a HAP-assisted MEC system, where multiple GDs process tasks locally or offload tasks to HAP. Our goal is to minimize system energy consumption. The local CPU cycle frequency of GDs, the size of computation tasks offloaded by GDs, and the resources allocated by the HAP are utilized to optimize system performance while taking into account the randomness of task arrival and the uncertainty of the communication quality.

  2. 2

    We employ stochastic optimization techniques to transform the original stochastic optimization problem into three sub-problems that can be solved in parallel, and design the EEDO algorithm to effectively reduce system energy consumption without prior statistical task arrival or communication information. Through theoretical analysis, the gap between the solution of algorithm and the optimal solution is proven.

  3. 3

    We conduct extensive experiments to evaluate the EEDO algorithm. Through parameter analysis, it is demonstrated that EEDO can achieve a balance between energy consumption and performance and effectively adapt to various task arrival rates and the number of GDs. And comparative experiments illustrate the algorithm significantly outperforms the comparison algorithms in reducing system energy consumption and ensuring system performance.

The remaining sections of this manuscript are structured as below: Section 2 builds the system model and formalizes the problem. Section 3 presents our algorithm, employing stochastic optimization to partition and resolve the original optimization problem. Section 4 provides a theoretical analysis of the EEDO algorithm. Section 5 conducts the parameter and comparison experiments. Section 6 discusses recent related works, and Section 7 concludes our works.

System model and problem formulation

System Model

This paper considers a HAP-assisted MEC framework including multiple GDs which can offload tasks to the edge server deployed on HAP, as shown in Fig. 1. The ground layer includes N GDs, denoted by \(\mathcal {N} = \{1,2,...,i,...,N\}\). Ascending to the aerial section, a HAP serves as the edge server, providing ground devices with computational AI services and data processing capabilities. Within our formulated system, time is segmented into discrete intervals as time slots, delineated as \(\mathcal {T} = \{0,1,...,t,...,T-1\}\), with the duration of each interval \(\tau\). Typically, GDs may have various computational demands within each time slot, thereby generating a substantial volume of computation-intensive tasks. The computational resource requirements of these tasks may surpass the processing capabilities of the local devices, making it unfeasible for the GDs to handle the tasks locally. Specifically, there are \(A_i(t)\) tasks that arrive at each GD in each time slot t, where the GD can process a portion of the tasks locally and offload a portion of the tasks to the HAP for processing. Upon receiving the offloaded tasks, the HAP allocates computational resources to these tasks from multiple GDs based on the backlog of the entire system during that time slot t (Table 1).

Fig. 1
figure 1

The HAP-assised MEC framework

Full size image
Table 1 Notations and definitions
Full size table

Communication model

GDs establish communication with the HAP, which is stationed at a consistent altitude within the stratosphere. Our analysis incorporates both direct Line-of-Sight (LoS) and indirect Non-Line-of-Sight (NLoS) transmission models to describe the communication model.

Based on [14], the path loss for communication between given GD i and the HAP is:

$$\begin{aligned} L_i = 20\log _{10}\left( \frac{4\pi f_c \sqrt{d_i^2 + r_i^2}}{c}\right) + \rho _i^{\text {LoS}}\eta _i^{\text {LoS}} + \left(1-\rho _i^{\text {LoS}}\right)\eta _i^{\text {NLoS}}. \end{aligned}$$
(1)

Here, \(f_c\) is defined as the carrier frequency utilized by the communication system, c represents the constant speed of light, and the variables \(d_i\) along with \(r_i\) respectively denote the vertical and horizontal distance between GD i and the HAP. The coefficients \(\eta _i^{\text {LoS}}\) and \(\eta _i^{\text {NLoS}}\) correspond to the path loss metrics for LoS and NLoS paths.

Additionally, \(\rho _i^{\text {LoS}}\) specifies the chance of employing the LoS model for transmissions between GD i and the HAP,

$$\begin{aligned} \rho _i^{\text {LoS}} = \frac{1}{1 + \varkappa _1 \exp \left\{-\varkappa _2 \left[\tan ^{-1}\left(\frac{d_i}{r_i}\right) - \varkappa _1\right]\right\}}, \end{aligned}$$
(2)

where the variables \(\varkappa _1\), \(\varkappa _2\), alongside the path loss parameters \(\eta _i^{\text {LoS}}\) and \(\eta _i^{\text {NLoS}}\), are determined by the prevailing environmental conditions.

Building upon the aforementioned path loss model, the channel gain \(h_i(t)\) between GD i and the HAP during slot t is deduced as:

$$\begin{aligned} h_i(t) = 10^{-\frac{L_i}{10}}. \end{aligned}$$
(3)

Furthermore, consider the GDs communicate with the HAP using Frequency Division Multiple Access (FDMA) technology [15]. Therefore, the data rate for GD i at given slot t can be represented as:

$$\begin{aligned} R_i(t) = W_i \log _2 \left( 1 + \frac{h_i(t)P_i(t)}{\sigma ^2}\right) . \end{aligned}$$
(4)

Here, \(W_i\) is the bandwidth spectrum apportioned to GD i by the HAP, \(P_i(t)\) the signal strength emitted by GD i, and \(\sigma ^2\) represents the intensity of the omnipresent Gaussian white noise.

Task and queue model

In the model, each GD i maintains a task queue denoted as \(Q_i(t)\) to store the tasks that arrive in each time slot [16]. GDs effectively allocate computational resources to handle tasks by adopting a partial offloading mechanism.

The size of tasks processed on-device by GD i is denoted by \(D_{i,l}(t)\), which indicates the size (in bits) of tasks processed by GD i itself in the given slot t, and is calculated as:

$$\begin{aligned} D_{i,l}(t) = \frac{f_i(t) \tau }{\varphi _i}. \end{aligned}$$
(5)

In this expression, \(\varphi _i\) is the CPU cycles number for GD i to process a single bit of data, \(f_i(t)\) represents the operational frequency of GD i’s CPU within slot t, constrained by \(0 \le f_i(t) \le f_i^{\text {max}}\), with \(f_i^{\text {max}}\) defining the upper limit of GD i’s CPU frequency.

Additionally, GDs can perform task offloading, with the size of tasks offloaded to the HAP represented as:

$$\begin{aligned} D_{i,o}(t) \le R_i(t) \tau . \end{aligned}$$
(6)

For each time slot t, the size of newly generated tasks at GD i are characterized as \(A_i(t)\). Following this, the evolution of the task queue for GD i is:

$$\begin{aligned} Q_i(t+1) = \max \{Q_i(t) - D_{i,l}(t) - D_{i,o}(t), 0\} + A_i(t). \end{aligned}$$
(7)

And \(\max \{Q_i(t) - D_{i,l}(t) - D_{i,o}(t), 0\}\) is used to ensure that the server does not process more tasks from GD i during time slot t than that already in the queue, in order to ensure the stability of the task queue.

In the multi-layer computing architecture we have considered, the HAP maintains a task queue for each GD to store the tasks offloaded from GD i to the HAP, denoted as \(H_i(t)\). This queue carries all tasks offloaded from the corresponding GD to the HAP, performing centralized processing and resource optimization.

At slot t, the size of tasks processed by the HAP for \(GD_i\) is denoted as \(C_i(t)\). The update process of the HAP task queue is described as follows:

$$\begin{aligned} H_i(t+1) = \max \{H_i(t) - C_i(t), 0\} + D_{i,o}(t). \end{aligned}$$
(8)

Energy consumption model

For this HAP-assisted MEC system, our focus is on minimizing the energy consumption, including the on-device energy consumption of GDs’ local computing, the energy for offloading data transmissions by GDs, and the energy required for computations by the HAP.

The energy consumed by the on-device computing of GDs is intricately related to the CPU chip design. For GD i, the on-device computing energy consumption labeled as \(E_{i,l}(t)\), is formulated as:

$$\begin{aligned} E_{i,l}(t) = \xi _i f_i^2(t) \varphi _i D_{i,l}(t). \end{aligned}$$
(9)

Here, \(\xi _i\) denotes the efficient switched capacitance, \(f_i(t)\) stands for the CPU’s processing frequency, and \(\varphi _i\) corresponds to the requisite CPU cycles for processing each data bit [17].

The energy consumed by GDs to offload tasks to the HAP is:

$$\begin{aligned} E_{i,o}(t) = \frac{D_{i,o}(t)}{R_i(t)} P_i(t). \end{aligned}$$
(10)

\(P_i(t)\) characterizes the power for transmission by GD i within the slot t.

The energy consumption of the HAP processing tasks from GD i is denoted as \(E_{i,h}(t)\) and is elucidated as:

$$\begin{aligned} E_{i,h}(t) = l_1 C_i(t). \end{aligned}$$
(11)

In this equation, \(l_1\) denotes the energy expenditure by the HAP for each bit of data processed.

The cumulative energy consumption for the system, designated as E(t) , aggregates all the three energy consumption parts. The goal is to minimize

$$\begin{aligned} E(t) = \sum \limits _{i=1}^{N}[E_{i,l}(t) + E_{i,o}(t) + E_{i,h}(t)]. \end{aligned}$$
(12)

Problem formulation

Minimizing energy consumption is crucial as it directly affects the system’s operational sustainability and costs. Our objective is to devise an online dynamic offloading strategy that minimizes the energy consumed by the following control variables: the computational frequencies of GDs, the offloading policy, and the resource allocation of the HAP. The variable set for decision-making is depicted as \(\mathcal {X}(t) = \{\mathbf {f(t)}, \mathbf {D_o(t)}, \mathbf {C(t)}\}\). Below is the problem formulation,

$$\begin{aligned} P_1: \quad \min _{\mathcal {X}(t)} \lim _{T \rightarrow \infty } \frac{1}{T} \sum \limits _{t=0}^{T-1} \textbf{E}\{E(t)\}, \end{aligned}$$
(13)

subject to the following constraints:

$$\begin{aligned}{} & {} C1 : 0 \le f_i(t) \le f_i^{\text {max}}, \\{} & {} C2 : 0 \le D_{i,o}(t) \le R_i(t)\tau , \\{} & {} C3 : D_{i,o}(t) \le Q_i(t), \\{} & {} C4 : 0 \le C_i(t) \le H_i(t). \end{aligned}$$

The problem presented is a stochastic optimization problem. Owing to the unpredictable arrival pattern of tasks and communication channels, the statistics information is difficult to predict. Therefore, we take advantage of stochastic optimization theory to solve problem \(P_1\).

Energy efficient dynamic offloading algorithm design

Here, we utilize stochastic optimization theory to convert the previously formulated problem \(P_1\) to a more manageable deterministic one. By decomposing the transformed problem into several subproblems, the complexity of problem-solving is reduced. Subsequently, we design the EEDO algorithm to address these issues. Due to the inherent nature of stochastic optimization techniques, the EEDO algorithm can still obtain asymptotically optimal offloading decisions, even in the absence of future statistical information.

Problem transformation

We designate \(\Theta (t) = [\mathbf {Q(t)}, \mathbf {H(t)}]\) as the vector representing the task queue backlog. The Lyapunov function is defined to quantify the queue backlog,

$$\begin{aligned} L(\Theta (t)) = \frac{1}{2} \sum \limits _{i=1}^{N} \left[Q_i^2(t) + H_i^2(t)\right]. \end{aligned}$$
(14)

To maintain system queue stability, we establish the Lyapunov drift function. This function quantifies the transition in the system’s state (queue’s state) from a given instant t to the subsequent instant \(t+1\), expressed as

$$\begin{aligned} \Delta (\Theta (t)) = \textbf{E}\{L(\Theta (t+1)) - L(\Theta (t)) | \Theta (t)\}. \end{aligned}$$
(15)

The aim is to reduce the system’s energy expenditure. In pursuing this goal, combing both queue length and energy consumption, we aim to optimize both the system’s energy consumption and queue performance. Hence, the drift-plus-penalty function is defined as

$$\begin{aligned} \Delta _V(\Theta (t)) = \Delta (\Theta (t)) + V\textbf{E}\{E(t) | \Theta (t)\}, \end{aligned}$$
(16)

where V is a penalty weight that trades off system energy consumption against queue stability.

Theorem 1

No matter what the queue backlog or the task offloading decisions are, Eq. (16) adheres to the subsequent relationship:

$$\begin{aligned}{} & {} \Delta (\Theta (t)) + V\textbf{E}\{E(t)|\Theta (t)\} \le Z + V\textbf{E}\{E(t)|\Theta (t)\}\nonumber \\{} & {} + \textbf{E}\left\{\sum \limits _{i=1}^{N} Q_i(t)[A_i(t) - D_{i,l}(t) - D_{i,o}(t)] | \Theta (t)\right\}\nonumber \\{} & {} + \textbf{E}\left\{\sum \limits _{i=1}^{N} H_i(t)[D_{i,o}(t) - C_i(t)] | \Theta (t)\right\}, \end{aligned}$$
(17)

where \(Z = \frac{1}{2} \sum \nolimits _{i=1}^{N} \left[(A_i^{\max })^2 + (C_i^{\max })^2 + (D_{i,l}^{\max } + D_{i,o}^{\max })^2 + (D_{i,o}^{\max })^2\right]\) is a constant.

Proof

By applying \(([a-b]^+ + c)^2 \le a^2 + b^2 + c^2 + 2a(c - b)\), we get

$$\begin{aligned} Q_i^2(t+1){} & {} \le Q_i^2(t) + A_i^2(t) + [D_{i,l}(t) + D_{i,o}(t)]^2 \nonumber \\{} & {} \quad + 2Q_i(t)[A_i(t) - D_{i,l}(t) - D_{i,o}(t)], \end{aligned}$$
(18)
$$\begin{aligned} H_i^2(t+1) \le H_i^2(t) + D_{i,o}^2(t) + C_i^2(t) + 2H_i(t)[D_{i,o}(t) - C_i(t)]. \end{aligned}$$
(19)

Then, we can derive

$$\begin{aligned} \frac{1}{2}\left[Q_i^2(t+1) - Q_i^2(t)\right]{} & {} \le \frac{1}{2}A_i^2(t) + \frac{1}{2}\left[D_{i,l}(t) + D_{i,o}(t)\right]^2 \nonumber \\{} & {} \quad + Q_i(t)[A_i(t) - D_{i,l}(t) - D_{i,o}(t)], \end{aligned}$$
(20)
$$\begin{aligned} \frac{1}{2}[H_i^2(t+1) - H_i^2(t)] \le \frac{1}{2}D_{i,o}^2(t) + \frac{1}{2}C_i^2(t) + H_i(t)[D_{i,o}(t) - C_i(t)]. \end{aligned}$$
(21)

Further, we can obtain

$$\begin{aligned} \Delta (\Theta (t)) + V\textbf{E}\{E(t) | \Theta (t)\}{} & {} = V\textbf{E}\{E(t) | \Theta (t)\}\nonumber \\ {} & {} \quad + \textbf{E}\left\{\frac{1}{2}\sum \limits _{i=1}^{N}\left[Q_i^2(t+1)-Q_i^2(t)\right] | \Theta (t)\right\}\nonumber \\ {} & {} \quad + \textbf{E}\left\{\frac{1}{2}\sum \limits _{i=1}^{N}\left[H_i^2(t+1)-H_i^2(t)\right] | \Theta (t)\right\}\nonumber \\ {} & {} \le Z + V\textbf{E}\left\{E(t) | \Theta (t)\right\} + \textbf{E}\left\{\sum \limits _{i=1}^{N}Q_i(t)\left[A_i(t) - D_{i,l}(t) - D_{i,o}(t)\right] | \Theta (t)\right\}\nonumber \\ {} & {} \quad + \textbf{E}\left\{\sum \limits _{i=1}^{N}H_i(t)\left[D_{i,o}(t) - C_i(t)\right] | \Theta (t)\right\}, \end{aligned}$$
(22)

where \(Z = \frac{1}{2} \sum \nolimits _{i=1}^{N} [(A_i^{\max })^2 + (C_i^{\max })^2 + (D_{i,l}^{\max } + D_{i,o}^{\max })^2 + (D_{i,o}^{\max })^2]\) is a constant. \(\square\)

The original stochastic optimization problem is converted as follows:

$$\begin{aligned} P_2: \quad{} & {} \min \limits _{\mathcal {X}(t)}\left\{\sum \limits _{i=1}^{N}\left[V\xi _if_i^3(t)\tau - \frac{f_i(t)\tau }{\varphi _i}Q_i(t)\right]\right.\nonumber \\{} & {} +\sum \limits _{i=1}^{N}\left[V\frac{P_i(t)}{R_i(t)}-Q_i(t)+H_i(t)\right]D_{i,o}(t)\nonumber \\{} &\left. {} +\sum \limits _{i=1}^{N}\left[Vl_1-H_i(t)\right]C_i(t)\right\}, \end{aligned}$$
(23)

subject to the constraints:

$$\begin{aligned}{} & {} C1 : 0\le f_i(t)\le f_i^{max}, \\{} & {} C2 : 0\le D_{i,o}(t)\le R_i(t)\tau , \\{} & {} C3 : D_{i,o}(t)\le Q_i(t), \\{} & {} C4 : 0 \le C_i(t) \le H_i(t). \end{aligned}$$

Energy efficient dynamic offloading algorithm

This part designs the online Energy Efficient Dynamic Offloading (EEDO) algorithm aimed at reducing the ceiling of Eq. (16). We can see that in the transformed problem, the decisions \(\mathbf {f(t)}, \mathbf {D_o(t)},\) and \(\mathbf {C(t)}\) are decoupled. Thus, problem \(P_2\) can be decoupled into three subproblems. Next, we will describe these subproblems one by one and provide their corresponding solutions.

Local CPU frequency allocation for GDs

By extracting the part related to decision \(\mathbf {f(t)}\) from problem \(P_2\), we obtain the local CPU frequency allocation subproblem for GDs as follows:

$$\begin{aligned} \min _{\mathbf {f(t)}} \sum \limits _{i=1}^{N} \left[ V\xi _i f_i^3(t)\tau - \frac{f_i(t)\tau }{\varphi _i}Q_i(t) \right] , \end{aligned}$$
(24)

subject to:

$$\begin{aligned} 0 \le f_i(t) \le f_i^{\max }. \end{aligned}$$

It is a convex optimization problem. By deducing the primary derivative to a null value, we can get \(f_i(t) = \sqrt{\frac{Q_i(t)}{3V\xi _i\varphi _i}}\). Consequently, the prime solution for the local CPU frequency is:

$$\begin{aligned} f_i^*(t) = \left\{ \begin{array}{ll} \sqrt{\frac{Q_i(t)}{3V\xi _i\varphi _i}}, &{} \text {if}\ 0 \le \sqrt{\frac{Q_i(t)}{3V\xi _i\varphi _i}} \le f^*, \\ f^*, &{} \text {otherwise}, \end{array}\right. \end{aligned}$$
(25)

where \(f^* = \min \left\{ \frac{Q_i(t)\varphi _i}{\tau }, f_i^{\max }\right\}\).

Offloading computation allocation for GDs

By extracting the part related to offloading computation, we can obtain the following optimization problem:

$$\begin{aligned} \min _{\mathbf {D_o(t)}} \sum \limits _{i=1}^{N} \left[ V\frac{P_i(t)}{R_i(t)} - Q_i(t) + H_i(t) \right] D_{i,o}(t), \end{aligned}$$
(26)

subject to:

$$\begin{aligned}{} & {} 0 \le D_{i,o}(t) \le R_i(t)\tau ,\\{} & {} \quad D_{i,o}(t) \le Q_i(t). \end{aligned}$$

This is a problem of linear programming, and the solution for GDs’ offloading computation is as follows:

$$\begin{aligned} D_{i,o}^*(t) = \left\{ \begin{array}{ll} \min \{R_i(t)\tau , Q_i(t)\}, &{} \text {if}\ V\frac{P_i(t)}{R_i(t)} - Q_i(t) + H_i(t) \le 0, \\ 0, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$
(27)

Computation resource allocation for HAP

By extracting the portion related to decision \(\mathbf {C(t)}\) from problem \(P_2\), we formulate the computation resource allocation subproblem for the HAP as follows:

$$\begin{aligned} \min _{\mathbf {C(t)}} \sum \limits _{i=1}^{N} [Vl_1 - H_i(t)] C_i(t), \end{aligned}$$
(28)

subject to:

$$\begin{aligned} 0 \le C_i(t) \le H_i(t). \end{aligned}$$

This problem is analogous to a knapsack problem, with the weight coefficient for \(C_i(t)\) being \(V_l - H_i(t)\). The capacity of the knapsack is the amount of tasks that the HAP can process. Below, we provide the solution process for this problem.

  1. (1)

    Set the baseline for tasks the HAP can process during slot t as \(C_h = \frac{f_{h}^{max} \tau }{\varphi _h}\). \(f_{h}^{\max }\) denotes the HAP’s maximum CPU frequency, and \(\varphi _h\) represents the CPU cycle number for the HAP to process a single bit of data.

  2. (2)

    Sort all GDs in ascending order of the weight \(Vl_1 - H_i(t)\) to obtain the order in which computational resources are allocated.

  3. (3)

    The HAP allocates computational resources to GDs according to the order of sorting, obtaining the amount of tasks that the HAP can process for GD i as follows:

    $$\begin{aligned} C_i^*(t) = \left\{ \begin{array}{ll} \min \{H_i(t), C_h\}, &{} \text {if}\ Vl_1 - H_i(t) \le 0, \\ 0, &{} \text {otherwise}. \end{array}\right. \end{aligned}$$
    (29)
  4. (4)

    Update the remaining size of tasks that the HAP can deal with as: \(C_h = C_h - C_i(t)\).

  5. (5)

    Repeat steps (3) and (4) until there are no tasks left for the HAP to deal with in slot t, or no GD requires further allocation of computational resources for task processing.

Subsequently, we present the detailed EEDO algorithm in Algorithm 1.

figure a

Algorithm 1 Energy Efficient Dynamic Offloading (EEDO) Algorithm

Analysis of the energy efficient dynamic offloading algorithm

Here, we examine the EEDO algorithm’s efficacy from a mathematical perspective. Lemma 1 is presented as follows.

Lemma 1

For any change in the task arrival rate \(\lambda\), we can obtain an offloading decision \(\pi ^*\), which is independent of the current task queue and satisfies

$$\begin{aligned} \textbf{E}\{\bar{E}^{\pi ^*}(t)\}\le & {} E^*(\lambda ),\nonumber \\ \textbf{E}\{A_i^{\pi ^*}(t)\}\le & {} \textbf{E}\{D_{i,l}^{\pi ^*}(t) + D_{i,o}^{\pi ^*}(t)\},\nonumber \\ \textbf{E}\{D_{i,o}^{\pi ^*}(t)\}\le & {} \textbf{E}\{C_i^{\pi ^*}(t)\}, \end{aligned}$$
(30)

where \(E^*(\lambda )\) symbolizes the minimum total energy consumption.

Proof

Caratheodory’s theorem [18] is utilized to derive Lemma 1. Similar to related works and for the sake of brevity, the details of the proof have been omitted here. \(\square\)

It is noteworthy that the task arrival rate is finite, which indicates that the system’s energy consumption is also finite. Thus, we denote the upper and lower bounds of the system’s energy consumption as \(\hat{E}\) and \(\check{E}\), respectively. Subsequently, we define the average queue length as \(\bar{J} = \lim \limits _{T \rightarrow \infty } \frac{1}{T} \sum \nolimits _{i=1}^{N} [Q_i(t) + H_i(t)]\). Building on Lemma 1, we establish the upper bounds of the system’s energy consumption and queue dimensions in Theorem 2.

Theorem 2

For any trade-off coefficient V and task arrival rate \(\lambda + \epsilon\), the upper bounds on system energy consumption and queue dimensions satisfy

$$\begin{aligned} E^{\text {EEDO}} \le E^* + \frac{Z}{V}. \end{aligned}$$
(31)
$$\begin{aligned} \bar{J} \le \frac{Z + V(\hat{E} - \check{E})}{\epsilon }. \end{aligned}$$
(32)

Proof

With Lemma 1, for any arbitrary stochastic offloading decision \(\pi\) and task arrival rate \(\lambda + \epsilon\), we have:

$$\begin{aligned}{} & {} \textbf{E}\{\bar{E}^{\pi }(t)\} \le E^*(\lambda + \epsilon ),\nonumber \\{} & {} \textbf{E}\{A_i^{\pi }(t)\} + \epsilon \le \textbf{E}\{D_{i,l}^{\pi }(t) - D_{i,o}^{\pi }(t)\},\nonumber \\{} & {} \textbf{E}\{D_{i,o}^{\pi }(t)\} + \epsilon \le \textbf{E}\{C_i^{\pi }(t)\}. \end{aligned}$$
(33)

For any offloading decision \(\pi\), we can derive:

$$\begin{aligned}{} & {} \Delta _V(\Theta (t)) \le Z + V\textbf{E}\{E(t)|\Theta (t)\}\nonumber \\{} & {} + \textbf{E}\{\sum \limits _{i=1}^{N}Q_i(t)[A_i^{\pi }(t) - D_{i,l}^{\pi }(t) - D_{i,o}^{\pi }(t)]|\Theta (t)\}\nonumber \\{} & {} + \textbf{E}\{\sum \limits _{i=1}^{N}H_i(t)[D_{i,o}^{\pi }(t) - C_i^{\pi }(t)]|\Theta (t)\}. \end{aligned}$$
(34)

By substituting Eq. (33) into Eq. (34) and summing over all time slots, the following is derived:

$$\begin{aligned} V\sum \limits _{t=0}^{T-1}\textbf{E}(E(t)) \le ZT + VTE^*(\lambda + \epsilon ) - \epsilon \sum \limits _{t=0}^{T-1} \sum \limits _{i=1}^{N} \textbf{E}\{Q_i(t) + H_i(t)\}. \end{aligned}$$
(35)

Since \(\epsilon , Q_i(t)\), and \(H_i(t)\) are all non-negative, we can deduce:

$$\begin{aligned} V\sum \limits _{t=0}^{T-1}\textbf{E}(E(t)) \le ZT + VTE^*(\lambda + \epsilon ). \end{aligned}$$
(36)

When Eq. (36) is divided by VT and as \(\epsilon \rightarrow 0, T \rightarrow \infty\), Eq. (31) is proven.

Furthermore, with Eq. (35), we also get:

$$\begin{aligned} \epsilon \sum \limits _{t=0}^{T-1} \sum \limits _{i=1}^{N} \textbf{E}\{Q_i(t) + H_i(t)\} \le ZT + VTE^*(\lambda + \epsilon ) - V\sum \limits _{t=0}^{T-1}\textbf{E}(E(t)). \end{aligned}$$
(37)

Given the non-negativity of \(\textbf{E}(E(t))\), the equation simplifies to:

$$\begin{aligned} \epsilon \sum \limits _{t=0}^{T-1} \sum \limits _{i=1}^{N} \textbf{E}\{Q_i(t) + H_i(t)\} \le ZT + VT(\hat{E} - \check{E}). \end{aligned}$$
(38)

By dividing both sides of Eq. (38) by \(\epsilon T\), and as \(T \rightarrow \infty\), Eq. (32) is proven. \(\square\)

Evaluation

Experiment settings

In this part, extensive experiments are done to evaluate the efficacy of the EEDO algorithm. A HAP is deployed to serve GDs across a \(1\text {km} \times 1\text {km}\) remote zone. GDs are distributed randomly in this area, while the HAP remains static at a predetermined elevation. The size of tasks arriving \(A_i(t)\) adheres to a uniform distribution ranging from \([0, 1.8] \times 10^6\) bits. GDs operate at a CPU cycle frequency \(1 \text {GHz}\), with transmission power described by a distribution \(P(t) \sim [0.01, 0.2]\) W [12]. The HAP has a maximum CPU cycle frequency of \(20 \text {GHz}\). The aggregate bandwidth available for communication between GDs and the HAP is \(100 \text {MHz}\). Additionally, \(\xi _i = 10^{-27}\), \(\sigma ^2 = 10^{-13}\) W, and \(\varphi _i = 1000\) cycles/bit [14]. The key parameter configurations are enumerated in Table 2.

Table 2 Parameter settings
Full size table

Parameter analysis

Impact of parameter V

We select a set of different V values for analysis to validate the impact on the system’s energy consumed and mean queue length. The change in energy consumed and queue length in response to varying V are depicted in Figs. 2 and 3. Figure 2 illustrates a decreasing trend in the system’s energy consumed correlating with ascending V values. This is because a larger control parameter V indicates the system’s tendency to prioritize energy optimization, which aligns with the results in Eq. (31). Figure 3 illustrates an increase in the queue length as V increases. This phenomenon can be ascribed to the bounded processing and data transmission capacities of GDs, which are capable of handling only a finite amount of tasks, consequently resulting in an accumulation of pending tasks. Such findings are in alignment with the results of Eq. (32). Therefore, the EEDO proves effective in reducing the energy consumption of the system whilst preserving the equilibrium of the task queue.

Fig. 2
figure 2

Energy consumption v.s. V

Full size image
Fig. 3
figure 3

Queue length v.s. V

Full size image

Impact of task arrival rate

Figures 4 and 5 illustrate the variations in the system’s energy consumed and the mean queue length corresponding to diverse arrival rates of the task. Here, the arrival rate of the task is denoted by \(\alpha A_i(t)\), and \(\alpha = 0.6\), 0.8, and 1.0. It is observed in Fig. 4 that the consumption of energy within the system rises with the rising arrival rate of the task. In a similar vein, Fig. 5 reveals a direct correlation between the arrival rate of the task and the average queue length. Nonetheless, it is observed that in a short time period, both energy consumption and queue length attain a state of equilibrium. Thus, the EEDO algorithm can dynamically adjust offloading decisions, allowing the system to quickly stabilize.

Fig. 4
figure 4

Energy consumption v.s. Task arrival rate

Full size image
Fig. 5
figure 5

Queue length v.s. Task arrival rate

Full size image

Impact of GDs number

Figures 6 and 7 illustrate the influence of varying numbers of GDs on the system’s energy consumed and mean queue length. Figure 6 reveals an increasing trend in energy consumed as the GD number increases. In contrast, Fig. 7 exhibits the continuous increase in mean queue length with more GDs, due to the HAP’s finite processing capacities. As the number of GDs increases, some tasks cannot be processed timely, resulting in a continuous increase in queue length.

Fig. 6
figure 6

Energy consumption v.s. GDs Number

Full size image
Fig. 7
figure 7

Queue length v.s. GDs Number

Full size image

Comparison experiment

Herein, we analyze the EEDO algorithm’s efficiency via comparative experiments. We compare the EEDO algorithm with three other algorithms, which are described as follows:

  • Local-only algorithm: Each GD processes all newly arrived tasks by itself.

  • Offload-only algorithm: Each GD offloads all newly arrived tasks to the HAP for processing.

  • GTCO-21 algorithm: Each GD adopts the greedy approach extended from [19] to perform task offloading.

Figures 8 and 9 illustrate the system’s energy consumed and queue length with these algorithms. Compared to the Offload-only and GTCO-21 algorithms, our EEDO algorithm can reduce system energy consumption while maintaining queue stability. With the Offload-only algorithm, the HAP’s finite computational capacity leads to unprocessed task accumulation and a continuous increase in queue length. For the GTCO-21 algorithm, since all GDs want to offload as many tasks as possible to the HAP to alleviate their burden, the excessive number of tasks exceeds the processing limit of the HAP, causing the queue length to keep increasing. Nevertheless, when compared with the Local-only approach, EEDO not only sustains task queue constancy but also reduces energy consumed. Collectively, the EEDO performs well in reducing energy consumed while maintaining task queue constancy.

Fig. 8
figure 8

Energy consumption v.s. Different algorithms

Full size image
Fig. 9
figure 9

Queue length v.s. Different algorithms

Full size image

Related work

The computational capacity limitations and battery energy constraints of GDs pose significant challenges in processing high-demand computational tasks. MEC has emerged as an innovative solution to these issues. Through proper offloading of computation tasks and allocation of resources, these issues can be effectively resolved [20].

Tang et al. [21] studied the offloading of indivisible and delay-sensitive computational tasks in MEC systems. They designed a distributed offloading algorithm to reduce task drop rate and average latency. Wu et al. [22] focused on task offloading within a decentralized and heterogeneous IoT network, augmented by blockchain technology. They presented an algorithm for real-time decision-making on task offloading to enhance offloading efficiency. Guo et al. [23] investigated the task offloading process within densely populated IoT environments, proposing a cyclical search mechanism to optimize CPU cycle frequency and transmission power. Tang et al. [24] drew on the idea of Intent-based Networking (IBN) and proposed a Service Intent-aware Task Scheduling (SIaTS) framework for CPNs. Nahum et al. [25] proposed an intent-aware reinforcement learning method to perform the RRS function in a RAN slicing scenario. Liao et al. [26] developed a novel task offloading framework for air-ground integrated vehicular edge computing (AGI-VEC) which could enabled a user vehicle to learn the long-term optimal task offloading strategy while satisfying the long-term ultra-reliable low-latency communication.

Moreover, many works have concentrated on partial task offloading. Tong et al. [27] explored minimizing the energy cost of the MEC system in a cooperative scenario. They established an online dynamic computational offloading algorithm to reduce additional overheads. Xia et al. [28] developed a model for a MEC offloading scheme powered by energy collection, employing a collaborative online optimization approach based on the game and stochastic theories. Hu et al. [29] contemplated the equilibrium between power efficiency and service latency within extensive MEC networks, proposing a dynamic offloading and resource management protocol.

However, when ground communication facilities are damaged or lacking, HAP-assisted aerial MEC networks become an alternative solution. Waqar et al. [14] investigated offloading problems within MEC-augmented vehicular networks, designing a decentralized strategy utilizing reinforcement learning. Wang et al. [30] researched energy efficiency in airborne MEC networks, and put forward an offloading strategy based on collective learning paradigms. Ren et al. [31] investigated caching and computational offloading issues with HAP assistance. They presented an algorithm based on the Lagrangian method.

Although many efforts have been made in the field of offloading and resource allocation, and some studies have also investigated issues related to HAP offloading, the offloading problem in the HAP-assisted MEC scenario is still challenging. This paper studies the task offloading and resource allocation problem in a HAP-assisted MEC system and designs the EEDO algorithm to reduce the consumption of system while considering the randomness of task arrival and the uncertainty of communication quality.

Conclusion

In our work, we study the dynamic multi-user computation offloading and resource allocation problem within a HAP-assisted MEC system. The problem is modeled as a stochastic optimization problem with objectives set on reducing energy consumption of the system, whilst preserving queue stability and adhering to resource constraints. By applying stochastic optimization techniques, we recast the initial stochastic problem into a deterministic problem. This reformulated problem is then strategically split into three distinct subproblems. Then, we design the online EEDO algorithm to solve these three subproblems, which require no prior statistical information on tasks. Our theoretical analysis proves that the EEDO algorithm maintains an equilibrium between energy consumed and queue stability within the system. Then, we conduct experimental analysis. The results from these experiments validate the EEDO algorithm’s effectiveness in reducing the system’s energy consumed while concurrently maintaining queue stability.