Abstract
Emerging technological advances in wireless communication and networking have led to the design of large scale networks and small sensor units with minimal power requirements and multifunctional processing. Though energy harvesting technologies are improving, the energy of sensors remains a scarce resource when designing routing protocols between sensor nodes and base station. This paper proposes a multi-hop graph-based approach for an energy-efficient routing (MH-GEER) protocol in wireless sensor networks which aims to distribute energy consumption between clusters at a balanced rate and thus extend networks’ lifespans. MH-GEER deals with node clustering and inter-cluster multi-hop routing selection. The clustering phase is built upon the centralized formation of clusters and the distributed selection of cluster heads similar to that of low-energy adaptive clustering hierarchy (LEACH). The routing phase builds a dynamic multi-hop path between cluster heads and the base station. Our strategy is about exploring the energy levels in the entire network and using these to select the next hop in a probabilistic, intelligent way. Performance evaluation shows that MH-GEER minimizes energy depletion in distant clusters and ensures load balancing in a network, thus improving the network’s lifetime and stability compared with single-hop conventional LEACH protocol.
Similar content being viewed by others
Introduction
Wireless sensor networks (WSNs) are communication infrastructures containing a large number of spatially distributed nodes equipped with micro-sensors. These small devices are used to sense data from a specific region and to collaborate in order to collect and process them. Data are then transmitted to a base station. Although WSNs have existed for several decades, they are one of the key components of Internet of Things (IoT)-based products and services [1]. Indeed, they play a significant role in various future IoT application scenarios such as health care [2], environmental monitoring [3] and smart cities [4]. Comparing sensor networks to ad-hoc networks, the number of sensor nodes in a sensor network can be several orders of magnitude higher than the nodes in an ad-hoc network. Sensor nodes are densely deployed and they are limited in power, computational capacities and memory [5]. Designing efficient-energy routing protocols is one of the major concerns in WSNs. Once deployed in the network, sensor nodes cannot be replaced. Thus, network operation is highly related to the adequate use and management of nodes’ power. Hierarchical routing protocols in WSNs are considered as the most energy-efficient systems that have been widely applied in the past few years [6]. They divide the network into clusters, each of which has a cluster head (CH) serving as an intermediate between the cluster nodes, aka member nodes, and the base station (BS) [7]. The CH has the highest energy level in the cluster; it gathers data, aggregates them and delivers them to the (BS) in a way that minimizes the overall energy consumption in the network.
Low energy adaptive clustering hierarchy (LEACH) [8] is the earliest hierarchically designed protocol using clustering to route information. It is a single-hop routing protocol where data are directly transmitted from the CHs to the BS. However, it has some limitations. First, CHs located far from the BS dissipate more energy than closer ones. As a result, the most distant clusters risk dying much earlier than closer clusters. The direct transmission process used in LEACH is not applicable for large scale networks because it affects the load balancing of the distribution and shortens the operational lifetime of the network. Second, the frequency of data transfer differs from one node to another based on the level of importance of the information detected at each area. This differentiation causes the early death of very active nodes compared to those with average activity, leading to an imbalance in the energy levels between the nodes of the network.
To tackle this problem, this paper proposes a distributed routing protocol based on multi-hop communication between CHs, modeled in a complete graph structure. A multipath routing process for the data was established to help to extend the network lifespan and to drain the nodes’ batteries at an evenly balanced rate. More specifically, our protocol builds a hierarchical organization of nodes based on their distance from each other, dividing the network into clusters. Then, it selects and rotates headers in these clusters, based on the differing levels of nodes’ energy, to minimize energy waste before the data routing phase to the BS. To establish the routing process, the proposed protocol takes advantage of a distributed intelligent technique inspired by the collective behaviors of ants in nature [9, 10]. It establishes energy-efficient paths, taking into consideration, at each round, the energy state of the whole network.
Contributions
This paper proposes a multi-hop graph-based approach for an energy-efficient routing protocol, known as MH-GEER, in wireless sensor networks, which aims to distribute energy consumption between clusters at a balanced rate and thus extend networks’ lifespans.
The salient contributions of this paper are as follows:
-
1.
Taking advantage of an ACO-based algorithm to achieve multi-hop routing;
-
2.
Optimizing the CH route selection chosen by agents by considering not only the residual energy of nodes and their positions but also the traffic load in the links (i.e. quantity of pheromones deposited) and the transmission cost of the latter compared to that of the complete path they have been part of in the past;
-
3.
Providing, using three different scenarios, a comparison of the routing phase of our protocol with that of the original LEACH protocol with regard to two metrics: the residual energy of distant CH nodes and the load balancing of the network.
Structure of the paper
“Related work” section discusses LEACH limitations and reviews the literature on the existing routing protocols that have been proposed to overcome them. “The MH-GEER protocol” section presents the proposed method and the system model used in the paper. A case illustrating the theoretical steps of our protocol and evaluating its performance compared to LEACH is given in “Performance evaluation” section and finally, conclusions and possible future work are described in “Conclusion and future work” section.
Related work
Several hierarchical routing protocols have been proposed for wireless sensor networks in the last few years [8, 11,12,13,14,15,16,17,18,19]. Many of them introduced a multi-hop inter-cluster communication approach to extend the network lifetime. LEACH [8] is the first well-known cluster-based protocol for WSN, built upon two phases: the setup phase and the steady state phase. In the setup phase, CHs are selected according to a distributed process, in which each node chooses, independently, to be a CH or not based on a probabilistic formula. The non-CH nodes join their cluster depending on the strength of the signal received from the CH. Next, each CH creates a time division multiple access schedule (TDMA) and sends it to all its cluster member nodes. In the steady state phase, a one-hop data transmission from each CH to the BS takes place in the relevant formed topology. LEACH uses a code division multiple access (CDMA) code to reduce inter-cluster interference. After each round, a randomized rotation of CH is conducted to ensure load balancing. However, LEACH has some limitations. It does not consider either the sensor node’s residual energy or its position during the CH election process. Moreover, it is a single-hop routing protocol where the direct transmission of data from the CH to the sink node makes it inappropriate for large scale networks since it will cause more energy dissipation and rapid death for distant CHs.
Rather than using single-hop inter-cluster communication, it has been shown that communications in a multi-hop fashion between CHs and the BS promote more energy conservation and scalability compared to the single-hop approach [20]. Therefore, Zhang et al. [13] proposed an intra-cluster multi-hop routing protocol for WSNs called LEACH-WM. Similar to LEACH, their approach has a setup phase and a steady state phase with optimizations. During the latter phase, information in the CH is forwarded through a weight relay node (WR) to the BS. This relay node is a cluster member elected depending on its residual energy and its distance away from the BS. This approach reduces cluster heads’ energy dissipation but suffers from unbalanced distribution of the energy in the network: clusters located far away from the BS exhaust their energy rapidly compared to other clusters.
Taj et al. [11] proposed an enhanced LEACH protocol for wireless sensor networks called ICH-LEACH. Their protocol consists of three phases: initialization, cluster setup, and a steady phase. After the BS coordinates have been transmitted to each node in the first phase, in the second phase, clusters are formed and for each a CH is elected. Information about other CHs in the network is recorded in the routing table of each CH. The main improvement in this approach compared to LEACH lies in the use of an intermediate CH as a relay between the sender CH and the BS. However, to evaluate the optimum relay CH in the path, the routing algorithm only considers the sender CH position along with the positions of the relay CH and the BS. A drawback is that this routing algorithm does not consider whether the intermediate CH’s state of energy is depleted or overloaded.
A multi-hop technique (MHT) for the improvement of LEACH was proposed by Alnawafi et al. [14]. It distributes all the CHs of the network into two groups based on their distance from the BS: the internal group and the external group. CHs from the first group transmit data directly to the BS, whereas CHs from the second group build their own routing table. The Improved MHT-LEACH protocol (IMHT) [15] extended the previous work by distributing all the CHs into more than two levels. It proposes a consecutive selection of next hop CH through the levels depending on comparisons between the distances separating a certain level CH from another lower level CH or a CH from a BS.
Although these approaches were designed in order to minimize the energy cost of communication, most of them depend only on the distance factor to design routes. The closest nodes to the BS are always selected to route data and hence deplete their energy faster than other nodes. Once routes are defined, they are unchangeable during the whole operational time of the network, thus influencing its load balance. In this respect, introducing the energy factor along with the distance factor when selecting the next hops of routing protocols in WSNs will optimize the load balance of the network.
An approach aiming to expand the network’s lifetime using efficient data delivery to the BS was proposed by Biradar et al. in [16]. It partitioned the entire network into various clusters and provided two sorts of communication operations. The first is an intra-cluster communication, in which the CH collects information from the member nodes and transfers it, after being aggregated, directly to the BS or through intermediate CHs. The second is an inter-cluster communication in which the CH is a considerable distance away from the BS. In this case, it forwards data to the BS through other CHs with a minimum hop count. Neto et al. [17] proposed a multi-hop LEACH (MH-LEACH) protocol to find the best routes to the BS through various intermediate CHs. Each CH transmits an advertisement message to build its routing table depending on the strength of the received signal. However, before using these routes, they are sent to the CH to check for potential looping or an opposite direction.
In [18], Xingguo et al. used LEACH but they modified the threshold formula responsible for the CH selection by introducing a remaining energy factor that depends on the residual energy of each node in the current round, the average energy of the rest of the nodes in the same round, and the total residual energy of rest nodes. Though this can avoid a node with very low energy becoming a CH and thus prolong the lifetime of the network, the protocol still uses a direct transmission mechanism between CHs and BS, which can lead to the death of nodes that are distant from the BS.
In [19], Razaque et al. proposed P-LEACH, which combines both the LEACH and the PEGASIS protocol models. They introduced a novel approach to improve the energy efficiency in routing. It is a cluster-based chain protocol, which chooses the nodes with maximum energy to be CHs and forms a chain of CHs to transfer data to the BS. Although this scheme improves the network lifetime, it misses some effective CH selections since each CH communicates only with its closest neighbour.
Using swarm intelligence (SI) algorithms and specifically ant colony optimization (ACO) in such routing protocols can be interesting. Indeed, the latter has been implemented in several engineering domains [21] and used as an optimization strategy for many activities such as task scheduling in cloud computing environments [22] or data routing in wireless sensor networks [23].
For instance, in [12], Ghasem et al. proposed MO-IAR, an ant colony-based data routing proposal in WSNs, which operates in two phases: a first phase where there is an exploration of the shortest paths between each source node and a particular destination and a second phase of actual data routing. Its unique characteristic is the use of a congestion awareness mechanism, minimizing collisions and the average latency.
In [24], Cheng et al. proposed EAACA, an energy-aware ant colony algorithm for routing in WSNs, which takes advantage of the ACO to construct the optimum route to the BS (sink node). More precisely, the next-hop selection depends on three parameters: the distance to the BS, the residual energy of the next node and the average energy of the path. The algorithm uses forward ants to establish valid paths to the destination and then generates response packets through backward ants.
In [25], Mohajerani et al. proposed an ACO-based routing algorithm called a lifetime aware routing algorithm for wireless sensor networks (LTAWSN) aiming to build a network system where energy dissipation is equally divided among nodes. It uses artificial ants to deposit a newly designed pheromone operator depending on energy consumption and hop count metrics. A location function is used when choosing the next-hop in the path, considering the distance to the destination or nodes nearer to the destination.
Although those strategies have shown good results compared to other variants of ACO, they remain flat routing protocols that deplete the energy of all the nodes in the network without any specific hierarchy or topology and can thus cause them to run out of energy very quickly. Moreover, their transmission schemes use two steps: a forward trip for route exploration and a backward trip for pheromone deposition. This increases the overheads and thus, the energy depletion of nodes due to transmission costs.
Based on the above discussions, we propose an improved multi-hop inter-cluster routing protocol enhancing the balance of the energy load between all the network clusters and achieving stability by extending the time before the first sensor node dies. It uses, in addition, intelligent mobile agents to select the next-hop node in the route, taking inspiration from the ant colony algorithm. In contrast to to the previous work, in our solution, agents do one trip only since the pheromone is deposited directly back by the BS.
The MH-GEER protocol
In this section, the detailed steps of the proposed routing protocol MH-GEER are presented.
MH-GEER is an inter-cluster multi-hop dynamic routing protocol, transferring information from one CH to another in order to reach the BS. Its main goal is to ensure the load balancing in the network and to give a long-lasting connectivity for all the clusters no matter how far they are located from the BS.
MH-GEER is built upon three phases: clustering; data collection and aggregation; and distributed routing between CHs. The data collection and aggregation phases within each cluster are similar to LEACH [8] in its steady state phase. It might be possible to use other aggregation techniques [26, 27]; however, since this field is not the primary interest in this study, these are not detailed in this paper.
Network and energy model
In this paper, the considered sensor network is a group of sensors randomly deployed over a large area to regularly monitor the environment. Sensors are grouped into clusters in which each cluster is headed by an elected node responsible for transmitting the cluster’s data to the BS. We denote the \(i_{th}\) CH by \(H_i\) where \(i\in \{1,2, , N-1\}\) and the BS by \(H_N\). Thus, the corresponding set of CHs and BS is denoted by \(H=\{H_1, H_2, ,H_{N-1}, H_N\}\) where \(|H| = N\). Each CH \(H_i\) makes its decision to dynamically select the next hop \(H_j\) for routing (which can be another cluster head or the BS) based on a probabilistic function. The source node chooses in a stochastic way between multi-hop transmission through other CHs and direct transmission to the BS.
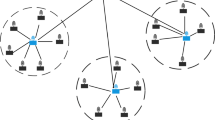
From the perspective of inter-cluster communication, the network consists of CHs and BS and can be modelled as a complete graph \(G=(\,N,E)\,\) where the set of vertices N represents the CHs and the BS and the edges set E represents the wireless links connecting each pair of CHs \((\,H_i , H_j)\,\) or pairs of CH-BS \((\,H_i , H_N)\,\) for \(i , j \in \{1, 2, ,N-1\}\). Figure 1 depicts the graph model used.
For our proposed MH-GEER protocol, we assume that the considered sensor network has the following properties:
-
Sensor nodes are location-aware, i.e. equipped with a global positioning system (GPS) or a similar device.
-
The sensed information within each cluster is highly correlated and the aggregation function opted for by the CHs is the average of received values; thus aggregate packets in all CHs always have the same size.
-
The BS has an unlimited amount of energy.
-
The sensor nodes are static after being deployed in the network.
-
All nodes in the network are homogeneous and energy-restricted.
A simplified dissipation energy model is used, similar to the one proposed in [8]. The energy required to transmit an l-bit message over a distance d is computed using the following equation:
where \(E_{elec}\) is the radio electronics energy, \(\varepsilon _{fs}\) and \(\varepsilon _{mp}\) are the transmitter amplifiers corresponding, respectively, to the free space propagation model (\(d^2\) power loss) and the multi-path fading propagation model (\(d^4\) power loss) depending on the transmission distance d. The \(d_0\) parameter is the threshold distance and can be computed by:
To receive an l-bit message, the energy expended is:
The energy required to transfer data from a CH node \(H_i\) to another \(H_j\), i.e. the transmission cost of the connection \((\,H_i,H_j)\,\), is denoted by \(e_{i,j}\) and given by the following expression:
The residual energy of a node \(H_i\) is denoted by \(e_i\).
Clustering phase
The BS is in charge of the network clustering. This is a centralized process where the BS, at the beginning of the algorithm, divides the network into \((N-1)\) groups and assigns the role of CH to the node with the highest energy level in each cluster. Then, at each round, the role of CH is given to another node within each cluster. In this paper, the clustering is static and settled by a centralized K-means algorithm [28, 29] where formed clusters remain fixed during the whole process. It is worth noting that the percentage of CHs in the network depends on several parameters chosen at the deployment of the network, the most important of which are the network topology and the chosen k value (for the K-means algorithm) that satisfies the properties requested by the application using this WSN.
More specifically, the clustering process is built upon two steps:
-
1.
Centralized clustering Each sensor node sends, initially, its position and energy level to the BS. This latter uses this positions to partition the network into dense clusters using the K-means technique. It also takes advantage of the information about the nodes’ energy to designate all the CHs in the network. Then, the BS directly transmits the clustering results back to each single node. In fact, depending of the nature of nodes, if the node is a member node, the BS directly sends an \(H_k\) parameter corresponding to the identity of the CH in the cluster k to which the node belongs where \(k \in [1,\ldots ,N-1]\); otherwise, if the node is a CH node, the BS directly sends it, along with the \(H_k\) parameter, the set of other CHs, their energy levels and their distances to this CH. The centralized process of network clustering is illustrated in Fig. 2.
The K-means algorithm randomly sets a first partition of K clusters, which are represented by their centroids. Then, it processes the unsupervised algorithm with the objective of minimizing the distance between each data point and its nearest center. This technique provides a very high density in each cluster and guarantees that all member nodes within each cluster are close to each other. This closeness provides reliable information detection in the zone monitored by the cluster even after the death of several nodes in charge of an alternative zone. Moreover, given that an active CH is close to its neighbors, it consumes less energy during inter-cluster communication.
-
2.
Cluster head declaration
At each node, if the \(H_i\) received from the BS corresponds to its own identity, it recognizes itself as the CH, creates a TDMA schedule for data transmission coordination within the cluster and broadcasts it to its member nodes. If this is not the case, then the node recognizes itself as a non-CH, and waits for a delay time D to ensure that all the CHs in the network have received the information about their selection and are prepared to receive joining requests from other nodes in their cluster. Then, this non-CH sends a JOIN message to the CH and waits for the transmission schedule.
After completing the CHs declaration within each cluster, the member nodes transmit sensed data as well as their residual energy level to their CH according to the schedule and then turn OFF their radios to reduce their energy consumption. The role of CH is examined in order to ensure the most lasting node takes the lead for its cluster at the beginning of the next round. In fact, each CH compares the stored energy values of its member nodes with its own and selects the node having the greatest remaining energy as the new CH. If the current CH does not find a node with a greater energy level than itself in the cluster, it remains the CH for the next round. Then, each CH aggregates the data and the new CH identity \(H_k\) of its cluster k in one packet and sends it to the BS through the multi-hop inter-cluster routing backbone.
At the end of the data routing phase, member nodes turn ON their radios and wait to receive the new \(H_k\) identity from their previous CH. Meanwhile, the BS directly transmits to each new CH of the next round the set of other new CHs, their energy levels and their distances to this CH. This means each CH is aware of the other CHs in the network and prepared for the selection process detailed later in the routing phase. Thus, the declaration of CH is a distributed process among member nodes and a centralized process among CH nodes for the rest of the operational network time. Figure 3 shows the flowchart for the CH declaration in the network.
Routing phase
In this section, we describe a new inter-cluster routing protocol between the N members of the vertices set of our graph G, i.e. a route from the set of the CHs to the BS in a single period.
As explained above, at the beginning of each period, each cluster head \(H_k\) of the cluster k is informed by the BS during the clustering phase about other CHs in the network, their locations and their energy levels. When \(H_k\) wants to route its data to the BS, it launches an agent \(A_k\) to carry data and find a path to the BS. We can denote the track of the agent in this path as \(pth_k\) which is built by sequentially adding the index of the CH node chosen by \(A_k\). Thus, the complete path will be \(pth_k^c = \{k,i,j,\ldots ,N\}\) starting from node \(H_k\) and finishing at the BS (i.e. \(H_N\)) where \(i, j \in \{1,\ldots ,N-1\}\setminus k\). \(A_k\) is also equipped with a memory table \(tab_k\) in which it stores the already visited nodes, their energy levels and the link cost.
\(A_k\) makes the choice of the next CH node according to a probabilistic rule \(p^k(i,j)\) ensuring network route exploration and efficient data transmission that balance the load distribution. \(p^k(i,j)\) is calculated as follows:
where \(p^k(i,j)\) is the probability of agent \(A_k\) moving from \(H_i\) to \(H_j\), N is the set of CHs in our network (graph). \(\tau _{i,j}\) represents the pheromone trail value associated with the edge \((H_i,H_j)\) and indicates the track taken. It is used and updated by the algorithm during the routing phase. \(\eta _{i,j}\) represents the visibility of the edge \((H_i,H_j)\). It assigns to each connection in the path a heuristic value called the heuristic information depending on the current routing round. The terms \(\alpha\) and \(\beta\) are constants that determine the relative weight of the pheromone values and the heuristic (visibility) values.
From a general perspective, the pheromone associated with the edge joining CHs \(H_i\) and \(H_j\), \(\tau _{i,j}\) is updated during the lifespan of the network as follows (it will be refined from the perspective of an agent \(A_k\) below in formula 12):
where \(\varDelta \tau ^k_{i,j}\) is the quantity of pheromone laid on edge \((H_i,H_j)\) by all the crossing agents \(A_k\). It is calculated as follows:
where \(E_{avr}\) and \(E_{min}\) are respectively the average and the minimum energy levels of all edges, stored in \(tab_k\), that belong to the complete path \(pth_k^c\) (i.e. the path from \(H_k\) to the BS). m is a small positive constant to avoid depositing a null pheromone amount in the particular case where the path is only one edge to the BS (otherwise the agent will continue choosing that particular path all the time and the algorithm detailed below will be blocked).
In summary, a small quantity of pheromone deposited at \((H_i, H_j)\) indicates that this connection belongs to an energy balanced path \(pth_k^c\) (which will be denoted hereafter as \(EB_k\)) and is initiated by a resourceful sensor node \(H_i\) (whose residual energy is \(e_i\)).
The visibility function is given by:
where \(e_j\) and \(e_{i,j}\) are defined earlier in “Network and energy model” section. We favor, with this formula, transitions toward nodes with high residual energy connected by low transmission cost edges.
In the selection probability \(p^k(i,j)\), we multiply the heuristic value \(\eta _{i,j}\) by the inverse of the corresponding pheromone \(\frac{1}{\eta _{i,j}}\) on the edge \((H_i, H_j)\). In this way, we favor the choice of edges that have a smaller amount of pheromone, i.e. less visited edges where there has been low traffic transfer.
Initially, the pheromone value \(\tau _{i,j}\) is set to a small positive constant \(\tau _{cte}\). The CH \(H_k\) that wants to route its data to the BS creates an agent \(A_k\). This latter, moving from an \(H_i\) to an \(H_j\), stores in its memory table \(tab_k\) the visited vertex node \(H_j\), its residual energy \(e_j\) and the link cost \(e_{i,j}\) between the two vertices. It continues in the same way from one CH to another until it reaches the BS. It transfers to it the carried information containing the sensed data, the complete list of nodes visited (\(tab_k\)) and the decisions of the new CHs in each cluster calculated in the clustering phase. The BS calculates \(EB_k\) using the data extracted from \(tab_k\) carried by agent \(A_k\) as follows:
where,
Next, agent \(A_k\) is destroyed and the BS proceeds with a pheromone update for all CHs by depositing the calculated amount of the pheromone trail at each edge in \(tab_k\) in reverse. In fact, each \(H_i\) in the complete path \(pth_k^c\) receives \(EB_k\) directly from the BS, computes \(\varDelta \tau _{i,j}\) based on its energy level \(e_i\) using formula 7 and then updates its pheromone value by:
Pheromone placed on the edges acts as a distributed long-term memory: this memory is not stored locally within the individual agents, but is distributed on the edges of the graph. This allows an indirect form of communication [30].
The routing table \(Rout_i\) for node \(H_i\) is obtained by integrating actual pheromone trail values \(\tau _{i,j}\) and heuristic values \(\eta _{i,j}.\)
Therefore, the pheromone value of each CH node, when visited by a new agent, is stored and updated by the BS at the end of data transmission. The BS is in charge of this task thanks to its unlimited energy, which reduces the energy consumption of the CH nodes.
The same routing process of the aggregate data to the BS is applied within each cluster by the CH, in each single round. Each source creates an agent traversing a certain path and chooses the edge with higher probability, then sends data to the next-hop, saves it in its list table and continues this way until it reaches the BS.
Each agent created both explores the route and transfers the data stored in its memory. Decisions relating to the next hop and the action of transmitting data are achieved locally and pseudo-simultaneously by the agents at each CH of the vertices set H of our graph. This allows the system to save more energy and promotes the distributed aspect of the routing protocol. The whole routing algorithm protocol is shown in Algorithm 1 where i and j are indexes from \(\{1, 2,\ldots , N\}\) referring to the set of CHs \(\{H_1,H_2,\ldots ,H_{N-1}\}\) and BS(\(H_N\)).

Performance evaluation
In this section, we present a case study illustrating the proposed inter-cluster routing protocol. Considering the clustering phase realized in each round, we evaluate the performance of the routing phase. The MH-GEER algorithm aims to improve the data routing approach applied in the LEACH protocol, which is based on a direct transmission from CHs to BS. This direct transmission technique suffers from a load balancing problem when the network is of a large scale. A distant CH that requires a large amount of energy will die much earlier than other CHs, affecting the network lifetime, energy consumption, coverage of distant areas, stability, and most importantly the load balancing between all clusters. Rather than using a single-hop communication, our protocol introduces a probabilistic multi-hop approach to transmit data to the BS. To evaluate and compare the performance of MH-GEER with the original LEACH, two metrics are used in this use case:
Residual energy of distant CH
The amount of energy remaining in the CH after the data transmission process.
Load balancing measure
We introduce a parameter LB to measure the load balancing in the networking as follows. The lower the maximum difference between two CHs \(H_i\) and \(H_j\) is, the more evenly the energy is distributed among all CHs.
Before describing the scenarios in detail, the specified parameters are summarized in Table 1. The initial energy of each sensor node is 0.1 J. From a communication perspective, a perfect-channel model is considered.
For evaluation purposes, three scenarios are proposed. The first two (S1 and S2) compare the remaining amount of energy of (i) one CH located far from the BS (S1) and (ii) three CHs deployed very far from the BS (S2) after a certain number of rounds. The third scenario (S3) compares the load balancing between the MH-GEER and LEACH routing protocols. For each scenario, the network topology was randomly generated using Python scripts, taking into account the defined constraints. The resulting topology of each scenario is illustrated in Figs. 4, 5 and 7, where the distances separating each pair of nodes are provided (in meters). CH nodes for each scenario and their distances to the BS (in meters) are listed in Table 2.
To simplify the scenario, we assume the CH nodes are fixed during the operational time. Although the routing process from each CH node is created consecutively in each round, we also assume that the CHs execute the routing process simultaneously. Third, intermediate nodes located very close to the BS are introduced in this use case. Their main function is to transfer received data from other CHs directly to the BS. Their energy transmission cost to the BS is insignificant and not of concern here. They symbolize the BS when running the algorithm to simplify calculations. The probabilistic choice of the next-hop CH is achieved each time with the roulette wheel selection function, known as the most frequently used selection strategy in genetic algorithms [31].
Scenario 1 (S1): one CH node is very far from the BS
Figure 4 shows four established CHs including the distant CH (\(H_1\)) along with two intermediate nodes, \(N_1\) and \(N_2.\)
We assume here that only \(H_1\) is transmitting data to the BS in each round. The routing table, \(Rout_1\), for \(H_1\) is presented in Table 3. At the beginning of the first round, after clustering is completed, \(H_1\) creates agent \(A_1\) with its memory \(tab_1\) consisting of the list of identities of visited nodes, their energy levels and the energy cost of each link in the path followed by the agent.
The agent calculates the probability value \(p^1(1,j)\) for each possible path from \(H_1\) to all other CH nodes in the graph. Since \(p^1(1,2)\) has the greatest value of the four possibilities, the agent chooses \(H_2\) to move and transfer data to. The agent updates its memory table with a new entry (\(H_2\)) in the visited nodes list and records the changed residual energy value of the previous CH. \(A_1\) continues travelling towards the BS until it reaches an intermediate node. Its final path is summarized in Table 4.
On reaching the intermediate node \(N_1\), agent \(A_1\) sends the sensed data and the collected information to the BS, which calculates the numerator amount, \(EB_1\) of the pheromone laid by previous agents, having used \(pth_1^c\) based on the collected information. Then the BS transfers it to each \(H_i\) on the way back so that they can calculate the complete amount of pheromone and update their routing tables. We can evaluate the energy efficiency of MH-GEER after manually running eight rounds. We compare the residual energy of \(H_1\) with MH-GEER using the multi-hop backbone and the single-hop backbone with LEACH. Table 5 illustrates the results for the two algorithms.
Scenario 2 (S2): three CH nodes are very far from the BS
Figure 5 shows seven established CHs including the distant ones \((H_1\), \(H_2\) and \(H_3)\) and two intermediate nodes, \(N_1\) and \(N_2\). In this scenario, we evaluate the energetic gain in a network with a larger scale than that in the first scenario.
In this scenario, we assume that only \(H_1\), \(H_2\) and \(H_3\) transmit data to the BS at each round. Figure 6 shows the residual energy of each node after running three rounds, manually, with MH-GEER compared to LEACH.
From Table 5 and Fig. 6, it is clear that the proposed protocol MH-GEER minimizes energy depletion in distant CHs compared to LEACH. A huge amount of energy is required by a single node to transfer data over a long distance to the BS. Use of other CHs as relays to reach the BS in a probabilistic way distributes this energy requirement into smaller energy amounts consumed by each of these relays.
Though the remaining energy in the first scenario was 976.8738 mJ and 968.5896 mJ for LEACH and MH-GEER respectively (i.e. the gain in the proposed approach was about 0.86%), in the second scenario, MH-GEER also achieved better values in comparison to LEACH. Although the residual energy of the first CH remained stable when applying the two algorithms, the second and third CHs showed an approximate gain in saving energy of 2.9% and 0.12%, respectively. Prolonging the lifetime of distant CHs maintains the coverage of distant areas, and also prolongs the whole network lifespan.
Scenario 3 (S3)
Figure 7 shows four established CHs including a distant CH (\(H_1\)) and an intermediate node, \(N_1\).
S3 investigates whether the energy consumption is well balanced among the CHs of the network when they are all functional and transmitting data to the BS. We measure the load balancing parameter, LB, introduced at the beginning of this section. D(x1,x2) is the energy level difference between a pair of nodes (x1,x2) where x1 and x2 can be a CH \(H_i\) or an intermediate node, \(N_1\). Figure 8 shows the energy level difference between each pair of nodes in the network after three rounds with MH-GEER and LEACH protocols. In this evaluation, MH-GEER appeared more stable than the LEACH protocol since the latter showed noticeable variations in the nodes’ energy levels compared to the proposed approach.
We computed the load balancing of the two protocols using formula 9. The results for LB after three rounds are presented in Table 6. To evaluate whether our algorithm increased the load balancing in the network, we took the energy differences between all pairs of CH nodes in the network and calculated the inverse of the maximum among all these differences. The greater the LB parameter, the less the pair’s maximum value of energy difference is, and the lower the energy difference values of the other CH pairs are. It is clear that MH-GEER provides a much greater value of LB than the direct transmission process used in LEACH. This proves that MH-GEER maintains low energy differences between all the CH nodes in the network compared to LEACH. The reason is that MH-GEER chooses to route data from one CH to another based on the information about the receiver node (energy and distance) and the link cost and its experience of routing in the previous rounds in a way that all CHs use their power at an even rate, thus prolonging the lifetime of the network.
We examined the residual energy of the nodes in this scenario, as depicted in Table 7, after data transmission from each CH to the BS. The distant node \(H_1\) profited from this approach and its remaining energy was higher, establishing the efficacy of MH-GEER with distant clusters. In contrast, the other nodes had their residual energies lowered when using MH-GEER.
However, we believe that this is justified because the network used in this scenario had a limited number of CH nodes; it was not a true simulation but a use case where there were fewer interactions between nodes.
Conclusion and future work
Routing protocols in wireless sensor networks have different requirements and challenges according to the network architecture and its field of application.
In this paper, the purpose of the work was to develop a multi-hop hierarchical routing protocol for a randomly large-scale distributed WSN with the fundamental objective of distributing energy consumption between clusters at a balanced rate and thus extending the network’s operational life. To accomplish this goal, we regarded the sensor network as a graph-based intelligent model using mobile agents within each CH. These agents choose the next hop CH in a route leading to the BS, learning from the experience stored as the pheromone variable and adapting the actual decision on the basis of the experience of previous agents. The proposal preceded the routing phase with a clustering phase. After setting up a group of static clusters with the intervention of the BS, the role of the CH was routing inside the cluster in each period in order to enable more effective exploitation of the sensors’ energy.
The use case section showed that MH-GEER improved the load balancing and the stability of the network in comparison with the LEACH protocol. It also maintained the coverage area of distant nodes for longer periods.
In future work, we intend to complete this proposition by implementing the proposed protocol to evaluate its performance in large-scale networks. Moreover, since it is well-known that, as in ad-hoc networks [32], routing protocols in WSNs can be affected by various malicious attacks such as black hole attacks or even selfish behaviours, we will study the effectiveness of such attacks against our protocol to decide whether we will have to include in our design some mechanisms [33] to secure data transmission from member nodes to CHs and then to the BS.
References
Lee I, Lee K (2015) The internet of things (IoT): applications, investments, and challenges for enterprises. Bus Horizons 58(4):431–440
Qiu T, Han M, Li M, Zhang Y (2017) SRTS : a self-recoverable time synchronization for sensor networks of healthcare IoT. Comput Netw 129:481–492
Lazarescu MT (2013) Design of a WSN platform for long-term environmental monitoring for IoT applications. IEEE J Emerg Select Topics Circuit Syst 3(1):45–54
Ghayvat H, Mukhopadhyay S, Gui X, Suryadevara N, Ghayvat H, Mukhopadhyay S, Gui X, Suryadevara N (2015) WSN- and IOT-based smart homes and their extension to smart buildings. Sensors 15(5):10350–10379
Bhende M, Wagh SJ, Utpat A (2014) A quick survey on wireless sensor networks. In: 2014 fourth international conference on communication systems and network technologies. pp 160–167
Sabri A, Al-Shqeerat K (2014) Hierarchical cluster-based routing protocols for wireless sensor networks a survey. Int J Comput Science 11(1):13
Misra S, Kumar R (2016) A literature survey on various clustering approaches in wireless sensor network. In: 2016 2nd international conference on communication control and intelligent systems (CCIS). pp 18–22
Heinzelman WR, Chandrakasan A, Balakrishnan H (2000) Energy-efficient communication protocol for wireless microsensor networks, vol 2. In: Proceedings of the 33rd annual Hawaii international conference on system sciences. p 10
Dorigo M, Bonabeau E, Theraulaz G (1999) Swarm intelligence: from natural to artificial systems. Oxford University Press, Oxford
Saleem M, Di Caro GA, Farooq M (2011) Swarm intelligence based routing protocol for wireless sensor networks: survey and future directions. Inf Sci 181(20):4597–4624
Taj MBM, Kbir MA (2016) ICH-LEACH: an enhanced LEACH protocol for wireless sensor network. In: 2016 international conference on advanced communication systems and information security (ACOSIS). pp 1–5
GhasemAghaei R, Rahman ASM, Rahman MA, Gueaieb W, El Saddik A (2008) Ant colony-based many-to-one sensory data routing in wireless sensor networks. In: IEEE/ACS international conference on computer systems and applications. AICCSA. pp 1005–1010
Zhang J, Chen J, Xu Z, Liu Y (2016) LEACH-WM: weighted and intra-cluster multi-hop energy-efficient algorithm for wireless sensor networks. In: 2016 35th Chinese control conference (CCC), pp 8325–8329
Alnawafa E, Marghescu I (2016) MHT: multi-hop technique for the improvement of leach protocol. In: 2016 15th RoEduNet cnference: networking in education and research. pp 1–5
Alnawafa E, Marghescu I (2017) Imht: improved mht-leach protocol for wireless sensor networks. In: 2017 8th international conference on information and communication systems (ICICS). pp 246–251
Biradar RV, Sawant SR, Mudholkar RR, Patil VC (2011) Multihop routing in self-organizing wireless sensor networks. Int J Comput Sci 8(1):10
Neto J, Henrique B, Rego A, Cardoso A, Celestino J (2014) Mh-leach: a distributed algorithm for multi-hop communication in wireless sensor networks. ICN, Chennai, pp 55–61
Xingguo L, Junfeng W, Linlin B (2016) LEACH protocol and its improved algorithm in wireless sensor network. In: 2016 international conference on cyber-enabled distributed computing and knowledge discovery (CyberC), pp 418–422
Razaque A, Abdulgader M, Joshi C, Amsaad F, Chauhan M (2016) P-leach: energy efficient routing protocol for wireless sensor networks. In: 2016 IEEE long island systems, applications and technology conference (LISAT), pp 1–5
Liu X, Liu X (2012) A survey on clustering routing protocols in wireless sensor networks. Sensors 12(8):11113–11153
Liu X (2017) Routing protocols based on ant colony optimization in wireless sensor networks: a survey. IEEE Access 5:26303–26317
Moon Y, Yu H, Gil JM, Lim J (2017) A slave ants based ant colony optimization algorithm for task scheduling in cloud computing environments. Hum Centric Comput Inf Sci 7:1
Chandra Mohan B, Baskaran R (2012) A survey: ant colony optimization based recent research and implementation on several engineering domain. Expert Syst Appl 39(4):4618–4627
Cheng D, Xun Y, Zhou T, Li W (2011) An energy aware ant colony algorithm for the routing of wireless sensor networks. In: Chen R (ed) Intelligent computing and information science, communications in computer and information science. Springer, Berlin, pp 395–401
Mohajerani A, Gharavian D (2016) An ant colony optimization based routing algorithm for extending network lifetime in wireless sensor networks. Wireless Netw 22(8):2637–2647
Dhand G, Tyagi SS (2016) Data aggregation techniques in WSN: survey. Procedia Comput Sci 92:378–384
Kim JJ (2018) Routing techniques for data aggregation in sensor networks. J Inf Process Syst 14:2
MacQueen J et al (1967) Some methods for classification and analysis of multivariate observations. In: Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, vol 1, Oakland, pp 281–297
Sasikumar P, Khara S (2012) K-means clustering in wireless sensor networks. In: 2012 Fourth international conference on computational intelligence and communication networks, pp 140–144
Dorigo M, Di Caro G, Gambardella LM (1999) Ant algorithms for discrete optimization. Artif Life 5(2):137–172
Mukhopadhyay DM, Balitanas MO, Jeon SH, Bhattacharyya D (2009) Genetic algorithm: a tutorial review. Int J Grid Distri Comput 2:8
Tseng FH, Chiang HP, Chao HC (2018) Black hole along with other attacks in MANETs: a survey. J Inf Process Syst 14(1):1
Md Zin S, Anuar NB, Mat Kiah L, Khan Pathan A-S (2014) Routing protocol design for secure WSN: review and open research issues. J Netw Comput Appl 41:517–530
Authors’ contributions
HR is the main contributor of this article. KT has suggested to use bio-inspired artificial intelligence methods for this kind of networks. RA has given advices to structure the proposal. DS has achieved lot of revisions related to scientific content and its organization to finalize the manuscript. SG has assessed quality of the article. All authors read and approved the final manuscript.
Acknowledgements
This work is supported by the ex-Rǵion Limousin, under grant for project “IoTSec”, by the MIRES research federation under grants for projects “UNITED2”, “SCOPE” and “SPOCK” and by the Région Nouvelle-Aquitaine under the Grant for project “SVP-IoT”.
Competing interests
The authors declare that they have no competing interests.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rhim, H., Tamine, K., Abassi, R. et al. A multi-hop graph-based approach for an energy-efficient routing protocol in wireless sensor networks. Hum. Cent. Comput. Inf. Sci. 8, 30 (2018). https://doi.org/10.1186/s13673-018-0153-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13673-018-0153-6