On solving the split generalized equilibrium problem and the fixed point problem for a countable family of nonexpansive multivalued mappings

Abstract

We consider the split generalized equilibrium problem and the fixed point problem for a countable family of nonexpansive multivalued mappings in real Hilbert spaces. Then, using the shrinking projection method, we prove a strong convergence theorem for finding a common solution of the considered problems. A numerical example is presented to illustrate the convergence result. Our results improve and extend the corresponding results in the literature.

1 Introduction

Let H be a real Hilbert space with inner product $\langle\cdot,\cdot\rangle$ and induced norm $\|\cdot\|$. Let C be a nonempty closed convex subset of H, $\varphi:C\times C\rightarrow\mathbb{R}$, and let $F: C\times C\rightarrow\mathbb{R}$ be two bifunctions. The generalized equilibrium problem is to find $x\in C$ such that

$$ F(x,y)+\varphi(x,y)\geq0, \quad \forall y \in C. $$

(1.1)

The solution set of generalized equilibrium problem is denoted by $\operatorname{GEP}(F,\varphi)$. In particular, if $\varphi=0$, then this problem reduces to the equilibrium problem to find $x\in C$ such that $F(x,y)\geq0$ for all $y \in C$. The solution set of the equilibrium problem is denoted by $\operatorname{EP}(F)$.

The generalized equilibrium problem is very general in the sense that it includes, as particular cases, optimization problems, variational inequality problems, minimization problems, fixed point problems, mixed equilibrium problem, Nash equilibrium problems in noncooperative games, and others; see, for example, [1–6].

In 2013, Kazmi and Rizvi [7] introduced and studied the following split generalized equilibrium problem. Let $C\subseteq H_{1}$ and $Q\subseteq H_{2}$, let $F_{1},\varphi_{1}:C\times C\rightarrow \mathbb{R}$ and $F_{2},\varphi_{2}:Q\times Q\rightarrow\mathbb{R}$ be nonlinear bifunctions, and let $A:H_{1}\rightarrow H_{2}$ be a bounded linear operator. The split generalized equilibrium problem is to find $x^{*}\in C$ such that

$$ F_{1}\bigl(x^{*},x\bigr)+\varphi_{1}\bigl(x^{*},x \bigr)\geq0,\quad \forall x\in C, $$

(1.2)

and such that

$$ y^{*}=Ax^{*}\in Q \quad \text{solves}\quad F_{2}\bigl(y^{*},y\bigr)+ \varphi_{2}\bigl(y^{*},y\bigr)\geq 0, \quad \forall y\in Q. $$

(1.3)

The solution set of the split generalized equilibrium problem is denoted by

$$\operatorname{SGEP}(F_{1},\varphi_{1},F_{2}, \varphi_{2}):=\bigl\{ x^{*}\in C: x^{*}\in \operatorname{GEP}(F_{1}, \varphi _{1}) \text{ and } Ax^{*}\in \operatorname{GEP}(F_{2}, \varphi_{2})\bigr\} . $$

The authors also gave an iterative algorithm to find a common element of the solution sets of the split generalized equilibrium problem in real Hilbert spaces; for more details, we refer to [7–9]. If $\varphi_{1}=0$ and $\varphi_{2}=0$, then the split generalized equilibrium problem reduces to the split equilibrium problem; see [10]. If $F_{2}=0$ and $\varphi_{2}=0$, the split generalized equilibrium problem reduces to the equilibrium problem considered by Cianciaruso et al. [11].

In 2008, Takahashi et al. [12] introduced the following iterative algorithm, which is known as the shrinking projection method, for finding a fixed point of a nonexpansive single-valued mapping in Hilbert spaces. The shrinking projection method is a popular method and plays an important role in studying the strong convergence for finding fixed points of nonlinear mappings. Many researchers developed the shrinking projection method for solving variational inequality problems, equilibrium problems, and fixed point problems in Hilbert spaces; see, for example, [13, 14].

Motivated and inspired by the results mentioned and related literature, we propose an iterative algorithm based on the shrinking projection method for finding a common element of the set of solutions of split generalized equilibrium problems and the set of common fixed points of a countable family of nonexpansive multivalued mappings in real Hilbert spaces. Then we prove strong convergence theorems that extend and improve the corresponding results of Kazmi and Rizvi [7], Suantai et al. [15], and others. Finally, we give some examples and numerical results to illustrate our main results.

2 Preliminaries

Let C be a nonempty closed convex subset of a real Hilbert space H. We denote the strong convergence and the weak convergence of a sequence $\{x_{n}\}$ to a point $x\in H$ by $x_{n}\to x$ and $x_{n}\rightharpoonup x$, respectively. It is also well known [16] that a Hilbert space H satisfies Opial’s condition, that is, for any sequence $\{x_{n}\}$ with $x_{n}\rightharpoonup x$, the inequality

$$\limsup_{n\to\infty}\|x_{n}-x\| < \limsup _{n\to\infty}\|x_{n}-y\| $$

holds for every $y\in H$ with $y\ne x$.

The following three lemmas are useful for our main results.

Lemma 2.1

In a real Hilbert space H, the following inequalities hold:

• (1) $\|x-y\|^{2} \leq\|x\|^{2}-\|y\|^{2} - 2\langle x-y,y\rangle$, $\forall x,y\in H$;

• (2) $\|x+y\|^{2} \leq\|x\|^{2} + 2\langle y, x + y\rangle$, $\forall x,y\in H$;

• (3) If $\{x_{n}\}$ is a sequence in H that converges weakly to $z\in H$, then

  $$\limsup_{n\rightarrow\infty}\|x_{n}-y\|^{2}= \limsup _{n\rightarrow\infty }\|x_{n}-z\|^{2}+\|z-y\|^{2}, \quad \forall y\in H. $$

Lemma 2.2

([17])

Let H be a Hilbert space. Let $x_{1},x_{2},\ldots,x_{N}\in H$, and let $\alpha_{1}$, $\alpha_{2},\ldots,\alpha_{N}$ be real numbers such that $\sum_{i=1}^{N}\alpha_{i}=1$. Then

$$\Biggl\Vert \sum_{i=1}^{N} \alpha_{i}x_{i} \Biggr\Vert ^{2} = \sum _{i=1}^{N}\alpha_{i} \Vert x_{i} \Vert ^{2} - \sum_{1\leq i,j\leq N} \alpha_{i}\alpha_{j} \Vert x_{i}-x_{j} \Vert ^{2}. $$

Lemma 2.3

([18])

Let H be a Hilbert space, and let $\{x_{n}\}$ be a sequence in H. Let $u,v\in H$ be such that $\lim_{n\rightarrow\infty}\|x_{n}-u\|$ and $\lim_{n\rightarrow\infty}\|x_{n}-v\|$ exist. If $\{x_{n_{k}}\}$ and $\{x_{m_{k}}\}$ are subsequences of $\{x_{n}\}$ that converge weakly to u and v, respectively, then $u=v$.

A single-valued mapping $T : C\to H$ is called δ-inverse strongly monotone [19] if there exists a positive real number δ such that

$$ \langle x-y,Tx-Ty\rangle\geq\delta\|Tx-Ty\|^{2},\quad \forall x,y\in C. $$

For each $\gamma\in(0,2\delta]$, we see that $I-\gamma T$ is a nonexpansive single-valued mapping, that is,

$$\bigl\Vert (I-\gamma T)x-(I-\gamma T)y \bigr\Vert \leq \Vert x-y \Vert , \quad \forall x,y\in C. $$

We denote by $\mathit{CB}(C)$ and $K(C)$ the collections of all nonempty closed bounded subsets and nonempty compact subsets of C, respectively. The Hausdorff metric $\mathcal{H}$ on $\mathit{CB}(C)$ is defined by

$$ \mathcal{H}(A,B):=\max \Bigl\{ \sup_{x\in A} \operatorname{dist} (x,B),\sup_{y\in B} \operatorname{dist} (y,A) \Bigr\} , \quad \forall A,B \in \mathit{CB}(C), $$

where $\operatorname{dist}(x,B)=\inf\{d(x,y):y\in B\}$ is the distance from a point x to a subset B. Let $S:C\rightarrow \mathit{CB}(C)$ be a multivalued mapping. An element $x\in C$ is called a fixed point of S if $x\in Sx$. The set of all fixed points of S is denoted by $F(S)$, that is, $F(S)=\{x\in C:x\in Sx\}$. Recall that a multivalued mapping $S:C\rightarrow \mathit{CB}(C)$ is called

• (i) nonexpansive if

  $$ \mathcal{H}(Sx,Sy)\leq\|x-y\|,\quad \forall x,y\in C; $$

• (ii) quasi-nonexpansive if $F(S)\neq\emptyset$ and

  $$ \mathcal{H}(Sx,Sp)\leq\|x-p\|,\quad \forall x\in C, \forall p \in F(S). $$

If S is a nonexpansive single-valued mapping on a closed convex subset of a Hilbert space, then $F(S)$ is closed and convex. The closedness of $F(S)$ can be easily extended to the multivalued case. However, the convexity of $F(S)$ cannot be extended (see, e.g., [20]). However, if S is a nonexpansive multivalued mapping and $Sp=\{p\}$ for each $p\in F(S)$, then $F(S)$ is always closed and convex as the following result shows.

Lemma 2.4

([21])

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $S : C\to \mathit{CB}(C)$ be a nonexpansive multivalued mapping with $F(S)\ne\emptyset$ and $Sp=\{p\}$ for each $p\in F(S)$. Then $F(S)$ is a closed and convex subset of C.

Lemma 2.5

([22])

Let C be a nonempty closed convex subset of a real Hilbert space H. Given $x,y,z\in H$ and a real number α, the set $\{u\in C:\|y-u\|^{2}\leq\|x-u\|^{2}+\langle z,u\rangle+\alpha\}$ is closed and convex.

Lemma 2.6

([23, 24])

Let C be a nonempty closed convex subset of a real Hilbert space H, and let $P_{C}:H\to C$ be the metric projection. Then

$$\|y-P_{C}x\|^{2}+\|x-P_{C}x\|^{2}\leq \|x-y\|^{2},\quad \forall x\in H, y\in C. $$

For solving the generalized equilibrium problem, we assume that the bifunctions $F_{1}:C\times C \rightarrow\mathbb{R}$ and $\varphi_{1}:C\times C \rightarrow\mathbb{R}$ satisfy the following assumption.

Assumption 2.7

Let C be nonempty closed and convex subset of a Hilbert space $H_{1}$. Let $F_{1}:C\times C \rightarrow\mathbb{R}$ and $\varphi_{1}:C\times C \rightarrow\mathbb{R}$ be two bifunctions satisfy the following conditions:

• (A1) $F_{1}(x,x)=0$ for all $x\in C$,

• (A2) $F_{1}$ is monotone, that is, $F_{1}(x,y)+F_{1}(y,x)\leq0$ for all $x,y \in C$,

• (A3) $F_{1}$ is upper hemicontinuous, that is, for all $x,y,z \in C$, $\lim_{t\downarrow0}F_{1}(tz+(1-t)x,y)\leq F_{1}(x,y)$,

• (A4) for each $x\in C$, $y\mapsto F_{1}(x,y)$ is convex and lower semicontinuous,

• (A5) $\varphi_{1}(x,x)\geq0$ for all $x\in C$,

• (A6) for each $y\in C$, $x\mapsto\varphi_{1}(x,y)$ is upper semicontinuous,

• (A7) for each $x\in C$, $y\mapsto\varphi_{1}(x,y)$ is convex and lower semicontinuous,

and assume that for fixed $r>0$ and $z\in C$, there exists a nonempty compact convex subset K of $H_{1}$ and $x\in C\cap K$ such that

$$F_{1}(y,x)+\varphi_{1}(y,x)+\frac{1}{r}\langle y-x,x-z\rangle< 0,\quad \forall y\in C\setminus K. $$

Lemma 2.8

([25])

Let C be nonempty closed and convex subset of a Hilbert space $H_{1}$. Let $F_{1}:C\times C\rightarrow \mathbb{R}$ and $\varphi_{1}:C\times C \rightarrow\mathbb{R}$ be two bifunctions satisfy Assumption 2.7. Assume that $\varphi_{1}$ is monotone. For $r>0$ and $x \in H_{1}$, define a mapping $T^{(F_{1},\varphi_{1})}_{r}:H_{1}\rightarrow C$ as follows:

$$T^{(F_{1},\varphi_{1})}_{r}(x)= \biggl\{ z\in C: F_{1}(z,y)+ \varphi_{1}(z,y)+\frac {1}{r}\langle y-z,z-x\rangle\geq0, \forall y\in C \biggr\} $$

for all $x\in H_{1}$. Then:

• (1) For each $x\in H_{1}$, $T^{(F_{1},\varphi_{1})}_{r}\neq \emptyset$,

• (2) $T^{(F_{1},\varphi_{1})}_{r}$ is single-valued,

• (3) $T^{(F_{1},\varphi_{1})}_{r}$ is firmly nonexpansive, that is, for any $x,y\in H_{1}$,

  $$\bigl\Vert T^{(F_{1},\varphi_{1})}_{r}x-T^{(F_{1},\varphi_{1})}_{r}y \bigr\Vert ^{2}\leq \bigl\langle T^{(F_{1},\varphi_{1})}_{r}x-T^{(F_{1},\varphi_{1})}_{r}y,x-y \bigr\rangle , $$

• (4) $F (T^{(F_{1},\varphi_{1})}_{r} )=\operatorname{GEP}(F_{1},\varphi_{1})$,

• (5) $\operatorname{GEP}(F_{1},\varphi_{1})$ is compact and convex.

Further, assume that $F_{2}:Q\times Q\rightarrow\mathbb{R}$ and $\varphi_{2}:Q\times Q\rightarrow\mathbb{R}$ satisfy Assumption 2.7, where Q is a nonempty closed and convex subset of a Hilbert space $H_{2}$. For all $s>0$ and $w\in H_{2}$, define the mapping $T^{(F_{2},\varphi_{2})}_{s}:H_{2}\rightarrow Q$ by

$$T^{(F_{2},\varphi_{2})}_{s}(v)= \biggl\{ w\in Q: F_{2}(w,d)+ \varphi_{2}(w,d)+\frac {1}{r}\langle d-w,w-v\rangle\geq0, \forall d \in Q \biggr\} . $$

Then we have:

• (6) For each $v\in H_{2}$, $T^{(F_{2},\varphi_{2})}_{s}\neq \emptyset$,

• (7) $T^{(F_{2},\varphi_{2})}_{s}$ is single-valued,

• (8) $T^{(F_{2},\varphi_{2})}_{s}$ is firmly nonexpansive,

• (9) $F (T^{(F_{2},\varphi_{2})}_{s} )=\operatorname{GEP}(F_{2},\varphi_{2})$,

• (10) $\operatorname{GEP}(F_{2},\varphi_{2})$ is closed and convex,

where $\operatorname{GEP}(F_{2},\varphi_{2})$ is the solution set of the following generalized equilibrium problem:

• Find $y^{*}\in Q$ such that $F_{2}(y^{*},y)+\varphi_{2}(y^{*},y)\geq0$ for all $y\in Q$.

Moreover, $\operatorname{SGEP}(F_{1},\varphi_{1},F_{2},\varphi_{2})$ is a closed and convex set.

Lemma 2.9

([11])

Let C be nonempty closed and convex subset of a Hilbert space $H_{1}$. Let $F_{1}:C\times C\rightarrow \mathbb{R}$ and $\varphi_{1}:C\times C \rightarrow\mathbb{R}$ be two bifunctions satisfying Assumption 2.7, and let $T^{(F_{1},\varphi_{1})}_{r}$ be defined as in Lemma 2.8 for $r>0$. Let $x,y\in H_{1}$ and $r_{1},r_{2}>0$. Then

$$\bigl\Vert T^{(F_{1},\varphi_{1})}_{r_{2}} y - T^{(F_{1},\varphi_{1})}_{r_{1}}x \bigr\Vert \leq\|y-x\| + \biggl\vert \frac{r_{2}-r_{1}}{r_{2}} \biggr\vert \bigl\Vert T^{(F_{1},\varphi_{1})}_{r_{2}}y -y \bigr\Vert . $$

3 Main results

In this section, we prove strong convergence theorems for finding a common element of the set of solutions of split generalized equilibrium problems and the set of common fixed points of a countable family of nonexpansive multivalued mappings in real Hilbert spaces and give a numerical example to support our main result.

We now state and prove our main result.

Theorem 3.1

Let C be a nonempty closed convex subset of a real Hilbert space $H_{1}$, and let Q be a nonempty closed convex subset of a real Hilbert space $H_{2}$. Let $A: H_{1}\rightarrow H_{2}$ be a bounded linear operator, and let $\{S_{i}\}$ be a countable family of nonexpansive multivalued mappings of C into $\mathit{CB}(C)$. Let $F_{1}, \varphi_{1}:C\times C\rightarrow\mathbb{R}$, $F_{2},\varphi_{2}:Q\times Q\rightarrow\mathbb{R}$ be bifunctions satisfying Assumption 2.7. Let $\varphi_{1}$, $\varphi_{2}$ be monotone, $\varphi_{1}$ be upper hemicontinuous, and $F_{2}$ and $\varphi_{2}$ be upper semicontinuous in the first argument. Assume that $\Gamma =\bigcap_{i=1}^{\infty}F(S_{i})\cap \operatorname{SGEP}(F_{1},\varphi_{1},F_{2},\varphi_{2}) \neq\emptyset$ and $S_{i}p=\{p\}$ for each $p\in\bigcap_{i=1}^{\infty}F(S_{i})$. Let $x_{1}\in C$ with $C_{1} =C$, and let $\{x_{n}\}$ be a sequence generated by

$$ \textstyle\begin{cases} u_{n}=T^{(F_{1},\varphi_{1})}_{r_{n}} (I-\gamma A^{*} (I-T^{(F_{2},\varphi _{2})}_{r_{n}} )A )x_{n}, \\ z_{n}= \alpha_{n}^{(0)} x_{n}+ \alpha_{n}^{(1)}y_{n}^{(1)} + \cdots +\alpha_{n}^{(n)}y_{n}^{(n)} ,\quad y_{n}^{(i)} \in S_{i}u_{n}, \\ C_{n+1} =\{p\in C_{n} : \|z_{n}-p\|\leq\|x_{n}-p\|\}, \\ x_{n+1} =P_{C_{n+1}} x_{1},\quad n\in\mathbb{N}, \end{cases} $$

(3.1)

where $\{\alpha_{n}^{(i)}\}\subset(0,1)$ satisfy $\sum_{i=0}^{n}\alpha_{n}^{(i)}=1$, $\{r_{n}\}\subset(0,\infty)$, and $\gamma\in(0,\frac{1}{L})$, where L is the spectral radius of $A^{*}A$, and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (C1) The limits $\lim_{n\to\infty}\alpha_{n}^{(i)}\in(0,1)$ exist for all $i\geq 0$,

• (C2) $\liminf_{n\rightarrow\infty} r_{n}>0$.

Then the sequence $\{x_{n}\}$ generated by (3.1) converges strongly to $P_{\Gamma}x_{1}$.

Proof

We divide our proof into six steps.

Step 1. We show that $\{x_{n}\}$ is well-defined for every $n\in\mathbb{N}$.

By Lemmas 2.4 and 2.8 we obtain that $\operatorname{SGEP}(F_{1},\varphi_{1},F_{2},\varphi_{2})$ and $\bigcap_{i=1}^{\infty}F(S_{i})$ are closed and convex subsets of C. Hence Γ is a closed and convex subset of C. It follows by Lemma 2.5 that $C_{n+1}$ is closed and convex for each $n\in\mathbb{N}$.

Let $p\in\Gamma$. Then we have $p=T^{(F_{1},\varphi_{1})}_{r_{n}}p$ and $Ap=T^{(F_{2},\varphi_{2})}_{r_{n}}(Ap)$. It follows that $p=(I-\gamma A^{*}(I-T^{(F_{2},\varphi_{2})}_{r_{n}})A)p$. Since $T^{(F_{1},\varphi_{1})}_{r_{n}}$ and $T^{(F_{2},\varphi_{2})}_{r_{n}}$ both are firmly nonexpansive, for $\gamma\in(0,\frac{1}{L})$, the mapping $T^{(F_{1},\varphi_{1})}_{r_{n}}(I-\gamma A^{*}(I-T^{(F_{2},\varphi_{2})}_{r_{n}})A)$ is nonexpansive; see [26]. This implies that

$$\begin{aligned} \Vert u_{n}-p \Vert &= \bigl\Vert T^{(F_{1},\varphi_{1})}_{r_{n}} \bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)A \bigr)x_{n}-T^{(F_{1},\varphi _{1})}_{r_{n}} \bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)A \bigr)p \bigr\Vert \\ &\leq \Vert x_{n}-p \Vert . \end{aligned}$$

(3.2)

Then, since $S_{i}p=\{p\}$ for all $p\in\bigcap_{i=1}^{\infty}F(S_{i})$, we have

$$\begin{aligned} \Vert z_{n}-p \Vert &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \alpha_{n}^{(1)} \bigl\Vert y_{n}^{(1)}-p \bigr\Vert + \cdots + \alpha_{n}^{(n)} \bigl\Vert y_{n}^{(n)}-p \bigr\Vert \\ &=\alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \alpha_{n}^{(1)}\operatorname{dist}\bigl(y_{n}^{(1)},S_{1}p \bigr) + \cdots +\alpha_{n}^{(n)}\operatorname{dist} \bigl(y_{n}^{(n)},S_{n}p\bigr) \\ &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \alpha_{n}^{(1)}\mathcal{H}(S_{1}u_{n},S_{1}p) + \cdots +\alpha_{n}^{(n)}\mathcal{H}(S_{n}u_{n},S_{n}p) \\ &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \alpha_{n}^{(1)} \Vert u_{n}-p \Vert + \cdots + \alpha_{n}^{(n)} \Vert u_{n}-p \Vert . \end{aligned}$$

(3.3)

This implies by (3.2) and $\sum_{i=0}^{n}\alpha_{n}^{(i)}=1$ that

$$ \|z_{n}-p\|\leq\|x_{n}-p\|. $$

(3.4)

This shows that $p\in C_{n+1}$ and hence $\Gamma\subset C_{n+1}\subset C_{n}$. Therefore, $P_{C_{n+1}}x_{1}$ is well-defined for every $x_{1}\in C$. Hence, $\{x_{n}\}$ is well-defined.

Step 2. We show that $\lim_{n\to\infty}x_{n}=q$ for some $q\in C$.

Since Γ is a nonempty closed convex subset of $H_{1}$, there exists a unique $\omega\in\Gamma$ such that $\omega=P_{\Gamma}x_{1}$. Since $x_{n}=P_{C_{n}}x_{1}$ and $x_{n+1}\in C_{n+1}\subset C_{n}$ for all $n\in\mathbb{N}$, we have $\|x_{n}-x_{1}\|\leq\|x_{n+1}-x_{1}\|$ for all $n\in\mathbb{N}$. On the other hand, since $\Gamma\subset C_{n}$, we obtain that $\|x_{n}-x_{1}\|\leq\|\omega-x_{1}\|$ for all $n\in \mathbb{N}$. Hence $\{\|x_{n}-x_{1}\|\}$ is bounded; so are $\{z_{n}\}$ and $\{y_{n}^{(i)}\}$. Therefore, $\lim_{n\rightarrow \infty}\|x_{n}-x_{1}\|$ exists. By the construction of the set $C_{n}$ we know that $x_{m}=P_{C_{m}} x_{1}\in C_{m} \subset C_{n}$ for $m>n \geq1$. This implies by Lemma 2.6 that

$$ \|x_{m}-x_{n}\|^{2}\leq \|x_{m}-x_{1}\|^{2}-\|x_{n}-x_{1} \|^{2}\to0\quad \mbox{as } m,n\to\infty. $$

(3.5)

Since $\lim_{n\rightarrow\infty}\|x_{n}-x_{1}\|$ exists, it follows that $\{x_{n}\}$ is a Cauchy sequence. By the completeness of $H_{1}$ and the closedness of C we get that there exists an element $q\in C$ such that $\lim_{n\rightarrow\infty} x_{n}=q$.

Step 3. We show that $\lim_{n\rightarrow \infty}\|y_{n}^{(i)}-x_{n}\|=0$ for all $i\in\mathbb{N}$.

From (3.5) we have

$$ \lim_{n\rightarrow\infty}\|x_{n+1}-x_{n} \|=0. $$

(3.6)

Since $x_{n+1}\in C_{n+1}$, we get that

$$ \Vert z_{n}-x_{n} \Vert \leq \Vert z_{n}-x_{n+1} \Vert + \Vert x_{n+1}-x_{n} \Vert \leq \Vert x_{n}-x_{n+1} \Vert + \Vert x_{n+1}-x_{n} \Vert \leq 2 \Vert x_{n+1}-x_{n} \Vert . $$

This implies by (3.6) that

$$ \lim_{n\rightarrow\infty}\|z_{n}-x_{n}\|=0. $$

(3.7)

Thus $\lim_{n\rightarrow\infty}z_{n}=q$.

For $p\in\Gamma$, by Lemma 2.2 we see that

$$\begin{aligned} \Vert z_{n}-p \Vert ^{2} &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2}+ \sum _{i=1}^{n}\alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-p \bigr\Vert ^{2} - \sum _{i=1}^{n}\alpha _{n}^{(0)} \alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2} \\ &=\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2} +\sum_{i=1}^{n} \alpha_{n}^{(i)}\operatorname {dist}\bigl(y_{n}^{(i)},S_{1}p \bigr)^{2} - \sum_{i=1}^{n} \alpha_{n}^{(0)}\alpha _{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2} \\ &=\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2} +\sum_{i=1}^{n} \alpha_{n}^{(i)}\mathcal {H}(S_{i}u_{n},S_{i}p)^{2} - \sum_{i=1}^{n}\alpha_{n}^{(0)} \alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2} \\ &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2} +\sum_{i=1}^{n} \alpha_{n}^{(i)} \Vert u_{n}-p \Vert ^{2} - \sum_{i=1}^{n} \alpha_{n}^{(0)}\alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2}. \end{aligned}$$

(3.8)

This implies by (3.2) and $\sum_{i=0}^{n}\alpha_{n}^{(i)}=1$ that

$$ \Vert z_{n}-p \Vert ^{2} \leq \Vert x_{n}-p \Vert ^{2}- \sum_{i=1}^{n} \alpha_{n}^{(0)}\alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2}. $$

Therefore we have

$$\begin{aligned} \alpha_{n}^{(0)}\alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2} &\leq \sum_{i=1}^{n}\alpha_{n}^{(0)} \alpha_{n}^{(i)} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert ^{2} \\ &\leq \Vert x_{n}-p \Vert ^{2}- \Vert z_{n}-p \Vert ^{2} \\ &\leq \Vert x_{n}-z_{n} \Vert \bigl( \Vert x_{n}-p \Vert + \Vert z_{n}-p \Vert \bigr). \end{aligned}$$

By the given control condition on $\{\alpha_{n}^{(i)}\}$ and (3.7) we obtain

$$ \lim_{n\rightarrow\infty} \bigl\Vert y_{n}^{(i)}-x_{n} \bigr\Vert =0, \quad \forall i\in \mathbb{N}. $$

(3.9)

Step 4. We show that $\lim_{n\rightarrow \infty}\|u_{n}-x_{n}\|=0$. For $p\in\Gamma$, we get that

$$\begin{aligned} \Vert u_{n}-p \Vert ^{2} =& \bigl\Vert T^{(F_{1},\varphi_{1})}_{r_{n}} \bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)A \bigr)x_{n}-T^{(F_{1},\varphi _{1})}_{r_{n}}p \bigr\Vert ^{2} \\ \leq& \bigl\Vert \bigl(I-\gamma A^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)A\bigr)x_{n}-p \bigr\Vert ^{2} \\ \leq& \Vert x_{n}-p \Vert ^{2}+\gamma^{2} \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert ^{2}+2\gamma\bigl\langle p-x_{n}, A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n}\bigr\rangle \\ \leq& \Vert x_{n}-p \Vert ^{2}+\gamma^{2} \bigl\langle Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}, AA^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\rangle \\ &{} + 2\gamma\bigl\langle A(p-x_{n}), Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\rangle \\ \leq& \Vert x_{n}-p \Vert ^{2}+L\gamma^{2} \bigl\langle Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}, Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr\rangle \\ &{} + 2\gamma\bigl\langle A(p-x_{n})+\bigl(Ax_{n}-T^{(F_{2},\varphi _{2})}_{r_{n}}Ax_{n} \bigr)-\bigl(Ax_{n}-T^{F_{2}}_{r_{n}}Ax_{n} \bigr), \\ &Ax_{n}-T^{(F_{2},\varphi _{2})}_{r_{n}}Ax_{n}\bigr\rangle \\ \leq& \Vert x_{n}-p \Vert ^{2}+L\gamma^{2} \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \\ &{} + 2\gamma \bigl(\bigl\langle Ap-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}, Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}\bigr\rangle - \bigl\Vert Ax_{n}-T^{(F_{2},\varphi _{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \bigr) \\ \leq& \Vert x_{n}-p \Vert ^{2}+L\gamma^{2} \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \\ &{} + 2\gamma \biggl(\frac{1}{2} \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2}- \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \biggr) \\ =& \Vert x_{n}-p \Vert ^{2}+\gamma(L\gamma-1) \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2}. \end{aligned}$$

Thus by (3.8) we have

$$\begin{aligned} \Vert z_{n}-p \Vert ^{2} &\leq\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2} +\sum _{i=1}^{n}\alpha_{n}^{(i)} \Vert u_{n}-p \Vert ^{2} \\ &\leq \alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \sum_{i=1}^{n}\alpha_{n}^{(i)} \bigl( \Vert x_{n}-p \Vert ^{2}+\gamma(L\gamma-1) \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \bigr) \\ &= \Vert x_{n}-p \Vert ^{2}+\gamma(L\gamma-1)\sum _{i=1}^{n}\alpha_{n}^{(i)} \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2} \\ &= \Vert x_{n}-p \Vert ^{2}-\gamma(1-L\gamma) \bigl(1- \alpha_{n}^{(0)}\bigr) \bigl\Vert Ax_{n}-T^{(F_{2},\varphi _{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2}. \end{aligned}$$

(3.10)

Therefore we have

$$\begin{aligned} \gamma(1-L\gamma) \bigl(1-\alpha_{n}^{(0)}\bigr) \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert ^{2}&\leq \Vert x_{n}-p \Vert ^{2}- \Vert z_{n}-p \Vert ^{2} \\ &\leq \Vert x_{n}-z_{n} \Vert \bigl( \Vert x_{n}-p \Vert + \Vert z_{n}-p \Vert \bigr). \end{aligned}$$

By the given control condition on $\{\alpha_{n}^{(0)}\}$, $\gamma(1-L\gamma)>0$, and (3.7) we obtain that

$$ \lim_{n\rightarrow\infty} \bigl\Vert Ax_{n}-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n} \bigr\Vert =0. $$

(3.11)

Since $T^{(F_{1},\varphi_{1})}_{r_{n}}$ is firmly nonexpansive and $I-\gamma A^{*}(I-T^{(F_{2},\varphi_{2})}_{r_{n}})A$ is nonexpansive, we have

$$\begin{aligned} \Vert u_{n}-p \Vert ^{2} =& \bigl\Vert T^{(F_{1},\varphi_{1})}_{r_{n}}\bigl(I-\gamma A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}} \bigr)A\bigr)x_{n}-T^{(F_{1},\varphi_{1})}_{r_{n}}p \bigr\Vert ^{2} \\ \leq&\bigl\langle T^{(F_{1},\varphi_{1})}_{r_{n}}\bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}}\bigr)A\bigr)x_{n}-T^{F_{1}}_{r_{n}}p, \\ & \bigl(I-\gamma A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}}\bigr)A \bigr)x_{n}-p\bigr\rangle \\ =& \bigl\langle u_{n}-p, \bigl(I-\gamma A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}} \bigr)A\bigr)x_{n}-p\bigr\rangle \\ =& \frac{1}{2}\bigl( \Vert u_{n}-p \Vert ^{2}+ \bigl\Vert \bigl(I-\gamma A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}}\bigr)A \bigr)x_{n}-p \bigr\Vert ^{2} \\ &{} - \bigl\Vert u_{n}-x_{n} -\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert ^{2}\bigr) \\ \leq&\frac{1}{2}\bigl( \Vert u_{n}-p \Vert ^{2}+ \Vert x_{n}-p \Vert ^{2}-\bigl( \Vert u_{n}-x_{n} \Vert ^{2} +\gamma^{2} \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert ^{2} \\ &{}-2\gamma\bigl\langle u_{n}-x_{n},A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\rangle \bigr) \bigr), \end{aligned}$$

which implies that

$$\begin{aligned} \Vert u_{n}-p \Vert ^{2} &\leq \Vert x_{n}-p \Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2}+2\gamma\bigl\langle u_{n}-x_{n},A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\rangle \\ &\leq \Vert x_{n}-p \Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2}+2\gamma \Vert u_{n}-x_{n} \Vert \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}} \bigr)Ax_{n} \bigr\Vert . \end{aligned}$$

(3.12)

This implies by (3.8) that

$$\begin{aligned} \Vert z_{n}-p \Vert ^{2} \leq&\alpha_{n}^{(0)} \Vert x_{n}-p \Vert ^{2}+ \sum _{i=1}^{n}\alpha _{n}^{(i)} \Vert u_{n}-p \Vert ^{2} \\ \leq& \alpha_{n}^{(0)} \Vert x_{n}-p \Vert + \sum_{i=1}^{n}\alpha_{n}^{(i)} \bigl( \Vert x_{n}-p \Vert ^{2}- \Vert u_{n}-x_{n} \Vert ^{2} \\ &{}+2\gamma \Vert u_{n}-x_{n} \Vert \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}} \bigr)Ax_{n} \bigr\Vert \bigr) \\ =& \Vert x_{n}-p \Vert ^{2}-\bigl(1- \alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert ^{2} \\ &{}+2\gamma\bigl(1-\alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert \bigl\Vert A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert \\ =& \Vert x_{n}-p \Vert ^{2}-\bigl(1- \alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert ^{2} \\ &{}+2\gamma\bigl(1-\alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert \bigl\Vert A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert . \end{aligned}$$

Therefore we have

$$\begin{aligned} &\bigl(1-\alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert ^{2} \\ &\quad \leq \Vert x_{n}-p \Vert ^{2}- \Vert z_{n}-p \Vert ^{2}+2\gamma\bigl(1- \alpha_{n}^{(0)}\bigr) \Vert u_{n}-x_{n} \Vert \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)Ax_{n} \bigr\Vert \\ &\quad \leq \Vert x_{n}-p \Vert ^{2}- \Vert z_{n}-p \Vert ^{2}+2\gamma\bigl(1-\alpha_{n}^{(0)} \bigr)M \bigl\Vert A^{*}\bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)Ax_{n} \bigr\Vert \\ &\quad \leq \Vert x_{n}-z_{n} \Vert \bigl( \Vert x_{n}-p \Vert + \Vert z_{n}-p \Vert \bigr)+2\gamma \bigl(1-\alpha_{n}^{(0)}\bigr)M \bigl\Vert A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}}\bigr)Ax_{n} \bigr\Vert , \end{aligned}$$

where $M=\sup\{\|u_{n}-x_{n}\|: n\in\mathbb{N}\}$. This implies by Condition (C1), (3.7), and (3.11) that

$$ \lim_{n\rightarrow\infty}\|u_{n}-x_{n}\|=0. $$

(3.13)

Step 5. We show that $q\in\bigcap^{\infty}_{i=1}F(S_{i})$.

By (3.9) and (3.13), for all $i\in\mathbb{N}$, we get that

$$\begin{aligned} \lim_{n\rightarrow\infty}\operatorname{dist}(u_{n},S_{i}u_{n})& \leq \lim_{n\rightarrow\infty} \bigl\Vert u_{n}-y_{n}^{(i)} \bigr\Vert \\ &\leq\lim_{n\rightarrow\infty} \Vert u_{n}-x_{n} \Vert + \lim_{n\rightarrow\infty} \bigl\Vert x_{n}-y_{n}^{(i)} \bigr\Vert \\ &=0. \end{aligned}$$

(3.14)

For each $i\in\mathbb{N}$, we get

$$\begin{aligned} \begin{aligned} \operatorname{dist}(q,S_{i}q) &\leq \Vert q-u_{n} \Vert + \bigl\Vert u_{n}-y^{(i)}_{n} \bigr\Vert + \operatorname {dist}\bigl(y^{(i)}_{n},S_{i}q\bigr) \\ &\leq \Vert q-u_{n} \Vert +\operatorname{dist}(u_{n},S_{i}u_{n})+ \mathcal {H}(S_{i}u_{n},S_{i}q) \\ &\leq2 \Vert q-u_{n} \Vert +\operatorname{dist}(u_{n},S_{i}u_{n}) \\ &\leq2\bigl( \Vert q-z_{n} \Vert + \Vert z_{n}-x_{n} \Vert \bigr)+\operatorname{dist}(u_{n},S_{i}u_{n}) . \end{aligned} \end{aligned}$$

Since $\lim_{n\rightarrow\infty} z_{n}=q$, it follows by (3.7) and (3.14) that

$$ \operatorname{dist}(q,S_{i}q)=0\quad \text{for all }i\in\mathbb{N}. $$

This shows that $q\in S_{i}q$ for all $i\in\mathbb{N}$, and hence $q\in\bigcap^{\infty}_{i=1} F(S_{i})$.

Step 6. We show that $q\in \operatorname{SGEP}(F_{1},\varphi_{1},F_{2},\varphi_{2})$.

First, we will show that $q\in \operatorname{GEP}(F_{1},\varphi_{1})$.

Since $u_{n}=T^{(F_{1},\varphi_{1})}_{r_{n}}(I-\gamma A^{*}(I-T^{(F_{2},\varphi_{2})}_{r_{n}})A)x_{n}$, we have

$$ F_{1}(u_{n},y)+\varphi_{1}(u_{n},y)+ \frac{1}{r_{n}} \bigl\langle y-u_{n},u_{n}-x_{n} -\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)Ax_{n} \bigr\rangle \geq0,\quad \forall y\in C, $$

which implies that

$$ F_{1}(u_{n},y)+\varphi_{1}(u_{n},y)+ \frac{1}{r_{n}}\langle y-u_{n},u_{n}-x_{n} \rangle-\frac{1}{r_{n}} \bigl\langle y-u_{n}, \gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)Ax_{n} \bigr\rangle \geq0, \quad \forall y\in C. $$

It follows from the monotonicity of $F_{1}$ and $\varphi_{1}$ that

$$ \frac{1}{r_{n}}\langle y-u_{n},u_{n}-x_{n} \rangle-\frac{1}{r_{n}} \bigl\langle y-u_{n}, \gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r_{n}} \bigr)Ax_{n} \bigr\rangle \geq F_{1}(y,u_{n})+\varphi_{1}(y,u_{n}), \quad \forall y\in C. $$

By (3.13) and $\lim_{n\rightarrow\infty} x_{n}=q$ we get that $\lim_{n\rightarrow\infty} u_{n}=q$. It follows by Condition (C2), (3.11), (3.13), Assumption 2.7, (A4) and (A7), that $0\geq F_{1}(y,q)+\varphi_{1}(y,q)$ for all $y\in C$. Put $y_{t}=ty+(1-t)q$ for all $t\in(0,1]$ and $y\in C$. Consequently, we get $y_{t}\in C$, and hence $F_{1}(y_{t},q)+\varphi_{1}(y_{t},q)\leq0$. So by Assumption 2.7, (A1)–(A7), we have

$$\begin{aligned} 0 &\leq F_{1}(y_{t},y_{t})+ \varphi_{1}(y_{t},y_{t}) \\ &\leq t\bigl(F_{1}(y_{t},y)+\varphi_{1}(y_{t},y) \bigr) + (1-t) \bigl(F_{1}(y_{t},q) +\varphi _{1}(y_{t},q)\bigr) \\ &\leq t\bigl(F_{1}(y_{t},y)+\varphi_{1}(y_{t},y) \bigr) + (1-t) \bigl(F_{1}(q,y_{t}) +\varphi_{1}(q,y_{t}) \bigr) \\ &\leq F_{1}(y_{t},y)+\varphi_{1}(y_{t},y). \end{aligned}$$

Hence we have

$$ F_{1}(y_{t},y)+\varphi_{1}(y_{t},y) \geq0, \quad \forall y\in C. $$

Letting $t\rightarrow0$, by Assumption 2.7 (A3) and the upper hemicontinuity of $\varphi_{1}$ we have

$$ F_{1}(q,y)+\varphi_{1}(q,y)\geq0, \quad \forall y\in C. $$

This implies that $q\in \operatorname{GEP}(F_{1},\varphi_{1})$.

Next, we show that $Aq\in \operatorname{GEP}(F_{2},\varphi_{2})$.

Since A is a bounded linear operator, we have $Ax_{n}\to Aq$. Then, it follows from (3.11) that

$$ T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}\to Aq. $$

(3.15)

By the definition of $T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}$ we have

$$ F_{2} \bigl(T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n},y \bigr)+ \varphi_{2} \bigl(T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n},y \bigr) +\frac{1}{r_{n}} \bigl\langle y-T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n},T^{(F_{2},\varphi_{2})}_{r_{n}}Ax_{n}-Ax_{n} \bigr\rangle \geq0 $$

for all $y\in Q$. Since $F_{2}$ and $\varphi_{2}$ are upper semicontinuous in the first argument, it follows by (3.15) that

$$ F_{2}(Aq,y)+\varphi_{2}(Aq,y)\geq0 , \quad \forall y\in Q. $$

This shows that $Aq\in \operatorname{GEP}(F_{2},\varphi_{2})$. Therefore $q\in \operatorname{SGEP}(F_{1},\varphi_{1},F_{2},\varphi_{2})$.

By Steps 5 and 6 we get that $q\in\Gamma$.

Step 7. Finally, we show that $q=P_{\Gamma}x_{1}$.

Since $x_{n}=P_{C_{n}}x_{1}$ and $\Gamma\subset C_{n}$, we obtain $\langle x_{1}-x_{n}, x_{n}-p\rangle\geq0$ for all $p\in\Gamma$. Thus we get $\langle x_{1}-q, q-p\rangle\geq0$ for all $p\in\Gamma$. This shows that $q=P_{\Gamma}x_{1}$.

By Steps 1–7 we can conclude that $\{x_{n}\}$ converges strongly to $P_{\Gamma}x_{1}$. This completes the proof. □

If $\varphi_{1}= \varphi_{2}=0$, then the split generalized equilibrium problem reduces to the split equilibrium problem. So, the following result can be immediately obtained from Theorem 3.1.

Corollary 3.2

Let C be a nonempty closed convex subset of a real Hilbert space $H_{1}$, and let Q be a nonempty closed convex subset of a real Hilbert space $H_{2}$. Let $A: H_{1}\rightarrow H_{2}$ be a bounded linear operator, and let $\{S_{i}\}$ be a countable family of nonexpansive multivalued mappings of C into $\mathit{CB}(C)$. Let $F_{1}:C\times C\rightarrow\mathbb{R}$, $F_{2}:Q\times Q\rightarrow\mathbb{R}$ be bifunctions satisfying Assumption 2.7. Let $F_{2}$ be upper semicontinuous in the first argument. Assume that $\Gamma =\bigcap_{i=1}^{\infty}F(S_{i})\cap SEP(F_{1},F_{2}) \neq\emptyset$ and $S_{i}p=\{p\}$ for each $p\in\bigcap_{i=1}^{\infty}F(S_{i})$. Let $x_{1}\in C$ with $C_{1} =C$, and let $\{x_{n}\}$ be a sequence generated by

$$ \textstyle\begin{cases} u_{n}=T^{F_{1}}_{r_{n}} (I-\gamma A^{*} (I-T^{F_{2}}_{r_{n}} )A )x_{n}, \\ z_{n}= \alpha_{n}^{(0)} x_{n}+ \alpha_{n}^{(1)}y_{n}^{(1)} + \cdots +\alpha_{n}^{(n)}y_{n}^{(n)} , \quad y_{n}^{(i)} \in S_{i}u_{n}, \\ C_{n+1} =\{p\in C_{n} : \|z_{n}-p\|\leq\|x_{n}-p\|\}, \\ x_{n+1} =P_{C_{n+1}} x_{1}, \quad n\in\mathbb{N}, \end{cases} $$

(3.16)

where $\{\alpha_{n}^{(i)}\}\subset(0,1)$ satisfy $\sum_{i=0}^{n}\alpha_{n}^{(i)}=1$, $\{r_{n}\}\subset(0,\infty)$, and $\gamma\in(0,\frac{1}{L})$, where L is the spectral radius of $A^{*}A$, and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (C1) The limits $\lim_{n\to\infty}\alpha_{n}^{(i)}\in(0,1)$ exist for all $i\geq 0$,

• (C2) $\liminf_{n\rightarrow\infty} r_{n}>0$.

Then the sequence $\{x_{n}\}$ generated by (3.16) converges strongly to $P_{\Gamma}x_{1}$.

If $F_{1}=F_{2}=F$, $H_{1}=H_{2}=H$, and $\varphi_{1}= \varphi_{2}=0$, then the following result can be immediately obtained from Theorem 3.1.

Corollary 3.3

Let C be a nonempty closed convex subset of a real Hilbert space H. Let $A: H\rightarrow H$ be a bounded linear operator, and let $\{S_{i}\}$ be a countable family of nonexpansive multivalued mappings of C into $\mathit{CB}(C)$. Let $F:C\times C\rightarrow\mathbb{R}$ be a bifunction satisfying Assumption 2.7. Assume that $\Gamma =\bigcap_{i=1}^{\infty}F(S_{i})\cap EP(F) \neq\emptyset$ and $S_{i}p=\{p\}$ for each $p\in\bigcap_{i=1}^{\infty}F(S_{i})$. Let $x_{1}\in C$ with $C_{1} =C$, and let $\{x_{n}\}$ be a sequence generated by

$$ \textstyle\begin{cases} u_{n}=T^{F}_{r_{n}} (I-\gamma A^{*} (I-T^{F}_{r_{n}} )A )x_{n}, \\ z_{n}= \alpha_{n}^{(0)} x_{n}+ \alpha_{n}^{(1)}y_{n}^{(1)} + \cdots +\alpha_{n}^{(n)}y_{n}^{(n)} ,\quad y_{n}^{(i)} \in S_{i}u_{n}, \\ C_{n+1} =\{p\in C_{n} : \|z_{n}-p\|\leq\|x_{n}-p\|\}, \\ x_{n+1} =P_{C_{n+1}} x_{1}, \quad n\in\mathbb{N}, \end{cases} $$

(3.17)

where $\{\alpha_{n}^{(i)}\}\subset(0,1)$ satisfy $\sum_{i=0}^{n}\alpha_{n}^{(i)}=1$, $\{r_{n}\}\subset(0,\infty)$, and $\gamma\in(0,\frac{1}{L})$, where L is the spectral radius of $A^{*}A$, and $A^{*}$ is the adjoint of A. Assume that the following conditions hold:

• (C1) The limits $\lim_{n\to\infty}\alpha_{n}^{(i)}\in(0,1)$ exist for all $i\geq 0$,

• (C2) $\liminf_{n\rightarrow\infty} r_{n}>0$.

Then the sequence $\{x_{n}\}$ generated by (3.17) converges strongly to $P_{\Gamma}x_{1}$.

4 Numerical example

In this section, we present a numerical example to demonstrate the performance and convergence of our theoretical results. All codes were written in Scilab.

Example 4.1

Let $H_{1}=H_{2}=\mathbb{R}$ and $C=Q=[0,10]$. Let $A:H_{1}\to H_{2}$ be defined by $Ax=x$ for each $x\in H_{1}$. Then $A^{*}y=y$ for each $y\in H_{2}$. For $x\in C$, $i=1,2,\ldots$ , we define the multivalued mappings $S_{i}$ on C as follows:

$$S_{i}x = \biggl[0, \frac{x}{10i} \biggr] \quad \text{for all }i \in \mathbb{N}. $$

Obviously, $S_{i}$ is nonexpansive for all $i\in\mathbb{N}$, $S_{i}(0)=\{ 0\}$, and $\bigcap_{i=1}^{\infty}F(S_{i})=\{0\}$. Define the bifunctions $F_{1},\varphi_{1}:C\times C\rightarrow \mathbb{R}$ by $F_{1}(x,y)=y^{2}+3xy-4x^{2}$ and $\varphi_{1}(x,y)=y^{2}-x^{2}$ for $x,y\in C$. Define $F_{2},\varphi_{2}:Q\times Q\rightarrow\mathbb{R}$ by $F_{2}(w,v)=2v^{2}+wv-3w^{2}$ and $\varphi_{2}(w,v)=w-v$ for $w\in Q$ and $v\in Q$. Choose $r_{n}=\frac{n}{n+1}$, $\gamma=\frac{1}{10}$, and the sequences $\{\lambda_{n}^{(i)}\}$ defined by

$$\lambda_{n}^{(i)} = \textstyle\begin{cases} \frac{1}{{b^{i + 1} }} ( {\frac{n}{{n + 1}}} ), & n \geq i + 1, \\ 1 - \frac{n}{{n + 1}} ( {\sum_{k = 1}^{n} {\frac{1}{{b^{k} }}} } ), & n = i, \\ 0, & n < i, \end{cases} $$

where $b> 1$. It is easy to check that $F_{1}$, $F_{2}$, $\varphi_{1}$, $\varphi_{2}$, $\{\lambda_{n}^{(i)}\}$, and $\{r_{n}\}$ satisfy all the conditions in Theorem 3.1 with $\Gamma=\{0\}$.

For all $x\in C$ and $n\in\mathbb{N}$, we compute $T^{(F_{2},\varphi_{2})}_{r}Ax$. Find w such that

$$\begin{aligned} \begin{aligned} 0&\leq F_{2}(w,v)+\varphi_{2}(w,v)+\frac{1}{r}\langle v-w,w-Ax\rangle \\ &= 2v^{2}+wv-3w^{2}+w-v + \frac{1}{r}(v-w) (w-x) \\ &\Leftrightarrow \\ 0&\leq2rv^{2}+rwv-3rw^{2}+r_{n}w-rv + (v-w) (w-x) \\ &=2rv^{2}+rwv-3rw^{2}+rw-rv+wv-vx-w^{2}+wx \\ &=2rv^{2}+(rw-r+w-x)v + \bigl(-3rw^{2}+rw-w^{2}+wx \bigr) \end{aligned} \end{aligned}$$

for all $v\in Q$. Let $J_{2}(v)=2rv^{2}+(rw-r+w-x)v + (-3rw^{2}+rw-w^{2}+wx)$. $J_{2}(v)$ is s a quadratic function of v with coefficients $a=2r$, $b=rw-r-x-w$, and $c=-3rw^{2}+rw-w^{2}+wx$. Determine the discriminant Δ of $J_{2}$:

$$\begin{aligned} \Delta&=b^{2}-4ac \\ &= (rw-r+w-x)^{2} -4(2r) \bigl(-3rw^{2}+rw-w^{2}+wx \bigr) \\ &= 25r^{2}w^{2}-10r^{2}w+10rw^{2}-10rwx+r^{2}-2rw+2rx+w^{2}-2wx+x^{2} \\ &=\bigl(25r^{2}+10r+1\bigr)w^{2}+\bigl(-10r^{2}-10rx-2r-2x \bigr)w+\bigl(2rx+x^{2}+r^{2}\bigr) \\ &=(5r+1)^{2}w^{2}-2w(5r+1) (x+r)+(x+r)^{2} \\ &=\bigl((5r+1)w-(x+r)\bigr)^{2}. \end{aligned}$$

We know that $J_{2}(v)\geq0$ for all $v\in\mathbb{R}$. If it has at most one solution in $\mathbb{R}$, then $\Delta\leq0$, so we have

$$ w=\frac{x+r}{5r+1}. $$

This implies that

$$ T^{(F_{2},\varphi_{2})}_{r}Ax=\frac{x+r}{5r+1}. $$

Furthermore, we get

$$\begin{aligned} \bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi_{2})}_{r} \bigr)A \bigr)x &=x- \gamma A^{*}\bigl(Ax-T^{(F_{2},\varphi_{2})}_{r}Ax\bigr) \\ &=x-\frac{1}{10}A^{*} \biggl(x-\frac{x+r}{5r+1} \biggr) \\ &=x-\frac{1}{10} \biggl(\frac{5rx-r}{5r+1} \biggr) \\ &=\frac{45xr+10x+r}{10(5r+1)}. \end{aligned}$$

Next, we find $u\in C$ such that $F_{1}(u,z)+\varphi_{1}(u,z)+\frac{1}{r}\langle z-u,u-s\rangle\geq0$ for all $z\in C$, where $s= (I-\gamma A^{*} (I-T^{(F_{2},\varphi_{2})}_{r} )A )x$. Note that

$$\begin{aligned} 0&\leq F_{1}(u,z)+\varphi_{1}(u,z)+\frac{1}{r} \langle z-u,u-s\rangle \\ &= 2z^{2}+3uz-5u^{2} + \frac{1}{r} \langle v-u,u-s \rangle \\ &\Leftrightarrow \\ 0&\leq2rz^{2}+3ruz-5ru^{2}+(z-u) (u-s) \\ &= 2rz^{2}+3ruz-5ru^{2}+uz-sz-u^{2}+us \\ &= 2rz^{2}+(3ru+u-s)z+\bigl(-5ru^{2}-u^{2}+us \bigr) \end{aligned}$$

for all $z\in C$. Let $J_{1}(z)=2rz^{2}+(3ru+u-s)z+(-5ru^{2}-u^{2}+us)$. $J_{1}(z)$ be a quadratic function of z with coefficients $a=2r$, $b=3ru+u-s$, and $c=-5ru^{2}-u^{2}+us$. Determine the discriminant Δ of $J_{1}$:

$$\begin{aligned} \Delta&= (3ru+u-s)^{2} -4(2r) \bigl(-5ru^{2}-u^{2}+us \bigr) \\ &= 49r^{2}u^{2}+14ru^{2}-14rus+u^{2}-2us+s^{2} \\ &=\bigl((7r+1)u-s\bigr)^{2}. \end{aligned}$$

We know that $J_{1}(z)\geq0$ for all $z\in\mathbb{R}$. If it has at most one solution in $\mathbb{R}$, then $\Delta\leq0$, so we have

$$ u=\frac{s}{7r+1}. $$

This implies that

$$\begin{aligned} u_{n}&=T^{(F_{1},\varphi_{1})}_{r_{n}} \bigl(I-\gamma A^{*} \bigl(I-T^{(F_{2},\varphi _{2})}_{r_{n}} \bigr)A \bigr)x_{n}, \\ &=\frac{45x_{n}r_{n}+10x_{n}+r_{n}}{10(5r_{n}+1)(7r_{n}+1)}. \end{aligned}$$

We put $y^{(i)}_{n}=\frac{u_{n}}{10i}$ for all $i\in\mathbb{N}$. Then algorithm (3.1) becomes:

$$ \textstyle\begin{cases} u_{n}=\frac{45x_{n}r_{n}+10x_{n}+r_{n}}{10(5r_{n}+1)(7r_{n}+1)},\quad r_{n}=\frac{n}{n+1}, \\ z_{n}= \lambda_{n}^{(0)}x_{n} + \frac{\lambda_{n}^{(1)}u_{n}}{10} +\frac{\lambda_{n}^{(2)}u_{n}}{20}+\cdots +\frac{\lambda_{n}^{(n)}u_{n}}{10n}, \\ C_{n+1} =\{p\in C_{n} : \|z_{n}-p\|\leq\|x_{n}-p\|\}, \\ x_{n+1} =P_{C_{n+1}} x_{1},\quad n\in\mathbb{N}. \end{cases} $$

(4.1)

For arbitrary $x_{1}\in C=C_{1}=[0,10]$, we get that $0\leq z_{1}\leq x_{1}\leq10$. Then $C_{2}=\{p\in C_{1}: |z_{1}-p|\leq |x_{1}-p|\}= [0,\frac{x_{1}+z_{1}}{2} ]$. Since $\frac{x_{1}+z_{1}}{2}\leq x_{1}$, it follows that $x_{2}=P_{C_{2}}x_{1} =\frac{x_{1}+z_{1}}{2}$. Continuing this process, we get $C_{n+1}= [0,\frac{x_{n}+z_{n}}{2} ]$, and hence $x_{n+1}=P_{C_{n+1}}x_{1} =\frac{x_{n}+z_{n}}{2}$. Now, we rewrite algorithm (4.1) as follows:

$$ \textstyle\begin{cases} u_{n}=\frac{45x_{n}r_{n}+10x_{n}+r_{n}}{10(5r_{n}+1)(7r_{n}+1)},\quad r_{n}=\frac{n}{n+1}, \\ z_{n}= \lambda_{n}^{(0)}x_{n} + \frac{\lambda_{n}^{(1)}u_{n}}{10} +\frac{\lambda_{n}^{(2)}u_{n}}{20}+\cdots +\frac{\lambda_{n}^{(n)}u_{n}}{10n}, \\ x_{n+1} =\frac{x_{n}+z_{n}}{2},\quad n\in\mathbb{N}. \end{cases} $$

(4.2)

In this example, we set the parameter on $\{\lambda_{n}^{(i)} \}$ by $b=9$. Then we obtain

$$\bigl(\lambda_{n}^{(i)} \bigr) = \left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{}} {\frac{1}{18}} & {\frac{17}{18}} & 0 & 0 & 0 & \cdots & 0 & \cdots \\ {\frac{2}{27}} & {\frac{2}{243}} & {\frac{223}{243}} & 0 & 0 & \cdots & 0 & \cdots \\ {\frac{1}{12}} & {\frac{1}{{108}}} & {\frac{1}{{972}}} & {\frac{{881}}{{972}}} & 0 & \cdots & 0 & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & {} & \vdots & {} \\ {\frac{n}{{9(n + 1)}}} & {\frac{n}{{9^{2}(n + 1)}}} & {\frac{n}{{9^{3}(n + 1)}}} & {\frac{n}{{9^{4}(n + 1)}}} & {\frac{n}{{9^{5}(n + 1)}}} & \cdots& {\frac{n}{{9^{i} (n + 1)}}} & \cdots \\ \vdots & \vdots & \vdots & \vdots & \vdots & {} & \vdots & {} \end{array}\displaystyle \right ). $$

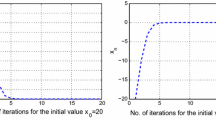
Figure 1 indicates the behavior of $x_{n}$ for algorithm (4.2), which converges to the same solution, that is, $0\in \Gamma$ as a solution of this example.

Figure 1

Behaviors of $x_{n}$ with three random initial points $x_{1}$

Now, we test the effect of the parameters in $\{\lambda_{n}^{(i)} \}$ on the convergence of algorithm (4.2). In this test, Figure 2 presents the behavior of $x_{n}$ by choosing three different parameters in $\{\lambda_{n}^{(i)} \}$, that is, $b=2$, $b=9$, and $b= 100$.

Figure 2

Behaviors of $x_{n}$ with three different parameters in $\{\lambda_{n}^{(i)} \}$

5 Conclusions

The results presented in this paper modify, extend, and improve the corresponding results of Kazmi and Rizvi [7], Suantai et al. [15], and others. The main aim of this paper is to propose an iterative algorithm based on the shrinking projection method to find an element for solving a class of split generalized equilibrium problems and fixed point problems for a countable family of nonexpansive multivalued mappings in real Hilbert spaces.