Fixed point results for set-contractions on metric spaces with a directed graph

Abstract

In this paper, we establish the existence of fixed points for set-valued mappings satisfying certain graph contractions with set-valued domain endowed with a graph. These results unify, generalize, and complement various known comparable results in the literature.

1 Introduction and preliminaries

Existence of fixed points in ordered metric spaces has been studied by Ran and Reurings [1]. Recently, many researchers have obtained fixed point results for single- and set-valued mappings defined on partially ordered metrics spaces (see, e.g., [2–6]). Jachymski and Jozwik [7] introduced a new approach in metric fixed point theory by replacing the order structure with a graph structure on a metric space. In this way, the results proved in ordered metric spaces are generalized (see also [8] and the references therein); in fact, in 2010, Gwozdz-Lukawska and Jachymski [9], developed the Hutchinson-Barnsley theory for finite families of mappings on a metric space endowed with a directed graph. Abbas and Nazir [10] obtained some fixed point results for power graph contraction pair endowed with a graph. Bojor [11] proved fixed point theorem of φ-contraction mapping on a metric space endowed with a graph. Recently, Bojor [12] proved fixed point theorems for Reich type contractions on metric spaces with a graph. For more results in this direction, we refer to [13–17] and the references mentioned therein. The reader interested in fixed point results of partial metric spaces is referred to [2, 10, 18]. In this paper, we prove fixed point results for set-valued maps, defined on the family of closed and bounded subsets of a metric space endowed with a graph and satisfying graph ϕ-contractive conditions. These results extend and strengthen various known results in [7, 8, 11, 19–21].

Consistent with Jachymski [8], let $(X,d)$ be a metric space and Δ denotes the diagonal of $X\times X$. Let G be a directed graph, such that the set $V(G)$ of its vertices coincides with X and $E(G)$ be the set of edges of the graph which contains all loops, that is, $\Delta \subseteq E(G)$. Also assume that the graph G has no parallel edges and, thus, one can identify G with the pair $(V(G),E(G))$.

Definition 1.1

[8]

An operator $f:X\rightarrow X$ is called a Banach G-contraction or simply a G-contraction if

• (a) f preserves edges of G; for each $x,y\in X$ with $(x,y)\in E(G)$, we have $(f(x),f(y))\in E(G)$,

• (b) f decreases weights of edges of G; there exists $\alpha \in (0,1)$ such that for all $x,y\in X$ with $(x,y)\in E(G)$, we have $d(f(x),f(y))\leq\alpha d(x,y)$.

If x and y are vertices of G, then a path in G from x to y of length $k\in \mathbb{N}$ is a finite sequence $\{x_{n}\}$ ($n\in\{0,1,2,\ldots,k\}$) of vertices such that $x_{0}=x$, $x_{k}=y$, and $(x_{i-1},x_{i})\in E(G)$ for $i\in \{1,2,\ldots,k\}$.

Notice that a graph G is connected if there is a directed path between any two vertices and it is weakly connected if $\widetilde{G}$ is connected, where $\widetilde{G}$ denotes the undirected graph obtained from G by ignoring the direction of the edges. Denote by $G^{-1}$ the graph obtained from G by reversing the direction of the edges. Thus,

$$ E \bigl( G^{-1} \bigr) = \bigl\{ ( x,y ) \in X\times X: ( y,x ) \in E ( G ) \bigr\} . $$

It is more convenient to treat $\widetilde{G}$ as a directed graph for which the set of its edges is symmetric; under this convention, we have

$$ E(\widetilde{G})=E(G)\cup E \bigl(G^{-1} \bigr). $$

If G is such that $E(G)$ is symmetric, then for $x\in V(G)$, the symbol $[x]_{G}$ denotes the equivalence class of the relation R defined on $V(G)$ by the rule:

$$ yRz\mbox{ if there is a path in }G\mbox{ from }y\mbox{ to }z. $$

Recall that if $f:X\rightarrow X$ is an operator, then by $F_{f}$ we denote the set of all fixed points of f. We set also

$$ X_{f}:= \bigl\{ x\in X: \bigl(x,f(x) \bigr)\in E(G) \bigr\} . $$

Jachymski and Jozwik [7] used the following property:

• (P) for any sequence $\{x_{n}\}$ in X, if $x_{n}\rightarrow x$ as $n\rightarrow\infty$ and $(x_{n},x_{n+1}) \in E(G)$, then $(x_{n},x)\in E(G)$.

Theorem 1.2

[7]

Let $(X,d)$ be a complete metric space and let G be a directed graph such that $V(G)=X$. Let $E(G)$ and the triplet $(X,d,G)$ have property (P). Let $f:X\rightarrow X$ be a G-contraction. Then the following statements hold:

• (1) $F_{f}\neq\emptyset$ if and only if $X_{f}\neq \emptyset$;

• (2) if $X_{f}\neq\emptyset$ and G is weakly connected, then f is a Picard operator, i.e., $F_{f}=\{x^{\ast}\}$ and sequence $\{f^{n}(x)\}\rightarrow x^{\ast}$ as $n\rightarrow\infty$, for all $x\in X$;

• (3) for any $x\in X_{f}$, $f|_{[ x]_{\widetilde{G}}}$ is a Picard operator;

• (4) if $X_{f}\subseteq E(G)$, then f is a weakly Picard operator, i.e., $F_{f}\neq\emptyset$ and, for each $x\in X$, we have sequence $\{f^{n}(x)\}\rightarrow x^{\ast}(x)\in F_{f}$ as $n\rightarrow\infty$.

For a detailed discussion concerning Picard and weakly Picard operators, we refer to Rus [22, 23] and to Berinde [24, 25].

Let $(X,d)$ be a metric space and let $CB(X)$ be the class of all nonempty closed and bounded subsets of X. For $A,B\in CB(X)$, let

$$ H(A,B)=\max \Bigl\{ \sup_{b\in B}d(b,A),\sup_{a\in A}d(a,B) \Bigr\} , $$

where $d(x,B)=\inf\{d(x,b):b\in B\}$ is the distance of a point x to the set B. The mapping H is said to be the Pompeiu-Hausdorff metric induced by d.

Throughout this paper, we assume that a directed graph G has no parallel edge and G is a weighted graph in the sense that each vertex x is assigned the weight $d(x,x)=0$ and each edge $(x,y)$ is assigned the weight $d(x,y)$. Since d is a metric on X, the weight assigned to each vertex x to vertex y need not be zero and, whenever a zero weight is assigned to some edge $(x,y)$, it reduces to a loop $(x,x)$ having weight 0. Further, in Pompeiu-Hausdorff metric induced by metric d, the Pompeiu-Hausdorff weight assigned to each $U,V\in CB ( X )$ need not be zero (that is, $H ( U,V ) \neq0$) and, whenever a zero Pompeiu-Hausdorff weight is assigned to some $U,V\in CB ( X )$, it reduces to $U=V$.

Definition 1.3

Let A and B be two nonempty subsets of X. Now we treat some terminology:

• (a) by ‘there is an edge between A and B’, we mean there is an edge between some $a\in A$ and $b\in B$ which we denote by $(A,B)\subset E ( G )$.

• (b) by ‘there is a path between A and B’, we mean that there is a path between some $a\in A$ and $b\in B$.

In $CB(X)$, we define a relation R in the following way:

For $A,B\in CB(X)$, we have $ARB$ if and only if there is a path between A and B.

We say that the relation R on $CB ( X )$ is transitive if there is a path between A and B, and there is a path between B and C, then there is a path between A and C.

For $A\in CB(X)$, the equivalence class of A induced by R is denoted by

$$ [ A]_{G}= \bigl\{ B \in CB(X) : ARB \bigr\} . $$

Now we consider the mapping $T:CB(X)\rightarrow CB(X)$ instead of $T:X\rightarrow X$ or $T:X\rightarrow CB(X)$ to study fixed points of graph contraction mappings.

For a mapping $T:CB ( X ) \rightarrow CB ( X )$, we define the following set:

$$ X_{T}:= \bigl\{ U\in CB ( X ) : \bigl( U,T ( U ) \bigr) \subseteq E(G) \bigr\} . $$

Definition 1.4

Let $T:CB(X)\rightarrow CB(X)$ be a set-valued mapping. The mapping T is said to be a graph ϕ-contraction if the following conditions hold:

• (i) There is an edge between A and B implies there is an edge between $T(A)$ and $T(B)$ for all $A,B\in CB(X)$.

• (ii) There is a path between A and B implies there is a path between $T(A)$ and $T(B)$ for all $A,B\in CB(X)$.

• (iii) There exists an upper semi-continuous and nondecreasing function $\phi:\mathbb{\mathbb{R} }^{+}\rightarrow\mathbb{\mathbb{R} }^{+}$ with $\phi(t)< t$ for each $t>0$ such that there is an edge between A and B implies

  $$ H \bigl( T ( A ) ,T ( B ) \bigr) \leq\phi \bigl(H(A,B) \bigr)\quad \mbox{for all }A,B\in CB ( X ) . $$

  (1.1)

Example 1.5

• (1) Any constant mapping $T:CB(X)\rightarrow CB(X)$ is a graph ϕ-contraction for $\Delta\subset E(G)$.

• (2) Any graph ϕ-contraction map for a graph G is also a graph ϕ-contraction for graph $G_{0}$, where the graph $G_{0}$ is defined by $E(G_{0})=X\times X$.

It is obvious if $T:CB(X)\rightarrow CB(X)$ is a graph ϕ-contraction for graph G, then T is also graph ϕ-contraction for the graphs $G^{-1}$ and $\widetilde{G}$.

A graph G is said to have property:

(P^∗):

if for any sequence $\{X_{n}\}$ in $CB(X)$ with $X_{n}\rightarrow X$ as $n\rightarrow\infty$, there exists an edge between $X_{n}$ and $X_{n+1}$ for $n\in \mathbb{N}$, implies that there is a subsequence $\{X_{n_{k}}\}$ of $\{X_{n}\}$ with an edge between $X_{n_{k}}$ and X for $n\in \mathbb{N}$.

Definition 1.6

Let $T:CB(X)\rightarrow CB(X)$. The set $A\in CB(X)$ is said to be a fixed point of T if $T(A)=A$. The set of all fixed points of T is denoted by $F ( T )$.

A subset Γ of $CB ( X )$ is said to be complete if for any set $X,Y\in\Gamma$, there is an edge between X and Y.

Definition 1.7

[19]

A metric space $(X,d)$ is called an ε-chainable metric space for some $\varepsilon >0$ if for given $x,y\in X$, there is $n\in \mathbb{N}$ and a sequence $\{x_{n}\}$ such that

$$ x_{0}=x,\qquad x_{n}=y\quad\mbox{and}\quad d(x_{i-1},x_{i})<\varepsilon\quad\mbox{for } i=1,\ldots,n. $$

We need of the following lemma of Nadler [21] (see also [26]).

Lemma 1.8

If $U,V\in CB(X)$ with $H(U,V)<\varepsilon$, then for each $u\in U$ there exists an element $v\in V$ such that $d(u,v)<\varepsilon$.

2 Fixed point results

In this section, we obtain several fixed point results for set-valued selfmaps on $CB(X)$ satisfying certain graph contraction conditions.

Theorem 2.1

Let $(X,d)$ be a complete metric space endowed with a directed graph G such that $V(G)=X$ and $E(G)\supseteq \Delta$. If $T:CB ( X ) \rightarrow CB ( X )$ is a graph ϕ-contraction mapping such that the relation R on $CB ( X )$ is transitive, then following statements hold:

• (i) If $F ( T )$ is complete, then the Pompeiu-Hausdorff weight assigned to the $U,V\in F(T)$ is 0.

• (ii) $X_{T}\neq\emptyset$ provided that $F ( T ) \neq \emptyset$.

• (iii) If $X_{T}\neq\emptyset$ and the weakly connected graph G satisfies the property (P^∗), then T has a fixed point.

• (iv) $F ( T )$ is complete if and only if $F ( T )$ is a singleton.

Proof

To prove (i), let $U,V\in F ( T )$. Suppose that the Pompeiu-Hausdorff weight assign to the U and V is not zero. Since T is a graph ϕ-contraction, we have

$$\begin{aligned} H(U,V) =&H \bigl(T ( U ) ,T ( V ) \bigr) \\ \leq&\phi \bigl(H(U,V) \bigr) \\ <&H(U,V), \end{aligned}$$

a contradiction. Hence (i) is proved.

To prove (ii), let $F ( T ) \neq\emptyset$. Then there exists $U\in CB(X)$ such that $T(U)=U$. Since $\Delta\subseteq E(G)$ and U is nonempty, we conclude that $X_{T}\neq\emptyset$.

To prove (iii), let $U\in X_{T}$. As T is a graph ϕ-contraction and $A,B\in CB(X)$, it follows by the hypothesis $CB(X)\subseteq [ A]_{\widetilde{G}}=P ( X )$, where $P(X)$ denotes the power set of X and so, $T(A)\in [ A]_{\widetilde{G}}$. Now for $A\in CB(X)$ and $B\in [ A]_{\widetilde{G}}$, there exists a path $\{x_{i}\}_{i=0}^{n}$ from some $x\in A$ and to $y\in T ( A )$, that is, $x_{0}=x$ and $x_{n}=y$ and $(x_{i-1},x_{i})\in E(\widetilde{G})$, for $i=1,2,\ldots,n$, such that $x_{0}\in A_{0}=A$, $x_{1}\in A_{1},\ldots, x_{n}\in A_{n}=T ( A )$, where each $A_{i}\in CB(X)$. Since T is also a graph ϕ-contraction for graph $\widetilde{G}$, for $i=1,2,\ldots,n$, we have

$$\begin{aligned}& H \bigl(T ( A_{i-1} ) ,T ( A_{i} ) \bigr) \leq\phi \bigl(H(A_{i-1},A_{i}) \bigr), \\& H \bigl(T ( A_{i-2} ) ,T ( A_{i-1} ) \bigr) \leq\phi \bigl(H(A_{i-2},A_{i-1}) \bigr), \\& \cdots \\& H \bigl(T ( A_{0} ) ,T ( A_{1} ) \bigr) \leq\phi \bigl(H(A_{0},A_{1}) \bigr), \end{aligned}$$

and so we obtain

$$ H \bigl(T^{n} ( A ) ,T^{n+1} ( A ) \bigr)\leq\phi ^{n} \bigl(H \bigl(A,T ( A ) \bigr) \bigr) $$

for all $n\in \mathbb{N}$. Now for $m,n\in \mathbb{N}$ with $m>n$,

$$\begin{aligned} H \bigl(T^{n} ( A ) ,T^{m} ( A ) \bigr) \leq&H \bigl(T^{n} ( A ) ,T^{n+1} ( A ) \bigr)+H \bigl(T^{n+1} ( A ) ,T^{n+2} ( A ) \bigr)+\cdots \\ &{}+H \bigl(T^{m-1} ( A ) ,T^{m} ( A ) \bigr) \\ \leq&\phi^{n} \bigl(H \bigl(A,T ( A ) \bigr) \bigr)+ \phi^{n+1} \bigl(H \bigl(A,T ( A ) \bigr) \bigr)+\cdots \\ &{}+\phi^{m-1} \bigl(H \bigl(A,T ( A ) \bigr) \bigr). \end{aligned}$$

On taking the upper limit as $n,m\rightarrow\infty$, we get $H(T^{n} ( A ) ,T^{m} ( A ) )$ converges to 0. Since $(X,d)$ is complete, we have $T^{n} ( A ) \rightarrow U^{\ast}$ as $n\rightarrow\infty$ for some $U^{\ast}\in CB ( X )$. There exists an edge between U and $T(U)$, the fact that T is a graph ϕ-contraction yields the result that there is an edge between $T^{n}(U)$ and $T^{n+1}(U)$ for all $n\in \mathbb{N}$. By property (P^∗), there exists a subsequence $\{ T^{n_{k}}(U)\}$ such that there is an edge between $T^{n_{k}}(U)$ and $U^{\ast}$ for every $n\in \mathbb{N}$. By the transitivity of the relation R, there is a path in G (and hence also in $\widetilde{G}$) between U and $U^{\ast}$. Thus $U\in [ U]_{\widetilde{G}}$. Now

$$ H \bigl(T^{n_{k}+1} ( U ) ,T \bigl( U^{\ast} \bigr) \bigr)\leq\phi \bigl(H \bigl(T^{n_{k}} ( U ) ,U^{\ast} \bigr) \bigr). $$

Now $T^{n_{k}} ( U ) \rightarrow U^{\ast}$ as $n\rightarrow \infty$ implies, on taking the upper limit as $n\rightarrow\infty$, $T^{n_{k}+1} ( U ) \rightarrow T ( U^{\ast} )$ as $n\rightarrow\infty$. Thus we obtain $U^{\ast}=T ( U^{\ast } )$.

Finally to prove (iv), suppose the set $F ( T )$ is complete. We are to show that $F(T)$ is singleton. Assume to the contrary that there exist $U,V\in CB ( X )$ such that $U,V\in F ( T )$ and $U\neq V$. By completeness of $F ( T )$, there exists an edge between U and V. As T is a graph ϕ-contraction, so we have

$$\begin{aligned} 0 <&H(U,V) \\ =&H \bigl(T ( U ) ,T ( V ) \bigr) \\ \leq&\phi \bigl(H(U,V) \bigr), \end{aligned}$$

a contradiction. Hence $U=V$.

Conversely, if $F(T)$ is singleton, then obviously $F(T)$ is complete. □

The following corollary is a direct consequence of Theorem 2.1(iii).

Corollary 2.2

Let $(X,d)$ be a complete metric space endowed with a directed graph G such that $V(G)=X$ and $E(G)\supseteq \Delta$. If G is weakly connected, then graph ϕ-contraction mapping $T:CB ( X ) \rightarrow CB(X)$ with $(A_{0},A_{1})\subset E(G)$ for some $A_{1}\in T ( A_{0} )$, has a fixed point.

Corollary 2.3

Let $(X,d)$ be a ε-chainable complete metric space for some $\varepsilon>0$, $T:CB ( X ) \rightarrow CB(X)$ and $\phi:\mathbb{R}^{+}\rightarrow\mathbb {R}^{+}$ be an upper semi-continuous and nondecreasing function with $\phi (t)< t$ for each $t>0$ with

$$ 0< H ( A,B ) <\varepsilon. $$

If

$$ H \bigl(T ( A ) ,T ( B ) \bigr)\leq\phi \bigl(H(A,B) \bigr)\quad\textit{for all } A,B\in CB ( X ) , $$

then T has a fixed point.

Proof

By Lemma 1.8, from $H ( A,B ) <\varepsilon$, we have for each $a\in A$, an element $b\in B$ such that $d(a,b)<\varepsilon$. Consider the graph G as $V(G)=X$ and

$$ E(G)= \bigl\{ (a,b)\in X\times X:0< d(a,b)<\varepsilon \bigr\} . $$

Then the ε-chainability of $(X,d)$ implies that G is connected. For $(A,B)\subset E(G)$, we have from the hypothesis

$$ H \bigl(T ( A ) ,T ( B ) \bigr)<\phi \bigl(H(A,B) \bigr). $$

This implies that T is a graph ϕ-contraction mapping.

Also, G has property (P^∗). Indeed, if $\{X_{n}\}$ in $CB(X)$ with $X_{n}\rightarrow X$ as $n\rightarrow\infty$ and $( X_{n},X_{n+1} ) \subset E ( G )$ for $n\in \mathbb{N}$, implies that there is a subsequence $\{X_{n_{k}}\}$ of $\{X_{n}\}$ such that $( X_{n_{k}},X ) \subset E ( G )$ for $n\in \mathbb{N}$. So by Theorem 2.1(iii), T has a fixed point. □

Example 2.4

Let $X=\{0,1,2,\ldots,n-1\}=V ( G )$ and

$$\begin{aligned} E ( G ) =& \bigl\{ (0,0), ( 1,1 ) ,(2,2),\ldots,(n-1,n-1), \\ &{}(0,1), ( 0,2 ) ,\ldots,(0,n-1),\\ &{}(1,2), ( 1,3 ) ,\ldots,(1,n-1),\\ &{}\cdots\\ &{}(n-2,n-1) \bigr\} . \end{aligned}$$

Let $V ( G )$ be endowed with metric $d:X\times X\rightarrow \mathbb{R} ^{+}$ defined by

$$\begin{aligned}& d ( 0,0 ) =d ( 1,1 ) =\cdots=d ( n-1,n-1 ) =0, \\& d ( 0,1 ) =d ( 1,0 ) =\frac{1}{n}, \\& d ( 0,2 ) =d ( 2,0 ) =d ( 1,2 ) =d ( 2,1 ) =\cdots=d ( n-2,n-1 ) =d ( n-1,n-2 ) =\frac {n}{n+1}. \end{aligned}$$

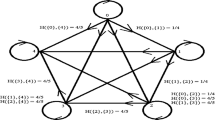
The Pompeiu-Hausdorff weights (for $n=4$) assigned to $A,B\in CB ( X )$ are shown in Figure 1.

Figure 1

Pompeiu-Hausdorff weighted graph.

Furthermore,

$$ H(A,B)=\left \{ \begin{array}{@{}l@{\quad}l} \frac{1}{n},& \mbox{if }A,B\subseteq\{0,1\}\mbox{ with }A\neq B, \\ \frac{n}{n+1}, &\mbox{if }A\mbox{ or }B\mbox{ (or both)}\nsubseteq\{0,1\} \mbox{ with }A\neq B, \\ 0, & \mbox{if }A=B. \end{array} \right . $$

Define $T:CB ( X ) \rightarrow CB(X)$ as follows:

$$ T(U)=\left \{ \begin{array}{@{}l@{\quad}l} \{0\}, & \mbox{if }U\subseteq\{0,1\}, \\ \{0,1\}, & \mbox{if }U\varsubsetneq\{0,1\}.\end{array} \right . $$

Note that, for all $A,B\in CB(X)$ with edge between A and B, there is an edge between $T(A)$ and $T(B)$. Also there is a path between A and B implies that there is a path between $T(A)$ and $T(B)$.

Define $\phi:[0,\infty)\rightarrow [0,\infty)$ by

$$ \phi(t)=\left \{ \begin{array}{@{}l@{\quad}l} \frac{4t}{5}, & \mbox{if }t\in [0,\frac{5}{2}), \\ \frac{2^{n}(2^{n+1}t-3)}{2^{2n+1}-1}, & \mbox{if }t\in [\frac{2^{2n}+1}{2^{n}},\frac{2^{2(n+1)}+1}{2^{n+1}}], n\in \mathbb{N} .\end{array} \right . $$

An easy computation shows that ϕ is continuous on $[0,\infty)$ and $\phi(t)< t$ for all $t>0$.

Now for all $A,B\in CB ( X )$, we consider the following cases:

• (a) For $A,B\subseteq\{0,1\}$, we have $H(T ( A ) ,T ( B ) )=0$.

• (b) If $A\subseteq \{ \{0\},\{1\},\{0,1\} \}$ and $B\varsubsetneq \{ \{0\},\{1\},\{0,1\} \}$, then we have

  $$\begin{aligned}[b] H \bigl(T ( A ) ,T ( B ) \bigr) &=H \bigl(\{0\},\{0,1\} \bigr)= \frac{1}{n}\\ &<\frac{4n}{5n+5}=\phi \biggl( \frac{n}{n+1} \biggr) =\phi \bigl(H(A,B) \bigr). \end{aligned} $$

• (c) In the case $A,B\varsubsetneq \{ \{0\},\{1\},\{0,1\} \}$, we have

  $$ H \bigl(T ( A ) ,T ( B ) \bigr)=H \bigl(\{0,1\},\{0,1\} \bigr)=0. $$

  Obviously, (1.1) is satisfied in the cases (a), (b), and (c).

Hence for all $A,B\in CB ( X )$ having an edge between A and B, (1.1) is satisfied and so T is a graph ϕ-contraction. Thus all the conditions of Theorem 2.1 are satisfied. Moreover, $\{0\}$ is the fixed point of T and $F ( T )$ is complete.

Remark 2.5

• (1) If $E(G):=X\times X$, then clearly G is connected and Theorem 2.1 improves and generalizes Theorem 2.5 in [19], Theorems 2.1-2.3 in [11] and Theorem 3.1 in [7].

• (2) Theorem 2.1 with the graph G improves and generalizes Theorem 2.1 in [20] from single valued to set-valued mappings.

• (3) If $E(G):=X\times X$, then clearly G is connected and our Corollary 2.2 extends and generalizes Theorem 2.5 in [19], Theorem 3.2 in [21], and Theorem 3.1 in [7].

• (4) If $E(G):=X\times X$, then clearly G is connected and our Corollary 2.3 improves and generalizes Theorem 3.2 in [21] and Theorem 3.1 in [7].

• (5) Corollary 2.3 extends and improves the Banach contraction theorem and Theorem 5.1 in [27].