Abstract
The abnormal aggregation of proteins into amyloid fibrils, usually implemented by a series of biochemical reactions, is associated with various neurodegenerative disorders. Considering the intrinsic stochasticity in the involving biochemical reactions, a general chemical master equation model for describing the process from oligomer production to fibril formation is established, and then the lower-order statistical moments of different molecule species are captured by the derivative matching closed system, and the long-time accuracy is verified using the Gillespie algorithm. It is revealed that the aggregation of monomers into oligomers is highly dependent on the initial number of misfolded monomers; the formation of oligomers can be effectively inhibited by reducing the misfolding rate, the primary nucleation rate, elongation rate, and secondary nucleation rate; as the conversion rate decreases, the number of oligomers increases over a long time scale. In particular, sensitivity analysis shows that the quantities of oligomers are more sensitive to monomer production and protein misfolding; the secondary nucleation is more important than the primary nucleation in oligomer formation. These findings are helpful for understanding and predicting the dynamic mechanism of amyloid aggregation from the viewpoint of quantitative analysis.
Similar content being viewed by others
1 Introduction
Spontaneous protein aggregation is referred to as a complex phenomenon in which the soluble protein monomers or protein fragments aggregate by self-association into insoluble amyloid fibrils through a series of intermediate species, such as oligomers in living systems. The normal aggregation of proteins is useful for many biological or biotechnological functions, such as the polymerization of actin [1], the structural strength of spider silk [2], and the storage of peptide hormone hormones within secretory cells [3], while the abnormal aggregation can be associated with various neurodegenerative disorders [4], including Alzheimer’s, Parkinson’s, Huntington’s, type II diabetes, and prion disease. Clearly, an overall understanding of the formation mechanism of the amyloid fibrils is vital for controlling or inhibiting the toxicity of the amyloid oligomers.
Increasing experimental and theoretical investigations reveal that the process of protein aggregation actually is a nucleation-dependent multi-stage polymerization mechanism [5–7], including nucleation, conversion and elongation, and is generally considered a type of crystallization [8, 9]. In the nucleation stage, the unstructured aggregates are stochastically generated from the protein monomers by a kind of self-association action. In the conversion stage, the unstructured oligomers are converted into short fibrillar aggregates. While in the stage of elongation, these fibrillar species undergo a rapid extension by monomer addition. After the fibrillar species was elongated, the freely moving monomers in solution can be adsorbed onto the fibril surface and then detach as oligomers, and this auto-catalytic process is the so-called monomer-dependent secondary nucleation. In fact, the earliest secondary nucleation in the formation of protein filaments was identified in mutant hemoglobin Hbs [10, 11]. It was later found in many other proteins such as amyloid-β peptide [7, 12], α-synuclein [13], and in the recent decade, the secondary nucleation of monomers on the fibril surface has been recognized as the main mechanism giving rise to the rapid generation of new aggregates [6, 14, 15]. Thus, the amyloid aggregation with secondary nucleation is like a positive feedback process.
Mathematical models, as bridges between macroscopic measurements and microscopic mechanisms [5–7] are useful in shedding light on the underlying mechanism for amyloid aggregation, which should be the first step to control and cure neurodegenerative disorders. For example, it is well known that the primary nucleation model proposed by Oosawa et al. for describing actin polymerization acts as the basis of the amyloid fibrillary nucleation mechanism [16], a coarse-grained coupled kinetic equation proposed by Knowles et al. revealed that the dynamics of amyloid growth is dominated by secondary rather than primary nucleation events [17]. The nucleation-conversion-elongation self-assembly reaction model proposed by Garcia et al. generalized the classical theory of nucleated polymerization by introducing a cascade of metastable intermediate species [18]. In a very recent study, a general chemical kinetic framework for amyloid oligomers developed by Dear et al. is the first systematic study of the oligomerization mechanisms of different types of amyloid proteins [19]. These achievements elucidate the aggregation mechanism to a certain extent. Nevertheless, most kinetic investigations for protein oligomers are based on deterministic mean-filed models.
Note that there are clear sources of stochasticity in amyloid aggregation. Amyloid aggregation is implemented through a series of biochemical reactions; some reactions are complex, while some are still to be uncovered, so these unknown reactions are the first source of uncertainty. The biochemical reactions involved usually occur in small-volume environments. The intrinsic molecular noise, which tends to make the inherent variability of the aggregation process prominent [11, 20–22], is the second source. Meanwhile, note that the chemical master equation is appropriate for describing the time evolution of a well-stirred chemically reacting system [23, 24], and its low-order statistical moments can be captured with the derivative matching moment closure [25, 26]. Thus, in this paper, we develop a unified probabilistic description of the chemical master equation for the relative process of protein self-assembly. Then, we apply the derivative matching moment closure method to disclose the factors that most impact the amyloid aggregation from the statistical average.
The paper is structured as follows: In Sect. 2, the chemical master equation for the amyloid aggregation process from misfolded monomers to toxic oligomers to fibrils is developed, and the resultant closed moment system is deduced. In Sect. 3, the accuracy of the moment closure method to the stochastic model is examined by means of stochastic simulation results. Particularly, the effects of the various aggregation rate parameters on the population of oligomers during nucleation are systematically studied, and the significance of the relevant parameters is analyzed. Finally, some concluding remarks are drawn in Sect. 4.
2 Model and method
2.1 Chemical master equation for protein amyloid aggregation
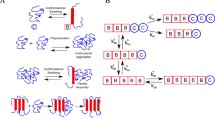
Biophysical experiments show that the subtle process of amyloid aggregation, which is usually implemented through a series of chemical reactions, can be divided into several stages, including primary nucleation, conversion from oligomer to fibril, fibril elongation, fragmentation, and secondary nucleation [11, 14, 27, 28]. The primary nucleation is the start of the aggregation, with the rate of formation of new aggregates dependent solely on the concentrations of monomers, while the secondary nucleation occurs at a rate dependent on the surface-catalyzed fibrils. That is, one or more monomers interact with the existing fibrils to generate new oligomers. Note that a long fibril can also break into shorter fibrils at any location along their length to yield new aggregates, independently of monomer concentration. Nevertheless, compared with the monomer-dependent secondary nucleation, the monomer-independent fibril fragmentation is negligible since it is not the main mechanism leading to the rapid formation of new aggregates. Based on these considerations, we aim to develop a chemical master equation to describe the aggregation process (Fig. 1), including slow primary nucleation, single-step conversion, fast elongation, and secondary nucleation stages in this subsection.
Note that the combined effect of these above different microscopic steps can be described by the master equation of the key experimental observable. In particular, increasing evidence suggests oligomers, the aggregation intermediate species, are correlated with cellular toxicity in various forms of amyloidogenesis [29] and neuronal death [30, 31], and thus, the intermediate species of oligomers should be incorporated. For simplicity, the evolution of the intermediate species of size not larger than \({n_{1}}\) is only considered, while the oligomer of the average size at conversion is used to denote the species of the maximal size. Here, we adopt the phase-structure method [32, 33] to distinguish between oligomers and fibrils. Compared with transient populations of oligomers, it is easier to obtain the average populations from experiments [34], and thus, this kind of treatment is appropriate. In fact, the same technique has been used in the fibril stage.
In order to derive the mathematical model, we still need to make the following assumptions:
(1) The monomer undergoes a conformational change to form a misfolded monomer with a misfolding rate \({K_{0}^{+}}\), and then two misfolded monomers form the minimum stable aggregate (i.e., dimer) as a critical nucleus [24, 35];
(2) Oligomers polymerize into larger intermediate species by adding monomers while dissociating into smaller intermediate species by subtracting monomers; the fibril elongation also occurs through monomer addition. Meanwhile, oligomer and fibril states are modeled as average stages O and \({P_{2} }\), respectively [32, 33];
(3) Oligomers are heterogeneous aggregates of different sizes that are structurally distinct from mature fibrils. It involves a conversion step from oligomers into short fibrillar species capable of further growth, which is assumed to be carried out by adding monomers to oligomers in reaction order \({n_{c}}\) [7, 19, 36];
(4) The secondary nucleation is also assumed to be a one-step nucleation process [12]. Note that the size of oligomers detached from the fibril surface is smaller than the average size \({O_{\alpha }}\) of the converting oligomers, so we assume the oligomers generated from the secondary nucleation are dimer [7];
(5) Reverse conversion of fibrils to oligomers is neglected as it is experimentally found that fibrils are far more stable than non-fibrillar oligomers [19].
Note that the concentration of monomers produced in vivo cannot grow unbounded. A saturated production function \({k_{p}} = f(N_{M_{0}}){N_{M_{0}}} = \delta N_{M_{0}}(1 - \frac{N_{M_{0}}}{\gamma })\) can be introduced to represent its production process [33], where \(f(N_{M_{0}}) = \delta (1 - \frac{N_{M_{0}}}{\gamma })\) is the corrected increase rate in the logistic equation, with δ being the growth rate of monomers and γ the carrying capacity. To keep up with the transthyretin oligomers [26], the average oligomer size \({O_{\alpha }} = 6\) is assumed, while following Ref. [37] the average fibril size is chosen as \({P_{\alpha }} = 10\) in the subsequent simulation. Let \({M_{0}},{M_{1}},{M_{2}},{M_{3}}\), and \({M_{4}}\) denote monomers, misfolded monomers, dimers, triamers, and tetramers, respectively. Let O be the oligomers of average size \({O_{\alpha }}\), \({P_{1}}\) be the converted oligomers (also known as fibrillar oligomers or fibrils), and \({P_{2}}\) be the fibrils of average size \({P_{\alpha }}\). Suppose \({n_{1}} = 4\) and \({n_{c}} = 2\), then the resultant biochemical reactions can be summarized, as shown in Table 1.
With \(N(t) = ({N_{{M_{0}}}},{N_{{M_{1}}}},{N_{{M_{2}}}},{N_{{M_{3}}}},{N_{{M_{4}}}},{N_{O}},{N_{{P_{1}}}},{N_{{P_{2}}}})\) denoting the number of \({M_{0}},{M_{1}}, {M_{2}},{M_{3}},{M_{4}},O,{P_{1}},{P_{2}}\) at time t and the \(8 \times 14\) stoichiometric matrix
in mind, where each row belongs to a reaction and each column involves a substance, then the chemical master equation [38] can be given as follows:
where \(P({N_{{M_{0}}}},{N_{{M_{1}}}},{N_{{M_{2}}}},{N_{{M_{3}}}},{N_{{M_{4}}}},{N_{O}},{N_{{P_{1}}}},{N_{{P_{2}}}},t)\) is the joint probability distribution of species at the state vector \(({N_{{M_{0}}}},{N_{{M_{1}}}},{N_{{M_{2}}}},{N_{{M_{3}}}},{N_{{M_{4}}}},{N_{O}},{N_{{P_{1}}}},{N_{{P_{2}}}})\) at time t. We remark that Eq. (1) is a probabilistic description of the formation process of protein aggregation, which contains more statistical information than the associated deterministic models in the mean-field sense [7, 33]. What is more, different from the stochastic master equation model constructed in Ref. [26], where only a primary nucleation process with intermediate oligomers was considered, the above model (1) covers the whole aggregation process from soluble protein monomers to insoluble fibrils.
2.2 The moment system and the derivative matching moment closure
Note that (1) is a chemical master equation of nonlinear reaction rates. For this type of equation, the analytical solution can usually not be acquired. The Gillespie stochastic simulation algorithm (SSA) [38, 39] can obtain the random solution, but it takes quite a long time to capture statistical moments. Instead, the method of moment evolutionary equations is the first and foremost technique in this regard.
For simplicity, we rewrite (1) into
where \({S_{r}}\) is the row vector of the stoichiometric matrix, and \({\omega _{r}}(N)\) is the propensity function for the rth chemical reaction governed by mass action kinetics [38]
with K being the reaction constant. Multiplying the both sides of (2) by \({e^{N\Theta }}\) and summing over all possible values of N, we arrive at
Then, note that the first term in the right-hand side of (4) is equal to
Thus, (4) can be reduced to
Note that the moment generating function is \(M(\Theta ,t) = \sum \limits _{N} {{e^{N\Theta }}P(N,t)} = \sum \limits _{{\mathbf{{m}}} = 0}^{14} {{\mu _{\mathbf{{m}}}}} \frac{{{\Theta ^{\mathbf{{m}}}}}}{{{\mathbf{{m}}}!}}\) with
being the moment of order \(\sum \nolimits _{i = 1}^{8} {{m_{i}}} \). Here, \({\Theta ^{m}} = \theta {{}_{1}^{{m_{1}}}}\theta {{}_{2}^{{m_{2}}}} \cdots \theta {{}_{8}^{{m_{8}}}}\), \({\mathbf{{m}}} = [{m_{1}}\,{m_{2}}\;...\;{m_{8}}] \in Z_{ \ge 0}^{8}\), and \(Z_{ \ge 0}^{8}\) stands for the eight-dimensional space of nonnegative integers. By extracting the coefficients for \({\theta _{1}},{\theta _{2}},\ldots,{\theta _{8}}\) from the both sides of (5), we acquire the moment evolutionary equations of general form as
Since the higher-order moments are involved in the evolution of the low-order moments, the moment system (6) is not self-closed. In order to close this system, various moment closure techniques [40, 41] have been proposed to approximate the higher-order moments by the lower-order ones. The derivative matching moment closure [25] is such a scheme that does not rely on the prior distribution but can lead to exact moment dynamics in many cases [26, 42].
The evolution of the first two order statistical moments of the relevant oligomers is of general interest. That is, the low-order moment system consists of \(2C_{8}^{1} + C_{8}^{2} = 44\) equations (see Appendix A), corresponding to the moment equations (6) for \(1 \le \sum \nolimits _{i = 1}^{8} {{m_{i}}} \le 2\). Let μ be the vector consisting of all the moments up to the second order and μ̄ be the vector of moments of order greater than two, then (6) can be rewritten as
where \(\mu = {[{\mu _{(1,0)}},{\mu _{(0,1)}},{\mu _{(2,0)}},{\mu _{(1,1)}},{ \mu _{(0,2)}}]^{T}}\), a is state-independent vector, A and B are state-independent matrices. The so-called moment closure is to approximate the higher order moments in μ̄ by functions of the lower order moments. That is, one needs to choose a vector-valued function ϕ̄ such that the original moment system can be approximated by
where ϕ̄ is the so-called closure function.
The so-called derivative matching moment closure is to approximate each of the higher-order moments with a divisible function under the requirement that the closed approximate moment system keeps the initial value and the initial rate of change of the original unclosed moment system. The divisible function is assumed to have a general form
where \({\alpha _{p}}(p = 1,2,\ldots,k)\) can be given by the unique solution to the following set of linear equations:
with \(\left ( { \begin{array}{c} h \\ l \end{array} } \right ) = \left \{ { \begin{array}{l} {\frac{{h!}}{{l!(h - l)!}},h \ge l;} \\ {0,h < l} \end{array} } \right. \) and \(\left ( { \begin{array}{c} {{h_{1}},\ldots,{h_{s}}} \\ {{l_{1}},\ldots,{l_{s}}} \end{array} } \right ) = \left ( { \begin{array}{c} {{h_{1}}} \\ {{l_{1}}} \end{array} } \right ) \cdots \left ( { \begin{array}{c} {{h_{s}}} \\ {{l_{s}}} \end{array} } \right )\). When applying this closure scheme to our low-order moment system, the higher-order moments can be replaced by the following functions of lower-order moments (see Appendix B).
2.3 Gillespie stochastic simulation algorithm
In order to verify the correctness and accuracy of the derivative matching moment method, let us use the stochastic simulation algorithm (SSA), which Gillespie proposed under the assumptions that the system is homogeneous and well-mixed [38, 39], to directly simulate the time evolution of the master equation system (1). The idea is to simulate the time evolution of the system in a series of steps in the way of a random walk. At each time step, the system is exactly in one state (i.e., the number of molecules of each species is determined). The algorithm determines the nature of the next reaction as well as the waiting time Δt, supposing that the system is at a given state at time t. The probability for a specific reaction to occur depends on its kinetics rate, which is a function of its corresponding kinetics constant and the number of molecules, while the waiting time is determined by the total transition probability. When applying the SSA to our system, there are 14 biochemical reactions involved (see Table 1 and Fig. 2), and the specific algorithm flow is as follows:
1) Set the initial number of \(t = 0\) for each species to
2) Calculate the transition rate \({\omega _{r}}(N)\) according to (3).
3) Set the total transition rate \({C_{14}}(N) = \sum \limits _{r = 1}^{14} {{\omega _{r}}(N)} \).
4) Generate two uniform random numbers \({z_{1}}\) and \({z_{2}}\).
5) Find \(r \in [1,\ldots,S]\) such that \(\sum \limits _{k = 1}^{r} {{\omega _{k}}(N)} > {z_{1}}{C_{14}}(N) > \sum \limits _{k = 1}^{r - 1} {{\omega _{k}}(N)}\).
6) Set \(\Delta t = - \frac{1}{{{C_{14}}(N)}}\ln {z_{2}}\).
7) Set \(t = t + \Delta t\) and update species populations based on the reaction r.
8) Return to step 2) and repeat until an end condition is met.
3 Results and discussion
For near isothermal reactions, considering that the activation energy plays a major role in determining the reaction rate constant, the following relation is obtained from the Arrhenius equation [43]:
That is, the oligomer formation rate increases with the increase in aggregate size. Specifically, we use the relations [33]:
Note that the process for protein to assembly into amyloid fibrils is similar to that in Ref. [19], the rate constants involved in the reactions relevant with oligomers are set as follows (with concentration units: \({\mathrm{{\mu M}}}\) and time units: h).
Here, the equilibrium constant \({{{k_{e}} = K_{1}^{-} } \mathord{\left / { \vphantom {{{k_{e}} = K_{1}^{-} } {K_{1}^{+} }} } \right . \kern -\nulldelimiterspace} {K_{1}^{+} }}\) is set around 0.01, which ensures that the oligomer is moderately more unstable than the monomer [7]. In addition, we assume that the misfolding rate \(K_{0}^{+} = 0.03\) is always less than refolding rate \(K_{0}^{-} \). Throughout the calculation, \(\delta = 5\) and \(\gamma = 4000\) are fixed, and the initial conditions are set as
Considering the biologically significant parameters in modeling the aggregation process may have very different order of magnitude ranges [33], we emphasize that the values used in the numerical simulations are only for illustrative purposes and may not accurately reflect the rate constants for specific protein (such as transthyretin) amyloid aggregation. In this paper, these parameters are chosen to satisfy the bounds of biological rationality [7, 19, 33]. In the diagram below, we use \({\bar{M}_{0}},\;{\bar{M}_{1}},{\bar{M}_{2}},{\bar{M}_{3}},{\bar{M}_{4}}, \bar{O},{\bar{P}_{1}},{\bar{P}_{2}}\) to represent the average of \({N_{{M_{0}}}},{N_{{M_{1}}}},{N_{{M_{2}}}},{N_{{M_{3}}}},{N_{{M_{4}}}},{N_{O}},{N_{{P_{1}}}},{N_{{P_{2}}}}\).
Figure 3 shows the mean we obtain for the various reaction species. It can be seen that the results obtained from the derivative matching moment method are consistent with those obtained from the SSA. This means that the moment method accurately captures the time evolution of the lower-order statistical moments. Therefore, we will analyze different amyloid aggregation processes using derivative matching moment closure schemes.
The mean number of \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O,{P_{1}},{P_{2}}\). Comparison of the mean by derivative matching moment closure method (red solid curves) and SSA (black dots). The initial values are set as \({N_{{M_{0}}}}(0) = 2000,\;{N_{{M_{1}}}}(0) = {N_{{M_{2}}}}(0) = {N_{{M_{3}}}}(0) = {N_{{M_{4}}}}(0) = {N_{O}}(0) = {N_{{P_{1}}}}(0) = {N_{{P_{2}}}}(0) = 0\), and the parameters are \({O_{\alpha }} = 6,{P_{\alpha }} = 10,\delta = 5,\gamma = 4000,K_{0}^{+} = 0.03,K_{1}^{+} = 3.8 \times {10^{ - 3}},K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4) ,\varepsilon = 1 \times {10^{ - 3}},{K_{c}} = 3.3 \times {10^{ - 2}}, {K_{+} } = 1,\;{K_{se}} = 2.9 \times {10^{ - 2}},\; {K_{d}} = 0.36\). The results obtained by SSA are based on 10000 realizations
3.1 Fibril-independent oligomers formation
Let \({K_{c}} = {K_{+} } = {K_{se}} = 0\) as in Table 1, then the amyloid aggregation process is reduced to the process of early amyloid aggregation, where only the primary oligomer formation with monomer addition and subtraction is involved.
Figure 4 shows the statistically quantitative evolution of the monomer, the misfolded monomer, the dimer, the triamer, the tetramer, the oligomer with average size 6, the converted oligomer, and the fibril. When \(\delta = 0\), that is \({k_{p}} = \delta N_{{M_{0}}}(1 - \frac{N_{M_{0}}}{\gamma }) = 0\), which means there is no monomer production in vitro experiment. When \(\delta \ne 0\), that is \({k_{p}} = \delta N_{M_{0}}(1 - \frac{N_{M_{0}}}{\gamma }) \ne 0\), which means there is production of monomers in vivo experiments. From this figure, it is clear that increasing the number of monomers would greatly increase the number of oligomers and thus accelerate the nucleation process in both cases. Moreover, it is also clear that the aggregation process is highly dependent on the initial number of monomers, and the more monomers there are at the initial time, the more oligomers there will be. This observation is consistent with the discovery disclosed by previous experimental and theoretical research [15, 26]. Note that the production of big molecular proteins varies from person to person, and thus the individual level of amino acid monomers fluctuates. Hence, the observation from Fig. 4 again can help explain why some people are more apt to suffer from amyloid disease to some extent.
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O\) at different parameters: \(\delta = 5, {N_{{M_{0}}}}(0) = 2000\) (red), \(\delta =0, {N_{{M_{0}}}}(0) = 2000\) (green) and \(\delta = 0, {N_{{M_{0}}}}(0) = 3000\) (blue). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \gamma = 4000, K_{0}^{+} = 0.03, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {{K_{c}} = {K_{+} } = {K_{se}} = 0}, {K_{d}} = 0.36\)
Figure 5 shows the effect of the misfolding rate \({K_{0}^{+}}\) on the average number of the monomer, the misfolded monomer, the dimer, the triamer, the tetramer, the oligomer, the converted oligomer, and the fibril. It is clear that as the misfolding rate increases, the number of all types of oligomers (Fig. 5(c)–(f)) increases at a given time, while it takes less time for these oligomers to reach a given level. Reversely, reducing the misfolding rate can help slow or inhibit the formation of protein aggregation. Note that the model (1) covers the description of the early protein aggregation in transthyroxin amyloid disease [26], decreasing the misfolding rate for the protein monomers should be of general importance for preventing amyloid disease. In fact, strategies to stabilize the folded state and avoid protein misfolding are now increasingly widely utilized in the clinic to treat familial amyloid polyneuropathy [44].
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O\) at different misfolding rates: \(K_{0}^{+} = 0.01\) (blue), 0.02 (green), and 0.03 (red). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 0,\gamma = 4000, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{c}} = {K_{+} } = {K_{se}} = 0, {{K_{d}} = 0.36}\)
Figure 6 shows the effect of the primary nucleation rate \({K_{1}^{+}}\) on the average number of the monomer, the misfolded monomer, the dimer, the triamer, the tetramer, the oligomer, the converted oligomer, and the fibril. It can be seen clearly that the number of oligomers (Fig. 6(c)–(f)) increases as the nucleation rate grows, suggesting that inhibiting the primary nucleation process can effectively slow the formation of amyloid disease. Note that in this process, the accumulation of toxic oligomers tends to play a leading role in amyloid disease [5, 30, 31, 34, 45], and therefore, it is necessary to reduce their formation in the primary pathway. For example, chaperone proteins have been used to inhibit protein aggregation in the primary nucleation process in cultured cells of mice [45].
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O\) at different primary nucleation rates: \(K_{1}^{+} = 1.8 \times {10^{ - 3}}\) (blue), \(2.8 \times {10^{ - 3}}\) (green), and \(3.8 \times {10^{ - 3}}\) (red). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 0,\gamma = 4000, K_{0}^{+} = 0.03, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{c}} = {K_{+} } = {K_{se}} = 0, {K_{d}} = 0.36\)
3.2 Fibril-dependent oligomers formation
Now let us turn to the general aggregation process where \({K_{c}},{K_{+} }\), and \({K_{se}}\) are all not vanishing. Besides the primary nucleation, the aggregation process involving fibrils, which contains the conversion stage of oligomers, the elongation stage of fibrils, and the fibril-dependent secondary nucleation, is also taken into account.
Figure 7 shows the effect of the conversion rate \({K_{c}}\) on the average number of the monomer, the misfolded monomer, the dimer, the triamer, the tetramer, the oligomer, the converted oligomer, and the fibril. The quantitative observation shows that in the early stage of aggregation, with the decrease of conversion rate, the number of oligomers (Fig. 7(c)–(d)) decreased somewhat. This corresponds to reactions in closed or open systems at an early stage, where a reduction in the conversion of oligomers slows down the aggregation reaction, corresponding to a reduction in the number of oligomers. However, over longer time scales, this strategy resulted in a significant increase in the number of oligomers. This effect occurs because the reduction of \({K_{c}}\) reduces the reaction flux from monomers to amyloid fiber precursors, which can rapidly expand into mature fibril(Fig. 7(g)–(h)), reflecting the complexity of the aggregation process [36]. Figure 7 also shows that the number of converted oligomer \({P_{1}}\) is far less than that of unconverted oligomer O, and this is consistent with the existing experimental findings [7, 19]. Thus, following Refs. [7, 19], this point actually reflects a basic fact: oligomers are a key source of fibrils, but due to the high free energy and low stability of intermediate oligomers species, most oligomers dissociate back to monomers rather than form new fibrils. As a result, it can be concluded that there are few oligomers on the pathway to fibrils but relatively many off-pathway oligomers.
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O,{P_{1}},{P_{2}}\) at different conversion rates: \(K_{c}= 3.3 \times {10^{ - 3}}\) (blue), \(8 \times {10^{ - 3}}\) (green), and \(3.3 \times {10^{ - 2}}\) (red). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 5,\gamma = 4000, K_{0}^{+} = 0.03, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{+} } = 1, {K_{se}} = 2.9 \times {10^{ - 2}}, {K_{d}} = 0.36\)
Figure 8 shows the effect of elongation rate \({K_{+} }\) on the average number of the monomer, the misfolded monomer, the dimer, the triamer, the tetramers, the oligomer, the converted oligomer, and the fibril. It can be seen that with the increase of elongation rate, the numbers of all the oligomers (Fig. 8(c)–(f)) increase at a given time, while it takes less time for these oligomers to reach a given level. In other words, reducing the elongation rate can inhibit the formation of toxic oligomers. In fact, there have been experimental research that used inhibitors to compete with fibril end and interact with sequence regions important for elongation reaction to achieve effective inhibition on fibril elongation [46].
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O,{P_{1}},{P_{2}}\) at different elongation rates: \(K_{+} = 5 \times {10^{ - 4}}\) (blue), \(1 \times {10^{ - 3}}\) (green), and 1 (red). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 5,\gamma = 4000, K_{0}^{+} = 0.03, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{c}} = 3.3 \times {10^{ - 2}}, {K_{se}} = 2.9 \times {10^{ - 2}}, {K_{d}} = 0.36\)
Figure 9 shows the effect of secondary rate \({K_{se}}\) on the average number of the monomer, the misfolded monomer, the dimer, the triamer, the tetramers, the oligomer, the converted oligomer, and the fibril. Again, it is observed that the number of converted oligomers is much lower than that of the unconverted oligomers. Particularly, it is observed that the quantitative results show that inhibition of secondary nucleation could reduce the number of oligomers. Note that the fibril structure itself is not toxic in vivo, but it promotes the formation of toxic oligomers by surface catalysis. It has been shown that toxicity tends to be most relevant in aggregation reactions involving fibrils and monomers [6, 14, 47]. Moreover, it is known that a distinctive feature of various amyloid diseases is the different patterns of spreading through adjacent tissues, but this spreading has to be explained by the mobility of oligomers derived from fibrils to a large extent [6]. Therefore, inhibition of secondary nucleation is expected to help reduce toxicity and its spreading, and to our knowledge, the employment of antibodies and molecular chaperone is for such a purpose, namely to selectively inhibit the catalytic cycle of the secondary nucleation pathway [46].
The mean number of oligomers \({M_{0}},{M_{1}},{M_{2}},{M_{3}},{M_{4}},O,{P_{1}},{P_{2}}\) at different secondary nucleation rates: \(K_{se} = 5 \times {10^{ - 3}}\) (blue), \(8 \times {10^{ - 3}}\) (green), and \(2.9 \times {10^{ - 2}}\) (red). The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 5,\gamma = 4000, K_{0}^{+} = 0.03, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{c}} = 3.3 \times {10^{ - 2}}, {K_{+} } = 1, {K_{d}} = 0.36\)
3.3 Primary via secondary nucleation
Now, let us compare the differences in generation of oligomers from primary and secondary pathways. First, let us show the change in the mean of the dimer with or without secondary processes. From Fig. 10(a), it is clear that more oligomers can be formed in the presence of secondary nucleation than in the absence of secondary nucleation. Next, let us compare the number of dimers produced in the primary and secondary processes. Theoretically, the means (\(\mu _{00100000}^{1*}\) and \(\mu _{00100000}^{2*}\)) of the dimer produced in the two processes can be derived from the following equations:
The numerical results are shown in Fig. 10(b). As shown in Fig. 10(b), in the early stage of aggregation, the dimers formed in the secondary process are less than the dimers formed in the primary process, but the dimer formed in the secondary process can experience very rapid growth, and thus, the number of the dimers formed in the primary process far falls behind. This can be explained as follows. The early stage of aggregation is dominated by the monomers-dependent primary nucleation, while secondary nucleation is fibril-dependent, but there are only monomers, and thus, the dimers generated from the primary nucleation are more abundant in quantity in this stage. Once fibril reaches a critical concentration, the secondary nucleation will replace the primary nucleation as the main origin of the new dimer, which causes a quick proliferation due to positive feedback [14]. It can be predicted that the dimer produced by subsequent secondary nucleation may be several orders of magnitude more than the dimer produced by primary nucleation. This prediction is consistent with the experimental research [14, 48]. Hence, from an overall perspective of preventing the protein amyloid disease, it is more vital to inhibit the secondary nucleation in order to reduce the oligomers. In this sense, it should be more effective for suppressing the production of neurotoxic oligomers by altering the secondary nucleation pathway.
(a) The mean number of \({M_{2}}\) with secondary nucleation rate \(K_{se} =2.9 \times {10^{ - 2}}\) (blue) and without secondary nucleation \(K_{se} =0\) (red); (b) In the presence of secondary nucleation, the mean number of oligomer \(M_{2}^{*}\) produced by primary (green) and secondary (magenta) processes in aggregation reactions. The other parameters are \({O_{\alpha }} = 6, {P_{\alpha }} = 10, \delta = 5,\gamma = 4000, K_{0}^{+} = 0.03, K_{1}^{+} = 3.8 \times {10^{ - 3}}, K_{i}^{+} = K_{i - 1}^{+} + \varepsilon (2 \le i \le 4), \varepsilon = 1 \times {10^{ - 3}}, {K_{c}} = 3.3 \times {10^{ - 2}}, {K_{+} } = 1, {K_{d}} = 0.36\)
3.4 Sensitivity analysis
More than ten parameters are involved in the model (1), and thus, it is natural to ask which parameters are most significant. Nevertheless, it is as difficult to solve this question from the viewpoint of experiments as to determine the value of model parameters. Considering the parameters of our model have different units and are of different orders of magnitude, We carry on the elasticity analysis [33, 49] to examine the proportional response to the scale change in the model parameters. Here the elasticity obtained from the proportional response measures the sensitivities of different parameters.
For the system (1), we define the \(8 \times 11\) elastic coefficient matrix as
where \(\bar{N} = \left ( {\bar{M}}_{0},{\bar{M}}_{1},{{\bar{M}}_{2}},{{\bar{M}}_{3}},{ \bar{M}}_{4},\bar{O},{\bar{P}}_{1},{\bar{P}}_{2} \right )\) and \(p = (\delta ,\gamma ,{K_{0}^{+}} ,{K_{1}^{+}}, {K_{2}^{+}}, {K_{3}^{+}}, {K_{4}^{+}}, {K_{d}}, {K_{c}}, {K_{+}} ,{ K_{se}})\). Then, we obtain the elastic coefficient by means of finite difference as
with \(\Delta {p_{j}} = 0.2{p_{j}}\). The transpose of the full elasticity coefficient matrix when \(t = 20\) is shown in Table 2. It is clear that the carrying capacity γ and the misfolding rate \(K_{0}^{+} \) of oligomers \({M_{2}},{M_{3}},{M_{4}}\) have relatively large elastic coefficient values of 1.0598, 1.0567, 1.0579, 1.0630, 1.0581, and 1.0615 respectively, which have extremely promoting effects, so both of them are the most sensitive parameters. Note that the elastic coefficient of the secondary nucleation rate \({K_{se}}\) with respect to the formation of dimer \({M_{2}}\) is 0.1737, which is much higher than that of the corresponding primary nucleation rate \(K_{1}^{+} \) of 0.0044, thus verifying that secondary nucleation is indeed more sensitive to its generation than primary nucleation. Similarly, it is also clear from the values of the elastic coefficients that the nucleation rates \(K_{2}^{+} \) and \(K_{3}^{+} \) markedly promotes the production of oligomers \({M_{3}}\) and \({M_{4}}\), respectively, while the conversion and elongation rates \({K_{c}}\) and \({K_{+} }\) only have relatively little impact, although \({K_{c}}\) can promote the formation of \({M_{2}}\) but inhibit the formation of \({M_{3}}\). As is known, there are few experiments dedicated to exploring the detailed process as ours, including the role of the conversion and elongation rates, and thus, the analysis presented here should be useful in shedding more light onto the aggregation mechanism of amyloid protein.
4 Conclusions
We have built a chemical master equation model for exploring oligomer formation in amyloid aggregation processes, including primary nucleation, structural conversion, fibril elongation, and secondary nucleation. With the derivative matching closure applied to the resultant evolutionary equations for the low-order statistical moments, a self-closed moment system is acquired. The long-time accuracy of the low-order statistical moments has also been verified and analyzed using the Gillespie simulation algorithm and sensitivity analysis.
Using the evolution of the low-order statistical moments, it has been revealed that the aggregation of monomers into toxic oligomers is highly dependent on the average number of monomers, the misfolding, the primary nucleation, and the secondary nucleation rates. It was also found that the conversion rate is an adjustable factor affecting amyloid aggregation. Particularly, when the secondary nucleation is present, the formation of oligomers is a process of auto-catalytic cycle. There is a lag stage before the early stage, and each species may not reach a stable state in a short time as well, but the sensitivity analysis shows that inhibiting the secondary nucleation is more critical than inhibiting the primary nucleation, as disclosed by previous experiments [14, 49]. From here, it is natural to infer that altering the secondary nucleation pathway should be an effective way to suppress the production of neurotoxic oligomers.
Note that the amyloid aggregation of protein is a complex multi-step process involving abundant factors, and thus, it is in general difficult and quite expensive to design every experiment to examine all the details. Nevertheless, a good mathematical model is capable of providing a guide towards different aspects, although it might not be that realistic. For instance, it is not easy to control the conversion rate and the elongation rate from the experimental design, but from the presented model, it can be concluded that both rates have relatively little impact. It should be emphasized that we model amyloid aggregation using stochastic chemical master equations rather than the mean-field model as used in most current literature. Specifically, we start from the probability density function, which can provide a more accurate description of the dynamics. We anticipate the chemical master equation model of this paper to be useful for clinical interventions and drug discovery in the near future. We also wish the model framework in the present study could be generalized to a wider range of biological aggregates, including human tissues affected by protein misfolding diseases with multiple oligomer and fibril stages.
Data availability
All data generated or analysed during this study are included in this published article.
References
Disanza, A., Steffen, A., Hertzog, M., Frittoli, E., Rottner, K., Scita, G.: Actin polymerization machinery: the finish line of signaling networks, the starting point of cellular movement. Cell. Mol. Life Sci. 62, 955–970 (2005)
Kenney, J.M., Knight, D., Wise, M.J., Vollrath, F.: Amyloidogenic nature of spider silk. Eur. J. Biochem. 269(16), 4159–4163 (2002)
Maji, S.K., Perrin, M.H., Sawaya, M.R., Jessberger, S., Vadodaria, K., Rissman, R.A., Singru, P.S., Nilsson, K.P.R., Simon, R., Schubert, D.: Functional amyloids as natural storage of peptide hormones in pituitary secretory granules. Science 325(5938), 328–332 (2009)
Chiti, F., Dobson, C.M.: Protein misfolding, amyloid formation, and human disease: a summary of progress over the last decade. Annu. Rev. Biochem. 86, 27–68 (2017)
Chatani, E., Yamamoto, N.: Recent progress on understanding the mechanisms of amyloid nucleation. Biophys. Rev. 10(2), 527–534 (2018)
Törnquist, M., Michaels, T.C., Sanagavarapu, K., Yang, X.T., Meisl, G., Cohen, S.I., Knowles, T.P., Linse, S.: Secondary nucleation in amyloid formation. Chem. Commun. 54(63), 8667–8684 (2018)
Michaels, T.C.T., Šarić, A., Curk, S., Bernfur, K., Arosio, P., Meisl, G., Dear, A.J., Cohen, S.I.A., Dobson, C.M., Vendruscolo, M., et al.: Dynamics of oligomer populations formed during the aggregation of Alzheimer’s Aβ42 peptide. Nat. Chem. 12(5), 445–451 (2020)
So, M., Hall, D., Goto, Y.: Revisiting supersaturation as a factor determining amyloid fibrillation. Curr. Opin. Struct. Biol. 36, 32–39 (2016)
Crespo, R., Rocha, F.A., Damas, A.M., Martins, P.M.: A generic crystallization-like model that describes the kinetics of amyloid fibril formation. J. Biol. Chem. 287(36), 30585–30594 (2012)
Ferrone, F.A., Hofrichter, J., Sunshine, H.R., Eaton, W.A.: Kinetic studies on photolysis-induced gelation of sickle cell hemoglobin suggest a new mechanism. Biophys. J. 32(1), 361–380 (1980)
Ferrone, F.A., Hofrichter, J., Eaton, W.A.: Kinetics of sickle hemoglobin polymerization: II. A double nucleation mechanism. J. Mol. Biol. 183(4), 611–631 (1985)
Meisl, G., Yang, X.T., Hellstrand, E., Frohm, B., Kirkegaard, J.B., Cohen, S.I.A., Dobson, C.M., Linse, S., Knowles, T.P.J.: Differences in nucleation behavior underlie the contrasting aggregation kinetics of the Aβ40 and Aβ42 peptides. Proc. Natl. Acad. Sci. 111(26), 9384–9389 (2014)
Iljina, M., Garcia, G.A., Horrocks, M.H., Tosatto, L., Choi, M.L., Ganzinger, K.A., Abramov, A.Y., Gandhi, S., Wood, N.W., Cremades, N., et al.: Kinetic model of the aggregation of alpha-synuclein provides insights into prion-like spreading. Proc. Natl. Acad. Sci. 113(9), 1206–1215 (2016)
Cohen, S.I.A., Linse, S., Luheshi, L.M., Hellstrand, E., White, D.A., Rajah, L., Otzen, D.E., Vendruscolo, M., Dobson, C.M., Knowles, T.P.J.: Proliferation of amyloid-β42 aggregates occurs through a secondary nucleation mechanism. Proc. Natl. Acad. Sci. 110(24), 9758–9763 (2013)
Michaels, T.C.T., Šarić, A., Habchi, J., Chia, S., Meisl, G., Vendruscolo, M., Dobson, C.M., Knowles, T.P.J.: Chemical kinetics for bridging molecular mechanisms and macroscopic measurements of amyloid fibril formation. Annu. Rev. Phys. Chem. 69, 273–298 (2018)
Oosawa, F., Kasai, M.: A theory of linear and helical aggregations of macromolecules. J. Mol. Biol. 4(1), 10–21 (1962)
Knowles, T.P.J., Waudby, C.A., Devlin, G.L., Cohen, S.I.A., Aguzzi, A., Vendruscolo, M., Terentjev, E.M., Welland, M.E., Dobson, C.M.: An analytical solution to the kinetics of breakable filament assembly. Science 326(5959), 1533–1537 (2009)
Garcia, G.A., Cohen, S.I.A., Dobson, C.M., Knowles, T.P.J.: Nucleation-conversion-polymerization reactions of biological macromolecules with prenucleation clusters. Phys. Rev. E 89(3), 032712 (2014)
Dear, A.J., Michaels, T.C.T., Meisl, G., Klenerman, D., Wu, S., Perrett, S., Linse, S., Dobson, C.M., Knowles, T.P.J.: Kinetic diversity of amyloid oligomers. Proc. Natl. Acad. Sci. 117(22), 12087–12094 (2020)
Szavits-Nossan, J., Eden, K., Morris, R.J., MacPhee, C.E., Evans, M.R., Allen, R.J.: Inherent variability in the kinetics of autocatalytic protein self-assembly. Phys. Rev. Lett. 113(9), 098101 (2014)
Michaels, T.C.T., Dear, A.J., Kirkegaard, J.B., Saar, K.L., Weitz, D.A., Knowles, T.P.J.: Fluctuations in the kinetics of linear protein self-assembly. Phys. Rev. Lett. 116(25), 258103 (2016)
Michaels, T.C.T., Dear, A.J., Knowles, T.P.J.: Stochastic calculus of protein filament formation under spatial confinement. New J. Phys. 20(5), 055007 (2018)
Zhou, T.S., Zhang, J.J.: Analytical results for a multistate gene model. SIAM J. Appl. Math. 72(3), 789–818 (2012)
Angstmann, C.N., Donnelly, I.C., Henry, T.A.M., Iand Langlands, B., Straka, P.: Generalized continuous time random walks, master equations, and fractional Fokker–Planck equations. SIAM J. Appl. Math. 75(4), 1445–1468 (2015)
Singh, A., Hespanha, J.P.: Approximate moment dynamics for chemically reacting systems. IEEE Trans. Autom. Control 56(2), 414–418 (2010)
Liu, R.N., Kang, Y.M.: Stochastic master equation for early protein aggregation in the transthyretin amyloid disease. Sci. Rep. 10(1), 12437 (2020)
Fodera, V., Librizzi, F., Groenning, M., Weert, M., Leone, M.: Secondary nucleation and accessible surface in insulin amyloid fibril formation. J. Phys. Chem. B 112(12), 3853–3858 (2008)
Eden, K., Morris, R., Gillam, J., MacPhee, C.E., Allen, R.J.: Competition between primary nucleation and autocatalysis in amyloid fibril self-assembly. Biophys. J. 108(3), 632–643 (2015)
Kayed, R., Head, E., Thompson, J.L., McIntire, T.M., Milton, S.C., Cotman, C.W., Glabe, C.G.: Common structure of soluble amyloid oligomers implies common mechanism of pathogenesis. Science 300(5618), 486–489 (2003)
Bucciantini, M., Giannoni, E., Chiti, F., Baroni, F., Formigli, L., Zurdo, J., Taddei, N., Ramponi, G., Dobson, C.M., Stefani, M.: Inherent toxicity of aggregates implies a common mechanism for protein misfolding diseases. Nature 416(6880), 507–511 (2002)
Cremades, N., Cohen, S.I.A., Deas, E., Abramov, A.Y., Chen, A.Y., Orte, A., Sandal, M., Clarke, R.W., Dunne, P., Aprile, F.A., et al.: Direct observation of the interconversion of normal and toxic forms of α-synuclein. Cell 149(5), 1048–1059 (2012)
Shammas, S.L., Garcia, G.A., Kumar, S., Kjaergaard, M., Horrocks, M.H., Shivji, N., Mandelkow, E., Knowles, T.P.J., Mandelkow, E., Klenerman, D.: A mechanistic model of tau amyloid aggregation based on direct observation of oligomers. Nat. Commun. 6(1), 7025 (2015)
Ackleh, A.S., Elaydi, S., Livadiotis, G., Veprauskas, A.: A continuous-time mathematical model and discrete approximations for the aggregation of β-amyloid. J. Biol. Dyn. 15(1), 109–136 (2021)
Bemporad, F., Chiti, F.: Protein misfolded oligomers: experimental approaches, mechanism of formation, and structure-toxicity relationships. Chem. Biol. 19(3), 315–327 (2012)
Kumar, S., Walter, J.: Phosphorylation of amyloid beta (Aβ) peptides–A trigger for formation of toxic aggregates in Alzheimer’s disease. Aging 3(8), 803 (2011)
Michaels, T.C.T., Dear, A.J., Cohen, S.I.A., Vendruscolo, M., Knowles, T.P.J.: Kinetic profiling of therapeutic strategies for inhibiting the formation of amyloid oligomers. J. Chem. Phys. 156(16), 164904 (2022)
Lomakin, A., Teplow, D.B., Kirschner, D.A., Benedek, G.B.: Kinetic theory of fibrillogenesis of amyloid β-protein. Proc. Natl. Acad. Sci. 94(15), 7942–7947 (1997)
Gillespie, D.T.: Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81(25), 2340–2361 (1977)
Lei, J.Z.: Stochastic modeling in systems biology. J. Adv. Math. Appl. 1(1), 76–88 (2012)
Lakatos, E., Ale, A., Kirk, P.D., Stumpf, M.P.: Multivariate moment closure techniques for stochastic kinetic models. J. Chem. Phys. 143(9), 094107 (2015)
Schnoerr, D., Sanguinetti, G., Grima, R.: Comparison of different moment-closure approximations for stochastic chemical kinetics. J. Chem. Phys. 143(18), 11 (2015)
Ding, Y.M., Kang, Y.M., Zhai, Y.J.: Rolling bearing fault diagnosis based on exact moment dynamics for underdamped periodic potential systems. IEEE Trans. Instrum. Meas. 72, 3510812 (2023)
Laidler, K.J.: Chemical Kinetics, vol. 1. Harper & Row, New York (1987)
Coelho, T., Merlini, G., Bulawa, C.E., Fleming, J.A., Judge, D.P., Kelly, J.W., Maurer, M.S., Planté-Bordeneuve, V., Labaudiniere, R., Mundayat, R., et al.: Mechanism of action and clinical application of tafamidis in hereditary transthyretin amyloidosis. Neurol. Ther. 5, 1–25 (2016)
Kakkar, V., Månsson, C., Mattos, E.P., Bergink, S., Der Zwaag, M., Waarde, M.A., Kloosterhuis, N.J., Melki, R., Cruchten, R.T., Al-Karadaghi, S., et al.: The S/T-rich motif in the DNAJB6 chaperone delays polyglutamine aggregation and the onset of disease in a mouse model. Mol. Cell 62(2), 272–283 (2016)
Shvadchak, V.V., Afitska, K., Yushchenko, D.A.: Inhibition of α-synuclein amyloid fibril elongation by blocking fibril ends. Angew. Chem., Int. Ed. Engl. 57(20), 5690–5694 (2018)
Cohen, S.I.A., Arosio, P., Presto, J., Kurudenkandy, F.R., Biverstål, H., Dolfe, L., Dunning, C., Yang, X.T., Frohm, B., Vendruscolo, M., et al.: A molecular chaperone breaks the catalytic cycle that generates toxic Aβ oligomers. Nat. Struct. Mol. Biol. 22(3), 207–213 (2015)
Cohen, S.I.A., Vendruscolo, M., Welland, M.E., Dobson, C.M., Terentjev, E.M., Knowles, T.P.J.: Nucleated polymerization with secondary pathways. I. Time evolution of the principal moments. J. Chem. Phys. 135(6), 065105 (2011)
Caswell, H.: Matrix Population Models, vol. 1 (2000)
Acknowledgements
We thank to the reviewers for their helpful comments and suggestions.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No 12172268).
Author information
Authors and Affiliations
Contributions
YK supervised and sponsored the study. LC also guided the research. YD built the model, made the deductions and calculations, and drew the figures. YD, LC, and YK drafted the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Moment equations
The moment system of the first two order moments is a system of \(C_{8}^{1} = 8\) equations, given by
The moment system of the two order raw moments is a system of \(C_{8}^{1} = 8\) equations, given by
The moment system of the two order mixed raw moments is a system of \(C_{8}^{2} = 28\) equations, given by
Appendix B: The moment closed functions
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ding, Y., Cai, L. & Kang, Y. Moment dynamics of oligomer formation in protein amyloid aggregation with secondary nucleation. Adv Cont Discr Mod 2024, 25 (2024). https://doi.org/10.1186/s13662-024-03819-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-024-03819-2