1 Introduction

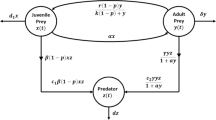
The disturbance caused by agricultural pests has always been a significant issue in agricultural production. Due to the excessive use of chemical pesticides, traditional pest-control methods have gradually shown their limitations. Therefore, the search for a more comprehensive and sustainable control strategy has become particularly urgent. Integrated Pest Management (IPM) combines various methods such as chemical control, biological control, and physical control [1–3], becoming the primary approach to pest control. In the early twentieth century, especially in the 1930s, mathematicians Volterra and Lotka conducted research on the mathematical models of interactions between predators and prey. They proposed the famous Lotka–Volterra model [4, 5], laying the theoretical foundation for later IPM strategies. Building upon the classical Lotka–Volterra model, we establish the following pest–enemy management model with a Holling-IV-type functional response function:

$$ \textstyle\begin{cases} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t), \end{cases} $$
(1)

where \(x(t)\) represents the density of pests and \(y(t)\) represents the density of enemies; r represents the intrinsic growth rate; K represents the capacity; δ denotes the natural death rate of the natural enemies; μ is the conversion rate of prey into predator; while β denotes the predation rate and η represents the antipredation coefficient.

The main objective of Integrated Pest Management strategy is not to completely eradicate pests, but to implement control measures when the pest-population density reaches economic thresholds, keeping pest density within a tolerable range [6–11]. Considering the intermittent use of pesticides, meaning the continuous adoption of integrated pest-management strategies for a period until the pest-population density falls below the economic damage threshold, it is necessary to characterize this intermittent control strategy using the Filippov nonsmooth dynamical system. Filippov nonsmooth dynamical systems have found widespread application across various fields, including mathematics, physics, life sciences, medicine, and engineering [12–21]. In recent years, extensive research by experts and scholars has led to rapid development in the theory of Filippov systems [22–28]. Based on model (1), we derive the following Filippov ecological system with intermittent control strategy:

$$ \textstyle\begin{cases} \left. \begin{gathered} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t), \end{gathered} \right \}x< ET, \\ \left . \begin{gathered} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t)-px(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t)+\tau, \end{gathered} \right\} x>ET, \end{cases} $$
(2)

where ET denotes the economic threshold; \(p\in [0,1)\) represents the mortality rate of pests caused by pesticide spraying; τ represents the number of enemies released at time t.

The model (2) can be expressed as:

$$ \textstyle\begin{cases} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t)-\varepsilon px(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t)+\varepsilon \tau, \end{cases} $$
(3)

where

$$ \varepsilon =\textstyle\begin{cases} 0,& H(Z)=x-ET< 0, \\ 1,& H(Z)=x-ET>0. \end{cases} $$
(4)

Let \(H(Z)=x-ET\) and vector field \(Z=(x(t),y(t))^{T}\). Furthermore, the discontinuity boundary Σ separating the two regions \(G_{1}=\{Z\in R^{2}_{+}|H(Z)<0\}\) and \(G_{2}=\{Z\in R^{2}_{+}|H(Z)>0\}\) is defined as

$$ \Sigma =\bigl\{ Z\in R^{2}_{+}|H(Z)=0\bigr\} , $$

then the Filippov system (3) and (4) can be modified to

$$ \frac{dZ(t)}{dt} =\textstyle\begin{cases} F_{G_{1}}(Z),& Z\in G_{1}, \\ F_{G_{2}}(Z),& Z\in G_{2}, \end{cases} $$
(5)

where

$$ F_{G_{1}}(Z) = \left[ \begin{aligned} & rx(t) \biggl(1-\frac{x(t)}{K} \biggr)-\beta x(t)y(t) \\ & \frac{\mu x(t)y(t)}{a+x^{2}(t)}-\delta y(t)-\eta x(t)y(t) \end{aligned} \right] $$

and

$$ F_{G_{2}}(Z) = \left[ \begin{aligned} & rx(t) \biggl(1-\frac{x(t)}{K} \biggr)-\beta x(t)y(t)-px(t) \\ & \frac{\mu x(t)y(t)}{a+x^{2}(t)}-\delta y(t)-\eta x(t)y(t)+\tau \end{aligned} \right]. $$

For convenience, let us denote the subsystems of Filippov system (5) on regions \(G_{1}\) and \(G_{2}\) as systems \(S_{1}\) and \(S_{2}\).

The structure of our paper is organized as follows: The next section delves into the examination of the existence and stability of equilibria for the two subsystems of the Filippov system. Section 3 explores the existence of various equilibria of the Filippov system, with special emphasis on the existence and stability of pseudoequilibrium. In Sect. 4, we investigate the nonexistence of boundary equilibrium bifurcation and limit cycles. This paper concludes with some biological implications drawn from theoretical analysis and numerical simulations.

2 Preliminaries

2.1 The existence and stability of the equilibria of subsystem \(S_{1}\)

If \(x< ET\), subsystem \(S_{1}\) is given by

$$ \textstyle\begin{cases} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t). \end{cases} $$
(6)

The two isoclines of model (6) are as follows

$$ y= \frac{r}{\beta} \biggl(1-\frac{x}{K} \biggr) $$

and

$$ \eta x^{3}+\delta x^{2}-(\mu -a\eta )x+a \delta =0. $$
(7)

We consider the second equation (7), which is a cubic equation in one dollar, let

$$ f(x)\doteq \eta x^{3}+\delta x^{2}-(\mu -a\eta )x+a\delta =0. $$

Taking the first and second derivatives of the function \(f(x)\) with respect to x gives:

$$ f'(x)=3\eta x^{2}+2\delta x-(\mu -a\eta );\qquad f''(x)=6\eta x+2\delta >0, $$

thus, \(f'(x)\) is strictly increasing. When \((\mu -a\eta )\leq 0\), we have \(f'(x)>0\), indicating that \(f(x)\) is monotonically increasing, with \(f(0)=a\delta >0\). Therefore, subsystem \(S_{1}\) does not have any internal equilibria. When \((\mu -a\eta )> 0\), \(f'(x)=0\) has a positive root

$$ x_{g}=\frac{-\delta +\sqrt {\delta ^{2}+3\eta (\mu -a\eta )}}{3\eta}. $$

Therefore, \(f(x)\) strictly decreases on the interval \((0,x_{g})\) and strictly increases on the interval \((x_{g},\infty )\). If \(f(x_{g})>0\), the equation \(f(x)=0\) has no positive roots, meaning that subsystem \(S_{1}\) has no internal equilibrium, If \(f(x_{g})=0\), subsystem \(S_{1}\) has an internal equilibrium \(E_{g}=(x_{g},y_{g})\), where

$$ y_{g}=\frac{r}{\beta} \biggl(1-\frac{x_{g}}{K} \biggr). $$

If \(f(x_{g})<0\), subsystem \(S_{1}\) has two internal equilibria, denoted as \(E_{11}=(x_{11},y_{11})\) and \(E_{12}=(x_{12},y_{12})\), where

$$\begin{aligned} &x_{11}= \frac{-\delta +\sqrt{A} (\cos \frac{\theta}{3}-\sqrt{3}\sin \frac{\theta}{3} )}{3\eta},\qquad y_{11}=\frac{r}{\beta} \biggl(1- \frac{-\delta +\sqrt{A} (\cos \frac{\theta}{3}-\sqrt{3}\sin \frac{\theta}{3} )}{3K\eta} \biggr);\\ &x_{12}= \frac{-\delta +\sqrt{A} (\cos \frac{\theta}{3}+\sqrt{3}\sin \frac{\theta}{3} )}{3\eta},\qquad y_{12}=\frac{r}{\beta} \biggl(1- \frac{-\delta +\sqrt{A} (\cos \frac{\theta}{3}+\sqrt{3}\sin \frac{\theta}{3} )}{3K\eta} \biggr), \end{aligned}$$

where \(A=\delta ^{2}+3\eta (\mu -a\eta )\), \(\theta =\arccos T\), \(T=\frac{2A\delta -3\eta B}{2\sqrt{A^{3}}}\), \(B=-\delta (\mu -a\eta )-9\eta a\delta \), and \(T\in (-1,1)\).

Next, let us analyze the local stability of equilibrium \(E_{g}=(x_{g},y_{g})\) for model (2). we first compute the Jacobian matrix of the model (2) as follows:

$$ J(x,y)= \begin{pmatrix} r (1-\frac{x}{K} )-\frac{rx}{K}-\beta y &-\beta x \\ \frac{\mu y}{a+x^{2}}-\frac{2\mu x^{2}y}{(a+x^{2})^{2}}-\eta y & \frac{\mu x}{a+x^{2}}-\delta -\eta x \end{pmatrix}, $$

upon substituting \(E_{x_{g}}\), we obtain:

$$ J(x_{g},y_{g})= \begin{pmatrix} -\frac{rx_{g}}{K} &-\beta x_{g} \\ \frac{\mu y_{g}}{a+x_{g}^{2}}- \frac{2\mu x_{g}^{2}y_{g}}{(a+x_{g}^{2})^{2}}-\eta y_{g} & 0 \end{pmatrix}, $$

we can easily calculate the determinant of \(\vert J(x_{g},y_{g}) \vert \) as:

| J ( x g , y g ) | = | − r x g K − β x g μ y g a + x g 2 − 2 μ x g 2 y g ( a + x g 2 ) 2 − η y g 0 | = β x g y g ( μ ( a − x g 2 ) ( a + x g 2 ) 2 − η ) .
(8)

It follows from \(f(x_{g})=0\) that \(a= \frac{\eta x_{g}^{3}+\delta x_{g}^{2}-\mu x_{g}}{-\delta -\eta x_{g}}\). By substituting this into (4) we obtain

$$ \bigl\vert J(x_{g},y_{g}) \bigr\vert = \frac{\beta}{\mu}x_{g}y_{g} \bigl(\mu \delta -2\eta ^{2} x_{g}^{3}-4\delta \eta x_{g}^{2}-2 \delta ^{2}x_{g} \bigr). $$

Let \(g(x)=\mu \delta -2\eta ^{2} x_{g}^{3}-4\delta \eta x_{g}^{2}-2 \delta ^{2}x_{g}\), taking the derivative of \(g(x)\) yields

$$ g'(x)=- \bigl(6\eta ^{2} x_{g}^{2}+8 \delta \eta x_{g}+2\delta ^{2} \bigr)< 0, $$

which indicates that \(g(x)\) is monotonically decreasing for \(x>0\). Since \(f'(x_{g})=3\eta x_{g}^{2}+2\delta x_{g}-(\mu -a\eta )=0\) and \(f(x_{g})=\eta x_{g}^{3}+\delta x_{g}^{2}-(\mu -a\eta )x_{g}+a\delta =0\) it follows that

$$ \begin{aligned} g(x_{g})&=\mu \delta -2\eta ^{2} x_{g}^{3}-4\delta \eta x_{g}^{2}-2 \delta ^{2}x_{g}=-2\eta ^{2} x_{g}^{3}- \delta \eta x_{g}^{2}+\delta \bigl( \mu -3\eta x_{g}^{2}-2\delta x_{g}\bigr) \\ &=-2\eta ^{2} x_{g}^{3}-\delta \eta x_{g}^{2}+\delta \bigl[(\mu -a\eta ) -3 \eta x_{g}^{2}-2\delta x_{g}+a\eta \bigr]=-2\eta ^{2} x_{g}^{3}-\delta \eta x_{g}^{2}+a \delta \eta \\ &=\eta \bigl[-2\eta x_{g}^{3}-\delta x_{g}^{2}- \eta x_{g}^{3}-\delta x_{g}^{2}+( \mu -a \eta )x_{g}\bigr] \\ &=\eta x_{g}\bigl[-3\eta x_{g}^{2}-2\delta x_{g}+(\mu -a\eta )\bigr]=0. \end{aligned} $$

Thus, \(\vert J(x_{2},y_{2}) \vert =0\), which means that \(E_{g}\) is a degenerate equilibrium.

Next, let us analyze the local stability of the equilibrium \(E_{2}=(x_{2},y_{2})\), where \(f'(x_{g})=3\eta x_{g}^{2}+2\delta x_{g}-(\mu -a\eta )=0\) and \(f(x_{g})=\eta x_{g}^{3}+\delta x_{g}^{2}-(\mu -a\eta )x_{g}+a\delta <0\), then we have

$$ \begin{aligned} g(x_{g})&=\mu \delta -2\eta ^{2} x_{g}^{3}-4\delta \eta x_{g}^{2}-2 \delta ^{2}x_{g}=-2\eta ^{2} x_{g}^{3}- \delta \eta x_{g}^{2}+a\delta \eta \\ &< \eta \bigl[-2\eta ^{2} x_{g}^{3}-\delta \eta x_{g}^{2}-\eta x_{g}^{3}- \delta x_{g}^{2}+(\mu -a\eta )x_{g}\bigr] \\ &=\eta x_{g}\bigl[-3\eta x_{g}^{2}-2\delta x_{g}+(\mu -a\eta )\bigr]=0 \end{aligned} $$

and \(x_{g}< x_{2}\), this implies \(g(x_{2})< g(x_{g})<0\). Thus, \(\vert J(x_{2},y_{2}) \vert <0\), which means that \(E_{2}\) is a saddle.

Similarly, for the stability of \(E_{1}\), where \(f'(x_{1})<0\) that

$$ \begin{aligned} g(x_{1})&=\mu \delta -2\eta ^{2} x_{1}^{3}-4\delta \eta x_{1}^{2}-2 \delta ^{2}x_{1}>-2\eta ^{2} x_{1}^{3}- \delta \eta x_{1}^{2}+a\delta \eta \\ &=\eta x_{1}\bigl[-3\eta x_{1}^{2}-2\delta x_{1}+(\mu -a\eta )\bigr]>0, \end{aligned} $$

which implies \(\vert J(x_{1},y_{1}) \vert >0\), the trace of \(J(x_{1},y_{1})\) is \(trJ(x_{1},y_{1})=-\frac{rx_{1}}{K}<0\), thus the positive equilibrium \(E_{1}\) is stable.

2.2 The existence and stability of the equilibria of subsystem \(S_{2}\)

Next, we will analyze the equilibria of subsystem \(S_{2}\). If \(x>ET\), subsystem \(S_{2}\) is given by

$$ \textstyle\begin{cases} \frac{{d}x(t)}{{d}t}= rx(t) (1-\frac{x(t)}{K} )-\beta x(t)y(t)-px(t), \\ \frac{{d}y(t)}{{d}t}=\frac{\mu x(t)y(t)}{a+x^{2}(t)}- \delta y(t)-\eta x(t)y(t)+\tau, \end{cases} $$
(9)

the two isoclines of model (8) are:

$$ y= \frac{1}{\beta} \biggl[r \biggl(1-\frac{x}{K} \biggr)-p \biggr] $$
(10)

and

$$ y=\frac{\tau}{\delta +\eta x-\frac{\mu x}{a+x^{2}}}= \frac{ (a+x^{2} )\tau}{\eta x^{3}+\delta x^{2}-(\mu -a\eta )x+a\delta}. $$

Obviously, there exists a boundary equilibrium (i.e., pest-extinction equilibrium) \((0, \frac{\tau}{\delta} )\) in subsystem \(S_{2}\).

Let us now analyze the internal equilibria of subsystem \(S_{2}\) by solving the equation

$$ \frac{1}{\beta} \biggl[r \biggl(1-\frac{x}{K} \biggr)-p \biggr]= \frac{ (a+x^{2} )\tau}{\eta x^{3}+\delta x^{2}-(\mu -a\eta )x+a\delta}. $$
(11)

Equation (11) can be transformed into a fourth-degree equation, indicating that it can have up to four solutions. To discuss the number of internal equilibria in model (9), let us modify equation (11) to:

$$ \frac{r}{\beta K\tau} \bigl[\eta x^{3}+\delta x^{2}-(\mu -a\eta )x+a \delta \bigr]+x=- \frac{ (K-\frac{pK}{r} )x+a}{x+\frac{pK}{r}-K}, $$

letting

$$ g_{1}(x)=\frac{r}{\beta K\tau} \bigl[\eta x^{3}+\delta x^{2}-(\mu -a \eta )x+a\delta \bigr]+x $$

and

$$ g_{2}(x)=-\frac{ (K-\frac{pK}{r} )x+a}{x+\frac{pK}{r}-K}. $$

Taking the derivative of \(g(x)\) with respect to x yields

$$ g_{1}'(x)=\frac{r}{\beta K\tau} \bigl[3\eta x^{2}+2\delta x-(\mu -a \eta ) \bigr]+1, $$

\(g_{1}'(x)\) is a quadratic equation with the concave downward opening shape, and its axis of symmetry is located at \(x=-\frac{\delta}{3\eta}\). When \(g_{1}'(-\frac{\delta}{3\eta})\geq 0\), \(g_{1}(x)\) is monotonically increasing in the interval \((-\infty,0)\), when \(g_{1}'(-\frac{\delta}{3\eta})<0\), there exists \(x_{p}<-\frac{\delta}{3\eta}\) such that \(g_{1}(x)\) is monotonically increasing in the interval \((-\infty,x_{p})\). At the same time, we have \(g_{1}(0) = \frac{ra\delta}{\beta K\tau}\) and \(\lim_{x\to -\infty}g_{1}(x)=-\infty \). Therefore, \(g_{2}(x)\) has at least one negative root.

\(g_{2}(x)\) is an inverse proportion function with a center of symmetry at \((K-Kp/r, (K-Kp/r ) )\). When \(K-\frac{Kp}{r}>0\), the graph of the function is located in the first, second, and fourth quadrants. When \(K-\frac{Kp}{r}<0\), the graph of the function is located in the second, third, and fourth quadrants.

To investigate the number of equilibria of the model, we plot \(g_{1}(x)\) and \(g_{2}(x)\) on the same coordinate axis to find the number of intersections, as shown in Fig. 1.

Figure 1
figure 1

Existence of equilibria in subsystem \(S_{2}\)

Full size image

(i) When \(-\frac{r}{\beta K\tau}(\mu -a\eta )+1>0\), \(g_{1}(x)\) is monotonically increasing in the interval \((0,+\infty )\). In this case, \(g_{1}(x)\) has no positive roots. As shown in Fig. 1[A], when \(K-\frac{Kp}{r}<0\), \(g_{1}(x)\) and \(g_{2}(x)\) have no intersections in the interval \((0,+\infty )\). As shown in Fig. 1[B], when \(K-\frac{Kp}{r}>0\), \(g_{1}(x)\) and \(g_{2}(x)\) have at most one intersection in the interval \((0,+\infty )\).

(ii) When \(-\frac{r}{\beta K\tau}(\mu -a\eta )+1<0\), \(g_{1}(x)\) may have two positive roots. As shown in Fig. 1[C], when \(K-\frac{Kp}{r}<0\), \(g_{1}(x)\) and \(g_{2}(x)\) have at most two intersections on the interval \((0,+\infty )\). As shown in Fig. 1[D], when \(K-\frac{Kp}{r}>0\), \(g_{1}(x)\) and \(g_{2}(x)\) have at most three intersections on the interval \((0,+\infty )\).

In conclusion, subsystem (8) can have a maximum of three positive equilibria. To examine the stability of equilibria \(E_{2i}(x_{2i},y_{2i})\) of subsystem \(S_{2}\), we calculate the Jacobian matrix as follows

$$ J(x,y)= \begin{pmatrix} r (1-\frac{x}{K} )-\frac{rx}{K}-\beta y-p &-\beta x \\ \frac{\mu y}{a+x^{2}}-\frac{2\mu x^{2}y}{(a+x^{2})^{2}}-\eta y & \frac{\mu x}{a+x^{2}}-\delta -\eta x \end{pmatrix}, $$

substituting \(E_{2i}\) into the equation, we obtain

$$ J(x_{2i},y_{2i})= \begin{pmatrix} -\frac{rx_{2i}}{K} &-\beta x_{2i} \\ \frac{\mu y_{2i}}{a+x_{2i}^{2}}- \frac{2\mu x_{2i}^{2}y_{2i}}{(a+x_{2i}^{2})^{2}}-\eta y_{2i} &-\tau \end{pmatrix}= \begin{pmatrix} A & B \\ C & D \end{pmatrix}. $$

The characteristic equation of \(E_{2i}\) is as follows:

$$ \lambda ^{2}-(A+D)\lambda +(AC-BD)=0, $$

the trace of \(J(x_{2i},y_{2i})\) is \(trJ(x_{2i},y_{2i})=(A+D)=-\frac{rx_{1}}{K}-\tau <0\), thus, if \(AD-BC>0\), \(E_{2i}\) is stable, if \(AD-BC<0\), \(E_{2i}\) is a saddle.

Furthermore, the existence and stability of the equilibria of subsystem \(S_{2}\) are investigated through numerical simulations, as shown in Fig. 2. In Fig. 2[A], subsystem \(S_{2}\) has a single positive equilibrium \(E_{21}\), which is a stable focus. In Fig. 2[B], we can observe that subsystem \(S_{2}\) has two positive equilibria, \(E_{21}\) (a stable node) and \(E_{22}\) (a stable node). Figure 2[C] demonstrates that subsystem \(S_{2}\) has three positive equilibria, \(E_{21}\), \(E_{22}\), and \(E_{23}\), with \(E_{21}\) being a stable focus, \(E_{22}\) being a saddle, and \(E_{23}\) being a stable node.

Figure 2
figure 2

Subsystem \(S_{2}\) has one, two, and three positive equilibria. Parameters are [A] \(r=1, K=5, \beta =0.5, \mu =0.4, a=1, \delta =0.2, \eta =0.1, p=0.2, \tau =0.21\); [B] \(r=1, K=5, \beta =0.5, \mu =0.2, a=.6, \delta =0.05, \eta =0.2, p=0.2, \tau =0.12\); [C] \(r=1, K=5, \beta =0.5, \mu =0.4, a=0.4, \delta =0.3, \eta =0.1, p=0.2, \tau =0.12\)

Full size image

3 Sliding dynamics

3.1 Sliding domain

In accordance with the Filippov system definition, the sliding domain is denoted as

$$ \Sigma =\bigl\{ Z\in \Sigma |\sigma (Z)\leq 0\bigr\} , $$

where \(\sigma =\{Z\in R_{+}^{2}|H(Z)=0\}\), while \(\sigma (Z)<0\) is equivalent to

$$ ET^{2} \biggl[r \biggl(1-\frac{ET}{K} \biggr)-\beta y \biggr] \cdot \biggl[r \biggl(1-\frac{ET}{K} \biggr)-\beta y-p \biggr]\leq 0, $$

that is

$$ \biggl[r \biggl(1-\frac{ET}{K} \biggr)-\beta y \biggr]\geq 0 $$

and

$$ \biggl[r \biggl(1-\frac{ET}{K} \biggr)-\beta y-p \biggr]\leq 0. $$

Solving the above two inequalities we obtain

$$ \frac{r(K-ET)-pK}{\beta K}\leq y\leq \frac{r(K-ET)}{\beta K}. $$

For convenience, let \(y_{\min}=\frac{r(K-ET)-pK}{\beta K}\) and \(y_{\max}=\frac{r(K-ET)}{\beta K}\). Therefore, the sliding segment of Filippov (5) can be defined as

$$ \Sigma _{S}=\bigl\{ (x,t)^{T}\in R_{+}^{2}|y_{\min}< y< y_{\max} \bigr\} . $$

Note. Due to the fact that the two inequalities \(F_{G_{1}}H(Z)\leq 0\) and \(F_{G_{2}}H(Z)\geq 0\) cannot be simultaneously satisfied, the Filippov system (5) lacks an escaping region.

3.2 Equilibria of Filippov system (5)

There are five types of equilibria in Filippov systems, boundary equilibrium (\(E_{b}\)), pseudoequilibrium (\(E_{p}\)), real equilibrium (\(E^{R}\)), virtual equilibrium (\(E^{V}\)), and tangency point (\(E_{t}\)).

Pseudoequilibrium: We employ Utkin’s equivalent control method to study the dynamical behavior of the Filippov system (5) in the sliding region \(\Sigma _{S}\). By considering \(H(Z)=0\) and the first equation of Filippov system (5), we obtain

$$ \frac{\partial H}{\partial t}=rx(t) \biggl(1-\frac{x(t)}{k} \biggr)- \beta x(t)y(t)- \varepsilon px(t)=0, \quad x(t)=ET, $$

solving the above equation yields

$$ \varepsilon =\frac{r(K-ET)-K\beta y(t)}{Kp}. $$

Substituting ε into the second equation of system (5) yields the dynamical equation of the Filippov system on the sliding domain \(\Sigma _{S}\) as follows:

$$ \frac{dy}{dt}= \frac{\mu pET-(\delta p+\eta pET+\tau \beta ) (a+ET^{2})}{(a+ET^{2})p}y+ \frac{r\tau (K-ET)}{KP}\doteq \phi (y), $$
(12)

which has a unique pseudoequilibrium state \(E_{p}(ET, y_{p})\), where

$$ y_{p}= \frac{r\tau (K-ET)(a+ET^{2})}{K [(\delta p+\eta pET+\tau \beta ) (a+ET^{2})-\mu pET ]}, $$
(13)

and \(y_{p}\in \Sigma _{S},y_{\min}\leq y_{p}\leq y_{\max}\). Next, we will discuss the stability of \(E_{p}(ET, y_{p})\). Taking the derivative of the scalar equation (11) with respect to y yields

$$ \phi '(y)= \frac{\mu pET-(\delta p+\eta pET+\tau \beta )(a+ET^{2})}{(a+ET^{2})p}. $$

Therefore, if the condition

$$ \mu pET< (\delta p+\eta pET+\tau \beta ) \bigl(a+ET^{2}\bigr) $$

holds, then, \(\phi '(y)<0\), and the pseudoequilibrium \(E_{p}\) is locally asymptotically stable on the sliding domain \(\Sigma _{S}\).

Boundary equilibrium: The two boundary equilibria of Filippov system (5) satisfy the following equations

$$ \textstyle\begin{cases} rx(t) (1-\frac{x(t)}{k} )-\beta x(t)y(t)=0, \\ \frac{\mu x(t)y(t)}{a+x^{2}(t)}-\delta y(t)-\eta x(t)y(t)=0, \\ x(t)=ET \end{cases} $$
(14)

and

$$ \textstyle\begin{cases} rx(t) (1-\frac{x(t)}{k} )-\beta x(t)y(t)-px(t)=0, \\ \frac{\mu x(t)y(t)}{a+x^{2}(t)}-\delta y(t)-\eta x(t)y(t)+\tau =0, \\ x(t)=ET. \end{cases} $$
(15)

It can be deduced by solving equation (14), if \(\delta =\frac{\mu ET}{a+ET(t)}-\eta ET\) holds, then Filippov system (5) has a boundary equilibrium \(E_{b}^{2}(ET,y_{\max})\). It can be deduced by solving equation (15), if \(y_{\min}=\frac{\tau}{\delta +\eta ET-\frac{\mu x}{a+ET^{2}}}\) holds, then Filippov system (5) has a boundary equilibrium \(E_{b}^{1}(ET,y_{\min})\). At the same time, to ensure biological significance, it must hold that \(y_{\min}>0\), that is,

$$ \delta >\frac{\mu x}{a+ET^{2}}-\eta ET. $$

Under this condition, the Filippov system (5) exhibits two boundary equilibria, namely, \(E_{b}^{1}(ET,y_{\min})\) and \(E_{b}^{2}(ET,y_{\max})\).

Tangent point: According to the definition of the Filippov system’s tangent point, it should satisfy

$$ \textstyle\begin{cases} rx(t) (1-\frac{x(t)}{k} )-\beta x(t)y(t)=0, \\ x(t)=ET \end{cases} $$

and

$$ \textstyle\begin{cases} rx(t) (1-\frac{x(t)}{k} )-\beta x(t)y(t)-px(t)=0, \\ x(t)=ET. \end{cases} $$

Therefore, the tangent points of the Filippov system (5) are \(E_{t}^{1}(ET,y_{\min})\) and \(E_{t}^{2}(ET,y_{\max})\), and they are the two endpoints of the sliding segment.

Regular equilibrium: To investigate the real and virtual equilibria of the Filippov system (5), it is necessary to conduct a relevant discussion on the equilibria of subsystems \(S_{1}\) and \(S_{2}\).

For subsystem \(S_{1}\), it has two internal equilibria \(E_{11}(x_{11}, y_{11})\) and \(E_{12}(x_{12}, y_{12})\), where \(x_{11} < x_{12}\). According to the definitions of real and virtual equilibria, we can classify them as follows:

(i) If \(x_{12}< ET\), then both internal equilibria of subsystem \(S_{1}\) are real equilibria, denoted as \(E_{r}^{11}\) and \(E_{r}^{12}\).

(ii) If \(x_{11}>ET\), then both internal equilibria of subsystem \(S_{1}\) are virtual equilibria, denoted as \(E_{v}^{11}\) and \(E_{v}^{12}\).

(iii) If \(x_{11}< ET< x_{12}\), then both internal equilibria of subsystem \(S_{1}\) have a real equilibrium and a virtual equilibrium, denoted as \(E_{r}^{11}\) and \(E_{v}^{12}\).

For subsystem \(S_{2}\), as shown in Fig. 2, it contains three internal equilibria \(E_{21}(x_{21}, y_{21})\), \(E_{22}(x_{22}, y_{22})\), and \(E_{23}(x_{23}, y_{23})\). According to the definitions of real and virtual equilibria, we can classify them as follows:

(i) If \(x_{23}< ET\), then three internal equilibria of subsystem \(S_{2}\) are virtual equilibria, denoted as \(E_{v}^{21}\), \(E_{v}^{22}\), and \(E_{v}^{23}\).

(ii) If \(x_{21}>ET\), then three internal equilibria of subsystem \(S_{2}\) are real equilibria, denoted as \(E_{r}^{21}\), \(E_{r}^{22}\), and \(E_{r}^{23}\).

(iii) If \(x_{21}< ET< x_{22}\), then three internal equilibria of subsystem \(S_{2}\) have two real equilibria and a virtual equilibrium, denoted as \(E_{r}^{22}\), \(E_{r}^{23}\), and \(E_{v}^{21}\).

(iiii) If \(x_{22}< ET< x_{23}\), then three internal equilibria of subsystem \(S_{2}\) have two virtual equilibria and a real equilibrium, denoted as \(E_{v}^{21}\), \(E_{v}^{22}\), and \(E_{r}^{23}\).

4 Sliding bifurcation analysis

4.1 Sliding mode bifurcation

According to the sliding region and sliding segments of the Filippov system (5), it can be determined whether or not there may be sliding segments. Under the control of the IPM strategy, the concentration of insecticide spraying and the release quantity of enemies have a significant impact on pest control. The parameters p and τ are selected below, and numerical simulations are employed for the study.

When the lethality of insecticides to pests is low, with the continuous variation of the control threshold ET, the length of the sliding segment remains constant, and the pseudoequilibrium changes from nonexistence to existence, as shown in Fig. 3[A] for \(p=0.4\). (i) With an increase in p, the length of the sliding segment grows, and when p reaches a certain threshold, the pseudoequilibrium persists and tends to stabilize, as shown in Fig. 3[B] for \(p=0.8\). (ii) With an increase in τ, the length of the sliding segment remains unchanged, and the pseudoequilibrium enlarges, as shown in Fig. 3[C], when τ increases to 1, the pseudoequilibrium consistently stays on the sliding segment. From the perspective of pest control, the presence of a stable pseudoequilibrium on the sliding segment in the Filippov system (5) is advantageous for pest control.

Figure 3
figure 3

Sliding mode bifurcation of Filippov system (5). Parameters are \(r=1, K=5, \beta =0.4, \mu =0.6, a=1, \delta =0.6, \eta =0.3\)

Full size image

4.2 Boundary equilibrium bifurcation

Boundary equilibrium bifurcation in the Filippov system occurs due to the collision of real equilibrium and tangent point (or pseudoequilibrium) at the discontinuity surface when one parameter passes through a threshold. When the corresponding equilibrium is a node, focus, or saddle, the resulting boundary bifurcation is referred to as the boundary node, focus, or saddle bifurcation.

Next, we will systematically study the bifurcation of boundary equilibria of the Filippov system (5) through numerical simulation.

Boundary-node bifurcation: As shown in Fig. 4[A], when \(ET=5\), the subsystem \(S_{2}\) of the Filippov system exhibits a real equilibrium \(E^{22}_{r}\), with \(E^{22}_{r}\) being a stable node; meanwhile, the system has a sliding segment \(\Sigma _{S}\), but no pseudoequilibrium. At this point, the trajectory tends towards the stable node \(E^{22}_{r}\). As shown in Fig. 4[B], when ET increases to the critical value \(ET=5.74\), the stable node \(E^{22}_{r}\) collides with tangent point \(E_{t}\) to form a point \(E_{b}\), and boundary-node bifurcation occurs at the boundary point \(E_{b}\) of the system. At this point, the trajectory approaches the boundary equilibrium \(E_{b}\). As shown in Fig. 4[C], when ET continues to increase to \(ET=6.2\), the boundary equilibrium of system (5) is separated into pseudoequilibrium \(E_{p}\), tangent point \(E_{t}\), and virtual equilibrium \(E^{22}_{v}\). At this point, the trajectory tends to the pseudoequilibrium \(E_{p}\).

Figure 4
figure 4

Boundary-node bifurcation for Filippov system (5). Parameters are \(r=0.8, K=10, \beta =0.5, \mu =0.2, a=5, \delta =0.8, \eta =0.02, p=0.25, \tau =0.16\), and [A] \(ET=5\); [B] \(ET=5.74\); [C] \(ET=6.2\)

Full size image

Boundary-focus bifurcation: As shown in Fig. 5[A], when \(ET=1\), the subsystem \(S_{2}\) of the Filippov system has real equilibrium \(E^{21}_{r}\) and tangent point \(E_{t}\), with \(E^{21}_{r}\) being a stable focus. At this time, the trajectory tends the stable focus \(E^{2}_{r}\). When ET increases to \(ET=1.13\), the boundary-node bifurcation occurs at the boundary point \(E_{b}\). At this point, the trajectory approaches \(E_{b}\), as shown in Fig. 5[B]. When ET continues to increase to \(ET=1.4\), the boundary equilibrium of system 5 is separated into pseudoequilibrium \(E_{p}\), tangent point \(E_{t}\), and virtual equilibrium \(E^{21}_{v}\). At this point, the trajectory tends to \(E_{p}\), as shown in Fig. 5[C].

Figure 5
figure 5

Boundary-focus bifurcation for Filippov system (5). Parameters are \(r=0.8, K=10, \beta =0.5, \mu =0.2, a=5, \delta =0.8, \eta =0.02, p=0.2, \tau =0.1\), and [A] \(ET=1\); [B] \(ET=1.13\); [C] \(ET=1.4\)

Full size image

Boundary-saddle bifurcation: The condition for the occurrence of a boundary-saddle bifurcation in the Filippov system is as follows: when the parameter ET reaches a critical value, the system’s real equilibrium (saddle), boundary equilibrium, and tangent point collide on a discontinuity surface, merging into a single point \(E_{B}\). As shown in Fig. 6[A], when \(ET=0.6\), the system has a virtual equilibrium \(E_{v}^{21}\), two real equilibria \(E_{r}^{22}\) and \(E_{r}^{22}\), a pseudoequilibrium \(E_{p}\), and a tangent point \(E_{t}\), where \(E_{r}^{22}\) is a saddle. As ET increases to the threshold \(ET=1.1\), the pseudoequilibrium \(E_{p}\), real equilibrium \(E_{r}^{22}\), and tangent point \(E_{t}\) collide and merge into a single point \(E_{b}\), leading to a boundary-saddle bifurcation, as shown in Fig. 6[B]. As ET continues to increase, \(E_{b}\) separates into a virtual equilibria \(E_{v}^{22}\) and a tangent point \(E_{t}\), as depicted in Fig. 6[C], where \(ET=1.5\).

Figure 6
figure 6

Boundary-saddle bifurcation for Filippov system (5). Parameters are \(r=1, K=4, \beta =0.5, \mu =0.4, a=0.35, \delta =0.3, \eta =0.1, \tau =0.12\), and [A] \(p=0.25, ET=0.6\); [B] \(p=0.25, ET=1.09065\); [C] \(p=0.25, ET=1.5\); [D] \(p=0.15, ET=1.09065\); [E] \(p=0.3, ET=1.09065\); [F] \(p=0.4, ET=1.09065\)

Full size image

From the perspective of pest control, the occurrence of boundary-node bifurcation and boundary-focus bifurcation is advantageous for pest control. As shown in Fig. 4[A] and Fig. 5[A], when the threshold ET is small, pests tend to stabilize at the real equilibria (node \(E_{r}^{22}\) or focus \(E_{r}^{21}\)). This indicates that despite the implementation of IPM strategies, the pest population is not effectively controlled. However, as the threshold ET increases, the Filippov system (5) undergoes boundary-node (or -focus) bifurcation, causing the system to stabilize at pseudoequilibrium, thereby preventing a large-scale outbreak of the pest population. With the increase of ET, the occurrence of boundary-saddle bifurcation is unfavorable for the control of the pest population. As shown in Fig. 6, the occurrence of boundary-saddle bifurcation leads to the trajectories of the Filippov system (5) to eventually approach the real equilibrium \(E_{r}^{23}\), resulting in a pest outbreak.

However, we can also choose p as the bifurcation parameter, as shown in Figs. 6[D]-[B]-[E]. When p is small (\(p=0.15\)), the trajectories tend toward the real equilibrium \(E_{r}^{23}\), as shown in Fig. 6[D]. As p increases to \(p=0.25\), the system’s virtual equilibrium \(E_{v}^{22}\) and tangent point \(E_{t}\) collide and merge into a single point \(E_{b}\), leading to a boundary-saddle bifurcation in the Filippov system (5), as shown in Fig. 6[B]. When p continues to increase to \(p=0.3\), \(E_{b}\) separates into a pseudoequilibrium \(E_{p}\), a real equilibrium \(E_{r}^{22}\), and a tangent point \(E_{t}\), as shown in Fig. 6[E]. At this point, the trajectories of the system tend toward either the pseudoequilibrium \(E_{p}\) or the real equilibrium \(E_{r}^{23}\). In this scenario, even with a low predator density, it can still result in a pest outbreak. As p continues to increase, the real equilibria \(E_{r}^{22}\) and \(E_{r}^{23}\) disappear, and the trajectories of the system eventually tend toward the pseudoequilibrium, avoiding a pest outbreak, as shown in Fig. 6[F].

4.3 Nonexistence of limit cycle

In Filippov systems, the following three types of limit cycles may exist:

(i) The limit cycle is entirely contained within the vector field \(F_{G_{i}}(Z),i=1,2 \), as shown in Fig. 7[A].

Figure 7
figure 7

Possible limit-cycle types in the invariant domain Ω of the Filippov system

Full size image

(ii) A limit cycle that contains only a tangency point (see Fig. 7[B]) or includes a part of the sliding segment \(\Sigma _{SL}\) (see Fig. 7[C]).

(iii) The limit cycle desieges the whole sliding segment \(\Sigma _{SL}\), as shown in Fig. 7[D].

Next, the existence of the above three types of limit cycles will be excluded. First, to exclude the existence of the first type of limit cycle, for the purpose of the proof, let the right-hand function of subsystem \(S_{i}\) be denoted as \(f_{G_{i}}(Z)= (f_{G_{i}}^{1}(Z)),f_{G_{i}}^{2}(Z) )\), where \(i=1,2\).

Lemma 1

There is no limit cycle totally in the vector field \(F_{G_{i}}(Z),i=1,2\).

Proof

Let the Dulac function be \(D(x,y)=1/xy\) for subsystem \(S_{1}\), we have

$$ \frac{\partial (Df_{G_{1}}^{1}(Z))}{\partial x}+ \frac{\partial (Df_{G_{1}}^{2}(Z))}{\partial y}=-\frac{r}{yK}< 0, $$

similarly, let \(D(x,y)=1/xy\) for subsystem \(S_{2}\), we have

$$ \frac{\partial (Df_{G_{2}}^{1}(Z))}{\partial x}+ \frac{\partial (Df_{G_{2}}^{2}(Z))}{\partial y}=-\frac{r}{yK}- \frac{\tau}{x^{2}y}< 0. $$

Therefore, the Filippov system does not have limit cycles that are entirely contained within the vector field \(F_{G_{i}}(Z),i=1,2\).

Next, we will exclude the existence of the second type of limit cycle. □

Lemma 2

There is no limit cycle that contains only a tangency point or includes a part of the sliding segment.

Proof

To prove Lemma 2, we consider the following two cases:

Case 1.

$$ \mu pET< (\delta p+\eta pET+\tau \beta ) \bigl(a+ET^{2}\bigr). $$

(i) When \(y_{\min} \leq y_{p} \leq y_{\max}\), the Filippov system has a unique pseudoequilibrium, and this pseudoequilibrium is stable. In this case, Lemma 2 holds.

(ii) When \(y_{\max} \geq y_{p}\) or \(y_{p}\leq y_{\min}\), there is no pseudoequilibrium in the Filippov system. In this case, because the real equilibria \(E_{r}^{21}\) and \(E_{r}^{23}\) are locally stable, the trajectories starting at the tangency point \(E_{t}\) either spiral towards the focus \(E_{r}^{21}\) (as shown in Fig. 8) or directly approach the node \(E_{r}^{23}\). Therefore, trajectories starting from \(E_{t}\) will not form a limit cycle.

Figure 8
figure 8

Phase plane \(x-y\) of Filippov system (5) to show the invariance region Ω, the sliding domain Σ, the equilibrium \(E_{r}^{21}\), and the null isoclines \(L_{2}\), The orbit Γ is plotted to show the asymptotical stability of the focus \(E_{r}^{21}\)

Full size image

Case 2.

$$ \mu pET>(\delta p+\eta pET+\tau \beta ) \bigl(a+ET^{2}\bigr), $$

that is

$$ \frac{\mu ET}{a+ET^{2}}-\delta -\eta ET-\frac{\tau \beta}{p}>0, $$

for this case, we have

$$ \frac{\mu ET}{a+ET^{2}}-\delta -\eta ET>0. $$

According to isocline (10), we have

$$ \frac{\mu yET}{a+ET^{2}}-\delta y-\eta yET+\tau -\frac{r\tau}{p} \biggl(1- \frac{ET}{K} \biggr)>0, $$

thus,

$$ \frac{\mu yET}{a+ET^{2}}-\delta y-\eta yET+\tau >0, $$

therefore, in the sliding domain \(\Sigma _{S}\), we have the direction on the sliding line segment is from bottom to top.

At the same time, it can also be obtained from equation (13) that

$$ y_{p}= \frac{r\tau (K-ET)}{K [(\delta p+\eta pET+\tau \beta ) -\frac{\mu pET}{a+ET^{2}} ]}< 0, $$

therefore, there is no pseudoequilibrium in the Filippov system. In this case, because the real equilibrium \(E_{r}^{11}\) is locally stable, the trajectories starting at the tangency point \(E_{t}^{2}\) either spiral towards the focus \(E_{r}^{11}\), as shown in Fig. 9, or directly approach the node \(E_{r}^{11}\). Therefore, trajectories starting from \(E_{t}^{2}\) will not form a limit cycle.

Figure 9
figure 9

Phase plane \(x-y\) of Filippov system (5) to show the invariance region Ω, the sliding domain Σ, the equilibrium \(E_{r}^{11}\), and the null isoclines \(L_{2}\), The orbit Γ is plotted to show the asymptotical stability of the focus \(E_{r}^{11}\)

Full size image

Finally, the existence of the third type of limit cycle is ruled out. □

Lemma 3

There are no admit limit cycles that include an entire sliding segment for the Filippov system (2).

Proof

Suppose there exists a limit cycle Γ containing an entire sliding segment within an invariant domain for the Filippov system (2), as shown in Fig. 10. The limit cycle Γ is divided by a discontinuous boundary Σ into left and right parts, and the intersection points of Γ and Σ are denoted as \(P_{1}\) and \(P_{2}\). Let the two parts of Γ be \(\Gamma _{1}\) and \(\Gamma _{2}\), respectively. Construct auxiliary lines \(A_{1}B_{1}=ET-\varepsilon \) and \(C_{1}D_{1}=ET+\varepsilon \), with \(C_{1}D_{1}\) intersecting with line \(\Gamma _{1}\) at points \(C_{1}\) and \(D_{1}\), and \(A_{1}B_{1}\) intersecting with line \(\Gamma _{2}\) at points \(A_{1}\) and \(B_{1}\), where ε is a sufficiently small positive number. As shown in Fig. 10, \(\Omega _{1}\) (\(\Omega _{2}\)) represents the region enclosed by \(\Gamma _{1}\) and \(C_{1}D_{1}\) (\(A_{1}B_{1}\)), and the direction of Γ is defined as counterclockwise. Denote the Dulac function as \(D(x,y)=1/xy\), using Green’s theorem [29–31], we can obtain

$$ \begin{aligned} & \iint _{\Omega _{1}} \biggl[ \frac{\partial (Df_{G_{1}}^{(1)})}{\partial x}+ \frac{\partial (Df_{G_{1}}^{(2)})}{\partial y} \biggr]\,dx\,dy \\ &\quad= \oint _{L_{1}}D \bigl[f_{G_{1}}^{(1)} \,dy-f_{G_{1}}^{(2)}\,dx \bigr] \\ &\quad= \int _{\Gamma _{1}}D \bigl[f_{G_{1}}^{(1)} \,dy-f_{G_{1}}^{(2)}\,dx \bigr]+ \int _{\overrightarrow{D_{1}C_{1}}}D \bigl[f_{G_{1}}^{(1)} \,dy-f_{G_{1}}^{(2)}\,dx \bigr] \\ &\quad=D \int _{t_{1}}^{t_{2}} \bigl[f_{G_{1}}^{(1)}f_{G_{1}}^{(2)}-f_{G_{1}}^{(2)}f_{G_{1}}^{(1)} \bigr]\,dt+D \int _{\overrightarrow{D_{1}C_{1}}} \bigl[f_{G_{1}}^{(1)} \,dy-f_{G_{1}}^{(2)}\,dx \bigr] \\ &\quad= \int _{\overrightarrow{D_{1}C_{1}}}Df_{G_{1}}^{(1)}\,dy. \end{aligned} $$
(16)
Figure 10
figure 10

Phase plane \(x-y\) of Filippov system (5)

Full size image

Similarly, we have

$$ \iint _{\Omega _{2}} \biggl[ \frac{\partial (Df_{G_{2}}^{(1)})}{\partial x}+ \frac{\partial (Df_{G_{2}}^{(2)})}{\partial y} \biggr]\,dx\,dy = \int _{ \overrightarrow{B_{1}A_{1}}}Df_{G_{2}}^{(1)}\,dy. $$
(17)

Denote the coordinates of points \(P_{1}\), \(P_{2}\), \(A_{1}\), \(B_{1}\), \(C_{1}\), \(D_{1}\) by \(y_{1}\), \(y_{2}\), \(y_{1}+h_{1}(\varepsilon )\), \(y_{2}-h_{2}(\varepsilon )\), \(y_{1}-h_{3}(\varepsilon )\), \(y_{2}+h_{4}(\varepsilon )\), where \(h_{i}(\varepsilon )>0\) and \(\lim_{\varepsilon \to 0}h_{i}(\varepsilon )=0\), thus

$$ \begin{aligned} \lim_{\varepsilon \to 0} \biggl[ \int _{ \overrightarrow{D_{1}C_{1}}}Df_{G_{1}}^{(1)}\,dy \biggr]&=\lim _{ \varepsilon \to 0} \int _{y_{1}+h_{3}(\varepsilon )}^{y_{2}-h_{4}( \varepsilon )} \biggl[\frac{r (1-\frac{x}{K} )}{y}-\beta \biggr]\,dy \\ &=r \biggl(1-\frac{x}{K} \biggr)\ln \frac{y_{2}}{y_{1}}-\beta (y_{2}-y_{1}). \end{aligned} $$

Similarly, we obtain

$$ \lim_{\varepsilon \to 0} \biggl[ \int _{ \overrightarrow{B_{1}A_{1}}}Df_{G_{2}}^{(1)}\,dy \biggr]=-r \biggl(1- \frac{x}{K} \biggr)\ln \frac{y_{2}}{y_{1}}+\beta (y_{2}-y_{1})+p\ln \frac{y_{2}}{y_{1}}. $$

Therefore,

$$ \lim_{\varepsilon \to 0} \biggl[ \int _{ \overrightarrow{D_{1}C_{1}}}Df_{G_{1}}^{(1)}\,dy \biggr]+\lim _{ \varepsilon \to 0} \biggl[ \int _{\overrightarrow{B_{1}A_{1}}}Df_{G_{2}}^{(1)}\,dy \biggr]=p\ln \frac{y_{2}}{y_{1}}>0. $$
(18)

According to Lemma 1, we have

$$ \zeta \doteq \iint _{\Omega _{1}} \biggl[ \frac{\partial (Df_{G_{1}}^{1}(Z))}{\partial x}+ \frac{\partial (Df_{G_{1}}^{2}(Z))}{\partial y} \biggr]< 0 $$

and

$$ \zeta \doteq \iint _{\Omega _{2}} \biggl[ \frac{\partial (Df_{G_{2}}^{1}(Z))}{\partial x}+ \frac{\partial (Df_{G_{2}}^{2}(Z))}{\partial y} \biggr]< 0, $$

thus,

$$ \lim_{\varepsilon \to 0} \biggl[ \int _{ \overrightarrow{D_{1}C_{1}}}Df_{G_{1}}^{(1)}\,dy \biggr]+\lim _{ \varepsilon \to 0} \biggl[ \int _{\overrightarrow{B_{1}A_{1}}}Df_{G_{2}}^{(1)}\,dy \biggr]< 0, $$

which contradicts (18). Therefore, there are no admit limit cycles that include an entire sliding segment for the Filippov system (5).

According to the above discussion, if the Filippov system (5) has pseudoequilibrium, then the pseudoequilibrium must be stable. In the Filippov system, when real equilibrium, virtual equilibrium, and pseudoequilibrium coexist, any trajectory starting from an initial value either converges to the real equilibrium of the Filippov system or tends towards the pseudoequilibrium, as shown in Fig. 11[A]. In this situation, although the system has pseudoequilibrium, when the population density of the pest is low, the trajectory of the system tends towards the real equilibrium \(E_{r}^{23}\). At this time, there is a pest outbreak, indicating poor pest control. Therefore, to address this issue, we increased the concentration of the insecticide. As the concentration of the insecticide increases, the real equilibrium \(E_{r}^{22}\) and \(E_{r}^{23}\) of the Filippov system disappear, and the trajectory of the Filippov system (5) eventually tends towards the real equilibrium \(E_{r}^{11}\) and the pseudoequilibrium \(E_{p}\), as shown in Fig. 11[B]. At this time, effective control of the pest is achieved. Additionally, we found that increasing the release quantity of natural enemies can also achieve the same pest-control effect.

Figure 11
figure 11

Schematic diagram illustrating the coexistence of real equilibrium, virtual equilibrium, and pseudoequilibrium in the Filippov system (5). Parameters are \(r=1, K=4, \beta =0.5, \mu =0.8, a=1.5, \delta =0.2, \eta =0.1, \tau =0.06, ET=1.5\). and [A] \(p=0.2\); [B] \(p=0.3\)

Full size image

 □

5 Biological conclusions

In comprehensive pest management, considering the application of insecticides and the release of enemies as an ideal scenario of instantaneous completion is common. However, in real-life situations, it is crucial to account for the persistence and lag effects of insecticide actions. Therefore, incorporating the intermittency of insecticide application into the model is highly necessary. To address this, we established a Filippov nonsmooth ecological system with antipredator behavior and conducted an indepth investigation of the proposed model through the utilization of Filippov system theory knowledge and numerical simulation techniques.

Specifically, we conducted a detailed analysis of the pseudoequilibrium bifurcation and sliding mode dynamics of the Filippov system (5). The results indicate that increasing the concentration of pesticides or the release of enemies will lead to the continued existence of pseudoequilibrium in the model, as shown in Fig. 3. Moreover, as discussed later, if a pseudoequilibrium exists, it must be stable. Although the existence of pseudoequilibrium helps control the pest population, when both the real equilibrium and pseudoequilibrium coexist in the system, different initial concentrations of pests and enemies will result in pest–enemy densities stabilizing at different attractors, as shown in Fig. 11[A]. This suggests that the implementation of control strategies is closely related to the initial density.

Simultaneously, this paper also investigates and discusses the boundary-node, -focus, and -saddle bifurcation of the system, as well as the nonexistence of limit cycles. The research results indicate that with the increase of ET, the occurrence of boundary-node and -focus bifurcation in the system will be beneficial for pest control. However, the occurrence of boundary-saddle bifurcation may lead to an outbreak in the pest population. When selecting p as the bifurcation parameter, the occurrence of boundary-saddle bifurcation is advantageous for pest control. It is worth noting that when p increases to a certain value, the equilibria of subsystem \(S_{2}\) will disappear, resulting in the pest–predator density stabilizing at the pseudoequilibrium or the real equilibrium \(E_{r}^{11}\), as shown in Fig. 4[F] and Fig. 11[B]. This achieves the goal of controlling pests.

One fundamental assumption of this article is that when the pest-population density reaches the economic threshold, an IPM strategy should be consistently employed for a period until the pest-population density falls below the economic threshold. However, a critical issue is overlooked here, namely, pest outbreaks and resurgence often coincide with shortages of resources such as chemical pesticides, physical insecticides, etc. This scarcity will significantly impact the control of pests. Addressing the challenge of limited resources, determining how to implement optimal control measures to prevent pest-population outbreaks will be a focal point of our future work.