1 Introduction

In the latter part of the 17th century, Isaac Newton and Gottfried Wilhelm Leibniz established the groundwork for differential and integral calculus. Today, this field stands as one of the most widely applicable branches of mathematics and it is referred to as Newtonian calculus. The fundamental operations of Newtonian calculus, integration and differentiation, correspond to the infinitesimal counterparts of the arithmetic operations of addition and its inverse, subtraction. Consequently, this calculus is sometimes termed additive calculus, highlighting that its primary operation is addition.

In 1967, Grossman and Katz [15] first introduced a type of non-Newtonian calculus, known as multiplicative calculus, where multiplication and division take the place of addition and subtraction, respectively. This approach proves particularly advantageous when handling exponentially varying mappings.

A comprehensive mathematical exposition of multiplicative calculus was presented by Bashirov et al. [5]. Furthermore, in the existing literature, traces of a similar calculation proposed by mathematical biologists Volterra and Hostinsky [28] in 1938 can be found, known as the Volterra calculation, which is recognized as a specific instance of multiplicative calculus.

The advantage of using multiplicative calculus, or non-Newtonian calculus, lies in its simplicity for modeling exponential growth phenomena, as it directly employs multiplication and division to handle proportional relationships and constant relative growth rates. This approach offers an intuitive representation of processes with multiplicative changes, making it particularly useful for analyzing natural phenomena exhibiting exponential or multiplicative behavior, such as population growth, compound interest, biological decay, and viral spread. Furthermore, the straightforward calculations and potential for computational efficiency make it versatile and applicable to various fields, offering novel insights and innovative solutions in mathematics, biology [13], economics and finance [6], physics and engineering [27], and other domains.

The concept of convexity holds significant and central importance across various domains, and it is closely intertwined with the development of the theory of inequalities. We recall that a function φ is considered convex on the interval \(I\subset \mathbb{R}\) if the inequality

$$ \varphi \bigl( tx+ ( 1-t ) y \bigr) \leq t\varphi ( x ) + ( 1-t ) \varphi (y) $$

holds for all \(x,y\in I\) and \(t\in {}[ 0,1]\) [24].

This theory serves as a fundamental tool in studying properties of solutions of differential equations and in error estimates of quadrature formulas. Several papers addressing quadrature methods can be found in [4, 9, 12, 26] and the references cited therein.

The Hermite–Hadamard inequality stands as the fundamental inequality for convex functions, and it can be expressed as follows: For any convex function φ on the interval \([ \varrho ,\kappa ]\) with \(\varrho <\kappa \), the inequality states that

$$ \varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) \leq \frac {1}{\kappa -\varrho} \int _{\varrho}^{\kappa}\varphi ( u )\,du\leq \frac {\varphi ( \varrho ) +\varphi ( \kappa ) }{2}. $$
(1)

The concept of convexity has undergone various extensions aimed at encompassing broader classes of functions. Among these extensions there is one that aligns with multiplicative calculus, referred to as logarithmic convexity or multiplicative convexity, defined as follows:

Definition 1.1

([20])

A function \(\varphi :I\subset \mathbb{R}\rightarrow \mathbb{R}^{+}\) is termed as log-convex or multiplicatively convex if

$$ \varphi \bigl( tx+ ( 1-t ) y \bigr) \leq \bigl[ \varphi ( x ) \bigr] ^{t} \bigl[ \varphi (y) \bigr] ^{1-t} $$

holds for all \(x,y\in I\) and all \(t\in {}[ 0,1]\).

In a recent study, Ali et al. [1] introduced the counterpart of inequality (1) specifically applicable to multiplicatively convex mappings. The corresponding expression is as follows:

$$ \varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) \leq \biggl( \int _{\varrho}^{\kappa}\varphi ( u ) ^{du} \biggr) ^{ \frac{1}{\kappa -\varrho}}\leq \sqrt{\varphi ( \varrho ) \varphi ( \kappa ) }. $$

Additionally, Khan et al. [16] established Hermite–Hadamard-type inequalities, including midpoint- and trapezoid-type inequalities, in the same context. In [3], Ali et al. investigated Ostrowski- and Simpson-type inequalities for multiplicatively convex mappings. Chasreechai et al. presented some Simpson- and Newton-type inequalities in [11], while the dual-Simpson- and Maclaurin-type inequalities for the same class of mappings were established in [18] and [17], respectively. For further insights into the latest advancements on this topic, we encourage readers to explore the referenced articles [2, 7, 8, 10, 14, 19, 21–23, 25] and the comprehensive bibliographies provided therein.

Motivated by the aforementioned cited papers, this study introduces a biparametrized multiplicative integral identity. Building upon this identity, we establish a set of one-, two-, and three-point Newton–Cotes-type inequalities for increasing multiplicatively differentiable convex mappings. The obtained results include both previously unknown findings and refinements of several other already established results.

The rest of this paper is structured as follows: Sect. 2 provides the essential background on multiplicative calculus. In Sect. 3, we introduce a novel biparametrized identity, which serves as the foundation for deriving a series of multiplicative inequalities applicable to the class of multiplicatively convex mappings. To support and validate our findings, an illustrative example with graphical representations is presented in Sect. 4. In Sect. 5, we showcase practical applications that demonstrate the significance of the obtained inequalities. Finally, Sect. 6 concludes the paper and outlines potential directions for future research.

2 Preliminaries

In this section, we review several definitions, properties, and concepts related to multiplicative differentiation and integration.

In [5], Bashirov et al. introduced the concept of ∗ derivative, called multiplicative derivative, in the following way:

Definition 2.1

([5])

Suppose a function \(\varphi :\mathbb{R}\rightarrow \mathbb{R}^{+}\) is positive. The multiplicative derivative denoted by \(\varphi ^{\ast }\) is given by

$$ \frac {d^{\ast }\varphi}{du}=\varphi ^{\ast } ( u ) = \lim_{h\rightarrow 0} \biggl( \frac {\varphi ( u+h ) }{\varphi ( u ) } \biggr) ^{\frac{1}{h}}. $$

The relation between \(\varphi ^{\ast }\) and the ordinary derivative \(\varphi ^{\prime }\) is as follows:

$$ \varphi ^{\ast } ( u ) =e^{ ( \ln \varphi ( u ) ) ^{\prime}}=e^{ \frac{\varphi ^{\prime } ( u ) }{\varphi ( u ) }}. $$

Based on this representation, we indicate that a mapping φ is increasing if and only if \(\varphi ^{\ast}\geq 1\).

Proposition 2.2

([5])

If the mappings φ and ϕ are both multiplicatively differentiable, and ψ is differentiable, then the mappings αφ, φϕ, \(\varphi +\phi \), \(\varphi /\phi \), \(\varphi ^{\psi}\), and \(\varphi \circ \psi \) all have multiplicative derivatives as well, where α is an arbitrary constant. In addition, the following properties hold:

  • \(( \alpha \varphi ) ^{\ast } (u ) =\varphi ^{ \ast } (u ) \),

  • \(( \varphi \phi ) ^{\ast } (u ) =\varphi ^{ \ast } (u ) \phi ^{\ast } (u ) \),

  • \(( \varphi +\phi ) ^{\ast } (u ) =\varphi ^{ \ast } (u ) ^{\frac{\varphi (u ) }{\varphi (u ) +\phi (u ) }} \phi ^{\ast } (u ) ^{ \frac{\phi (u ) }{\varphi (u ) +\phi ( u ) }}\),

  • \(( \frac{\varphi}{\phi} ) ^{\ast } (u ) = \frac{\varphi ^{\ast } (u ) }{\phi ^{\ast } (u ) }\),

  • \(( \varphi ^{\psi} ) ^{\ast } (u ) =\varphi ^{ \ast } (u ) ^{\psi (u ) }\varphi (u ) ^{\psi ^{\prime } (u ) }\),

  • \((\varphi \circ \psi )^{\ast}(u)=\varphi ^{\ast} ( \psi (u) )^{\psi ^{\prime}(u)}\).

Bashirov et al. also introduced the multiplicative integral operator in the following manner:

$$ \int ^{\kappa}_{\varrho} \bigl( \varphi (u ) \bigr) ^{du}=\exp \biggl( \int ^{\kappa}_{\varrho}\ln \bigl( \varphi (u ) \bigr)\,du \biggr) . $$

Proposition 2.3

([5])

If φ and ϕ are positive and Riemann integrable mappings on \([\varrho ,\kappa ]\), then φ is multiplicatively integrable on \([\varrho ,\kappa ]\) and

  • \(\int ^{\kappa}_{\varrho} ( ( \varphi (u ) ) ^{p} ) ^{du}= ( \int ^{\kappa}_{\varrho} ( \varphi (u ) ) ^{du} ) ^{p}\),

  • \(\int ^{\kappa}_{\varrho} ( \varphi (u ) \phi ( u ) ) ^{du}= \int ^{\kappa}_{\varrho} ( \varphi ( u ) ) ^{du}\int ^{\kappa}_{\varrho} ( \phi ( u ) ) ^{dt}\),

  • \(\int ^{\kappa}_{\varrho} ( \frac{\varphi (u ) }{\phi (u ) } ) ^{du}= \frac{\int ^{\kappa}_{\varrho} ( \varphi (u ) ) ^{du}}{\int ^{\kappa}_{\varrho} ( \phi (u ) ) ^{du}}\),

  • \(\int ^{\kappa}_{\varrho} ( \varphi (u ) ) ^{du}=\int ^{c}_{\varrho} ( \varphi (u ) ) ^{du}\int ^{\kappa}_{c} ( \varphi (u ) ) ^{du}\), \(\varrho < c<\kappa \),

  • \(\int ^{\varrho}_{\varrho} ( \varphi (u ) ) ^{du}=1\) and \(\int ^{\kappa}_{\varrho} ( \varphi (u ) ) ^{du}= ( \int ^{\varrho}_{\kappa} ( \varphi (u ) ) ^{du} ) ^{-1}\).

Theorem 2.4

([5])

Suppose \(\varphi :[\varrho ,\kappa ]\rightarrow \mathbb{R}\) is multiplicatively differentiable, and \(\phi :[\varrho ,\kappa ]\rightarrow \mathbb{R}\) is differentiable. Then the mappings \((\varphi ^{\ast} )^{\phi}\) and \(\varphi ^{\phi ^{\prime}}\) are multiplicatively integrable, and we have that

$$ \int ^{\kappa}_{\varrho} \bigl( \varphi ^{\ast } (u ) ^{\phi ( u ) } \bigr) ^{du}= \frac {\varphi ( \kappa ) ^{\phi ( \kappa ) }}{\varphi ( \varrho ) ^{\phi ( \varrho ) }} \times \frac {1}{\int ^{b}_{\varrho} ( \varphi (u ) ^{\phi ^{\prime } (u ) } ) ^{du}}. $$

This relation is known as multiplicative integration by parts.

Lemma 2.5

([3])

Let \(\varphi :[\varrho ,\kappa ]\rightarrow \mathbb{R}\) be multiplicatively differentiable, \(\phi :J\subset \mathbb{R}\rightarrow \mathbb{R}\) and \(\psi :[\varrho ,\kappa ]\rightarrow \mathbb{R}\) be two differentiable mappings. Then we have

$$ \int ^{\kappa}_{\varrho} \bigl( \varphi ^{\ast } \bigl( \psi (u ) \bigr) ^{\psi ^{\prime } (u ) \phi (u ) } \bigr) ^{dt}= \frac {\varphi ( \psi ( \kappa ) ) ^{\phi ( \kappa ) }}{\varphi ( \psi ( \varrho ) ) ^{\phi ( \varrho ) }} \times \frac {1}{\int ^{\kappa}_{\varrho} ( \varphi ( \psi (u ) ) ^{\phi ^{\prime } (u ) } ) ^{du}}. $$

3 Main results

Throughout the rest of the paper, we make the assumption that \([\varrho ,\kappa ]\) is a subinterval of \([0,\infty )\), and \(\varphi : [\varrho ,\kappa ] \rightarrow \mathbb{R}^{+}\) is a multiplicatively differentiable function on \([\varrho ,\kappa ]\), with \(\varphi ^{\ast}\in L^{1} [\varrho ,\kappa ]\). Before proceeding to state the results, the following notation is used:

$$ \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi )= \varphi ( x ) ^{ \frac { ( \varrho +\kappa -2x ) \lambda +2 ( x-\varrho ) }{2 ( \kappa -\varrho ) }}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) ^{ \frac { ( \varrho +\kappa -2x ) ( 1-\lambda ) }{ ( \kappa -\varrho ) }} \varphi ( \varrho +\kappa -x ) ^{ \frac { ( \varrho +\kappa -2x ) \lambda +2 ( x-\varrho ) }{2 ( \kappa -\varrho ) }}, $$
(2)

with \(\lambda \geq 0\) and \(x\in [\varrho ,\frac {\varrho +\kappa}{2} ]\).

To establish our findings, we must rely on the following lemma.

Lemma 3.1

For all \(\lambda \geq 0\) and \(x \in [\varrho , \frac{\varrho + \kappa}{2}]\), the following identity for multiplicative integrals holds:

$$\begin{aligned} &\mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \\ &\quad = \biggl( \int _{0}^{1} \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr)^{t} \bigr) ^{dt} \biggr) ^{\frac { ( x-\varrho ) ^{2}}{\kappa -\varrho}} \\ &\qquad {}\times \biggl( \int _{0}^{1} \biggl( \varphi ^{ \ast } \biggl( ( 1-t ) x+t\frac {\varrho +\kappa}{2} \biggr)^{ t-\lambda} \biggr) ^{dt} \biggr) ^{ \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } } \\ &\qquad {}\times \biggl( \int _{0}^{1} \biggl(\varphi ^{ \ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) \biggr)^{t- ( 1-\lambda )} \biggr) ^{dt} \biggr) ^{ \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }} \\ &\qquad {}\times \biggl( \int _{0}^{1} \bigl( \varphi ^{ \ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t \kappa \bigr)^{t-1} \bigr) ^{dt} \biggr) ^{\frac { ( x-\varrho ) ^{2}}{\kappa -\varrho}}, \end{aligned}$$

where \(\mathcal{Z}\) is defined in (2).

Proof

Let

$$\begin{aligned}& I_{1} = \biggl( \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) ^{t} \bigr) ^{dt} \biggr) ^{\frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}}, \\& I_{2} = \biggl( \int _{0}^{1} \biggl( \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x+t \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{t-\lambda } \biggr) ^{dt} \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }}, \\& I_{3} = \biggl( \int _{0}^{1} \biggl( \varphi ^{ \ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) \biggr) ^{t- ( 1-\lambda ) } \biggr) ^{dt} \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }}, \end{aligned}$$

and

$$ I_{4}= \biggl( \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t\kappa \bigr) \bigr) ^{t-1} \bigr) ^{dt} \biggr) ^{ \frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}}. $$

Using Lemma 2.5, from \(I_{1}\) we have

$$\begin{aligned} I_{1} ={}& \biggl( \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) ^{t} \bigr) ^{dt} \biggr) ^{\frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}} \\ ={}& \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) ^{ ( x- \varrho ) \frac{ ( x-\varrho ) }{\kappa -\varrho}t} \bigr) ^{dt} \\ ={}& \frac {\varphi ( x ) ^{\frac{x-\varrho}{\kappa -\varrho}}}{1} \frac {1}{\int _{0}^{1} ( \varphi ( ( ( 1-t ) \varrho +tx ) ) ^{\frac{x-\varrho}{\kappa -\varrho}} ) ^{dt}} \\ ={}&\varphi ( x ) ^{\frac {x-\varrho}{\kappa -\varrho}} \frac {1}{\exp \int _{0}^{1} ( \frac{x-\varrho}{\kappa -\varrho}\ln \varphi ( ( ( 1-t ) \varrho +tx ) ) )\,dt} \\ ={}&\varphi ( x ) ^{\frac {x-\varrho}{\kappa -\varrho}} \frac {1}{\exp \int _{\varrho }^{x} ( \frac{1}{\kappa -\varrho}\ln \varphi ( u ) )\,du} \\ ={}&\varphi ( x ) ^{\frac {x-\varrho}{\kappa -\varrho}} \frac {1}{ ( \int _{\varrho}^{x}\varphi ( u ) ^{du} ) ^{\frac {1}{\kappa -\varrho}}} \\ ={}&\varphi ( x ) ^{\frac {x-\varrho}{\kappa -\varrho}} \biggl( \int _{\varrho}^{x}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}}. \end{aligned}$$
(3)

Likewise,

$$\begin{aligned}& I_{2} ={} \biggl( \int _{0}^{1} \biggl( \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x+t \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{t-\lambda } \biggr) ^{dt} \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }} \\& \hphantom{I_{2}}={} \int _{0}^{1} \biggl( \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x+t\frac {\varrho +\kappa}{2} \biggr) \biggr) ^{\frac{\varrho +\kappa -2x}{2} \frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( t-\lambda ) } \biggr) ^{dt} \\& \hphantom{I_{2}}={} \frac { ( \varphi ( \frac{\varrho +\kappa}{2} ) ) ^{\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( 1-\lambda ) }}{ ( \varphi ( x ) ) ^{-\frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}} \frac {1}{\int _{0}^{1} ( ( \varphi ( ( 1-t ) x+t\frac{\varrho +\kappa}{2} ) ) ^{\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} ) ^{dt}} \\& \hphantom{I_{2}}={} \frac { ( \varphi ( \frac{\varrho +\kappa}{2} ) ) ^{\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( 1-\lambda ) }}{ ( \varphi ( x ) ) ^{-\frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}} \frac {1}{\exp \int _{0}^{1}\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }\ln ( \varphi ( ( 1-t ) x+t\frac{\varrho +\kappa}{2} ) )\,dt} \\& \hphantom{I_{2}}={} \biggl( \varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( 1-\lambda ) } \bigl( \varphi ( x ) \bigr) ^{ \frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} \frac {1}{\exp \int _{x}^{\frac{\varrho +\kappa}{2}}\frac{1}{\kappa -\varrho}\ln ( \varphi ( u ) )\,du} \\& \hphantom{I_{2}}={} \biggl( \varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( 1-\lambda ) } \bigl( \varphi ( x ) \bigr) ^{ \frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} \biggl( \int _{x}^{\frac{\varrho +\kappa}{2}} \bigl( \varphi ( u ) \bigr) ^{du} \biggr) ^{ \frac{1}{\varrho -\kappa}}, \end{aligned}$$
(4)
$$\begin{aligned}& I_{3} = \biggl( \int _{0}^{1} \biggl( \biggl( \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) \biggr) \biggr) ^{t- ( 1-\lambda ) } \biggr) ^{dt} \biggr) ^{ \frac{ ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }} \\& \hphantom{I_{3}}= \int _{0}^{1} \biggl( \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho + \kappa -x ) \biggr) ^{\frac{\varrho +\kappa -2x}{2} \frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) } ( t- ( 1-\lambda ) ) } \biggr) ^{dt} \\& \hphantom{I_{3}}= \frac {\varphi ( \varrho +\kappa -x ) ^{\frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}}{\varphi ( \frac{\varrho +\kappa}{2} ) ^{-\frac{ ( 1-\lambda ) ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}} \frac {1}{\int _{0}^{1} ( \varphi ( ( 1-t ) \frac{\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) ) ^{\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} ) ^{dt}} \\& \hphantom{I_{3}}= \frac {\varphi ( \varrho +\kappa -x ) ^{\frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}}{\varphi ( \frac{\varrho +\kappa}{2} ) ^{-\frac{ ( 1-\lambda ) ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}} \frac {1}{\exp \int _{0}^{1}\frac{ ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }\ln ( \varphi ( ( 1-t ) \frac{\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) ) )\,dt} \\& \hphantom{I_{3}}= \varphi ( \varrho +\kappa -x ) ^{ \frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) ^{ \frac{ ( 1-\lambda ) ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} \frac {1}{\exp \int _{\frac{\varrho +\kappa}{2}}^{\varrho +\kappa -x}\frac{1}{\kappa -\varrho}\ln ( \varphi ( u ) )\,du} \\& \hphantom{I_{3}}= \varphi ( \varrho +\kappa -x ) ^{ \frac{\lambda ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr) ^{ \frac{ ( 1-\lambda ) ( \varrho +\kappa -2x ) }{2 ( \kappa -\varrho ) }} \biggl( \int _{\frac{\varrho +\kappa}{2}}^{\varrho +\kappa -x} \bigl( \varphi ( u ) \bigr) ^{du} \biggr) ^{\frac{1}{\varrho -\kappa}}, \end{aligned}$$
(5)

and

$$\begin{aligned} I_{4} ={}& \biggl( \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t\kappa \bigr) \bigr) ^{t-1} \bigr) ^{dt} \biggr) ^{ \frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}} \\ ={}& \int _{0}^{1} \bigl( \bigl( \varphi ^{\ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t \kappa \bigr) \bigr) ^{ ( x-\varrho ) \frac{ ( x-\varrho ) }{\kappa -\varrho} ( t-1 ) } \bigr) ^{dt} \\ ={}& \frac {1}{ ( \varphi ( \varrho +\kappa -x ) ) ^{-\frac{x-\varrho}{\kappa -\varrho}}} \frac {1}{\int _{0}^{1} ( ( \varphi ( ( 1-t ) ( \varrho +\kappa -x ) +t\kappa ) ) ^{\frac{x-\varrho}{\kappa -\varrho}} ) ^{dt}} \\ ={}& \bigl( \varphi ( \varrho +\kappa -x ) \bigr) ^{ \frac{x-\varrho}{\kappa -\varrho}} \frac {1}{\exp \int _{0}^{1}\frac{x-\varrho}{\kappa -\varrho}\ln ( \varphi ( ( 1-t ) ( \varrho +\kappa -x ) +t\kappa ) )\,dt} \\ ={}& \bigl( \varphi ( \varrho +\kappa -x ) \bigr) ^{ \frac{x-\varrho}{\kappa -\varrho}} \frac {1}{\exp \int _{\varrho +\kappa -x}^{\kappa}\frac{1}{\kappa -\varrho}\ln ( \varphi ( u ) )\,du} \\ ={}& \bigl( \varphi ( \varrho +\kappa -x ) \bigr) ^{ \frac{x-\varrho}{\kappa -\varrho}} \biggl( \int _{\varrho +\kappa -x}^{\kappa} \bigl( \varphi ( u ) \bigr) ^{du} \biggr) ^{\frac{1}{\varrho -\kappa}}. \end{aligned}$$
(6)

By multiplying the equalities (3)–(6), we obtain the desired result, and thus, the proof is completed. □

Theorem 3.2

For an increasing multiplicatively differentiable mapping \(\varphi : [ \varrho ,\kappa ] \rightarrow \mathbb{R}^{+}\) on \([ \varrho ,\kappa ] \), if \(\varphi ^{\ast}\) is multiplicatively convex on \([\varrho ,\kappa ]\), then the following inequality holds for \(\lambda \geq 0\):

$$\begin{aligned} \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho} \varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \leq {}& \bigl(\varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \bigr)^{ \frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac {\mathcal{C}_{1} (\lambda )(\varrho +\kappa -2x)^{2}}{12(\kappa -\varrho )}} \\ &{}\times \bigl(\varphi ^{\ast } (x )\varphi ^{\ast } ( \varrho + \kappa -x ) \bigr)^{ \frac {8 (x-\varrho )^{2}+\mathcal{C}_{2} (\lambda )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}}, \end{aligned}$$

where

$$\begin{aligned}& \mathcal{C}_{1} (\lambda )=\textstyle\begin{cases} 2-3\lambda +2\lambda ^{3} & \textit{for } 0\leq \lambda \leq 1, \\ 3\lambda -2 & \textit{for } \lambda >1, \end{cases}\displaystyle \end{aligned}$$
(7)
$$\begin{aligned}& \mathcal{C}_{2} (\lambda )=\textstyle\begin{cases} 1-3\lambda +6\lambda ^{2}-2\lambda ^{3} & \textit{for } 0\leq \lambda \leq 1, \\ 3\lambda -1 & \textit{for } \lambda >1, \end{cases}\displaystyle \end{aligned}$$
(8)

and \(\mathcal{Z}\) is defined in (2).

Proof

Based on Lemma 3.1 and the properties of multiplicative integrals, we can deduce the following:

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho} \varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0} \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) ^{t} \bigr) \bigr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \biggl\vert \ln \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x +t \frac {\varrho +\kappa}{2} \biggr) ^{t-\lambda} \biggr) \biggr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \biggl\vert \ln \biggl( \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t(\varrho +\kappa -x) \biggr) ^{t- (1- \lambda )} \biggr) \biggr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0} \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) ( \varrho +\kappa -x)+t \kappa \bigr) ^{t-1} \bigr) \bigr\vert \,dt \biggr\} \\& \quad = \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0}t \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) \bigr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \vert t-\lambda \vert \biggl\vert \ln \biggl( \varphi ^{ \ast } \biggl( ( 1-t ) x +t\frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert \biggl\vert \ln \biggl( \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t(\varrho +\kappa -x) \biggr) \biggr) \biggr\vert \,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0} (1-t ) \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) (\varrho +\kappa -x)+t \kappa \bigr) \bigr) \bigr\vert \,dt \biggr\} . \end{aligned}$$

Using the multiplicative convexity of \(\varphi ^{\ast }\), we get

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho} \varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0}t \ln \bigl( \varphi ^{\ast } ( \varrho )^{ 1-t} \varphi ^{\ast } (x )^{ t} \bigr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \vert t-\lambda \vert \ln \biggl( \varphi ^{\ast } ( x )^{1-t} \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{t} \biggr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert \ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{1-t}+ \varphi ^{\ast } ( \varrho +\kappa -x )^{t} \biggr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0} (1-t )\ln \bigl( \varphi ^{\ast } (\varrho +\kappa -x )^{ 1-t} \varphi ^{\ast } ( \kappa )^{ t} \bigr)\,dt \biggr\} \\& \quad = \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0}t \bigl( (1-t) \ln \bigl( \varphi ^{\ast } ( \varrho ) \bigr) + t \ln \bigl(\varphi ^{\ast } (x ) \bigr) \bigr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \vert t-\lambda \vert \biggl( (1-t) \ln \bigl( \varphi ^{ \ast } (x ) \bigr) + t\ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert \\& \qquad {}\times \biggl( (1-t)\ln \biggl( \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr) \biggr) + t\ln \bigl( \varphi ^{\ast } (\varrho +\kappa -x ) \bigr) \biggr)\,dt \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \int ^{1}_{0} (1-t ) \bigl( (1-t) \ln \bigl( \varphi ^{\ast } ( \varrho +\kappa -x ) \bigr) + t\ln \bigl( \varphi ^{\ast } ( \kappa ) \bigr) \bigr)\,dt \biggr\} . \end{aligned}$$
(9)

Here, we distinguish two cases:

1. For \(0\leq \lambda \leq 1\), (9) gives

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho} \varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad = \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \biggl( \frac{ \ln ( \varphi ^{\ast } ( \varrho ) )}{6}+ \frac{ \ln ( \varphi ^{\ast } (x ) )}{3} \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \biggl( \frac{1-3\lambda +6\lambda ^{2}-2\lambda ^{3}}{6} \ln \bigl( \varphi ^{\ast } (x ) \bigr) \\& \qquad {}+ \frac{2-3\lambda +2\lambda ^{3}}{6} \ln \biggl( \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \biggl( \frac{2-3\lambda +2\lambda ^{3}}{6} \ln \biggl( \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr) \biggr) \\& \qquad {}+ \frac{1-3\lambda +6\lambda ^{2}-2\lambda ^{3}}{6}\ln \bigl( \varphi ^{ \ast } (\varrho +\kappa -x ) \bigr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \biggl( \frac{\ln ( \varphi ^{\ast } (\varrho +\kappa -x ) )}{3}+ \frac{\ln ( \varphi ^{\ast } ( \kappa ) )}{6} \biggr) \biggr\} \\& \quad = \bigl\{ \exp \bigl(\ln \bigl( \varphi ^{\ast } ( \varrho )^{\frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{ \ast } (x )^{\frac {(x-\varrho )^{2}}{3(\kappa -\varrho )}} \bigr) \bigr) \bigr\} \\& \qquad {}\times \biggl\{ \exp \biggl( \ln \biggl( \varphi ^{\ast } (x )^{ \frac { (1-3\lambda +6\lambda ^{2}-2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr)^{ \frac { (2-3\lambda +2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \biggr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \biggl( \ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac { (2-3\lambda +2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \varphi ^{\ast } (\varrho +\kappa -x )^{ \frac { (1-3\lambda +6\lambda ^{2}-2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \biggr) \biggr) \biggr\} \\& \qquad {}\times \bigl\{ \exp \bigl( \ln \bigl( \varphi ^{\ast } ( \varrho +\kappa -x )^{ \frac {(x-\varrho )^{2}}{3(\kappa -\varrho )}}\varphi ^{\ast } ( \kappa )^{\frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \bigr) \bigr) \bigr\} \\& \quad = \bigl(\varphi ^{\ast } ( \varrho )\varphi ^{\ast } ( \kappa ) \bigr)^{ \frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac { (2-3\lambda +2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{12(\kappa -\varrho )}} \\& \qquad {}\times \bigl(\varphi ^{\ast } (x )\varphi ^{\ast } ( \varrho + \kappa -x ) \bigr)^{ \frac {8 (x-\varrho )^{2}+ (1-3\lambda +6\lambda ^{2}-2\lambda ^{3} )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}}, \end{aligned}$$

where we have used the facts that

$$\begin{aligned}& \int ^{1}_{0} ( 1-t )^{2}\,dt= \int ^{1}_{0}t^{2}\,dt= \frac{1}{3}, \end{aligned}$$
(10)
$$\begin{aligned}& \int ^{1}_{0}t ( 1-t )\,dt=\frac{1}{6}, \end{aligned}$$
(11)
$$\begin{aligned}& \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert t \,dt= \int ^{1}_{0} \vert t-\lambda \vert ( 1-t )\,dt \\& \hphantom{\int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert t \,dt}= \int ^{\lambda}_{0} ( \lambda -t ) (1-t)\,dt+ \int ^{1}_{\lambda} ( t-\lambda ) (1-t)\,dt \\& \hphantom{\int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert t \,dt}= \frac{1-3\lambda +6\lambda ^{2}-2\lambda ^{3}}{6}, \end{aligned}$$
(12)

and

$$\begin{aligned} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert (1-t )\,dt&= \int ^{1}_{0} \vert t-\lambda \vert t \,dt \\ &= \int ^{\lambda}_{0} ( \lambda -t ) t \,dt+ \int ^{1}_{\lambda} ( t-\lambda ) t \,dt \\ &=\frac{2-3\lambda +2\lambda ^{3}}{6}. \end{aligned}$$
(13)

2. For \(\lambda > 1\), (9) gives

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ; \varphi ) \times \biggl( \int ^{\kappa}_{\varrho} \varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad = \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \biggl( \frac{ \ln ( \varphi ^{\ast } ( \varrho ) )}{6}+ \frac{\ln ( \varphi ^{\ast } (x ) )}{3} \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \biggl( \frac{3\lambda -1}{6} \ln \bigl( \varphi ^{\ast } (x ) \bigr) +\frac{3\lambda -2}{6} \ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(\varrho +\kappa -2x)^{2}}{4(\kappa -\varrho )} \biggl( \frac{3\lambda -2}{6} \ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr)+ \frac{3\lambda -1}{6}\ln \bigl( \varphi ^{\ast } (\varrho +\kappa -x ) \bigr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \frac {(x-\varrho )^{2}}{\kappa -\varrho} \biggl( \frac{\ln ( \varphi ^{\ast } (\varrho +\kappa -x ) )}{3}+ \frac{ \ln ( \varphi ^{\ast } ( \kappa ) )}{6} \biggr) \biggr\} \\& \quad = \bigl\{ \exp \bigl(\ln \bigl( \varphi ^{\ast } ( \varrho )^{\frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{ \ast } (x )^{\frac {(x-\varrho )^{2}}{3(\kappa -\varrho )}} \bigr) \bigr) \bigr\} \\& \qquad {}\times \biggl\{ \exp \biggl(\ln \biggl( \varphi ^{\ast } (x )^{ \frac { (3\lambda -1 )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr)^{ \frac { (3\lambda -2 )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \biggr) \biggr) \biggr\} \\& \qquad {}\times \biggl\{ \exp \biggl( \ln \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac { (3\lambda -2 )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \varphi ^{\ast } (\varrho +\kappa -x )^{ \frac { (3\lambda -1 )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}} \biggr) \biggr) \biggr\} \\& \qquad {}\times \bigl\{ \exp \bigl( \ln \bigl( \varphi ^{\ast } ( \varrho +\kappa -x )^{ \frac {(x-\varrho )^{2}}{3(\kappa -\varrho )}}\varphi ^{\ast } ( \kappa )^{\frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \bigr) \bigr) \bigr\} \\& \quad = \bigl(\varphi ^{\ast } ( \varrho )\varphi ^{\ast } ( \kappa ) \bigr)^{ \frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac { (3\lambda -2 )(\varrho +\kappa -2x)^{2}}{12(\kappa -\varrho )}} \\& \qquad {}\times \bigl(\varphi ^{\ast } (x )\varphi ^{\ast } ( \varrho + \kappa -x ) \bigr)^{ \frac {8 (x-\varrho )^{2}+ (3\lambda -1 )(\varrho +\kappa -2x)^{2}}{24(\kappa -\varrho )}}, \end{aligned}$$

where we have used (10), (11), and the facts that

$$\begin{aligned} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert t \,dt= \int ^{1}_{0} \vert t-\lambda \vert ( 1-t )\,dt=& \int ^{1}_{0} ( \lambda -t ) (1-t)\,dt = \frac{3\lambda -1}{6} \end{aligned}$$
(14)

and

$$\begin{aligned} \int ^{1}_{0} \bigl\vert t- (1-\lambda ) \bigr\vert (1-t )\,dt= \int ^{1}_{0} \vert t-\lambda \vert t \,dt=& \int ^{1}_{0} ( \lambda -t ) t \,dt = \frac{3\lambda -2}{6}. \end{aligned}$$
(15)

This completes the proof. □

Corollary 3.3

In Theorem 3.2, if we take \(x=\varrho \), we obtain the following parametrized Simpson-type inequalities via multiplicative convexity

$$\begin{aligned} & \biggl\vert \biggl(\varphi ( \varrho )^{ \frac {\lambda}{2}}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr)^{(1- \lambda )}\varphi ( \kappa )^{\frac {\lambda}{2}} \biggr) \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\ &\quad \leq \bigl(\varphi ^{\ast } ( \varrho ) \varphi ^{ \ast } ( \kappa ) \bigr)^{ \frac {\mathcal{C}_{2} (\lambda )(\kappa -\varrho )}{24}} \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr)^{ \frac {\mathcal{C}_{1} (\lambda ) (\kappa -\varrho )}{12}}, \end{aligned}$$

where \(\mathcal{C}_{1}\) and \(\mathcal{C}_{2}\) are defined in (7) and (8), respectively.

Corollary 3.4

In Corollary 3.3, if we take \(\lambda =1\), we obtain the following trapezoid-type inequalities:

$$ \biggl\vert \sqrt{\varphi ( \varrho )\varphi ( \kappa )} \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \leq \biggl( \varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \varphi ^{\ast } \biggl(\frac {\varrho +\kappa}{2} \biggr) \biggr)^{\frac {\kappa -\varrho}{12}}. $$

Remark 3.5

  • The result of Corollary 3.4 is an improvement of that established by Khan et al. in Theorem 4.2 of [16]. The latter can be deduced by utilizing the multiplicative convexity of \(\varphi ^{\ast}\), i.e., \(\varphi ^{\ast} (\frac {\varrho +\kappa}{2} )\leq \sqrt{ \varphi ^{\ast} ( \varrho )\varphi ^{\ast} ( \kappa )}\).

  • Taking \(\lambda =0\), Corollary 3.3 will be reduced to Theorem 3.3 from [7] which provides a refinement of that established by Khan et al. in Theorem 3.3 of [16].

  • By setting \(\lambda =\frac{1}{3}\) in Corollary 3.3, we can simplify it to Corollary 3 from [19], which provides a refinement of that established by Chasreechai et al. in Theorem 4.1 of [11], specifically related to the Simpson rule.

  • By choosing \(\lambda =\frac {1}{2}\) in Corollary 3.3, we recover Corollaries 3 and 4 from [8], related to Bullen formula.

Corollary 3.6

Taking \(\lambda =\frac {4}{3}\) in Corollary 3.3, we obtain the following Milne-type inequalities via multiplicative convexity

$$\begin{aligned} & \biggl\vert \biggl[\varphi ( \varrho )^{2}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr)^{-1}\varphi ( \kappa )^{2} \biggr]^{\frac {1}{3}} \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \\ &\quad \leq \bigl( \varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \bigr)^{\frac {(\kappa -\varrho )}{8}} \varphi ^{ \ast } \biggl(\frac {\varrho +\kappa}{2} \biggr)^{ \frac {(\kappa -\varrho )}{6}}. \end{aligned}$$

Moreover, using the multiplicative convexity of \(\varphi ^{\ast}\), we obtain

$$ \biggl\vert \biggl[\varphi ( \varrho )^{2}\varphi \biggl( \frac {\varrho +\kappa}{2} \biggr)^{-1}\varphi ( \kappa )^{2} \biggr]^{\frac {1}{3}} \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \leq \bigl( \varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \bigr)^{\frac {5(\kappa -\varrho )}{24}}. $$

Corollary 3.7

In Theorem 3.2, if we take \(\lambda =1\), we get the following analogue of Ostrowski’s inequalities for multiplicatively differentiable convex mappings:

$$\begin{aligned} \biggl\vert \sqrt{\varphi (x )\varphi (\varrho + \kappa -x )} \times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{\frac {1}{\varrho -\kappa}} \biggr\vert \leq {}& \bigl( \varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \bigr)^{ \frac {(x-\varrho )^{2}}{6(\kappa -\varrho )}} \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr)^{ \frac {(\varrho +\kappa -2x)^{2}}{12(\kappa -\varrho )}} \\ &\times \bigl(\varphi ^{\ast } (x )\varphi ^{\ast } ( \varrho + \kappa -x ) \bigr)^{ \frac {4 (x-\varrho )^{2}+(\varrho +\kappa -2x)^{2}}{12(\kappa -\varrho )}}. \end{aligned}$$

Remark 3.8

  • When substituting \(x=\frac {5\varrho +\kappa}{6}\) and \(\lambda =\frac {5}{8}\) into Theorem 3.2, one gets an equivalent statement to Theorem 3.2 presented in [17].

  • By choosing \(x=\frac {3\varrho +\kappa}{4}\) and \(\lambda =\frac {5}{3}\) in Theorem 3.2, we can simplify it to Theorem 3.2 in [18].

Continuing in the same direction, Theorem 3.2 enables us to derive a variety of entirely novel results, including formulas such as Corrected Simpson, Corrected dual Simpson, Corrected Euler–Maclaurin, and more. This is accomplished by substituting appropriate respective values for x and λ.

Now, we present another result that holds when \((\ln \varphi ^{\ast} )^{q}\) is convex.

Theorem 3.9

For an increasing multiplicatively differentiable mapping \(\varphi : [ \varrho ,\kappa ] \rightarrow \mathbb{R}^{+}\) on \([ \varrho ,\kappa ] \), if \(( \ln \varphi ^{\ast } ) ^{q}\) is convex on \([\varrho ,\kappa ]\) for \(q>1\) with \(\frac{1}{p}+\frac{1}{q}=1\), then the following inequality holds for \(\lambda \geq 0\):

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ;\varphi )\times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{ \frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \biggl( \bigl( \varphi ^{\ast } ( \varrho ) \varphi ^{\ast } ( \kappa ) \bigr) ^{\frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}} \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{ (\mathcal{C}_{3} (\lambda ,p ) )^{\frac{1}{p}} \frac{ ( \varrho +\kappa -2x ) ^{2}}{2 ( \kappa -\varrho ) }} \\& \qquad {}\times \bigl( \varphi ^{\ast } ( x ) \varphi ^{ \ast } ( \varrho +\kappa -x ) \bigr) ^{ \frac{4 ( x-\varrho ) ^{2}+ (\mathcal{C}_{3} (\lambda ,p ) )^{\frac{1}{p}} ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }} \biggr) ^{ ( \frac{1}{p+1} ) ^{\frac{1}{p}} ( \frac{1}{2} ) ^{\frac{1}{q}}}, \end{aligned}$$

where \(\mathcal{C}_{3} (\lambda ,p )\) is given by

$$ \mathcal{C}_{3} (\lambda ,p )=\textstyle\begin{cases} \lambda ^{p+1}+ (1-\lambda )^{p+1} & \textit{for } 0\leq \lambda \leq 1, \\ \lambda ^{p+1}- (\lambda -1 )^{p+1} & \textit{for } \lambda >1, \end{cases} $$
(16)

and \(\mathcal{Z}\) is defined in (2).

Proof

Using Lemma 3.1, the modulus function, and Hölder’s inequality, we obtain

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ;\varphi )\times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{ \frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \int _{0}^{1}t \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) \bigr\vert \,dt \biggr) \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \int _{0}^{1} \vert t-\lambda \vert \biggl\vert \ln \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x+t\frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr\vert \,dt \biggr) \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \int _{0}^{1} \bigl\vert t- ( 1- \lambda ) \bigr\vert \biggl\vert \ln \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho + \kappa -x ) \biggr) \biggr\vert \,dt \biggr) \\& \qquad {}\times \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \int _{0}^{1} ( 1-t ) \bigl\vert \ln \varphi ^{\ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t\kappa \bigr) \bigr\vert \,dt \biggr) \\& \quad \leq \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \int _{0}^{1}t^{p}\,dt \biggr) ^{\frac{1}{p}} \biggl( \int _{0}^{1} \bigl\vert \ln \bigl( \varphi ^{\ast } \bigl( ( 1-t ) \varrho +tx \bigr) \bigr) \bigr\vert ^{q}\,dt \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \int _{0}^{1} \vert t-\lambda \vert ^{p}\,dt \biggr) ^{ \frac{1}{p}} \biggl( \int _{0}^{1} \biggl\vert \ln \biggl( \varphi ^{\ast } \biggl( ( 1-t ) x+t \frac {\varrho +\kappa}{2} \biggr) \biggr) \biggr\vert ^{q}\,dt \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \int _{0}^{1} \bigl\vert t- ( 1-\lambda ) \bigr\vert ^{p}\,dt \biggr) ^{\frac{1}{p}} \\& \qquad {}\times \biggl( \int _{0}^{1} \biggl\vert \ln \varphi ^{\ast } \biggl( ( 1-t ) \frac {\varrho +\kappa}{2}+t ( \varrho +\kappa -x ) \biggr) \biggr\vert ^{q}\,dt \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \int _{0}^{1} ( 1-t ) ^{p}\,dt \biggr) ^{\frac{1}{p}} \\& \qquad {}\times \biggl( \int _{0}^{1} \bigl\vert \ln \varphi ^{ \ast } \bigl( ( 1-t ) ( \varrho +\kappa -x ) +t \kappa \bigr) \bigr\vert ^{q}\,dt \biggr) ^{\frac{1}{q}}. \end{aligned}$$
(17)

Now, it is easy to show that

$$ \int _{0}^{1} ( 1-t ) ^{p}\,dt= \int _{0}^{1}t^{p}\,dt= \frac{1}{p+1} $$
(18)

and

$$ \int _{0}^{1} \vert t-\lambda \vert ^{p}\,dt= \int _{0}^{1} \bigl\vert t- ( 1-\lambda ) \bigr\vert ^{p}\,dt=\frac {\mathcal{C}_{3} (\lambda ,p )}{p+1}=\textstyle\begin{cases} \frac {\lambda ^{p+1}+ (1-\lambda )^{p+1}}{p+1} & \text{for } 0\leq \lambda \leq 1, \\ \frac {\lambda ^{p+1}- (\lambda -1 )^{p+1}}{p+1} & \text{for } \lambda >1. \end{cases} $$
(19)

Inserting (18) and (19) into (17), and making use of the convexity of \(( \ln \varphi ^{\ast } ) ^{q}\), we get

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ;\varphi )\times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{ \frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \int _{0}^{1} \bigl( ( 1-t ) \bigl( \ln \bigl( \varphi ^{\ast } ( \varrho ) \bigr) \bigr) ^{q}+t \bigl( \ln \bigl( \varphi ^{\ast } ( x ) \bigr) \bigr) ^{q} \bigr)\,dt \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \\& \qquad {}\times \biggl( \int _{0}^{1} \biggl( ( 1-t ) \bigl( \ln \varphi ^{\ast } ( x ) \bigr) ^{q}+t \biggl( \ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{q} \biggr)\,dt \biggr) ^{ \frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \\& \qquad {}\times \biggl( \int _{0}^{1} \biggl( ( 1-t ) \biggl( \ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{q}+t \bigl( \ln \varphi ^{\ast } ( \varrho +\kappa -x ) \bigr) ^{q} \biggr)\,dt \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \int _{0}^{1} \bigl( ( 1-t ) \bigl( \ln \varphi ^{\ast } ( \varrho +\kappa -x ) \bigr) ^{q}+t \bigl( \ln \varphi ^{\ast } ( \kappa ) \bigr) ^{q} \bigr)\,dt \biggr) ^{\frac{1}{q}} \\& \quad = \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{ \frac{1}{q}} \bigl( \bigl( \ln \bigl( \varphi ^{\ast } ( \varrho ) \bigr) \bigr) ^{q}+ \bigl( \ln \bigl( \varphi ^{ \ast } ( x ) \bigr) \bigr) ^{q} \bigr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \biggl( \bigl( \ln \varphi ^{\ast } ( x ) \bigr) ^{q}+ \biggl( \ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{q} \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \\& \qquad {}\times \biggl( \biggl( \ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{q}+ \bigl( \ln \varphi ^{ \ast } ( \varrho +\kappa -x ) \bigr) ^{q} \biggr) ^{ \frac{1}{q}} \\& \qquad {}\times \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \bigl( \bigl( \ln \varphi ^{\ast } ( \varrho +\kappa -x ) \bigr) ^{q}+ \bigl( \ln \varphi ^{\ast } ( \kappa ) \bigr) ^{q} \bigr) ^{\frac{1}{q}}. \end{aligned}$$
(20)

Using the fact that \(M^{q}+N^{q}\leq (M+N)^{q}\) for \(M\geq 0\), \(N\geq 0\) with \(q\geq 1\), (20) gives

$$\begin{aligned}& \biggl\vert \mathcal{Z} ( \varrho ,\kappa ,x,\lambda ;\varphi )\times \biggl( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} \biggr) ^{ \frac {1}{\varrho -\kappa}} \biggr\vert \\& \quad \leq \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \bigl( \ln \bigl( \varphi ^{\ast } ( \varrho ) \bigr) +\ln \bigl( \varphi ^{\ast } ( x ) \bigr) \bigr) \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \biggl( \ln \varphi ^{\ast } ( x ) +\ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) \\& \qquad {}\times \exp \frac { ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) } \biggl( \frac {\mathcal{C}_{3} (\lambda ,p )}{p+1} \biggr) ^{ \frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \biggl( \ln \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) +\ln \varphi ^{\ast } ( \varrho +\kappa -x ) \biggr) \\& \qquad {}\times \exp \frac { ( x-\varrho ) ^{2}}{\kappa -\varrho} \biggl( \frac {1}{p+1} \biggr) ^{\frac{1}{p}} \biggl( \frac {1}{2} \biggr) ^{\frac{1}{q}} \bigl( \ln \varphi ^{\ast } ( \varrho + \kappa -x ) +\ln \varphi ^{\ast } ( \kappa ) \bigr) \\& \quad = \biggl( \bigl( \varphi ^{\ast } ( \varrho ) \varphi ^{ \ast } ( \kappa ) \bigr) ^{\frac{ ( x-\varrho ) ^{2}}{\kappa -\varrho}} \biggl( \varphi ^{\ast } \biggl( \frac {\varrho +\kappa}{2} \biggr) \biggr) ^{ ( \mathcal{C}_{3} (\lambda ,p ) ) ^{\frac{1}{p}} \frac{ ( \varrho +\kappa -2x ) ^{2}}{2 ( \kappa -\varrho ) }} \\& \qquad {}\times \bigl( \varphi ^{\ast } ( x ) \varphi ^{ \ast } ( \varrho +\kappa -x ) \bigr) ^{ \frac{4 ( x-\varrho ) ^{2}+ (\mathcal{C}_{3} (\lambda ,p ) ) ^{\frac{1}{p}} ( \varrho +\kappa -2x ) ^{2}}{4 ( \kappa -\varrho ) }} \biggr) ^{ ( \frac{1}{p+1} ) ^{\frac{1}{p}} ( \frac{1}{2} ) ^{\frac{1}{q}}}. \end{aligned}$$

This completes the proof. □

Similar to Theorem 3.2, Theorem 3.9 allows us to derive results concerning all the Newton–Cotes formulas with 1, 2, and 3 points by substituting the appropriate values for x and λ. The specific calculations are left to the reader.

4 Numerical example

This section is devoted to confirming the accuracy of the obtained results through an example comprising multiple cases, with the results presented graphically using the Matlab software.

Example 4.1

Let us consider the function \(\varphi :[0,1]\rightarrow \mathbb{R}^{+}\), defined by \(\varphi (u )=e^{u^{2}}\), and whose multiplicative derivative \(\varphi ^{\ast} (u )=e^{2u}\) is multiplicatively convex.

From Theorem 3.2, we have for all \(x\in [0,\frac {1}{2} ]\) and \(\lambda \geq 0\),

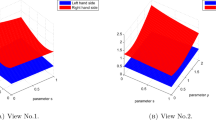
$$ e^{ (\frac {(1-2x) (1-\lambda )}{4}+ (x^{2}+ (1-x )^{2} )\frac {(1-2x)\lambda +2x}{2}- \frac {1}{3} )} \leq \textstyle\begin{cases} e^{ \frac {10x^{2}+3 (1-2\lambda +2\lambda ^{2} )(1-2x)^{2}}{12}} & \text{for } 0\leq \lambda \leq 1, \\ e^{\frac {10x^{2}+3 (2\lambda -1 )(1-2x)^{2}}{12}} & \text{for } 1< \lambda . \end{cases} $$

The above results are illustrated in Fig. 1, where the left-hand term is shown in blue, and the right-hand term is shown in red. From this graphical representation, we observe that the values of the left-hand term are lower than those of the right-hand term for all \(x\in [0,\frac {1}{2} ]\) and \(\lambda \in [0,2]\), which justifies the correctness of the obtained results.

Figure 1
figure 1

Illustration for Theorem 3.2 in Example 4.1 when \(x\in [0,\frac{1}{2}]\) and \(\lambda \in [0,2]\)

Full size image

Now, if we attempt to fix \(\lambda =1\), Corollary 3.7 gives

$$ e^{ (\frac {x^{2}+ (1-x )^{2}}{2}-\frac {1}{3} )} \leq e^{\frac {10x^{2}+3(1-2x)^{2}}{12}}. $$

The above result is detailed in Table 1 and depicted in Fig. 2.

Figure 2
figure 2

Illustration for Corollary 3.7 in Example 4.1 when \(\lambda =1\) and \(x\in [0,\frac{1}{2} ]\)

Full size image
Table 1 Numerical validation of Corollary 3.7
Full size table

From Table 1 and Fig. 2, it can be observed that the value on the left is less than that on the right for all \(x\in [0,\frac {1}{2} ]\), which confirms the accuracy and correctness of the obtained results.

5 Applications

5.1 Multiplicative differential equation

Assume that a bank offers various growth factors at different points in time, denoted as \(\varphi (t)\). If \(\psi (t)\) represents the value of the deposit at time t, then, employing the financial interpretation of the multiplicative derivative, we straightforwardly deduce the following multiplicative differential equation modeling the accumulated value in the bank account at time t:

$$ \psi ^{\ast}(t)=\varphi (t), \qquad \psi (0)=\mathcal{C}, $$
(21)

where \(\mathcal{C}\) denotes the value in the account at the initial time moment.

The following is the solution to the multiplicative differential equation (21):

$$ \psi (t)=\mathcal{C} \int^{t}_{0} \bigl(\varphi (u) \bigr)^{du}. $$

Firstly, it is important to note that the equation in this example is the multiplicative form of the ordinary linear differential equation \(\psi ^{\prime}(t) = \mathcal{N}(t)\psi (t)\), where \(\mathcal{N}(t) = \ln (\varphi (t) )\). Although this equation is widely used in applications without involving multiplicative differential equations, the financial interpretation of the multiplicative derivative facilitates a straightforward approach to the same result.

Now, suppose we consider that the value in the account at time \(t=0\) is equal to 1 unit and the growth factor is described by the function \(\varphi (t)=e^{t^{2}}\), and we want to calculate the accumulated value in the bank at time \(t=1\). In this case, exact calculation of the integral becomes impossible, and only an approximation of it is feasible.

Instead of starting with an a priori selection of our quadrature formula, the findings presented in this study enable a posteriori choice based on the estimation of the error in order to minimize it as much as possible. Indeed, using the quadrature formula described by (2) with \(\lambda \in [0,1]\) and the fact that \(\varphi ^{\ast}(u)=e^{2u}\), we get

$$ \psi (1)= \int^{1}_{0} \bigl(e^{u^{2}} \bigr)^{du} \simeq e^{ [ (x^{2}+(1-x)^{2} ) \frac{(1-2x)\lambda +2x}{2}+\frac{(1-2x)(1-\lambda )}{4} ]}, $$
(22)

and the corresponding error estimate is as follows:

$$ \mathrm{Er} (x,\lambda )\leq e^{ [ \frac {12x^{2}+ (3-6\lambda +6\lambda ^{2} )(1-2x)^{2}}{12} ]}. $$

Finally, based on the preceding estimate, we can select specific values for x and λ to minimize the error.

5.2 Special means

Consider the following means of arbitrary real numbers \(\varrho _{1},\varrho _{2},\dots ,\varrho _{n}\):

  • The arithmetic mean \(M ( \varrho _{1},\varrho _{2},\dots ,\varrho _{n} ) = \frac{\varrho _{1}+\varrho _{2}+\cdots +\varrho _{n}}{n}\);

  • The harmonic mean \(H ( \varrho _{1},\varrho _{2},\dots ,\varrho _{n} ) = \frac{n}{\frac{1}{\varrho _{1}}+\frac{1}{\varrho _{2}}+\cdots +\frac{1}{\varrho _{n}}}\);

  • The logarithmic means \(L ( \varrho _{1},\varrho _{2} ) = \frac{\varrho _{2}-\varrho _{1}}{\ln \varrho _{2}-\ln \varrho _{1}}\), \(\varrho _{1},\varrho _{2}>0\) and \(\varrho _{1}\neq \varrho _{2}\);

  • The k-logarithmic means \(L_{k} ( \varrho _{1},\varrho _{2} ) = ( \frac{\varrho _{2}^{k+1}-\varrho _{1}^{k+1}}{ ( k+1 ) ( \varrho _{2}-\varrho _{1} ) } ) ^{\frac{1}{k}}\), \(\varrho _{1},\varrho _{2}>0\), \(\varrho _{1}\neq \varrho _{2}\), and \(k\in \mathbb{R}\setminus \{ -1,0\} \).

Proposition 5.1

For two positive real numbers \(0<\varrho <\kappa \) and \(p\geq 2\), we have

$$\begin{aligned} &e^{ \frac{M^{p} ( \varrho ,\varrho ,\kappa ) +M^{p} ( \varrho ,\kappa ) +M^{p} ( \varrho ,\kappa ,\kappa ) -3L_{p}^{p} ( \varrho ,\kappa ) }{3}} \leq \bigl( e^{4\varrho ^{p-1}+9 ( \frac{2\varrho +\kappa}{3} ) ^{p-1}+4 ( \frac{\varrho +\kappa}{2} ) ^{p-1}+9 ( \frac{\varrho +2\kappa}{3} ) ^{p-1}+4\kappa ^{p-1}} \bigr) ^{ \frac{p ( \kappa -\varrho ) }{216}}. \end{aligned}$$

Proof

It suffices to apply Theorem 3.2 with \(x=\frac{2\varrho +\kappa}{3}\) and \(\lambda =0\), taking as function \(\varphi ( u ) =e^{u^{p}}\) with \(p\geq 2\) whose multiplicative derivative and integral are given by \(\varphi ^{\ast } ( u ) =e^{pu ^{p-1}}\) and \(( \int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} ) ^{\frac {1}{\varrho -\kappa}}=\exp \{ -L_{p}^{p} ( \varrho ,\kappa ) \} \), respectively. □

Proposition 5.2

For two positive real numbers \(0<\varrho <\kappa \) and \(p\geq 2\), we have

$$\begin{aligned} &e^{ \frac{M^{p} ( \varrho ,\varrho ,\kappa ) +M^{p} ( \varrho ,\kappa ,\kappa ) -2L_{p}^{p} ( \varrho ,\kappa ) }{2}} \leq \bigl( e^{ \varrho ^{4 ( p-1 ) }+ ( \frac{2\varrho +\kappa}{3} ) ^{10 ( p-1 ) }+ ( \frac{\varrho +\kappa}{2} ) ^{2 ( p-1 ) }+ ( \frac{\varrho +2\kappa}{3} ) ^{10 ( p-1 ) }+\kappa ^{4 ( p-1 ) }} \bigr) ^{\frac{p ( \kappa -\varrho ) }{216}}. \end{aligned}$$

Proof

It suffices to apply Theorem 3.2 with \(x=\frac{2\varrho +\kappa}{3}\) and \(\lambda =1\), taking as function \(\varphi ( u ) =e^{u ^{p}}\) with \(p\geq 2\) whose multiplicative derivative and integral are given by \(\varphi ^{\ast } ( u ) =e^{pu ^{p-1}}\) and \((\int ^{\kappa}_{\varrho}\varphi ( u ) ^{du} ) ^{\frac {1}{\varrho -\kappa}}=\exp \{ -L_{p}^{p} ( \varrho ,\kappa ) \} \), respectively. □

6 Conclusion

In this research, we have introduced a significant biparametrized multiplicative integral identity, which served as a fundamental tool in deriving a set of one-, two-, and three-point Newton–Cotes-type inequalities. These inequalities are applicable to increasing multiplicatively differentiable convex mappings. Our study has contributed new and valuable results to the field, building upon existing knowledge and refining certain previously established findings.

The provided illustrative example has further demonstrated the validity of our results, emphasizing the significance of the proposed approach. The graphical representations have visually corroborated the inequalities’ behavior and reinforced their reliability. Moreover, the potential applications of these findings are expected to have broad implications in various mathematical and scientific disciplines.

In conclusion, this study has contributed to advancing our understanding of inequalities for multiplicative integrals and has brought to light novel insights. We hope that our work will inspire further research in this area and find application in diverse theoretical and practical contexts.