1 Introduction

Over the past thirty years, fractional derivatives have fascinated multiple researchers as compared to classical derivatives. Also, fractional derivatives are more credible in mathematical modeling of real-world problems. The methodology of a fractional operator involves regular derivatives and the kernel of a fractional operator with a convolution relation. Initially, Caputo [1] and Riemann–Liouville adopted a power-law kernel to produce a fractional operator. However, this fractional operator faced a few obstructions in real-world applications. Caputo and Fabrizio [2] instead adopted a localized exponential kernel to construct a modern fractional operator. Furthermore, Atangana and Baleanu [3] suggested an advanced fractional operator by using an optimized Mittag–Leffler function, being a nonsingular and nonlocal kernel. This fractional operator counters local and singular kernel restrictions of the preceding fractional operators, keeping certain of their features. Applications of fractional calculus have not only been used in the disciplines of engineering and physical sciences but also in other disciplines, such as ecology, geology, viscoelasticity, economics, probability and statistics and fluid dynamics [4–11].

Among different kinds of rate-type fluids, the Maxwell fluid has gained attention in many research areas. It is a viscoelastic fluid that has properties both of viscosity and elasticity. Maxwell fluids are widely used in polymeric industries due to their lower complexity. The impact of MHD recounts the movement of a conducting flow under the influence of a magnetic field. MHD consequently intensifies conductivity during flow, being a sensation in chemical, mechanical and electrical engineering. Cao et al. [12] analyzed a fractional model of a MHD Maxwell nanofluid over a moving plate. Results for a Maxwell fluid on a vibrating plate utilizing CF derivatives and Laplace transforms were acquired by other investigators [13, 14]. Abro et al. [15] solved the model of a MHD Maxwell fluid for velocity and temperature in a porous medium by using the ABC definition. Bai et al. [16] conducted a thermal analysis in fractional MHD Maxwell flow with viscous dissipation. Asif et al. [17] used the CF definition in order to explore a Maxwell fluid with slip effects.

Normally, thermal convection discussion are connected with distinct physical state, for example, surface heat flux, ramped surface heating and uniform boundary temperature. However, the aforementioned conditions are not applicable for some real-life phenomena. For these phenomena, fluids are placed under Newtonian heating conditions. Newtonian heating expresses that the heat-transfer rate through a sidewall is proportional to the local sidewall temperature. Merkin [18] conducted an introductory study on Newtonian heating. Newtonian heating has several applications, including engine cooling, solar radiations, exploration and extraction processes of petroleum industries, and conjugate heat transport around fins. Nowadays, Newtonian heating has attracted many researchers as a result of its efficient prominence in various engineering systems like radiators. Riaz et al. [19, 20] considered a Maxwell fluid with the contribution of Newtonian heating via fractional operators. Imran et al. [21] employed a CF time derivative to investigate a Maxwell fluid with Newtonian heating on a moving plate. Imran et al. [22] analyzed exact solutions of a rate-type model with Newtonian heating by using Laplace, C and CF time derivatives. Also, they studied the comparison between them. Raza and Asad Ullah [23] used Newtonian heating conditions in a fractional Maxwell fluid and analyzed heat transfer by using C and CF derivatives. Vieru et al. [24] found the solutions for velocity, temperature, and concentration profile for flow under Newtonian heating conditions. Said Mad Zain et al. [25] generalized a fractional Bézier curve with shape parameters. Ghomanjani and Noeiaghdam [26] studied the application of a ball curve for solving fractional differential-algebraic equations.

The basic incentive of this paper was to observe the efficacy of fractional-order derivatives to reveal the memory effect for the Maxwell model under Newtonian heating conditions. The impact of emerging parameters onto momentum, mass and energy solutions are plotted from different graphs accompanied by real justifications. Finally, a comparison has been made among C, CF and ABC fractional models.

2 Mathematical model

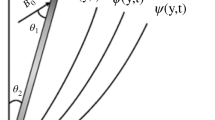
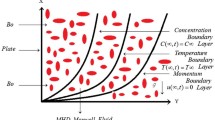
Assume a Maxwell fluid upon an upright and unbounded plate under the impact of a magnetic field having strength \(B_{0}\). The plate is perpendicular to the y-axis and parallel to the x-axis. Initially, the fluid and the plate are stationary at a fixed temperature \(\tilde{\Upsilon }_{\infty } \). The local sidewall temperature ϒ̃ and the thermal transfer rate through the bounding wall to the fluid are in proportion to each other. The physical model is shown in Fig. 1 and is given in [19, 20].

Figure 1
figure 1

Physical model

Full size image

The governing equations are given by [19, 20]:

$$\begin{aligned}& \begin{aligned}[b] \biggl(1 + \lambda _{m}\frac{\partial }{\partial \widetilde{t}}\biggr) \frac{\partial \tilde{W}}{\partial \widetilde{t}} &= \upsilon \frac{\partial ^{2}\tilde{W}}{\partial \tilde{\zeta }^{2}} + \biggl(1 + \tilde{\lambda } \frac{\partial }{\partial \widetilde{t}}\biggr)g\beta _{\tilde{\Upsilon }} (\tilde{\Upsilon } - \tilde{\Upsilon }_{\infty } ) \\ & {}+ \biggl(1 + \tilde{\lambda } \frac{\partial }{\partial \widetilde{t}}\biggr)g\beta _{\tilde{\Lambda }} (\tilde{\Lambda } - \tilde{ \Lambda }_{\infty } ) - \frac{\sigma B_{o}^{2}}{\rho } \biggl(1 + \tilde{\lambda } \frac{\partial }{\partial \widetilde{t}}\biggr)\tilde{W}, \end{aligned} \end{aligned}$$
(1)
$$\begin{aligned}& \frac{\partial \tilde{\Upsilon }}{\partial \widetilde{t}} = \frac{k}{\rho C_{p}}\frac{\partial ^{2}\tilde{\Upsilon }}{\partial \tilde{\zeta }^{2}}, \end{aligned}$$
(2)
$$\begin{aligned}& \frac{\partial \tilde{\Lambda }}{\partial \widetilde{t}} = D_{m}\frac{\partial ^{2}\tilde{\Lambda }}{\partial \tilde{\zeta }^{2}}. \end{aligned}$$
(3)

Suitable initial and boundary conditions are:

$$\begin{aligned}& \forall \tilde{\zeta } \ge 0 \quad \Rightarrow\quad \tilde{W}(\tilde{ \zeta },0) = 0,\qquad \frac{\partial \tilde{W}(\tilde{\zeta },0)}{\partial \widetilde{t}} \bigg\vert _{t = 0} = 0, \\& \tilde{\Upsilon } (\tilde{\zeta },0) = \tilde{ \Upsilon }_{\infty }, \qquad \tilde{\Lambda } (\tilde{\zeta },0) = \tilde{ \Lambda }_{\infty }, \\& \forall \widetilde{t}>0\quad \Rightarrow \quad \tilde{W}(0,\tilde{t}) = 0, \qquad \frac{\partial \tilde{\Upsilon } (0,\tilde{t})}{\partial \tilde{\zeta }} \bigg\vert _{\xi = 0} = \frac{ - h}{k}\tilde{\Upsilon } (0,\tilde{t}), \qquad \tilde{\Lambda } (0, \tilde{t}) = \tilde{\Lambda }_{\infty } + \tilde{\Lambda }_{w} \tilde{t}, \\& \tilde{W}(\tilde{\zeta },\tilde{t}) \to 0,\qquad \tilde{\Upsilon } (\tilde{\zeta },\tilde{t}) \to \tilde{\Upsilon }_{\infty } \quad \mbox{and} \quad \tilde{ \Lambda } (\tilde{\zeta },\tilde{t}) \to \tilde{\Lambda }_{\infty } \quad \mbox{as } \tilde{\zeta } \to \infty . \end{aligned}$$

The dimensionless parameters to nondimensionalize the above equations are:

$$\begin{aligned}& \Upsilon = \frac{\tilde{\Upsilon } - \tilde{\Upsilon }_{\infty }}{\tilde{\Upsilon }_{\infty }}, \qquad \Lambda = \frac{\tilde{\Lambda } - \tilde{\Lambda }_{\infty }}{\tilde{\Lambda }_{\infty }},\qquad W = \frac{\upsilon h^{2}}{gk^{2}}\tilde{W}, \\& t = \frac{\upsilon h^{2}}{k^{2}}\tilde{t},\qquad \zeta = \frac{h}{k}\tilde{\zeta }, \qquad \Pr = \frac{\mu C_{p}}{k},\qquad Sc = \frac{\upsilon }{D_{m}}, \\& \lambda = \frac{\upsilon h^{2}}{k^{2}}\tilde{\lambda },\qquad M = \frac{\sigma B_{o}^{2}k^{2}}{\mu h^{2}},\qquad Gr = \beta _{\tilde{\Upsilon }} \tilde{\Upsilon }_{\infty } \quad \mbox{and}\quad Gm = \beta _{\tilde{\Lambda }} \tilde{\Lambda }_{w}. \end{aligned}$$

Therefore, the dimensionless momentum, energy and mass equations are:

$$\begin{aligned}& \biggl(1 + \lambda \frac{\partial }{\partial t}\biggr)\frac{\partial W}{\partial t} = \frac{\partial ^{2}W}{\partial \zeta ^{2}} + \biggl(1 + \lambda \frac{\partial }{\partial t}\biggr)Gr\Upsilon + \biggl(1 + \lambda \frac{\partial }{\partial t}\biggr)Gm\Lambda - M\biggl(1 + \lambda \frac{\partial }{\partial t}\biggr)W, \end{aligned}$$
(4)
$$\begin{aligned}& \Pr \frac{\partial \Upsilon }{\partial t} = \frac{\partial ^{2}\Upsilon }{\partial \zeta ^{2}}, \end{aligned}$$
(5)
$$\begin{aligned}& Sc\frac{\partial \Lambda }{\partial t} = \frac{\partial ^{2}\Lambda }{\partial \zeta ^{2}}. \end{aligned}$$
(6)

The required nondimensional initial and boundary conditions are:

$$\begin{aligned}& \forall \zeta \ge 0\quad \Rightarrow \quad W(\zeta ,0) = 0,\qquad \frac{\partial W(\zeta ,0)}{\partial t} \bigg\vert _{t = 0} = 0,\qquad \Upsilon (\zeta ,0) = 0,\qquad \Lambda (\zeta ,0) = 0, \\& \forall t>0 \quad \Rightarrow\quad W(0,t) = 0,\qquad \frac{\partial \Upsilon (0,t)}{\partial \zeta } \bigg\vert _{\zeta = 0} = - \bigl[ \Upsilon (0,t) + 1 \bigr],\qquad \Lambda (0,t) = t, \\& W(\zeta ,t) \to 0,\qquad \Upsilon (\zeta ,t) \to 0 \quad \mbox{and}\quad \Lambda ( \zeta ,t) \to 0 \quad \mbox{as } \zeta \to \infty . \end{aligned}$$

3 Preliminaries

3.1 Caputo derivative and its Laplace transform

The Caputo derivative and its Laplace transform are given below:

$$ {}^{C}D_{t}^{\gamma } i(\zeta ,t) = \frac{1}{\Gamma (m - \gamma )} \int _{0}^{t} \frac{i^{(m)}(\tau )}{(t - \tau )^{\gamma + 1 - m}} \,d\tau , $$
(7)

where \(\Gamma ( \cdot )\) represents the Gamma function.

$$ \mathcal{L} \bigl( {}^{C}D_{t}^{\gamma } i(\zeta ,t) \bigr) = q^{\gamma } \mathcal{L} \bigl( i(\zeta ,t) \bigr) - q^{\gamma - 1}i(\zeta ,0). $$
(8)

3.2 Caputo–Fabrizio derivative and its Laplace transform

The Caputo–Fabrizio derivative and its Laplace transform are given below:

$$ {}^{CF}D_{t}^{\gamma } i(\zeta ,t) = \frac{N(\gamma )}{1 - \gamma } \int _{a}^{t} \frac{\partial i(\zeta ,\tau )}{\partial \tau } \exp \biggl( - \gamma \frac{t - \tau }{1 - \gamma } \biggr)\,d\tau , $$
(9)

where \(N(\gamma )\) is the normalization function or a constant depending on γ. Here, consider \(N(\gamma ) = 1\).

$$ \mathcal{L} \bigl( {}^{CF}D_{t}^{\gamma } i(\zeta ,t) \bigr) = \frac{q\mathcal{L} ( i(\zeta ,t) ) - i(\zeta ,0)}{(1 - \gamma )q + \gamma }. $$
(10)

3.3 Atangana–Baleanu derivative and its Laplace transform

The Atangana–Baleanu derivative and its Laplace transform are given below:

$$ {}^{ABC}D_{t}^{\gamma } i(\zeta ,t) = \frac{AB(\gamma )}{1 - \gamma } \int _{a}^{t} \frac{\partial i(\zeta ,\tau )}{\partial \tau } E_{\gamma } \biggl( - \gamma \frac{(t - \tau )^{\gamma }}{1 - \gamma } \biggr)\,d\tau , $$
(11)

where \(AB(\gamma )\) represents the normalization function. Here, \(AB(\gamma ) = 1\).

$$ \mathcal{L} \bigl( {}^{ABC}D_{t}^{\gamma } i(\zeta ,t) \bigr) = \frac{q^{\gamma } \mathcal{L} ( i(\zeta ,t) ) - q^{\gamma - 1}i(\zeta ,0)}{(1 - \gamma )q^{\gamma } + \gamma }. $$
(12)

4 Solutions for temperature profile

The temperature fields for integer-order, C and CF time-fractional derivatives have been already calculated by Vieru et al. [24], Asjad et al. [22], Raza and Asad Ullah [23] and Riaz et al. [20], respectively.

5 Solutions for concentration profile

The concentration fields for integer-order, C and CF time-fractional derivatives have been already calculated by Riaz et al. [20].

6 Solutions for velocity profile

6.1 Integer-order solution

Theorem 1

Let \(\mathcal{L}\) be the Laplace operator, applying this operator to Eq. (4) along with initial and boundary conditions, the exact solution of velocity is given in Eq. (19).

Proof

Applying the Laplace transform to Eq. (4), we obtain:

$$\begin{aligned}& \mathcal{L} \biggl[ \frac{\partial \bar{W}}{\partial \zeta } + \lambda \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} \biggr] \\& \quad = \mathcal{L} \biggl[ \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} + Gr \biggl( \bar{\Upsilon } + \lambda \frac{\partial \bar{\Upsilon }}{\partial \zeta } \biggr) + Gm \biggl( \bar{\Lambda } + \frac{\partial \bar{\Lambda }}{\partial \zeta } \biggr) - M \biggl( \bar{W} + \lambda \frac{\partial \bar{W}}{\partial \zeta } \biggr) \biggr]. \end{aligned}$$
(13)

After some simplifications, we obtain:

$$\begin{aligned}& ( 1 + \lambda q )q\bar{W} = \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} + Gr ( 1 + \lambda q )\bar{ \Upsilon } + Gm ( 1 + \lambda q )\bar{\Lambda } - M ( 1 + \lambda q ) \bar{W}, \end{aligned}$$
(14)
$$\begin{aligned}& \biggl[ \frac{\partial ^{2}}{\partial \zeta ^{2}} - \lambda q^{2} - ( 1 + \lambda M )q - M \biggr]\bar{W} = Gr \bigl[ ( 1 + \lambda q )\bar{\Upsilon } \bigr] + Gm \bigl[ ( 1 + \lambda q )\bar{\Lambda } \bigr]. \end{aligned}$$
(15)

Equation (15) is a 2nd-order nonhomogeneous linear equation.

The standard solution of Eq. (15) is

$$ \bar{W} ( \zeta ,q ) = \bar{W}_{1} ( \zeta ,q ) + \bar{W}_{2} ( \zeta ,q ). $$
(16)

where \(\bar{W}_{1} ( \zeta ,q )\) and \(\bar{W}_{2} ( \zeta ,q )\) are the complementary and particular solutions, respectively.

$$\begin{aligned}& \bar{W}_{1} ( \zeta ,q ) = c_{1}e^{\zeta \sqrt{\lambda q^{2} + ( 1 + \lambda M )q + M}} + c_{2}e^{ - \zeta \sqrt{\lambda q^{2} + ( 1 + \lambda M )q + M}}, \end{aligned}$$
(17)
$$\begin{aligned}& \begin{aligned}[b] \bar{W}_{2} ( \zeta ,q ) &= Gr \biggl[ \frac{1 + \lambda q}{\lambda q ( \sqrt{\Pr q} - 1 ) ( q^{2} - a_{1}q + a_{2} )} \biggr]e^{ - \zeta \sqrt{\Pr q}} \\ &\quad {}+ Gm \biggl[ \frac{1 + \lambda q}{\lambda q^{2} ( q^{2} - b_{1}q + a_{2} )} \biggr]e^{ - \zeta \sqrt{scq}}. \end{aligned} \end{aligned}$$
(18)

Here, \(a_{1} = \frac{\Pr - ( 1 + \lambda M )}{\lambda } \), \(a_{2} = \frac{M}{\lambda } \) and \(b_{1} = \frac{Sc - ( 1 + \lambda M )}{\lambda } \).

Putting Eqs. (17) and (18) into Eq. (16), we obtain:

$$ \begin{aligned} \bar{W} ( \zeta ,q ) &= c_{1}e^{\zeta \sqrt{\lambda q^{2} + ( 1 + \lambda M )q + M}} + c_{2}e^{ - \zeta \sqrt{\lambda q^{2} + ( 1 + \lambda M )q + M}} \\ &\quad {}+ Gr \biggl[ \frac{1 + \lambda q}{\lambda q ( \sqrt{\Pr q} - 1 ) ( q^{2} - a_{1}q + a_{2} )} \biggr]e^{ - \zeta \sqrt{\Pr q}} \\ &\quad {}+ Gm \biggl[ \frac{1 + \lambda q}{\lambda q^{2} ( q^{2} - b_{1}q + a_{2} )} \biggr]e^{ - \zeta \sqrt{scq}}. \end{aligned} $$

After applying initial and boundary conditions to the above equation, we obtain the Laplace solution for velocity:

$$ \begin{aligned}[b] \bar{W} ( \zeta ,q ) &= Gr \biggl[ \frac{1 + \lambda q}{\lambda ( \sqrt{\Pr q} - 1 )} \biggl( \frac{4}{A_{3}q} + \frac{1}{A_{4} ( q - A_{2} )} + \frac{1}{A_{5} ( q - A_{1} )} \biggr) \\ &\quad {}\times \bigl( e^{ - \zeta \sqrt{\Pr q}} - e^{ - \zeta \sqrt{\lambda \{ ( q - a_{3} )^{2} - a_{4}^{2} \} }} \bigr) \biggr] \\ &\quad {}+ Gm \biggl[ \frac{1 + \lambda q}{\lambda } \biggl( \frac{2}{q} \biggl( \frac{1}{B_{3}} - \frac{1}{B_{4}} \biggr) + \frac{4}{B_{5}q^{2}} + \frac{2}{B_{2} ( q - B_{2} )} + \frac{2}{B_{4} ( q - B_{1} )} \biggr) \\ &\quad {}\times\bigl( e^{ - \zeta \sqrt{scq}} - e^{ - \zeta \sqrt{\lambda \{ ( q - a_{3} )^{2} - a_{4}^{2} \} }} \bigr) \biggr], \end{aligned} $$
(19)

where \(a_{3} = \frac{1 + \lambda M}{2\lambda } \), \(a_{4} = \sqrt{\frac{ ( 1 + \lambda M )^{2} - 4\lambda M}{4\lambda ^{2}}}\), \(A_{1} = \frac{a_{1}}{2} - z\), \(A_{2} = \frac{a_{1}}{2} + z\), \(A_{3} = a_{1}^{2} - 4z^{2}\), \(A_{4} = 2z^{2} - a{}_{1}z\), \(A_{5} = 2z^{2} + a{}_{1}z\), \(z = \sqrt{\frac{a_{1}^{2} - 4a_{2}}{4}}\), \(B_{1} = \frac{b_{1}}{2} - z_{1}\), \(B_{2} = \frac{b_{1}}{2} + z_{1}\), \(B_{3} = z_{1}(b_{1} - 2z_{1})^{2}\), \(B_{4} = z_{1}(b_{1} + 2z_{1})^{2}\), \(B_{5} = b_{1}^{2} - 4z_{1}^{2}\) and \(z_{1} = \sqrt{\frac{b_{1}^{2} - 4a_{2}}{4}}\). □

6.2 Caputo fractional derivative

Theorem 2

Let \({}^{C}D_{t}^{\gamma } i(\zeta ,t)\) be the Caputo fractional derivative and L be the Laplace operator, applying these operators to Eq. (4) along with initial and boundary conditions, the exact solution of velocity is given in Eq. (26).

Proof

Applying the Caputo time derivative Eq. (7) to the nondimensional velocity Eq. (4) and taking the Laplace transform, we obtain:

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{L} \biggl[ \bigl( 1 + \lambda {}^{C}D_{t}^{\gamma } \bigr)\frac{\partial \bar{W}}{\partial \zeta } \biggr] \\ &\quad = \mathcal{L} \biggl[ \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} + Gr \bigl( 1 + \lambda {}^{C}D_{t}^{\gamma } \bigr) \bar{\Upsilon } + Gm \bigl( 1 + {}^{C}D_{t}^{\gamma } \bigr)\bar{\Lambda } - M \bigl( 1 + \lambda {}^{C}D_{t}^{\gamma } \bigr)\bar{W} \biggr], \end{aligned} \end{aligned}$$
(20)
$$\begin{aligned}& \bigl( 1 + \lambda q^{\gamma } \bigr)q\bar{W}_{C} = \frac{\partial ^{2}\bar{W}_{C}}{\partial \zeta ^{2}} + Gr \bigl( 1 + \lambda q^{\gamma } \bigr)\bar{ \Upsilon }_{C} + Gm \bigl( 1 + \lambda q^{\gamma } \bigr)\bar{ \Lambda }_{C} - M \bigl( 1 + \lambda q^{\gamma } \bigr) \bar{W}_{C}, \end{aligned}$$
(21)
$$\begin{aligned}& \begin{aligned}[b] &\biggl[ \frac{\partial ^{2}}{\partial \zeta ^{2}} - \bigl( 1 + \lambda q^{\gamma } \bigr)q - M \bigl( 1 + \lambda q^{\gamma } \bigr) \biggr]\bar{W}_{C} \\ &\quad = Gr \bigl[ - \bigl( 1 + \lambda q^{\gamma } \bigr)\bar{\Upsilon }_{C} \bigr] + Gm \bigl[ - \bigl( 1 + \lambda q^{\gamma } \bigr)\bar{\Lambda }_{C} \bigr]. \end{aligned} \end{aligned}$$
(22)

The general solution of the nonhomogeneous linear equation, Eq. (22), is:

$$ \bar{W}_{C} ( \zeta ,q ) = \bar{W}_{1} ( \zeta ,q ) + \bar{W}_{2} ( \zeta ,q ). $$
(23)

Here,

$$ \bar{W}_{1} ( \zeta ,q ) = c_{1}e^{\zeta \sqrt{ ( 1 + \lambda q^{\gamma } ) ( q + M )}} + c_{2}e^{ - \zeta \sqrt{ ( 1 + \lambda q^{\gamma } ) ( q + M )}}, $$
(24)

and

$$ \bar{W}_{2} ( \zeta ,q ) = Gr \biggl[ \frac{1 + \lambda q^{\gamma }}{q ( \sqrt{\Pr q^{\gamma }} - 1 ) ( pq^{\gamma } + m_{1} )}e^{ - \zeta \sqrt{\Pr q^{\gamma }}} \biggr] + Gm \biggl[ \frac{1 + \lambda q^{\gamma }}{q^{2} ( sq^{\gamma } + m_{1} )}e^{ - \zeta \sqrt{Scq^{\gamma }}} \biggr]. $$
(25)

Substituting Eq. (24) and Eq. (25) into Eq. (23) and applying initial and boundary conditions, the Laplace solution of Eq. (23) is

$$ \begin{aligned}[b] \bar{W}_{C}(\zeta ,q) &= Gr \biggl[ \frac{1 + \lambda q^{\gamma }}{q ( \sqrt{\Pr q^{\gamma }} - 1 ) ( pq^{\gamma } + m_{1} )} \bigl( e^{ - \zeta \sqrt{\Pr q^{\gamma }}} - e^{ - \zeta \sqrt{m_{1} ( 1 + \lambda q^{\gamma } )}} \bigr) \biggr] \\ &\quad {}+ Gm \biggl[ \frac{1 + \lambda q^{\gamma }}{q^{2} ( sq^{\gamma } + m_{1} )} \bigl( e^{ - \zeta \sqrt{Scq^{\gamma }}} - e^{ - \zeta \sqrt{m_{1} ( 1 + \lambda q^{\gamma } )}} \bigr) \biggr], \end{aligned} $$
(26)

where \(m_{1} = q + M\), \(p = \lambda ( q + M ) - \Pr \) and \(s = \lambda ( q + M ) - Sc\). □

6.3 Caputo–Fabrizio fractional derivative

Theorem 3

Let \({}^{CF}D_{t}^{\gamma } i(\zeta ,t)\) be the Caputo–Fabrizio fractional derivative and L be the Laplace operator, applying these operators to Eq. (4) along with initial and boundary conditions, the exact solution of velocity is given in Eq. (33).

Proof

Applying the Caputo–Fabrizio time derivative Eq. (9) and then its Laplace transform Eq. (10) to Eq. (4), we obtain:

$$\begin{aligned}& \mathcal{L} \biggl[ \bigl( 1 + \lambda {}^{CF}D_{t}^{\gamma } \bigr)\frac{\partial \bar{W}}{\partial \zeta } \biggr] \\& \quad = \mathcal{L} \biggl[ \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} + Gr \bigl( 1 + \lambda {}^{CF}D_{t}^{\gamma } \bigr) \bar{\Upsilon } + Gm \bigl( 1 + {}^{CF}D_{t}^{\gamma } \bigr)\bar{\Lambda } - M \bigl( 1 + \lambda {}^{CF}D_{t}^{\gamma } \bigr)\bar{W} \biggr], \end{aligned}$$
(27)
$$\begin{aligned}& \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr)q\bar{W}_{CF} \\& \quad = \frac{\partial ^{2}\bar{W}_{CF}}{\partial \zeta ^{2}} + Gr \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr)\bar{\Upsilon }_{CF} \\& \qquad {}+ Gm \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr)\bar{\Lambda }_{CF} - M \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr) \bar{W}_{CF}. \end{aligned}$$
(28)

After some calculations we obtain a second-order nonhomogeneous linear equation:

$$\begin{aligned}& \biggl[ \frac{\partial ^{2}}{\partial \zeta ^{2}} - \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr)q - M \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr) \biggr]\bar{W}_{CF} \\& \quad = - \biggl( 1 + \frac{\lambda q}{ ( 1 - \gamma )q + \gamma } \biggr) ( Gr\bar{\Upsilon }_{CF} + Gm \bar{\Lambda }_{CF} ). \end{aligned}$$
(29)

The solution of Eq. (29) is

$$ \bar{W}_{CF} ( \zeta ,q ) = \bar{W}_{1} ( \zeta ,q ) + \bar{W}_{2} ( \zeta ,q ), $$
(30)

where

$$ \bar{W}_{1} ( \zeta ,q ) = c_{1}e^{\zeta \sqrt{ ( \frac{dq + \gamma }{lq + \gamma } )m_{1}}} + c_{2}e^{ - \zeta \sqrt{ ( \frac{dq + \gamma }{lq + \gamma } )m_{1}}} , $$
(31)

and

$$\begin{aligned} \bar{W}_{1} ( \zeta ,q ) =& Gr \biggl[ \frac{dq + \gamma }{q ( \sqrt{\frac{\Pr q}{lq + \gamma }} - 1 ) ( p_{2}q + m_{1}\gamma )}e^{ - \zeta \sqrt{\frac{\Pr q}{lq + \gamma }}} \biggr] \\ &{}+ Gm \biggl[ \frac{dq + \gamma }{q^{2} ( s_{2}q + m_{1}\gamma )}e^{ - \zeta \sqrt{\frac{Scq}{lq + \gamma }}} \biggr]. \end{aligned}$$
(32)

Inserting the values of Eq. (31) and Eq. (32) into Eq. (30) and applying initial and boundary conditions, we have:

$$\begin{aligned} \bar{W}_{\mathbf{C}F} ( \zeta ,q ) =& Gr \biggl[ \frac{dq + \gamma }{q ( p_{2}q + m_{1}\gamma ) ( \sqrt{\frac{\Pr q}{lq + \gamma }} )} \bigl( e^{ - \zeta \sqrt{\frac{\Pr q}{lq + \gamma }}} - e^{ - \zeta \sqrt{m_{1} ( \frac{dq + \gamma }{lq + \gamma } )}} \bigr) \biggr] \\ &{}+ Gm \biggl[ \frac{dq + \gamma }{q^{2} ( s_{2}q + m_{1}\gamma )} \bigl( e^{ - \zeta \sqrt{\frac{Scq}{lq + \gamma }}} - e^{ - \zeta \sqrt{m_{1} ( \frac{dq + \gamma }{lq + \gamma } )}} \bigr) \biggr], \end{aligned}$$
(33)

where \(m_{1} = q + M\), \(l = 1 - \gamma \), \(d = 1 - \gamma + \lambda \), \(p_{2} = m_{1}d - \Pr \) and \(s_{2} = m_{1}d - Sc\). □

6.4 Atangana–Baleanu fractional derivative

Theorem 4

Let \({}^{ABC}D_{t}^{\gamma } i(\zeta ,t)\) be the Atangana–Baleanu fractional derivative and L be the Laplace operator, applying these operators to Eq. (4) along with initial and boundary conditions, the exact solution of velocity is given in Eq. (40).

Proof

Applying the Atangana–Baleanu time derivative Eq. (11) and then its Laplace transform Eq. (12) to Eq. (4), we obtain:

$$\begin{aligned}& \mathcal{L} \biggl[ \bigl( 1 + \lambda {}^{ABC}D_{t}^{\gamma } \bigr)\frac{\partial \bar{W}}{\partial \zeta } \biggr] \\& \quad = \mathcal{L} \biggl[ \frac{\partial ^{2}\bar{W}}{\partial \zeta ^{2}} + Gr \bigl( 1 + \lambda {}^{ABC}D_{t}^{\gamma } \bigr) \bar{\Upsilon } + Gm \bigl( 1 + {}^{ABC}D_{t}^{\gamma } \bigr)\bar{\Lambda } - M \bigl( 1 + \lambda {}^{ABC}D_{t}^{\gamma } \bigr)\bar{W} \biggr], \end{aligned}$$
(34)
$$\begin{aligned}& \biggl( 1 + \frac{\lambda q^{\gamma }}{ ( 1 - \gamma )q^{\gamma } + \gamma } \biggr)q\bar{W}_{ABC} \\& \quad = \frac{\partial ^{2}\bar{W}_{ABC}}{\partial \zeta ^{2}} + Gr \biggl( 1 + \frac{\lambda q^{\gamma }}{ ( 1 - \gamma )q^{\gamma } + \gamma } \biggr)\bar{ \Upsilon }_{ABC} \\& \qquad {} + Gm \biggl( 1 + \frac{\lambda q^{\gamma }}{ ( 1 - \gamma )q^{\gamma } + \gamma } \biggr)\bar{ \Lambda }_{ABC} - M \biggl( 1 + \frac{\lambda q^{\gamma }}{ ( 1 - \gamma )q^{\gamma } + \gamma } \biggr)\bar{W}_{ABC}, \end{aligned}$$
(35)
$$\begin{aligned}& \biggl[ \frac{\partial ^{2}}{\partial \zeta ^{2}} - \biggl( 1 + \frac{\lambda q^{\gamma }}{lq^{\gamma } + \gamma } \biggr)q - M \biggl( 1 + \frac{\lambda q^{\gamma }}{lq^{\gamma } + \gamma } \biggr) \biggr]\bar{W}_{ABC} \\& \quad = - \biggl( 1 + \frac{\lambda q^{\gamma }}{lq^{\gamma } + \gamma } \biggr) ( Gr\bar{\Upsilon }_{ABC} + Gm\bar{\Lambda }_{ABC} ). \end{aligned}$$
(36)

Equation (36) is a 2nd-order nonhomogeneous linear equation. So, its exact solution is:

$$ \bar{W}_{ABC} ( \zeta ,q ) = \bar{W}_{1} ( \zeta ,q ) + \bar{W}_{2} ( \zeta ,q ). $$
(37)

Here,

$$ \bar{W}_{1} ( \zeta ,q ) = c_{1}e^{\zeta \sqrt{ ( \frac{dq^{\gamma } + \gamma }{lq^{\gamma } + \gamma } )m_{1}}} + c_{2}e^{ - \zeta \sqrt{ ( \frac{dq^{\gamma } + \gamma }{lq^{\gamma } + \gamma } )m_{1}}} , $$
(38)

and

$$\begin{aligned} \bar{W}_{2} ( \zeta ,q ) =& Gr \biggl[ \frac{dq^{\gamma } + \gamma }{q ( \sqrt{\frac{\Pr q^{\gamma }}{lq^{\gamma } + \gamma }} - 1 ) ( p_{3}q^{\gamma } + m_{1}\gamma )}e^{ - \zeta \sqrt{\frac{\Pr q^{\gamma }}{lq^{\gamma } + \gamma }}} \biggr] \\ &{}+ Gm \biggl[ \frac{dq^{\gamma } + \gamma }{q^{2} ( s_{3}q^{\gamma } + m_{1}\gamma )}e^{ - \zeta \sqrt{\frac{Scq^{\gamma }}{lq^{\gamma } + \gamma }}} \biggr]. \end{aligned}$$
(39)

Putting values of the solution of \(\bar{W}_{1} ( \zeta ,q )\) and \(\bar{W}_{2} ( \zeta ,q )\) into Eq. (37) and after some simplifications, we obtain:

$$\begin{aligned} \bar{W}_{ABC} ( \zeta ,q ) =& Gr \biggl[ \frac{dq^{\gamma } + \gamma }{q ( \sqrt{\frac{\Pr q^{\gamma }}{lq^{\gamma } + \gamma }} ) ( p_{3}q^{\gamma } + m_{1}\gamma )} \bigl( e^{ - \zeta \sqrt{\frac{\Pr q^{\gamma }}{lq^{\gamma } + \gamma }}} - e^{ - \zeta \sqrt{m_{1} ( \frac{dq^{\gamma } + \gamma }{lq^{\gamma } + \gamma } )}} \bigr) \biggr] \\ &{}+ Gm \biggl[ \frac{dq^{\gamma } + \gamma }{q^{2} ( s_{3}q^{\gamma } + m_{1}\gamma )} \bigl( e^{ - \zeta \sqrt{\frac{Scq^{\gamma }}{lq^{\gamma } + \gamma }}} - e^{ - \zeta \sqrt{m_{1} ( \frac{dq^{\gamma } + \gamma }{lq^{\gamma } + \gamma } )}} \bigr) \biggr], \end{aligned}$$
(40)

where \(m_{1} = q + M\), \(l = 1 - \gamma \), \(d = 1 - \gamma + \lambda \), \(p_{3} = m_{1}d - \Pr \) and \(s_{3} = m_{1}d - Sc\). □

Stehfest’s formula [22] is one of the simplest algorithms we use to determine the inverse Laplace transform:

$$ W ( r,t ) = \frac{e^{4.7}}{t} \Biggl[ \frac{1}{2}\bar{W} \biggl( r,\frac{4.7}{t} \biggr) + \operatorname{Re} \Biggl\{ \sum _{k = 1}^{N_{1}} ( - 1 )^{k}\bar{W} \biggl( r,\frac{k\pi i + 4.7}{t} \biggr) \Biggr\} \Biggr], $$

where \(N_{1}\) is a natural number, \(\operatorname{Re} (\cdot)\) and i are the real part and the imaginary unit, respectively [22].

7 Limiting case

7.1 Case 1

By ignoring the concentration profile, we recover the results presented in Riaz and Iftikhar [19].

7.2 Case 2

By removing the magnetic field in Eq. (4), we obtain the results presented in Riaz et al. [20].

7.3 Case 3

By eliminating the concentration and magnetic field simultaneously we obtain the results shown in Raza and Asad Ullah [23].

8 Results and discussion

In this article, the effects of Newtonian heating on MHD Maxwell flow over a vertical plate are studied. The C, CF and ABC derivatives are interpolated to form three particular fractional models for flow, energy and mass equations. Fractional derivatives and Laplace transforms are applied to examine the solutions for nondimensional fractional models. Limiting cases of the fractional models are discussed. Several graphs are presented to illustrate the physical effects of parameters γ, λ, Sc, Pr, Gr, Gm and M on velocity.

  1. 1.

    Effect of γ: Fig. 2 shows that the fluid velocity increases when the fractional parameter γ increases, as time varies. The rate of change increases, and the velocity profile increases. All curves, Caputo, Caputo–Fabrizio and Atangana–Baleanu, converge as y tends to infinity. For both large and small time and among all three MHD fractional Maxwell models, the fluid velocity is maximum for the Atangana–Baleanu case as it has a nonsingular and nonlocal kernel. For the Caputo fractional model, the fluid velocity is minimum, while for the Caputo–Fabrizio model, the fluid velocity is moderate among all three models because it has a nonsingular kernel and a maximum for the ABC model. The fractional-order derivative converts into a classical model as \(\alpha \rightarrow 1\).

    Figure 2
    figure 2

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of γ, where \(M = 4\), \(\Pr = 6\), \(Sc = 8\), \(Gr = 6\), \(Gm = 8\) and \(\lambda = 0.2\)

    Full size image
  2. 2.

    Effect of M: Fig. 3 reveals the deviation in velocity distribution under the effect of a magnetic field. The magnetic field causes a frictional force (Lorentz force) due to which the fluid velocity decreases. For different values of M, an increase in the Lorentz force effectively decreases flow-accelerating forces, and as a result, the velocity is decelerated. The fluid velocity is maximum, moderate and minimum for Atangana–Baleanu, Caputo–Fabrizio and Caputo models, respectively

    Figure 3
    figure 3

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of M, where \(\gamma = 0.1\), \(\Pr = 6\), \(Sc = 8\), \(Gr = 6\), \(Gm = 8\) and \(\lambda = 0.2\)

    Full size image
  3. 3.

    Effect of λ: Fig. 4 shows that as λ increases, the velocity profile decreases. The velocity function has also been determined for variable time. Relaxation time enhances the backward flow and reduces the velocity. Also, when λ rises, the thickness of the momentum boundary layer minimizes, which leads to a downshift of the flow. Since the increment in relaxation time suggests that fluid will acquire additional time to relax, it affirms a decrease in velocity.

    Figure 4
    figure 4

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of λ, where \(\gamma = 0.1\), \(\Pr = 6\), \(Sc = 8\), \(Gr = 6\), \(Gm = 8\) and \(M = 4\)

    Full size image
  4. 4.

    Effect of Sc: The fluid velocity decreases when Sc increases, as shown in Fig. 5. As the Maxwell fractional model concerns the effect of a magnetic field, this causes a decrease in molecular or mass diffusivity and hence velocity decreases. Moreover, Sc is also inversely proportional to the molecular diffusivity due to which the fluid velocity decreases. Among all three fractional solutions, the velocity profile is significant for the Atangana–Baleanu model.

    Figure 5
    figure 5

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of Sc, where \(\gamma = 0.1\), \(\Pr = 6\), \(\lambda = 0.2\), \(Gr = 6\), \(Gm = 8\) and \(M = 4\)

    Full size image
  5. 5.

    Effect of Gm: Fig. 6 shows that the fluid velocity increases with increasing Gm. Physically, the increment in buoyancy forces reduces the viscous force that leads to a further increase in the velocity field with higher values of Gm. Velocity curves show maximum behavior for the ABC model as compared to the other two models.

    Figure 6
    figure 6

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of Gm, where \(\gamma = 0.1\), \(\Pr = 6\), \(\lambda = 0.2\), \(Gr = 6\), \(Sc = 8\) and \(M = 4\)

    Full size image
  6. 6.

    Effect of Gr: Fig. 7 describes the variability of the momentum profile with increasing values of Grashof number. Physically, large values of Gr correspond to a significant buoyancy force as it is related to strong convection currents. For increasing Gr, all buoyancy forces dominate frictional forces and hence the momentum profile is amplified.

    Figure 7
    figure 7

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of Gr, where \(\gamma = 0.1\), \(\Pr = 6\), \(\lambda = 0.2\), \(Sc = 8\), \(Gm = 8\) and \(M = 4\)

    Full size image
  7. 7.

    Effect of Pr: Fig. 8 illustrates the effects of Pr on the flow. It is noted that the flow declines as Pr increases. Clearly, as Pr increases, thermal diffusivity decreases. This causes an increase in viscosity, which results in a decrease in velocity. Moreover, the velocity profile of the MHD Maxwell fractional model is minimum for the Caputo case and maximum for the Atangana–Baleanu case.

    Figure 8
    figure 8

    (a, b, c). Velocity curves belonging to C, CF and ABC for various values of Pr, where \(\gamma = 0.1\), \(Gr = 6\), \(\lambda = 0.2\), \(Sc = 8\), \(Gm = 8\) and \(M = 4\)

    Full size image
  8. 8.

    Comparison among C, CF and ABC: Fig. 9 shows a comparison among the three fractional models. Clearly, velocity curves for ABC show a significant change for different values of the fractional parameter.

    Figure 9
    figure 9

    Velocity curves for C, CF and ABC for various values of γ

    Full size image
  9. 9.

    Velocity profile without concentration: Fig. 10 presents the velocity curves for C, CF and ABC without concentration. It is observed that as the fractional parameter tends to 1 the fractional model approaches to an integer-order model [21].

    Figure 10
    figure 10

    (a, b, c). Velocity curves for C, CF and ABC for various values of γ approaching to integer order

    Full size image

9 Conclusions

This article studies a time-dependent, Maxwell MHD fluid on an unbounded upright plate with Newtonian heating. The C, CF and ABC operators are used to construct a flow-directing equation for a rate-type fluid. Solutions of the model equations are presented from Laplace transforms. Several graphs are presented to illustrate the impact of various parameters on the solutions. Significant findings of this study are noted as follows:

  1. 1.

    The velocity of the fluid increases with increasing fractional parameter for the Caputo, Caputo–Fabrizio and Atangana Baleanu models.

  2. 2.

    The flow profile is maximum for the ABC model as compared to the C and CF models.

  3. 3.

    As the magnetic field increases for variable time, the fluid velocity decreases for local, nonlocal and nonsingular kernels.

  4. 4.

    An increment in the Maxwell parameter λ causes a decrease in the fluid velocity for all fractional models.

  5. 5.

    The fluid velocity declines as the values of Pr and Sc increase, whereas, the fluid velocity exhibits a reverse profile for higher values of Gr and Gm.