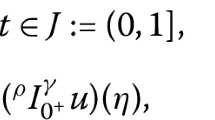1 Introduction

The theory of singular fractional boundary value problems has become an area of research investigation in the last three decades (see [1, 3, 6, 7, 16, 21]). One of the equations describing this type of problems is the very important Lane–Emden equation, which was published by Lane in 1870 [18] and detailed by Emden [8]. Lane–Emden differential equations are singular initial value problems of the second order, they describe a variety of phenomena in mathematical physics and astrophysics such as aspects of the stellar structure. For more information and some applications, one can consult Refs. [2, 13, 23].

The classical Lane–Emden equation has the following form [5, 8]:

$$ x^{{\prime \prime }} ( t ) +\frac{a}{t}x^{{\prime }} ( t ) +f \bigl( t,x ( t ) \bigr) =g ( t ) , \quad t\in [ 0,1 ] , $$

under the conditions

$$ x ( 0 ) =A, \qquad x^{{\prime }} ( 0 ) =B, $$

where A and B are constants and f and g are continuous real functions.

The above problem has attracted many researchers attention. In fact, in [20], the authors have used the method of collocation to study the following Lane–Emden problem:

$$ \textstyle\begin{cases} D^{\alpha }y ( t ) + \frac{k}{t^{\alpha -\beta }}D^{\beta }y ( t ) +f ( t,y ( t ) ) =g ( t ) , \quad t\in [ 0,1 ] , \\ k\geq 0,\qquad 1< \alpha \leq 2,\qquad 0< \beta \leq 1, \end{cases}$$

Ibrahim [15] has been concerned with the stability of Ulam Hyers for the following fractional Lane–Emden problem:

$$ \textstyle\begin{cases} D^{\beta } ( D^{\alpha }+\frac{a}{t} ) u ( t ) +f ( t,u ( t ) ) =g ( t ) , \\ u ( 0 ) =\mu , \qquad u ( 1 ) =\nu , \\ 0< \alpha ,\beta \leq 1,\qquad 0\leq t\leq 1,\qquad a\geq 0,\end{cases}$$

under the conditions: \(D^{\gamma }\) is the Caputo derivative, f is a continuous function and \(g\in C ( [ 0,1 ] ) \).

Very recently, Y. Gouari et al. [10] have investigated the following nonlocal fractional problem of Lane–Emden type:

$$ \textstyle\begin{cases} D^{\beta }(D^{\alpha }+\frac{k}{t^{\lambda }})y(t)+\Delta _{1}f(t,y(t),D^{ \delta }y(t))+\Delta _{2}g(t,y(t),I^{\rho }y(t))+h(t,y(t))=l(t), \\ y(0)=0, \qquad y(1)=b\int _{0}^{\eta }y(s)\,ds,\quad 0< \eta < 1, \qquad I^{q}y(u)=y(1),\quad 0< u< 1, \\ k>0,\qquad 0< \lambda \leq 1,\qquad 1\leq \beta \leq 2,\qquad 0\leq \alpha , \delta \leq 1, \qquad t\in\, ]0,1[, \end{cases} $$

Motivated by the above cited papers, in [25] we have proved the existence and uniqueness of solutions by application of the Banach contraction principle for the following anti periodic fractional differential problem:

$$ \textstyle\begin{cases} D^{\alpha }D^{\beta }y(t)+\frac{k}{t^{\lambda }}D^{\alpha }y(t)+a_{1}F (t,y(t),D^{\gamma }y(t),J^{p}y(t) ) \\ \quad {}+a_{2}G (t,y(t),D^{\gamma }y(t) )+a_{3}H (t,y(t) )=L(t). \\ y(0)+y(1)=0, \qquad y^{\prime }(0)+y^{\prime }(1)=0,\qquad D^{\gamma }(0)+D^{\gamma }(1)=0, \\ k>0,\qquad 1\leq \beta \leq 2, \qquad 0\leq \gamma \leq \alpha \leq 1, \qquad 0< \lambda < 1,\qquad p>0,\qquad t\in {}[ 0,1], \end{cases} $$
(1)

where \(I:=[0,1]\), the derivatives of the problem are in the sense of Caputo, \(J^{p}\) denotes the Riemann–Liouville integral of order p and \(F:I\times \mathbb{R}^{3}\rightarrow \mathbb{R}\), \(G:I\times \mathbb{R}^{2}\rightarrow \mathbb{R}\), \(H:I\times \mathbb{R}^{2}\rightarrow \mathbb{R}\) and \(L:I\rightarrow \mathbb{R} \) are four given functions, and \(\mathbb{R} \) being the set of real numbers.

In this work, we continue studying the above problem by investigating certain types of Ulam stability for the problem (1). Then, using a numerical approach of the derivative Caputo, we analyze certain behavior of the problem by means of the fourth-order Runge–Kutta integrator method.

2 Preliminaries

We present some necessary lemmas and theorems which will be used in this paper.

As it is proved in our last work [25], the integral solution of (1) is given by the following auxiliary result.

Lemma 1

Let \(L_{1}\in C([0,1])\), \(t\in I\), \(0\leq \gamma \leq \alpha \leq 1\), \(1<\beta <2\). Then the integral solution of the problem

$$ \textstyle\begin{cases} D^{\alpha }(D^{\beta })y(t)+(\frac{k}{t^{\lambda }})D^{\alpha }y(t)=L_{1}(t), \\ y(0)+y(1)=0, \qquad y^{\prime }(0)+y^{\prime }(1)=0,\qquad D^{\gamma }(0)+D^{\gamma }(1)=0,\end{cases} $$
(2)

is given by the following expression:

$$\begin{aligned} y(t) =& \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L_{1}(u)-\frac{k}{u^{\lambda }}D^{\alpha }y(u) \biggr] \,du\,ds \\ &{}+ \bigl[ K_{1}t^{\beta }+K_{2}t+K_{3} \bigr] \biggl[ \int _{0}^{1} \frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L_{1}(u)-\frac{k}{u^{\lambda }}D^{\alpha }y(u) \biggr] \,du\,ds \biggr] \\ &{}+ \bigl[ K_{4}t^{\beta }+K_{5}t-K_{6} \bigr] \biggl[ \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L_{1}(u)-\frac{k}{u^{\lambda }}D^{\alpha }y(u) \biggr] \,du\,ds \biggr] \\ &{}- [ K_{7} ] \biggl[ \int _{0}^{1} \frac{(1-s)^{\beta -1}}{\Gamma (\beta )} \int _{0}^{s} \frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L_{1}(u)-\frac{k}{u^{\lambda }}D^{\alpha }y(u) \biggr] \,du\,ds \biggr] , \end{aligned}$$
(3)

where

$$\begin{aligned} L_{1}(u) =&L(u)-a_{1}F \bigl(u,y(u),D^{\gamma }y(u),J^{p}y(u) \bigr)-a_{2}G \bigl(u,y(u),D^{ \gamma }y(u) \bigr) \\ &{}-a_{3}H \bigl(u,y(u) \bigr)-\frac{k}{u^{\lambda }}D^{\alpha }y(u) \end{aligned}$$

and

$$\begin{aligned}& K_{1}= \frac{\Gamma ( \beta -\gamma +1 ) }{ \beta [ \Gamma ( \beta -\gamma +1 ) -2\Gamma ( \beta ) \Gamma ( 2-\gamma ) ] }, \\& K_{2}= \frac{\Gamma ( \beta ) \Gamma ( 2-\gamma ) }{2\Gamma ( \beta ) \Gamma ( 2-\gamma ) -\Gamma ( \beta -\gamma +1 ) }, \\& K_{3}= \frac{\Gamma ( \beta +1 ) \Gamma ( 2-\gamma ) -\Gamma ( \beta -\gamma +1 ) }{2\beta \Gamma ( \beta -\gamma +1 ) -4\Gamma ( \beta +1 ) \Gamma ( 2-\gamma ) }, \\& K_{4}= \frac{2\Gamma ( 2-\gamma ) \Gamma ( \beta -\gamma +1 ) }{ \beta [ \Gamma ( \beta -\gamma +1 ) -2\Gamma ( \beta ) \Gamma ( 2-\gamma ) ] }, \\& K_{5}=\frac{\Gamma ( 2-\gamma ) \Gamma ( \beta -\gamma +1 ) }{2\Gamma ( \beta ) \Gamma ( 2-\gamma ) -\Gamma ( \beta -\gamma +1 ) }, \\& K_{6}= \frac{2\Gamma ( 2-\gamma ) \Gamma ( \beta -\gamma +1 ) -\beta \Gamma ( 2-\gamma ) \Gamma ( \beta -\gamma +1 ) }{2\beta \Gamma ( \beta -\gamma +1 ) -4\Gamma ( \beta +1 ) \Gamma ( 2-\gamma ) }, \\& K_{7}= \frac{\Gamma ( \beta -\gamma +1 ) -2\Gamma ( \beta ) \Gamma ( 2-\gamma ) }{2\Gamma ( \beta -\gamma +1 ) -4\Gamma ( \beta ) \Gamma ( 2-\gamma ) }. \end{aligned}$$

Before presenting our main results, we shall introduce also the Banach space

$$ X:= \bigl\{ y\in C(I,\mathbb{R}),D^{\alpha }y\in C(I,\mathbb{R}),D^{ \gamma }y \in C(I,\mathbb{R}) \bigr\} , $$

and the norm

$$ \Vert y \Vert _{X}=\max \bigl\{ \Vert y \Vert _{\infty }, \bigl\Vert D^{\alpha }y \bigr\Vert _{ \infty }, \bigl\Vert D^{\gamma }y \bigr\Vert _{\infty } \bigr\} , $$

where

$$ \Vert x \Vert _{\infty }=\sup_{t\in I} \bigl\vert x(t) \bigr\vert , \qquad \bigl\Vert D^{\alpha }x \bigr\Vert _{\infty }= \sup_{t\in I} \bigl\vert D^{\alpha }x(t) \bigr\vert ,\qquad \bigl\Vert D^{ \gamma }x \bigr\Vert _{\infty }=\sup_{t\in I} \bigl\vert D^{\gamma }x(t) \bigr\vert . $$

Also, we consider the following hypotheses:

  1. (H1):

    There exist nonnegative constants \(W_{i}\), \(i=1,\ldots,6\), such that for each \(t\in I\) and for all \(x_{1},x_{2},x_{3},y_{1},y_{2},y_{3}\in \mathbb{R}\) we have

    $$\begin{aligned}& \bigl\vert F(t,x_{1},x_{2},x_{3})-F(t,y_{1},y_{2},y_{3}) \bigr\vert \leq W_{1} \vert x_{1}-y_{1} \vert +W_{2} \vert x_{2}-y_{2} \vert +W_{3} \vert x_{3}-y_{3} \vert , \\& \bigl\vert G(t,x_{1},x_{2})-G(t,y_{1},y_{2}) \bigr\vert \leq W_{4} \vert x_{1}-y_{1} \vert +W_{5} \vert x_{2}-y_{2} \vert , \\& \bigl\vert H(t,x_{1})-H(t,y_{1}) \bigr\vert \leq W_{6} \vert x_{1}-y_{1} \vert . \end{aligned}$$

The following quantities are also needed in this paper:

$$\begin{aligned}& \begin{aligned} N_{1} ={}&(a_{1}W_{1,2}+a_{2}W_{4,5}+a_{3}W_{6}) \biggl[ \frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta +1)} \\ &{}+ \frac{ \vert K_{1} \vert + \vert K_{2} \vert + \vert K_{3} \vert }{ \Gamma (\alpha +\beta )}+ \frac{ \vert K_{4} \vert + \vert K_{5} \vert + \vert K_{6} \vert }{\Gamma (\alpha +\beta -\gamma +1)} \biggr] \\ &{}+a_{1}W_{3} \biggl[ \frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta +p+1)}+ \frac{ \vert K_{1} \vert + \vert K_{2} \vert + \vert K_{3} \vert }{\Gamma (\alpha +\beta +p)}+ \frac{ \vert K_{4} \vert + \vert K_{5} \vert + \vert K_{6} \vert }{\Gamma (\alpha +\beta -\gamma +p+1)} \biggr] \\ &{}+ \vert k \vert \Gamma (1-\lambda ) \biggl[ \frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta -\lambda +1)}+ \frac{ \vert K_{1} \vert + \vert K_{2} \vert + \vert K_{3} \vert }{\Gamma (\alpha +\beta -\lambda )}+ \frac{ \vert K_{4} \vert + \vert K_{5} \vert + \vert K_{6} \vert }{\Gamma (\alpha +\beta -\gamma -\lambda +1)} \biggr], \end{aligned} \\& \begin{aligned} N_{2} ={}&(a_{1}W_{1,2}+a_{2}W_{4,5}+a_{3}W_{6}) \biggl[\frac{1+ \vert K_{7} \vert }{\Gamma (\beta +1)} +\frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\alpha )+ \vert K_{2} \vert \Gamma (\beta -\alpha +1)}{\Gamma (\beta )\Gamma (\beta -\alpha +1)\Gamma (2-\alpha )} \\ &{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\alpha )+ \vert K_{5} \vert \Gamma (\beta -\alpha +1)}{ \Gamma (\beta -\gamma +1)\Gamma (\beta -\alpha +1)\Gamma (2-\alpha )} \biggr] \\ &{}+a_{1}W_{3} \biggl[ \frac{1+ \vert K_{7} \vert }{\Gamma (\beta +p+1)} + \frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\alpha ) + \vert K_{2} \vert \Gamma (\beta -\alpha +1)}{\Gamma (\beta +p)\Gamma (\beta -\alpha +1)\Gamma (2-\alpha )} \\ &{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\alpha ) + \vert K_{5} \vert \Gamma (\beta -\alpha +1)}{\Gamma (\beta -\gamma +p+1)\Gamma (\beta -\alpha +1) \Gamma (2-\alpha )} \biggr] \\ &{}+ \vert k \vert \Gamma (1-\lambda ) \biggl[\frac{1+ \vert K_{7} \vert }{\Gamma (\beta -\lambda +1)} + \frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\alpha ) + \vert K_{2} \vert \Gamma (\beta -\alpha +1)}{\Gamma (\beta -\lambda )\Gamma (\beta -\alpha +1)\Gamma (2-\alpha )} \\ &{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\alpha ) + \vert K_{5} \vert \Gamma (\beta -\alpha +1)}{\Gamma (\beta -\gamma -\lambda +1)\Gamma (\beta -\alpha +1)\Gamma (2-\alpha )} \biggr], \end{aligned} \\& N_{3} =(a_{1}W_{1,2}+a_{2}W_{4,5}+a_{3}W_{6}) \biggl[\frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta -\gamma +1)} \\& \hphantom{N_{3} ={}}{}+\frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\gamma ) + \vert K_{2} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -\gamma )\Gamma (\beta -\gamma +1) \Gamma (2-\gamma )} \\& \hphantom{N_{3} ={}}{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\gamma ) + \vert K_{5} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -2\gamma +1)\Gamma (\beta -\gamma +1) \Gamma (2-\gamma )} \biggr] \\& \hphantom{N_{3} ={}}{}+a_{1}W_{3} \biggl[ \frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta -\gamma +p+1)} + \frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\gamma )+ \vert K_{2} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -\gamma +p)\Gamma (\beta -\gamma +1) \Gamma (2-\gamma )} \\& \hphantom{N_{3} ={}}{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\gamma )+ \vert K_{5} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -2\gamma +p+1)\Gamma (\beta -\gamma +1) \Gamma (2-\gamma )} \biggr] \\& \hphantom{N_{3} ={}}{}+ \vert k \vert \Gamma (1-\lambda ) \biggl[\frac{1+ \vert K_{7} \vert }{\Gamma (\alpha +\beta -\gamma -\lambda +1)} + \frac{ \vert K_{1} \vert \Gamma (\beta +1)\Gamma (2-\gamma ) + \vert K_{2} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -\gamma -\lambda ) \Gamma (\beta -\gamma +1)\Gamma (2-\gamma )} \\& \hphantom{N_{3} ={}}{}+\frac{ \vert K_{4} \vert \Gamma (\beta +1)\Gamma (2-\gamma ) + \vert K_{5} \vert \Gamma (\beta -\gamma +1)}{\Gamma (\alpha +\beta -2\gamma -\lambda +1) \Gamma (\beta -\gamma +1)\Gamma (2-\gamma )} \biggr] , \\& \quad \text{where }W_{1,2}:=\max (W_{1},W_{2})\text{ and } W_{4,5}:=\max (W_{4},W_{5}). \end{aligned}$$

We recall the following result [25], which allows us to study the stability phenomena of the considered problem.

Theorem 2

([25])

Assume that (H1) holds and suppose that \(0< N<1\), where \(N=\max (N_{1},N_{2},N_{3})\). Then the problem (1) has a unique solution on I.

3 Ulam type stabilities

The notion of the stability problem of functional equations originated from a problem of Stanislaw Ulam [26], posed in 1940: When can we assert that approximate solution of a functional equation can be approximated by a solution of the corresponding equation. In 1941, Hyers [14] solved it. This approach can guarantee that there exists a close exact solution useful in many applications. For more details on the recent advances on the Hyers–Ulam stability (see for example [9, 11, 24, 27]).

In order to study some types of Ulam stability for the problem (1), we consider the following fractional differential equation:

Let \(1\leq \beta \leq 2\), \(0\leq \gamma \leq \alpha \leq 1\) and ϵ a positive real numbers and the function \(T\in C(I,\mathbb{R}^{+})\). We consider the following fractional differential equation:

$$\begin{aligned}& D^{\alpha }D^{\beta }y(t)+\frac{k}{t^{\lambda }}D^{\alpha }y(t)+a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\& \quad {}+a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr)+a_{3}H \bigl(t,y(t) \bigr)=L(t),\quad t\in I, \end{aligned}$$
(4)

and the following fractional differential inequality:

$$\begin{aligned}& \biggl\vert D^{\alpha }D^{\beta }x(t)+ \frac{k}{t^{\lambda }}D^{\alpha }x(t)+a_{1}F \bigl(t,x(t),D^{\gamma }x(t),J^{p}x(t) \bigr)+a_{2}G \bigl(t,x(t),D^{\gamma }x(t) \bigr) \\& \quad {}+a_{3}H \bigl(t,x(t) \bigr)-L(t) \biggr\vert \leq \epsilon ,\quad t\in I, \end{aligned}$$
(5)
$$\begin{aligned}& \biggl\vert D^{\alpha }D^{\beta }x(t)+ \frac{k}{t^{\lambda }}D^{\alpha }x(t)+a_{1}F \bigl(t,x(t),D^{\gamma }x(t),J^{p}x(t) \bigr)+a_{2}G \bigl(t,x(t),D^{\gamma }x(t) \bigr) \\& \quad {}+a_{3}H \bigl(t,x(t) \bigr)-L(t) \biggr\vert \leq \epsilon T ( t ) ,\quad t\in I, \end{aligned}$$
(6)
$$\begin{aligned}& \biggl\vert D^{\alpha }D^{\beta }x(t)+ \frac{k}{t^{\lambda }}D^{\alpha }x(t)+a_{1}F \bigl(t,x(t),D^{\gamma }x(t),J^{p}x(t) \bigr)+a_{2}G \bigl(t,x(t),D^{\gamma }x(t) \bigr) \\& \quad {}+a_{3}H \bigl(t,x(t) \bigr)-L(t) \biggr\vert \leq T ( t ) ,\quad t\in I. \end{aligned}$$
(7)

Definition 3

The problem (1) is Ulam–Hyers stable, if there exists a real number \(S>0\), such that, for each \(\epsilon >0\), \(t\in I\), and for each \(x\in X\) solution of (5), there exists a solution \(y\in X\) of (4) (with the same conditions as in (1)), such that

$$ \Vert x-y \Vert _{X}\leq S\epsilon ,\quad t\in I. $$

Definition 4

The problem (1) is generalized Ulam–Hyers stable, if there exists an increasing function \(Z\in C(\mathbb{R}^{+},\mathbb{R}^{+})\), \(Z(0)=0\), such that, for all \(\epsilon >0\), and for each solution \(x\in X\) of (5), there exists a solution \(y\in X\) of (4) (with the same conditions as in (1)), such that

$$ \Vert x-y \Vert _{X}\leq Z(\epsilon ),\quad t\in I. $$

Definition 5

The problem (1) is Ulam–Hyers–Rassias stable, if there exists a function \(T\in C(\mathbb{I},\mathbb{R}^{+})\) and \(\sigma >0\), such that for each \(\epsilon >0\) and for all solutions \(x\in X\) of (6) there exists a solution \(y\in X\) of (4) (with the same conditions as in (1)), such that

$$ \bigl\vert x ( t ) -y ( t ) \bigr\vert \leq \sigma \epsilon T ( t ) ,\quad t \in I. $$

Definition 6

The problem (1) is generalized Ulam–Hyers–Rassias stable, if there exists a function \(T\in C(\mathbb{I},\mathbb{R}^{+})\) and \(\sigma >0\), such that for all solutions \(x\in X\) of (7) there exists a solution \(y\in X\) of (4) (with the same conditions as in (1)), such that

$$ \bigl\vert x ( t ) -y ( t ) \bigr\vert \leq \sigma T ( t ) ,\quad t\in I. $$

Now, we are ready to prove the following result.

Theorem 7

Assume that (H1) is fulfilled and \(N=\max (N_{1},N_{2},N_{3})<1\). Then the problem (1) is Ulam–Hyers stable in X.

Proof

Let us note

$$\begin{aligned}& O = \biggl\vert \int _{0}^{t}\frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}+ \bigl[ K_{1}t^{\beta }+K_{2}t+K_{3} \bigr] \int _{0}^{1}\frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \\& \hphantom{O ={}}{}\times\biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}+ \bigl[ K_{4}t^{\beta }+K_{5}t-K_{6} \bigr] \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )} \int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \\& \hphantom{O ={}}{}\times\biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}- [ K_{7} ] \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )} \int _{0}^{s} \frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}- \int _{0}^{t}\frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}- \bigl[ K_{1}t^{\beta }+K_{2}t+K_{3} \bigr] \int _{0}^{1}\frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}- \bigl[ K_{4}t^{\beta }+K_{5}t-K_{6} \bigr] \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )} \int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \\& \hphantom{O ={}}{}\times\biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\& \hphantom{O ={}}{}+ [ K_{7} ] \times \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )} \int _{0}^{s} \frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\& \hphantom{O ={}}{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \biggr\vert , \\& \begin{aligned} M_{1} ={} & \biggl\vert x(t)- \int _{0}^{t}\frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\ &{}- \bigl[ K_{1}t^{\beta }+K_{2}t+K_{3} \bigr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\ &{}- \bigl[ K_{4}t^{\beta }+K_{5}t-K_{6} \bigr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )} \int _{0}^{s} \frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \\ &{}+ [ K_{7} ] \\ &{}\times \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,du\,ds \biggr\vert , \end{aligned}\\& \begin{aligned} M_{2} ={} & \biggl\vert D^{\alpha }x(t)- \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )} \biggl[L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \\ &{}- \biggl[ \frac{K_{1}\Gamma (\beta +1)t^{\beta -\alpha }}{\Gamma (\beta -\alpha +1)}+ \frac{K_{2}t^{1-\alpha }}{\Gamma (2-\alpha )} \biggr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \\ &{}- \biggl[ \frac{K_{4}\Gamma (\beta +1)t^{\beta -\alpha }}{\Gamma (\beta -\alpha +1)}+ \frac{K_{5}t^{1-\alpha }}{\Gamma (2-\alpha )} \biggr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \\ &{}+ [ K_{7} ] \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \biggr\vert , \end{aligned}\\ & \begin{aligned} M_{3} ={} & \biggl\vert D^{\gamma }x(t)- \int _{0}^{t} \frac{(t-s)^{\alpha +\beta -\gamma -1}}{\Gamma (\alpha +\beta -\gamma )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr)-a_{2} \\ &{}\times G \bigl(u,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{ \alpha }x(s) \biggr] \,ds \\ &{}- \biggl[ \frac{K_{1}\Gamma (\beta +1)t^{\beta -\gamma }}{\Gamma (\beta -\gamma +1)}+ \frac{K_{2}t^{1-\gamma }}{\Gamma (2-\gamma )} \biggr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\alpha +\beta -\gamma -2}}{\Gamma (\alpha +\beta -\gamma -1)} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \\ &{}- \biggl[ \frac{K_{4}\Gamma (\beta +1)t^{\beta -\gamma }}{\Gamma (\beta -\gamma +1)}+ \frac{K_{5}t^{1-\gamma }}{\Gamma (2-\gamma )} \biggr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\alpha +\beta -2\gamma -1}}{\Gamma (\alpha +\beta -2\gamma )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \\ &{}+ [ K_{7} ] \int _{0}^{t} \frac{(t-s)^{\alpha +\beta -\gamma -1}}{\Gamma (\alpha +\beta -\gamma )} \biggl[ L(s)-a_{1}F \bigl(s,x(s),D^{\gamma }x(s),J^{p}x(s) \bigr) \\ &{}-a_{2}G \bigl(s,x(s),D^{\gamma }x(s) \bigr)-a_{3}H \bigl(s,x(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }x(s) \biggr] \,ds \biggr\vert . \end{aligned} \end{aligned}$$

Let now \(x\in X\) be a solution of (5). Then, by integrating (5), we obtain

$$ M_{1} \leq \frac{\epsilon t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}. $$

Thanks to Theorem 2, the unique solution of (1) is given by

$$\begin{aligned} y(t) =& \int _{0}^{t}\frac{(t-s)^{\beta -1}}{\Gamma (\beta )}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\ &{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\ &{}+ \bigl[ K_{1}t^{\beta }+K_{2}t+K_{3} \bigr] \\ &{}\times \int _{0}^{1}\frac{(1-s)^{\beta -2}}{\Gamma (\beta -1)}\int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\ &{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\ &{}+ \bigl[ K_{4}t^{\beta }+K_{5}t-K_{6} \bigr] \\ &{}\times \int _{0}^{1} \frac{(1-s)^{\beta -\gamma -1}}{\Gamma (\beta -\gamma )} \int _{0}^{s}\frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\ &{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds \\ &{}- [ K_{7} ] \times \int _{0}^{t} \frac{(t-s)^{\beta -1}}{\Gamma (\beta )} \int _{0}^{s} \frac{(s-u)^{\alpha -1}}{\Gamma (\alpha )} \biggl[ L(s)-a_{1}F \bigl(s,y(s),D^{\gamma }y(s),J^{p}y(s) \bigr) \\ &{}-a_{2}G \bigl(s,y(s),D^{\gamma }y(s) \bigr)-a_{3}H \bigl(s,y(s) \bigr)- \frac{k}{s^{\lambda }}D^{\alpha }y(s) \biggr] \,du\,ds. \end{aligned}$$

Then, from all \(t\in I\), we get

$$\begin{aligned} \bigl\vert x(t)-y(t) \bigr\vert \leq &\frac{\epsilon t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}+ O. \end{aligned}$$

This implies that

$$ \Vert x-y \Vert _{\infty }\leq \frac{\epsilon }{\Gamma (\alpha +\beta +1)}+N_{1} \Vert x-y \Vert _{X}. $$
(8)

By integrating and differentiating (5), we get

$$ M_{2} \leq \frac{\epsilon t^{\beta }}{\Gamma (\beta +1)}. $$

Similarly, we show that

$$ \bigl\Vert D^{\alpha }x-D^{\alpha }y \bigr\Vert _{\infty }\leq \frac{\epsilon }{\Gamma (\beta +1)}+N_{2} \Vert x-y \Vert _{X}. $$
(9)

On the other hand, we have

$$ M_{3} \leq \frac{\epsilon t^{\alpha +\beta -\gamma }}{\Gamma (\alpha +\beta -\gamma +1)}. $$

Also, we have

$$ \bigl\Vert D^{\gamma }x-D^{\gamma }y \bigr\Vert _{\infty }\leq \frac{\epsilon }{\Gamma (\alpha +\beta -\gamma +1)}+N_{3} \Vert x-y \Vert _{X}. $$
(10)

Using the inequalities (8), (9) and (10), we get

$$ \Vert x-y \Vert _{X}\leq \max \biggl( \frac{\epsilon }{\Gamma (\alpha +\beta +1)}, \frac{\epsilon }{\Gamma (\beta +1)}, \frac{\epsilon }{\Gamma (\alpha +\beta -\gamma +1)} \biggr) +N \Vert x-y \Vert _{X}. $$

Thus,

$$ \Vert x-y \Vert _{X}\leq S \epsilon , $$

such that

$$ S= \frac{\max ( \frac{1}{\Gamma (\alpha +\beta +1)},\frac{1}{\Gamma (\beta +1)},\frac{1}{\Gamma (\alpha +\beta -\gamma +1)} ) }{1-N} > 0. $$

Consequently, the problem (1) shows the Ulam–Hyers stability. □

Taking \(Z(\epsilon )=S\epsilon \), we can state that the problem (1) is generalized Ulam–Hyers stable.

In the following, we introduce the following hypothesis to study Rassias stability.

  1. (H2):

    \(T\in C(\mathbb{I},\mathbb{R}^{+})\) is continuous, nondecreasing function, and there exists \(\lambda _{T,\alpha }>0\) such that \(J^{\alpha }T ( t ) \leq \lambda _{T,\alpha }T ( t ) \) for each \(t\in I\).

We present the following result.

Theorem 8

Assume that (H1)–(H2) are satisfied and \(N:=\max (N_{1},N_{2},N_{3})<1\).

Then the problem (1) is Ulam–Hyers–Rassias stable in X.

Proof

Let \(x\in X\) be a solution of (6). Then, by integrating (6), we obtain

$$ M_{1} \leq \epsilon J^{\beta }J^{\alpha }T ( t ). $$

Let y be the unique solution of the problem (1). Then, for each \(t\in I\), we have

$$ \bigl\vert x(t)-y(t) \bigr\vert \leq \epsilon J^{\beta }J^{\alpha }T ( t ) + O. $$

In view of (H2), we have

$$\begin{aligned}& \bigl\vert x(t)-y(t) \bigr\vert \leq \epsilon J^{\beta }J^{\alpha }T ( t ) +N_{1} \Vert x-y \Vert _{X}\leq \epsilon \lambda _{T,\beta +\alpha }T ( t ) +N_{1} \Vert x-y \Vert _{X}, \\& \quad \text{which implies that } \bigl\vert x(t)-y(t) \bigr\vert \leq \epsilon \lambda _{T,\beta +\alpha }T ( t ) +N_{1} \Vert x-y \Vert _{X}. \end{aligned}$$
(11)

On the other hand, by integrating and differentiating (6), we get

$$ M_{2} \leq \epsilon J^{\beta }T ( t ) . $$

Also, we can show that

$$ \bigl\vert D^{\alpha }x-D^{\alpha }y \bigr\vert \leq \epsilon \lambda _{T,\beta }T ( t ) +N_{2} \Vert x-y \Vert _{X} . $$
(12)

We have also

$$ M_{3} \leq \epsilon J^{\alpha +\beta -\gamma }T ( t ). $$

By the same arguments as before, we observe that

$$ \bigl\vert D^{\gamma }x ( t ) -D^{\gamma }y ( t ) \bigr\vert \leq \epsilon \lambda _{T,\alpha +\beta - \gamma }T ( t ) +N_{3} \Vert x-y \Vert _{X} . $$
(13)

Using the inequalities (11), (12) and (13) yields

$$ \textstyle\begin{cases} \vert x(t)-y(t) \vert \leq \epsilon \max ( \lambda _{T,\alpha +\beta }, \lambda _{T,\beta },\lambda _{T,\alpha +\beta -\gamma } ) T ( t ) +N_{1} \Vert x-y \Vert _{X},& t\in I, \\ \vert D^{\alpha }x ( t ) -D^{\alpha }y ( t ) \vert \leq \epsilon \max ( \lambda _{T,\alpha + \beta },\lambda _{T,\beta },\lambda _{T,\alpha +\beta -\gamma } ) T ( t ) +N_{2} \Vert x-y \Vert _{X},& t\in I, \\ \vert D^{\gamma }x ( t ) -D^{\gamma }y ( t ) \vert \leq \epsilon \max ( \lambda _{T,\alpha + \beta },\lambda _{T,\beta },\lambda _{T,\alpha +\beta -\gamma } ) T ( t ) +N_{3} \Vert x-y \Vert _{X},& t\in I. \end{cases}$$

Hence, it follows that there exists a real number

$$ \sigma = \frac{\max ( \lambda _{T,\alpha +\beta },\lambda _{T,\beta },\lambda _{T,\alpha +\beta -\gamma } )}{1-N}, $$

such that

$$ \Vert x-y \Vert _{X}\leq \sigma \epsilon T ( t ),\quad t\in I. $$

Consequently, the problem (1) shows the Ulam–Hyers–Rassias stability. □

4 Numerical simulations

In this section, we recall a numerical approach for the Caputo derivative. Then, for some fixed parameters, we investigate behavior of the above fractional Lane–Emden problem. To do this, we shall first obtain a reduced fractional differential system that is equivalent to our studied problem. Using a fourth-order Runge–Kutta integrator, the numerical simulations recover the convective behavior of the integer model in astrophysics [4]. In order to ensure the effect of the fractional order in Lane–Emden dynamics, we consider judicious values for α and β.

  • Hydrodynamic simulations of giant stars, where the stellar profiles can be modeled in [12, 22, 28] as

    $$ \frac{1}{t}\frac{d}{d t} \biggl(t^{2} \frac{dy}{d t} + t^{2} \frac{g_{c}(a t)}{4 a \pi G p_{0} } \biggr)+ y^{n}=0 , $$

    where y is the polytropic temperature with index n, \(t\equiv \frac{r}{a} \), and \(p_{0}\) the central gas density. For \(r \leq \frac{h}{2}\) and \(x \equiv \frac{r}{h}\), the smoothed gravitational force of the core is defined by

    $$ g_{c}(r):= G m_{c} \frac{x (\frac{32}{3}+x^{2} (\frac{-192}{5}+32x ) )}{h^{2}} . $$

  • Self-similar profiles of nonlinear wave equations in flat space-time were modeled in [4, 17] as

    $$ \bigl(1-t^{2} \bigr)\frac{d^{2}y}{d t^{2}}+ \biggl( \frac{A}{t}+ B t \biggr) \frac{dy}{d t} - C y + D y^{E} =0 . $$

4.1 Numerical approach for Caputo derivative

In this subsection, we presented an important numerical approach for the Riemann–Liouville fractional integral and the Caputo derivative; we recall the theorems of [6, 19].

Theorem 9

Assume that \(y\in \mathcal{C}^{1}([0,1],\mathbb{R})\). The fractional integration approach is given by

$$ J^{\alpha }y(t_{i})\simeq \frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^{i}y(t_{j}) \sigma _{j}(\alpha ), \quad i=0, \dots ,n+1, $$

where

$$ \sigma _{j}(\alpha )= \textstyle\begin{cases} (n+2-j)^{(\alpha +1)}+(n-j)^{(\alpha +1)}-2(n-j+1)^{(\alpha +1)},& j=1,\dots, i-1, \\ (n)^{(\alpha +1)}-(n-\alpha )(n+1)^{\alpha },& j=0, \textit{and } 1, j=i . \end{cases}$$

Theorem 10

Assume that \(y\in \mathcal{C}^{1}([0,1],\mathbb{R})\) and \(0<\alpha \leq 1\). Then we have

$$ D^{\alpha }y(t_{i})\simeq \frac{h^{1-\alpha }}{\Gamma (1-\alpha +2)}\sum _{j=0}^{i}y^{(j)}(t_{j}) \sigma _{j}(1-\alpha ) ,\quad i=0,\dots ,n, $$

where

$$ y^{(j)}= \textstyle\begin{cases} \frac{y_{1}-y_{0}}{h}, \quad j=0,\qquad \frac{y_{j+1}-y_{j-1}}{2h},\quad j=1,\dots, i-1,\qquad \frac{y_{i}-y_{i-1}}{h},\quad j=i. \end{cases} $$

4.2 Simulation for Lane–Emden behaviors

We note that the problem (1) can be reduced to the following system:

$$\begin{aligned}& D^{\beta }y(t) = z(t), \\& \begin{aligned} D^{\alpha }z(t) ={}& {-}\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr)-a_{3}H \bigl(t,y(t) \bigr)+L(t). \end{aligned} \end{aligned}$$

In order to achieve the mentioned phenomena, we take \(1<\alpha +\beta \leq 2\), and \(\lambda =1\). Taking into account our problem parameters, three cases can be observed:

  1. Case 1:

    \(\alpha =\beta =1\), we get

    $$\begin{aligned}& Dy(t) = z(t), \\& \begin{aligned} Dz(t) ={}& {-}\frac{k}{t^{\lambda }}Dy(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t). \end{aligned} \end{aligned}$$
  2. Case 2:

    \(0<\alpha \leq 1\), \(\beta =1\), we obtain

    $$\begin{aligned}& Dy(t) = z(t), \\& \begin{aligned} D^{\alpha }z(t) ={}& {-}\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t). \end{aligned} \end{aligned}$$

    As a consequence,

    $$\begin{aligned}& Dy(t) = z(t), \\& \begin{aligned} Dz(t) = {}& D^{1-\alpha } \biggl( -\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl( t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t) \biggr). \end{aligned} \end{aligned}$$
  3. Case 3:

    \(0<\alpha \leq 1\), \(1\leq \beta \leq 2\), we have

    $$\begin{aligned}& D^{\beta }y(t) = z(t), \\& \begin{aligned} D^{\alpha }z(t) ={}& {-}\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t), \end{aligned} \end{aligned}$$

    that is,

    $$\begin{aligned}& J^{2-\beta }D \bigl[Dy(t) \bigr] = z(t), \\& \begin{aligned} D^{\alpha }z(t) = {}& {-}\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t). \end{aligned} \end{aligned}$$

    Therefore,

    $$\begin{aligned}& Dy(t) = z(t), \\& J^{2-\beta }D z = w(t), \\& \begin{aligned} D^{\alpha }w(t) ={}& {-}\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t). \end{aligned} \end{aligned}$$

    Consequently,

    $$\begin{aligned}& Dy(t) = z(t), \\& Dz(t) = D^{2-\beta } w(t), \\& \begin{aligned} Dw(t) = {}& D^{1-\alpha } \biggl( -\frac{k}{t^{\lambda }}D^{\alpha }y(t)-a_{1}F \bigl( t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) \\ &{} - a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) -a_{3}H \bigl(t,y(t) \bigr)+L(t) \biggr). \end{aligned} \end{aligned}$$

I: As a first simulation, we consider the hydrodynamic simulations of giant stars, where \(k=2\), \(p =\gamma =0.01\), and f, H, G, H, L are given by

$$\begin{aligned}& a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) = \frac{16a^{4}m_{c}}{\pi p_{0}h^{6}} t^{4}+\frac{289}{51t} \bigl(J^{p}y(t) \bigr)^{n} , \\& a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) = - \frac{48a^{3}m_{c}}{\pi p_{0}h^{5}} t^{3}- \frac{663}{255t} \bigl(D^{\gamma }y(t) \bigr)^{n}, \\& a_{3}H \bigl(t,y(t) \bigr) = \frac{32a^{4}m_{c}}{\pi p_{0}h^{6}} t^{4}-\frac{527}{255t} \bigl(y(t) \bigr)^{n}, \\& L(t) = \frac{8am_{c}}{\pi p_{0}h^{3}} t. \end{aligned}$$

For the first case, with initial conditions \((0,0)\), \(h =0.001\), and \(n =\{ 1, 1.5, 2, 2.5 \}\), the numerical simulations are carried out only by the fourth-order Runge–Kutta method, for specific parameters, we have Fig. 1.

Figure 1
figure 1

Numerical simulation of Case 1 for different values of the polytropic index n and \(\alpha = \beta =1\)

Full size image

Remark 11

Through ongoing evaluation, we observe that the change in value of n has no impact on the attitude of the remaining cases.

For the following simulation we take \(n=1.5\) as it is more adequate. Now, to ensure that all three cases are convenient, we should be looking for a suitable fractional order.

For the second case, with initial conditions \((0,0)\), \(h=0.001\), and \(\alpha =\{0.55,0.35,0.2\}\), numerical simulations are realized by a combination of the Caputo approach and the fourth-order Runge–Kutta method, we acquire Fig. 2. By comparing the above result with the one of the first case, we conclude that both cases are adequate for \(\alpha =0.35\) (see Fig. 3).

Figure 2
figure 2

Numerical simulations of Case 2 for \(\alpha =\{0.55,0.35,0.2\}\) and \(\beta =1\)

Full size image
Figure 3
figure 3

Comparative simulation (Case 1–Case 2)

Full size image

For the third case, with initial conditions \((0,0,0.5)\), \(h=0.001\), \(\beta =\{1.45,1.3,1.05\}\), for any β value, we take \(\alpha =\{0.55,0.35,0.2\}\). Numerical simulations are carried out by a combination of the Caputo approach and the fourth-order Runge–Kutta method, we see, according to Figs. 4–6, that \(\beta =1.3\) is the valid value. It is obvious from Fig. 7 that \(\alpha =0.35\) is the appropriate value.

Figure 4
figure 4

Numerical simulations of Case 3 for \(\beta =1.45\) and \(\alpha =\{0.55,0.35,0.2\}\)

Full size image
Figure 5
figure 5

Numerical simulations of Case 3 for \(\beta =1.3\) and \(\alpha =\{0.55,0.35,0.2\}\)

Full size image
Figure 6
figure 6

Numerical simulations of Case 3 for \(\beta =1.05\) and \(\alpha =\{0.55,0.35,0.2\}\)

Full size image
Figure 7
figure 7

Comparative simulation (Case 1–Case 3)

Full size image

II: As a second simulation, we consider self-similar profiles of nonlinear wave equation in flat space-time, where \(k=A\), \(p =\gamma =0.01\), and f, H, G, H, L are given by

$$\begin{aligned}& a_{1}F \bigl(t,y(t),D^{\gamma }y(t),J^{p}y(t) \bigr) = \frac{C}{1-t^{2}}J^{p}y(t), \\& a_{2}G \bigl(t,y(t),D^{\gamma }y(t) \bigr) = - \frac{B t}{1-t^{2}}D^{\gamma }y(t), \\& a_{3}H \bigl(t,y(t) \bigr) = -\frac{D}{1-t^{2}} \bigl(y(t) \bigr)^{E}, \\& L(t) = 0, \end{aligned}$$

with initial conditions \((0.576037116,0.24090)\), and \(A=2\), \(B=\frac{-25}{12}\), \(C=\frac{1}{4}\), \(D=1\), \(E=2\), \(h=0.01\). The integration for the first case is carried out by the fourth-order Runge–Kutta method, now, we are trying to determine an appropriate fractional order (see Fig. 8).

Figure 8
figure 8

Numerical simulation of Case 1

Full size image

For the second case, we take the same data as above, and \(\alpha =\{0.95,0.9,0.8\}\). Numerical simulations are realized by a combination of the Caputo approach and the fourth-order Runge–Kutta method (see Fig. 9).

Figure 9
figure 9

Numerical simulation of Case 2

Full size image

Comparing our outcome to that in the first case, we summarize that the two cases are consistent in terms of \(\alpha =0.95\) (see Fig. 10).

Figure 10
figure 10

Comparative simulation (Case 1–Case 2)

Full size image

For the third case, with initial conditions \((0.576037116,0.24090,0)\), and \(h=0.01\), \(\beta =\{1.2,1.15,1.05\}\), for each β, we take \(\alpha =\{0.95,0.9,0.8\}\). Numerical simulations are carried out by a combination of the Caputo approach and the fourth-order Runge–Kutta method.

It appeared from Figs. 11–13 that \(\beta =1.2\) and \(\alpha =0.8\) are the most acceptable values too.

Figure 11
figure 11

Numerical simulations of Case 3 for \(\beta =1.2\) and different values of α, on the left side. Comparative simulation (Case 1–Case 3), on the right side

Full size image
Figure 12
figure 12

Numerical simulations of Case 3 for \(\beta =1.15\) and different values of α, on the left side. Comparative simulation (Case 1–Case 3), on the right side

Full size image
Figure 13
figure 13

Numerical simulations of Case 3 for \(\beta =1.05\) and different values of α, on the left side. Comparative simulation (Case 1–Case 3), on the right side

Full size image

5 Conclusions

In this manuscript, we study some types of Ulam stability for a nonlinear fractional differential equation of Lane–Emden type with antiperiodic conditions. Then, by using a numerical approach for the Caputo derivative, we investigate the behaviors of the considered system.