Extinction and persistence of a stochastic SICA epidemic model with standard incidence rate for HIV transmission

Abstract

In this paper, a stochastic SICA epidemic model with standard incidence rate for HIV transmission is proposed. The sufficient conditions of the extinction and persistence in mean for the disease are established. Numerical simulations show that random perturbations can suppress disease outbreaks and the risk of HIV transmission can be reduced by reducing the transmission coefficient of HIV while increasing the strength of the stochastic perturbation.

1 Introduction

To the best of our knowledge, the human immunodeficiency virus (HIV) is a retrovirus that causes HIV infection and, over time, acquired immunodeficiency syndrome (AIDS). There is no cure or vaccine to AIDS. However, antiretroviral (ART) treatment improves health, prolongs life, and substantially reduces the risk of HIV transmission. As more people receive antiretroviral therapy, the number of new HIV infections worldwide is approximately 2.3 million, a 33 per cent decline in new infections compared to 2001. At the same time, the number of AIDS deaths is also declining, with approximately 1.6 million AIDS deaths in 2012, down from 2.3 million in 2005 [1]. This goes to show that access to antiretroviral therapy has a huge impact on HIV prevention. Parvaiz et al. consider a fractional-order HIV epidemic model with the inclusion of prostitution in the population and its consequences on the disease transmission [2]. In [3], the authors consider a nonlinear fractional order epidemic model for HIV transmission and analyze by including an extra compartment, namely the exposed class, to the basic SIR epidemic model. They show through numerical simulations that the control measures effectively increase the quality of life and age limit of the HIV patients. The authors in [4] consider the following model:

$$ \textstyle\begin{cases} {\frac{dS(t)}{dt} =\lambda -\mu {S(t)}-\frac{\beta S(t)I(t)}{N(t)},} \\ {\frac{dI(t)}{dt} = \frac{\beta S(t)I(t)}{N(t)}-(\mu +\gamma +\rho )I(t)+ \alpha {A(t)}+\omega {C(t)},} \\ {\frac{dC(t)}{dt} =\gamma {I(t)}-(\mu +\omega )C(t),} \\ {\frac{dA(t)}{dt} =\rho {I(t)}-(\alpha +\mu +d)A(t),} \end{cases} $$

(1.1)

where the parameters are:

• $N(t)$: The total population at time t;

• $S(t)$: Susceptible individuals at time t;

• $I(t)$: HIV-infected individuals with no clinical symptoms of AIDS at time t;

• $C(t)$: HIV-infected individuals under ART treatment with a viral load remaining low at time t;

• $A(t)$: HIV-infected individuals with AIDS clinical symptoms at time t;

• λ: Recruitment rate;

• μ: Natural death rate;

• β: HIV transmission rate;

• γ: HIV treatment rate for I individuals;

• ρ: Default treatment rate for I individuals;

• α: AIDS treatment rate;

• ω: Default treatment rate for C individuals;

• d: AIDS induced death rate.

They found that when $R_{0}<1$, the disease-free equilibrium of system (1.1) is asymptotically stable; when $R_{0}>1$, the disease-free equilibrium is unstable and there is a globally asymptotically stable endemic equilibrium. Here, $R_{0}= \frac{\beta (\alpha +\mu +d)(\mu +\omega )}{\mu [(\mu +\omega )(\rho +\alpha +\mu +d)+\gamma (\alpha +\mu +d)+\rho d]+\rho \omega d}$ is the basic reproduction number.

The above studies did not consider the effect of white noise in the environment on the model; in fact, infectious diseases are inevitably affected by random white noise in the environment. May [5] finds that because of the fluctuation of the environment, the parameters of the deterministic system, such as the death rate and the transmission coefficient, and other parameters of the deterministic system show a certain degree of random fluctuation. Therefore, the transmission coefficient may be affected by many environmental factors, such as temperature, wind, rain, and snow. In [6], the authors extend the classical SIS epidemic model from a deterministic framework to a stochastic one and formulate it as a stochastic differential equation (SDE) for the number of infectious individuals $I(t)$. They discuss perturbation by stochastic noise. In the case of persistence they show the existence of a stationary distribution and derive expressions for its mean and variance. In [7], the authors present the threshold of a stochastic SIQS epidemic model which determines the extinction and persistence of the disease and find that noise can suppress the disease outbreak. Therefore, when establishing the corresponding mathematical model, we must consider the impact of white noise on the disease. Many scholars have introduced white noise into the infectious disease model [8–12]. In addition, there are a number of other types of stochastic models that have been developed to further explain that stochastic factors are integral to the modeling of infectious diseases, see [13–16].

In this paper, our aim is to introduce random white noise in the environment into the deterministic model and to study the effect of random disturbance on the number of HIV infected people and the conditions between the random disturbance and the parameters of the model, and if the number of HIV infected people can be controlled. Motivated by [6], we consider here random white noise in the environment, which is assumed to demonstrate itself as fluctuations in the parameter β, so that $\beta \rightarrow \beta +\sigma \,dB(t)$, where $B(t)$ is a standard Brownian motion with intensity $\sigma ^{2}>0$. Hence, we can derive the following stochastic model:

$$ \textstyle\begin{cases} {dS(t)=[\lambda -\mu {S(t)}-\frac{\beta S(t)I(t)}{N(t)}]\,dt- \frac{\sigma S(t)I(t)}{N(t)}\,dB(t),} \\ {dI(t)=[ \frac{\beta S(t)I(t)}{N(t)}-(\mu +\gamma +\rho )I(t)+\alpha {A(t)}+ \omega {C(t)}]\,dt+\frac{\sigma S(t)I(t)}{N(t)}\,dB(t),} \\ {dC(t) =[\gamma {I(t)}-(\mu +\omega )C(t)]\,dt,} \\ {dA(t) =[\rho {I(t)}-(\alpha +\mu +d)A(t)]\,dt.} \end{cases} $$

(1.2)

This paper is organized as follows. In Sect. 2, we prove that there is a unique global positive solution for system (1.2). In Sect. 3, we show that the disease goes to extinction exponentially under certain conditions and the persistence of the disease, that is to say, the disease will prevail. In Sect. 4, we carry out the numerical simulations to demonstrate the analytical results. In Sect. 5, we give some conclusions.

Throughout this paper, we let $(\Omega , \mathcal{F}, \{\mathcal{F}\}_{t\geq 0}, \mathbb{P})$ be a complete probability space with filtration $\{\mathcal{F}\}_{t\geq 0}$ satisfying the usual conditions (that is to say, it is increasing and right continuous while $\mathcal{F}_{0}$ contains all $\mathbb{P}$-null sets). On the other hand, we define $\mathbb{R}_{+}^{d}=\{x\in \mathbb{R}^{d}|x_{i}>0\mbox{ for all }1\leq i\leq d\}$.

Generally speaking, consider the d-dimensional stochastic differential equation

$$ dx(t) = f\bigl(x(t), t\bigr)\,dt + g\bigl(x(t), t\bigr) \,dB_{t}, $$

(1.3)

where $f(t,x(t))$ is a function in $\mathbb{R}^{d}$ defined in $[t_{0},\infty ]\times \mathbb{R}^{d}$, and $g(x(t), t)$ is a $d\times {m}$ matrix, f, g are locally Lipschitz functions in x. $B_{t}$ denotes an m-dimensional standard Brownian motion defined on the complete probability space $(\Omega ,\mathcal{F},\{\mathcal{F}\}_{t\geq 0},\mathbb{P})$. Denote by $C^{2,1}(\mathbb{R}^{d}\times [t_{0},\infty ];\mathbb{R}_{+})$ the family of all nonnegative functions $V (x(t), t)$ defined on $\mathbb{R}^{d}\times [t_{0},\infty ]$ such that they are continuously twice differentiable in x and once in t. We define the differential operator L of equation (1.3) by [17]

$$ L=\frac{\partial }{\partial {t}}+\sum_{i=1}^{d}f_{i}(x,t) \frac{\partial }{\partial {x_{i}}}+\frac{1}{2}\sum_{i,j=1}^{d} \bigl[g^{T}(x,t)g(x,t)\bigr]_{ij} \frac{\partial ^{2}}{\partial {x_{i}}\partial {x_{j}}}. $$

If L acts on a function $V\in {C^{2,1}(\mathbb{R}^{d}\times [t_{0},\infty ],\mathbb{R}_{+})}$, then

$$ LV(x,t)=V_{t}(x,t)+V_{x}(x,t)f(x,t)+ \frac{1}{2}\operatorname{trace}\bigl[g^{T}(x,t)V_{xx}(x,t)g(x,t) \bigr], $$

where $V_{t}(x,t)=\frac{\partial {V}}{\partial {t}}$, $V_{x}(x,t)=( \frac{\partial {V}}{\partial {x_{i}}},\ldots, \frac{\partial {V}}{\partial {x_{d}}})$, $V_{xx}(x,t)=( \frac{\partial ^{2}{V}}{\partial {x_{i}}\partial {x_{j}}})_{d\times {d}}$.

From Itô’s formula, if $x(t)\in \mathbb{R}^{d}$, then

$$ dV(x,t)=LV(x,t)\,dt+V_{x}(x,t)g(x,t)\,dB_{t}. $$

2 Existence and uniqueness of positive solution

Theorem 2.1

There is a unique solution $(S (t ),I (t ),C (t ),A (t ) )$ of system (1.2) on $t\geq 0$ for any initial value $(S(0),I(0),C(0),A(0))\in \mathbb{R}_{+}^{4}$, and the solution will remain in $\mathbb{R}_{+}^{4}$ with probability one, namely $(S (t ),I (t ),C (t ),A (t ) ) \in \mathbb{R}_{+}^{4}$ for all $t\geq 0$ almost surely. Moreover,

$$ \begin{aligned} \frac{\lambda }{(\mu +d)}< \lim_{t\rightarrow \infty }N(t)= \frac{\lambda }{\mu }, \end{aligned} $$

(2.1)

where $N(t)=S (t )+I (t )+C (t )+A (t )$.

Proof

We can easily know that the coefficients of system (1.2) are locally Lipschitz continuous, then for any given initial value $(S(0),I(0),C(0),A(0))\in \mathbb{R}_{+}^{4}$, there is a unique local solution $(S(t),I(t),C(t),A(t))$ on $t\in [0,\tau _{e})$, where $\tau _{e}$ is the explosion time (see [17]). To show that this solution is global, we only need to prove that $\tau _{e}=\infty$ almost surely. Let $k_{0}\geq 0$ be sufficiently large so that $(S(0),I(0),C(0),A(0))$ all lie within the interval $[\frac{1}{k_{0}},k_{0}]$. For each integer $k\geq {k_{0}}$, define the following stopping time:

$$ \begin{aligned} \tau _{k}={}&\inf \biggl\{ t\in [0,\tau _{e}): \min \bigl\{ \bigl(S (t ),I (t ),C (t ),A (t ) \bigr) \bigr\} \leq \frac{1}{k} \\ &{} \mbox{or } \max \bigl\{ \bigl(S (t ),I (t ),C (t ),A (t ) \bigr)\bigr\} \geq {k}\biggr\} , \end{aligned} $$

where throughout this paper, we set $\inf \emptyset =\infty$ (as usual ∅ denotes the empty set). According to the definition of the stopping time, $\tau _{k}$ is increasing as $k\rightarrow \infty$. Set $\tau _{\infty }{=}\lim_{k\rightarrow \infty }\tau _{k}$, whence $\tau _{\infty }\leq \tau _{e}$ almost surely. Namely, we need to show that $\tau _{\infty }{=}\infty$ almost surely. We assumed that there exists a pair of constants $T>0$ and $\epsilon \in (0,1 )$ such that

$$ P\{\tau _{\infty }\leq {T}\}>\epsilon . $$

As a result, there is an integer $k_{1}\geq {k_{0}}$ such that

$$ \begin{aligned} P\{\tau _{k}\leq {T}\}>\epsilon \quad \mbox{for all } k\geq {k_{1}}. \end{aligned} $$

(2.2)

Now define a $C^{2}$-function $V:\mathbb{R}_{+}^{4}\rightarrow \mathbb{R}_{+}$ by

$$ V(t)=\bigl(S(t)-1-\ln S(t)\bigr)+ \bigl(I(t)-1-\ln I(t)\bigr)+\bigl(C(t)-1-\ln C(t)\bigr)+\bigl(A(t)-1- \ln A(t)\bigr). $$

Applying Itô’s formula, we obtain

$$ \begin{aligned} dV(t)=LV(t)\,dt- \biggl[\frac{\sigma (S(t)-1)I(t)}{N(t)}- \frac{\sigma (I(t)-1)S(t)}{N(t)} \biggr]\,dB(t), \end{aligned} $$

where

$$\begin{aligned} LV(t)={}& \biggl(1-\frac{1}{S(t)} \biggr) \biggl(\lambda -\mu {S(t)}- \frac{\beta S(t)I(t)}{N(t)} \biggr)+\frac{1}{2S^{2}(t)} \frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{N^{2}(t)} \\ &{}+ \biggl(1-\frac{1}{I(t)} \biggr) \biggl(\frac{\beta S(t)I(t)}{N(t)}-( \mu + \gamma +\rho )I(t)+\alpha {A(t)}+\omega {C(t)} \biggr) \\ &{}+\frac{1}{2I^{2}(t)}\frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{N^{2}(t)}+ \biggl(1-\frac{1}{C(t)} \biggr)\bigl[\gamma {I(t)}-(\mu +\omega )C(t)\bigr] \\ &{}+ \biggl(1-\frac{1}{A(t)} \biggr)\bigl[\rho {I(t)}-(\alpha +\mu +d)A(t)\bigr] \\ ={}&\lambda +4\mu +\gamma +\rho +\alpha +\omega +d+ \frac{\beta I(t)}{N(t)}+ \frac{\sigma ^{2}I^{2}(t)}{2N^{2}(t)}+ \frac{{\sigma ^{2}S^{2}(t)}}{2N^{2}(t)}-\mu {N(t)}-dA(t) \\ &{}-\frac{\lambda }{S(t)}-\frac{\beta S(t)}{N(t)}- \frac{\alpha {A(t)}+\omega {C(t)}}{I(t)}- \frac{\gamma {I(t)}}{C(t)}- \frac{\rho {I(t)}}{A(t)} \\ \leq{} &\lambda +4\mu +\gamma +\rho +\alpha +\omega +d+\beta +\sigma ^{2} \doteq K. \end{aligned}$$

Thus

$$ dV(t)=K\,dt- \biggl[\frac{\sigma (S(t)-1)I(t)}{N(t)}- \frac{\sigma (I(t)-1)S(t)}{N(t)} \biggr]\,dB(t). $$

(2.3)

Integrating both sides of (2.3) from 0 to $T\wedge {\tau _{k}}$ and taking expectations, we can obtain

$$\begin{aligned}& \mathbb{E}V \bigl(S(T\wedge {\tau _{k}}),I(T\wedge {\tau _{k}}),C(T \wedge {\tau _{k}}),A(T\wedge {\tau _{k}}) \bigr) \\& \quad \leq {V \bigl(S (0 ),I (0 ),C (0 ),A (0 ) \bigr)}+KT< \infty . \end{aligned}$$

(2.4)

Set $\Omega _{k}=\{\tau _{k}\leq {t}\}$ for $k\geq {k_{1}}$ by (2.2), $P (\Omega _{k} )\geq \epsilon$. Notice that, for every $\omega \in \Omega _{k}$, there is at least one of $(S (\tau _{k},\omega ),I (\tau _{k},\omega ),C (\tau _{k},\omega ),A (\tau _{k},\omega ) )$ that equals to k or $\frac{1}{k}$. Consequently,

$$ V \bigl(S(\tau _{k},\omega ),I(\tau _{k}, \omega ),C(\tau _{k},\omega ),A( \tau _{k},\omega ) \bigr)\geq {(k-1-\log {k})}\wedge \biggl(\frac{1}{k}-1+ \log {k}\biggr), $$

(2.5)

where $a\wedge {b}$ denotes the minimum of a and b. In view of (2.4) and (2.5), we have

$$\begin{aligned} V \bigl(S (0 ),I (0 ),C (0 ),A (0 ) \bigr)+KT&\geq {\mathbb{E}} \bigl[1_{\Omega _{k}}V \bigl(S(\tau _{k}, \omega ),I(\tau _{k},\omega ),C(\tau _{k},\omega ),A(\tau _{k}, \omega ) \bigr)\bigr] \\ &\geq \epsilon \biggl[(k-1-\log {k})\wedge \biggl(\frac{1}{k}-1+\log {k}\biggr)\biggr], \end{aligned}$$

where $1_{\Omega _{k}}$ is the indicator function of $\Omega _{k}$. Let $k\rightarrow \infty$ lead to the contradiction

$$ \infty >V \bigl(S (0 ),I (0 ),C (0 ),A (0 ) \bigr)+KT=\infty . $$

Therefore, we must have $\tau _{\infty }=\infty$ almost surely.

In view of system (1.2), we have

$$ \begin{aligned} \frac{dN(t)}{dt}=\lambda -\mu N (t )-dA(t). \end{aligned} $$

Solving this equation, we obtain that

$$ N(t)=\frac{\lambda }{\mu }+ \biggl(N(0)-\frac{\lambda }{\mu } \biggr)e^{- \mu t}-d \int _{0}^{t}A(s)e^{-\mu (t-s)}\,ds, $$

which implies that

$$ \lim_{t\rightarrow \infty }N(t)=\frac{\lambda }{\mu } \quad \mbox{almost surely}. $$

On the other hand, we have

$$ \frac{dN(t)}{dt}>\lambda -(\mu +d) N(t). $$

Then we can obtain

$$ N(t)>\frac{\lambda }{\mu +d}+e^{-(\mu +d)t} \biggl(N (0 )- \frac{\lambda }{\mu +d} \biggr), $$

which implies that

$$ \lim_{t\rightarrow \infty }N(t)>\frac{\lambda }{\mu +d} \quad \mbox{almost surely}. $$

The proof of Theorem 2.1 is complete. □

3 Extinction and persistence in mean

In this section, we discuss under what conditions the disease will be extinct and the persistence of the disease, namely, under what condition the disease will prevail. For convenience, firstly, we define $\langle X(t)\rangle =\frac{1}{t}\int _{0}^{t}X(s)\,ds$.

Theorem 3.1

If $R_{1}<1$ or $\sigma ^{2}\leq \beta$ and $R_{2}<1$ hold, then the disease $I(t)$ will die out exponentially with probability one, that is,

$$ I(t),C(t),A(t)\rightarrow 0 \quad \textit{as } t\rightarrow +\infty \quad \textit{and}\quad S(t) \rightarrow \frac{\lambda }{\mu } \quad \textit{as } t \rightarrow +\infty , $$

where

$$ R_{1}=\frac{\beta ^{2}}{2\sigma ^{2}\mu }, \qquad R_{2}= \frac{\beta }{(\mu +\frac{\sigma ^{2}}{2})}. $$

Proof

Let $Q(t)=I(t)+C(t)+A(t)$. Making use of Itô’s formula, we can have

$$\begin{aligned} d\ln Q(t)={}&\frac{1}{I(t)+C(t)+A(t)} \biggl[ \frac{\beta S(t)I(t)}{N(t)}-\mu I(t)-\mu C(t)-(\mu +d)A(t) \biggr]\,dt \\ &{}-\frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{2N^{2}(I(t)+C(t)+A(t))^{2}}\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ \leq {}& \biggl[ \frac{\beta S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}-\mu - \frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{2N^{2}(t)(I(t)+C(t)+A(t))^{2}} \biggr]\,dt \\ \begin{aligned} &{}+\frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ ={}& \biggl[- \biggl(\frac{\sigma S(t)I(t)}{\sqrt{2}N(t)(I(t)+C(t)+A(t))}- \frac{\beta \sqrt{2}}{2\sigma } \biggr)^{2}+ \frac{\beta ^{2}}{2\sigma ^{2}}-\mu \biggr]\,dt \end{aligned} \\ &{}+\frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ \leq {}& \biggl[\frac{\beta ^{2}}{2\sigma ^{2}}-\mu \biggr]\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))} \,dB(t) \\ ={}& \bigl[\mu (R_{1}-1) \bigr]\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t). \end{aligned}$$

(3.1)

Integrating on both sides of equation (3.1) from 0 to t, and then dividing by t, we can obtain

$$ \begin{aligned} \frac{\ln Q(t)}{t}\leq &\frac{\ln Q(0)}{t}+\mu (R_{1}-1)+ \frac{M(t)}{t}, \end{aligned} $$

(3.2)

where

$$ M(t)= \int _{0}^{t}\frac{\sigma S(s)I(s)}{N(s)(I(s)+C(s)+A(s))}\,dB(s). $$

By the large number theorem for martingale (see [17]), we can get

$$ \begin{aligned} \lim_{t\rightarrow +\infty }\frac{M(t)}{t}=0, \quad \mbox{almost surely}. \end{aligned} $$

(3.3)

In the light of (3.2) and (3.3), if $R_{1}<1$, then

$$ \begin{aligned} \limsup_{t\rightarrow +\infty } \frac{\ln Q(t)}{t}\leq \mu (R_{1}-1)< 0, \quad \mbox{almost surely}, \end{aligned} $$

which implies that

$$ \lim_{t\rightarrow +\infty }I(t)=0,\qquad \lim_{t\rightarrow +\infty }C(t)=0, \qquad \lim_{t\rightarrow +\infty }A(t)=0, \quad \mbox{almost surely}. $$

On the other hand, we consider the function $f(x)=\beta x -\frac{\sigma ^{2}x^{2}}{2}$, where $x\in (0,1]$. One can obtain that if $\frac{\sigma }{\sqrt{2}}\leq \frac{\beta \sqrt{2}}{2\sigma }$, that is, $\sigma ^{2}\leq \beta$, $f(x)$ has the max value $f(1)=\beta -\frac{\sigma ^{2}}{2}$. Let $x= \frac{ S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}$, we have

$$ f(x)=- \biggl(\frac{\sigma S(t)I(t)}{\sqrt{2}N(t)(I(t)+C(t)+A(t))}- \frac{\beta \sqrt{2}}{2\sigma } \biggr)^{2}+ \frac{\beta ^{2}}{2\sigma ^{2}}\leq \beta -\frac{\sigma ^{2}}{2}. $$

Therefore,

$$\begin{aligned} d\ln Q(t)={}&\frac{1}{I(t)+C(t)+A(t)} \biggl[ \frac{\beta S(t)I(t)}{N(t)}-\mu I(t)-\mu C(t)-(\mu +d)A(t) \biggr]\,dt \\ &{}-\frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{2N^{2}(I(t)+C(t)+A(t))^{2}}\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ \leq{} & \biggl[ \frac{\beta S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}-\mu - \frac{\sigma ^{2}S^{2}(t)I^{2}(t)}{2N^{2}(t)(I(t)+C(t)+A(t))^{2}} \biggr]\,dt \\ \begin{aligned} &{}+\frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ ={}& \biggl[- \biggl(\frac{\sigma S(t)I(t)}{\sqrt{2}N(t)(I(t)+C(t)+A(t))}- \frac{\beta \sqrt{2}}{2\sigma } \biggr)^{2}+ \frac{\beta ^{2}}{2\sigma ^{2}}-\mu \biggr]\,dt \end{aligned} \\ &{}+\frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ \leq {}& \biggl[\beta -\frac{\sigma ^{2}}{2}-\mu \biggr]\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t) \\ ={}& \biggl[ \biggl(\mu +\frac{\sigma ^{2}}{2} \biggr) (R_{2}-1) \biggr]\,dt+ \frac{\sigma S(t)I(t)}{N(t)(I(t)+C(t)+A(t))}\,dB(t). \end{aligned}$$

(3.4)

Hence, if $R_{2}<1$, we obtain

$$ \begin{aligned} \limsup_{t\rightarrow +\infty } \frac{\ln Q(t)}{t}\leq \biggl(\mu + \frac{\sigma ^{2}}{2}\biggr) (R_{2}-1)< 0, \quad \mbox{almost surely}, \end{aligned} $$

which implies that

$$ \lim_{t\rightarrow +\infty }I(t)=0,\qquad \lim_{t\rightarrow +\infty }C(t)=0, \qquad \lim_{t\rightarrow +\infty }A(t)=0 \quad \mbox{almost surely}. $$

Based on the above analysis, in view of (2.1), if $R_{1}<1$ or $\sigma ^{2}\leq \beta$ and $R_{2}<1$, we have

$$ \lim_{t\rightarrow +\infty }S(t)=\frac{\lambda }{\mu } \quad \mbox{almost surely}. $$

The proof is completed. □

Theorem 3.2

For any initial value $(S(0),I(0),C(0),A(0))\in \mathbb{R}_{+}^{4}$, if $R_{3}>1$, the disease is persistence in mean. Furthermore,

$$\begin{aligned} \liminf_{t\rightarrow +\infty }\bigl\langle I(t)\bigr\rangle \geq{} & \frac{\lambda (\omega +\mu )(\alpha +\mu +d)(\mu +\gamma +\rho +\frac{\sigma ^{2}}{2})}{\beta (\mu +d) [(\omega +\mu )(\alpha +\mu +d+\rho )+\gamma (\alpha +\mu +d) ]} (R_{3}-1 ) \\ >{}&0 \quad \textit{almost surely}, \end{aligned}$$

where

$$ R_{3}=\frac{\beta }{\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}}. $$

Proof

Integrating system (1.2) from 0 to t, we can obtain

$$\begin{aligned} &\frac{S(t)-S(0)}{t}+\frac{I(t)-I(0)}{t}+ \frac{\alpha }{\mu +\alpha +d} \frac{A(t)-A(0)}{t}+ \frac{\omega }{\omega +\mu }\frac{C(t)-C(0)}{t} \\ &\quad =\lambda -\mu \bigl\langle S(t) \bigr\rangle + \biggl[ \frac{\alpha \rho }{\mu +\alpha +d}+\frac{\omega \gamma }{\omega +\mu }-( \mu +\gamma +\rho ) \biggr]\bigl\langle I(t) \bigr\rangle . \end{aligned}$$

Then

$$ \begin{aligned} \bigl\langle S(t) \bigr\rangle =\frac{\lambda }{\mu }+ \frac{1}{\mu } \biggl[ \frac{\alpha \rho }{\mu +\alpha +d}+\frac{\omega \gamma }{\omega +\mu }-( \mu + \gamma +\rho ) \biggr]\bigl\langle I(t) \bigr\rangle -\frac{H(t)}{\mu }, \end{aligned} $$

(3.5)

where

$$ H(t)=\frac{S(t)-S(0)}{t}+\frac{I(t)-I(0)}{t}+ \frac{\alpha }{\mu +\alpha +d} \frac{A(t)-A(0)}{t}+ \frac{\omega }{\omega +\mu }\frac{C(t)-C(0)}{t}. $$

In addition,

$$ \begin{aligned} \frac{C(t)-C(0)}{t}=\gamma \bigl\langle I(t) \bigr\rangle -(\omega +\mu ) \bigl\langle C(t) \bigr\rangle , \end{aligned} $$

then

$$ \begin{aligned} \bigl\langle C(t) \bigr\rangle =- \frac{C(t)-C(0)}{(\omega +\mu )t}+ \frac{\gamma }{\omega +\mu }\bigl\langle I(t)\bigr\rangle . \end{aligned} $$

(3.6)

Furthermore,

$$ \begin{aligned} \frac{A(t)-A(0)}{t}=\rho \bigl\langle I(t) \bigr\rangle -(\alpha +\mu +d) \bigl\langle A(t) \bigr\rangle , \end{aligned} $$

then

$$ \begin{aligned} \bigl\langle A(t) \bigr\rangle =- \frac{A(t)-A(0)}{(\alpha +\mu +d)t}+ \frac{\rho }{\alpha +\mu +d}\bigl\langle I(t)\bigr\rangle . \end{aligned} $$

(3.7)

Define

$$ V(t)=-\ln I(t)+e, $$

where e is a constant. $e=-\min \{-\ln I(t)\}$ to keep the nonnegativity of $V(t)$. Applying Itô’s formula, we obtain

$$ \begin{aligned} d\bigl(V(t)\bigr)={}&-\frac{1}{I(t)} \biggl[ \frac{\beta S(t)I(t)}{N(t)}-(\mu + \gamma +\rho )I(t)+\alpha {A(t)}+\omega {C(t)} \biggr]\,dt \\ &{}-\frac{\sigma S(t)}{N(t)}\,dB(t)+\frac{\sigma ^{2}S^{2}(t)}{2N^{2}(t)}\,dt \\ ={}& \biggl[ -\frac{\beta S(t)}{N(t)}+(\mu +\gamma +\rho )- \frac{\alpha {A(t)}+\omega {C(t)}}{I(t)}+ \frac{\sigma ^{2}S^{2}(t)}{2N^{2}(t)} \biggr]\,dt- \frac{\sigma S(t)}{N(t)}\,dB(t) \\ \leq {}& \biggl[ -\frac{\beta (N(t)-I(t)-C(t)-A(t))}{N(t)}+\mu +\gamma + \rho + \frac{\sigma ^{2}}{2} \biggr]\,dt-\frac{\sigma S(t)}{N(t)}\,dB(t) \\ ={}& \biggl[-\beta +\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}+ \frac{\beta I(t)}{N(t)}+\frac{\beta C(t)}{N(t)}+ \frac{\beta A(t)}{N(t)} \biggr]\,dt- \frac{\sigma S(t)}{N(t)}\,dB(t). \end{aligned} $$

According to $N(t)>\frac{\lambda }{\mu +d}$, we have

$$ \begin{aligned} d\bigl(V(t)\bigr)\leq {}& \biggl[-\beta +\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}+ \frac{\beta I(t)}{N(t)}+\frac{\beta C(t)}{N(t)}+ \frac{\beta A(t)}{N(t)} \biggr]\,dt-\frac{\sigma S(t)}{N(t)}\,dB(t) \\ \leq {}& \biggl[-\beta +\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}+ \frac{\beta (\mu +d)}{\lambda }\bigl(I(t)+C(t)+A(t)\bigr) \biggr]\,dt \\ &{}- \frac{\sigma S(t)}{N(t)} \,dB(t). \end{aligned} $$

Hence

$$ \begin{aligned} \frac{\ln I(0)}{t}-\frac{\ln I(t)}{t}\leq {}&- \beta +\mu +\gamma +\rho + \frac{\sigma ^{2}}{2}+\frac{\beta (\mu +d)}{\lambda }\bigl(\bigl\langle I(t) \bigr\rangle +\bigl\langle C(t)\bigr\rangle +\bigl\langle A(t)\bigr\rangle \bigr) \\ &{}-\frac{1}{t} \int _{0}^{t}\frac{\sigma S(s)}{N(s)}\,dB(s). \end{aligned} $$

In the light of (3.6) and (3.7), we have

$$\begin{aligned} \bigl\langle I(t)\bigr\rangle \geq {}&\frac{\lambda }{\beta (\mu +d)} \biggl[ \beta -\biggl( \mu +\gamma +\rho +\frac{\sigma ^{2}}{2}\biggr)+ \frac{\ln I(0)}{t}- \frac{\ln I(t)}{t}+\frac{1}{t} \int _{0}^{t}\frac{\sigma S(s)}{N(s)}\,dB(s) \biggr] \\ &{}-\bigl\langle C(t)\bigr\rangle -\bigl\langle A(t)\bigr\rangle \\ ={}&\frac{\lambda }{\beta (\mu +d)} \biggl[\beta -\biggl(\mu +\gamma +\rho + \frac{\sigma ^{2}}{2}\biggr)+\frac{\ln I(0)}{t}-\frac{\ln I(t)}{t}+ \frac{1}{t} \int _{0}^{t}\frac{\sigma S(s)}{N(s)}\,dB(s) \biggr] \\ &{}+\frac{C(t)-C(0)}{(\omega +\mu )t}-\frac{\gamma }{\omega +\mu } \bigl\langle I(t)\bigr\rangle + \frac{A(t)-A(0)}{(\alpha +\mu +d)t}- \frac{\rho }{\alpha +\mu +d}\bigl\langle I(t)\bigr\rangle . \end{aligned}$$

Furthermore,

$$ \begin{aligned} \bigl\langle I(t)\bigr\rangle \geq & \frac{\lambda (\omega +\mu )(\alpha +\mu +d)(\mu +\gamma +\rho +\frac{\sigma ^{2}}{2})}{\beta (\mu +d) [(\omega +\mu )(\alpha +\mu +d+\rho )+\gamma (\alpha +\mu +d) ]} (R_{3}-1 ) +F(t), \end{aligned} $$

where

$$\begin{aligned} F(t)={}&\frac{(\omega +\mu )(\alpha +\mu +d)}{(\omega +\mu )(\alpha +\mu +d+\rho )+\gamma (\alpha +\mu +d)} \\ &{}\times \biggl\{ \frac{\lambda }{\beta (\mu +d)} \biggl( \frac{\ln I(0)}{t}- \frac{\ln I(t)}{t} \\ &{}+\frac{1}{t} \int _{0}^{t}\frac{\sigma S(s)}{N(s)}\,dB(s) \biggr)+\frac{C(t)-C(0)}{(\omega +\mu )t}+ \frac{A(t)-A(0)}{(\alpha +\mu +d)t} \biggr\} . \end{aligned}$$

If $R_{3}>1$, then

$$\begin{aligned} \liminf_{t\rightarrow +\infty }\bigl\langle I(t)\bigr\rangle \geq {}&\frac{\lambda (\omega +\mu )(\alpha +\mu +d)(\mu +\gamma +\rho +\frac{\sigma ^{2}}{2})}{\beta (\mu +d) [(\omega +\mu )(\alpha +\mu +d+\rho )+\gamma (\alpha +\mu +d) ]} (R_{3}-1 ) \\ >{}&0 \quad \mbox{almost surely}. \end{aligned}$$

 □

4 Numerical simulations

In this section, we use Milstein’s method [18] to simulate stochastic model (1.2) with a numerical scheme for stochastic model (1.2) given by

$$ \textstyle\begin{cases} S_{k+1}=S_{k}+[\lambda -\mu {S_{k}}- \frac{\beta S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}}]\Delta t \\ \hphantom{S_{k+1}=}{}-\frac{\sigma S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}}\sqrt{\Delta t} \xi _{k}-\frac{\sigma ^{2}}{2} ( \frac{ S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}} )^{2}(\xi _{k}^{2}-1) \Delta t, \\ I_{k+1}=I_{k}+[ \frac{\beta S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}}-( \mu +\gamma +\rho )I_{k}+\alpha {A_{k}}+\omega {C_{k}}]\Delta t \\ \hphantom{I_{k+1}=}{}+\frac{\sigma S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}}\sqrt{\Delta t} \xi _{k}+\frac{\sigma ^{2}}{2} ( \frac{ S_{k}I_{k}}{S_{k}+I_{k}+C_{k}+A_{k}} )^{2}(\xi _{k}^{2}-1) \Delta t, \\ C_{k+1} =C_{k}+[\gamma {I_{k}}-(\mu +\omega )C_{k}]\Delta t, \\ A_{k+1} =A_{k}+[\rho {I_{k}}-(\alpha +\mu +d)A_{k}]\Delta t, \end{cases} $$

where $\xi _{k}$, $k = 1,2,\ldots ,n$, are independent Gaussian random variables $N(0,1)$.

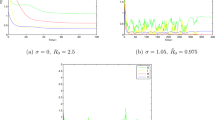
Firstly, we choose $\sigma =0.8$, $\gamma =0.07$, $\omega =0.9$, and other parameter values given by Table 1. In this case, we have

$$\begin{aligned}& R_{1}=\frac{\beta ^{2}}{2\sigma ^{2}\mu }=0.651< 1, \\& R_{2}=\frac{\beta }{(\mu +\frac{\sigma ^{2}}{2})}=0.806< 1, \qquad \sigma ^{2}- \beta =0.14>0, \\& R_{3}=\frac{\beta }{\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}}=0.633< 1, \end{aligned}$$

then the disease $I(t)$ will die out (see Theorem 3.1 and Fig. 1(b)). In addition, the basic reproduction number of the corresponding deterministic model $R_{0} =1.259>1$, this means that the corresponding deterministic model (1.1) has an endemic equilibrium which is globally asymptotically stable, as shown in Fig. 1(a)–(d).

Figure 1

The path $S(t)$, $I(t)$, $C(t)$, and $A(t)$ for models (1.1) and (1.2), when $R_{1} = 0.651<1$ and $R_{0} =1.259>1$

Table 1 Parameters of the HIV/AIDS model (1.2)

Secondly, we choose $\sigma =0.645$, $\gamma =0.05$, $\omega =0.8$, and other parameter values given by Table 1. In this case, we have

$$\begin{aligned}& R_{1}=\frac{\beta ^{2}}{2\sigma ^{2}\mu }=1.002>1, \\& R_{2}=\frac{\beta }{(\mu +\frac{\sigma ^{2}}{2})}=0.9842< 1,\qquad \sigma ^{2}- \beta =-0.084< 0, \\& R_{3}=\frac{\beta }{\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}}=0.7599< 1, \end{aligned}$$

then the disease $I(t)$ will die out (see Theorem 3.1 and Fig. 2(b)). In addition, the basic reproduction number of the corresponding deterministic model $R_{0} =1.271>1$, this means that the corresponding deterministic model (1.1) also has an endemic equilibrium which is globally asymptotically stable, as shown in Fig. 2. Furthermore, we choose $\gamma =0.07$, $\omega =0.9$, and $\sigma =0.8,1,1.2,1.4$, and other parameter values given by Table 1 to study the impact of σ on the dynamics for the SDE SICA model (1.2). In this case, we can obtain the values given in Table 2. Theorem 3.1 reveals the numerical results shown in Fig. 3.

Figure 2

The path $S(t)$, $I(t)$, $C(t)$, and $A(t)$ for model (1.1) and (1.2), when $R_{2} = 0.9842<1$, $\sigma ^{2}-\beta =-0.084<0$, and $R_{0} =1.271>1$

Figure 3

The path of $(S(t),I(t),C(t),A(t))$ for stochastic model (1.2) when $\sigma =0.8,1,1.2,1.4$

Table 2 The values with $\sigma =0.8, 1, 1.2, 1.4$

Our results reveal that random perturbations in the environment can restrain the spread of the disease (see Fig. 2), and the bigger the intensity of the random perturbation, the faster the disease dies out (see Fig. 3). However, deterministic models ignore this, so it is essential to introduce stochastic perturbations into deterministic models.

Thirdly, we fix $\sigma =0.8$ and choose $\beta =0.2, 0.4, 0.6, 0.8, 1, 1.2$ and other parameters taken as in Table 1 to study the impact of β on the dynamics for the SDE SICA model (1.2). In this case, we can obtain the values given in Table 3, and the numerical results show that the smaller the transmission rate, the faster the disease dies out (see Fig. 4).

Figure 4

The path of $(S(t),I(t),C(t),A(t))$ for stochastic model (1.2) when $\sigma =0.8$

Table 3 The values with $\beta =0.2, 0.4, 0.6, 0.8, 1, 1.2$

Finally, we choose $\sigma =0.2$, $\gamma =0.01$, $\omega =0.1$ and other parameter values given by Table 1. In this case, we have

$$\begin{aligned}& R_{1}=\frac{\beta ^{2}}{2\sigma ^{2}\mu }=10.417, \\& R_{2}=\frac{\beta }{(\mu +\frac{\sigma ^{2}}{2})}=1.563>1, \qquad \sigma ^{2}- \beta =-0.46< 0, \\& R_{3}=\frac{\beta }{\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}}=1.163>1, \end{aligned}$$

then the disease $I(t)$ will be persistence in mean, namely, the disease will prevail (see Theorem 3.2 and Fig. 5(b)).

Figure 5

The path $S(t)$, $I(t)$, $C(t)$, and $A(t)$ for models (1.1) and (1.2), when $R_{3} =1.163>1$ and $R_{0} =1.291>1$

By numerical simulation, the results of numerical simulations show that HIV can be controlled by increasing the intensity of interference and reducing the transmission rates shown in Fig. 6 (e.g., increased HIV prevention campaigns, condom use, etc.)

Figure 6

The path of $(S(t),I(t),C(t),A(t))$ for stochastic model (1.2) when $\sigma =0.8,1,1.2,1.4$ and $\beta =0.5,0.4,0.3,0.2$

5 Conclusion

This paper studied the extinction and persistence of a stochastic SICA epidemic model with standard incidence rate for HIV transmission. Firstly, we analyze that model (1.2) has a unique global positive solution for any initial value. Secondly, by Theorem 3.1, we can find that when $R_{1}=\frac{\beta ^{2}}{2\sigma ^{2}\mu }<1$ or $\sigma ^{2}<\beta$ and $R_{2}=\frac{\beta }{(\mu +\frac{\sigma ^{2}}{2})}<1$, disease will die out (see Theorem 3.1 and Fig. 1 and Fig. 2). Furthermore, $\lim_{t\rightarrow +\infty }S(t)=\frac{\lambda }{\mu }$ (see Theorem 3.1), but for the corresponding deterministic model (1.2), $R_{0} > 1$, there exists an endemic equilibrium, which means that a stochastic perturbation can suppress the outbreak of the disease (see Fig. 1 and Fig. 2), and the bigger the intensity of the random perturbation, the faster the disease dies out (see Fig. 3). However, deterministic models do not take this into account, so it is essential to include a stochastic element in deterministic models. In addition, we fix σ to study the impact of β on the dynamics for the SDE SICA model (1.2). In this case, we can find that the greater the rate of transmission, the higher the number of people infected (see Fig. 4).

Finally, if $R_{3}=\frac{\beta }{\mu +\gamma +\rho +\frac{\sigma ^{2}}{2}}>1$, the disease will be persistence in mean, namely, the disease will prevail (see Theorem 3.2 and Fig. 5).

Through numerical simulations, we can conclude that it is possible to reduce the transmission coefficient of HIV while increasing the strength of the stochastic perturbation to reduce the risk of HIV transmission, the simulation results are shown in Fig. 6.

On the other hand, in this paper, we only consider the effect of random perturbations on HIV transmission rate β, we can also study the effect of random perturbations on another parameter such as natural death rate, HIV treatment rate, AIDS induced death rate, and so on. In addition, in this paper, we only consider the effect of white noise. In fact, there are some random perturbations which cannot be modeled by white noises, for example, the telephone and Lévy noise, see [23–26] and the references therein. On the other hand, there have also been extensive numerical works to establish the positive property of numerical solutions for certain physical models (see [27–29]). We leave these investigations for future work.