1 Introduction

The nonlinear partial differential equation is a physical and natural model which can be used for model constructs by scientists and researchers. Different types of differential equations of both ODEs and PDEs in various fields of science, like fluid flow, mechanics, and biology, are expressed in the special forms [1, 2]. There is no particular method for accessing the exact type solutions of nonlinear PDEs but some approximate and analytical solutions have been determined [3, 4]. As is well known, the model of many natural phenomena and the differential equations in the sciences and engineering are nonlinear and it is very important to obtain analytically or numerically accurate solutions. In order to achieve this goal, various methods have been developed for linear and nonlinear equations, such as the Exp-function method [5], the homotopy analysis method [6], the homotopy perturbation method [7], the (G’/G)-expansion method [8], the improved \(\tan (\phi /2)\)-expansion method [9, 10], the Hirota bilinear method [11, 12, 59–67], the He variational principle [13, 14], the binary Darboux transformation [15], the Lie group analysis [16, 17], the Bäcklund transformation method [18], and the multiple Exp-function method [19, 20]. Moreover, many powerful methods have been used to investigate the new properties of mathematical models which are symbolizing serious real world problems [21, 22, 68, 69]. The utilized methods which employed by powerful researchers are such methods as the Exp-function method, the multiple Exp-function method, (G’-G)-expansion method—but we should not forget to mention that these methods continue to attract a wave of criticism. This criticism is focused on two aspects of these methods. First of all, it has been demonstrated that the mentioned methods can produce wrong solutions. Secondly, these methods cannot produce necessary and sufficient conditions for the existence of analytic solutions, neither in the system parameter space nor in the space of initial conditions. These aspects can be useful for investigating in future research and combining these methods in work which will have a link with special transformations.

The main idea of the following equations is finding the exact solution of any models which can be expressed by a Hirota bilinear method. Big varieties of mathematical and physical phenomena are governed by NLPDEs which play a crucial role in the nonlinear sciences. It provides much physical information and more insight into the physical aspects of the problem and thus leads to further applications. Bogoyavlensky introduced a model equation describing the nonisospectral scattering problems [23], namely, the \((2+1)\)-dimensional Bogoyavlenski equation

$$\begin{aligned} & 4\Psi _{t}+\Psi _{xxy}-4\Psi ^{2}\Psi _{y}-4\Psi _{x}\Phi =0, \\ &\Psi \Psi _{y}=\Phi _{x}. \end{aligned}$$
(1.1)

Kudryashov and Pickering [24] proposed the above equation as a member of a \((2+1)\) Schwarzian breaking soliton hierarchy. Clarkson and co-authors [25] investigated Eq. (1.1) as one of the equations associated to nonisospectral scattering problems. Estevez and Prada [26] presented a generalization of the sine-Gordon equation that possesses the Painlevé feature. Zhran and Khater [27] probed the Bogoyavlensky equation by utilizing the modified extended tanh-function method. The authors of [28] showed that the above equation is a modified version of the following nonlinear equation:

$$ 4\Psi _{xt}+8\Psi _{x}\Psi _{xy}+4 \Psi _{y}\Psi _{xx}+\Psi _{xxxy}=0, $$
(1.2)

which is called the breaking soliton equation. Also, Eq. (1.2) is a particular version of the Bogoyavlensky–Konopelchenko (BK) equation given as

$$ a\Psi _{xt}+b\Psi _{xxxx}+c\Psi _{xxy}+d\Psi _{x}\Psi _{xx}+e\Psi _{x} \Psi _{xy}+k\Psi _{xx}\Psi _{y}=0. $$
(1.3)

Equation BK explains the \((2+1)\)-dimensional interaction of a Riemann wave propagation along the y-axis with a long wave along the x-axis, and it also is a two-dimensional generalization of the well-known Korteweg–de Vries equation [29, 30]. This study is aimed at investigating the following generalized Bogoyavlensky–Konopelchenko (BK) equation [31]:

$$ \Psi _{t}+\alpha (6\Psi \Psi _{x}+\Psi _{xxx})+\beta (\Psi _{xxy}+3 \Psi \Psi _{y}+3\Psi _{x}\Phi _{y})+\gamma _{1}\Psi _{x} + \gamma _{2} \Psi _{y}+\gamma _{3}\Phi _{yy}=0, $$
(1.4)

in which \(\Phi _{x}=\Psi \), and \(\alpha, \beta, \gamma _{1}, \gamma _{2}\), and \(\gamma _{3}\) are determined values. Equation (1.4) can be written as

$$\begin{aligned} &\Phi _{xt}+\alpha (6\Phi _{x}\Phi _{xx}+\Phi _{xxxx})+\beta (\Phi _{xxxy}+3 \Phi _{x}\Phi _{xy}+3\Phi _{xx}\Phi _{xy}) \\ &\quad{}+ \gamma _{1}\Phi _{xx} + \gamma _{2}\Phi _{xy}+\gamma _{3}\Phi _{yy}=0, \end{aligned}$$
(1.5)

and by applying the bilinear transformation \(\Psi =2(\ln f)_{xx}\) and \(\Phi =2(\ln f)_{x}\) Eq. (1.5) is transformed to the bilinear form

$$\begin{aligned} &\bigl(\alpha D_{x}^{4}+\beta D_{x}^{3}D_{y}+D_{t}D_{x}+ \gamma _{1}D_{x}^{2}+ \gamma _{2}D_{x} D_{y}+\gamma _{3} D_{y}^{2} \bigr)f. f=0, \\ &D_{x}^{4} f. f=2\bigl(ff_{xxxx}-4f_{x}f_{xxx}+3f_{xx}^{2} \bigr),\qquad D_{x}^{3}D_{y} f. f=2(ff_{xxx y}-f_{y}f_{xxx }-3f_{x}f_{xx y}+3f_{xx}f_{x y}), \\ &D_{x}^{2} f. f=2\bigl(ff_{xx}-f_{x}^{2} \bigr),\qquad D_{x} D_{t} f. f=2(ff_{x t}-f_{x}f_{t}), D_{x} D_{y} f. f=2(ff_{x y}-f_{x}f_{y}), \\ & D_{y}^{2} f. f=2\bigl(ff_{yy}-f_{y}^{2} \bigr). \end{aligned}$$
(1.6)

The aim of this study is to construct the invariant solutions of the \((2+1)\)-dimensional fractional generalized CBS-BK equation in the following form:

$$\begin{aligned} & D_{t}^{\alpha }\Psi +\Psi _{xxy}+3\Psi _{x}\Psi _{y}+\delta _{1}\Psi _{y}+ \delta _{2} \Phi _{yy}+\delta _{3} \Psi _{x}\\ &\quad{}+\delta _{4}\bigl(3\Psi _{x}^{2}+ \Psi _{xxx}\bigr)+\delta _{5}\bigl(3\Phi _{yy}^{2}+ \Psi _{yyyy}\bigr) \\ &\quad{}+\delta _{6}(3\Psi _{y}\Phi _{yy}+\Psi _{yyy})=0, \quad\Psi _{x}=\Phi, 0< \alpha \leq 1, \end{aligned}$$
(1.7)

in which \(\delta _{i}, i=1,\ldots,6\), are the determined values. By employing the following fractional transformation [32]:

$$ \tau =\frac{t^{\alpha }}{\Gamma (\alpha +1)}, $$
(1.8)

Equation (1.7) changes to the nonlinear fractional generalized CBS-BK equation as follows:

$$\begin{aligned} &\Psi _{\tau }+\Psi _{xxy}+3\Psi _{x} \Psi _{y}+\delta _{1}\Psi _{y}+ \delta _{2} \Phi _{yy}+\delta _{3} \Psi _{x}+ \delta _{4}\bigl(3\Psi _{x}^{2}+ \Psi _{xxx}\bigr)+\delta _{5}\bigl(3\Phi _{yy}^{2}+ \Psi _{yyyy}\bigr) \\ &\quad{}+\delta _{6}(3\Psi _{y}\Phi _{yy}+\Psi _{yyy})=0, \quad\Psi _{x}=\Phi, 0< \alpha \leq 1. \end{aligned}$$
(1.9)

The propagation and the dynamical behavior of these solutions can be analyzed for the different choices of α, the fractional order. When \(\alpha =1, N=1\) in an N-soliton, it is verified that the velocity of the soliton cannot be influenced by the variable coefficients. Furthermore, the shape and the amplitude of the soliton cannot be affected. For \(\alpha =1\), when the arbitrary constants are supposed \(\delta _{3}=\delta _{4}=\delta _{5}=\delta _{6}=0\), Eq. (1.9) changes as a generalized Calogero–Bogoyavlensky–Schiff (CBS) equation where has been cited in Refs. [33, 34]. While the arbitrary constants supposed \(\delta _{5}=\delta _{6}=0\), then Eq. (1.9) becomes a generalized Bogoyavlensky–Konopelchenko (BK) equation as cited in Refs. [34–36].

We address solving the fractional generalized CBS-BK equation in the sense of the modified Riemann–Liouville derivative which has been derived by [37]. These equations can be reduced to the nonlinear ordinary differential equations via integer orders utilizing some fractional complex transformations. Jumarie’s modified Riemann–Liouville derivative of order α is given by

$$ D_{t}^{\alpha }u(t)= \textstyle\begin{cases} \frac{1}{\Gamma (1-{\alpha })} \int _{0}^{t} (t-\tau )^{-\alpha } (u(\tau )-u(0) )\,\mathrm{d}\tau& \text{if } 0< {\alpha }\leq 1, \\ [u^{(n)}(t) ]^{(\alpha -n)}& \text{if } n\leq \alpha < n+1, n\geq 1. \end{cases} $$
(1.10)

We list some valuable properties of the Riemann–Liouville fractional derivative [38–40] as follows:

{ D J α ( f ( x ) g ( x ) ) = ∑ j = 0 + ∞ ( α j ) f ( j ) ( x ) g R − L ( α − j ) ( x ) − f ( 0 ) g ( 0 ) x α Γ ( 1 − α ) , D J α ( f ( g ( x ) ) ) = ∑ j = 0 + ∞ ( α j ) x j − α j ! Γ ( j − α + 1 ) ∑ m = 1 j f ( m ) ( g ) ∑ ∏ k = 1 j 1 P k ! ( g ( k ) k ! ) P k D J α ( f ( g ( x ) ) ) = + f ( g ( x ) ) − f ( g ( 0 ) ) x α Γ ( 1 − α ) , D t α t γ = Γ ( γ + 1 ) Γ ( 1 + α − γ ) t γ − α , γ > 0 ,
(1.11)

where Γ denotes the Gamma function.

In this paper, we will study the multiple rogue waves for determining the multiple soliton solutions. The multiple rogue waves method used by some of powerful authors for the various nonlinear equations, including constructing rogue waves with a controllable center in the nonlinear systems [41], a \((3+1)\)-dimensional Hirota bilinear equation [42], the generalized \((3+1)\)-dimensional KP equation [43], and the Boussinesq equation [44]. There are many new papers about this fields, such as lump solutions (constructing the lump–soliton and mixed lump strip solutions of \((3+1)\)-dimensional soliton equation [45]; utilizing the linear superposition principle to discuss the \((3+1)\)-dimensional Boiti–Leon–Manna–Pempinelli equation [46]; obtaining periodic solutions for many non-linear evolution equations in the integrable systems theory [47]), rogue wave solutions (utilizing the Hirota bilinear form of the extended \((3+1)\)-dimensional JM equation to find 30 classes of rogue wave type solutions [48]; resonant multiple wave solutions to some integrable soliton equations [49]). Some important work related with recent development in fractional calculus and its applications can be pointed out referring to the valuable papers containing studies of general fractional derivatives: theory, methods and applications by Yang [50]; anomalous diffusion equations with the decay exponential kernel by the Laplace transform [51]; new fractal nonlinear Burgers’ equation arising in the acoustic signals propagation by Yang and Machado [52]; time fractional nonlinear diffusion equation from diffusion process by fractional Lie group approach [53]; the generalized time fractional diffusion equation by symmetry analysis [54]; investigating a time fractional nonlinear heat conduction equation with applications in mathematics physics, integrable system, fluid mechanics and nonlinear areas, by means of applying the fractional symmetry group method [55]; and determining the time fractional extended \((2+1)\)-dimensional Zakharov–Kuznetsov equation in quantum magneto-plasmas by using a group analysis approach [56]. In [57], an operator-based framework for the construction of analytical soliton solutions to fractional differential equations was showed to fractional differential equations were mapped from Caputo algebra to Riemann–Liouville algebra.

The rest of this paper is structured as follows. The Hirota bilinear scheme has been summarized in Sect. 2. In Sects. 3–5, the lump solution, lump–kink, and lump–soliton solution to the fractional generalized CBS-BK equation, respectively, have been given. In Sect. 6, the conclusions have been given.

2 Hirota bilinear method

Take the fractional generalized CBS-BK of the form

$$\begin{aligned} \mathbb{P}_{ g\text{CBS-BK}}(\Upsilon ):={}&\Psi _{\tau }+\Psi _{xxy}+3\Psi _{x} \Psi _{y}+\delta _{1} \Psi _{y}+\delta _{2} \Psi _{xyy}+\delta _{3} \Psi _{x}+\delta _{4}\bigl(3\Psi _{x}^{2}+\Psi _{xxx}\bigr)\\ &{}+\delta _{5} \bigl(3\Psi _{xyy}^{2}+ \Psi _{yyyy}\bigr) +\delta _{6}(3\Psi _{y}\Psi _{xyy}+\Psi _{yyy})=0. \end{aligned}$$
(2.1)

Assume the Hirota derivatives according to the functions \(\phi (x)\), \(\varphi (x)\) can be presented as

$$ \prod_{i=1}^{3}D_{\lambda _{i}}^{\pi _{i}} \phi.\varphi = \prod_{i=1}^{3} \biggl( \frac{\partial }{\partial \lambda _{i}}- \frac{\partial }{\partial \mu _{i}} \biggr)^{o_{i}}\phi (\lambda ) \varphi (\mu )\bigg|_{\mu =\lambda }, $$
(2.2)

where the vectors \(\lambda =(\lambda _{1},\lambda _{2},\lambda _{3})\), \(\mu =(\mu _{1},\mu _{2},\mu _{3})\) and \(o_{1},o_{2},o_{3}\) are optional nonnegative integers. It is clear that the fractional generalized CBS-BK equation above possesses the following Hirota bilinear:

$$\begin{aligned} &\mathbb{B}_{g\text{CBS-BK}}(f)\\ &\quad:= \bigl(\delta _{4} D_{x}^{4}+ D_{x}^{3}D_{y}+ \delta _{3}D_{x}^{2}+D_{x}D_{\tau }+ \delta _{2}D_{y}^{2}+\delta _{1}D_{x} D_{y}+\delta _{5} D_{y}^{4}+\delta _{6}D_{y}^{3}D_{x} \bigr)f. f \\ &\quad=2 \bigl[\delta _{4}\bigl(ff_{xxxx}-4f_{x}f_{xxx}+3f_{xx}^{2} \bigr)+ (ff_{xxx y}-f_{y}f_{xxx }-3f_{x}f_{xx y}+3f_{xx}f_{x y}) \\ &\qquad{}+ \delta _{3}\bigl(ff_{xx}-f_{x}^{2}\bigr)+ (ff_{x \tau }-f_{x}f_{\tau }) \\ &\qquad{}+ \delta _{2}\bigl(ff_{yy}-f_{y}^{2} \bigr)+\delta _{1} (ff_{x y}-f_{x}f_{y})+ \delta _{5} \bigl(ff_{yyyy}-4f_{y}f_{yyy}+3f_{yy}^{2} \bigr) \\ &\qquad{}+ \delta _{6}(ff_{yyy x}-f_{x}f_{yyy }-3f_{y}f_{yy x}+3f_{yy}f_{yx}) \bigr]. \end{aligned}$$
(2.3)

We utilize the following relationship between the functions \(f(x,y,\tau )\) and \(\Psi (x,y,\tau )\):

$$ \Psi (x,y,\tau )=\Psi _{0}+2\bigl(\ln f(x,y,\tau ) \bigr)_{x}, \qquad\Phi (x,y,\tau )=2\bigl(\ln f(x,y,\tau ) \bigr)_{xx}. $$
(2.4)

According to the Bell polynomial theories of soliton equations [58], we can obtain the following relationship:

$$ \mathbb{P}_{g\text{CBS-BK}}(\Psi )= \biggl[\frac{\mathbb{B}_{g\text{CBS-BK}}(f)}{f} \biggr]_{x}. $$
(2.5)

Theorem 2.1

f solves (2.4) if and only if \(\Psi =2(\ln f)_{x}\) is demonstrated to be a solution to Eq. (2.1),

$$\begin{aligned} &\bigl(\delta _{4} D_{x}^{4}+ D_{x}^{3}D_{y}+\delta _{3}D_{x}^{2}+D_{x}D_{\tau }+ \delta _{2}D_{y}^{2}+\delta _{1}D_{x} D_{y}+\delta _{5} D_{y}^{4}+ \delta _{6}D_{y}^{3}D_{x} \bigr)f. f \\ &\quad=2 \bigl[\delta _{4}\bigl(ff_{xxxx}-4f_{x}f_{xxx}+3f_{xx}^{2} \bigr)+ (ff_{xxx y}-f_{y}f_{xxx }-3f_{x}f_{xx y}+3f_{xx}f_{x y}) \\ &\qquad{}+ \delta _{3}\bigl(ff_{xx}-f_{x}^{2}\bigr)+ (ff_{x \tau }-f_{x}f_{\tau }) \\ &\qquad{}+ \delta _{2}\bigl(ff_{yy}-f_{y}^{2} \bigr)+\delta _{1} (ff_{x y}-f_{x}f_{y})+ \delta _{5} \bigl(ff_{yyyy}-4f_{y}f_{yyy}+3f_{yy}^{2} \bigr) \\ &\qquad{}+ \delta _{6}(ff_{yyy x}-f_{x}f_{yyy }-3f_{y}f_{yy x}+3f_{yy}f_{yx}) \bigr]. \end{aligned}$$
(2.6)

Proof

By supposing \(\theta =\partial _{x}(\ln f)\), from Eq. (2.4), we get

$$ \Psi =2 \theta \quad\Longleftrightarrow\quad f=\exp \biggl( \frac{1}{2} \int \Psi \,\mathrm{d}x \biggr), $$
(2.7)

then, by considering \(f=\exp (\partial _{x}^{-1}\theta )\) and \(f>0\), the expressions \(f_{x}\), \(f_{y}\), \(f_{\tau }\), \(f_{xx}\), \(f_{yy}\), \(f_{xy}\), \(f_{x\tau }\), \(f_{xxy}\), \(f_{xyy}\), \(f_{xxx}\), \(f_{xxyy}\), and \(f_{xxxx}\), respectively, can be written as

$$\begin{aligned} &f_{x}=\theta \exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.8)
$$\begin{aligned} &f_{y}=\partial _{x}^{-1}\theta _{y}\exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.9)
$$\begin{aligned} &f_{\tau }=\partial _{x}^{-1}\theta _{\tau }\exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.10)
$$\begin{aligned} &f_{xx}=\bigl(\theta ^{2}+\theta _{x}\bigr)\exp \bigl(\partial _{x}^{-1}\theta \bigr), \end{aligned}$$
(2.11)
$$\begin{aligned} &f_{yy}=\bigl(\bigl(\partial _{x}^{-1} \theta _{y}\bigr)^{2}+\partial _{x}^{-1} \theta _{yy}\bigr) \exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.12)
$$\begin{aligned} &f_{xy}=\bigl(\theta \partial _{x}^{-1} \theta _{y}+\theta _{y}\bigr)\exp \bigl( \partial _{x}^{-1}\theta \bigr), \end{aligned}$$
(2.13)
$$\begin{aligned} &f_{x\tau }=\bigl(\theta \partial _{x}^{-1} \theta _{t}+\theta _{t}\bigr)\exp \bigl(\partial _{x}^{-1}\theta \bigr), \end{aligned}$$
(2.14)
$$\begin{aligned} &f_{xxx}=\bigl(\theta ^{3}+3\theta \theta _{x}+\theta _{xx}\bigr)\exp \bigl( \partial _{x}^{-1}\theta \bigr), \end{aligned}$$
(2.15)
$$\begin{aligned} &f_{xxy}= \bigl[\bigl(\theta ^{2}+\theta _{x}\bigr)\partial _{x}^{-1}\theta _{y}+2 \theta \theta _{y}+\theta _{xy} \bigr]\exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.16)
$$\begin{aligned} & f_{xyy}= \bigl[\theta \bigl(\partial _{x}^{-1}\theta _{y}\bigr)^{2}+\theta \partial _{x}^{-1}\theta _{yy}+ 2\theta _{y}\partial _{x}^{-1}\theta _{y}+ \theta _{yy} \bigr]\exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.17)
$$\begin{aligned} &f_{xxxx}= \bigl[\theta ^{4}+6\theta ^{2}\theta _{x}+4\theta \theta _{xx}+3( \theta _{x})^{2}+\theta _{xxx} \bigr] \exp \bigl(\partial _{x}^{-1} \theta \bigr), \end{aligned}$$
(2.18)
$$\begin{aligned} &f_{xxyy}= \bigl[\bigl(\theta ^{2}+\theta _{x}\bigr) \bigl(\bigl(\partial _{x}^{-1}\theta _{y}\bigr)^{2}+ \partial _{x}^{-1} \theta _{yy}\bigr)+4\theta \theta _{y}\partial _{x}^{-1} \theta _{y}+ 2\theta _{xy} \partial _{x}^{-1}\theta _{y}\\ &\phantom{f_{xxyy}= }{}+2\theta \theta _{yy}+2(\theta _{y})^{2}+\theta _{xyy} \bigr] \exp \bigl( \partial _{x}^{-1}\theta \bigr). \end{aligned}$$
(2.19)

Plugging (2.8)–(2.19) into (2.3) yields the bilinear form of Eq. (2.3) as

$$\begin{aligned} &2 \bigl[\delta _{4}\bigl(ff_{xxxx}-4f_{x}f_{xxx}+3f_{xx}^{2} \bigr)+ (ff_{xxx y}-f_{y}f_{xxx }-3f_{x}f_{xx y}+3f_{xx}f_{x y})\\ &\qquad{}+ \delta _{3}\bigl(ff_{xx}-f_{x}^{2}\bigr)+ (ff_{x \tau }-f_{x}f_{\tau }) \\ &\qquad{}+ \delta _{2}\bigl(ff_{yy}-f_{y}^{2} \bigr)+\delta _{1} (ff_{x y}-f_{x}f_{y})+ \delta _{5} \bigl(ff_{yyyy}-4f_{y}f_{yyy}+3f_{yy}^{2} \bigr) \\ &\qquad{}+ \delta _{6}(ff_{yyy x}-f_{x}f_{yyy }-3f_{y}f_{yy x}+3f_{yy}f_{yx}) \bigr] \\ &\quad=2\exp \bigl(2\partial _{x}^{-1}\theta \bigr) \biggl[6 \biggl( \int {\frac{\partial ^{2}}{\partial {y}^{2}}}\theta ( x,y, \tau ) {\,\mathrm{d}}x \biggr) ^{2}\delta _{{5}} \\ &\qquad{}+6 \int { \frac{\partial ^{2}}{\partial {y}^{2}}}\theta ( x,y,\tau ) {\,\mathrm{d}}x \biggl( { \frac{\partial }{\partial y}}\theta ( x,y,\tau ) \biggr) \delta _{{6}}+6 \biggl( { \frac{\partial }{\partial x}}\theta ( x,y,\tau ) \biggr) ^{2}\delta _{{4}} \\ &\qquad{}+ \biggl( { \frac{\partial ^{3}}{\partial {x}^{3}}}\theta ( x,y,\tau ) \biggr) \delta _{{4}}+ \int { \frac{\partial ^{4}}{\partial {y}^{4}}} \theta ( x,y,\tau ) {\,\mathrm{d}}x\delta _{{5}} \\ &\qquad{}+ \int { \frac{ \partial ^{2}}{\partial {y}^{2}}}\theta ( x,y,\tau ) { \,\mathrm{d}} x\delta _{{2}}+6 \biggl( {\frac{\partial }{\partial x}} \theta ( x,y,\tau ) \biggr) { \frac{\partial }{\partial y}}\theta ( x, y,\tau ) \\ &\qquad{}+ \biggl( {\frac{\partial }{\partial x}}\theta ( x,y, \tau ) \biggr) \delta _{{3}}+ \biggl( { \frac{\partial ^{3}}{ \partial {y}^{3}}}\theta ( x,y,\tau ) \biggr) \delta _{{6}}+ \biggl( {\frac{\partial }{\partial y}}\theta ( x,y,\tau ) \biggr) \delta _{{1}} \\ &\qquad{}+{ \frac{\partial ^{3}}{\partial {x}^{2}\partial y}}\theta ( x,y, \tau ) +{\frac{\partial }{\partial \tau }} \theta ( x,y, \tau ) \biggr] \\ &\quad=2{f}^{2} \bigl[6\delta _{{5}} \bigl(\partial _{x}^{-1}\theta _{yy} \bigr) ^{2}+6 \delta _{{6}}\theta _{y} \bigl(\partial _{x}^{-1} \theta _{yy} \bigr)+ 6\delta _{{4}}\theta _{x}^{2}+ \delta _{4} \theta _{xxx}+\delta _{5}\partial _{x}^{-1}\theta _{yyyy}+\delta _{2} \partial _{x}^{-1}\theta _{yy}+6\theta _{x}\theta _{y} \\ &\qquad{}+\delta _{3}\theta _{x}+\delta _{6} \theta _{yyy}+\delta _{1} \theta _{y}+\theta _{xxy}+\theta _{\tau } \bigr] \end{aligned}$$
(2.20)

or it can be rewritten as

$$\begin{aligned} &\frac{1}{f^{2}}2 \bigl[\delta _{4} \bigl(ff_{xxxx}-4f_{x}f_{xxx}+3f_{xx}^{2} \bigr)+ (ff_{xxx y}-f_{y}f_{xxx }-3f_{x}f_{xx y}+3f_{xx}f_{x y})\\ &\qquad{}+ \delta _{3}\bigl(ff_{xx}-f_{x}^{2}\bigr)+ (ff_{x \tau }-f_{x}f_{\tau }) \\ &\qquad{}+ \delta _{2}\bigl(ff_{yy}-f_{y}^{2} \bigr)+\delta _{1} (ff_{x y}-f_{x}f_{y})+ \delta _{5} \bigl(ff_{yyyy}-4f_{y}f_{yyy}+3f_{yy}^{2} \bigr) \\ &\qquad{}+ \delta _{6}(ff_{yyy x}-f_{x}f_{yyy }-3f_{y}f_{yy x}+3f_{yy}f_{yx}) \bigr] \\ &\quad=\frac{ (\delta _{4} D_{x}^{4}+ D_{x}^{3}D_{y}+\delta _{3}D_{x}^{2}+D_{x}D_{\tau }+\delta _{2}D_{y}^{2}+\delta _{1}D_{x} D_{y}+\delta _{5} D_{y}^{4}+\delta _{6}D_{y}^{3}D_{x} )\mathfrak{f}. f}{2f^{2}}, \end{aligned}$$
(2.21)

in which \(\theta =\frac{1}{2}\Psi =\partial _{x}(\ln f)\) and \(\partial _{x}^{-1}(\cdot)=\int (\cdot)\,\mathrm{d}x\). Therefore, Eq. (2.21) is the fractional generalized CBS-BK equation. Therefore, the theorem is complete. □

3 Rogue wave solutions of a \((2+1)\)-D fractional gCBS-BK equation

For Eq. (2.1) with the obtained nonlinear PDE containing f, we get the combinations of positive functions, called a lump solution function:

$$ \begin{aligned}&f(x,y,\tau )= \Biggl(\sum_{i=1}^{4}a_{i}x_{i} \Biggr)^{2}+ \Biggl( \sum_{i=5}^{8}a_{i}x_{i} \Biggr)^{2}+a_{9},\\ &(x_{1}, x_{2}, x_{3}, x_{4})=(x_{5}, x_{6}, x_{7}, x_{8})=(x,y,\tau,1), \end{aligned} $$
(3.1)

and \(\tau =\frac{t^{\alpha }}{\Gamma (\alpha +1)}\) where \(a_{i}, i=1,\ldots,9\) are the optional parameters which we are to find subsequently. Plugging (3.1) into Eq. (2.6), we get ten sets of nonlinear algebraic equations and then collecting the coefficients including \(t,x,y\) and a constant, we obtain the following results for determining the solution function \(\Psi =\Psi _{0}+2 \partial _{x} (\ln f)\).

Case I:

$$\begin{aligned} &\Psi _{1}(x,y,t)\\ &\quad =\Psi _{0}+ \frac{4 ( \Omega a_{{2}}x+a_{{2}}y-{\frac{a_{{2}} ( {\Omega }^{ 2}\delta _{{3}}+\Omega \delta _{{1}}+\delta _{{2}} ) {t}^{\alpha } }{\Omega \Gamma ( \alpha +1 ) }}+a_{{4}} ) \Omega a _{{2}}+4 ( a_{{5}}x+{\frac{a_{{5}}y}{\Omega }}-{\frac{a_{{5}} ( {\Omega }^{2}\delta _{{3}}+\Omega \delta _{{1}}+\delta _{{2}} ) {t}^{\alpha }}{{\Omega }^{2}\Gamma ( \alpha +1 ) }}+ a_{{8}} ) a_{{5}} }{ ( \Omega a_{{2}}x+a_{{2}}y-{\frac{a_{{2}} ( {\Omega }^{2} \delta _{{3}}+\Omega \delta _{{1}}+\delta _{{2}} ) {t}^{\alpha }}{ \Omega \Gamma ( \alpha +1 ) }}+a_{{4}} ) ^{2}+ ( a_{{5}}x+{\frac{a_{{5}}y}{\Omega }}-{\frac{a_{{5}} ( { \Omega }^{2}\delta _{{3}}+\Omega \delta _{{1}}+\delta _{{2}} ) {t}^{\alpha }}{{\Omega }^{2}\Gamma ( \alpha +1 ) }}+a_{{8}} ) ^{2}+a_{{9}} }, \end{aligned}$$
(3.2)

where Ω solves \(\delta _{{4}}{\Omega }^{4}+{\Omega }^{3}+\delta _{{6}}\Omega +\delta _{{5}}=0, a_{9}>0\) and \(\Psi _{1}(x,y,t)\) is the lump solution.

Case II:

$$\begin{aligned} & a_{1}=a_{1},\qquad a_{2}=a_{2},\\ &a_{3}=- \frac{ ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ( a_{{1}}\delta _{{3} }+a_{{2}}\delta _{{1}} ) +\delta _{{2}} ( a_{{1}}{a_{{2}}}^{2 }-a_{{1}}{a_{{6}}}^{2}+2 a_{{2}}a_{{5}}a_{{6}} ) }{a_{1}^{2}+a_{5}^{2}},\qquad a_{4}=a_{4}, \\ &a_{5}=a_{5},\qquad a_{7}=a_{7}, \\ &a_{7}=- \frac{ ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ( a_{{5}}\delta _{{3} }+a_{{6}}\delta _{{1}} ) +\delta _{{2}} ( 2 a_{{1}}a_{{2}}a_{{6}}-{a_{{2}}}^{2}a_{{5}}+a_{{5}}{a_{{6}}}^{2} ) }{a_{1}^{2}+a_{5}^{2}},\qquad a_{8}=a_{8}, \\ &a_{9}=- \bigl(3 \bigl( \bigl( {a_{{1}}}^{2}+{a_{{5}}}^{2}\bigr) ^{2} ( a_{{1}}a_{{2}} +a_{{5}}a_{{6}}) +\delta _{{4}} \bigl( {a_{{1}}}^{2}+{a_{{5}}}^{ 2}\bigr) ^{3}+\delta _{{5}}( {a_{{2}}}^{2}+{a_{{6}}}^{2} ) ^{2} \bigl( {a_{{1}}}^{2}+{a_{{5}}}^{2} \bigr) \\ &\phantom{a_{9}=}{}+\delta _{{6}} \bigl( {a_{{2}}}^{2}+{a_{{6}}}^{2} \bigr) \bigl( {a_{{1}}}^{2}+{a_{ {5}}}^{2}\bigr) ( a_{{1}}a_{{2}}+a_{{5}}a_{{6}} ) \bigr)\bigr) \\ &\phantom{a_{9}=}{}/\bigl(\delta _{{2}} \bigl( a_{{1}}a_{{6}}-a_{{2}}a_{{5}}\bigr) ^{2}\bigr), \end{aligned}$$
(3.3)

then the function f will be

$$\begin{aligned} &f_{2}(x,y,t)= \biggl(a_{1}x+a_{2}y+a_{3} \frac{t^{\alpha }}{\Gamma (\alpha +1)}+a_{4} \biggr)^{2}+ \biggl(a_{5}x+a_{6}y+a_{7} \frac{t^{\alpha }}{\Gamma (\alpha +1)}+a_{8} \biggr)^{2}+a_{9}, \\ &\Psi _{2}(x,y,t) \\ &\quad=\Psi _{0}+ \frac{4a_{1} (a_{1}x+a_{2}y+a_{3}\frac{t^{\alpha }}{\Gamma (\alpha +1)}+a_{4} )+ 4a_{5} (a_{5}x+a_{6}y+a_{7}\frac{t^{\alpha }}{\Gamma (\alpha +1)}+a_{8} )}{f_{2}(x,y,t)}. \end{aligned}$$
(3.4)

Also, indeed we need to be ensured of the well-posedness, the positivity of \(f_{2}(x,y,t)\) and rational analysis and localization of the function \(\Psi _{2}\), respectively, which can be stated as

$$\begin{aligned} & \Delta = \begin{vmatrix} a_{1} & -a_{5} \\ a_{5} & a_{1} \end{vmatrix}\neq 0, \\ &\delta _{2} \bigl( \Delta ^{2}( a_{{1}}a_{{2}} +a_{{5}}a_{{6}}) + \delta _{{4}} \Delta ^{3}+\delta _{{5}}\Delta \bigl( {a_{{2}}}^{2}+{a_{{6}}}^{2} \bigr) ^{2} +\delta _{{6}} \Delta \bigl( {a_{{2}}}^{2}+{a_{{6}}}^{2} \bigr) ( a_{{1}}a_{{2}}+a_{{5}}a_{{6}} ) \bigr)< 0, \end{aligned}$$
(3.5)

and

$$ a_{{1}}a_{{6}}-a_{{2}}a_{{5}}\neq 0. $$

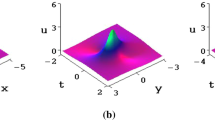
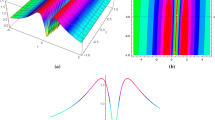
Moreover, by selecting the suitable values of parameters, the analytical treatment of periodic wave solution is presented in Figs. 1–3 including 3D plot, contour plot, density plot, and 2D plot when three spaces arise at spaces \(y=-5\), \(y=0\), and \(y=5\). By taking the new value parameters such as \(a_{1}= 1, a_{2}= 2, a_{4}= 2, a_{5}= 3, a_{6}= 1.2, a_{8}= 1, \delta _{1}= 1, \delta _{2}= -5, \delta _{3}= 1.5, \delta _{4}= 1.2, \delta _{5}= 1.4, \delta _{6}= 1.5, \Psi _{0}= 0, t = 2\), the corresponding the moving velocity and moving pass of the obtained lump in Case II are \(v=29.05009176\) and \(y=-1.030640668x+1.086367345x\). Also, a 2D plot of the lump–soliton by selecting the values of the different fractional order α is depicted in Fig. 4.

Figure 1
figure 1

The plot of rogue wave (3.5) with fractional order \(\alpha =0.5\)

Full size image
Figure 2
figure 2

The plot of rogue wave (3.5) with fractional order \(\alpha =0.8\)

Full size image
Figure 3
figure 3

The plot of rogue wave (3.5) with fractional order \(\alpha =1.0\)

Full size image
Figure 4
figure 4

The 2D plot of lump–soliton (3.5) with the different fractional orders

Full size image

Remark 3.1

Because of using a simple computation, the lump has two critical points, but we investigate only one point \((x_{1}, y_{1}) = ({\frac{1}{a_{{1}}a_{{6}}-a_{{2}}a_{{5}}} ( { \frac{{t}^{\alpha } ( a_{{2}}a_{{7}}-a_{{3}}a_{{6}} ) }{\Gamma ( \alpha + 1 ) }}+a_{{2}}a_{{8}}-a_{{4}}a_{{6}} ) }+{ \frac{ \sqrt{a_{{9}} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) }}{{a_{{1}}}^{2}+{a_{ {5}}}^{2}}}, -{ \frac{1}{a_{{1}}a_{{6}}-a_{{2}}a_{{5}}} ( { \frac{{t}^{\alpha } ( a_{{1}}a_{{7}}-a_{{3}}a_{{5}} ) }{\Gamma ( \alpha + 1 ) }}+a_{{1}}a_{{8}}-a_{{4}}a_{{5}} ) } )\). At the point \((x_{1}, y_{1})\), the second-order derivative and the Hessian matrix can be determined given by [12]

$$ \textstyle\begin{cases} \Theta {1}= \frac{\partial ^{2}}{\partial x^{2}}\Psi (x,y) |_{(x_{1},y_{1})}= -{ \frac{2 \sqrt{a_{{9}} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) } ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) }{{a_{{9}}}^{2}}}, \\ \Delta _{1}= \det \begin{pmatrix} \frac{\partial ^{2}}{\partial x^{2}}\Psi (x,y) & \frac{\partial ^{2}}{\partial x \,\partial y}\Psi (x,y) \\ \frac{\partial ^{2}}{\partial x \,\partial y}\Psi (x,y) & \frac{\partial ^{2}}{\partial y^{2}}\Psi (x,y) \end{pmatrix}_{(x_{1},y_{1})}={ \frac{ 4 ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ( {a_{{1} }}^{2}{a_{{6}}}^{2}-2 a_{{1}}a_{{2}}a_{{5}}a_{{6}}+{a_{{2}}}^{2}{a_{{ 5}}}^{2} ) }{{a_{{9}}}^{3}}}. \end{cases} $$
(3.6)

If \({a_{{9}}}^{3} ( {a_{{1}}}^{2}{a_{{6}}}^{2}-2 a_{{1}}a_{{2}}a_{{5 }}a_{{6}}+{a_{{2}}}^{2}{a_{{5}}}^{2} ) >0\), then the point \((x_{1}, y_{1})\) is an extreme value point. Based on above analysis, the point \((x_{1}, y_{1})\) is a maximum value point at \(\Psi _{\max }\). By using the different values of \(\delta _{i}, i=1,\ldots,5\), the lump solution \(\Psi (x,y)\) has one maximum value containing

$$ \Psi _{\max }={ \frac{2\sqrt{a_{{9}} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) } }{a_{{9}}}}. $$

Remark 3.2

For three cases, it can be seen from Eqs. (3.3)–(3.5) in which the lump solution tends to 0 at any given time t when \((\sum_{i=1}^{4}a_{i}x_{i} )^{2}+ (\sum_{i=5}^{8}a_{i}x_{i} )^{2}\rightarrow 0\), or equivalently, \(x^{2}+y^{2}\rightarrow 0\). By utilizing

$$ \frac{\partial \Psi }{\partial x}=0, \qquad\frac{\partial \Psi }{\partial y}=0, $$
(3.7)

in which \(\Psi =\Psi _{0}+2 \partial _{x} (\ln (\sum_{i=1}^{4}a_{i}x_{i} )^{2}+ (\sum_{i=5}^{8}a_{i}x_{i} )^{2}+a_{9} )\) the moving path of this lump can be determined as

$$ \textstyle\begin{cases} x={\frac{1}{a_{{1}}a_{{6}}-a_{{2}}a_{{5}}} ( { \frac{{t}^{\alpha } ( a_{{2}}a_{{7}}-a_{{3}}a_{{6}} ) }{\Gamma ( \alpha + 1 ) }}+a_{{2}}a_{{8}}-a_{{4}}a_{{6}} ) }+{ \frac{ \sqrt{a_{{9}} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) }}{{a_{{1}}}^{2}+{a_{ {5}}}^{2}}}, \\ y=-{\frac{1}{a_{{1}}a_{{6}}-a_{{2}}a_{{5}}} ( { \frac{{t}^{\alpha } ( a_{{1}}a_{{7}}-a_{{3}}a_{{5}} ) }{\Gamma ( \alpha + 1 ) }}+a_{{1}}a_{{8}}-a_{{4}}a_{{5}} ) }, \end{cases} $$
(3.8)

also the moving velocity and the maximum amplitude, respectively, read

$$ v=\sqrt{{ \frac{ ( a_{{2}}a_{{7}}-a_{{3}}a_{{6}} ) ^{2}+ ( a_{ {1}}a_{{7}}-a_{{3}}a_{{5}} ) ^{2}}{a_{{1}}a_{{6}}-a_{{2}}a_{{5}} }} }, \qquad H=4, $$
(3.9)

and the moving pass will be

$$ y={ \frac{a_{{3}}a_{{8}}-a_{{4}}a_{{7}}}{a_{{2}}a_{{7}}-a_{{3}}a_{{6}} }}+{ \frac{a_{{1}}a_{{7}}-a_{{3}}a_{{5}} \sqrt{a_{{9}} ( {a_{{1}} }^{2}+{a_{{5}}}^{2} ) }}{ ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ( a_{{2}}a_{{7}}-a_{{3}}a_{{6}} ) }}-{ \frac{ ( a_{{1}}a_{{7}}-a_{{3}}a_{{5}} ) x}{a_{{2}}a_{{7}}-a_{{3} }a_{{6}}}}. $$
(3.10)

It is worth mentioning that this rogue wave has the following features:

$$ \lim_{x\longrightarrow \pm \infty }\Psi (x,y)=\Psi _{0},\qquad \lim_{y\longrightarrow \pm \infty }\Psi (x,y)=\Psi _{0}. $$
(3.11)

4 Lump–kink solutions

In this section, for Eq. (2.1) with the obtained nonlinear PDE containing f, we get the combinations of positive functions and exponential function called a lump–kink solution. Necessary and sufficient conditions for positive quadratic functions to solve the Hirota bilinear equations conclude the study of lump solutions. Take the following function form:

$$ \begin{aligned}&f(x,y,\tau )= \Biggl(\sum_{i=1}^{4}a_{i}x_{i} \Biggr)^{2}+ \Biggl( \sum_{i=5}^{8}a_{i}x_{i} \Biggr)^{2}+\exp \Biggl(\sum_{i=9}^{12}a_{i}x_{i} \Biggr)+a_{13},\\ & (x_{1,5,9}, x_{2,6,10}, x_{3,7,11}, x_{4,8,12})=(x,y,\tau,1), \end{aligned} $$
(4.1)

where \(\tau =\frac{t^{\alpha }}{\Gamma (\alpha +1)}\) and \(a_{i}, i=1,\ldots,13\), are the optional parameters which we are to find subsequently. Putting (4.1) into Eq. (2.6), we get 20 sets of nonlinear algebraic equations and then collecting the coefficients including \(e^{\sum _{i=9}^{12}a_{i}x_{i}}\), \(\tau,x,y\) and a constant, we obtain the following results for finding the solution function \(\Psi =\Psi _{0}+2 \partial _{x} (\ln f)\).

Case I:

$$\begin{aligned} & \Psi _{1}(x,y,t)\\ &\quad =\Psi _{0}+ \frac{4 ( a_{{5}}x+{\frac{a_{{7}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} ) a_{{5}} }{ ( a_{{2}}y-{\frac{a_{{2}}\delta _{{1}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{4}} ) ^{2}+ ( a_{{5}}x+{ \frac{a_{{7}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} ) ^{2}+a_{{13}}+{{\mathrm{e}}^{a_{{10}}y-{\frac{a_{{10}} ( {a_{{10}}}^{2}\delta _{{6}}+\delta _{{1}} ) {t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{12}}}}}. \end{aligned}$$
(4.2)

Case II:

$$\begin{aligned} & \Psi _{2}(x,y,t)\\ &\quad =\Psi _{0}+ \frac{2 a_{{9}}{{\mathrm{e}}^{-a_{{9}} ( {a_{{9}}}^{2}\delta _{{4}}+\delta _{ {3}} ) t+a_{{9}}x+a_{{12}}}} }{ ( -ta_{{2}} ( {a_{{9}}}^{2}+\delta _{{1}} ) +a_{{2}}y+ a_{{4}} ) ^{2}+ ( ( -a_{{6}}{a_{{9}}}^{2}-a_{{6}} \delta _{{1}} ) t+ya_{{6}}+a_{{8}} ) ^{2}+a_{{13}}+{{\mathrm{e}} ^{-a_{{9}} ( {a_{{9}}}^{2}\delta _{{4}}+\delta _{{3}} ) t+a_{ {9}}x+a_{{12}}}} }. \end{aligned}$$
(4.3)

Case III:

$$\begin{aligned} &f_{3}(x,y,t)= \biggl( a_{{2}}y+{ \frac{a_{{3}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{4}} \biggr) ^{2}+ \biggl( a_{{5}}x+{ \frac{a_{{5}}a_{{ 10}}y}{a_{{9}}}}+{ \frac{a_{{7}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+4 { \frac{a_{{5}}}{a_{{9}}}} \biggr) ^{2} \end{aligned}$$
(4.4)
$$\begin{aligned} &\phantom{f_{3}(x,y,t)= }{}-\frac{1}{2}{ \frac{3 {a_{{2}}}^{2}{a_{{9}}}^{5}-2 {a_{{5}}}^{2}{a_{{10}}}^{3}\delta _{{2} }}{{a_{{9}}}^{2}{a_{{10}}}^{3}\delta _{{2}}}}+{{\mathrm{e}}^{a_{{9}}x+a_{{10 }}y-\frac{1}{3}{ \frac{a_{{9}} ( 2 {a_{{2}}}^{2}\delta _{{2}}-3 a_{{5} }a_{{7}} ) {t}^{\alpha }}{{a_{{5}}}^{2}\Gamma ( \alpha +1 ) }}+a_{{12}}}}, \\ & \Psi _{3}(x,y,t)\\ &\quad =\Psi _{0}+ \frac{4 ( a_{{5}}x+{\frac{a_{{5}}a_{{10}}y}{a_{{9}}}}+{\frac{a_{{7} }{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+4 {\frac{a_{{5}}}{ a_{{9}}}} ) a_{{5}}+2a_{{9}}{{\mathrm{e}}^{a_{{9}}x+a_{{10}}y-\frac{1}{3}{ \frac{a_{{9}} ( 2 {a_{{2}}}^{2}\delta _{{2}}-3 a_{{5}}a_{{7}} ) {t}^{\alpha }}{{a_{{5}}}^{2}\Gamma ( \alpha +1 ) }} +a_{{12}}}} }{f_{3}(x,y,t)}. \end{aligned}$$
(4.5)

Moreover, by selecting the suitable values of parameters, the analytical treatment of periodic wave solution is presented in Figs. 5 and 6 including 3D plot, contour plot, density plot, and 2D plot when three spaces arise at spaces \(y=-5\), \(y=0\), and \(y=5\). By taking the new value parameters \(a_{2}= 1.2, a_{3}= 1.4, a_{4}= 2, a_{5}= 1.5, a_{9}= 1.7, a_{10}= 1.2, a_{12}=1.5, \delta _{2}= 3, \Psi _{0}= 1, t = 2\), the obtained lump–kink solutions in Case II are presented with two different fractional orders. Also, 2D plot of the lump–soliton by selecting the values of the different fractional order α is depicted in Fig. 7.

Figure 5
figure 5

The plot of lump–kink (4.5) with fractional order \(\alpha =0.5\)

Full size image
Figure 6
figure 6

The plot of lump–kink (4.5) with fractional order \(\alpha =0.95\)

Full size image
Figure 7
figure 7

The 2D plot of lump–kink (4.5) with the different fractional orders

Full size image

Case IV:

$$\begin{aligned} &f_{4}(x,y,t)= \biggl( ta_{{3}}+{ \frac{ \sqrt{{a_{{5}}}^{2}{a_{{10}}}^{2}-{a_{{6}}}^{2}{a_{{9}}}^{2}}y}{a_{{9}}}}+a_{{4}} \biggr) ^{2}+ \biggl( a_{{7}}t+xa _{{5}}+ya_{{6}}+4 {\frac{a_{{5}}}{a_{{9}}}} \biggr) ^{2} \end{aligned}$$
(4.6)
$$\begin{aligned} &\phantom{f_{4}(x,y,t)=}{}+a_{{13}}+{ {\mathrm{e}}^{{ \frac{ ( \sqrt{{a_{{5}}}^{2}{a_{{10}}}^{2}-{a_{{6}}}^{2}{a_{{9}}}^{2}}a_{{7}}+a_{{3}}a_{{5}}a_{{10}}-a_{{3}}a_{{6}}a_{{9}} ) a_{{9}}t}{a_{{5}} \sqrt{{a_{{5}}}^{2}{a_{{10}}}^{2}-{a_{{6}}} ^{2}{a_{{9}}}^{2}}}}+a_{{9}}x+a_{{10}}y+a_{{12}}}}, \\ &\Psi _{4}(x,y,t)\\ &\quad =\Psi _{0}+ \frac{4 ( a_{{7}}t+xa_{{5}}+ya_{{6}}+4 {\frac{a_{{5}}}{a_{{9}}}} ) a_{{5}}+2a_{{9}}{{\mathrm{e}}^{{\frac{ ( \sqrt{{a_{{5}}}^{2} {a_{{10}}}^{2}-{a_{{6}}}^{2}{a_{{9}}}^{2}}a_{{7}}+a_{{3}}a_{{5}}a_{{10 }}-a_{{3}}a_{{6}}a_{{9}} ) a_{{9}}t}{a_{{5}}\sqrt{{a_{{5}}}^{2} {a_{{10}}}^{2}-{a_{{6}}}^{2}{a_{{9}}}^{2}}}}+a_{{9}}x+a_{{10}}y+a_{{12 }}}} }{f_{4}(x,y,t)}. \end{aligned}$$
(4.7)

Case V:

$$\begin{aligned} &\Psi _{4}(x,y,t)\\ &\quad =\Psi _{0}+{ \frac{4 ( -ta_{{1}}\delta _{{3}}+xa_{{1}}+a_{{4}} ) a _{{1}}+2 ( -ta_{{5}}\delta _{{3}}+xa_{{5}}+a_{{8}} ) a_{{5 }}}{ ( -ta_{{1}}\delta _{{3}}+xa_{{1}}+a_{{4}} ) ^{2}+2 ( -ta_{{5}}\delta _{{3}}+xa_{{5}}+a_{{8}} ) ^{2}+a_{{13}}+{ {\mathrm{e}}^{ ( -{a_{{10}}}^{3}\delta _{{6}}-a_{{10}}\delta _{{1}} ) t+a_{{10}}y+a_{{12}}}}}}. \end{aligned}$$
(4.8)

5 Lump–soliton solutions

In this section, to obtain to lump–soliton solutions, assume f to be as follows:

$$ \begin{aligned}&f(x,y,\tau )= \Biggl(\sum_{i=1}^{4}a_{i}x_{i} \Biggr)^{2}+ \Biggl( \sum_{i=5}^{8}a_{i}x_{i} \Biggr)^{2}+\cosh \Biggl(\sum_{i=9}^{12}a_{i}x_{i} \Biggr)+a_{13}, \\ &(x_{1,5,9}, x_{2,6,10}, x_{3,7,11}, x_{4,8,12})=(x,y,\tau,1), \end{aligned} $$
(5.1)

where \(\tau =\frac{t^{\alpha }}{\Gamma (\alpha +1)}\) and \(a_{i}, i=1,\ldots,13\), are the optional parameters in which are to find subsequently. Substituting (4.8) into Eq. (2.6), we get 24 sets of nonlinear algebraic equations and then collecting the coefficients including \(\cosh (\sum_{i=9}^{12}a_{i}x_{i} )\), \(\sinh (\sum_{i=9}^{12}a_{i}x_{i} )\), \(t,x,y\) and a constant, we obtain the following results for determining the solution function \(\Psi =\Psi _{0}+2 \partial _{x} (\ln f)\).

Case I:

$$\begin{aligned} f_{1}={}& \biggl( xa_{{1}}-{ \frac{y ( {a_{{1}}}^{2}\delta _{{4}}+{a_{{5}}}^{2}\delta _{{4}}+a_{{5}}a_{{6}} ) }{a_{{1}}}} \end{aligned}$$
(5.2)
$$\begin{aligned} &{}+{ \frac{ ( {a_{{1}}}^{2}\delta _{{1}}\delta _{{4}}+{a_{{5}}}^{2}\delta _{{1}}\delta _{{4 }}-{a_{{1}}}^{2}\delta _{{3}}+a_{{5}}a_{{6}}\delta _{{1}} ) {t}^{ \alpha }}{a_{{1}}\Gamma ( \alpha +1 ) }}+a_{{4}} \biggr) ^{2 } \\ &{}+\biggl( xa_{{5}}+ya_{{6}}+{ \frac{ ( -a_{{5}}\delta _{{3}}-a_{{6 }}\delta _{{1}} ) {t}^{\alpha }}{\Gamma ( \alpha +1 ) } }+a_{{8}} \biggr) ^{2}+a_{{13}}+\cosh \biggl( a_{{10}}y-{ \frac{a_{{10} }\delta _{{1}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{12}} \biggr), \\ \Psi _{1}={}&\Psi _{0}+ \biggl(4 \biggl( xa_{{1}}-{\frac{y ( {a_{{1}}}^{2}\delta _{{4}}+{a_{{5} }}^{2}\delta _{{4}}+a_{{5}}a_{{6}} ) }{a_{{1}}}}\\ &{}+{\frac{ ( {a_{{1}}}^{2}\delta _{{1}}\delta _{{4}}+{a_{{5}}}^{2}\delta _{{1}}\delta _{{4}}-{a_{{1}}}^{2}\delta _{{3}}+a_{{5}}a_{{6}}\delta _{{1}} ) {t} ^{\alpha }}{a_{{1}}\Gamma ( \alpha +1 ) }}+a_{{4}} \biggr) a _{{1}} \\ &{}+4 \biggl( xa_{{5}}+ya_{{6}}-{\frac{ ( a_{{5}}\delta _{{3 }}+a_{{6}}\delta _{{1}} ) {t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} \biggr) a_{{5}}\biggr)\Big/f_{1}. \end{aligned}$$
(5.3)

Case II:

$$\begin{aligned} f_{2}={}& \biggl( xa_{{1}}-{\frac{a_{{5}}a_{{6}}y}{a_{{1}}}}-{ \frac{ ( {a _{{1}}}^{2}\delta _{{3}}+{a_{{5}}}^{2}\delta _{{3}}+a_{{5}}a_{{7}} ) {t}^{\alpha }}{a_{{1}}\Gamma ( \alpha +1 ) }}+a_{{4 }} \biggr) ^{2} \end{aligned}$$
(5.4)
$$\begin{aligned} &{}+\biggl( xa_{{5}}+ya_{{6}}+{ \frac{a_{{7}}{t}^{\alpha } }{\Gamma ( \alpha +1 ) }}+a_{{8}} \biggr) ^{2}+a_{{13}} \\ &{}+ \cosh \biggl( a_{{10}}y+{ \frac{a_{{10}} ( -a_{{6}}{a_{{10}}}^{2} \delta _{{6}}+a_{{5}}\delta _{{3}}+a_{{7}} ) {t}^{\alpha }}{a_{{6}} \Gamma ( \alpha +1 ) }}+a_{{12}} \biggr), \\ \Psi _{2}={}&\Psi _{0}\\ &{}+ \frac{4 ( xa_{{1}}-{\frac{a_{{5}}a_{{6}}y}{a_{{1}}}}-{\frac{ ( {a_{{1}}}^{2}\delta _{{3}}+{a_{{5}}}^{2}\delta _{{3}}+a_{{5}}a_{ {7}} ) {t}^{\alpha }}{a_{{1}}\Gamma ( \alpha +1 ) }}+a _{{4}} ) a_{{1}}+4 ( xa_{{5}}+ya_{{6}}+{\frac{a_{{7}}{t} ^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} ) a_{{5}} }{f_{2}}. \end{aligned}$$
(5.5)

Case III:

$$\begin{aligned} &a_{{1}}= \frac{ \sqrt{ ( 16 \delta _{{4}}{\delta _{{5}}}^{3}-{ \delta _{{6}}}^{4}-8 {\delta _{{5}}}^{2}\delta _{{6}} ) ( - 16 {a_{{5}}}^{2}\delta _{{4}}{\delta _{{5}}}^{3}+{a_{{5}}}^{2}{\delta _{ {6}}}^{4}+8 {a_{{5}}}^{2}{\delta _{{5}}}^{2}\delta _{{6}}+2 \sqrt{-16 {\delta _{{2}}}^{2}\delta _{{4}}{\delta _{{5}}}^{5}+{\delta _{{2}}}^{2}{ \delta _{{5}}}^{2}{\delta _{{6}}}^{4}+8 {\delta _{{2}}}^{2}{\delta _{{5}} }^{4}\delta _{{6}}} ) }}{16 \delta _{{4}}{\delta _{{5}}}^{3}-{ \delta _{{6}}}^{4}-8 {\delta _{{5}}}^{2}\delta _{{6}}}, \end{aligned}$$
(5.6)
$$\begin{aligned} &a_{{2}}=\frac{1}{2}{ \frac{a_{{1}}{a_{{10}}}^{2}\delta _{{6}}}{\delta _{{2}}}},\qquad a_{{3}}=- \frac{1}{4}{ \frac{a_{{1}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2}- 2 a_{{10}}a_{{11}}\delta _{{6}}+4 \delta _{{2}}\delta _{{3}} ) }{ \delta _{{2}}}},\qquad a_{4}=a_{4}, \\ & a_{5}=a_{5},\qquad a_{{6}}=\frac{1}{2}{ \frac{a_{{5}}{a_{{10}}}^{2}\delta _{{6}}}{\delta _{{2}}}}, \\ &a_{{7}}=-{ \frac{a_{{5}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2}- 2 a_{{10}}a_{{11}}\delta _{{6}}+4 \delta _{{2}}\delta _{{3}} ) }{ 4\delta _{{2}}}},\qquad a_{8}=a_{8},\qquad a_{9}=0, \\ & a_{{10}}={ \frac{ \sqrt{-\delta _{{5}}\delta _{{2}}}}{\delta _{{5}}}},\qquad a_{{11}}=-{ \frac{\delta _{{1}} \sqrt{-\delta _{{5}}\delta _{{2}}}}{ \delta _{{5}}}},\qquad a_{12}=a_{12} \\ &\Psi _{3}=\Psi _{0}+ \frac{4 ( a_{{1}}x+a_{{2}}y+{\frac{a_{{3}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{4}} ) a_{{1}}+4 ( a_{{5}} x+a_{{6}}y+{\frac{a_{{7}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} ) a_{{5}} }{ ( a_{{1}}x+a_{{2}}y+{\frac{a_{{3}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{4}} ) ^{2}+ ( a_{{5}}x+a_{{6}}y+{ \frac{a_{{7}}{t}^{\alpha }}{\Gamma ( \alpha +1 ) }}+a_{{8}} ) ^{2}+{{\mathrm{e}}^{a_{{10}}y+{\frac{a_{{11}}{t}^{\alpha }}{ \Gamma ( \alpha +1 ) }}+a_{{12}}}}+a_{{13}} }. \end{aligned}$$
(5.7)

The existence condition of solution is of the form

$$\begin{aligned} &\bigl( 16 \delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{6}}}^{4}-8 { \delta _{{5}}}^{2}\delta _{{6}} \bigr) \bigl( -16 {a_{{5}}}^{2} \delta _{{4}}{\delta _{{5}}}^{3}+{a_{{5}}}^{2}{ \delta _{{6}}}^{4}+8 {a_{{5}}}^{2}{\delta _{{5}}}^{2}\delta _{{6}} \\ &\quad{}+2 \sqrt{-16 {\delta _{{2}}}^{2} \delta _{{4}}{\delta _{{5}}}^{5}+{ \delta _{{2}}}^{2}{\delta _{{5}}}^{2}{ \delta _{{6}}}^{4}+8 {\delta _{{2}}}^{2}{ \delta _{{5}}}^{4}\delta _{{6}}} \bigr) >0 \end{aligned}$$

and

$$ 16 \delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{6}}}^{4}-8 {\delta _{{5}} }^{2}\delta _{{6}}< 0. $$

Case IV:

$$\begin{aligned} &f_{4}= \biggl( -\frac{1}{4}{ \frac{ta_{{1}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2} +2 {a_{{10}}}^{2}\delta _{{1}}\delta _{{6}}+4 \delta _{{2}}\delta _{{3}} ) }{\delta _{{2}}}}+a_{{1}}x+1/2 { \frac{ya_{{1}}{a_{{10}}}^{2} \delta _{{6}}}{\delta _{{2}}}}+a_{{4}} \biggr) ^{2} \end{aligned}$$
(5.8)
$$\begin{aligned} &\phantom{f_{4}=}{}+\biggl( -\frac{1}{4}{ \frac{ta_{{5}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2}+2 {a_{{10}}}^{2}\delta _{{1}}\delta _{{6}}+4 \delta _{{2}}\delta _{{3}} ) }{ \delta _{{2}}}}+a_{{5}}x+{ \frac{ya_{{5}}{a_{{10}}}^{2}\delta _{{6} }}{2\delta _{{2}}}}+{\frac{a_{{4}}a_{{5}}}{a_{{1}}}} \biggr) ^{2} \\ &\phantom{f_{4}=}{}+a_{{ 13}}+ \cosh ( -ta_{{10}}\delta _{{1}}+a_{{10}}y+a_{{12}} ), \\ &\Psi _{4}=\Psi _{0}+\frac{1}{f_{4}} \biggl[ 4 \biggl( -{ \frac{ta_{{1}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2}+2 {a_{{10}}}^{2}\delta _{{1}}\delta _{{6}}+4 \delta _{{2}}\delta _{{ 3}} ) }{4\delta _{{2}}}}+a_{{1}}x+{ \frac{ya_{{1}}{a_{{10}}}^{2}\delta _{{6}}}{2\delta _{{2}}}}+a_{{4}} \biggr) a_{{1}} \\ &\phantom{\Psi _{4}=}{}+ 4 \biggl( -{ \frac{ta_{{5}} ( {a_{{10}}}^{4}{\delta _{{6}}}^{2}+2 {a_{{10 }}}^{2}\delta _{{1}}\delta _{{6}}+4 \delta _{{2}}\delta _{{3}} ) }{4\delta _{{2}}}}+a_{{5}}x+{ \frac{ya_{{5}}{a_{{10}}}^{2}\delta _{{6} }}{2\delta _{{2}}}}+{\frac{a_{{4}}a_{{5}}}{a_{{1}}}} \biggr) a_{{5}} \biggr], \end{aligned}$$
(5.9)

in which

$$\begin{aligned} &a_{10}={\frac{ \sqrt{-\delta _{{5}}\delta _{{2}}}}{\delta _{{5}}}},\\ & a_{1}={ \frac{ \sqrt{ ( 16\delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{6} }}^{4}-8{\delta _{{5}}}^{2}\delta _{{6}} ) ( -{a_{{5}}}^{2 } ( 16\delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{6}}}^{4}-8{ \delta _{{5}}}^{2}\delta _{{6}} ) +2 \sqrt{-{\delta _{{2}}}^{2}{ \delta _{{5}}}^{2} ( 16\delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{ 6}}}^{4}-8{\delta _{{5}}}^{2}\delta _{{6}} ) } ) }}{16 \delta _{{4}}{\delta _{{5}}}^{3}-{\delta _{{6}}}^{4}-8{\delta _{{5}}}^{2 }\delta _{{6}}}}. \end{aligned}$$

Case V:

$$\begin{aligned} & a_{1}=a_{1},\qquad a_{{2}}= \frac{1}{2}{ \frac{a_{{9}}a_{{10}} ( 2 {a_{{1}}}^{2}a_{{13}}-{ a_{{9}}}^{2} ) }{a_{{1}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1 }}}^{2} ) }},\qquad a_{4}=a_{4},\qquad a_{5}=0, \end{aligned}$$
(5.10)
$$\begin{aligned} & a_{8}=a_{8},\qquad a_{9}=a_{9},\qquad a_{10}=a_{10},\qquad a_{12}=a_{12}, \\ &a_{{3}}=-{ \frac{1}{2{a_{{9}} }^{2} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) ^{2}{a_{{ 1}}}^{3}}} \bigl[{a_{{1}}}^{2}{a_{{9}}}^{3}a_{{10}} \delta _{{1}} \bigl( 2 {a_{{1}}}^{2}a_{{13}}-{a_{{9}}}^{2} \bigr) \bigl( -{a_{{9 }}}^{2}a_{{13}}+2 {a_{{1}}}^{2} \bigr) \\ &\phantom{a_{{3}}=}{}- {a_{{10}}}^{2}\delta _{{2}} \bigl( -2 {a_{{1}}}^{4}{a_{{9}}}^{4}{a_{{13}}}^{2}-8 {a_{{1}}}^{6}{ a_{{9}}}^{2}a_{{13}}+4 {a_{{1}}}^{2}{a_{{9}}}^{6}a_{{13}}+8 {a_{{1}} }^{8}-{a_{{9}}}^{8} \bigr) \\ &\phantom{a_{{3}}=}{}+2 {a_{{1}}}^{4}{a_{{9}}}^{2} \delta _{{3}} \bigl( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} \bigr) ^{2} \bigr], \\ &a_{6}=\frac{1}{2}{ \frac{a_{{10}} \sqrt{-16 {a_{{1}}}^{6}{a_{{9}}}^{2}a_{{13}}+4 {a_{{1}}}^{2}{a_{{9}}}^{6}a_{{13}}+16 {a_{{1}}}^{8}-{a_{{9}}}^{8}} }{ ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) a_{{9}}a_{{1 }}}}, \\ &a_{{7}}=-\frac{1}{2} \bigl(a_{{10}} \sqrt{-16 {a_{{1}}}^{6}{a_{{9}}}^{2}a_{{13}}+4 {a_{{1}}}^{2}{a_{{9}}}^{6}a_{{13}}+16 {a_{{1}}}^{8}-{a_{{9} }}^{8}} \bigl( {a_{{1}}}^{2}\delta _{{1}} ( -{a_{{9}}}^{2}a_{{13}} +2 {a_{{1}}}^{2} ) \\ &\phantom{a_{{7}}=}{}+a_{{9}}a_{{10}}\delta _{{2}} \bigl( 2 {a_{{ 1}}}^{2}a_{{13}}-{a_{{9}}}^{2} \bigr) \bigr)\bigr) \\ &\phantom{a_{{7}}=}/\bigl( \bigl( -{a_{{9}}}^{ 2}a_{{13}}+2 {a_{{1}}}^{2} \bigr) ^{2}a_{{9}}{a_{{1}}}^{3}\bigr), \\ &a_{{11}}=-\frac{1}{3}{ \frac{{a_{{10}}}^{2}\delta _{{2}} ( {a_{{9}}}^{2} a_{{13}}{a_{{1}}}^{2}+2 {a_{{1}}}^{4}-{a_{{9}}}^{4} ) +3 {a_{{ 1}}}^{2}a_{{9}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) ( a_{{9}}\delta _{{3}}+a_{{10}}\delta _{{1}} ) }{{a _{{1}}}^{2}a_{{9}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) }}, \\ & f_{5}= \biggl(a_{1}x+a_{2}y+ \frac{a_{3}t^{\alpha }}{\Gamma (\alpha +1)}+a_{4} \biggr)^{2}+ \biggl(a_{6}y+ \frac{a_{6}t^{\alpha }}{\Gamma (\alpha +1)}+a_{8} \biggr)^{2}\\ &\phantom{f_{5}=}{}+ \cosh \biggl(a_{9}x+a_{10}y+ \frac{a_{11}t^{\alpha }}{\Gamma (\alpha +1)}+a_{12} \biggr)+a_{13}, \\ &\Psi _{5}=\Psi _{0}+\frac{2 d f_{5}/dx}{f_{5}}. \end{aligned}$$
(5.11)

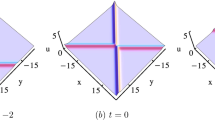
Also, by selecting the suitable values of parameters, the analytical treatment of periodic wave solution is presented in Figs. 8 and 9 including 3D plot, contour plot, density plot, and 2D plot when three spaces arise at spaces \(x=-1\), \(x=-3\), and \(x=-5\). By taking the new value parameters \(a_{1}= 1.2, a_{4}= 2, a_{5}= 1.5, a_{8}= 1.1, a_{9}= 2, a_{10}= 1, a_{12}= 1.5, a_{13}= 3, \delta _{1}= 2, \delta _{2} = -2, \delta _{3}= 1.5, \delta _{6}= 1.5, \Psi _{0}= 1, y = 1.5, t = 2\), the obtained lump–soliton solutions in Case V are presented with two different fractional orders. Also, a 2D plot of the lump–soliton by selecting values of the different fractional order α is depicted in Fig. 10. As pointed out above the positive polynomial functions and hyperbolic cosine function have the forms

$$\begin{aligned} &\Delta _{1}=\Delta _{11}^{2}= \biggl(a_{1}x+a_{2}y+ \frac{a_{3}t^{\alpha }}{\Gamma (\alpha +1)}+a_{4} \biggr)^{2}, \qquad\Delta _{2}=\Delta _{12}^{2}= \biggl(a_{6}y+ \frac{a_{6}t^{\alpha }}{\Gamma (\alpha +1)}+a_{8} \biggr)^{2}, \\ &\Delta _{3}=\cosh (\Delta _{13})=\cosh \biggl(a_{9}x+a_{10}y+ \frac{a_{11}t^{\alpha }}{\Gamma (\alpha +1)}+a_{12} \biggr), \end{aligned}$$

by investigating the asymptotic behavior of a lump and resonance soliton pairs we have the following relations between \(\Delta _{11}\) and \(\Delta _{13}\):

$$\begin{aligned} \Delta _{11}={}&\frac{1}{2}{ \frac{a_{{9}} ( 2 {a_{{1}}}^{2}a_{{13}}-{a_{{9}}}^{2} ) }{a_{{1}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) }}\Delta _{13}+{ \frac{-4 {a_{{9}}}^{2}a_{{13}}{a_{{1}}}^{2}+4 {a_{{1}}}^{4}+{ a_{{9}}}^{4}}{2a_{{1}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) }}x\\ &{}+{ \frac{-2 {a_{{1}}}^{2}a_{{9}}a_{{12}}a_{{13}}-2 a_{{1}}a_{{4} }{a_{{9}}}^{2}a_{{13}}+4 {a_{{1}}}^{3}a_{{4}}+{a_{{9}}}^{3}a_{{12}}}{2 a_{{1}} ( -{a_{{9}}}^{2}a_{{13}}+2 {a_{{1}}}^{2} ) }} \\ &{}-\frac{1}{6} \bigl( \bigl( -4{a_{{9}}}^{2}a_{{13}}{a_{{1}}}^{2}+4{a_{{1 }}}^{4}+{a_{{9}}}^{4} \bigr) \\ &{}\times \bigl( -3{a_{{1}}}^{2}{a_{{9}}}^{4}a_{{13}}\delta _{{3}}-{a_{{1}}}^{2}{a_{{9}}}^{2}{a_{{10}}}^{2}a_{{13}} \delta _{{2}}+6{a_{{1}}}^{4}{a_{{9}}}^{2}\delta _{{3}}-6{a_{{1}}}^{4 }{a_{{10}}}^{2}\delta _{{2}}+2{a_{{9}}}^{4}{a_{{10}}}^{2}\delta _{{2}} \bigr) \bigr)\\ &{}/\bigl({a_{{9}}}^{2} \bigl( -{a_{{9}}}^{2}a_{{13}}+2{a_{{1}}}^{2 } \bigr) ^{2}{a_{{1}}}^{3}\bigr)\frac{t^{\alpha }}{\Gamma (\alpha +1)}, \end{aligned}$$

also the limited relations in which arise for \(\Delta _{11}\) and \(\Delta _{13}\) are of the form

$$\begin{aligned} &\lim_{t\rightarrow \pm \infty } \frac{\Delta _{11}}{\Delta _{12}}\\ &\quad= \bigl(6\Gamma (\alpha +1){a_{{9}}}^{2} \bigl( -{a_{{9}}}^{2}a_{{13}}+2{a_{{1}}}^{2 } \bigr) ^{2}{a_{{1}}}^{4}\bigr)\\ &\qquad{}/\bigl( \bigl(4{a_{{1 }}}^{4}+{a_{{9}}}^{4} -4{a_{{9}}}^{2}a_{{13}}{a_{{1}}}^{2} \bigr) \\ &\qquad{}\times \bigl( -3{a_{{1}}}^{2}{a_{{9}}}^{4}a_{{13}}\delta _{{3}}-{a_{{1}}}^{2}{a_{{9}}}^{2}{a_{{10}}}^{2}a_{{13}} \delta _{{2}}+6{a_{{1}}}^{4}{a_{{9}}}^{2}\delta _{{3}}-6{a_{{1}}}^{4 }{a_{{10}}}^{2}\delta _{{2}}+2{a_{{9}}}^{4}{a_{{10}}}^{2}\delta _{{2}} \bigr) \bigr), \\ &\lim_{t\rightarrow \pm \infty } \frac{\Delta _{11}}{\Delta _{3}}=0,\qquad \lim_{t\rightarrow \pm \infty } \frac{\Delta _{12}}{\Delta _{3}}=0, \end{aligned}$$

since one can consider \(\Delta _{11}\) in its relation with \(\Delta _{13}\), therefore at this time, the resonance soliton pairs occur when \(\Delta _{11}\) contains \(\Delta _{13}\).

Figure 8
figure 8

The plot of lump–soliton (5.11) with fractional order \(\alpha =0.5\)

Full size image
Figure 9
figure 9

The plot of lump–soliton (5.11) with fractional order \(\alpha =0.95\)

Full size image
Figure 10
figure 10

The 2D plot of lump–soliton (5.11) with the different fractional orders

Full size image

Case VI:

$$\begin{aligned} f_{6}={}& \biggl( {\frac{ta_{{1}}a_{{7}}}{a_{{5}}}}+xa_{{1}}+ya_{{2}}+a_{{4}} \biggr) ^{2}+ \biggl( ta_{{7}}+xa_{{5}}+{ \frac{ya_{{2}}a_{{5}}}{a_{{1 }}}}+a_{{8}} \biggr) ^{2}+a_{{13}} \\ &{}+\cosh \biggl( 2 { \frac{ ( 2 {a_{{2}}}^{3}a_{{5}}\delta _{{6}} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ^{2}+ {a_{{1}}}^{2} ( {a_{{1}}}^{2}+{a_{{5}}}^{2} ) ( 2 {a_{{1}}}^{2}a_{{2}}a_{{5}}+2 a_{{2}}{a_{{5}}}^{3 }+2 a_{{2}}a_{{5}}\delta _{{1}}+a_{{1}}a_{{7}} ) ) t}{{a_{{1}}}^{3}a_{{5}} \sqrt{2 {a_{{1}}}^{2}+2 {a_{{5}}}^{2}}}} \\ &{}+ x \sqrt{2 {a_{{1}}}^{2}+2 {a_{{5}}}^{2}}-{ \frac{ya_{{2}} \sqrt{2 {a_{{1}}}^{2}+2 {a_{{5}}}^{2}}}{a_{{1}}}}+a_{{12}} \biggr) ,\qquad \Psi _{6}=\Psi _{0}+\frac{d f_{6}/dx}{f_{6}}, \\ &\delta _{{2}}=-\frac{1}{2}{ \frac{-{a_{{2}}}^{2} ( {a_{{1}}}^{2}+{a_{{5} }}^{2} ) ( 3 a_{{1}}\delta _{{6}}-8 a_{{2}}\delta _{{5}} ) +{a_{{1}}}^{5}+{a_{{1}}}^{3}{a_{{5}}}^{2}}{{a_{{1}}}^{2}a_{{2 }}}}, \qquad\delta _{{4}}=-{ \frac{{a_{{2}}}^{4}\delta _{{5}}}{{a_{{1}}}^{4}}}, \\ &\delta _{{3}}=\frac{1}{2} \bigl(-2{a_{{1}}}^{3}a_{{2}}a_{{5}}\delta _{{1}}- {a_{{2}}}^{3}a_{{5}} \bigl( {a_{{1}}}^{2}+{a_{{5}}}^{2} \bigr) \bigl( 3a_{{1}}\delta _{{6}}-8 a_{{2}}\delta _{{5}} \bigr) \\ &\phantom{\delta _{{3}}=}{} +a_{{1}} \bigl( -3{a_{{2}}}^{3}{a_{{5}}}^{3}\delta _{{6}}+{a_{{1}}}^{4}a_{{2} }a_{{5}}+{a_{{1}}}^{2}a_{{2}}{a_{{5}}}^{3}-2{a_{{1}}}^{3}a_{{7}} \bigr)\bigr) \\ &\phantom{\delta _{{3}}=}{}/{\bigl({a_{{1}}}^{4}a_{{5}}\bigr)}. \end{aligned}$$
(5.12)

Remark

In system (1.7), by utilizing \(\alpha =1\) we get the original system. Also, by choosing the different α we can get attractive physical interpretations of the obtained solutions. In Figs. 1–10 the graphical illustrations of some solutions of the considered model have been plotted.

6 Conclusion

In this article, the localized waves, lump–solitons and solutions between lumps and rogue waves for the fractional generalized Calogero–Bogoyavlensky–Schiff–Bogoyavlensky–Konopelchenko (CBS-BK) equation are investigated. The Hirota bilinear method is utilized which contain three cases including lump, lump–kink as the interaction between a lump and one line soliton and lump–soliton as the interaction between a lump and two-line solitons. The second-order derivative and the Hessian matrix for only one point investigated and the lump solution for the first-order rouge wave solution is obtained with one maximum value. The moving path of the lump solution and also the moving velocity and the maximum amplitude are obtained. The graphs for the various fractional order α are plotted containing 3D plot, contour plot, density plot and 2D plot. The results are beneficial to the study of the mathematics physics, fluid dynamics, and applied mechanics. All calculations in this paper have been made quickly with the aid of the Maple.