n-Expansively super-homogeneous and $(n,k)$-contractively sub-homogeneous fuzzy control functions and stability results with numerical examples

Abstract

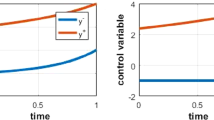
We consider fuzzy sets and generalized triangular norms on positive elements of order commutative $C^{*}$-algebras to study the concept of $C^{*}$-algebra valued normed algebras with uncertainty. Using n-expansively super-homogeneous and $(n,k)$-contractively sub-homogeneous control functions, we make stochastic $(\Theta,\Upsilon,\Xi )$-derivations stable and get a better estimated error. We present some numerical examples of control functions and approximations to illustrate the applicability of the main results.

1 Introduction

In this paper, we define some new control functions with uncertainty named n-expansively super-homogeneous and $(n,k)$-contractively sub-homogeneous mappings. These control functions help us to make stochastic derivations stable. Also, we can get a better approximation for these stochastic derivations.

We consider the positive cone of an order commutative $C^{*}$-algebra and generalize the concept of triangular norm and fuzzy sets on it; we refer the reader to [1–3] for more details. Also, we define $C^{*}$-algebra valued normed algebras using generalized triangular norms and fuzzy sets.

Definition 1

Let $\mathcal{A}$ be an order commutative $C^{*}$-algebra and $\mathcal{A}^{+}$ be the positive cone of $\mathcal{A}$. Let $U\neq \emptyset$. A $C^{*}$-algebra valued fuzzy set (in short, $C^{*}$-AVF set) $\mathcal{C}$ on U is a function $\mathcal{C}:U \longrightarrow \mathcal{A}^{+}$. For each u in U, ${\mathcal{C}}(u)$ represents the degree (in $\mathcal{A}^{+}$) to which u satisfies $\mathcal{A}^{+}$.

We put $\mathbf{0}= \inf \mathcal{A}^{+}$ and $\mathbf{1}= \sup \mathcal{A}^{+}$. Now, we define a class of generalized t-norms (triangular norm) on $\mathcal{A}^{+}$.

Definition 2

A t-norm on $\mathcal{A}^{+}$ is an operation $\odot: \mathcal{A}^{+}\times \mathcal{A}^{+} \to \mathcal{A}^{+}$ satisfying the following conditions:

(a) $t\odot \mathbf{1}=t$ for every $t \in {\mathcal{A}}^{+}$ (boundary condition);

(b) $t\odot s = s\odot t$ for every $(t,s)\in ({\mathcal{A}}^{+})^{2}$ (commutativity);

(c) $t\odot (s\odot p) = (t\odot s)\odot p$ for every $(t,s,p)\in ({\mathcal{A}}^{+})^{3}$ (associativity);

(d) $t\preceq t^{\prime } \text{and} s\preceq s^{\prime } \Longrightarrow t \odot s \preceq t^{\prime }\odot s^{\prime }$ for every $(t,t^{\prime },s,s^{\prime })\in ({\mathcal{A}}^{+})^{4}$ (monotonicity).

Now suppose that, for $t, s \in \mathcal{A}^{+}$ and sequences $\{t_{n}\}$ and $\{s_{n}\}$ converging to t and s, we have

$$ \lim_{n}(t_{n}\odot s_{n})= t\odot s. $$

Then ⊙ on $\mathcal{A}^{+}$ is continuous (in short, CTN).

Definition 3

Assume that a decreasing mapping $\mathcal{F}: \mathcal{A}^{+} \to \mathcal{A}^{+}$ satisfies $\mathcal{F}(\mathbf{0}) = \mathbf{1}$ and $\mathcal{F}(\mathbf{1}) = \mathbf{0}$. Then $\mathcal{F}$ is called a negation on $\mathcal{A}^{+}$.

Example 1

Let

$$ \operatorname{diag} M_{n}\bigl([0,1]\bigr)= \left\{ \begin{bmatrix} t_{1} & & \\ & \ddots & \\ & & t_{n} \end{bmatrix} =\operatorname{diag}[t_{1}, \ldots,t_{n}], t_{1},\ldots,t_{n}\in [0,1] \right \}. $$

We denote $\operatorname{diag}[t_{1},\ldots,t_{n}]\preceq \operatorname{diag}[s_{1},\ldots,s_{n}]$ if and only if $t_{i}\leq s_{i}$ for all $i=1,\ldots,n$; also, ${\mathbf{1}}=\operatorname{diag}[1,\ldots,1]$ and ${\mathbf{0}}=\operatorname{diag}[0,\ldots,0]$. Now, we know that if ${\mathcal{A}}=\operatorname{diag} M_{n}([0,1])$, then $\operatorname{diag} M_{n}([0,1])=\mathcal{A}^{+}$. Define $\odot _{P}: \operatorname{diag} M_{n}([0,1])\times \operatorname{diag} M_{n}([0,1]) \to \operatorname{diag} M_{n}([0,1])$ such that

$$ \operatorname{diag}[t_{1},\ldots,t_{n}]\odot _{P} \operatorname{diag}[s_{1},\ldots,s_{n}] = \operatorname{diag}[t_{1}.s_{1}, \ldots,t_{n}.s_{n}]. $$

Then $\odot _{P}$ is a t-norm (product t-norm). Also note that $\odot _{P}$ is a CTN.

Example 2

Let $\operatorname{diag} M_{n}([0,1])=\mathcal{A}^{+}$. Define $\odot _{M}: \operatorname{diag} M_{n}([0,1])\times \operatorname{diag} M_{n}([0,1]) \to \operatorname{diag} M_{n}([0,1])$ such that

$$ \operatorname{diag}[t_{1},\ldots,t_{n}]\odot _{M} \operatorname{diag}[s_{1},\ldots,s_{n}]= \operatorname{diag}\bigl[ \min (t_{1},s_{1}),\ldots,\min (t_{n},s_{n})\bigr]. $$

Then $\odot _{M}$ is a t-norm (minimum t-norm). Also note that $\odot _{M}$ is a CTN.

Definition 4

The triple $(T,\mathcal{N},\odot )$ is called a $C^{*}$-AVF normed space (in short, $C^{*}$AVFN-space) if T is a vector space over $\mathbb{C}$, ⊙ is a CTN on $\mathcal{A}^{+}$, and $\mathcal{N}$ is a $C^{*}$AVF-set on $T \times [0,+\infty )$ such that, for each $t,s\in T$ and $\tau,\varsigma$ in $[0,+\infty )$, we have

• (a) ${\mathcal{N}}(t,0) = {\mathbf{0}}$;

• (b) ${\mathcal{N}}(t,\tau ) = {\mathbf{1}}$ for all $\tau > 0$ if and only if $t = 0$;

• (c) ${\mathcal{N}}(\alpha t,\tau )={\mathcal{N}}(t, \frac{\tau }{|\alpha |})$ for all $\alpha \neq 0$;

• (d) ${\mathcal{N}}(t+s,\tau +\varsigma )\succeq {\mathcal{N}}(t,\tau ) \odot {\mathcal{N}}(s,\varsigma )$;

• (e) ${\mathcal{N}}(t,\cdot ): [0,\infty ) \to \mathcal{A}^{+}$ is left continuous;

• (f) $\lim_{t\rightarrow \infty }{\mathcal{N}}(t,\tau )={\mathbf{1}}$.

Also, $\mathcal{N}$ is called a $C^{*}$-AVF norm.

Let $(T,\mathcal{N},\odot )$ be a $C^{*}$-AVFN-space. For $\tau >0$, define the open ball $O_{(t,\varrho )}(\tau )$ as

$$ O_{(t,\varrho )}(\tau ) = \bigl\{ s \in T: {\mathcal{N}}(t-s,\tau ) \succ \mathcal{F}(\varrho )\bigr\} , $$

in which $t \in T$ is the center and $\varrho \in \mathcal{A}^{+} \setminus \{{\mathbf{0}}, {\mathbf{1}}\}$ is the radius. We say that $A \subseteq T$ is open if for each $t \in A$, there exist $\tau > 0$ and $\varrho \in \mathcal{A}^{+} \setminus \{{\mathbf{0}}, {\mathbf{1}}\}$ such that $O_{(t,\varrho )}(\tau ) \subseteq A$. We denote the family of all open subsets of T by $\tau _{\mathcal{N}}$ and so $\tau _{\mathcal{N}}$ is the ${C}^{*}$-AVF topology induced by the $C^{*}$-AVF norm $\mathcal{N}$.

Example 3

Consider a normed space $(T,\|\cdot \|)$. Let $\odot =\odot _{M}$ and define the fuzzy set $\mathcal{N}$ on $T\times (0,\infty )$ as

$$\begin{aligned} {\mathcal{N}}(t,\tau )=\operatorname{diag}\biggl[\frac{h \tau }{h \tau +m \Vert t \Vert }, \exp \biggl(-\frac{ \Vert t \Vert }{\tau }\biggr)\biggr] \end{aligned}$$

for all $\tau,h,m\in {\mathbb{R}}^{+}$. Then $(T,\mathcal{N},\odot _{M})$ is a $C^{*}$-AVFN-space.

Example 4

Let $(T,\|\cdot \|)$ be a normed space,

$$\begin{aligned} u\odot v=\bigl(u_{1}v_{1},\min \{u_{2},v_{2} \}\bigr) \end{aligned}$$

for all $u=(u_{1},u_{2}), v=(v_{1},v_{2})\in \mathcal{A}^{+}$, and define the fuzzy set $\mathcal{N}$ on $T\times (0,\infty )$ as

$$\begin{aligned} {\mathcal{N}}(s,\zeta )=\operatorname{diag} \biggl[\frac{\zeta }{\zeta + \Vert s \Vert }, \frac{\zeta }{\zeta + \Vert s \Vert } \biggr],\quad \forall \zeta \in {\mathbb{R}}^{+}. \end{aligned}$$

Then $(T,\mathcal{N},\odot )$ is a $C^{*}$-AVFN-space.

Lemma 1

([4])

Let $(T,\mathcal{N},\odot )$ be a $C^{*}$-AVFN-space. Then ${\mathcal{N}}(t,\tau )$ is nondecreasing with respect to τ for all $t\in T$.

Definition 5

Let $\{t_{n}\}_{n \in \mathbb{N}}$ be a sequence $C^{*}$-AVFN-space $(T, \mathcal{N}, \odot )$. If

$$ \forall \varepsilon \in {\mathcal{A }}^{+} \setminus \{{\mathbf{0}}\} \text{ and } \tau > 0, \exists n_{0} \in {\mathbb{N}} \text{ such that } \forall m\geq n \ge n_{0}, {\mathcal{N}}(t_{m}-t_{n}, \tau ) \succeq {\mathcal{F}}(\varepsilon ), $$

then $\{t_{n}\}_{n \in \mathbf{{N}}}$ is a Cauchy sequence. Also $\{t_{n}\}_{n \in \mathbf{{N}}}$ is convergent to $t \in T$ ($t_{n} \stackrel{\mathcal{N}}{\longrightarrow } t$) if ${\mathcal{N}}(t_{n}-t,\tau ) \to \mathbf{1}$ whenever $n \to +\infty$ for every $\tau > 0$. When all Cauchy sequences are convergent in a $C^{*}$AVFN-space, the space is complete. A complete $C^{*}$AVFN-space is called a $C^{*}$AVF Banach space (in short, $C^{*}$AVFB-space).

Definition 6

A $C^{*}$-AVFN algebra $(T,{\mathcal{N}},\odot,\odot ^{\prime })$ is a $C^{*}$-AVFN-space $(T,{\mathcal{N}},\odot )$ satisfying

(g) ${\mathcal{N}}(wz,\tau \zeta )\succeq {\mathcal{N}}(w,\tau )\odot ^{\prime } {\mathcal{N}}(z,\zeta )$ for every $w,z\in T$ and $\tau,\zeta > 0$ in which ⊙′ is a CTN.

Consider a normed algebra $(T,\|\cdot \|)$. Define a $C^{*}$-AVFN algebra $(T,{\mathcal{N}},\odot _{M},\odot _{M})$, in which

$$ {\mathcal{N}}(w,\zeta )=\operatorname{diag} \biggl[\frac{\zeta }{\zeta + \Vert w \Vert },\exp \biggl(-\frac{ \Vert w \Vert }{\zeta } \biggr) \biggr] $$

for all $\zeta >0$ if and only if

$$ \Vert wz \Vert \le \Vert w \Vert \Vert z \Vert + \zeta \Vert w \Vert + \tau \Vert z \Vert \quad(w,z \in T; \tau,\zeta > 0), $$

for which we name the standard $C^{*}$-AVFN algebra.

Definition 7

Consider a complete $C^{*}$AVF-algebra $({\mathcal{V}},{\mathcal{N}},\odot,\odot ^{\prime })$. An involution on $\mathcal{V}$ is a mapping $v\to v^{*}$ from $\mathcal{V}$ into $\mathcal{V}$ with

• (i) $v^{**}=v$ for $v\in \mathcal{V}$;

• (ii) $(\Upsilon v+ \Theta w)^{*}=\overline{\Upsilon } v^{*} + \overline{\Theta } w^{*}$;

• (iii) $(vw)^{*}=w^{*}v^{*}$ for $v,w\in \mathcal{V}$.

If, in addition, ${\mathcal{N}}(v^{*}v,\Theta \Upsilon )={\mathcal{N}}(v,\Theta )\odot ^{\prime }{ \mathcal{N}}(v,\Upsilon )$ for $v\in \mathcal{V}$ and $\Theta,\Upsilon >0$, then $\mathcal{V}$ is a $C^{*}$AVF $C^{*}$-algebra.

Novotný and Hrivnák [5] considered $(\Theta,\Upsilon,\Xi )$-derivations on Lie algebras. Let $\mathcal{B}$ be a Lie $C^{*}$-algebra. We say that a $\mathbb{C}$-linear mapping $\mathcal{D}: \mathcal{B} \to \mathcal{B}$ is a Lie derivation on $\mathcal{B}$ if $\mathcal{D}: \mathcal{B} \to \mathcal{B}$ satisfies that

$$ {\mathcal{D}}[t,s]=\bigl[{\mathcal{D}}(t),s\bigr]+\bigl[t,{ \mathcal{D}}(s)\bigr] $$

(1.1)

for all $t,s \in \mathcal{B}$ [6, 7]. Also the $\mathbb{C}$-linear mapping $\mathfrak{H}: \mathcal{B} \to \mathcal{B}$ is a Lie $(\Theta,\Upsilon,\Xi )$-derivation on $\mathcal{B}$ if there exist $\Theta,\Upsilon,\Xi \in \mathbb{C}$ such that

$$ \Theta {\mathfrak{H}}[t,s]=\Upsilon \bigl[{\mathfrak{H}}(t),s \bigr]+\Xi \bigl[t,{ \mathfrak{H}}(s)\bigr] $$

(1.2)

for all $t,s \in \mathcal{B}$. A $C^{*}$AVF $C^{*}$-algebra $\mathcal{B}$ with a Lie product $[t,s]=ts-st$ is said to be a $C^{*}$AVF Lie $C^{*}$-algebra. Assume that $\mathcal{B}$ is a $C^{*}$AVF Lie $C^{*}$-algebra. A $\mathbb{C}$-linear mapping $H: \mathcal{B} \to \mathcal{B}$ is said to be a $C^{*}$AVF Lie derivation on $\mathcal{B}$ if $H: \mathcal{B} \to \mathcal{B}$ satisfies (1.1). A $\mathbb{C}$-linear mapping $\mathfrak{H}: \mathcal{B} \to \mathcal{B}$ is said to be a $C^{*}$AVF Lie $(\Theta,\Upsilon,\Xi )$-derivation on $\mathcal{B}$ if there exist $\Theta,\Upsilon,\Xi \in \mathbb{C}$ satisfying (1.2).

Consider a probability measure space $(\Gamma, \Sigma, \xi )$ and Borel measurable spaces $(T,{\mathfrak{B}}_{T})$ and $(S,{\mathfrak{B}}_{S})$, where T and S are $C^{*}$AVFB-spaces. If for $\digamma:\Gamma \times T\to S$ we have $\{\gamma: \digamma (\gamma,t)\in R\}\in \Sigma$ for every t in T and $R\in {\mathfrak{B}}_{S}$, we say that Ϝ is a random operator. If $\digamma (\gamma,\alpha t_{1}+\beta t_{2})=\alpha \digamma (\gamma,t_{1})+ \beta \digamma (\gamma, t_{2})$ almost everywhere for $t_{1},t_{2}$ in T and scalers $\alpha,\beta$, then Ϝ is a linear random operator, also if we can find an $M(\gamma )>0$ such that

$$ \nu \bigl(\digamma (\gamma,t_{1})-\digamma (\gamma,t_{2}),M( \gamma ) \tau \bigr)\ge \nu (t_{1}-t_{2},\tau ) $$

almost everywhere for $t_{1},t_{2}$ in T and $\tau >0$, then Ϝ is a bounded random operator.

2 Cauchy–Jensen random operator

In this paper, let $\mathcal{G}=[0,\infty ]$ and $\mathcal{G}^{\circ }=(0,\infty )$.

Theorem 1

([8, 9])

Let S be a set with the complete $\mathcal{G}$-valued metric δ, and let a self-mapping Λ on S satisfy

$$ \delta (\Lambda s,\Lambda t)\le \kappa \delta (t,s),\quad\kappa < 1 \textit{ is a Lipschitz constant.} $$

Let $s\in S$. Then we have two options

• (I) $\delta (\Lambda ^{m}s,\Lambda ^{m+1}s) = \infty, \forall m\in \mathbb{N}$ or

• (II) we can find $m_{0}\in \mathbb{N}$ such that

  • (1) $\delta (\Lambda ^{m}s,\Lambda ^{m+1}s)<\infty, \forall m\ge m_{0}$;

  • (2) the fixed point $t^{*}$ of Λ is the convergent point of the sequence $\{\Lambda ^{m} s\}$;

  • (3) in the set $V = \{t\in S \mid \delta (\Lambda ^{m_{0}}s,t) <\infty \}$, $t^{*}$ is the unique fixed point of Λ;

  • (4) $(1-\kappa )\delta (t,t^{\ast }) \le \delta (t,\Lambda t)$ for every $s \in V$.

In this paper, assume that $({\mathcal{B}},{\mathcal{N}},\odot _{M},\odot _{M})$ is a $C^{*}$-AVF Lie $C^{*}$-algebra. Also, we use the random operator $g:\Gamma \times {\mathcal{B}}\rightarrow \mathcal{B}$:

$$\begin{aligned} &\Delta _{\nu }g (\gamma,t_{1},\ldots,t_{n} ):=\sum ^{n}_{i=1}g \Biggl(\gamma,\nu t_{i}+ \frac{1}{n-1}\sum^{n}_{j=1,j\neq i} \nu t_{j} \Biggr)-2\nu \sum^{n}_{i=1}g( \gamma,t_{i}), \\ &\Delta _{\Theta,\Upsilon,\Xi } g (\gamma,t,s ):=\Theta g[ \gamma,t,s]-\Upsilon \bigl[g( \gamma,t),s\bigr]-\Xi \bigl[t,g(\gamma,s)\bigr] \end{aligned}$$

for all $t_{1},\ldots,t_{n}\in \mathcal{B},\gamma \in \Gamma$, all $\nu \in \Omega$ for some set $\Omega \in D_{\mathbb{C}}$ and $\Theta,\Upsilon,\Xi \in \mathbb{C}$. Denote

$$ D_{\mathbb{C}}=\{\Omega \subseteq {\mathbb{C}}| g: \Omega \longrightarrow \mathcal{B} \text{ is additive, bounded and continuous}\}. $$

For more details, see [10–13]. Also, ${\mathbb{T}}_{1/n_{0}}^{1}:=\{e^{i\theta }; 0\leq \theta \leq 2 \pi /n_{0} \}\in D_{\mathbb{C}}$.

Lemma 2

([14])

A random operator $g:\Gamma \times T \rightarrow S$ satisfies the equation

$$\begin{aligned} &g \biggl(\gamma,t_{1}+ \frac{1}{2}(t_{2}+t_{3}) \biggr)+g \biggl( \gamma,t_{2}+ \frac{1}{2}(t_{1}+t_{3}) \biggr)+g \biggl(\gamma,t_{3}+ \frac{1}{2}(t_{1}+t_{2}) \biggr) \\ &\quad=2 \bigl(g(\gamma,t_{1})+g(\gamma,t_{2})+g( \gamma,t_{3}) \bigr) \end{aligned}$$

(2.1)

for all $t_{1},t_{2},t_{3}\in T,\gamma \in \Gamma$ if and only if g is additive.

If we set $t_{3}=0$ in (2.1), then we get that the Cauchy–Jensen random operator

$$ g \biggl( \gamma,\frac{1}{2}(t_{1}+t_{2}) \biggr)+g \biggl(\gamma,t_{1}+ \frac{t_{2}}{2} \biggr)+g \biggl(\gamma, \frac{t_{1}}{2}+t_{2} \biggr)=2 \bigl(g(\gamma,t_{1})+g( \gamma,t_{2}) \bigr) $$

is equivalent to $g(\gamma,t_{1}+t_{2})=g(\gamma,t_{1})+g(\gamma,t_{2})$ for all $t_{1},t_{2}\in T,\gamma \in \Gamma$.

Lemma 3

([15])

A random operator $g:\Gamma \times T \rightarrow S$ satisfies $\Delta _{\nu }g=0$ for all $t_{1},\ldots,t_{n}\in T,\gamma \in \Gamma$ if and only if g is additive.

Lemma 4

([10])

Let $g:\Gamma \times {\mathcal{B}} \rightarrow \mathcal{B}$ be an additive random operator such that $g(\gamma,\nu t)=\nu g(\gamma,t)$ for all $\nu \in \Omega,\gamma \in \Gamma$ where the bounded set Ω is in $D_{\mathbb{C}}$. Then the random operator g is $\mathbb{C}$-linear.

3 Hyers–Ulam–Rassias stability

In this section, we present some stability results. In real phenomena, the concept of stability also appears in mechanical applications as a consequence of real equilibrium problems. Related stability problems take part in mathematical models from mechanics when equilibrium equations are imposed (see [16, 17]). The stability results have numerous applications in the study of stability of porous medium problems (see [18]). For further applications, we refer to [19–21].

Definition 8

Let $n\in \mathbb{N}$. A $C^{*}$AVF mapping ${\mathcal{R}}: {\mathcal{B}}^{n}\times (0,\infty ) \rightarrow { \mathcal{A }}^{+}$ is called a $C^{*}$AVF n-expansively super-homogeneous function if there is a fixed number $\ell \in (0,1)$ such that

$$\begin{aligned} &{\mathcal{R}} \bigl( \bigl(\mu ^{-1}t_{1}, \ldots,\mu ^{-1}t_{n} \bigr),\tau \bigr)\succeq {\mathcal{R}} \biggl( (t_{1},\ldots,t_{n} ), \frac{\mu ^{n}\tau }{\ell ^{n}} \biggr), \end{aligned}$$

(3.1)

$$\begin{aligned} &\lim_{\varsigma \to \infty }{\mathcal{R}}\bigl((t_{1}, \ldots,t_{n}), \varsigma \bigr)={\mathbf{1}} \end{aligned}$$

(3.2)

for all $t_{i}\in {\mathcal{B}} (1\leq i\leq n)$, $1<\mu \in \mathbb{N}$, and $\tau \in \mathcal{G}^{\circ }$.

Example 5

Consider a real function $r:\mathbb{R}\to \mathbb{R}$ defined as $r(t)=|t|^{4}$. Define

$$ {\mathcal{R}}\bigl((t_{1},t_{2},t_{3}),\tau \bigr)=\operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{3} r(t_{j})},\exp \biggl(- \frac{\sum_{j=1}^{3} r(t_{j})}{\tau } \biggr) \biggr] $$

for all $t_{1},t_{2},t_{3}\in \mathbb{R}$ and $\tau \in \mathcal{G}^{\circ }$. Put $\ell =\frac{1}{\sqrt[3]{2}}$. Then ${\mathcal{R}}$ is a 3-expansively super-homogeneous function.

Theorem 2

Consider a $C^{*}$-AVF expansively super-homogeneous function $\varphi: {\mathcal{B}}^{n}\times (0,\infty )\rightarrow { \mathcal{A }}^{+}$ and a $C^{*}$VAF 2-expansively super-homogeneous function $\psi:{\mathcal{B}}^{2}\times (0,\infty ) \rightarrow {\mathcal{A }}^{+}$ with a fixed number ℓ such that a random operator $g:\Gamma \times \mathcal{B}\rightarrow \mathcal{B}$ satisfies

$$\begin{aligned} &{\mathcal{N}}\bigl(\Delta _{\eta }g (\gamma,t_{1}, \ldots,t_{n} ),t\bigr) \succeq \varphi \bigl((t_{1}, \ldots,t_{n}),\tau \bigr), \end{aligned}$$

(3.3)

$$\begin{aligned} & {\mathcal{N}}\bigl(\Delta _{\Theta,\Upsilon,\Xi } g (\gamma,t,s ),\tau \bigr)\succeq \psi \bigl((t,s),\tau \bigr) \end{aligned}$$

(3.4)

for all $t_{1},\ldots,t_{n},t,s\in \mathcal{B},\gamma \in \Gamma$, $\eta \in \Omega$, $\tau \in \mathcal{G}^{\circ }$ and some $\Theta,\Upsilon,\Xi \in \mathbb{C}$, where $\Omega \in D_{\mathbb{C}}$ is bounded. Then we can find a unique $C^{*}$VAF Lie $(\Theta,\Upsilon,\Xi )$-derivation ${\mathfrak{H}}: \Gamma \times {\mathcal{B}}\rightarrow \mathcal{B}$ which satisfies $\Delta _{\nu }g=0$ and the inequality

$$ {\mathcal{N}}\bigl(g(\gamma,z)-{\mathfrak{H}}(\gamma,z),\varsigma \bigr) \succeq \varphi \biggl(\bigl(\overbrace{z,\ldots,z}^{n{\textit{-times}}}\bigr), \frac{(2^{n} n-2n\ell ^{n})\varsigma }{\ell ^{n}} \biggr) $$

(3.5)

for all $z\in \mathcal{B},\gamma \in \Gamma$ and $\varsigma \in \mathcal{G}^{\circ }$.

Proof

Consider $M:=\{k: \Gamma \times \mathcal{B}\rightarrow \mathcal{B}, k( \varpi,0)=0, \forall \varpi \in \Gamma \}$ and define

$$\begin{aligned} \delta (k,h): ={}&\inf \biggl\{ P\in \Xi ^{\circ }: {\mathcal{N}}\bigl(k( \varpi,w) - h(\varpi,w),\tau \bigr) \succeq \varphi \biggl( (w,\ldots,w), \frac{\tau }{P} \biggr), \\ &{} \forall \varpi \in \Gamma, w\in \mathcal{B}, \tau \in \mathcal{G}^{\circ } \biggr\} . \end{aligned}$$

In [22], Miheţ and Radu showed that $(M, \delta )$ is a complete $\mathcal{G}$-valued metric space (see [23]).

Define a linear mapping $\Lambda: M\rightarrow M$ as

$$ (\Lambda k) (\varpi,w) = 2k \biggl(\varpi,\frac{w}{2} \biggr), \quad\forall k \in M \text{ and } w\in {\mathcal{B}} \varpi \in \Gamma. $$

Let $k,h\in M$ and consider a sequence of positive real numbers $P_{m}$ with $\lim_{m\to \infty }P_{m}=\delta (k,h)$ and $\delta (k,h) \leq P_{m}$. Fix m and, for convenience, let $P_{m}=P$. Then

$$ {\mathcal{N}}\bigl(k(\varpi,w) -h(\varpi,w),\varsigma \bigr) \succeq \varphi \biggl((w,\ldots,w),\frac{\varsigma }{P} \biggr) $$

for all $w\in \mathcal{B},\varpi \in \Gamma$ and $\varsigma \in \Xi ^{\circ }$. Now we have

$$\begin{aligned} {\mathcal{N}}\bigl((\Lambda k) (\varpi,w) - (\Lambda h) (\varpi,w), \varsigma \bigr)& = {\mathcal{N}} \biggl(2 k \biggl(\varpi,\frac{w}{2} \biggr) - 2h \biggl(\varpi,\frac{w}{2} \biggr),\varsigma \biggr) \\ & = {\mathcal{N}} \biggl( k \biggl(\varpi,\frac{w}{2} \biggr) - h \biggl(\varpi,\frac{w}{2} \biggr),\frac{\varsigma }{2} \biggr) \\ &\succeq \varphi \biggl(\biggl(\frac{w}{2},\ldots,\frac{w}{2} \biggr), \frac{\varsigma }{2P} \biggr) \\ &\succeq \varphi \biggl((w,\ldots,w), \frac{2^{n-1}\varsigma }{\ell ^{n} P} \biggr) \end{aligned}$$

for all $w\in \mathcal{B}$ and $\varsigma \in \mathcal{G}^{\circ },\varpi \in \Gamma$, and so $\delta (\Lambda k,\Lambda h) \leq \frac{\ell ^{n}}{2^{n-1}}P = \frac{\ell ^{n}}{2^{n-1}}P_{m}$ for any $k,h \in M$. Now let $m \to \infty$, and we get $\delta (\Lambda k,\Lambda h) \leq \frac{\ell ^{n}}{2^{n-1}} \delta (k,h)$ for any $k,h \in M$.

Let g be as in the statement of the theorem. Putting $t_{1},\ldots,t_{n} = w$ and $\eta = 1$ in (3.3), we obtain

$$ {\mathcal{N}}\bigl(g(\gamma,2w) - 2 g(\gamma,w),\tau \bigr)\succeq \phi \bigl((w,\ldots,w),n \tau \bigr) $$

for all $w\in \mathcal{B}$, $\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Thus

$$\begin{aligned} {\mathcal{N}} \biggl(2g \biggl(\gamma,\frac{w}{2} \biggr)-g(\gamma,w), \tau \biggr)&\succeq \varphi \biggl( \biggl(\frac{w}{2},\ldots, \frac{w}{2} \biggr),n\tau \biggr) \\ &\succeq \varphi \biggl((w,\ldots,w),\frac{2^{n} n\tau }{\ell ^{n}} \biggr) \end{aligned}$$

for all $w\in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Hence $\delta (\Lambda g,g)\leq \frac{\ell ^{n}}{2^{n} n}$. Now Theorem 1 guarantees that $\{\Lambda ^{n} g\}$ converges to a unique fixed point ${\mathfrak{H}}\in M$ of Λ such that ${\mathfrak{H}}(\gamma,2w)=2{\mathfrak{H}}(\gamma,w)$, i.e.,

$$\begin{aligned} {\mathfrak{H}}(\gamma,w) =\lim_{m\to \infty }2^{m} g \biggl(\gamma, \frac{w}{2^{m}} \biggr) \end{aligned}$$

(3.6)

for all $w \in \mathcal{B},\gamma \in \Gamma$. Also (see Theorem 1)

$$ \delta (g,{\mathfrak{H}})\le \frac{1}{1-\frac{\ell ^{n}}{2^{n-1}}} \delta (g, \Lambda g) \le \frac{\ell ^{n}}{2^{n} n-2n\ell ^{n}}, $$

i.e., (3.5) holds for all $t \in \mathcal{B}$ and $\tau \in \mathcal{G}^{\circ }$. From the property of $\mathfrak{H}$, we get that

$$\begin{aligned} {\mathcal{N}} \bigl(\Delta _{\eta }{\mathfrak{H}} (\gamma,t_{1}, \ldots,t_{n} ),\tau \bigr) &=\lim_{m\to \infty } { \mathcal{N}} \biggl(\Delta _{\eta }g \biggl(\gamma,\frac{t_{1}}{2^{m}}, \ldots, \frac{t_{n}}{2^{m}} \biggr), \frac{\tau }{2^{m}} \biggr) \\ &\succeq \lim_{m\to \infty } \varphi \biggl( \biggl( \frac{t_{1}}{2^{m}}, \ldots,\frac{t_{n}}{2^{m}} \biggr),\frac{\tau }{2^{m}} \biggr)={1} \end{aligned}$$

holds for all $t_{1},\ldots,t_{n}\in \mathcal{B},\gamma \in \Gamma$, $\eta \in \Omega$, and $\tau \in \mathcal{G}^{\circ }$. Thus $\Delta _{\eta }{\mathfrak{H}} (\gamma,t_{1},\ldots,t_{n} )=0$ for all $t_{1},\ldots,t_{n}\in \mathcal{B},\gamma \in \Gamma$ and all $\eta \in \Omega$. If we put $\eta =1$ in the above equality, then Lemma 3 implies that $\mathfrak{H}$ is additive. Putting $t_{1}=t$ and $t_{2}=\cdots =t_{n}=0$ in the above equality, we get ${\mathfrak{H}}(\gamma,\eta t)= \eta {\mathfrak{H}}(\gamma,t)$ and Lemma 4 implies that ${\mathfrak{H}}\in M$ is $\mathbb{C}$-linear. Also (3.1) and (3.4) imply that

$$\begin{aligned} {\mathcal{N}}\bigl(\Delta _{\Theta,\Upsilon,\Xi } {\mathfrak{H}} (\gamma,t,s ),\tau \bigr)&=\lim_{m\to \infty } {\mathcal{N}} \biggl(\Delta _{\Theta, \Upsilon,\Xi } g \biggl(\gamma,\frac{t}{2^{m}},\frac{s}{2^{m}} \biggr), \frac{\tau }{2^{m}} \biggr) \\ &\succeq \lim_{m\to \infty } \psi \biggl( \biggl(\frac{t}{2^{m}}, \frac{s}{2^{m}} \biggr),\frac{\tau }{2^{m}} \biggr) \\ &\succeq \lim_{m\to \infty }\psi \biggl((t,s), \frac{2^{2m}\tau }{\ell ^{2} 2^{m}} \biggr) \\ &=\lim_{m\to \infty }\psi \biggl((t,s),\frac{2^{m}\tau }{\ell ^{2} } \biggr) \\ &=1 \end{aligned}$$

for all $t,s\in \mathcal{B}$, some $\Theta,\Upsilon,\Xi \in \mathbb{C}$ and $\tau \in \mathcal{G}^{\circ }$. Then, for some $\Theta,\Upsilon,\Xi \in \mathbb{C}$,

$$ \Theta {\mathfrak{H}}[\gamma,t,s]=\Upsilon \bigl[{\mathfrak{H}}(\gamma,t),s \bigr]+ \Xi \bigl[t,{\mathfrak{H}}(\gamma,s)\bigr] $$

for all $t,s\in \mathcal{B},\gamma \in \Gamma$. So the random operator ${\mathfrak{H}}\in M$ is a $C^{*}$VAF Lie $(\Theta,\Upsilon,\Xi )$-derivation on the $C^{*}$VAF Lie $C^{*}$-algebra $\mathcal{B}$ and (3.5) holds. □

Example 6

Let a random operator $g:\Gamma \times \mathcal{B}\rightarrow \mathcal{B}$ satisfy

$$\begin{aligned} &{\mathcal{N}}\bigl(\Delta _{\eta }g (\gamma,t_{1}, \ldots,t_{4} ),t\bigr) \succeq \operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{4} \Vert t_{j} \Vert ^{5}}, \exp \biggl(-\frac{\sum_{j=1}^{4} \Vert t_{j} \Vert ^{5}}{\tau } \biggr) \biggr], \end{aligned}$$

(3.7)

$$\begin{aligned} &{\mathcal{N}}\bigl(\Delta _{\Theta,\Upsilon,\Xi } g ( \gamma,t_{1},t_{2} ),\tau \bigr)\succeq \operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{2} \Vert t_{j} \Vert ^{5}},\exp \biggl(- \frac{\sum_{j=1}^{2} \Vert t_{j} \Vert ^{5}}{\tau } \biggr) \biggr] \end{aligned}$$

(3.8)

for all $t_{1},\ldots,t_{4}\in \mathcal{B},\gamma \in \Gamma$, $\eta \in \Omega$, $\tau \in \mathcal{G}^{\circ }$ and some $\Theta,\Upsilon,\Xi \in \mathbb{C}$, where $\Omega \in D_{\mathbb{C}}$ is bounded. Then we can find a unique $C^{*}$VAF Lie $(\Theta,\Upsilon,\Xi )$-derivation ${\mathfrak{H}}: \Gamma \times {\mathcal{B}}\rightarrow \mathcal{B}$ which satisfies $\Delta _{\nu }g=0$ and the inequality

$$ {\mathcal{N}}\bigl(g(\gamma,z)-{\mathfrak{H}}(\gamma,z),\tau \bigr)\succeq \operatorname{diag} \biggl[\frac{30\tau }{30\tau + \Vert z \Vert ^{5}},\exp \biggl(- \frac{ \Vert z \Vert ^{5}}{30\tau } \biggr) \biggr] $$

(3.9)

for all $z\in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$.

Define

$$ \varphi \bigl((t_{1},t_{2},t_{3},t_{4}), \tau \bigr)=\operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{4} \Vert t_{j} \Vert ^{5}},\exp \biggl(- \frac{\sum_{j=1}^{4} \Vert t_{j} \Vert ^{5}}{\tau } \biggr) \biggr] $$

and

$$ \psi \bigl((t_{1},t_{2}),\tau \bigr)=\operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{2} \Vert t_{j} \Vert ^{5}},\exp \biggl(- \frac{\sum_{j=1}^{2} \Vert t_{j} \Vert ^{5}}{\tau } \biggr) \biggr] $$

for all $t_{1},t_{2},t_{3}\in \mathbb{B}$ and $\tau \in \mathcal{G}^{\circ }$. Put $\ell =\frac{1}{\sqrt[4]{2}}$. Then φ and ψ are 4-expansively super-homogeneous function and 2-expansively super-homogeneous function, respectively. Now, applying Theorem 2, we get (3.9).

Definition 9

Let $n,k\in \mathbb{N}$. A $C^{*}$AVF map ${\mathcal{O}}: {\mathcal{B}}^{n}\times (0,\infty ) \rightarrow { \mathcal{A }}^{+}$ is called a $C^{*}$AVF $(n,k)$-contractively sub-homogeneous if there exists a fixed number ℓ with $0 < \ell < 1$ such that

$$\begin{aligned} &{\mathcal{O}}(\mu t_{1},\ldots,\mu t_{n},\tau )\succeq { \mathcal{O}} \biggl((t_{1},\ldots,t_{n}), \frac{\tau }{\ell ^{k}\mu ^{\frac{1}{k}}} \biggr), \\ &\lim_{\varsigma \to \infty }{\mathcal{O}}(t_{1},\ldots,t_{n}, \varsigma )={ \mathbf{1}} \end{aligned}$$

for all $t_{1},\ldots,t_{n}\in {\mathcal{B}}$, $1<\mu \in \mathbb{N}$ and $\tau \in \mathcal{G}^{\circ }$.

Example 7

Consider a real function $r:\mathbb{R}\to \mathbb{R}$ defined as $r(t)=|t|^{\frac{1}{4}}$. Define

$$ {\mathcal{O}}\bigl((t_{1},t_{2},t_{3}),\tau \bigr)=\operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{3} r(t_{j})},\exp \biggl(- \frac{\sum_{j=1}^{3} r(t_{j})}{\tau } \biggr) \biggr] $$

for all $t_{1},t_{2},t_{3}\in \mathbb{R}$ and $\tau \in \mathcal{G}^{\circ }$. Put $\ell =\frac{1}{\sqrt[8]{2}}$. Then ${\mathcal{O}}$ is a $(3,2)$-contractively sub-homogeneous function.

Theorem 3

Consider a $C^{*}$AVF (n+2,k)-contractively sub-homogeneous function $\varphi:{\mathcal{B}}^{n+2}\times (0,\infty ) \rightarrow { \mathcal{A }}^{+}$ with a fixed number ℓ such that a random operator $g: \Gamma \times {\mathcal{B}}\rightarrow \mathcal{B}$ holds

$$ {{\mathcal{N}}} \bigl(\Delta _{\eta }g ( \gamma,t_{1},\ldots,t_{n} )+\Delta _{\Theta,\Upsilon,\Xi } g ( \gamma,t,s ), \tau \bigr)\succeq \varphi \bigl( (t_{1}, \ldots,t_{n},t,s ),\tau \bigr) $$

(3.10)

for all $t_{1},\ldots,t_{n},t,s\in \mathcal{B},\gamma \in \Gamma$, all $\eta \in \Omega$ in which $\Omega \in D_{\mathbb{C}}$ is a bounded set, $\Theta,\Upsilon,\Xi \in \mathbb{C}$ and $\tau \in \mathcal{G}^{\circ }$. Then there is a unique $C^{*}$VAF Lie $(\Theta,\Upsilon,\Xi )$-derivation ${\mathfrak{H}}:\Gamma \times { \mathcal{B}}\rightarrow \mathcal{B}$ which satisfies $\Delta _{\nu }g=0$ and the inequality

$$ {\mathcal{N}}\bigl(g(\gamma,w)-{\mathfrak{H}}(\gamma,w),\tau \bigr)\succeq \varphi \biggl(\bigl(\overbrace{w,\ldots,w}^{{n}{\textit{-times}}}, 0,0 \bigr), \frac{2n(\sqrt[k]{2^{k-1}}-\ell ^{k})}{\sqrt[k]{2^{k-1}}}\tau \biggr) $$

(3.11)

for all $w\in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$.

Proof

Putting $t_{1},\ldots, t_{n} =t$ and $\eta =1$ in (3.10), we get

$$ {\mathcal{N}}\bigl(ng(\gamma,2t)-2ng(\gamma,t),\tau \bigr)\succeq \varphi \bigl( (t,\ldots,t,0,0 )\tau \bigr) $$

(3.12)

for all $t\in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Let $M:=\{f:\Gamma \times \mathcal{B}\rightarrow \mathcal{B}, f(\varpi,0)=0 \forall \varpi \in \Gamma \}$. We introduce a function on M as

$$\begin{aligned} \delta (f,h): ={}& \inf \biggl\{ u>0: {\mathcal{N}}\bigl(f(\gamma,t) - h( \gamma,t), \tau \bigr) )\succeq \varphi \biggl( (t,\ldots,t,0,0), \frac{\tau }{u} \biggr), \\ & \forall t\in {\mathcal{B}}, \gamma \in \Gamma \text{ and } \tau \in \mathcal{G}^{\circ }\biggr\} . \end{aligned}$$

In [22], Miheţ and Radu showed that $(B, \delta )$ is a complete Ξ-valued metric space (see [23]).

Define $\Lambda:M\rightarrow M$ as

$$ (\Lambda f) (\gamma,t)= \frac{1}{2}f(\gamma,2t) \quad\text{for all } f \in E \text{ and } t \in \mathcal{B}. $$

Now, we have

$$\begin{aligned} {\mathcal{N}}\bigl((\Lambda f) (\varpi,w) - (\Lambda h) (\varpi,w), \varsigma \bigr)& = {\mathcal{N}} \biggl(\frac{1}{2}f(\gamma,2t) - \frac{1}{2}h(\gamma,2t),\varsigma \biggr) \\ & = {\mathcal{N}} \bigl( f(\gamma,2t) - h(\gamma,2t),2\varsigma \bigr) \\ &\succeq \varphi \biggl((2w,\ldots,2w,0,0),\frac{2\varsigma }{u} \biggr) \\ &\succeq \varphi \biggl((w,\ldots,w,0,0), \frac{2^{1-\frac{1}{k}}\varsigma }{\ell ^{k} u} \biggr) \end{aligned}$$

for all $w\in \mathcal{B}$ and $\varsigma \in \mathcal{G}^{\circ },\varpi \in \Gamma$, and so $\delta (\Lambda f, \Lambda h) \le \frac{\ell ^{k}}{2^{1-\frac{1}{k}}}\delta (f, h)$ for any $f, h \in E$. Let g be as in the statement of the theorem. Using (3.12) we get

$$ {\mathcal{N}} \biggl(\frac{1}{2}g(\gamma,2t)-g(\gamma,t),\tau \biggr) \succeq \varphi \bigl( (t,\ldots,t,0,0 ),2n\tau \bigr) $$

for all $t \in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Then $\delta (\Lambda g,g) \le \frac{1}{2n}$. Applying Theorem 1, we get that $\{\Lambda ^{m} g\}$ converges to a unique fixed point ${\mathfrak{H}}\in M$ of Λ such that ${\mathfrak{H}}(\gamma,2t)=2{\mathfrak{H}}(\gamma,t)$, i.e.,

$$\begin{aligned} {\mathfrak{H}}(\gamma,t)= \lim_{m\to \infty } \frac{1}{2^{m}} g \bigl( \gamma,2^{m}t \bigr) \end{aligned}$$

(3.13)

for all $t \in \mathcal{B}$. Also

$$ \delta (g,{\mathfrak{H}})\le \frac{1}{1-\frac{\ell ^{k}}{{2^{1-\frac{1}{k}}}}} \delta (g, \Lambda g) \le \frac{1}{2n(1-\frac{\ell ^{k}}{{2^{1-\frac{1}{k}}}})}= \frac{\sqrt[k]{2^{k-1}}}{2n(\sqrt[k]{2^{k-1}}-\ell ^{k})}, $$

i.e., (3.5) is true for every $t \in \mathcal{B}$. Then (3.11) is true. Using Theorem 2, we can complete the proof. □

Example 8

Let a random operator $g: \Gamma \times {\mathcal{B}}\rightarrow \mathcal{B}$ satisfy

$$\begin{aligned} &{{\mathcal{N}}} \bigl(\Delta _{\eta }g ( \gamma,t_{1}, t_{2} )+\Delta _{\Theta,\Upsilon,\Xi } g ( \gamma,t_{3},t_{4} ),\tau \bigr) \\ &\quad \succeq \operatorname{diag} \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{4} \Vert t_{j} \Vert ^{\frac{1}{6}}},\exp \biggl(- \frac{\sum_{j=1}^{4} \Vert t_{j} \Vert ^{\frac{1}{6}}}{\tau } \biggr) \biggr] \end{aligned}$$

(3.14)

for all $t_{1},\ldots,t_{4}\in \mathcal{B},\gamma \in \Gamma$, all $\eta \in \Omega$ in which $\Omega \in D_{\mathbb{C}}$ is a bounded set, $\Theta,\Upsilon,\Xi \in \mathbb{C}$ and $\tau \in \mathcal{G}^{\circ }$. Then there is a unique $C^{*}$VAF Lie $(\Theta,\Upsilon,\Xi )$-derivation ${\mathfrak{H}}:\Gamma \times { \mathcal{B}}\rightarrow \mathcal{B}$ which satisfies $\Delta _{\nu }g=0$ and the inequality

$$\begin{aligned} &{\mathcal{N}}\bigl(g(\gamma,w)-{\mathfrak{H}}(\gamma,w),\tau \bigr) \\ &\quad\succeq \operatorname{diag} \biggl[ \frac{8(\sqrt[6]{32}-1)\tau }{8(\sqrt[6]{32}-1)\tau + 2\sqrt[6]{32} \Vert w \Vert ^{\frac{1}{6}}}, \exp \biggl(- \frac{\sqrt[6]{32} \Vert w \Vert ^{\frac{1}{6}}}{4(\sqrt[6]{32}-1)\tau } \biggr) \biggr] \end{aligned}$$

(3.15)

for all $w\in \mathcal{B},\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$.

Define

$$ \varphi \bigl((t_{1},t_{2},t_{3},t_{4}), \tau \bigr)= \biggl[ \frac{\tau }{\tau +\sum_{j=1}^{4} \Vert t_{j} \Vert ^{\frac{1}{6}}},\exp \biggl(-\frac{\sum_{j=1}^{4} \Vert t_{j} \Vert ^{\frac{1}{6}}}{\tau } \biggr) \biggr] $$

for all $t_{1},t_{2},t_{3},t_{4}\in \mathbb{R}$ and $\tau \in \mathcal{G}^{\circ }$. Put $\ell =\frac{1}{\sqrt[18]{2}}$. Then φ is a $(4,3)$-contractively sub-homogeneous function. Now, applying Theorem 3, we get (3.15).

4 $C^{*}$-ternary algebra stochastic homomorphism

A $\mathbb{C}$-linear random operator $\eta: \Gamma \times T \rightarrow S$ is said to be a $C^{*}$-ternary algebra stochastic homomorphism ($C^{*}$-tash) if

$$ \eta \bigl(\gamma,[t,s,p]\bigr) = \bigl[\eta (\gamma,t), \eta (\gamma,s), \eta ( \gamma,p)\bigr] $$

for all $t,s,p \in T$ and $\gamma \in \Gamma$ (see [6, 24]).

Consider a random operator $g: \Gamma \times T \to S$ and define

$$ \Xi _{\xi }g(\gamma,t_{1},\dots,t_{p},s_{1}, \dots,s_{d}):= 2g \Biggl( \gamma,\frac{\sum_{j=1}^{p}\xi t_{j}}{2}+\sum _{j=1}^{d}\xi s_{j} \Biggr)-\sum _{j=1}^{p}\xi g(\gamma,t_{j})-2\sum _{j=1}^{d}\xi g( \gamma,s_{j}) $$

for all $\xi \in {\mathbb{T}}^{1}:=\{ \lambda \in \mathbb{C}: | \lambda |=1 \}$ and all $t_{1},\dots,t_{p},s_{1},\dots,s_{d}\in T$ and $\gamma \in \Gamma$.

It is easy to show that a random operator $g: \Gamma \times T \to S$ satisfies

$$ \Xi _{\xi }g(\gamma,t_{1}, \ldots, t_{p}, s_{1}, \ldots, s_{d}) =0 $$

for all $\xi \in {\mathbb{T}}^{1}$, $t_{1},\ldots,t_{p},s_{1},\ldots,s_{d}\in T$ and $\gamma \in \Gamma$ if and only if

$$ g(\gamma,\xi t+\lambda s)=\xi g(\gamma,t)+\lambda g(\gamma,s) $$

for all $\xi, \lambda \in {\mathbb{T}}^{1}$, $t,s \in T$ and $\gamma \in \Gamma$.

Theorem 4

Consider q and σ such that $q<1$ and $\sigma < 3$. Let $\varphi:T ^{p+d}\times (0,\infty )\rightarrow {\mathcal{A}}^{+}$ ($d \geq 2$) and $\psi:T^{3}\times (0,\infty ) \rightarrow {\mathcal{A }}^{+}$ be a $C^{*}$-AVF control function satisfying

$$\begin{aligned} &\varphi \bigl(a(t_{1},\dots,t_{p},s_{1}, \dots,s_{d}),\tau \bigr)=\varphi \biggl( (t_{1}, \dots,t_{p},s_{1},\dots,s_{d}),\frac{\tau }{a^{q}} \biggr), \end{aligned}$$

(4.1)

$$\begin{aligned} &\psi \bigl( a(t,s,p),\tau \bigr)=\psi \biggl((t,s,p), \frac{\tau }{a^{\sigma }} \biggr) \end{aligned}$$

(4.2)

and

$$\begin{aligned} \lim_{\mu \to \infty } \varphi \bigl( (t_{1}, \dots,t_{p},s_{1},\dots,s_{d}), \mu \bigr)= \lim _{\mu \to \infty } \psi \bigl((t,s,p),\mu \bigr)=1 \end{aligned}$$

(4.3)

for all $t_{1},\dots,t_{p},s_{1},\dots,s_{d},t,s,p\in T$, $a>0$, and $\tau, \nu \in \mathcal{G}^{\circ }$. Suppose that $g: \Gamma \times T \rightarrow S$ is a random operator with $g(\gamma,0)=0$ satisfying

$$ {\mathcal{N}}\bigl(\Xi _{\eta } g(\gamma,t_{1}, \dots,t_{p},s_{1},\dots,s_{d}), \tau \bigr) \succeq \varphi \bigl((t_{1},\dots,t_{p},s_{1}, \dots,s_{d}),\tau \bigr) $$

(4.4)

and

$$ {\mathcal{N}}\bigl(g\bigl(\gamma,[t,s,p]\bigr) - \bigl[g( \gamma,t), g(\gamma,s), g( \gamma,p)\bigr],\tau \bigr)\succeq \psi \bigl((t,s,p), \tau \bigr) $$

(4.5)

for all $\eta \in \mathbb{T}$¹ and all $t_{1},\dots,t_{p},s_{1},\dots,s_{d},t,s,p \in T$ and $\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Then there exists a unique $C^{*}$-tash ${\mathfrak{H}}: \Gamma \times T \rightarrow S$ such that

$$ {\mathcal{N}}\bigl(g(\gamma,t)-{\mathfrak{H}}(\gamma,t),\tau \bigr)\succeq \varphi \bigl(\bigl(\overbrace{0,\ldots,0,t,\ldots,t}^{{n+d}{\textit{-times}}} \bigr),2 \tau \bigl(d-d^{q}\bigr) \bigr) $$

(4.6)

for all $t\in T,\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$.

Proof

Let $0< q<1$ and $0<\sigma <3$ (the other cases are similar).

Putting $\eta =1$, $t_{1}=\cdots =t_{p}=0$ and $s_{1}=\cdots =s_{d}=t$ in (4.4), we get

$$ {\mathcal{N}}\bigl(2g(\gamma,dt)-2dg(\gamma,t),\tau \bigr)\succeq \varphi \bigl(\bigl( \overbrace{0,\dots,0}^{p},\overbrace{t, \dots,t}^{d}\bigr),\tau \bigr) $$

(4.7)

for all $t\in T,\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Replacing t by $d^{n} t$ in (4.7), we get

$$ {\mathcal{N}} \biggl(\frac{1}{d^{n+1}}g\bigl(\gamma,d^{n+1}t\bigr)- \frac{1}{d^{n}}g\bigl(\gamma,d^{n}t\bigr),\tau \biggr) \succeq \varphi \bigl(\bigl( \overbrace{0,\dots,0}^{p},\overbrace{t, \dots,t}^{d}\bigr),2d\tau d^{(1-q)n}\bigr) $$

for all $t\in T,\gamma \in \Gamma$, all nonnegative integers n and $\tau \in \mathcal{G}^{\circ }$. Therefore,

$$\begin{aligned} &{\mathcal{N}} \biggl(\frac{1}{d^{n+m}}g\bigl( \gamma,d^{n+m}t\bigr)- \frac{1}{d^{m}}g\bigl(\gamma,d^{m}t \bigr),\tau \biggr) \\ &\quad\succeq \varphi \biggl(\bigl( \overbrace{0, \dots,0}^{p},\overbrace{t,\dots,t}^{d}\bigr), \frac{2d\tau }{\sum_{k=m}^{m+n}d^{(q-1)k}} \biggr) \end{aligned}$$

(4.8)

for all $t\in T$, $n,m\in \mathbb{N}$ and $\tau \in \mathcal{G}^{\circ }$, and it follows that $\{\frac{1}{d^{n}} g(\gamma,d^{n} t)\}$ is a Cauchy sequence for every $t \in A$. The completeness of B implies that $\{\frac{1}{d^{n}} g(\gamma,d^{n} t)\}$ converges. Thus we can define the random operator ${\mathfrak{H}}: \Gamma \times T \rightarrow S$ by

$$ {\mathfrak{H}}(\gamma,t): = \lim_{n\to \infty } \frac{1}{d^{n}} g \bigl( \gamma,d^{n} t\bigr) $$

for all $t \in T,\gamma \in \Gamma$. Putting $m =0$ and letting $n \to \infty$ in (4.8), we get (4.6). We conclude from (4.1), (4.3), and (4.4) that

$$\begin{aligned} & {\mathcal{N}} \Biggl(2{\mathfrak{H}}\Biggl(\gamma, \frac{\sum_{j=1}^{p} \eta t_{j}}{2}+\sum _{j=1}^{d} \eta s_{j}\Biggr) - \sum_{j=1}^{p} \eta {\mathfrak{H}}( \gamma,t_{j})-2 \sum_{j=1}^{d} \eta {\mathfrak{H}}(\gamma,s_{j}),\tau \Biggr) \\ & \quad = \lim_{n\to \infty } {\mathcal{N}} ( \frac{1}{d^{n}} \Biggl( 2 g\Biggl( \gamma,d^{n}\frac{\sum_{j=1}^{p} \eta t_{j}}{2}+d^{n}\sum _{j=1}^{d} \eta s_{j}\Biggr) \\ &\qquad{}- \sum _{j=1}^{p} \eta g\bigl(\gamma,d^{n} t_{j}\bigr)-2 \sum_{j=1}^{d} \eta g\bigl(\gamma,d^{n}s_{j}\bigr),\tau \Biggr) \\ & \quad \succeq \lim_{n\to \infty } \varphi \bigl(\bigl(d^{n}(t_{1}, \dots,t_{p},s_{1}, \dots,s_{d}) \bigr),{d^{n}} \tau \bigr) \\ & \quad = \lim_{n\to \infty } \varphi \biggl(( t_{1}, \dots,t_{p},s_{1}, \dots,s_{d}), \frac{d^{n}}{d^{nq}}\tau \biggr) \\ & \quad=1 \end{aligned}$$

for all $\eta \in \mathbb{T}$¹, $t_{1}, \dots, t_{p}, s_{1}, \dots, s_{d} \in T$, $\gamma \in \Gamma$, and $\tau \in \mathcal{G}^{\circ }$. Hence

$$ 2{\mathfrak{H}} \Biggl(\gamma,\frac{\sum_{j=1}^{p} \eta t_{j}}{2}+\sum _{j=1}^{d} \eta s_{j} \Biggr) = \sum _{j=1}^{p} \eta {\mathfrak{H}}( \gamma,t_{j})+2 \sum_{j=1}^{d} \eta {\mathfrak{H}}(\gamma,s_{j}) $$

for all $\eta \in \mathbb{T}$¹ and all $t_{1}, \dots, t_{p}, s_{1}, \dots, s_{d} \in T$. Thus ${\mathfrak{H}}(\lambda t+\eta s)=\lambda {\mathfrak{H}}(\gamma,t)+ \eta {\mathfrak{H}}(\gamma,s)$ for all $\lambda, \eta \in \mathbb{T}$¹ and all $t, s \in T$.

Therefore, from Lemma 4 the random operator ${\mathfrak{H}}: \Gamma \times T \rightarrow S$ is $\mathbb{C}$-linear.

We conclude from (4.2), (4.3), and (4.5) that

$$ \begin{aligned} & {\mathcal{N}} \bigl({\mathcal{H}}\bigl(\gamma,[t, s, p]\bigr)- \bigl[{\mathcal{H}}( \gamma,t), {\mathcal{H}}(\gamma,s), { \mathcal{H}}(\gamma,p)\bigr],\tau \bigr) \\ &\quad =\lim_{n\to \infty }{\mathcal{N}}\biggl(\frac{1}{d^{3n}} \bigl(g \bigl( \gamma,\bigl[d^{n} t, d^{n} s, d^{n} p \bigr] \bigr) - \bigl[g\bigl(\gamma,d^{n} t\bigr), g\bigl( \gamma,d^{n} s\bigr), g\bigl(\gamma,d^{n} p\bigr) \bigr] \bigr),\tau \biggr) \\ & \quad=\lim_{n\to \infty }{\mathcal{N}} \bigl( g \bigl(\gamma, \bigl[d^{n} t, d^{n} s, d^{n} p\bigr] \bigr) - \bigl[g\bigl(\gamma,d^{n} t\bigr),g\bigl(\gamma,d^{n} s \bigr), g\bigl( \gamma,d^{n} p\bigr) \bigr],{d^{3n}}\tau \bigr) \\ &\quad\succeq \lim_{n\to \infty }\psi \bigl(\bigl(d^{n} t, d^{n} s, d^{n} p\bigr),{d^{3n}} \tau \bigr) \\ &\quad= \lim_{n\to \infty }\psi \biggl((t,s,p), \frac{d^{3n}}{d^{n\sigma }} \tau \biggr)=1 \end{aligned} $$

for all $t, s,p \in T,\gamma \in \Gamma$, and $\tau \in \mathcal{G}^{\circ }$. Thus

$$ {\mathcal{H}}\bigl(\gamma,[t, s, p]\bigr) = \bigl[ {\mathcal{H}}(\gamma,t), { \mathcal{H}}(\gamma,s), {\mathcal{H}}(\gamma,p)\bigr] $$

for all $t, s, p \in T$ and $\gamma \in \Gamma$.

Consider another generalized Cauchy–Jensen additive random operator ${\mathcal{K}}: \Gamma \times T \rightarrow S$ satisfying (4.6). Then we have

$$\begin{aligned} {\mathcal{N}}\bigl({\mathcal{H}}(\gamma,t)-{\mathcal{K}}(\gamma,t),\tau \bigr)&=\lim_{n \to \infty }{\mathcal{N}} \biggl(\frac{1}{d^{n}} \bigl(g\bigl(\gamma,d^{n} t\bigr)-{ \mathcal{K}}\bigl( \gamma,d^{n} t\bigr)\bigr),\tau \biggr) \\ &= \lim_{n\to \infty }{\mathcal{N}} \bigl( g\bigl( \gamma,d^{n} t\bigr)-{ \mathcal{K}}\bigl(\gamma,d^{n} t \bigr),d^{n}\tau \bigr) \\ &\succeq \lim_{n\to \infty } \varphi \bigl(\bigl(\overbrace{0, \dots,0}^{p}, \overbrace{d^{n}t,\dots,d^{n}t}^{d} \bigr),2\tau d^{n}\bigl(d-d^{q}\bigr) \bigr) \\ &= \lim_{n\to \infty } \varphi \biggl(\bigl(\overbrace{0, \dots,0}^{p}, \overbrace{t,\dots,t}^{d}\bigr), \biggl( \frac{2\tau d^{n}(d-d^{q})}{d^{nq}} \biggr) \biggr) \\ &=1 \end{aligned}$$

for all $t \in T,\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Then ${\mathcal{H}}(\gamma,t)={\mathcal{K}}(\gamma,t)$ for all $t \in T$. Thus the random operator ${\mathcal{H}}: \Gamma \times T\rightarrow S$ is a unique $C^{*}$-tash satisfying (4.6), as desired. □

Theorem 5

Let $q<1$ and $\sigma <2$. Let $g:\Gamma \times T \rightarrow S$ be a random operator satisfying (4.1), (4.2), (4.3), (4.4), and (4.5). If there exist a real number $\lambda >1 (0<\lambda <1)$ and an element $t_{0}\in T$ such that $\lim_{n\rightarrow \infty } \frac{1}{\lambda ^{n}} g(\gamma, \lambda ^{n} t_{0}) = e' (\lim_{n\rightarrow \infty } \lambda ^{n} g(\gamma,\frac{t_{0}}{\lambda ^{n}}) = e' )$ (identity element), then the random operator $g: \Gamma \times T \rightarrow S$ is a $C^{*}$-tash.

Proof

Applying Theorem 4, we get that there exists a unique $C^{*}$-tash ${\mathcal{H}}:\Gamma \times T \rightarrow S$ satisfying (4.6). Now,

$$ {\mathcal{H}}(\gamma,t)=\lim_{n\rightarrow \infty } \frac{1}{\lambda ^{n}} g\bigl(\gamma,\lambda ^{n} t\bigr), \quad\biggl({ \mathcal{H}}(\gamma,t)=\lim_{n\rightarrow \infty } \lambda ^{n} g \biggl( \gamma,\frac{t}{\lambda ^{n}}\biggr) \biggr) $$

(4.9)

for all $t\in T$ and all real numbers $\lambda >1 (0<\lambda <1)$. Therefore, from the assumption we get that ${\mathcal{H}}(\gamma,t_{0})=e'$. Let $\lambda >1$ and $\lim_{n\rightarrow \infty } \frac{1}{\lambda ^{n}} g(\gamma, \lambda ^{n} t_{0}) = e'$. It follows from (4.5) and (4.9) that

$$\begin{aligned} & {\mathcal{N}}\bigl(\bigl[{\mathcal{H}}(\gamma,t),{\mathcal{H}}(\gamma,s),{ \mathcal{H}}(\gamma,p)\bigr]-\bigl[{\mathcal{H}}(\gamma,t),{\mathcal{H}}( \gamma,s),g( \gamma,p)\bigr],\tau \bigr) \\ &\quad={\mathcal{N}}\bigl({\mathcal{H}}[\gamma,t,s,p]-\bigl[{\mathcal{H}}( \gamma,t),{ \mathcal{H}}(\gamma,s),{\mathcal{H}}(\gamma,p)\bigr],\tau \bigr) \\ &\quad=\lim_{n\rightarrow \infty }{\mathcal{N}} \biggl( \frac{1}{\lambda ^{2n}}\bigl(g \bigl(\bigl[\gamma,\lambda ^{n} t,\lambda ^{n} s, p\bigr] \bigr) - \bigl[g\bigl(\gamma,\lambda ^{n} t\bigr),g\bigl(\lambda ^{n} s\bigr),g(\gamma,z) \bigr]\bigr),\tau \biggr) \\ &\quad=\lim_{n\rightarrow \infty }{\mathcal{N}} \bigl( g\bigl(\bigl[\gamma,\lambda ^{n} t,\lambda ^{n} s, p\bigr]\bigr) - \bigl[g\bigl(\gamma, \lambda ^{n} t\bigr),g\bigl(\gamma,\lambda ^{n} s\bigr),g( \gamma,p) \bigr],\lambda ^{2n}\tau \bigr) \\ &\quad\succeq \lim_{n\rightarrow \infty } \psi \bigl(\bigl(\lambda ^{t}, \lambda ^{s}, \lambda ^{p}\bigr),\lambda ^{2n}\tau \bigr) \\ &\quad= \lim_{n\rightarrow \infty } \psi \biggl((t,s,p), \frac{\lambda ^{2n}}{\lambda ^{2n\sigma }}\tau \biggr) \\ &\quad =1 \end{aligned}$$

for all $t\in T,\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Thus $[{\mathcal{H}}(\gamma,t),{\mathcal{H}}(\gamma,s),{\mathcal{H}}( \gamma,p)]=[{\mathcal{H}}(\gamma,t),{\mathcal{H}}(\gamma,s),g( \gamma,p)]$ for all $t,s,p\in T$. Letting $t=s=t_{0}$ in the last equality, we get $g(\gamma,t)={\mathcal{H}}(\gamma,p)$ for all $p\in T$.

Similarly, one can show that ${\mathcal{H}}(\gamma,t)=g(\gamma,t)$ for all $t\in T$ when $0<\lambda <1$ and $\lim_{n\rightarrow \infty } \lambda ^{n} g(\gamma, \frac{t_{0}}{\lambda ^{n}})=e'$. Therefore, the random operator $g:\Gamma \times T \rightarrow S$ is a $C^{*}$-tash. □

Theorem 6

Let $q>1$ and $\sigma >3$. Let $g:\Gamma \times T \rightarrow S$ be a random operator satisfying (4.4) and (4.5). If there exist a real number $0<\lambda <1\ (\lambda >1)$ and an element $t_{0}\in T$ such that $\lim_{n\rightarrow \infty } \frac{1}{\lambda ^{n}} g(\gamma, \lambda ^{n} t_{0}) = e' (\lim_{n\rightarrow \infty } \lambda ^{n} g(\gamma,\frac{t_{0}}{\lambda ^{n}}) = e' )$, then the random operator $g:\Gamma \times T \rightarrow S$ is a $C^{*}$-tash.

Proof

The proof is similar to the proof of Theorem 5, and so we omit it. □

Example 9

Consider q and σ such that $q<1$ and $\sigma < 3$. Suppose that $g: \Gamma \times T \rightarrow S$ is a random operator with $g(\gamma,0)=0$ satisfying

$$\begin{aligned} & {\mathcal{N}}\bigl(\Xi _{\eta } g(\gamma,t_{1}, \dots,t_{p},s_{1},\dots,s_{d}), \tau \bigr) \\ &\quad\succeq \operatorname{diag} \biggl[ \frac{\tau }{\tau +(\sum_{j=1}^{p} \Vert t_{j} \Vert ^{q} +\sum_{j=1}^{d} \Vert s_{j} \Vert ^{q})}, \exp \biggl(- \frac{\sum_{j=1}^{p} \Vert t_{j} \Vert ^{q} +\sum_{j=1}^{d} \Vert s_{j} \Vert ^{q}}{\tau } \biggr) \biggr] \end{aligned}$$

(4.10)

and

$$\begin{aligned} &{\mathcal{N}}\bigl(g\bigl(\gamma,[t,s,p]\bigr) - \bigl[g( \gamma,t), g(\gamma,s), g( \gamma,p)\bigr],\tau \bigr)\\ &\quad \succeq \operatorname{diag} \biggl[ \frac{\tau }{\tau ( \Vert t \Vert ^{q} + \Vert s \Vert ^{q})}, \exp \biggl(- \frac{ \Vert t \Vert ^{q} + \Vert s \Vert ^{q}}{\tau } \biggr) \biggr] \end{aligned}$$

(4.11)

for all $\eta \in \mathbb{T}$¹ and all $t_{1},\dots,t_{p},s_{1},\dots,s_{d},t,s,p \in T$ and $\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Then there exists a unique $C^{*}$-tash ${\mathfrak{H}}: \Gamma \times T \rightarrow S$ such that

$$ {\mathcal{N}}\bigl(g(\gamma,t)-{\mathfrak{H}}(\gamma,t),\tau \bigr)\succeq \operatorname{diag} \biggl[\frac{2\tau (d-d^{q})}{2\tau (d-d^{q})+(d \Vert t \Vert ^{q})}, \exp \biggl(- \frac{d \Vert t \Vert ^{q}}{2\tau (d-d^{q})} \biggr) \biggr] $$

(4.12)

for all $t\in T,\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$.

To see this, put

$$\begin{aligned} &\varphi \bigl((t_{1},\dots,t_{p},s_{1}, \dots,s_{d}),\tau \bigr) \\ &\quad =\operatorname{diag} \biggl[ \frac{\tau }{\tau +(\sum_{j=1}^{p} \Vert t_{j} \Vert ^{q} +\sum_{j=1}^{d} \Vert s_{j} \Vert ^{q})}, \exp \biggl(- \frac{\sum_{j=1}^{p} \Vert t_{j} \Vert ^{q} +\sum_{j=1}^{d} \Vert s_{j} \Vert ^{q}}{\tau } \biggr) \biggr] \end{aligned}$$

(4.13)

and

$$\begin{aligned} \psi \bigl((t,s,p),\tau \bigr)=\operatorname{diag} \biggl[ \frac{\tau }{\tau ( \Vert t \Vert ^{q} + \Vert s \Vert ^{q})}, \exp \biggl(- \frac{ \Vert t \Vert ^{q} + \Vert s \Vert ^{q}}{\tau } \biggr) \biggr] \end{aligned}$$

(4.14)

for all $t_{1},\dots,t_{p},s_{1},\dots,s_{d},t,s,p \in T$ and $\gamma \in \Gamma$ and $\tau \in \mathcal{G}^{\circ }$. Now, applying Theorem 4, we get (4.12).

Example 10

Let $q<1$ and $\sigma <2$. Let $g:\Gamma \times T \rightarrow S$ be a random operator satisfying (4.10), (4.11). If there exist a real number $\lambda >1 (0<\lambda <1)$ and an element $t_{0}\in T$ such that $\lim_{n\rightarrow \infty } \frac{1}{\lambda ^{n}} g(\gamma, \lambda ^{n} t_{0}) = e' (\lim_{n\rightarrow \infty } \lambda ^{n} g(\gamma,\frac{t_{0}}{\lambda ^{n}}) = e' )$ (identity element), then the random operator $g: \Gamma \times T \rightarrow S$ is a $C^{*}$-tash.

Define control functions φ and ψ as in (4.13) and (4.14). Theorem 5 guarantees the result.

5 Conclusion

In this paper we defined a new generalization of uncertain normed spaces by replacing the classical range by $C^{*}$-AV fuzzy sets and using triangular norms defined on the positive section of an order commutative $C^{*}$-algebra, named $C^{*}$-AVF-spaces. Also, by a super $C^{*}$-AVF controller, we considered Hyers–Ulam–Rassias stability of stochastic $(\Theta,\Upsilon,\Xi )$-derivations on $C^{*}$-AVF Lie $C^{*}$-algebras.