1 Introduction

Various mathematical models have been proposed to understand the various phenomena better. Proposing biological models [1] has become most important as it helps scientists in better understanding and bringing new insight into it, such as epidemic modeling that may help in control of the epidemic. Most of the biological models [2, 3] that have been proposed fall in the category of non-linear biological systems. Chaos, antimonotonicity, different types of bifurcations, multi-stability are the many properties [4] which have been visualized in many biological models. In order to analyze the proposed non-linear dynamical models [5–8], one should use non-linear methods such as Lyapunov exponents, stagnation points analysis, basins of attraction, and bifurcation diagrams. In order to model the changing dynamics, the considered parameter values can be changed over a wide range.

Since a very long time ago, the Hopfield neural network (HNN) has been carefully studied and applied in various fields such as in image encryption, data storage, information processing, and associative memory. Because of the exceptional non-linearity of the neuron activation function, the HNN model is stoutly non-linear [9]. Like the chaotic time delay systems, Chua circuit, and coupled HR neuron circuits [10], the HNN model generates very complex behaviors like hyper-chaos, periodic chaos and quasi-period [11], which implies that the HNN model simulates the prominent chaotic behavior like that of the brain [12, 13]. Therefore, one must investigate these systems as they have a theoretical significance as well as practical significance. Up to now various HNN models have been studied and proposed in the literature; such as the two dimensional neuronal model [14], three dimensional neuronal model [15] and four dimensional neuronal model [16]. For these systems a variety of studies has been done, such as multi-stability, coexisting attractors, circuit implementation, and synchronization [17–23].

Many chaos control methods [24–27] have been developed in the recent past to tame chaos and increase its application across various disciplines. Some of the popular methods used are active control, tracking control, sliding mode, and the parameter estimation method. Chaos synchronization is also a way to contain chaos between master and slave systems. Some popular synchronization methods use the anti-synchronization, projective synchronization, difference synchronization, and matrix synchronization [28] methods [29–32].

We study fractional [33, 34] HNN model varying parameter values and fractional orders. Some basic dynamic methods [35–37] have been used such as Lyapunov exponents [38, 39], bifurcation diagrams [40], phase portraits, and time series. We have also discussed the existence of the solution of the considered system. As the considered system did not have any stagnation point, we have used chaos control using adaptive sliding mode about two arbitrarily chosen desired points considering external disturbances and uncertainties. The disturbances have been estimated and the error converging to zero has been achieved, which have been plotted using MATLAB software.

2 The fractional Hopfield neural network

The fractional HNN model is [41]:

$$ \begin{aligned} &\dot{Z_{1}}=-Z_{1}-1.4 \tanh(Z_{1})+1.2\tanh(Z_{2})-7\tanh(Z_{3}), \\ &\dot{Z_{2}}=-Z_{2}+1.1\tanh(Z_{1})+2.8 \tanh(Z_{3}), \\ &\dot{Z_{3}}=-{Z_{3}}+P \tanh(Z_{1})-2 \tanh(Z_{2})+4\tanh(Z_{3}). \end{aligned} $$
(1)

For \(P=0.8\) and I.C. \((0,0.01,0)\), system (1) shows chaotic behavior. Here we introduce the fractional version of HNN, perform its thorough dynamical analysis and chaos control. Caputo’s derivative is used in the paper:

$$\begin{aligned} {{}_{t_{0}} D^{\alpha}_{t} f(t)}= \frac{1}{\Gamma(n-\alpha)} \int_{t_{0}}^{t} \frac{f^{(n)}(\tau)}{(t-\tau)^{\alpha-n+1}}\,d\tau, \quad t>t_{0}. \end{aligned}$$

The fractional HNN model is given as

$$ \begin{aligned} &D^{q}{V_{1}}=-Z_{1}-1.4 \tanh(Z_{1})+1.2\tanh(Z_{2})-7\tanh(Z_{3}), \\ &D^{q}{V_{2}}=-Z_{2}+1.1 \tanh(Z_{1})+2.8\tanh(Z_{3}), \\ &D^{q}{V_{3}}=-{Z_{3}}+P \tanh(Z_{1})-2\tanh(Z_{2})+4\tanh(Z_{3}), \end{aligned} $$
(2)

where \(Z=(Z_{1},Z_{2},Z_{3})^{T}\in{R}^{3}\) are the state variables and \(P\in R\) is a parameter value.

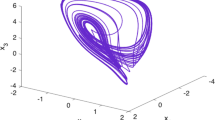
For \(P=0.8\) and initial condition (I.C.) \((0,0.01,0)\) the fractional system is chaotic for \(q=0.987\) as is seen in Fig. 1 and Fig. 2.

Figure 1
figure 1

State trajectories of (2)

Full size image
Figure 2
figure 2

Chaotic attractors of (2)

Full size image

3 Dynamics of fractional HNN model

The dynamics of the fractional HNN with tanhyperbolic terms is explored here, studying the symmetry, dissipative, uniqueness of the solution, bifurcation and Lyapunov dynamics, fixed point analysis, etc.

3.1 Symmetry, stagnation point analysis and dissipativity

System (2) in matrix form can be written as

[ D q Z 1 D q Z 2 D q Z 3 ] = [ G 1 ( Z ) G 2 ( Z ) G 3 ( Z ) ]

where

[ G 1 ( Z ) G 2 ( Z ) G 3 ( Z ) ] = [ − Z 1 − 1.4 tanh ( Z 1 ) + 1.2 tanh ( Z 2 ) − 7 tanh ( Z 3 ) − Z 2 + 1.1 tanh ( Z 1 ) + 2.8 tanh ( Z 3 ) − Z 3 + P tanh ( Z 1 ) − 2 tanh ( Z 2 ) + 4 tanh ( Z 3 ) ] .

The fractional HNN model (2) does not remain invariant under the \(Z_{i} \rightarrow-Z_{i}\), \(Z_{j} \rightarrow-Z_{j}\), \(Z_{k} \rightarrow Z_{k}\) transformation i.e. the system possesses asymmetric behavior about all the axes. However, the system is symmetric about the origin as under the transformation \(Z_{1} \rightarrow-Z_{1}\), \(Z_{2} \rightarrow-Z_{2}\), \(Z_{3} \rightarrow-Z_{3}\), the system remains invariant.

The divergence of G is

$$\begin{aligned} \nabla G&=\frac{\partial(G_{1}(Z))}{\partial Z_{1}}+ \frac{\partial(G_{2}(Z))}{\partial Z_{2}}+ \frac{\partial(G_{3}(Z)}{\partial Z_{3}} \\ &=-1-1.4\operatorname{sech}^{2} Z_{1}-1-1+4\operatorname{sech}^{2} Z_{3} \\ &=-1-1.4-1-1+4 \end{aligned}$$

i.e.

$$ \nabla G=-0.4< 0. $$

Therefore (2) is dissipative.

Equating \(G_{i}(Z_{1},Z_{2},Z_{3})\) for \(i=1,2,3\) to 0, the system can be explored for stagnation points i.e.

$$\begin{aligned}& -Z_{1}-1.4\tanh(Z_{1})+1.2\tanh(Z_{2})-7 \tanh(Z_{3})=0, \\& -Z_{2}+1.1\tanh(Z_{1})+2.8\tanh(Z_{3})=0, \\& -{Z_{3}}+P \tanh(Z_{1})-2\tanh(Z_{2})+4 \tanh(Z_{3})=0. \end{aligned}$$

For \(P=0.8\) we obtain no stagnation points. The absence of stagnation points hints at the complex nature of the chaotic system.

3.2 Solution of HNN model

Theorem

The I.V.P. of system (2)

$$ D^{q}Z(t)=B_{1} Z(t)+B_{2}Z(t),\qquad Z(0)=Z_{o} $$

where

B 1 = [ − 1 0 0 0 − 1 0 0 0 − 1 ] , B 2 = [ − 1.4 1.2 − 7 1.1 0 2.8 0.8 − 2 4 ] , Z o = [ Z 1 o Z 2 o Z 3 o ] ,

\(q=(q_{1},q_{2},q_{3})^{T}\), \(0< q_{i}<1\) for \(i=1, 2, 3\) for some constant \(\tau>0\), then a unique solution exists.

Proof

Let \(G(Z)=B_{1}Z(t)+B_{2}\tanh(Z(t))\), then \(G(Z)\) is continuous and bounded on \([Z_{0}-\epsilon,Z_{0}+\epsilon]\) for any \(\epsilon>0\), therefore Lipschitz continuity over \([Z_{0}-\epsilon,Z_{0}+\epsilon]\) proves the existence and uniqueness of the solution.

We have

$$\begin{aligned} \bigl\vert G(Z)-G(W) \bigr\vert &= \bigl\vert \bigl(B_{1}Z(t)+B_{2} \tanh\bigl(Z(t)\bigr)\bigr)-\bigl(B_{1}W(t)+B_{2}\tanh \bigl(W(t)\bigr)\bigr) \bigr\vert \\ &= \bigl\vert B_{1}(Z-W)+B_{2}\bigl(\tanh\bigl(Z(t) \bigr)-\tanh\bigl(W(t)\bigr)\bigr) \bigr\vert \\ &\leq \Vert B_{1} \Vert \vert Z-W \vert + \Vert B_{2} \Vert \bigl( \bigl\vert \tanh\bigl(Z(t)\bigr) \bigr\vert + \bigl\vert \tanh\bigl(W(t)\bigr) \bigr\vert \bigr) \vert . \end{aligned}$$

We have

$$\begin{aligned} \bigl\vert \tanh\bigl(Z(t)\bigr) \bigr\vert &\leq1 \\ &\leq \Vert B_{1} \Vert \vert Z-W \vert +2 \Vert B_{2} \Vert . \end{aligned}$$

Thus

$$\begin{aligned} \bigl\vert G(Z)-G(W) \bigr\vert &\leq\bigl( \Vert B_{1} \Vert +2 \Vert B_{2} \Vert \bigr) \vert Z-W \vert \\ &=D \vert Z-W \vert , \end{aligned}$$

where \(D=(\|B_{1}\|+2\|B_{2}\|)[2|Z_{o}|+2 \epsilon]))\) and \(W(t) \in R^{3}\).

Hence system (2) possesses a unique solution. □

3.3 Lyapunov dynamics and bifurcation

For \(P=0.8\) and I.C. \((0,0.01,0)\) the Lyapunov spectrum of the system for \(q=0.987\) is

$$ 0.1584, 0.0067 \approx0, -0.5987. $$

The positive component confirms the presence of chaos. The L.E. shows the separation rate of trajectories starting closely. The Lyapunov values help to find the chaotic dimension of the chaotic attractor, called the Kaplan–Yorke dimension.

From the formula

$$ D_{YK}=p+\frac{\sum_{s=1}^{p}L.E._{s}}{ \vert L.E._{s+1} \vert + \vert L.E._{s+2} \vert }, $$

where p is such that \(\sum_{s=1}^{p}L.E._{s} \geq0\) and \(\sum_{s=1}^{p+1}L.E._{s} <0 \), we get the chaotic attractor’s dimension. Hence the K.Y. dimension is 2.27576.

Chaotic systems are highly sensitive to parameter values and I.C. By varying the parameter values and I.C. the nature of the dynamical system may vary from regular, periodic to chaotic nature. Bifurcations give the nature of chaotic system by changing parameters in a range. The bifurcations determine the route to chaos. For the HNN model by varying the parameter in the range \((0.5, 1)\) the bifurcations can be seen in Fig. 3. Figure 4 shows Lyapunov and bifurcations for varying q between 0.8 to 1. The phase portrait of the system for varying q is also shown in Fig. 5.

Figure 3
figure 3

Bifurcation diagram for \(P\in(0.5,1)\)

Full size image
Figure 4
figure 4

System dynamics for \(0.8 \leq q \leq1\)

Full size image
Figure 5
figure 5

Chaotic attractors for (2) at q= (a) 0.95, (b) 0.98, (c) 0.99, (d) 1

Full size image

4 Controlling chaos

Chaos in fractional HNN model exposed to uncertainties and disturbances is controlled using an adaptive SMC technique. Suitably designed controllers are constructed to stabilize chaos in the trajectories of the system about an arbitrarily chosen point \((p_{1},p_{2},p_{3})\). The fractional HNN model exposed to uncertainties and external disturbances is

$$ \begin{aligned} &D^{q}{Z_{1}}=-Z_{1}-1.4 \tanh(Z_{1})+1.2\tanh(Z_{2})-7\tanh(Z_{3})+ \bigtriangleup H_{1}+D_{1}+{v_{1}}, \\ &D^{q}{Z_{2}}=-Z_{2}+1.1 \tanh(Z_{1})+2.8\tanh(Z_{3})+\bigtriangleup H_{2}+D_{2}+{v_{2}}, \\ &D^{q}{Z_{3}}=-{Z_{3}}+P \tanh(Z_{1})-2\tanh(Z_{2})+4\tanh(Z_{3})+ \bigtriangleup H_{3}+D_{3}+{v_{3}}, \end{aligned} $$
(3)

where \(\bigtriangleup H_{i} \) are uncertainties and \(D_{i}\) are disturbances, \({v_{i}}\) are controllers designed about desired point. Figures 6 and 7 give the trajectories and plots of the exposed system. Consider \(|\bigtriangleup H_{i}| \) and \(D_{i} \) to be bounded by positive values \(C_{i} \) and \(F_{i}\) with \(\hat{C_{i}}\), \(\hat{F_{i}}\) being their estimates.

Figure 6
figure 6

Trajectories of exposed system (3)

Full size image
Figure 7
figure 7

Chaotic attractors of exposed system (3)

Full size image

Define the control error about the desired point \((p_{1},p_{2},p_{3})\) as

$$ \begin{aligned} &e_{1}=Z_{1}-p_{1}, \\ &e_{2}=Z_{2}-p_{2}, \\ &e_{3}=Z_{3}-p_{3}. \end{aligned} $$
(4)

Differentiating (4) we get

$$ \begin{aligned} &D^{q}{e_{1}}=-(e_{1}+p_{1})-1.4 \tanh(e_{1}+a)+1.2\tanh(e_{2}+p_{2}) \\ &\hphantom{D^{q}{e_{1}}=}{}-7\tanh(e_{3}+p_{3})+ \bigtriangleup H_{1}+D_{1}+v_{1}, \\ &D^{q}{e_{2}}=-(e_{2}+p_{2})+1.1 \tanh(e_{1}+a)+2.8\tanh(e_{3}+p_{3}) \\ &\hphantom{D^{q}{e_{2}}=}{}+ \bigtriangleup H_{2}+D_{2}+v_{2}, \\ &D^{q}{e_{3}}=-(e_{3}+p_{3})+0.8 \tanh(e_{1}+p_{1})-2\tanh(e_{2}+p_{2}) \\ &\hphantom{D^{q}{e_{3}}=}{}+4\tanh(e_{3}+p_{3})+ \bigtriangleup H_{3}+D_{3}+v_{3}. \end{aligned} $$
(5)

The sliding surface is defined as

$$ s_{i}(t)=D^{q-1}e_{i}(t)+ \lambda_{i} \int_{0}^{t}e_{i}(\xi)\,d \xi.$$
(6)

To have (5) in sliding mode, the necessary condition is

$$ s_{i}(t)=0, \qquad\dot{s_{i}}(t)=0. $$
(7)

Differentiating (6):

$$ \dot{s_{i}}(t)=D^{q}e_{i}(t)+{ \lambda}_{i}e_{i}(t), \quad i=1,2,3. $$
(8)

Then from (7), we have

$$ D^{q}e_{i}(t)=-{\lambda}_{i}e_{i}(t). $$
(9)

Equation (9) is stable using Matignon’s theorem [42]. The designed controllers are

$$ \begin{aligned} &v_{1} =(e_{1}+p_{1})+1.4\tanh(e_{1}+a)-1.2 \tanh(e_{2}+p_{2}) \\ &\hphantom{v_{1} =}{}+7\tanh(e_{3}+p_{3})- \lambda_{1} e_{1}-(\hat{C_{1}}+ \hat{F_{1}}+r_{1})\operatorname{sign}(s_{1}), \\ &v_{2} =(e_{2}+p_{2})-1.1 \tanh(e_{1}+a)-2.8\tanh(e_{3}+p_{3}) \\ &\hphantom{v_{2} =}{}-\lambda_{2} e_{2}-( \hat{C_{2}}+\hat{F_{2}}+r_{2}) \operatorname{sign}(s_{2}), \\ &v_{3}=(e_{3}+p_{3})-0.8 \tanh(e_{1}+p_{1})+2\tanh(e_{2}+p_{2}) \\ &\hphantom{v_{3}=}{}-4\tanh(e_{3}+p_{3})- \lambda_{3} e_{3}-(\hat{C_{3}}+ \hat{F_{3}}+r_{3})\operatorname{sign}(s_{3}), \end{aligned} $$
(10)

with \(\operatorname{sign}(\cdot) \), the signum function.

Parameter update conditions are

$$ \begin{aligned} &\dot{\hat{C}}_{i}=c_{i} \vert s_{i} \vert , \\ &\dot{\hat{E}}_{i}=f_{i} \vert s_{i} \vert , \end{aligned} $$
(11)

with \(c_{i}, f_{i} > 0\) are constants.

Theorem 4.1

Trajectories of fractional HNN model exposed to uncertainties and disturbances achieve stability about any desired point \((p_{1},p_{2},p_{3})\) using (10)–(11).

Proof

The proof is based on Lyapunov’s direct method, defining [43] the Lyapunov function by

$$ V=V_{1}+V_{2}+V_{3}, $$
(12)

where

$$ \begin{aligned} &V_{1}= \frac{1}{2}s_{1}^{2}+\frac{1}{2c_{1}}( \hat{C}_{1}-C_{1})^{2}+ \frac{1}{2f_{1}}(\hat{F}_{1}-F_{1})^{2}, \\ &V_{2}=\frac{1}{2}s_{2}^{2}+ \frac{1}{2c_{2}}(\hat{C}_{2}-C_{2})^{2}+ \frac{1}{2f_{2}}(\hat{F}_{2}-F_{2})^{2}, \\ &V_{3}=\frac{1}{2}s_{3}^{2}+ \frac{1}{2c_{3}}(\hat{C}_{3}-C_{3})^{2}+ \frac{1}{2f_{3}}(\hat{F}_{3}-F_{3})^{2}. \end{aligned} $$
(13)

Differentiating (13):

$$ \begin{aligned} &\dot{V}_{1}=s_{1} \dot{s_{1}}+\frac{1}{c_{1}}(\hat{C}_{1}-C_{1}) \dot{\hat{C}}_{1}+\frac{1}{f_{1}}(\hat{F}_{1}-F_{1}) \dot{\hat{F}}_{1}, \\ &\dot{V}_{2}=s_{2}\dot{s_{2}}+ \frac{1}{c_{2}}(\hat{C}_{2}-C_{2}) \dot{ \hat{C}}_{2}+\frac{1}{f_{2}}(\hat{F}_{2}-F_{2}) \dot{\hat{F}}_{2}, \\ &\dot{V}_{3}=s_{3}\dot{s_{3}}+ \frac{1}{c_{3}}(\hat{C}_{3}-C_{3}) \dot{ \hat{C}}_{3}+\frac{1}{f_{3}}(\hat{F}_{3}-F_{3}) \dot{\hat{F}}_{3}. \end{aligned} $$
(14)

From (8), we have

$$ \begin{aligned} &\dot{V}_{1}=s_{1} \bigl(D^{q}e_{1}+\lambda_{1}e_{1} \bigr)+\frac{1}{c_{1}}( \hat{C}_{1}-C_{1})\dot{ \hat{C}}_{1}+\frac{1}{f_{1}}(\hat{F}_{1}-F_{1}) \dot{\hat{F}}_{1}, \\ &\dot{V}_{2}=s_{2}\bigl(D^{q}e_{2}+ \lambda_{2}e_{2}\bigr)+\frac{1}{c_{2}}( \hat{C}_{2}-C_{2})\dot{\hat{C}}_{2}+ \frac{1}{f_{2}}(\hat{F}_{2}-F_{2}) \dot{ \hat{F}}_{1}, \\ &\dot{V}_{3}=s_{3}\bigl(D^{q}e_{3}+ \lambda_{3}e_{3}\bigr)+\frac{1}{c_{3}}( \hat{C}_{3}-C_{3})\dot{\hat{C}}_{3}+ \frac{1}{f_{3}}(\hat{F}_{3}-F_{3}) \dot{ \hat{F}}_{3}. \end{aligned} $$
(15)

Substituting \(D^{q}e_{i}\), \(\dot{\hat{C}}_{i} \) and \(\dot{\hat{F}}_{i} \) in (15):

$$\begin{aligned} \dot{V}_{i} & =s_{1}\bigl[( \bigtriangleup H_{i} +D_{i}) -( \hat{C}_{i}+ \hat{F}_{i}+r_{i})\operatorname{sign} s_{i} \bigr]+(\hat {C}_{i}-F_{i}) \vert s_{i} \vert +( \hat{C}_{i}-F_{i}) \vert s_{i} \vert \\ & \leq\bigl( \vert \bigtriangleup H_{i} \vert + \vert D_{i} \vert \bigr) \vert s_{i} \vert +( \hat{C}_{i}-F_{i}) \vert s_{i} \vert +( \hat{C}_{i}-F_{i}) \vert s_{i} \vert \\ & < (C_{i}+F_{i}) \vert s_{i} \vert -(\hat{C}_{i}+\hat{F}_{i}+r_{i}) \vert \operatorname{sign}s_{i} \vert +( \hat{C}_{i}-F_{i}) \vert s_{i} \vert +(\hat{C}_{i}-F_{i}) \vert s_{i} \vert \\ & =-T_{i} \vert s_{i} \vert . \end{aligned}$$

Finally,

$$ \begin{aligned} \dot{V}&=\sum _{i=1}^{3}\dot{V}_{i} \\ & < -\sum_{i=1}^{3}\bigl(T_{i} \vert s_{i} \vert \bigr). \end{aligned} $$
(16)

Thus ∃ a real T ≥0 so that

$$ \sum_{i=1}^{3}T_{i} \vert s_{i} \vert > T $$

then

$$ \begin{aligned} \dot{V} &< -T \sqrt{s_{1}^{2}+s_{2}^{2}+s_{3}^{2}} \\ &< 0. \end{aligned} $$
(17)

From Lyapunov stability theory \(\Vert s_{i}\Vert \rightarrow0 \) as \(t\rightarrow\infty\). Hence the errors converge to \(s_{i}=0 \) implying stability about the desired point. □

4.1 Simulations

For performing simulations, the following assumptions have been made: \(P=0.8\) for \(q=0.987\) and I.C. as \((0,0.01,0)\), \(\bigtriangleup H_{1}=\sin(Z_{1})\), \(D_{1}=0\), \(\bigtriangleup H_{2}=0\), \(D_{2}=\sin(7t)\), \(\bigtriangleup H_{3}=0\), \(D_{3}=\cos (7t)\). Here \(v_{1}\), \(v_{2}\), \(v_{3}\) are controllers about any point \((p_{1},p_{2},p_{3})\), \(\lambda_{1}=1\), \(\lambda_{2}=2\), \(\lambda_{3}=3\), \(r_{1}=1\), \(r_{2}=2\), \(r_{3}=3\). Figure 8 gives the controlled trajectories, errors, surface with estimated disturbances about \((1,2,3)\) and Fig. 9 gives results about \((-1,-2,-3)\).

Figure 8
figure 8

Controlling chaos about \((1,2,3)\) (b) with error, surface and estimated disturbances

Full size image
Figure 9
figure 9

Controlling chaos about \((-1,-2,-3)\) (b) with error, surface and estimated disturbances

Full size image

5 Conclusion

Dynamical properties of fractional order HNN model are studied in the paper by analyzing the system’s symmetry, uniqueness of the solution, dissipativity and fixed points. Lyapunov dynamics and bifurcations of the system are studied for specific order as well as variable order. The chaos in a fractional system exposed to uncertainties and disturbances is contained by designing suitable controllers based on an adaptive sliding mode control technique about two arbitrarily chosen desired points. The simulations performed in Matlab have been displayed and discussed.

Synchronization of the fractional HNN model with some other system involves future scope of work in this direction. Also studying the system as regards its hidden attractors as well as its electronic circuit would be interesting.