Abstract
In this paper, we consider a diffusive predator–prey model with a time delay and prey toxicity. The effect of time delay on the stability of the positive equilibrium is studied by analyzing the eigenvalue spectrum. Delay-induced Hopf bifurcation is also investigated. By utilizing the normal form method and center manifold reduction for partial functional differential equations, the formulas for determining the property of Hopf bifurcation are given.
Similar content being viewed by others
1 Introduction
Since the relationship of different biological species is very common in nature, many scholars have done a lot of works in this field [1–4]. In the real world, some biological species can release toxic substances that can affect the growth of other species. These toxic substances can even affect the living environment of human beings, so it is important to study the dynamics of the population models. In [5], Chattopadhyay studied the local and global stability of the interior equilibrium of a two-species competitive system with toxic substances. This work suggests that the toxic substance has the stabilizing effect on the model. In [6], Kar and Chaudhuri considered a two-species competing fish model with harvesting effect and toxic substances. They mainly studied the stability of the interior equilibrium. In addition, reaction–diffusion models arise in a variety of real world problems, such as in physical [7], chemical [8] and biological [9] applications. In [9], Zhang and Zhao proposed a diffusive predator–prey model with the toxic substance of the following form:
All parameters are positive; u and v denote the densities of prey and predator, respectively; r and ϵ denote the growth rates of prey and predator, respectively; \(D_{1}\) and \(D_{2}\) are diffusion coefficients of prey and predator, respectively; K is the environmental capacity of prey. The functional response is of Holling II-type; β represents the efficiency toxic substance released by prey. They mainly studied the stability of the constant positive steady states and existence of the nonconstant positive steady states.
In the real world, time delay and asymptotic behaviors are widely studied toward the comprehension of growth process for biological species [10–13], such as gestation delay, maturation time, capturing time, and so on. Additionally, related analysis of characteristic equations also appear in the description of equilibrium models for other sciences, as, for instance, in civil engineering; see [14]. Differential equations with time delay often cause periodic oscillations, and show more abundant dynamic properties [15, 16]. In [17], the authors studied the Hopf–Hopf bifurcation in a predator–prey with predator cannibalism and time delay. In [18], the authors studied the Hopf–zero bifurcation in a delayed predator–prey model with dormancy of predators. These results all suggest that the time delay can enrich the dynamic properties of the predator–prey models.
Using the following parameters transformation:
the model (1.1) becomes
Based on the model (1.2), we consider the following delay model:
All parameters are positive; τ is the resource limitation of the prey logistic equation. For convenience, we denote \(\Omega =(0, l\pi )\). The aim of this paper is to study the effect of time delay on the model (1.3). Compare with the model (1.1), whether some new dynamical phenomena occurs.
The organization of this paper is as follows. In Sect. 2, we study the existence of equilibria. In Sect. 3, we analyze the stability of the positive equilibrium, the existence of Hopf bifurcation, and the property of bifurcating periodic solutions. In Sect. 4, we give a numerical simulation. At last, we give a brief conclusion.
2 Existence of equilibria
The equilibria of model (1.3) are the roots of the following equations:
Lemma 2.1
For the model (1.3), the following statements are true:
-
(1)
The model (1.3) has a boundary equilibrium \((1,0)\).
-
(2)
The model (1.3) has at least one positive equilibrium.
-
(3)
Under hypothesis \({(\mathbf{H}_{\mathbf{0}})}\), \(0< s< a<1\), the model (1.3) has a unique positive equilibrium.
Proof
Obviously, the model (1.3) has a boundary equilibrium \((1,0)\). Now, we consider the existence of positive equilibrium denoted as \((u_{*},v_{*})\). From the first equation in (2.1), we have \(v_{*}=\frac{(1-u_{*}) (a u_{*}+1)}{b}\). From the second equation in (2.1), we have \(v_{*}=\frac{u_{*}}{s u_{*}^{2}+1}>0\). Then we can obtain that \(u_{*}\) is the positive root of the following equation:
It is not difficult to obtain that \(h(0)=-1\), \({\lim_{x \to \infty }} h(u)=+\infty \). Thus Eq. (2.2) has at least one positive root, which means that the model (1.3) has at least one positive equilibrium. In addition, by the Descartes’s rule of signs, Eq. (2.2) has a unique positive root under condition \(0< s< a<1\), which means that the model (1.3) has a unique positive equilibrium. □
In the rest of this paper, we denote the positive equilibrium as \((u_{*},v_{*})\), where \(v_{*}=\frac{u_{*}}{s u_{*}^{2}+1}\).
3 Stability analysis
Linearize system (1.3) at \((u_{*},v_{*})\) as follows:
where
and
The characteristic equation of (3.1) is
where \(I=\operatorname{diag}\{1,1\}\) and \(M_{n}=-n^{2}/l^{2}\operatorname{diag}\{d_{1},d_{2}\}\), \(n \in \mathbb{N}_{0}\). Then, we have
where
3.1 The case of \(\tau =0\)
When \(\tau =0\), the characteristic Eq. (1.3) reduces to the following equation:
where
for \(n \in \mathbb{N}_{0}\). The eigenvalues are given by
We consider the following hypotheses:
By direct calculation, we can get the following remark.
Remark 3.1
Hypothesis \({(\mathbf{H}_{\mathbf{0}})}\) is a sufficient condition for \(\tilde{c}>0\). If Hypothesis \({(\mathbf{H}_{\mathbf{1}})}\) holds, then \(T_{n}<0\) for \(n \in \mathbb{N}_{0}\). If Hypothesis \({(\mathbf{H}_{\mathbf{2}})}\) holds, then \(D_{n}>0\) for \(n \in \mathbb{N}_{0}\).
Theorem 3.1
When \(\tau =0\), the equilibrium \((u_{*},v_{*})\) is locally asymptotically stable under Hypotheses \({(\mathbf{H}_{\mathbf{1}})}\) and \({(\mathbf{H}_{\mathbf{2}})}\).
Proof
When \(\tau =0\), by Remark 3.1, we have \(T_{n}<0\) and \(D_{n}>0\) for \(n \in \mathbb{N}_{0}\) under Hypotheses \({(\mathbf{H}_{\mathbf{1}})}\) and \({(\mathbf{H}_{\mathbf{2}})}\). Then the eigenvalues (3.7) all have negative real parts, which can guarantee the statement in Theorem 3.1. □
3.2 The case of \(\tau >0\)
To study the stability of \(E_{*}(u_{*},v_{*})\) when \(\tau >0\), we suppose \({{(\mathbf{H}_{\mathbf{1}})}}\) and \({(\mathbf{H}_{\mathbf{2}})}\) hold. Let iω (\(\omega >0\)) be a solution of Eq. (3.4). We have
Then we have
leading to
Denote \(z = \omega ^{2}\). Then (3.10) can be changed into
and the roots of (3.11) are
By direct computation,
Fix parameters a, b, c, s, define
Under \({{(\mathbf{H}_{\mathbf{1}})}}\) and \({(\mathbf{H}_{\mathbf{2}})}\), we can obtain
and
This means that Eq. (3.11) has at least a pair of positive roots \(z_{0}^{\pm }\). Then \(\mathcal{D}\neq \emptyset \).
For \(n\in \mathcal{D}\), if \(z^{+}>0\), then Eq. (3.4) has a pair of purely imaginary roots \(\pm {\mathrm{i}}\omega ^{+}_{n}\) at \(\tau ^{j,+}_{n}\), \(j \in \mathbb{N}_{0}\). If \(z^{-}>0\), then Eq. (3.4) has a pair of purely imaginary roots \(\pm {\mathrm{i}}\omega ^{-}_{n}\) at \(\tau ^{j,-}_{n}\), \(j \in \mathbb{N}_{0}\), where
From (3.13), we have \(\tau ^{0,\pm }_{n}<\tau ^{j,\pm }_{n}\) \((j\in \mathbb{N})\). For \(k\in \mathcal{D}\), define the smallest τ so that the stability will change, \(\tau _{*}=\min\{\tau ^{0,\pm }_{k} \mbox{ or } \tau ^{0,+}_{k} \mid k \in \mathcal{D} \}\).
Lemma 3.1
Suppose \({{(\mathbf{H}_{\mathbf{1}})}}\) (or \({(\mathbf{H}_{\mathbf{2}})}\)) holds. If \((A_{n}^{2}-2 B_{n}- u_{*}^{2})^{2}-4(B_{n}^{2}-C_{n}^{2})>0\), then \(\operatorname{Re}(\frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,+}_{n}}>0\), \(\operatorname{Re} ( \frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,-}_{n}}<0\) for \(\tau \in \mathcal{D}\) and \(j \in \mathbb{N}_{0}\).
Proof
Differentiating two sides of (3.4) with respect τ, we have
Then
where \(\Lambda =\omega ^{2} u_{*}^{2} +C^{2}_{n} >0\). Therefore \(\operatorname{Re}(\frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,+}_{n}}>0\), \(\operatorname{Re} ( \frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,-}_{n}}<0\). □
Theorem 3.2
Suppose \({{(\mathbf{H}_{\mathbf{1}})}}\) and \({(\mathbf{H}_{\mathbf{2}})}\) hold. For system (1.3), the following statements are true:
-
(1)
\(E_{*}(u_{*},v_{*})\) is locally asymptotically stable for \(\tau \in [0,\tau _{*})\), and unstable for \(\tau \in [\tau _{*},\tau _{*}+\epsilon )\) with some ϵ.
-
(2)
System (1.3) undergoes a Hopf bifurcation at the equilibrium \(E_{*}(u_{*},v_{*})\) when \(\tau =\tau ^{j,+}_{n}\) (or \(\tau =\tau ^{j,-}_{n}\)), \(j\in \mathbb{N}_{0}\), \(n \in \mathcal{D}\), where \(\tau ^{j,\pm }_{n}\) is defined in (3.13).
Remark 3.2
From Lemma (3.1), we obtain \(\operatorname{Re}(\frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,+}_{n}}>0\), \(\operatorname{Re} ( \frac{d \lambda }{d \tau })|_{\tau =\tau ^{j,-}_{n}}<0\) for \(\tau \in \mathcal{D}\) and \(j \in \mathbb{N}_{0}\), then the stability switch may exist.
3.3 Properties of Hopf bifurcation
Now, we will study the property of Hopf bifurcation by the method exploited in [19, 20]. For a critical value \(\tau ^{j,+}_{n}\) (or \(\tau ^{j,-}_{n}\)), we denote it as τ̃. Let \(\tilde{u}(x,t)=u(x,\tau t)-u_{*}\) and \(\tilde{v}(x,t)=v(x,\tau t)-v_{*}\). Then the system (1.3) is (dropping the tilde)
Denote \(\tau =\tilde{\tau }+\varepsilon \), and \(U=(u(x,t),v(x,t))^{T}\). In the phase space \(\mathscr{C}_{1}:=C([-1,0],X)\), (3.14) can be rewritten as
where \(L_{\varepsilon }(\varphi )\) and \(F(\varphi ,\varepsilon )\) are
with
respectively, for \(\phi =(\phi _{1}, \phi _{2})^{T} \in \mathscr{C}_{1}\).
Consider the linear equation
We know that \(\Lambda _{n}:=\{{\mathrm{i}}\omega _{n} \tilde{\tau },-{\mathrm{i}}\omega _{n} \tilde{\tau }\}\) are characteristic roots of
Choose
where
Then
for \(\phi \in C([-1,0],\mathbb{R}^{2})\).
Define the bilinear paring
for \(\varphi \in C([-1,0],\mathbb{R}^{2})\), \(\psi \in C([0,1],\mathbb{R}^{2})\); \(A(\tilde{\tau })\) has a pair of simple purely imaginary eigenvalues \(\pm {\mathrm{i}}\omega _{n} \tilde{\tau }\), and they are also eigenvalues of \(A^{*}\).
Define \(p_{1}(\sigma )=(1,\xi )^{T}e^{{\mathrm{i}}\omega _{n} \tilde{\tau } \sigma }\) (\(\sigma \in [-1,0]\)), \(q_{1}(r)=(1,\eta )e^{-{\mathrm{i}}\omega _{n} \tilde{\tau } r}\) (\(r \in [0,1]\)), where
Let \(\Phi =(\Phi _{1},\Phi _{2})\) and \(\Psi ^{*}=(\Psi ^{*}_{1},\Psi ^{*}_{2})^{T}\) with
for \(\sigma \in [-1,0]\), and
for \(r \in [0,1]\). Then we can compute by (3.22)
Define and \(\Psi =(\Psi _{1},\Psi _{2})^{T}=(\Psi ^{*},\Phi )^{-1}\Psi ^{*} \). Then \((\Psi ,\Phi )_{0}=I_{2}\). In addition, define \(f_{n}:=(\beta ^{1}_{n},\beta ^{2}_{n})\), where
We also define
and
for \(u=(u_{1},u_{2})^{T}\), \(v=(v_{1},v_{2})^{T}\), \(u,v\in X\) and \(\langle \varphi ,f_{0}\rangle =(\langle \varphi ,f^{1}_{0}\rangle , \langle \varphi ,f^{2}_{0}\rangle )^{T}\).
Rewrite Eq. (3.14) as
where
The solution is
where , and \(h(x_{1},x_{2},\varepsilon ) \in P_{S} \mathscr{C}_{1}\), \(h(0,0,0)=0\), \(Dh(0,0,0)=0 \). Then
Let \(z=x_{1}-{\mathrm{i}} x_{2}\). Then
and
Equation (3.26) is
where
From [19], z satisfies
where
Let
then
and
with
Hence,
with
and
Denote
Notice that
and we have
Then by (3.29), (3.31) and (3.37), we have \(g_{20}=g_{11}=g_{02}=0\), for \(n=1,2,3,\dots \).
If \(n=0\), \(\Gamma =\frac{1}{l\pi } \int _{0}^{l\pi }\cos ^{3}\frac{n x}{l}\,dx=1\), then we have
And for \(n\in \mathbb{N}_{0}\), \(g_{21}=\tilde{\tau }( \gamma _{1} \kappa _{1} +\gamma _{2} \kappa _{2})\). Next, we just need to compute \(W_{11}(\theta ):=(W_{11}^{(1)}(\theta ), W_{11}^{(2)}(\theta ))^{T}\) and \(W_{20}(\theta ):=(W_{20}^{(1)}(\theta ),W_{20}^{(2)}(\theta ))^{T}\).
By (3.30), we can obtain
From [19], we have
where
Hence, we have
that is,
For \(-1\leq \theta < 0\), we have
Therefore,
and
where
By the definition of \(A_{\tilde{\tau }}\) and (3.39), we have
That is,
where
By the definition of \(A_{\tilde{\tau }}\) and (3.39), we have that for \(-1\le \theta <0\),
As
and
we have
That is,
Similarly, from (3.40), we have
That is,
Then, we have
Thus, we can obtain
Theorem 3.3
For any critical value \(\tau ^{j,\pm }_{n}\), the bifurcating periodic solutions exists for \(\tau >\tau ^{j,\pm }_{n}\) (or \(\tau <\tau ^{j,\pm }_{n}\)) when \(\mu _{2}>0\) (or \(\mu _{2}<0\)), and are orbitally asymptotically stable (or unstable) when \(\beta _{2}<0\) (or \(\beta _{2}>0\)).
4 A numerical simulation
In this section, we give a numerical simulation done with Matlab. The numerical simulation of the systems is implemented by finite-difference methods. In the model (1.3), we fix the following parameters:
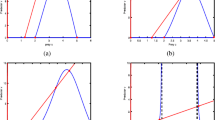
The model (1.3) has a unique positive equilibrium \((u_{*},v_{*})\approx (0.4691, 0.3845)\). By direct computation, we have \(\mathcal{D}=\{0,1 \}\neq \emptyset \), and \(\tau _{*} \approx 2.0053\). By Theorem 3.2, we know that \((u_{*},v_{*})\) is locally asymptotically stable when \(\tau \in [0,\tau _{*})\) (shown in Fig. 1). Hopf bifurcation occurs when \(\tau =\tau _{*}\). By Theorem 3.3, we have
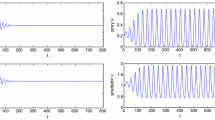
Hence, the locally asymptotically stable bifurcating periodic solutions exists for \(\tau >2.0053\), and the periods of bifurcating periodic solutions increase (shown in Fig. 2).
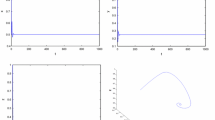
Numerical simulations of system (1.3) for \(\tau =1.5\)
Numerical simulations of system (1.3) for \(\tau =2.1\)
5 Conclusion
In this paper, we considered a delayed diffusive predator–prey model with toxic substances released by prey. We mainly analyzed the effect of the time delay on the stability of the positive equilibrium, and time delay induced Hopf bifurcation. We gave some parameters that determine the properties of Hopf bifurcation, namely bifurcation direction and the stability of the bifurcating periodic solution. Compared with the model (1.1), time delay is an important factor in relationship between prey and predator, since it may affect the stability of the positive equilibrium and induce Hopf bifurcation.
Availability of data and materials
Data sharing not applicable to this paper as no datasets were generated or analyzed during the current study.
References
Yi, F., Wei, J., Shi, J.: Bifurcation and spatiotemporal patterns in a homogeneous diffusive predator–prey system. J. Differ. Equ. 246(5), 1944–1977 (2009)
Wang, J., Shi, J., Wei, J.: Dynamics and pattern formation in a diffusive predator–prey system with strong Allee effect in prey. J. Differ. Equ. 251(4), 1276–1304 (2011)
Song, Y., Jiang, H., Yuan, Y.: Turing–Hopf bifurcation in the reaction–diffusion system with delay and application to a diffusive predator–prey model. J. Appl. Anal. Comput. 9(3), 1132–1164 (2019)
Cao, X., Jiang, W.: Turing–Hopf bifurcation and spatiotemporal patterns in a diffusive predator–prey system with Crowley–Martin functional response. Nonlinear Anal., Real World Appl. 43, 428–450 (2018)
Chattopadhyay, J.: Effect of toxic substances on a two-species competitive system. Ecol. Model. 84(1–3), 287–289 (1996)
Kar, T.K., Chaudhuri, K.S.: On non-selective harvesting of two competing fish species in the presence of toxicity. Ecol. Model. 161(1–2), 125–137 (2003)
Li, T., Pintus, N., Viglialoro, G.: Properties of solutions to porous medium problems with different sources and boundary conditions. Z. Angew. Math. Phys. 70(3), 1–18 (2018)
Wei, X., Wei, J.: Turing instability and bifurcation analysis in a diffusive bimolecular system with delayed feedback. Commun. Nonlinear Sci. Numer. Simul. 50, 241–255 (2017)
Zhang, X., Zhao, H.: Dynamics and pattern formation of a diffusive predator–prey model in the presence of toxicity. Nonlinear Dyn. 95, 2163–2179 (2019)
Beretta, E., Solimano, F., Takeuchi, Y.: Global stability and periodic orbits for two-patch predator–prey diffusion-delay models. Math. Biosci. 85(2), 153–183 (1987)
Martin, A., Ruan, S.: Predator–prey models with delay and prey harvesting. J. Math. Biol. 43(3), 247–267 (2001)
Viglialoro, G., Woolley, T.E.: Boundedness in a parabolic–elliptic chemotaxis system with nonlinear diffusion and sensitivity and logistic source. Math. Methods Appl. Sci. 41(5), 1809–1824 (2017)
Gourley, S.A.: Instability in a predator–prey system with delay and spatial averaging. IMA J. Appl. Math. 56(2), 121–132 (1996)
Li, T., Viglialoro, G.: Analysis and explicit solvability of degenerate tensorial problems. Bound. Value Probl. 2018, 2 (2018). https://doi.org/10.1186/s13661-017-0920-8
Chiu, K., Li, T.: Oscillatory and periodic solutions of differential equations with piecewise constant generalized mixed arguments. Math. Nachr. 292(10), 2153–2164 (2019)
Yang, R., Zhang, C.: Dynamics in a diffusive predator–prey system with a constant prey refuge and delay. Nonlinear Anal., Real World Appl. 31, 1–22 (2016)
Duan, D., Niu, B., Wei, J.: Coexistence of periodic oscillations induced by predator cannibalism in a delayed diffusive predator–prey model. Int. J. Bifurc. Chaos 29(7), 1950089 (2019)
Wang, J., Jiang, W.: Hopf-zero bifurcation of a delayed predator–prey model with dormancy of predators. J. Appl. Anal. Comput. 7(3), 1051–1069 (2017)
Wu, J.: Theory and Applications of Partial Functional Differential Equations. Springer, Berlin (1996)
Hassard, B.D., Kazarinoff, N.D., Wan, Y.H.: Theory and Applications of Hopf Bifurcation. Cambridge University Press, Cambridge (1981)
Acknowledgements
The authors wish to express their gratitude to the editors and the reviewers for the helpful comments.
Funding
This research was supported by Fundamental Research Funds for the Central Universities (No. 2572019BC01), Heilongjiang Provincial Natural Science Foundation (No. A2018001), and the College Students Innovations Special Project funded by Northeast Forestry University (No. 202010225137).
Author information
Authors and Affiliations
Contributions
The idea of this research was introduced by RY. All authors contributed to the main results and numerical simulations. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yang, R., Ma, Y. & Zhang, C. Time delay induced Hopf bifurcation in a diffusive predator–prey model with prey toxicity. Adv Differ Equ 2021, 47 (2021). https://doi.org/10.1186/s13662-020-03161-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03161-3