Abstract
In this paper, we discuss fixed point theorems for a new χ-set contraction condition in partially ordered Banach spaces, whose positive cone \(\mathbb{K}\) is normal, and then proceed to prove some coupled fixed point theorems in partially ordered Banach spaces. We relax the conditions of a proper domain of an underlying operator for partially ordered Banach spaces. Furthermore, we discuss an application to the existence of a local fractional integral equation.
Similar content being viewed by others
1 Introduction and preliminaries
A measure of non-compactness (MNC) for the first time was given by Kuratowski [1]. It is combined with the algebraically and analytically studies for establishing the existence of nonlinear problems [2]. The fractional calculus is a subject of a long history and has gained great interest in different fields of applied science, and many authors considered this topic [3–7].
Let \((\mathbb{X}, \|\cdot \|)\) be an infinite dimensional Banach space and θ be its zero element. \(\mathcal{B}(\vartheta ,\zeta )\) will denote the closed ball with center ϑ are radius ζ and \(\mathcal{B}_{\zeta }\) will stand for \(\mathcal{B}(\theta ,\zeta )\). Moreover, \(\mathfrak{M}_{\mathbb{X}}\) will denote the family of nonempty bounded subsets of \(\mathbb{X}\) and \(\mathfrak{N}_{\mathbb{X}}\) is its subfamily consisting of all relatively compact sets.
Definition 1.1
([8])
A mapping \(\mu : \mathfrak{M}_{\mathbb{X}} \to \mathbb{R}^{+}\) is said to be a measure of non-compactness (MNC, for short) in \(\mathbb{X}\) if it satisfies the following conditions (\(\mathcal{Y},\mathcal{Y}_{1},\mathcal{Y}_{2} \in \mathfrak{M}_{\mathbb{X}}\)):
- \((1^{\circ })\):
-
\(\operatorname{ker} \mu := \{\mathcal{Y} \in \mathfrak{M}_{\mathbb{X}} : \mu ( \mathcal{Y}) = 0\}\ne \emptyset \) and \(\operatorname{ker} \mu \subset \mathfrak{N}_{\mathbb{X}}\),
- \((2^{\circ })\):
-
\(\mathcal{Y}_{1} \subseteq \mathcal{Y}_{2} \Rightarrow \mu ( \mathcal{Y}_{1}) \leq \mu (\mathcal{Y}_{2})\),
- \((3^{\circ })\):
-
\(\mu (\overline{\mathcal{Y}}) = \mu (\mathcal{Y})\),
- \((4^{\circ })\):
-
\(\mu (\overline{\operatorname{conv} \mathcal{Y}}) = \mu (\mathcal{Y})\),
- \((5^{\circ })\):
-
\(\mu ( \lambda \mathcal{Y}_{1} + (1 - \lambda ) \mathcal{Y}_{2} ) \leq \lambda \mu (\mathcal{Y}_{1}) + (1 - \lambda ) \mu (\mathcal{Y}_{2})\) for \(\lambda \in [0, 1]\),
- \((6^{\circ })\):
-
\(\mu (\mathcal{Y}_{1} \cup \mathcal{Y}_{2})=\max \{\mu (\mathcal{Y}_{1}), \mu (\mathcal{Y}_{2})\}\),
- \((7^{\circ })\):
-
if \((\mathcal{Y}_{n})\) is a decreasing sequence of nonempty closed sets in \(\mathfrak{M}_{\mathbb{X}}\) and if \(\lim_{n\rightarrow \infty }\mu (\mathcal{Y}_{n})=0\), then the set \(\mathcal{Y}_{\infty }=\bigcap_{n=1}^{\infty }\mathcal{Y}_{n}\) is nonempty and compact.
A map \(\alpha :\mathfrak{M}_{\mathbb{X}}\rightarrow \mathbb{R}^{+}\) is said to be a Kuratowski MNC [1] if
We denote by \(\Lambda (\mathbb{X})\) a nonempty, bounded, closed and convex set on Banach space \(\mathbb{X}\).
The following extensions of the topological Schauder fixed point theorem and classical Banach fixed point theorem were proved by Darbo (DFPT, in short) in 1955.
Theorem 1.2
([8])
Let \(\mathbb{X}\) be a Banach space, \(\mathcal{Y} \in \Lambda (\mathbb{X})\) and \(\mathfrak{F} : \mathcal{Y} \to \mathcal{Y}\) be a continuous operator such that there exists a \(\lambda \in [0,1)\) with
for any \(\emptyset \neq \mathcal{A} \subset \mathcal{Y}\), here μ is the Kuratowski MNC on \(\mathbb{X}\). Then we can conclude that \(\mathfrak{F}\) has a fixed point.
We define \(\Psi := \{\psi : \mathbb{R}^{+} \to \mathbb{R}^{+}\}\) is a non-decreasing function, and \(\lim_{n \to \infty } \psi ^{n}(t) = 0\) for each \(t \geq 0\).
Definition 1.3
([9])
Denote by \(\mathbb{H}\) the collection of all functions \(\hbar : \mathbb{R}_{+} \to \mathbb{R}_{+}\) and let Δ be the collection of all functions
satisfying:
-
(i)
\(\Theta (\hbar ; \zeta ) > 0\) for \(\zeta > 0\) and \(\Theta (\hbar ; 0) = 0\),
-
(ii)
\(\Theta (\hbar ; \zeta ) \leq \Theta (\hbar , \xi )\) for \(\zeta \leq \xi \),
-
(iii)
\(\lim_{n\to \infty } \Theta (\hbar ; \zeta _{n}) = \Theta (\hbar ; \lim_{n\to \infty } \zeta _{n})\),
-
(iv)
\(\Theta (\hbar ; \max \{\zeta , \}) = \max \{\Theta (\hbar ; \zeta ), \Theta (\hbar ; \xi )\}\) for some \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\).
Arab [10] used Definition 1.3 to generalize the result of Aghajani et al. [11].
Theorem 1.4
Let \(\mathcal{Y} \in \Lambda (\mathbb{X})\) and let \(\mathfrak{F}: \mathcal{Y}\rightarrow \mathcal{Y}\) be a continuous operator satisfying
for any \(\emptyset \neq \Xi \subset \mathcal{Y}\), where χ is an arbitrary MNC, \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\psi \in \Psi \), \(\Theta (\circ ; \cdot ) \in \Delta \) and a continuous function \(\varphi : \mathbb{R}^{+} \to \mathbb{R}^{+}\). Then we find that \(\mathfrak{F}\) has at least one fixed point.
With the above discussion in mind, an attempt has been made to give a monotone version of Lemma 1.4 with the relaxed conditions of domain of an underlying operator into partially ordered Banach spaces. To achieve the proposed results in partially ordered Banach spaces, we define a notion of MNC. Then we use this notion to prove some FPTs for χ-set contraction condition in partially ordered Banach spaces whose positive cone K is norm. We will relax the conditions of bounds, closed and convexity of the domain of operator at the expense of the operator being monotone and bounded. Next, we use the obtained FPTs to establish the existence of the solution of local fractional integral equation.
2 FPTs
Let \(\mathbb{X}\) be a Banach space with the norm \(\|\cdot \|\) whose positive cone is defined by \(\mathbb{K}=\{x\in \mathbb{X}: x\geq 0\}\). \((\mathbb{X}, \|\cdot \|)\) is a partially ordered Banach space with the order relation ⊑ induced by cone \(\mathbb{K}\).
Denote by Ω a collection of continuous and strictly increasing function \(\omega : \mathbb{R}_{+}\rightarrow \mathbb{R}_{+}\).
We now discuss our results in partially ordered Banach spaces.
Theorem 2.1
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all bounded subset Ξ in \(\mathbb{X}\), where χ denotes the arbitrary MNC, \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\Theta (\circ ; \cdot ) \in \Delta \), \(\psi \in \Psi \), \(\omega \in \Omega \).
If ∃ an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) of successive iterations converges monotonically to \(\varrho ^{*}\).
Proof
Assume \(\varsigma _{0} \in \mathbb{X}\) and define a sequence \(\{\varsigma _{n}\} \subset \mathbb{X}\) by
Since \(\mathfrak{F}\) is non-decreasing and \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), we have
Denote \(\mathfrak{B}_{n} = \overline{\operatorname{conv}}\{\varsigma _{n}, \varsigma _{n+1}, \ldots \}\) for \(n \in \mathbb{N}^{*}\). By (2.2) and (2.3), each \(\mathfrak{B}_{n}\) is a bounded and closed subset in \(\mathbb{X}\) and
Following (2.1), we obtain
Taking the limit \(n \to \infty \) in (2.5), we have by the virtue of \(\psi \in \Psi \)
By the virtue of (iii) of Definition 1.1, we get
and therefore
Since \(\mathfrak{B}_{n} \subset \mathfrak{B}_{n-1}\), we have
Hence, for every \(\epsilon > 0\) there exists an \(n_{0} \in \mathbb{N}\) such that
From this we conclude that \(\overline{\mathfrak{B}}_{n_{0}}\) and consequently \(\mathfrak{B}_{0}\) is a compact chain in \(\mathbb{X}\). Hence, \(\{\varsigma _{n}\}\) has a convergent subsequence. Applying the monotone property of \(\mathfrak{F}\) and the normality of cone K, the whole sequence \(\{\varsigma _{n}\} = \{\mathfrak{F}^{n}\varsigma _{0}\}\) converges monotonically to a point, say \(\varrho ^{*} \in \mathfrak{B}_{0}\). Finally, from the continuity of \(\mathfrak{F}\), we get
□
On different setting of functions \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\Theta (\circ ; \cdot ) \in \Delta \), \(\omega : \mathbb{R}^{+} \to \mathbb{R}^{+}\) satisfying the condition (2.1) in Theorems 2.1, we can get some new DFPTs. For example, if we set first \(\omega (t)=0\) and secondly \(\psi (\zeta )=\lambda \zeta \) (\(\lambda \in (0,1)\)) and finally ħ= identity map with \(\Theta (\hbar ; \zeta ) =\zeta \), then we have following DFPTs, respectively.
Theorem 2.2
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all bounded subset \(\mathfrak{B}\) in \(\mathbb{X}\), where χ denotes the arbitrary MNC, \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\). \(\Theta (\circ ; \cdot ) \in \Delta \), \(\psi \in \Psi \).
If ∃ an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) converges monotonically to \(\varrho ^{*}\).
Theorem 2.3
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all bounded subset \(\mathfrak{B}\) in \(\mathbb{X}\), where χ denotes the arbitrary MNC, \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\Theta (\circ ; \cdot ) \in \Delta \), \(\psi \in \Psi \), \(\omega \in \Omega \).
If ∃ an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) of successive iterations converges monotonically to \(\varrho ^{*}\).
Theorem 2.4
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all bounded subset \(\mathfrak{B}\) in \(\mathbb{X}\), where χ denotes the arbitrary MNC, \(\psi \in \Psi \), \(\omega \in \Omega \).
If ∃ an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) of successive iterations converges monotonically to \(\varrho ^{*}\).
If we take \(\operatorname{diam} (\mathfrak{B}) =\) diameter of \(\mathfrak{B}\), then we have the following.
Proposition 2.5
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone K is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all bounded subset \(\mathfrak{B}\) in \(\mathbb{X}\), where \(\psi \in \Psi \), \(\omega \in \Omega \).
If there exists an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) of successive iterations converges monotonically to \(\varrho ^{*}\).
Proof
Theorem 2.1 and Proposition 3.2 [12] claim the existence of a \(\mathfrak{F}\)-invariant nonempty closed convex subset \(\mathfrak{B}\) with \(\operatorname{diam}(\mathfrak{B}_{\infty }) = 0\), that is, \(\mathfrak{B}_{\infty }\) has a singleton element, hence we have a fixed point of \(\mathfrak{F} \neq \emptyset \).
To prove uniqueness, we suppose that there exist two distinct fixed points \(\zeta , \xi \in \mathfrak{B}\), then we may define the set \(\Lambda := \{\zeta ,\xi \}\). In this case \(\operatorname{diam}(\Lambda ) = \operatorname{diam}(\mathfrak{F}(\Lambda )) = \|\xi -\zeta \| > 0\). Then using (2.10), we get
a contradiction with the property of \(\psi \in \Psi \), \(\psi (t)< t\) for each \(t > 0\) and hence \(\xi = \zeta \). □
The following is the generalized classical fixed point result derived from Proposition 2.3.
Theorem 2.6
Let \((\mathbb{X}, \|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space, whose positive cone K is normal. Suppose that \(\mathfrak{F}: \mathbb{X}\rightarrow \mathbb{X}\) is a continuous, non-decreasing and bounded mapping satisfying the following contraction:
for all \(\zeta ,\xi \in \mathbb{X}\), where \(\psi \in \Psi \), \(\omega \in \Omega \). If there exists an element \(\varsigma _{0}\in \mathbb{X}\) such that \(\varsigma _{0} \sqsubseteq \mathfrak{F}\varsigma _{0}\), then \(\mathfrak{F}\) has a unique fixed point \(\varrho ^{*}\) and the sequence \(\{\mathfrak{F}^{n}\varsigma _{0}\}\) of successive iterations converges monotonically to \(\varrho ^{*}\).
Proof
Let \(\chi :\mathfrak{M}_{\mathbb{X}}\rightarrow \mathbb{R}^{+}\) be a set quantity defined by the formula \(\chi(\mathbb{X})=\operatorname{diam}\mathbb{X}\), where \(\operatorname{diam}\mathbb{X}=\sup \{\Vert \zeta -\xi \Vert :\zeta ,\xi \in \mathbb{X}\}\) stands for the diameter of \(\mathcal{X}\). It is easily seen that χ is a MNC in a space \(\mathbb{X}\) in the sense of Definition 1.1. Therefore from (2.11) we have
which implies that
Thus following Proposition 2.3, \(\mathfrak{F}\) has an unique fixed point. □
3 Coupled FPTs
In this section, we prove some coupled fixed point theorems. We begin our discussion by recalling some definitions and notions.
Definition 3.1
([13])
An element \((\varrho ^{*}, \sigma ^{*}) \in \mathbb{X}^{2}\) is called a coupled fixed point of a mapping \(\mathcal{G}: \mathbb{X}^{2} \to \mathbb{X}\) if \(\mathcal{G}(\varrho ^{*}, \sigma ^{*}) = \varrho ^{*}\) and \(\mathcal{G}(\sigma ^{*}, \varrho ^{*}) = \sigma ^{*}\).
Definition 3.2
Let \((\mathbb{X},\|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space and let \(\mathcal{G}: \mathbb{X}^{2}\rightarrow \mathbb{X}\) be a mapping. A map \(\mathcal{G}\) is said to have the monotone property if \(\mathcal{G}(\varrho ,\sigma )\) is monotone non-decreasing in both variables ϱ and σ, that is, for any \(\varrho ,\sigma \in \mathbb{X}\),
and
Lemma 3.3
[14] Suppose that \(\beta _{1}, \beta _{2},\ldots , \beta _{n}\) are MNCs (in Banach spaces \(\mathbb{X}_{1}, \mathbb{X}_{2},\ldots ,\mathbb{X}_{n}\)), respectively. We assume that the function \(\mathcal{G}: \mathbb{R}_{+}^{n} \to \mathbb{R}_{+}\) is convex and \(\mathcal{G}(\zeta _{1}, \zeta _{2},\ldots , \zeta _{n}) = 0\) if and only if \(\zeta _{i} = 0\) for \(i = 1, 2, 3, \ldots , n\). Then
defines a MNCs in \(\mathbb{X}_{1} \times \mathbb{X}_{2} \times \mathbb{X}_{3} \times \cdots \times \mathbb{X}_{n}\) where \(\mathfrak{B}_{i}\) denotes the natural projection of \(\mathfrak{B}\) into \(\mathbb{X}_{i}\), for \(i = 1, 2, 3, \ldots , n\).
Theorem 3.4
Let \((\mathbb{X},\|\cdot \|, \sqsubseteq )\) be a partially ordered Banach space whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathcal{G}: \mathbb{X}^{2} \rightarrow \mathbb{X}\) is a continuous and bounded mapping, having the monotone property and satisfying
for all bounded subsets \(\mathfrak{B}_{1}\), \(\mathfrak{B}_{2}\) in \(\mathbb{X}\), where β denotes the MNC in \(\mathbb{X}^{2}\), \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\Theta (\circ ; \cdot ) \in \Delta \), \(\psi \in \Psi \), \(\omega \in \Omega \).
If ∃ elements \(\varrho _{0}, \sigma _{0}\in \mathbb{X}\) such that \(\varrho _{0} \sqsubseteq \mathcal{G}(\varrho _{0},\sigma )\) for any \(\sigma \in \mathbb{X}\) and \(\sigma _{0} \sqsubseteq \mathcal{G}(\sigma _{0},\varrho )\) for any \(\varrho \in \mathbb{X}\), then \(\mathcal{G}\) has at least a coupled fixed point \((\varrho ^{*},\sigma ^{*})\).
Proof
We consider the following map \(\widehat{\mathcal{G}} : \mathbb{X}^{2} \to \mathbb{X}^{2}\):
Due to the assumption, \(\widehat{\mathcal{G}}\) is also a continuous and bounded mapping, having the monotone property.
Following Lemma 3.3, for \(\mathfrak{B}=\mathfrak{B}_{1}\times \mathfrak{B}_{2}\), we define a new MNC as
where \(\mathfrak{B}_{i}\), \(i = 1, 2\), denote the natural projections of \(\mathfrak{B}\). Now let \(\mathfrak{B}=\mathfrak{B}_{1}\times \mathfrak{B}_{2} \subset \mathbb{X}^{2}\) be a nonempty bounded subset. Due to (3.1) we conclude that
that is,
Next, we show that there is a \(\widehat{\varrho }_{0}\in \mathfrak{B}\) such that \(\widehat{\varrho }_{0}\sqsubseteq \widehat{\mathcal{G}}( \widehat{\varrho }_{0})\). Indeed, there exist two elements \(\varrho _{0}, \sigma _{0}\in \mathbb{X}\) such that \(\varrho _{0} \sqsubseteq \mathcal{G}(\varrho _{0},\sigma )\) for any \(\sigma \in \mathbb{X}\) and \(\sigma _{0} \sqsubseteq \mathcal{G}(\sigma _{0},\varrho )\) for any \(\varrho \in \mathbb{X}\), set \(\widehat{\varrho }_{0}=(\varrho _{0}, \sigma _{0})\). Then, by the definition of \(\widehat{\mathcal{G}}\), we have
Theorem 2.1 implies that \(\widehat{\mathcal{G}}\) has a fixed point, and hence \(\mathcal{G}\) has a coupled fixed point. □
Theorem 3.5
Let \((\mathbb{X},\|\cdot \|, \mathfrak{\sqsubseteq })\) be a partially ordered Banach space whose positive cone \(\mathbb{K}\) is normal. Suppose that \(\mathcal{G}: \mathbb{X}^{2} \rightarrow \mathbb{X}\) is a continuous and bounded mapping, having the monotone property and satisfying
for all bounded subsets \(\mathfrak{B}_{1}\), \(\mathfrak{B}_{2}\) in \(\mathbb{X}\), where β denotes the MNC in \(\mathbb{X}^{2}\), \(\hbar \in \mathbb{H}(\mathbb{R}_{+})\), \(\Theta (\circ ; \cdot ) \in \Delta \), \(\psi \in \Psi \), \(\omega \in \Omega \). If there exist elements \(\varrho _{0}, \sigma _{0}\in \mathbb{X}\) such that \(\varrho _{0} \sqsubseteq \mathcal{G}(\varrho _{0},\sigma )\) for any \(\sigma \in \mathbb{X}\) and \(\sigma _{0} \sqsubseteq \mathcal{G}(\sigma _{0},\varrho )\) for any \(\varrho \in \mathbb{X}\), then \(\mathcal{G}\) has at least a coupled fixed point \((\varrho ^{*},\sigma ^{*})\).
Proof
We consider the map \(\widehat{\mathcal{G}} : \mathbb{X}^{2} \to \mathbb{X}^{2}\) defined by
Then \(\widehat{\mathcal{G}}\) is a continuous and bounded mapping, having the monotone property.
For any \(\mathfrak{B}=\mathfrak{B}_{1}\times \mathfrak{B}_{2}\), we define a new MNC in the space \(\mathbb{X}^{2}\) as
where \(\mathfrak{B}_{i}\), \(i = 1, 2\), denote the natural projections of \(\mathfrak{B}\). Now let \(\mathfrak{B} \subset \mathbb{X}^{2}\) with \(\mathfrak{B}=\mathfrak{B}_{1}\times \mathfrak{B}_{2}\) be a nonempty bounded subset. We can conclude
That is,
Next, we show that there is a \(\widehat{\varrho }_{0}\in \mathfrak{B}\) such that \(\widehat{\varrho }_{0}\sqsubseteq \widehat{\mathcal{G}}( \widehat{\varrho }_{0})\). There exist elements \(\varrho _{0}, \sigma _{0}\in \mathbb{X}\) such that \(\varrho _{0} \sqsubseteq \mathcal{G}(\varrho _{0},\sigma )\) for any \(\sigma \in \mathbb{X}\) and \(\sigma _{0} \sqsubseteq \mathcal{G}(\sigma _{0},\varrho )\) for any \(\varrho \in \mathbb{X}\), set \(\widehat{\varrho }_{0}=(\varrho _{0}, \sigma _{0})\). Then, by the definition of \(\widehat{\mathcal{G}}\), we have
Theorem 2.1 implies that \(\widehat{\mathcal{G}}\) has a fixed point, and hence \(\mathcal{G}\) has a coupled fixed point. □
4 Fractals
Recently, a fractional derivative without singular kernel with its details was given in [15, 16]. The local fractional derivative of \(\mathfrak{K}(\varrho )\) of order \(0<\gamma \leq 1\) is inserted by
where the expression \(d^{\gamma }[\mathfrak{K}(\varrho )-\mathfrak{K}(\varrho _{0})]/ [d( \varrho -\varrho _{0})]^{\gamma }\) is the Riemann–Liouville fractional derivative given by
and we have the integral operator as follows:
The operator in (4.1) is well defined and it is represented to the classical fractional calculus. The function \(\mathfrak{K}\) is called local fractional continuous at \(\varrho _{0}\) if for all \(\varepsilon >0\) there is a κ that satisfies
provided \(|\varrho -\varrho _{0}|< \kappa \). We denote the space of all local fractional continuous functions by \(\mathrm{C}_{\gamma }\). For \(\mathfrak{K} \in \mathrm{C}_{\gamma } \), the local fractional integral is defined by
where (see [17])
The goal of this part is to study the existence and uniqueness of the generalized fractional integral equation
For this investigation, we shall apply Theorem 2.6. For our setting, we make the following assumptions:
-
(A1)
The function \(\mathfrak{K}: [0,1]\times C_{\gamma }[0,1] \rightarrow C_{\gamma }[0,1] \) is a non-decreasing function in \(C_{\gamma }[0,1]\) satisfying that there occurs a positive constant \(\ell > 0\) such that
$$ \bigl\vert \mathfrak{K}(\varsigma ,\varrho )-\mathfrak{K}(\varsigma , \eta ) \bigr\vert \leq \ell \vert \varrho - \eta \vert . $$ -
(A2)
There is a positive constant L satisfying
$$ L:=\frac{\ell +\lambda }{\Gamma (1+\gamma )\Gamma (2-\gamma )} < 1. $$
Theorem 4.1
Suppose that [A1], [A2] are achieved. If
then Eq. (4.2) admits a unique solution in \(C_{\gamma }[0,1]\).
Proof
Define the operator \(\Lambda : C_{\gamma }[0,1] \rightarrow C_{\gamma }[0.1]\), it is well defined and given by
Set \(\widetilde{\mathfrak{K}}(\varsigma ) = \mathfrak{K}(\varsigma , 0)\) and the ball \(\mathcal{B}_{r} = \{ \varrho \in C_{\gamma }[0,1]: \Vert \varrho \Vert \leq r \} \). Now we subdivide the operator Λ into two operator \(\Lambda _{1}\) and \(\Lambda _{2}\) on \(B_{r}\) as follows:
and
where λ is a positive constant. Since \(\mathfrak{K}\) is a non-decreasing and continuous function, this leads to Λ being also a non-decreasing and continuous mapping.
The proof is as follows.
Step 1. (Boundedness) \(\Lambda \varrho := \Lambda _{1}\varrho +\Lambda _{2} \varrho \in \mathcal{B}_{r}\) for every \(\varrho \in B_{r}\). In view of [A1], we have
This implies that
Hence, Λ is bounded, continuous and non-decreasing in \(\mathcal{B}_{r}\).
Step 2. Λ is ψ-contraction mapping (condition (2.11)).
For any \(\varrho , \eta \in \mathcal{B}_{r}\), we obtain
This gives
Define two continuous functions φ and ψ as follows:
From the last inequality, we obtain
In view of [A2], the operator Λ is a ψ-contraction mapping. Taking the sup. over \(\mathcal{B}_{r}\), we have
Thus, Λ obeys all the conditions of Theorem 2.6. That is, Λ has a unique fixed point in \(\mathcal{B}_{r}\). □
Example 1
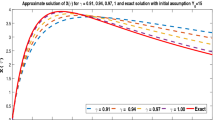
For the initial point \(\varrho _{0}=0.1\) and \(\gamma =0.5\), we have
Then, for all \(\lambda \in (0,1)\), Eq. (4.6) has a unique solution in \(C_{0.5}[0,1]\). The fixed point approximates the value \(\varsigma \approx 1\), whenever \(\lambda = 113{,}261/500{,}000 \approx 0.22\). Furthermore, for \(\gamma =0.9\) we have
Equation (4.7) has a unique solution in \(C_{0.9}[0,1]\). The fixed point is approximated to the value \(\varsigma \approx 1\), whenever \(\lambda = 1{,}372{,}727/10{,}000{,}000 \approx 0.137\). We proceed by assuming the following integral equation:
Equation (4.8) has a unique solution in \(C_{0.9}[0,1]\). The fixed point is approximated to the value \(\varsigma \approx 1\), whenever \(\lambda = 71{,}017/100{,}000 \approx 0.7\). Finally, we consider the following fractal integral:
Equation (4.9) has a unique solution in \(C_{0.9}[0,1]\). The fixed point approximates the value \(\varsigma \approx 1\), whenever \(\lambda = 101{,}527/1{,}000{,}000 \approx 0.1\).
Remark 4.2
-
By applying Theorem 3.5, one can show that the coupled system
$$\begin{aligned} &\varrho _{1}(\varsigma ) = \frac{\varrho _{o}}{\Gamma (2-\gamma )\Gamma (1+\gamma )} - \frac{\lambda _{1}}{\Gamma (1+\gamma )} \int _{0}^{1} \varrho _{2}( \varsigma ) (d\varsigma )^{\gamma } \\ & \hphantom{\varrho _{1}(\varsigma ) =}{}+ \frac{1}{\Gamma (1+\gamma )} \int _{0}^{1} \mathfrak{K}_{1} \bigl( \varsigma , \varrho (\varsigma )\bigr) (d\varsigma )^{\gamma }, \\ &\varrho _{2}(\varsigma ) = \frac{\varrho _{o}}{\Gamma (2-\gamma )\Gamma (1+\gamma )} - \frac{\lambda _{2}}{\Gamma (1+\gamma )} \int _{0}^{1} \varrho _{1}( \varsigma ) (d\varsigma )^{\gamma } \\ &\hphantom{\varrho _{2}(\varsigma ) =}{}+ \frac{1}{\Gamma (1+\gamma )} \int _{0}^{1} \mathfrak{K}_{2} \bigl( \varsigma , \varrho (\varsigma )\bigr) (d\varsigma )^{\gamma }, \end{aligned}$$where \(\varrho =(\varrho _{1},\varrho _{2})\) and \(\varrho _{1}(0)=\varrho _{2}(0)=\varrho _{0}\), has at least one fixed point.
-
All the above fixed point theorems are applicable for both convex and non-convex domains.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
References
Kuratowski, K.: Sur les espaces completes. Fundam. Math. 15, 301–309 (1930)
Nashine, H.K., Ibrahim, R.W.: Monotone solutions of iterative fractional equations found by modified Darbo-type fixed-point theorems. J. Fixed Point Theory Appl. 19(14), 3217–3229 (2017)
Tuan, N.H., Huynh, L.N., Baleanu, D., Can, N.H.: On a terminal value problem for a generalization of the fractional diffusion equation with hyper-Bessel operator. Math. Methods Appl. Sci. 43(6), 2858–2882 (2020)
Tuan, N.H., Baleanu, D., Thach, T.N., O’Regan, D., Can, N.H.: Final value problem for nonlinear time fractional reaction-diffusion equation with discrete data. J. Comput. Appl. Math. 2020, 112883 (2020)
Almeida, R., Girejko, E., Hristova, S., Malinowska, A.B.: Leader-following consensus for fractional multi-agent systems. Adv. Differ. Equ. 2019, 301 (2019)
Agarwal, R., Almeida, R., Hristova, S., O’Regan, D.: Caputo fractional differential equation with state dependent delay and practical stability. Dyn. Syst. Appl. 28(3), 715–742 (2019)
Hristova, S., Ivanova, K.: Caputo fractional differential equations with non-instantaneous random erlang distributed impulses. Fractal Fract. 3(2), 28 (2019)
Banas, J., Goebel, K.: Measures of Noncompactness in Banach Spaces. Lecture Notes in Pure and Applied Mathematics. Dekker, New York (1980)
Altun, I., Turkoglu, D.: A fixed point theorem for mappings satisfying a general contractive condition of operator type. J. Comput. Anal. Appl. 9(1), 9–14 (2007)
Arab, R.: Some fixed point theorems in generalized Darbo fixed point theorem and the existence of solutions for system of integral equations. J. Korean Math. Soc. 52(1), 125–139 (2015)
Aghajani, A., Banas, J., Sabzali, N.: Some generalizations of Darbo fixed point theorem and applications. Bull. Belg. Math. Soc. Simon Stevin 20, 345–358 (2013)
Falset, J.G., Latrach, K.: On Darbo-Sadovskii’s fixed point theorems type for abstract measures of (weak) noncompactness. Bull. Belg. Math. Soc. Simon Stevin 22, 797–812 (2015)
Guo, D., Lakshmikantham, V., Liu, X.: Nonlinear Integral Equations in Abstract Spaces. Mathematics and Its Applications, vol. 373. Kluwer Academic, Dordrecht (1996)
Akmerov, R., Kamenski, M., Potapov, A., Rodkina, A., Sadovskii, B.: Measures of Noncompactness and Condensing Operators. Birkhäuser, Basel (1992)
Caputo, M., Fabrizio, M.: A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 1(2), 73–85 (2015)
Yang, X., Baleanu, D., Srivastava, H.M.: Local Fractional Integral Transforms and Their Applications. Elsevier, Amsterdam (2016)
Cattani, C., Srivastava, H.M., Yang, X.-J.: Fractional Dynamics. de Gruyter, Berlin (2015)
Acknowledgements
The authors would like to thank the reviewers and editor for their constructive comments and valuable suggestions, which improved the quality of our paper.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript. All authors contributed equally to the writing of this paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nashine, H.K., Ibrahim, R.W., Agarwal, R.P. et al. Existence of local fractional integral equation via a measure of non-compactness with monotone property on Banach spaces. Adv Differ Equ 2020, 697 (2020). https://doi.org/10.1186/s13662-020-03153-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03153-3