Abstract
In this study, an efficient numerical scheme based on shifted Chebyshev polynomials is established to obtain numerical solutions of the Bagley–Torvik equation. We first derive the shifted Chebyshev operational matrix of fractional derivative. Then, by the use of these operational matrices, we reduce the corresponding fractional order differential equation to a system of algebraic equations, which can be solved numerically by Newton’s method. Furthermore, the maximum absolute error is obtained through error analysis. Finally, numerical examples are presented to validate our theoretical analysis.
Similar content being viewed by others
1 Introduction
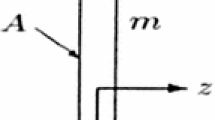
Over the past few decades, many natural phenomena have been successfully modeled using the fractional differential equation [1–6]. As an example, the authors in [7] constructed the following equation that describes the motion of a rigid plate immersed in a Newtonian fluid:
and
where the operator \(D^{\frac{3}{2}}\) is a Liouville–Caputo derivative, \(A\neq 0,B\) are constants, and the function \(f(t)\) is known. The existence and uniqueness of the problem have been established in [8, 9]. Many methods have been developed to deal with the problem in the literature [10–14]. Podlubny also investigated this equation and introduced an approximate analytical solution by Green’s function in his monograph [15]. Ray and Bera [16] adopted a semi-analytical method for solving Bagley–Torvik equation and obtained the same solution as Podlubny’s solution. Rajarama and Chakraverty [17] adopted the Sumudu transformation method to obtain the analytical solution of the problem. Cenesiz et al. [18–20] suggested a Taylor polynomial along with the collocation method for dealing with a class of fractional differential equations including the Bagley–Torvik equation. In [21–24], the wavelet method was used to deal with the problems. Diethelm and Ford [25] solved the problem by using Adams predictor and corrector methods. In [26–28] the spectral collocation method based on a hybrid function and Chebyshev polynomial were employed to handle the equation. Moreover, shifted Legendre polynomial based Galerkin and collocation methods were utilized in delay Bagley–Torvik equations in [29]. Most recently, Hou and Ji [30, 31] introduced Jacobi polynomials and Laplace transform together with Laguerre polynomials to solve the equation.
Papers [26, 27] and [32] focused on the Chebyshev polynomial method for the Bagley–Torvik equation. In these studies, the operational matrix of fractional integration and Tau method were applied to tackle the problem. The objective of the current study is to develop a modified Chebyshev spectral collocation method to handle the Bagley–Torvik equation. We generate the operational matrices of derivative for shifted Chebyshev polynomials in the physical space. Thereafter, we obtain a discrete numerical scheme, in which the nonhomogeneous terms are not approximated. A rigorous error analysis in \(L^{\infty }\)-norm is provided.
2 The fractional integration and differentiation
In this section, we mainly introduce the widely used Riemann–Liouville fractional integral and Liouville–Caputo fractional derivative.
Definition 1
([33])
The Riemann–Liouville fractional integral operator \(J^{\alpha }\), \(\alpha >0\), is defined as follows:
Definition 2
([33])
The Liouville–Caputo fractional derivative operator \(D^{\alpha }\) is defined as follows:
for \(n-1< \alpha \leq n\), \(n\in \mathbb{N}\), \(t>0\), \(f(t)\in C_{-1}^{n}\).
For the Liouville–Caputo derivative (3), we have
Here, \(\lceil \alpha \rceil \) and \(\lfloor \alpha \rfloor \) are the ceiling and floor functions, respectively. Also \(\mathbb{N}_{0}=\{0,1,2,\ldots \}\).
3 Shifted Chebyshev polynomials and their properties
The well-known Chebyshev polynomials are defined on the interval \([-1,1]\) and are obtained by expanding the following formulae:
To use these polynomials on the interval \(t\in [0,L]\) for any real \(L>0\), we introduce the change of variable \(x=2t/L-1\), \(0\leq t \leq L\), and obtain the shifted Chebyshev polynomials
The shifted Chebyshev polynomials \(T^{*}_{Ln}(t)\) satisfy the recurrence relation
where \(T^{*}_{L0}(t)=1\), \(T^{*}_{L1}(t)=2t/L-1\). The analytic form of the shifted Chebyshev polynomials \(T^{*}_{Li}(t)\) of degree i is given by
where \(T^{*}_{Li}(0)=(-1)^{i}\), \(T^{*}_{Li}(L)=1\). The \(T^{*}_{Li}(t)\) also satisfy a discrete orthogonality condition

where the interpolation points are chosen to be the Chebyshev–Gauss–Lobatto points associated with the interval \([0,L]\), \(t_{k}=\frac{L}{2}(1-\cos (k\pi /N))\), \(k=0,1,2,\ldots ,N\). Here, the summation symbol with double primes denotes a sum with both the first and last terms halved.
4 The operational matrix of derivative
A continuous and bounded function \(y(t)\) can be approximated in terms of shifted Chebyshev polynomials in the interval \([0,L]\) by the formula

Using the discrete orthogonality relation, the coefficient \(c_{k}\) in (6) is given by the explicit formula

Applying (6), (7), the function \(y_{N}(t)\) can be written collectively in a matrix form
where
and
The derivative \(y_{N}'(t)\) is as follows:
We know that
in which M is the \((N+1)\times (N+1)\) operational matrix of derivative given by
so that \(m_{1}\), \(m_{2}\), and \(m_{3}\) are respectively N, 0, 2N for odd N and 0, 2N, 0 for even N. Then, we substitute equation (10) into (9) to get
Therefore \(y_{N}'(t)\) can be expressed in a discretized form as follows:
where
and
So, we can get the operational matrix of derivative
Furthermore, the operational matrix of derivative of the n-order derivative can be completely determined from those of the first derivative
5 Calculation of the operational matrix of fractional order derivatives
According to the definition of Liouville–Caputo fractional derivative, we can write
where \(\alpha >0\). Applying (5), the Liouville–Caputo fractional derivative of the vector \(T(x)\) in (13) can be expressed as
where
and
Using (4) we have
where
Employing (13), (14) and (15), we get
where
and
Then we get the operational matrix of fractional derivative
For simplicity, the operational matrix of the fractional derivative in (16) can be written collectively in the following form:
6 Applications to the Bagley–Torvik equation
To show the fundamental importance of the operational matrix of fractional order derivatives, we apply it for solving the Bagley–Torvik equation. To solve the problem, we first consider incorporating boundary conditions
By substituting the approximation (18) in (19) and by using the boundary conditions (2), we get a system of algebraic equations:
Solving the system of algebraic equations, we can obtain the vector Y. Then, using (8), we can get the output response
7 Some useful lemmas
In this section, we give some useful lemmas, which play a significant role in the convergence analysis later. We first introduce some notations that will be used. Let \(I:=(-1,1)\) and \(L^{2}_{\omega ^{\alpha ,\beta }}(I)\) be the space of measurable functions whose square is Lebesgue integrable in I relative to the weight function \(\omega ^{\alpha ,\beta }(x)\). The inner produce and norm of \(L^{2}_{\omega ^{\alpha ,\beta }}(I)\) are defined by
For a nonnegative integer m, define
with the seminorm and the norm as follows:
Particularly, let
be the Chebyshev weight function. Denote by \(L^{\infty }(-1,1)\) the measurable functions space with the norm
For a given positive integer N, we denote the points by \(\{x_{i}\}_{i=0}^{N}\), which is a set of \(N+1\) Gauss–Lobatto points, corresponding to the weight \(\omega (x)\). By \(P_{N}\) we denote the space of all polynomials of degree not exceeding N. For all \(v\in C[-1,1]\), we define the Lagrange interpolating polynomial \(I_{N}v\in P_{N}\), satisfying
The Lagrange interpolating polynomial can be written in the form
where \(F_{i}(x)\) is the Lagrange interpolation basis function associated with \(\{x_{i}\}_{i=0}^{N}\).
Lemma 3
([34])
Assume that \(v\in H^{m}_{\omega }\), and denote \(I_{N}v\) its interpolation polynomial associated with the Gauss–Lobatto points \(\{x_{i}\}_{i=0}^{N}\), namely
Then the following estimates hold:
8 Convergence analysis
In this section, an error estimate of the applied method for the solutions of the Bagley–Torvik equation is provided. For the sake of applying the theory of orthogonal polynomials, we use the variable transformations \(t=T(1+x)/2\), \(x\in [-1,1]\) to rewrite (1), (2) as follows:
and
where
Theorem 4
Let \(u(x)\) be the exact solution of the Bagley–Torvik equation differential equation (22), which is assumed to be sufficiently smooth. Let the approximate solution \(u_{N}(x)\) be obtained by using the proposed method. If \(u(x)\in H^{m}_{\omega }(I)\), then for sufficiently large N the following error estimate holds:
Proof
We use \(u_{i}\approx u(x_{i})\), \(u^{(\alpha )}_{i}\approx u^{\alpha }(x_{i}), 0\leq i \leq N \), and
where \(F_{j}\), \(j=0,1,2,\ldots ,N\), is the Lagrange interpolation basis function. Consider equation (22). By using Chebyshev–Gauss–Lobatto collocation points \(\{x_{i}\}_{i=0}^{N}\), we have
Then the numerical scheme (20) can be written as
We now subtract (24) from (26) and subtract (25) from (27) to get the error equation
Multiplying by \(F_{i}(x)\) both sides of (28), (29) and summing from 0 to N yield
Consequently,
where
It follows from the Gronwall inequality and [35] that
then we have
Using Lemma 3, we have
We now estimate \(J_{4}\). By virtue of Lemma() with \(m=2\), we have
Therefore, a combination of (30), (31), (32), and (33) yields estimate (23). □
9 Illustrative examples
To illustrate the effectiveness of the proposed method in the present paper, some test examples are carried out in this section. The results obtained by the present methods reveal that the present method is very effective and convenient for fractional differential equations.
Example 9.1
As the first example, we consider the following Bagley–Torvik differential equation [36–38]:
with the boundary conditions \(y(0)=0\) and \(y(1)=0\). With \(N=3\), from (16) we get
The following system of algebraic equations will be obtained:
Applying the boundary conditions \(y(0)=0\), \(y(1)=0\) and solving (35), we obtain \(y(1/2)=-0.025\). Thus
which is the exact solution \(y(t)=t^{2}-t\).
Example 9.2
In this example we consider the following equation:
where
The analytical solution can be found in [15]. The problem is considered in [18, 20, 22, 28, 39]. First, we consider the boundary conditions \(y(0)=0\), \(y(20)=-1.48433\) and apply the present method to solve the problem with \(N=8,16,32,64,128\). In Table 1, we list the \(L^{\infty }\), \(L^{2}\) errors and CPU time for the differential values of N. The numerical solutions obtained by the present method and some other numerical methods, such as the wavelet method [22] and the hybrid functions method [28], are given in Tables 2 and 3. Clearly, numerical results show that the present method is working well and the accuracy is comparable with the existing methods. Also, the numerical results with \(N=16,32\) and the exact solution are plotted in Fig. 1. For Example 9.2, Fig. 1 shows that the approximate solutions using the present method are in high agreement with the exact solutions. Second, we solve this problem with the boundary conditions \(y(0)=0\), \(y(1)=2.95179355\). We compare the absolute errors of the present method, the Taylor collocation method [18], and the fractional Taylor method [20] in Table 4. This indicates that our results are better than given by [18, 20].
10 Conclusion
In this work, the shifted Chebyshev operational matrix of fractional derivatives has been derived. Also, the operational matrix in combination with a collocation method is used to approximate the unknown function of the Bagley–Torvik equation. Moreover, a convergence analysis was performed under the \(L^{\infty }\) norm. Finally, numerical examples were presented to demonstrate the validity and applicability of the proposed numerical scheme. From examples, we observed that our scheme is simple and accurate. We believe that the ideas introduced in this study can be extended for systems of nonlinear fractional differential equations and fractional integro-differential equations.
Availability of data and materials
This paper focuses on theoretical analysis and does not involve experiments and data.
References
Singh, H., Sahoo, M.R., Singh, O.P.: Numerical method based on Galerkin approximation for the fractional advection-dispersion equation. Int. J. Appl. Comput. Math. 3(3), 2171–2187 (2017)
Singh, H., Singh, C.S.: A reliable method based on second kind Chebyshev polynomial for the fractional model of Bloch equation. Alex. Eng. J. 57(3), 1425–1432 (2018)
Singh, H., Srivastava, H.M.: Numerical investigation of the fractional-order Liénard and Duffing equations arising in oscillating circuit theory. Front. Phys. (2020). https://doi.org/10.3389/fphy.2020.00120
Jena, R.M., Chakraverty, S.: Boundary characteristic orthogonal polynomials-based Galerkin and least square methods for solving Bagley–Torvik equations. In: Recent Trends in Wave Mechanics and Vibrations. Lecture Notes in Mechanical Engineering, pp. 327–342. Springer, Berlin (2020)
Chakraverty, S., Jena, R.M., Jena, S.K.: Time-Fractional Order Biological Systems with Uncertain Parameters. Synthesis Lectures on Mathematics and Statistics. Morgan & Claypool Publishers, San Rafael (2020)
Srivastava, H.M., Saad, K.M.: A comparative study of the fractional-order clock chemical model. Mathematics 8(9), 1436 (2020)
Torvik, P., Bagley, R.L.: On the appearance of the fractional derivative in the behavior of real materials. J. Appl. Mech. 51(2), 725–728 (1984)
Luchko, Y., Gorenflo, R.: An operational method for solving fractional differential equations with the Caputo derivatives. Acta Math. Vietnam. 24(2), 207–233 (1999)
Rehman, M.U., Idrees, A., Saeed, U.: A quadrature method for numerical solutions of fractional differential equations. Appl. Math. Comput. 307(15), 38–49 (2017)
Singh, H., Srivastava, H.M., Kumar, D.: A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons Fractals 103, 131–138 (2017)
Singh, H., Pandey, R.K., Srivastava, H.M.: Solving non-linear fractional variational problems using Jacobi polynomials. Mathematics 7(3), 224 (2019)
Singh, H., Srivastava, H.M.: Jacobi collocation method for the approximate solution of some fractional-order Riccati differential equations with variable coefficients. Phys. A, Stat. Mech. Appl. 523, 1130–1149 (2019)
Srivastava, H.M., Saad, K.M., Khader, M.M.: An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 140, 110174 (2020)
Srivastava, H.M., Jena, R.M., Chakraverty, S., Jena, S.K.: Dynamic response analysis of fractionally-damped generalized Bagley–Torvik equation equation subject to external loads. Russ. J. Math. Phys. 27(2), 254–268 (2020)
Podlubny, I.: Fractional Differential Equations, vol. 198. Academic Press, San Diego (1998)
Ray, S.S., Bera, R.K.: Analytical solution of the Bagley–Torvik equation by Adomian decomposition method. Appl. Math. Comput. 168(1), 398–410 (2005)
Jena, R.M., Chakraverty, S.: Analytical solution of Bagley–Torvik equations using Sumudu transformation method. SN Appl. Sci. 1(3), 246 (2019)
Çenesiz, Y., Keskin, Y., Kurnaz, A.: The solution of the Bagley–Torvik equation with the generalized Taylor collocation method. J. Franklin Inst. 347(2), 452–466 (2010)
Gülsu, M., Öztürk, Y., Anapali, A.: Numerical solution the fractional Bagley–Torvik equation arising in fluid mechanics. Int. J. Comput. Math. 11(7), 1–12 (2015)
Krishnasamy, V.S., Razzaghi, M.: The numerical solution of the Bagley–Torvik equation with fractional Taylor method. J. Comput. Nonlinear Dyn. 11(5), 051010 (2016)
Li, Y., Zhao, W.: Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl. Math. Comput. 216(8), 2276–2285 (2010)
Ray, S.S.: On Haar wavelet operational matrix of general order and its application for the numerical solution of fractional Bagley–Torvik equation. Appl. Math. Comput. 218(9), 5239–5248 (2012)
Fakhrodin, M.: Numerical solution of Bagley–Torvik equation using Chebyshev wavelet operational matrix of fractional derivative. Int. J. Adv. Appl. Math. Mech. 2(1), 83–91 (2014)
Srivastava, H.M., Shah, F.A., Abass, R.: An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley–Torvik equation. Russ. J. Math. Phys. 26(1), 77–93 (2019)
Diethelm, K., Ford, J.: Numerical solution of the Bagley–Torvik equation. BIT Numer. Math. 42(3), 490–507 (2002)
Bhrawy, A.H., Alofi, A.S.: The operational matrix of fractional integration for shifted Chebyshev polynomials. Appl. Math. Lett. 26(1), 25–31 (2013)
Mokhtary, P.: Numerical treatment of a well-posed Chebyshev tau method for Bagley–Torvik equation with high-order of accuracy. Numer. Algorithms 72(4), 875–891 (2016)
Mashayekhi, S., Razzaghi, M.: Numerical solution of the fractional Bagley–Torvik equation by using hybrid functions approximation. Math. Methods Appl. Sci. 39(3), 353–365 (2016)
Jena, R.M., Chakraverty, S., Edeki, S.O., Ofuyatan, O.M.: Shifted Legendre polynomial based Galerkin and collocation methods for solving fractional order delay differential equations. J. Theor. Appl. Inf. Technol. 98(4), 535–547 (2020)
Ji, T., Hou, J.: Numerical solution of the Bagley–Torvik equation using Laguerre polynomials. SeMA J. 77(1), 97–106 (2020)
Hou, J., Yang, C., Lv, X.: Jacobi collocation methods for solving the fractional Bagley–Torvik equation. IAENG Int. J. Appl. Math. 50(1), 114–120 (2020)
Bhrawy, A.H., Tharwat, M.M., Yildirim, A.: A new formula for fractional integrals of Chebyshev polynomials: application for solving multi-term fractional differential equations. Appl. Math. Model. 37(6), 4245–4252 (2013)
Kilbas, A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, vol. 204. Elsevier, Amsterdam (2006)
Canuto, C.G., Hussaini, M.Y., Quarteroni, A., Zang, T.A.: Spectral Methods: Fundamentals in Single Domains. Scientific Computation, vol. 23. Springer, Berlin (2007)
Yang, Y., Chen, Y.P., Huang, Y.Q.: Convergence analysis of the Jacobi spectral-collocation method for fractional integro-differential equations. Acta Math. Sci. 34(3), 673–690 (2014)
Diethelm, K., Ford, N.J., Freed, A.D.: Detailed error analysis for a fractional Adams method. Numer. Algorithms 36(1), 31–52 (2004)
Esmaeili, S., Shamsi, M.: A pseudo-spectral scheme for the approximate solution of a family of fractional differential equations. Commun. Nonlinear Sci. Numer. Simul. 16(9), 3646–3654 (2011)
Yüzbaşı, Ş.: Numerical solution of the Bagley–Torvik equation by the Bessel collocation method. Math. Methods Appl. Sci. 36(3), 300–312 (2013)
Al-Mdallal, Q.M., Syam, M.I., Anwar, M.N.: A collocation-shooting method for solving fractional boundary value problems. Commun. Nonlinear Sci. Numer. Simul. 15(12), 3814–3822 (2010)
Acknowledgements
Not applicable.
Funding
This research received no external funding.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with the same responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ji, T., Hou, J. & Yang, C. Numerical solution of the Bagley–Torvik equation using shifted Chebyshev operational matrix. Adv Differ Equ 2020, 648 (2020). https://doi.org/10.1186/s13662-020-03110-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03110-0