Abstract
In this study, a hybrid technique for improving the differential transform method (DTM), namely the modified differential transform method (MDTM) expressed as a combination of the differential transform method, Laplace transforms, and the Padé approximant (LPDTM) is employed for the first time to ascertain exact solutions of linear and nonlinear pantograph type of differential and Volterra integro-differential equations (DEs and VIDEs) with proportional delays. The advantage of this method is its simple and trusty procedure, it solves the equations straightforward and directly without requiring large computational work, perturbations or linearization, and enlarges the domain of convergence, and leads to the exact solution. Also, to validate the reliability and efficiency of the method, some examples and numerical results are provided.
Similar content being viewed by others
1 Introduction
Mathematical modeling of various phenomena in science and engineering such as biological population management, chemistry, physics, physiological and pharmaceutical kinetics and chemical kinetics, medicine, infectious diseases, economy, nonlinear dynamical system, communication networks, number theory, electrodynamics, the navigational control of ships and aircraft and control problems and electronic systems leads to one of the most important kinds of delay differential equations (DDEs), namely pantograph equation [1–7]. The term pantograph was first used by Ockendon and Tayler in [8] which modeled and redesigned the collection system for an electric locomotive.
At this point, it is usually difficult to solve these kinds of DDEs analytically. Therefore, in the literature, there are some valuable efforts that focus on finding the analytical and numerical methods for solving the pantograph type of DEs and VIDEs with proportional delays. (see, e.g., [9–21] and the references therein). The differential transform method (DTM) is an analytical-numerical technique introduced for the first time by Zhou [22] to study the electrical circuits. Like any subject in mathematics, DTM has grown over a period of time. In 1999, Chen and Ho [23] developed this method for partial differential equations with two independent variables. In 2004, Ayaz [24] extended the two-dimensional DTM into the three-dimensional DTM and used it to solve linear and nonlinear partial differential equations. In 2005, Arikoglu and Ozkol [25] used the differential transform method for integro-differential equations. With the advent of fractional calculus, the differential transform method was also modified to solve derivative and integral problems of any order. In 2007, Arikoglu and Ozkol [26] proposed a numerical-analytical method similar to the DTM, called the fractional differential transform method (FDTM), which they used to solve fractional differential equations. In 2008, Odibat and Momani [27] introduced the generalized differential transform method (GDTM) based on the differential transform method and generalized Taylor’s formula and the Caputo fractional derivative and used it to solve fractional partial differential equations. Also in the same year, Momani and Erturk [28] learned to correct and improve the accuracy of the solution of convergent series obtained by the differential transform method, they introduced the modified differential transform method (MDTM), and Chang [29] used the DTM for one-dimensional nonlinear functions. In 2009, Keskin [30, 31] introduced the reduced form of the DTM as the reduced differential transform method (RDTM), which Keskin and Oturanc [32, 33] used to solve partial differential equations and fractional differential equations. Many authors, during recent years, have used this method for solving various types of equations. For example, differential-algebraic equations [34–36], Volterra integral equation [37–39], integro-differential equations [40–43] and fractional differential equations [44–47] are solved using this method. This suggested technique is highly efficient and powerful in obtaining the exact solutions and approximate solutions of mathematical modeling of many problems, gives the solution in the form of rapidly convergent successive approximations, and is capable of handling linear and nonlinear equations in a similar manner. Moreover the comparison of our method with other analytical methods available in the literature show that although the results of these methods are the same, RDTM is a lot easier, more convenient, and reliable than them [48–55].
In this paper, we present the application of the modified differential transform method (MDTM) as a hybrid approach, for improving DTM’s truncated series solutions in convergence rate combining DTM, Laplace transforms, and Padé approximant. The solutions series obtained by the differential transform method, even if they contain a large number of terms, may converge in a limited area. Therefore, the domain of convergence of the truncated power series expands by the Laplace–Padé differential transform method (LPDTM) and often leads to the exact solution. To improve the solution of convergent series obtained by the DTM, we apply Laplace transform to it, and then by forming its Padé approximant, the transformed series convert into a meromorphic function. Finally, to obtain the analytical solution, we take the inverse Laplace transform from the function obtained of the Padé approximant. Therefore, in the light of the above-mentioned method, we will study the exact solution of linear and nonlinear pantograph type of DEs and VIDEs with proportional delays
where u is the unknown function and the functions F, G, and K are analytic in the domain of interest.
The rest of this study is presented in the following sections: In Sect. 2, The main idea behind the Padé approximant is introduced. In Sect. 3, we simply introduce the modified differential transform method (MDTM) as a combined form of the DTM with Laplace transforms, and the Padé approximant. In Sect. 4, we prove several important Theorems. In Sect. 5, we apply the MDTM to obtain the exact solutions for linear and nonlinear pantograph type of DEs and VIDEs with proportional delays. Finally, we offer some summaries and a conclusion in Sect. 6.
2 Padé approximant
The best approximation of a function with a rational function of a certain order is the Padé approximant. Under this technique, the approximant’s power series agrees with the power series of the function it is approximating.
Let \(u(t) \) be an analytical function that corresponds to the Maclaurin series:
Then the Padé approximant to \(u(t) \) is a rational fraction which we denote as \([\frac{m}{n} ] \) and is defined by [56, 57]
there are \(m+1 \) independent numerator coefficients and n independent denominator coefficients, making \(m+n+1 \) unknown coefficients in all. We have
From Eq. (2.3), we have
From Eq. (2.4), we get the following algebraic linear systems:
and
We determine first all the denominator coefficients \(b_{j} \), \(1\leq j\leq n \), from Eq. (2.5). Then, we calculate the numerator coefficients \(a_{i} \), \(0\leq i \leq m \), from Eq. (2.6).
Remark 2.1
For a fixed value of \(m+n+1 \), error Eq. (2.3) is the smallest when the numerator has one degree higher than the denominator of (2.2) or when the numerator and denominator have the same degree.
The advantage of Padé approximant is that it often gives a better approximation than the truncated series solutions from the Taylor series. This is because sometimes the Taylor series may not be convergent, and the Padé approximant has the potential to expand the domain of convergence of solutions or includes finding exact solutions.
3 Summary of the method
We present some important definitions and mathematical preliminaries operations of the modified differential transform method which can help to gain more understanding of the method stated in this section.
Definition 3.1
The differential transform function of \(u(t)\) can be written in the following form:
where \(u(t)\) represents the main original analytic and differentiated continuously function with regard to time t, in the domain of interest, and \(\mathcal{U}(k) \) describes the transformed function.
Definition 3.2
The differential inverse transform of \(\mathcal{U}(k)\) is determined as
Then, consolidating Eqs. (3.2) and (3.1) yields
By the help of the upper definitions, to illustrate the basic idea of the DTM, consider the following form of nonlinear ordinary differential equations:
with the following initial condition:
where \(f(u(t),t)\) indicates a nonlinear smooth function.
After applying the DTM definition on both sides of Eq. (3.4), we can write the following iteration formula:
where \(\mathcal{F}(\mathcal{U}(0), \ldots ,\mathcal{U}(k),k)\) is the differential transform functions of \(f(u(t),t)\).
Implementing the aforesaid method to the initial condition (3.5), we have
To discover the remaining iteration, we plug Eq. (3.7) into Eq. (3.6) and by simple reiterative calculation, we get the subsequent \(\mathcal{U}(k)\) values. Then, by using the inverse transformation of the set of values \(\{\mathcal{U}(k)\}^{n}_{k=0}\), the approximation solution can be written as follows:
Thus, the exact solution of the considered equation can be gained by
The solutions series derived from the DTM, even if they contain a large number of terms, may converge in a limited area. To improve the solution obtained in convergent series form using the DTM, and enlarge the domain of convergence of solutions we apply the Laplace–Padé method by following steps.
-
Step 1: Applying Laplace transformation with respect to t for the obtained power series (3.8).
-
Step 2: Substituting s by \(\frac{1}{t} \) in the resulting equation.
-
Step 3: Creating the Padé approximant of order \([\frac{m}{n} ] \) for the transformed series and convert it into a meromorphic function.
Remark 3.3
m and n are arbitrarily chosen, but they should be of smaller values than the order of the power series. In this step, to obtain better convergence and accuracy, the Padé approximant enlarges the domain of the truncated series solution.
-
Step 4: Substituting t by \(\frac{1}{s} \).
-
Step 5: Applying the inverse Laplace transformation with respect to s for obtaining the exact or approximate solution.
Table 1 contains the basic mathematical operations carried out by DTM.
4 Main results
The principal main of this section is to study the fundamental Theorem of this paper.
Theorem 4.1
If \(w(t) =u(\alpha t) \), then \(\mathcal{W}(k)=\alpha ^{k} \mathcal{U}(k)\) where \(\alpha \in (0,1)\).
Proof
From Eq. (3.1), we get
where \(\hat{t}=\alpha t\), then
□
Theorem 4.2
If \(w(t) =u(\alpha _{1}t) v(\alpha _{2}t) \), then, for \(\alpha _{1}, \alpha _{2}\in (0,1)\), we have
Proof
From Eq. (3.1), we get
where \(\hat{t}=\alpha _{1} t\) and \(\tilde{t}=\alpha _{2} t\), then
□
Theorem 4.3
If \(w(t)=\frac{d^{r}}{dt^{r}} u(\alpha t) \), then \(\mathcal{W}(k)=\alpha ^{k+r} \frac{(k+r) !}{k !} \mathcal{U}(k+r)\).
Proof
From Eq. (3.1), we have
therefore
□
Theorem 4.4
If \(w(t) =\frac{d^{m}}{dt^{m}} u(\alpha _{1}t) \frac{d^{n}}{dt^{n}} v( \alpha _{2}t) \), then
Proof
From Eq. (3.1), we have
where \(\hat{t}=\alpha _{1} t\) and \(\tilde{t}=\alpha _{2} t\), then
□
Theorem 4.5
If \(w(t)=\int _{0}^{lt}u(\alpha \xi ) \,\mathrm{d}\xi \), then \(\mathcal{W}(k)=\frac{1}{k} l^{k} \alpha ^{k-1} \mathcal{U}(k-1)\).
Proof
therefore
□
Theorem 4.6
If \(w(t)=\int _{0}^{lt}u(\alpha _{1}\xi ) v(\alpha _{2}\xi )\,\mathrm{d} \xi \), then
Proof
where \(\hat{t}=l\alpha _{1} t\) and \(\tilde{t}=l\alpha _{2} t\), then
□
Theorem 4.7
If \(w(t)=v(\beta t)\int _{0}^{lt}u_{1}(\alpha _{1}\xi ) u_{2}(\alpha _{2} \xi )\,\mathrm{d}\xi \), then
Proof
Let \(y(t)=\int _{0}^{lt}u_{1}(\alpha _{1}\xi ) u_{2}(\alpha _{2}\xi ) \,\mathrm{d}\xi \). From Theorem 4.6 we have
where \(\bar{t}=\beta t\) and from Theorem 4.5 we have
where \(\hat{t}=l\alpha _{1} t\) and \(\tilde{t}=l\alpha _{2} t\), then
therefore
□
Theorem 4.8
If \(w(t)=\int _{0}^{lt} \frac{d^{m}}{dt^{m}} u(\alpha _{1}\xi ) \frac{d^{n}}{dt^{n}} v(\alpha _{2}\xi )\,\mathrm{d}\xi \), then for \(k\geq 1 \)
Proof
where \(\hat{t}=l\alpha _{1} t\) and \(\tilde{t}=l\alpha _{2} t\), then
□
Theorem 4.9
If \(w(t)=\frac{d^{\lambda }}{dt^{\lambda }} v(\beta t)\int _{0}^{lt} \frac{d^{m}}{dt^{m}} u_{1}(\alpha _{1}\xi ) \frac{d^{n}}{dt^{n}} u_{2}( \alpha _{2}\xi )\,\mathrm{d}\xi \), then for \(k\geq 1 \)
Proof
Let \(y(t)=\int _{0}^{lt} \frac{d^{m}}{dt^{m}}u_{1}(\alpha _{1}\xi ) \frac{d^{n}}{dt^{n}} u_{2}(\alpha _{2}\xi )\,\mathrm{d}\xi \). From Theorem 4.8 we have
where \(\bar{t}=\beta t\) and from Theorem 4.5 we have
where \(\hat{t}=l\alpha _{1} t\) and \(\tilde{t}=l\alpha _{2} t\), then
therefore
□
5 Applications
The principal aim of this section is to apply the modified differential transform method to a class of linear and nonlinear pantograph type of DEs and VIDEs with proportional delays. We present the following examples to illustrate the accuracy of the presented method and compare the new method with the previous result.
Example 5.1
As the first example, we consider the following linear pantograph equation:
subject to the initial condition
By using Table 1 and Theorem 4.1, Eq. (5.1) transforms to the following recurrence relations:
and from the initial condition (5.2), we write
Substituting Eq. (5.4) in Eq. (5.3) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.1), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.9) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.10) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.11), we arrive at the improved solution that corresponds to the exact solution \(u(t)=e^{-t} \).
Example 5.2
As the second example, we consider the following linear pantograph equation:
subject to the initial conditions
By using Table 1, Theorems 4.1 and 4.2, Eq. (5.12) transforms to the following recurrence relations:
and from the initial conditions (5.13), we write
Consequently, we find
Therefore, from (3.2) we have
To improve Eq. (5.12), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.20) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.21) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.22), we arrive at an improved solution that corresponds to the exact solution \(u(t)=e^{-t} \cos (t) \).
Example 5.3
As the third example, we consider the following nonlinear pantograph equation:
subject to the initial conditions
First, we rewrite the equation as follows:
By using Table 1 and Theorem 4.2, Eq. (5.15) transforms to the following recurrence relations:
and from the initial conditions (5.24), we write
Substituting Eq. (5.27) in Eq. (5.26) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.23), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.32) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.33) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.34), we arrive at an improved solution that corresponds to the exact solution \(u(t)=te^{-t} \).
Example 5.4
As the fourth example, we consider the following nonlinear pantograph equation:
subject to the initial conditions
By using Table 1, Theorems 4.3 and 4.4, Eq. (5.35) transforms to the following recurrence relations:
and from the initial conditions (5.36), we write
Substituting Eq. (5.38) in Eq. (5.37) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.35), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 6 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.43) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.44) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.45), we arrive at an improved solution that corresponds to the exact solution \(u(t)=e^{t}-e^{-t} \).
Example 5.5
As the fifth example, we consider the following linear VIDEs with proportional delay:
subject to the initial conditions
By using Table 1, Theorems 4.1, 4.5 and 4.6, Eq. (5.46) transforms to the following recurrence relations:
and from the initial conditions (5.47), we write
Substituting Eq. (5.49) in Eq. (5.48) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.46), we implement the (LPDTM) for the fourth-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.54) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.55) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.56), we arrive at an improved solution that corresponds to the exact solution \(u(t)=\sin (t) \).
Example 5.6
As the sixth example, we consider the following nonlinear VIDEs with proportional delay:
subject to the initial condition
By using Table 1 and Theorems 4.1, 4.2 and 4.7, Eq. (5.57) transforms to the following recurrence relations:
and from the initial condition (5.58), we write
Substituting Eq. (5.60) in Eq. (5.59) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.57), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.65) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.66) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.67), we arrive at an improved solution that corresponds to the exact solution \(u(t)=e^{t} \).
Example 5.7
Lastly, we consider the following nonlinear VIDEs with proportional delay:
subject to the initial condition
By using Table 1, Theorems 4.2, 4.3, 4.8 and 4.9 Eq. (5.68) transforms to the following recurrence relations:
and from the initial conditions (5.69), we write
Substituting Eq. (5.71) in Eq. (5.70) recursively we derive the following results:
Therefore, from (3.2) we have
To improve Eq. (5.68), we implement the (LPDTM) for the third-order approximation solution
Applying the Laplace transformation with respect to t for \(u(t) \) yields
Let \(s=\frac{1}{t} \), we have
For \(m\geq 1 \), \(n\geq 1 \), and \(m+n\leq 4 \), all of the \([\frac{m}{n} ](t) \)-Padé approximants of Eq. (5.76) yield
In this step, by writing \(\frac{1}{s} \) instead of t in Eq. (5.77) we obtain
Finally, using the inverse Laplace transform on the Padé approximants (5.78), we arrive at an improved solution that corresponds to the exact solution \(u(t)=e^{-t} \).
Comparing our result with the solutions obtained in [13, 14, 17, 58, 59], we can see that the results are the same.
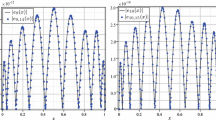
Results for Examples 5.1–5.7 are reported in Figs. 1–7 and Tables 2–8, respectively. In these tables, the terms \(u_{E}\), \(u_{n,R}\) and \(e(u)\) stand for exact solution, nth order approximate solution of DTM and their absolute error, respectively.
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.1
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.2
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.3
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.4
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.5
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.6
Comparison of the exact solution (blue) and the approximate solutions (red) of Example 5.7
6 Conclusion
Most pantograph equations with proportional delays are usually difficult to solve analytically. In many cases, it is required to obtain approximate solutions. In this work, for this purpose, the modified differential transform method, a combined form of the differential transform method with Laplace transforms, and the Padé approximant (LPDTM) is effectively used to find the exact solution of linear and nonlinear pantograph type of differential and Volterra integro-differential equations (DEs and VIDEs) with proportional delays. In fact, the main advantage of this method is its capability of combining the two strongest methods for finding a fast convergent series solution of pantograph equations. Furthermore, as seen from the examples, the results indicate the reliability and efficiency of the method and show that it needs less effort to achieve the results, and is a promising and powerful method over other methods for solving many linear and nonlinear pantograph type of DEs and VIDEs with proportional delays arising in mathematical physics. The method can be extended easily with some modifications to the fractional delay differential equations. It is our aim for future work.
Availability of data and materials
Not applicable.
References
Farah, N., Seadawy, A.R., Ahmad, S., et al.: Interaction properties of soliton molecules and Painleve analysis for nano bioelectronics transmission model. Opt. Quantum Electron. 52, 329 (2020)
Ali, S., Younis, M.: Rogue wave solutions and modulation instability with variable coefficient and harmonic potential. Front. Phys. 7, 255 (2020)
Younis, M.: Optical solitons in \((n+1)\) dimensions with Kerr and power law nonlinearities. Mod. Phys. Lett. B 31(15), 1750186 (2017)
Arif, A., Younis, M., Imran, M., et al.: Solitons and lump wave solutions to the graphene thermophoretic motion system with a variable heat transmission. Eur. Phys. J. Plus 134, 303 (2019)
Sardar, A., Husnine, S.M., Rizvi, S.T.R., Younis, M., Ali, K.: Multiple travelling wave solutions for electrical transmission line model. Nonlinear Dyn. 82(3), 1317–1324 (2015)
Rizvia, S.T.R., Younis, M., Baleanu, D., Iqbal, H.: Lump and rogue wave solutions for the Broer–Kaup–Kupershmidt system. Chin. J. Phys. 68, 19–27 (2020)
Younis, M., Yousaf, U., Ahmed, N., Rizvi, S.T.R., Iqbal, M.S., Baleanu, D.: Investigation of electromagnetic wave structures for a coupled model in antiferromagnetic spin-ladder medium. Front. Phys. (2020). https://doi.org/10.3389/fphy.2020.00372
Ockendon, J.R., Tayler, A.B.: The dynamics of a current collection system for an electric locomotive. Proc. R. Soc. A 322(1551), 447–468 (1971)
Sedaghat, S., Ordokhani, Y., Dehghan, M.: Numerical solution of the delay differential equations of pantograph type via Chebyshev polynomials. Commun. Nonlinear Sci. Numer. Simul. 17, 4815–4830 (2012)
Yu, Z.H.: Variational iteration method for solving the multi-pantograph delay equation. Phys. Lett. A 372(43), 6475–6479 (2008)
Feng, X.: An analytic study on the multi-pantograph delay equations with variable coefficients. Bull. Math. Soc. Sci. Math. Roum. 56(104), 205–215 (2013)
Ahmed, I., Kumam, P., Abubakar, J., Borisut, P., Sitthithakerngkiet, K.: Solutions for impulsive fractional pantograph differential equation via generalized anti-periodic boundary condition. Adv. Differ. Equ. 2020, 477 (2020)
Hou, C.C., Simos, T.E., Famelis, I.-T.: Neural network solution of pantograph type differential equations. Math. Methods Appl. Sci. 43(6), 3369–3374 (2020)
Trif, D.: Direct operatorial tau method for pantograph-type equations. Appl. Math. Comput. 219, 2194–2203 (2012)
Sezer, M., Yalçinbaş, S., Gülsu, M.: A Taylor polynomial approach for solving generalized pantograph equations with nonhomogeneous term. Int. J. Comput. Math. 85(7), 1055–1063 (2008)
Cakir, M., Arslan, D.: The Adomian decomposition method and the differential transform method for numerical solution of multi-pantograph delay differential equations. Appl. Math. 6, 1332–1343 (2015)
Ezz-Eldien, S.S., Doha, E.H.: Fast and precise spectral method for solving pantograph type Volterra integro-differential equations. Numer. Algorithms 81, 57–77 (2019)
Yuzbasi, S., Karacayir, M.: A numerical approach for solving high-order linear delay Volterra integro-differential equations. Int. J. Comput. Methods 15(3), Article ID 1850042 (2018)
Rebenda, J., Šmarda, Z.: A differential transformation approach for solving functional differential equations with multiple delays. Commun. Nonlinear Sci. Numer. Simul. 48, 246–257 (2017)
Rameh, R.B., Cherry, E.M., Weber dos Santos, R.: Single-variable delay-differential equation approximations of the Fitzhugh–Nagumo and Hodgkin–Huxley models. Commun. Nonlinear Sci. Numer. Simul. 82, Article ID 105066 (2020)
Chena, X., Wang, L.: The variational iteration method for solving a neutral functional-differential equation with proportional delays. Comput. Math. Appl. 59, 2696–2702 (2010)
Zhou, J.K.: Differential Transformation and Its Application for Electrical Circuits. Huazhong University Press, Wuhan (1986)
Chen, C.K., Ho, S.H.: Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 106(2–3), 171–179 (1999)
Ayaz, F.: Solutions of the system of differential equations by differential transform method. Appl. Math. Comput. 147(2), 547–567 (2004)
Arikoglu, A., Ozkol, I.: Solution of boundary value problems for integro-differential equations by using differential transform method. Appl. Math. Comput. 168(2), 1145–1158 (2005)
Arikoglu, A., Ozkol, I.: Solution of fractional differential equations by using differential transform method. Chaos Solitons Fractals 34(5), 1473–1481 (2007)
Odibat, Z., Momani, S.: A generalized differential transform method for linear partial differential equations of fractional order. Appl. Math. Lett. 21, 194–199 (2008)
Momani, S.M., Erturk, V.S.: Solutions of nonlinear oscillators by the modified differential transform method. Comput. Math. Appl. 55, 833–842 (2008)
Chang, S.-H., Chang, I.L.: A new algorithm for calculating one-dimensional differential transform of nonlinear functions. Appl. Math. Comput. 195, 799–808 (2008)
Keskin, Y., Oturanc, G.: Reduced differential transform method for partial differential equations. Int. J. Nonlinear Sci. Numer. Simul. 10(6), 741–749 (2009)
Keskin, Y.: Ph.D. Thesis, Selcuk University, in Turkish (2010)
Keskin, Y., Oturanc, G.: The reduced differential transform method: a new approach to fractional partial differential equations. Nonlinear Sci. Lett. A 1(2), 207–217 (2010)
Keskin, Y., Oturanc, G.: The reduced differential transformation method for solving linear and nonlinear wave equations. Iran. J. Sci. Technol. 34(2), 113–122 (2010)
Ayaz, F.: Applications of differential transform method to differential-algebraic equations. Appl. Math. Comput. 152(3), 649–657 (2004)
Benhammouda, B., Vazquez-Leal, H.: Analytical solution of a nonlinear index-three DAEs system modelling a slider-crank mechanism. Discrete Dyn. Nat. Soc. 2015, Article ID 206473 (2015)
Benhammouda, B.: Solution of nonlinear higher-index Hessenberg DAEs by Adomian polynomials and differential transform method. SpringerPlus 4, Article ID 648 (2015)
Celik, E., Tabatabaei, K.: Solving a class of Volterra integral equation systems by the differential transform method. Int. J. Nonlinear Sci. 16(1), 87–91 (2013)
Odibat, Z.: Differential transform method for solving Volterra integral equation with separable kernels. Math. Comput. Model. 48, 1144–1149 (2008)
Moosavi Noori, S.R., Taghizadeh, N.: Application of reduced differential transform method for solving two-dimensional Volterra integral equations of the second kind. Appl. Appl. Math. 14(2), 1003–1019 (2019)
Moosavi Noori, S.R., Taghizadeh, N.: Study on solving two-dimensional linear and nonlinear Volterra partial integro-differential equations by reduced differential transform method. Appl. Appl. Math. 15(1), 394–407 (2020)
Arikoglu, A., Ozkol, I.: Solutions of integral and integro-differential equation systems by using differential transform method. Comput. Math. Appl. 56, 2411–2417 (2008)
Tari, A., Shahmorad, S.: Differential transform method for the system of two-dimensional nonlinear Volterra integro-differential equations. Comput. Math. Appl. 61, 2621–2629 (2011)
Moghadam, M.M., Saeedi, H.: Application of differential transform for solving the Volterra integro-partial equations. Iran. J. Sci. Technol. 34(1), 59–70 (2010)
Eslami, M., Taleghani, S.A.: Differential transform method for conformable fractional partial differential equations. Iran. J. Numer. Anal. Optim. 9(2), 17–29 (2019)
Secer, A., Akinlar, M.A., Cevikel, A.: Efficient solutions of systems of fractional PDEs by the differential transform method. Adv. Differ. Equ. 2012, 188 (2012)
Deepanjan, D.: The generalized differential transform method for solution of a free vibration linear differential equation with fractional derivative damping. J. Appl. Math. Comput. Mech. 18(2), 19–29 (2019)
Acan, O., Al Qurashi, M.M., Baleanu, D.: Reduced differential transform method for solving time and space local fractional partial differential equations. J. Nonlinear Sci. Appl. 10(10), 5230–5238 (2017)
Durur, H., Ilhan, E., Bulut, H.: Novel complex wave solutions of the \((2+ 1)\)-dimensional hyperbolic nonlinear Schrödinger equation. Fractal Fract. 4(3), 41 (2020)
Gao, W., Senel, M., Yel, G., Baskonus, H.M., Senel, B.: New complex wave patterns to the electrical transmission line model arising in network system. AIMS Math. 5(3), 1881–1892 (2020)
Hajipour, M., Jajarmi, A., Baleanu, D.: On the accurate discretization of a highly nonlinear boundary value problem. Numer. Algorithms 79(3), 679–695 (2018)
Al-Refai, M.: Maximum principles for nonlinear fractional differential equations in reliable space. Prog. Fract. Differ. Appl. 6(2), 95–99 (2020)
Singh, J., Kumar, D., Hammouch, Z., Atangana, A.: A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 316, 504–515 (2018)
Gao, W., Veeresha, P., Prakasha, D.G., Senel, B., Baskonus, H.M.: Iterative method applied to the fractional nonlinear systems arising in thermoelasticity with Mittag-Leffler kernel. Fractals (2020). https://doi.org/10.1142/S0218348X2040040X
Yel, G., Baskonus, H.M., Gao, W.: New dark–bright soliton in the shallow water wave model. AIMS Math. 5(4), 4027–4044 (2020)
García Guirao, J.L., Baskonus, H.M., Kumar, A.: Regarding new wave patterns of the newly extended nonlinear \((2 + 1)\)-dimensional Boussinesq equation with fourth order. Mathematics 8(3), 341 (2020)
Baker, G.A.: Essentials of Padé Approximants. Academic Press, San Diego (1975)
Benhammouda, B., Vazquez-Leal, H., Sarmiento-Reyes, A.: Modified reduced differential transform method for partial differential algebraic equations. J. Appl. Math. 2014, Article ID 279481 (2014)
Bahsi, M.M., Çevik, M.: Numerical solution of pantograph-type delay differential equations using perturbation-iteration algorithms. J. Appl. Math. 2015, Article ID 139821 (2015)
Yuzbasi, S.: Laguerre approach for solving pantograph-type Volterra integro-differential equations. Appl. Math. Comput. 232, 1183–1199 (2014)
Acknowledgements
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
The authors declare that the study was realized in collaboration with equal responsibility. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Abbreviations
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Moosavi Noori, S.R., Taghizadeh, N. Modified differential transform method for solving linear and nonlinear pantograph type of differential and Volterra integro-differential equations with proportional delays. Adv Differ Equ 2020, 649 (2020). https://doi.org/10.1186/s13662-020-03107-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03107-9