Abstract
In this paper, we investigate the external stability and \(H_{\infty }\) control of switching systems with time-varying delay and impulse. First of all, a modified two-direction inequality (relation) between the switching numbers and the maximum, minimum dwell time is proposed. This new inequality is applied to proving the external stability of switching systems with delay and impulse consisting of subsystems with Hurwitz stable matrices of internal dynamics. By using this new inequality, a normal \(L_{2}\) norm constraint is derived rather than weighted \(L_{2}\) norm constraint. In addition, by a realizable switching law, the obtained result is extended to the switching systems comprised of subsystems with both Hurwitz stable and unstable matrices of internal dynamics. The results are finally applied to \(H_{\infty }\) control and illustrated by a numerical example.
Similar content being viewed by others
1 Introduction
External stability (ES) is defined as a property of control systems: every \(L_{2}\) input generates an \(L_{2}\) zero-state output [1–4], which plays an essential role in system analysis. As one type of systems, switching systems(SSs), consisting of a family of subsystems, and a switching rule that orchestrates the switching between them [5–8], have been an important framework in the area of input–output analysis. In practice, effects of time delay [9, 10] and impulse [11, 12] are usually inevitable. Therefore, there are lots of results on system and input–output analysis of delayed SSs [11–21]. For example of a discrete-time framework, the problem of robust exponential \(H_{\infty }\) filtering for switched fuzzy delayed systems was investigated in [15]; for example of a continuous-time framework, in [11], fault-tolerant synchronization for SSs with delay and impulse was considered.
In the field of ES, \(H_{\infty }\) control, \(H_{\infty }\) model reduction, \(L_{2}\)-gain analysis and disturbance attenuation for the SSs, how to obtain the \(L_{2}\) norm bound constraint is a critical part of our study. Owing to the essence of SSs and average dwell time(DT) scheme, the concept of weighted \(L_{2}\) norm bound constraint, instead of the normal \(L_{2}\) norm bound constraint, has been proposed [16, 17, 22]. However, this weighted concept changes the original physical meaning of \(L_{2}\). Recently, some researchers tried to remove this label “weighted”, see [18] in 2012, [23] in 2016 and [19] in 2017. However, there are still some doubtful problems. Specifically, Liu and Yuan adopted a normal \(L_{2}\) relation between input and output in [18] but where the average DT could not be substituted into the integral in (36); In [23], Eq. (21) could not be directly derived because \(\Psi (s)\) could not be guaranteed greater than zero; Syed Ali et al. employed the square of \(L_{2}\) norm, see (6) in [19], but it is questionable for the cancelation of \(e^{\alpha (T-s)}\) on both sides of the inequality right below (57). Very recently, a two-direction inequality (\(\frac{t-\tau }{T_{\mathrm{max}}}\leq N_{\sigma }(t,\tau )\leq \frac{t-\tau }{T_{\mathrm{min}}}\)) between the switching numbers and the maximum, minimum DT was proposed in [11] such that the label “weighted” can be removed properly. Furthermore, an improved two-direction inequality (\(\frac{t-\tau }{T_{\mathrm{max}}}-1\leq N_{\sigma }(t,\tau )\leq \frac{t-\tau }{T_{\mathrm{min}}}+1\)) was provided in [24, 25]. But this improved inequality is still not precise enough. A more accurate two-direction inequality (\(\max \{\frac{t-\tau }{T_{\mathrm{max}}}-1,0\}\leq N_{\sigma }(t,\tau )\leq \frac{t-\tau }{T_{\mathrm{min}}}+1\)) was given in [21]. To the best of our knowledge, this more accurate two-direction inequality has not been used to study the ES and \(H_{\infty }\) control of SSs with delay and impulse.
In order to study the ES of SSs comprised of subsystems with both Hurwitz stable and unstable matrices, a suitable switching law is necessary. There are a few results that have been reported in [22, 25–29]. Some state-dependent switching laws were proposed in [27, 28], while some time-dependent switching laws were presented [22, 25, 26, 29]. The authors of [29] applied fast switching and slow switching, respectively, to unstable and stable subsystems. In [26], the precondition \(\inf_{t\geq t_{0}}[\frac{T^{-1}(t)}{T^{+}(t)}]\geq - \frac{\beta }{\alpha }\) was given to guarantee that \(-\gamma t=T^{-1}(t)\alpha +T^{+}(t)\beta <0\) holds. But this precondition cannot make sure that \(-\gamma t=T^{-1}(t)\alpha +T^{+}(t)\beta \) holds or that \(T^{-1}(t)\alpha +T^{+}(t)\beta \) is a linear function as desired. Only \(T^{-1}(t)\alpha +T^{+}(t)\beta <0\) can be deduced there. Another resolution was proposed in [22], a new separation of switching instants was arranged in advance. By a given parameter \(c_{*}>0\) without a specified sequence of time instants, the switching law in [25] is easier and clearer to implement than the one in [22]. This makes it worth to study how to adopt the switching law in [25] to investigate the ES and \(H_{\infty }\) control of SSs with delay and impulse.
Motivated by the above discussion, the problem of ES and \(H_{\infty }\) control of SSs with delay and impulse is investigated in this paper. The main contribution of the paper is as follows. First, a two-direction inequality (relation) between the switching numbers and the maximum, minimum DT is used such that the label “weighted” can be removed properly and the normal \(L_{2}\) norm constraint is derived. Second, a suitable switching law is adopted to deal with the SSs with both Hurwitz stable and unstable subsystems. Third, we take the overlooked case \(0<\mu <1\) into consideration (in almost all mentioned results above the range of μ is only larger or equal to 1), i.e. the range of switching parameters μ is extended to the set of all positive real numbers. Fourth, the non-weighted \(H_{\infty }\) control [30–32] of switching control systems with delay and impulse is established, in which the matrices of internal dynamics of the controlled system are not necessarily all Hurwitz as usual. Finally, the effectiveness of the results is illustrated by a numerical example.
2 Problem statement and preliminaries
Let \(\mathbb{R}^{n}\) denote the n-dimensional real Euclidean space. For \(x\in \mathbb{R}^{n}\), \(\|x\|\) denotes the Euclidean norm of x. We use the notation \(L_{2}([0,\infty ),\mathbb{R}^{n})\) to denote the class of square integrable functions from \([0,\infty )\) to \(\mathbb{R}^{n}\), i.e. for each \(x\in L_{2}([0,\infty ),\mathbb{R}^{n})\), the \(L_{2}\) norm of x is \(\|x\|_{L_{2}}=(\int _{0}^{\infty }\|x(t)\|^{2}\,\mathrm{d}t)^{\frac{1}{2}}< \infty \). Define \(x_{t}(s)=x(t+s)\), \(-d\leq s\leq 0\), and \(\|x_{t}\|_{d}=\sup_{-d\leq s\leq 0}\|x(t+s)\|\). The notation \(P>0\) indicates that matrix P is positive definite. \(\lambda _{\mathrm{max}}(P)\) (\(\lambda _{\mathrm{min}}(P)\)) denotes the maximum (minimum) eigenvalue of matrix P. \(\alpha _{-}\) means such a positive number that the inequality \(A_{i}^{T}P_{i}+P_{i}A_{i}+\alpha _{-}P_{i}<0\) holds where \(A_{i}\) is Hurwitz stable, while \(\alpha _{+}\) means such a positive number that \(A_{i}^{T}P_{i}+P_{i}A_{i}-\alpha _{+}P_{i}<0\) holds where \(A_{i}\) is not Hurwitz stable.
Consider the following switching control system with delay and impulse:
where \(x(t)\in \mathbb{R}^{n}\), \(u(t)\in \mathbb{R}^{m}\) and \(y(t)\in \mathbb{R}^{p}\) represent the state vector, external input vector and output vector, respectively. \(A_{\sigma (t)}\), \(A_{d\sigma (t)}\), \(B_{\sigma (t)}\), \(C_{\sigma (t)}\), \(C_{d\sigma (t)}\), \(E_{\sigma (t)}\) and \(I_{\sigma (t)}\) are constant matrices with appropriate dimensions, where \(\sigma (t)\) is the switching signal, which takes values from \(\mathscr{P}=\{1,2,\ldots \}\) and \(\sigma (t)=i\in \mathscr{P}\) means the subsystem i is active at t. The switching time instants \(t_{k}\) (\(k=1,2,\ldots \)) satisfy \(0\leq t_{0}< t_{1}< t_{2}<\cdots <t_{k}<\cdots \) , \(\lim_{k\to \infty }t_{k}= \infty \). The initial function \(\phi (\theta )\) is piecewise continuous on \([-d,0]\). The delay function \(\tau (t)\) is differentiable and satisfies \(0\leq \tau (t)\leq d\), \(\dot{\tau }(t)\leq \rho <1\).
Remark 2.1
Here ẋ is considered as the right derivative of x based on two considerations. On the one hand, the derivative at \(t_{0}\) is taken to be a right derivative, since \(\phi (\theta )\) may not admit a left derivative at \(t_{0}\) or this left derivative even exists but may not equal the right hand function. To be consistent with the derivative at \(t_{0}\), \(\dot{x}(t_{k})\) needs to be the notation of the right derivative at \(t_{k}\). On the other hand, at \(t_{k}\), the subsystem \(\sigma (t_{k})=\sigma (t_{k}^{+})\) is already active, i.e. \(\dot{x}(t)=A_{\sigma (t_{k}^{+})}x(t)+A_{d\sigma (t_{k}^{+})}x(t- \tau (t))+B_{\sigma (t_{k}^{+})}u(t)\). It follows that \(\dot{x}(t_{k})\) also denotes the right derivative at \(t_{k}\).
Remark 2.2
The solution \(x(t)\) is right continuous at \(t_{k}\), i.e. \(x(t_{k}^{+})=x(t_{k})\), since \(\dot{x}(t_{k})\) represents the right derivative at \(t_{k}\) and the right derivative is defined based on right continuity.
Definition 2.1
([1])
The \(L_{2}\) gain of an externally stable system is
(Here θ indicates the zero function.) The \(L_{2}\) gain is the maximum ratio of \(\|y\|_{L_{2}}/\|u\|_{L_{2}}\).
Lemma 2.1
([21])
For any \(t\geq \tau \geq t_{0}\), \(N_{\sigma }(t,\tau )\) denote the number of discontinuities of region over \((\tau ,t)\), i.e., the number of region switching over \((\tau ,t)\),
where \(T_{\mathrm{max}}={\sup_{k=1,2,\ldots}}(t_{k}-t_{k-1})\), \(T_{\mathrm{min}}={\inf_{k=1,2,\ldots}}(t_{k}-t_{k-1})\) are the maximum and minimum DT of system (1).
3 Main results
At the beginning of this section, the ES of SSs with delay and impulse consisting of subsystems with Hurwitz \(A_{i}'s\) is proved. Then the obtained result is extended to the ES of SSs, in which not all subsystems are Hurwitz stable, by employing a switching law. In obtained results, the normal \(L_{2}\) norm constraint, rather than a weighted \(L_{2}\) norm constraint, is derived by using the new proposed relation (2). Finally, the derived results of ES is applied to \(H_{\infty }\) control.
3.1 External stability
In this subsection, by using Eq. (2), the ES of SSs with delay and impulse consisting of subsystems that are all Hurwitz stable, and subsystems that are not all Hurwitz stable, is proved, respectively.
3.1.1 All subsystems are Hurwitz stable
Theorem 3.1
Given scalars \(\alpha >0\), \(\mu >0\) and the numbers of any two consecutive subsystems \(i, j\in \mathscr{P}\) (σ switches from j to i), the system (1) is externally stable with a \(L_{2}\) gain γ, if there exist \(n\times n\) positive definite matrices \(P_{i}\), \(Q_{i}\), \(P_{j}\), \(Q_{j}\) such that
and
where \(\digamma _{\mu }=\frac{\gamma }{\mu } \sqrt{ \frac{\alpha -\ln \mu /T_{\mathrm{min}}}{\alpha -\ln \mu /T_{\mathrm{max}}}}\) if \(\mu >1\); \(\digamma _{\mu }=\gamma \) if \(\mu =1\); \(\digamma _{\mu }=\gamma \mu \sqrt{ \frac{\alpha -\ln \mu /T_{\mathrm{max}}}{\alpha -\ln \mu /T_{\mathrm{min}}}}\) if \(0<\mu <1\).
Proof
Consider the following Lyapunov functional candidate:
where \(V_{1\sigma (t)}(t,x_{t})=x^{T}(t)P_{\sigma (t)}x(t)\) and \(V_{2\sigma (t)}(t,x_{t})=\int _{t-\tau (t)}^{t}x^{T}(s)\) \(\mathrm{e}^{\alpha (s-t)}Q_{\sigma (t)}\) \(x(s)\,\mathrm{d}s\). For simplicity, we shall use \(V_{\sigma (t)}(t)\) to denote \(V_{\sigma (t)}(t,x_{t})\).
Suppose \(\sigma (t)=i\) for \(t\in [t_{k-1},t_{k})\), then the derivatives of \(V_{1\sigma (t)}(t)\) and \(V_{2\sigma (t)}(t)\) are
and
respectively.
Denote \(\Delta (t)=y^{T}(t)y(t)-\digamma _{\mu }^{2}u^{T}(t)u(t)\). Then we get
where \(\eta (t)=[x^{T}(t),x^{T}(t-\tau (t)),u^{T}(t)]^{T}\) and \((1,1)=A_{i}^{T}P_{i}+P_{i}A_{i}+\alpha P_{i}+Q_{i}+ C_{i}^{T}C_{i}\).
From (3), by using the Schur complement [33], we obtain
Therefore, we can deduce that
Thus, integrating the inequality (9) from \(t_{k-1}\) to t, \(t\in [t_{k-1},t_{k})\), produces
Since σ switches from j to i, \(\sigma (t_{k-1}^{-})=j\) and \(\sigma (t_{k-1}^{+})=\sigma (t_{k-1})=i\). Now we consider the change of \(V_{\sigma (t)}(t)\) at \(t=t_{k-1}\) as follows. Firstly,
Using the Schur complement again, it follows from the first inequality in (4) that \((I+I_{j})^{T}P_{i}(I+I_{j})-\mu p_{j}\leq 0\) such that \(V_{1i}(t_{k-1})=V_{1i}(t_{k-1}^{+})\leq \mu V_{1j}(t_{k-1}^{-})\). Secondly,
The second inequality in (4) and the calculation above together imply that \(V_{2i}(t_{k-1})=V_{2i}(t_{k-1}^{+})\leq \mu V_{2j}(t_{k-1}^{-})\). Thus, one has
Using the technique in (2.7) of [22], it follows from (10) and (11) that
Under the zero initial condition, we acquire
That is,
To obtain the ES, we discuss (14) in three cases, that is, \(\mu >1\), \(\mu =1\) and \(0<\mu <1\). For the case of \(\mu >1\) (\(\ln \mu >0\)). It follows from (2) that \(\frac{\ln \mu }{T_{\mathrm{max}}}(t-s)-\ln \mu \leq N_{\sigma }(t,s)\ln \mu \leq \frac{\ln \mu }{T_{\mathrm{min}}}(t-s)+\ln \mu \). Then inequality (14) can be rearranged as follows:
where \(\alpha -\frac{\ln \mu }{T_{\mathrm{max}}}>0\) and \(\alpha -\frac{\ln \mu }{T_{\mathrm{min}}}>0\) due to (5) and \(\alpha >0\).
Integrating both sides of (15) from \(t=t_{0}\) to ∞ and interchanging the order of integrals lead to
By substituting \(\digamma _{\mu }=\frac{\gamma }{\mu } \sqrt{ \frac{\alpha -\ln \mu /T_{\mathrm{min}}}{\alpha -\ln \mu /T_{\mathrm{max}}}}\) into (17), we obtain
The remaining arguments for the other two cases, \(\mu =1\) and \(0<\mu <1\), are analogous to the above analysis and will not be reproduced here. Consider \(u(s)=0\), for \(s\in [0, t_{0}]\), then we have
which implies that the system (1) is externally stable with a \(L_{2}\) gain γ. □
Remark 3.1
The switching parameter \(0<\mu <1\) was usually overlooked, as mentioned also in [11]. Only \(\mu \geq 1\) was considered in [16–18, 22] and in [19] that was \(\eta \geq 1\). If the sets of those matrices (such as \(P_{i}\), \(Q_{i}\) in this work) were finite, as assumed in [16–19, 22], it would be not easy to consider this overlooked case. However, in [11, 25] and this work, the switching index set, see \(\mathscr{P}\) below (1), is not restricted to be finite such that the just mentioned sets of matrices can be infinite. Moreover, in conditions like \(Q_{i}\leq \mu Q_{j}\), i and j are only any two consecutive (j is just after i) rather than two arbitrary indices as in [16–19, 22]. These together make the case \(0<\mu <1\) feasible, i.e. the range of μ can be all positive real numbers.
Remark 3.2
It follows from (12) and Theorem 3.1, the zero-input state \(\|x(t)\|\) ≤ \(K_{\mu }\) \(\|x_{t_{0}}\|_{d}\) \(e^{-\alpha _{\mu }(t-t_{0})}\), where \(K_{\mu }=\sqrt{ \frac{\mu [\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})]}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\alpha _{\mu }=\frac{1}{2}(\alpha -\frac{\ln \mu }{T_{\mathrm{min}}})\) if μ > 1; \(K_{\mu }= \sqrt{ \frac{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\alpha _{\mu }=\frac{1}{2}\alpha \) if \(\mu =1\); \(K_{\mu }=\sqrt{ \frac{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})}{\mu \inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\alpha _{\mu }= \frac{1}{2}(\alpha -\frac{\ln \mu }{T_{\mathrm{max}}})\) if \(0<\mu <1\).
3.1.2 Not all subsystems are Hurwitz stable
In the following, we consider to investigate the ES of SSs consisting of subsystems that are not all Hurwitz stable.
For a subsystem \(A_{i}\) (Hurwitz stable), similar to (6)–(10), \(A_{di}\), \(B_{i}\), \(C_{i}\), \(D_{i}\) on \([t_{k-1},t_{k})\), replacing α with \(\alpha _{-}\) under the condition (3), then, for \(t\in [t_{k-1},t_{k})\), we can derive that
For a subsystem \(A_{i}\) (not Hurwitz), there always exist \(P_{i}>0\) and \(\alpha _{+}>0\) (as long as \(\alpha _{+}\) is large enough), such that \(A_{i}^{T}P_{i}+P_{i}A_{i}-\alpha _{+}P_{i}<0\). If the condition
holds, we can deduce that
then
Therefore, the following inequality holds:
Under the inequality in (4), using the same arguments as in (12), (13) and (14), from \(t_{0}\) to t, \(t\in [t_{k-1},t_{k})\), we can get
And then
where \(T_{+}(t,\tau )\), \(T_{-}(t,\tau )\) denote the total active time of those subsystems with Hurwitz \(A_{i}'s\), not Hurwitz \(A_{i}'s\) over \((\tau ,t)\), respectively.
Taking the case \(\mu >1\) as an example, the exponential index on the left side of (26): \(\alpha _{+} T_{+}(t,s)-\alpha _{-} T_{-}(t,s)+N_{\sigma }(t,s)\ln \mu \) may be reduced to be \(-(\alpha _{-}-\frac{\ln \mu }{T_{\mathrm{max}}})(t-s)\), while the same index on the right side of (26) may not be immediately increased to be in the form: \(-\lambda (t-s)\), \(\lambda >0\). Now, we choose a scalar \(\alpha _{*}\in (0,\alpha _{-})\) arbitrarily and propose the following switching law.
Switching Law 3.1
([25])
Given a sequence of time instants \(t_{1}< t_{2}<\cdots <t_{k}<\cdots \) , \(\lim_{k\rightarrow \infty }t_{k}=\infty \), where \(t_{k}\), \(k=1,2,\ldots \) , is the switching instant and \(t_{1}>t_{0}\), such that, for given scalars \(\alpha _{+}>0\), \(\alpha _{-}>0\), \(0<\alpha _{*}<\alpha _{-}\) and \(c_{*}>0\), the inequality \(\alpha _{+}T_{+}(t,\tau )-\alpha _{-}T_{-}(t,\tau )\leq c_{*}- \alpha _{*}(t-\tau )\) holds, for any \(t\geq \tau \geq t_{0}\).
Theorem 3.2
Given scalars \(\alpha >0\), \(0<\alpha _{-}<\alpha \), \(\alpha _{+}>0\), \(c_{*}>0\), \(\mu >0\) and the numbers of any two consecutive subsystems i, \(j\in \mathscr{P}\) (σ switches from j to i), the system (1), under Switching Law 3.1, is externally stable with a \(L_{2}\) gain γ, if there exist real \(n\times n\) positive definite matrices \(P_{i}\), \(Q_{i}\), \(P_{j}\), \(Q_{j}\) such that, for each subsystem (\(A_{i}\) is Hurwitz),
for each subsystem (\(A_{i}\) is not Hurwitz),
and
where \(\digamma _{\mu }=\frac{\gamma }{\mu } \sqrt{ \frac{\alpha _{*}-\ln \mu /T_{\mathrm{min}}}{e^{c_{*}}(\alpha _{-}-\ln \mu /T_{\mathrm{max}})}}\) if \(\mu >1\); \(\digamma _{\mu }=\gamma \sqrt{ \frac{\alpha _{*}}{e^{c_{*}}\alpha _{-}}}\) if \(\mu =1\); \(\digamma _{\mu }={\gamma }{\mu } \sqrt{ \frac{\alpha _{*}-\ln \mu /T_{\mathrm{max}}}{e^{c_{*}}(\alpha _{-}-\ln \mu /T_{\mathrm{min}})}}\) if \(0<\mu <1\).
Proof
Under Switching Law 3.1, one has
To obtain the ES, we also investigate (26) in three cases, that is \(\mu >1\), \(\mu =1\) and \(0<\mu <1\). For the case of \(\mu >1\). It follows from (2) that \(\frac{\ln \mu }{T_{\mathrm{max}}}(t-s)-\ln \mu \leq N_{\sigma }(t,s)\ln \mu \leq \frac{\ln \mu }{T_{\mathrm{min}}}(t-s)+\ln \mu \). From (26), we obtain
Then
Using \(\alpha _{*}>\frac{\ln \mu }{T_{\mathrm{min}}}\) (then \(\alpha _{*}-\frac{\ln \mu }{T_{\mathrm{min}}}>0\) and \(\alpha _{-}-\frac{\ln \mu }{T_{\mathrm{max}}}>0\) due to \(\alpha _{*}<\alpha _{-}\)) and selecting \(\digamma _{\mu }=\frac{\gamma }{\mu } \sqrt{ \frac{\alpha _{*}-\ln \mu /T_{\mathrm{min}}}{e^{c_{*}}(\alpha _{-}-\ln \mu /T_{\mathrm{max}})}}\), then following a similar process to (16) to (19), we can conclude that the control system (1), under Switching Law 3.1 is externally stable with a \(L_{2}\) gain γ. □
Remark 3.3
It follows from (25), Switching Law 3.1 and Theorem 3.2 that the state \(\|x(t)\|\) ≤ \(\hat{K}_{\mu }\|x_{t_{0}}\|_{d}\) \(e^{-\hat{\alpha }_{\mu }(t-t_{0})}\), where \(\hat{K}_{\mu }=e^{\frac{c_{*}}{2}}\sqrt{ \frac{\mu [\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}}(Q_{\sigma (t_{0})})]}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\hat{\alpha }_{\mu }=\frac{1}{2}(\alpha _{*}- \frac{\ln \mu }{T_{\mathrm{min}}})\) if \(\mu >1\); \(\hat{K}_{\mu }= e^{\frac{c_{*}}{2}}\sqrt{ \frac{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}}(Q_{\sigma (t_{0})})}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\hat{\alpha }_{\mu }=\frac{1}{2}\alpha _{*}\) if \(\mu =1\); \(\hat{K}_{\mu }=e^{\frac{c_{*}}{2}}\sqrt{ \frac{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}}(Q_{\sigma (t_{0})})}{\mu \inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\hat{\alpha }_{\mu }= \frac{1}{2}(\alpha _{*}-\frac{\ln \mu }{T_{\mathrm{max}}})\) if \(0<\mu <1\).
In fact, for the case \(0<\mu <1\), without Switching Law 3.1, we also have the following conclusion.
Corollary 3.1
Given scalars \(\alpha >0\), \(0<\alpha _{-}<\alpha \), \(\alpha _{+}>0\), \(0<\mu <1\) and the numbers of any two consecutive subsystems i, \(j\in \mathscr{P}\) (σ switches from j to i), the system (1) is externally stable with a \(L_{2}\) gain γ, if there exist real \(n\times n\) positive definite matrices \(P_{i}\), \(Q_{i}\), \(P_{j}\), \(Q_{j}\) such that, for each subsystem (\(A_{i}\) is Hurwitz),
for each subsystem (\(A_{i}\) is not Hurwitz),
and
where \(\digamma _{\mu }=\gamma \mu \sqrt{ \frac{-\alpha _{+}+|\ln \mu | /T_{\mathrm{max}}}{\alpha _{-}+|\ln \mu |/T_{\mathrm{min}}}}\).
Proof
Taking a similar process to (20) to (26), we have
Since \(\frac{t-s}{T_{\mathrm{max}}}-1\leq N_{\sigma }(t,s)\leq \frac{t-s}{T_{\mathrm{min}}}+1\), \(\frac{-|\ln \mu |}{T_{\mathrm{min}}}(t-s)+\ln \mu \leq N_{\sigma }(t,s)\ln \mu \leq \frac{-|\ln \mu |}{T_{\mathrm{max}}}(t-s)-\ln \mu \). Then
Suppose \(\alpha _{+}<\frac{|\ln \mu |}{T_{\mathrm{max}}}\) and choose \(\digamma _{\mu }=\gamma \mu \sqrt{ \frac{-\alpha _{+}+|\ln \mu | /T_{\mathrm{max}}}{\alpha _{-}+|\ln \mu |/T_{\mathrm{min}}}}\). Then following a similar process to (16) to (19), we can prove that the control system (1), consisting of both subsystems with Hurwitz \(A_{i}'s\) and subsystems with \(A_{i}'s\) that are not Hurwitz, is externally stable with a \(L_{2}\) gain γ. □
Remark 3.4
It follows from (25) and the Corollary 3.1 that, for the case \(0<\mu <1\), we have the zero-input state
Remark 3.5
The Corollary 3.1 does not use Switching Law 3.1, the right side of inequality (38) is enlarged as \(\digamma _{\mu }^{2}\int _{t_{0}}^{t} u^{T}(s)u(s)e^{\alpha _{+}(t-s)+N_{\sigma }(t,s)\ln \mu } \,\mathrm{d}s\) instead of \(\digamma _{\mu }^{2}\int _{t_{0}}^{t} u^{T}(s)u(s) e^{-\alpha _{*}(t-s)+N_{\sigma }(t,s)\ln \mu } \,\mathrm{d}s\). As an additional condition, \(\alpha _{+}<\frac{|\ln \mu |}{T_{\mathrm{max}}}\) is imposed. Therefore, Theorem 3.2 is less conservative.
Remark 3.6
By employing the new proposed two-direction inequality (2), after the steps (15)–(19), (33) and (39), the normal \(L_{2}\) norm constraint instead of the weighted \(L_{2}\) norm constraint is obtained. However, only the weighted \(L_{2}\) norm constraint was derived in [16, 17, 22]. This can be easily seen in the proof steps (2.10)–(2.15) in [22], (33)–(34) in [16] and (49)–(50) in [17]. The “average dwell time” method is adopted in these references, that is, the one-direction inequality \(N_{\sigma }(0,\tau )\leq \frac{\tau }{\tau _{a}}\) is applied.
3.2 Application to \(H_{\infty }\) control
In this section, we apply the derived results of ES to \(H_{\infty }\) control. The so-called \(H_{\infty }\) control is named from the \(H_{\infty }\) functions defined on the \(H_{\infty }\) (Hardy) space (see page 1 in [30]): \(H_{\infty }:=\{F:C\to C|F \text{ is analytic}, \sup_{\operatorname{Re}(s)>0}|F(s)|< \infty \}\) equipped with the norm \(\|F\|_{\infty }:=\sup_{\operatorname{Re}(s)>0}|F(s)|\), for \(F\in H_{\infty }\). As is well known (also see page 4 in [31]), transfer functions for finite dimensional linear control systems are rational functions with real coefficients. Thus, we may consider the subset of \(H_{\infty }\) consisting of real-rational functions: \(RH_{\infty }\subset H_{\infty }\). In fact [31], a transfer function \(F(s)\in RH_{\infty }\) if and only if F is proper (\(\lim_{s\to \infty }F(s)<\infty \)) and stable (F has no poles in the closed right half complex plane). In this case, \(\|F\|_{\infty }=\sup_{\omega \in R}|F(j\omega )|=\sup_{u\in L_{2},u \neq \theta }\|y\|_{L_{2}}/\|u\|_{L_{2}}\), where u, y denote the input, output of the considered control system [1]. Therefore, the transfer function of a linear control system \(F(s)\) is a real-rational \(H_{\infty }\) function implies that the control system is externally stable, i.e. every \(L_{2}\) input only excites an \(L_{2}\) zero-state output. If the input is considered to be a disturbance, then ES measures the robustness of the zero-state output on the disturbance, i.e. it ensures that the zero-state output excited by the energy-bounded (because the square of the \(L_{2}\) norm of a signal can be considered as the energy content of the signal) disturbance will not blow up.
For linear control systems, \(H_{\infty }\) control is to find a control (consisting of measured variables) such that the norm of the transfer function from the disturbance (input) \(u_{d}\) to the output y (something we want to minimize) \(\|F_{d\to y}\|_{\infty }\) is minimized, i.e. the zero-state output excited by disturbance \(y_{d}\) is minimized [32]. For nonlinear control systems including the system considered in this paper, they do not have transfer functions as the linear ones do. However, the same name \(H_{\infty }\) control is employed for the following control objective: to find a control such that the controlled system is asymptotically stable when no disturbances are present, and moreover, has finite \(L_{2}\) gain from \(u_{d}\) to y, under the zero initial condition (is externally stable from \(u_{d}\) to y), see page 6 in [31]. As we see above, for either linear or nonlinear control systems, \(H_{\infty }\) control has the same physical meaning: the \(H_{\infty }\) controller starts to stabilize the system after the energy-bounded disturbance has already decayed to zero, then maintains the stabilized system to be externally stable from the disturbance to the output such that effect of the disturbance on the output is attenuated during the steady period. This specializes the practical importance of \(H_{\infty }\) control in industry roared with noises. However, by the existing average dwell time approach, those results obtained for switched system are only on weak noise attenuation index of weighted form than cannot truly reflect the practical meaning of \(H_{\infty }\) problems [17].
In this section, by adopting maximum, minimum dwell time and the new proposed two-direction inequality (2), we state the details for the non-weighted \(H_{\infty }\) control of switching control systems with delay and impulse. Consider (1) with both control input \(u_{c}\) and disturbance input \(u_{d}\) as follows:
As just discussed, the control (input) \(u_{c}\) is comprised of measured variables. A special (and common) form is \(u_{c}=K_{\sigma (t)}x\) (state feedback), where \(K_{\sigma (t)}\) is the control gain to be designed and x is the state variable that is pre-assumed to be measurable (available). Generally, \(u_{c}\) may be also designed as a function of \(x_{t}\) (delayed state feedback), \(x(t^{-}_{k})\) (impulsive state feedback) and y (output feedback) as needed, if they can be measured.
Controlled by \(u_{c}=K_{\sigma (t)}x\), the system above can be rewritten as
where \(\bar{A}_{\sigma (t)} =A_{\sigma (t)}+B_{\sigma (t)}K_{\sigma (t)}\) and \(\bar{C}_{\sigma (t)} =C_{\sigma (t)}+E_{\sigma (t)}K_{\sigma (t)}\). The \(H_{\infty }\) control problem is to find \(K_{\sigma (t)}\) such that (41) is asymptotically stable when \(u_{d}=0\), and is externally stable from \(u_{d}\) to y, i.e. \(\|y(t)\|_{L_{2}}\leq \gamma ^{*}\|u_{d}(t)\|_{L_{2}}\) for some prescribed constant \(\gamma ^{*}\), when \(\phi (\theta )=0\).
Comparing (41) with (1), it can be concluded that the objectives of \(H_{\infty }\) control are all achieved (since exponential stability implies asymptotic stability and the ES is already proven) in different cases if \(A_{\sigma (t)}\), \(C_{\sigma (t)}\) are replaced by \(\bar{A}_{\sigma (t)}\), \(\bar{C}_{\sigma (t)}\), respectively, in the corresponding theorems. To avoid tediousness, we only state a theorem for the \(H_{\infty }\) control corresponding to Theorem 3.2. The result corresponding to Theorem 3.1 is left to the reader.
Theorem 3.3
Given scalars \(\alpha >0\), \(0<\alpha _{-}<\alpha \), \(\alpha _{+}>0\), \(c_{*}>0\), \(\mu >0\) and the numbers of any two consecutive subsystems i, \(j\in \mathscr{P}\) (σ switches from j to i), the \(H_{\infty }\) control problem of (40), under the switching law S3.1, is solved, if there exist real \(n\times n\) positive definite matrices \(P_{i}\), \(Q_{i}\), \(P_{j}\), \(Q_{j}\) and appropriate dimensions matrices \(K_{i}\), \(K_{j}\) such that, for each subsystem (\(\bar{A}_{i}\) is Hurwitz),
for each subsystem (\(\bar{A}_{i}\) is not surely Hurwitz),
and
where \(\digamma _{\mu }=\frac{\gamma ^{*}}{\mu } \sqrt{ \frac{\alpha _{*}-\ln \mu /T_{\mathrm{min}}}{e^{c_{*}}(\alpha _{-}-\ln \mu /T_{\mathrm{max}})}}\), if \(\mu >1\); \(\digamma _{\mu }={\gamma ^{*}} \sqrt{ \frac{\alpha _{*}}{e^{c_{*}}\alpha _{-}}} \) if \(\mu =1\); \(\digamma _{\mu }={\gamma ^{*}}{\mu } \sqrt{ \frac{\alpha _{*}-\ln \mu /T_{\mathrm{max}}}{e^{c_{*}}(\alpha _{-}-\ln \mu /T_{\mathrm{min}})}}\) if \(0<\mu <1\).
Remark 3.7
It follows from Remark 3.3, under the same conditions as in Theorem 3.3, the state \(\|x(t)\|\leq \tilde{K}_{\mu }\|x_{t_{0}}\|_{d}e^{- \tilde{\alpha }_{\mu }(t-t_{0})}\), where \(\tilde{K}_{\mu }=e^{\frac{c_{*}}{2}}\sqrt{ \frac{\mu [{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})}]}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\tilde{\alpha }_{\mu }= \frac{1}{2}(\alpha _{*}-\frac{\ln \mu }{T_{\mathrm{min}}})\) if \(\mu >1\); \(\tilde{K}_{\mu }=e^{\frac{c_{*}}{2}}\sqrt{ \frac{{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})}}{\inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\tilde{\alpha }_{\mu }=\frac{1}{2}\alpha _{*}\) if \(\mu =1\); \(\tilde{K}_{\mu }= e^{\frac{c_{*}}{2}}\sqrt{ \frac{\lambda _{\mathrm{max}}(P_{\sigma (t_{0})})+d\lambda _{\mathrm{max}} (Q_{\sigma (t_{0})})}{\mu \inf_{i\in \mathscr{P}}(\lambda _{\mathrm{min}}(P_{i}))}}\), \(\tilde{\alpha }_{\mu }= \frac{1}{2}(\alpha _{*}-\frac{\ln \mu }{T_{\mathrm{max}}})\) if \(0<\mu <1\).
Remark 3.8
After substituting \(\bar{A}_{i}\), \(\bar{C}_{i}\), nonlinear terms like \(P_{i}B_{i}K_{i}\) and \(K_{i}^{T}B_{i}^{T}P_{i}\) appear in (42) and (43). We can first left and right multiply (42), (43) by \(\operatorname{diag}(P_{i}^{-1},I,I,I)\). Then we apply the Schur complement and use \(-Q_{i}^{-1}\leq -2\epsilon _{i}I+\epsilon _{i}^{2}Q_{i}\), \(\epsilon _{i}>0\) to derive the following linear matrix inequalities of \(P_{i}^{-1}\), \(Q_{i}\) and \(Y_{i}\):
where \((1,1)_{1}=A_{i}P_{i}^{-1}+P_{i}^{-1}A_{i}^{T}+\alpha _{-} P_{i}^{-1}+B_{i}Y_{i}+Y_{i}^{T}B_{i}^{T}\), \((1,1)_{2}=A_{i}P_{i}^{-1}+P_{i}^{-1}A_{i}^{T}-\alpha _{+} P_{i}^{-1}+B_{i}Y_{i}+Y_{i}^{T}B_{i}^{T}\) and \(Y_{i}=K_{i}P_{i}^{-1}\), obeying (42), (43), respectively. It follows that \(K_{i}=Y_{i}P_{i}\).
As for the first inequality in (44), we can first left and right multiply it by \(\operatorname{diag}(P_{j}^{-1},I)\). Then left and right multiply it by \(\operatorname{diag}(I,P_{i}^{-1})\) to derive an equivalent linear matrix inequality as
Thus, all matrix inequalities in Theorem 3.3 are already transformed to linear matrix inequalities of \(P_{i}^{-1}\), \(Q_{i}\) and \(Y_{i}\) that can be solved by Matlab.
Remark 3.9
It is arbitrary to pre-assume that a certain \(\bar{A}_{i}\) is Hurwitz or not surely Hurwitz, as long as feasible solutions for the inequalities can be found; see Example 4.1, where \(\bar{A}_{1}\) is pre-assumed to be Hurwitz.
4 Illustrative example
In this section, we provide an example of \(H_{\infty }\) control with numerical simulations to illustrate previous results.
Example 4.1
Consider the switching control system with delay and impulse initialized as follows:
Let \(\alpha _{-}=1\), \(\alpha _{+}=2\), \(\alpha _{*}=0.25<\alpha _{-}\) and \(c_{*}=2.25\), then we can select the switching signal \(\sigma (t)\) satisfied Switching Law 3.1. From Remark 3.6 in [25], here we choose a simple switching law realization as shown in Fig. 1. The first active subsystem is a Hurwitz stable subsystem. And the switching time is periodic. Let \(t_{2j}-t_{2j-1}=T_{+}=1\), \(t_{2j-1}-t_{2j-2}=T_{-}=6\), \(j=1,2,\ldots \) , then \(T_{+}\leq c_{*}/(\alpha _{+}+\alpha _{*})\) and \(T_{-}\geq 2T_{+}(\alpha _{+}+\alpha _{*})/(\alpha _{-}-\alpha _{*})\) are satisfied. Therefore, \(T_{\mathrm{max}}=T_{-}=6\), \(T_{\mathrm{min}}=T_{+}=1\). In fact, any switching signal can be selected as long as Switching Law 3.1 is satisfied.
Select the disturbance input \(u_{d}(t)=\sin (\frac{2\pi }{7}t)[H(t)-H(t-7)]+\sin (\frac{2\pi }{7}(t-14))[H(t-14)-H(t-21)] \in L_{2}[0,\infty )\) as shown in Fig. 2 and the initial condition \(\phi (\theta )=\phi (\theta _{1},\theta _{2})=[\theta _{1}+1,\theta _{2}+1]^{T}\), where \(H(t)\) is the Heaviside step function. Given the delay function \(\tau (t)=0.1+0.1\sin t\), then we can select \(d=0.2\) and \(\rho =0.1\) such that \(\tau (t)\leq d\), \(\dot{\tau }(t)\leq \rho <1\) as required.
All other common parameters for three cases are given as \(\gamma ^{*}=1\), \(\alpha =1.01 (\alpha >\alpha _{-})\), \(\epsilon _{1}=0.6\) and \(\epsilon _{2}=0.6\).
Case 1: \(0<\mu <1\). Select \(\mu =0.98\), then \(\digamma _{\mu }=0.1586\) and \(\alpha _{*}>\ln \mu /T_{\mathrm{min}}=-0.0202\). In this case, we consider \((A_{1}+B_{1}K_{j}, A_{d1}, B_{1}, I_{1}, C_{1}+E_{1}K_{j}, C_{d1}, E_{1})\), \(j=1,3,5,\ldots,9\) as the controlled subsystem \(j=1,3,5,\ldots,9\), and \((A_{2}+B_{2}K_{i}, A_{d2}, B_{2}, I_{2}, C_{2}+E_{2}K_{i}, C_{d2}, E_{2})\), \(j=2,4,6,\ldots,10\), as the controlled subsystem \(j=2,4,6,\ldots,10\). Note that in the switching signal, see Fig. 1, the lower ‘1’s represent \(1, 3, 5, \ldots, 9\) and the upper ‘2’s represent \(2, 4, 6, \ldots, 10\), from left to right. Employing the linear matrix inequality tool box of Matlab, we derive
Then the conditions for this case in Theorem 3.3, where \(\bar{A}_{1}\) (or \(A_{1}+B_{1}Kj\)) is pre-assumed to be Hurwitz, are satisfied. From Remark 3.7, \(K_{\mu }= 8.1513\) and \(\alpha _{\mu }=0.1267\).
Case 2: \(\mu =1\). In this case, \(\digamma _{\mu }=0.1623\) and \(\alpha _{*}>\ln \mu /T_{\mathrm{min}}=0\). Using Matlab, we obtain
Thus, all conditions in Theorem 3.3 (where \(\bar{A}_{1}\) is pre-assumed to be Hurwitz) hold. It follows from Remark 3.7 that \(K_{\mu }=4.3379\) and \(\alpha _{\mu }=0.1250\).
Case 3: \(\mu >1\). Select \(\mu =1.01\), then \(\digamma _{u}=0.1576\) and \(\alpha _{*}>\ln \mu /T_{\mathrm{min}}=0.0100\). By Matlab, we get
Therefore, conditions in Theorem 3.3 (where \(\bar{A}_{1}\) is pre-assumed to be Hurwitz) are all satisfied. According to Remark 3.7, \(K_{\mu }=4.6746\) and \(\alpha _{\mu }=0.1200\).
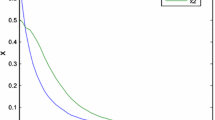
As expected, the zero-input (\(u_{d}(t)\equiv 0\)) states with the initial condition \(\phi (\theta )\) in these three cases are bounded by \(K_{\mu }\|x_{t_{0}}\|_{d}e^{-\alpha _{\mu }(t-t_{0})}\): \(11.5277e^{-0.1267t}\) (case 1), \(6.6109e^{-0.1200t}\) (case 2) and \(6.1347e^{-0.1250t}\) (case 3), see Fig. 3, respectively; and \(\gamma _{0}(t)\) defined as \((\int _{0}^{t}y^{2}(s)\,\mathrm{d}s/ \int _{0}^{t}u_{d}^{2}(s)\,\mathrm{d}s)^{\frac{1}{2}}\), under the zero initial condition, for each case, is less than \(\gamma =1\); see Fig. 4. Therefore, the \(H_{\infty }\) control goal has been achieved.
As introduced before, the \(H_{\infty }\) controller \(u_{c}=K_{\sigma (t)}x\) starts to stabilize the system (the state \(x_{1}\) with the initial condition \(\phi (\theta )\) completely equaling \(x_{2}\) in each case is almost stabilized between \(t=7~\mbox{s}\) and \(t=14~\mbox{s}\), and after \(t=21~\mbox{s}\), see Fig. 5) after the energy-bounded disturbance \(u_{d}\) has already decayed to zero (between \(t=7~\mbox{s}\) and \(t=14~\mbox{s}\), and after \(t=21~\mbox{s}\); see Fig. 2), then maintains the stabilized system to be externally stable from the disturbance to the output such that the effect of the disturbance on the output is attenuated during the steady period, see \(\gamma _{2}(t)\) of each case in Fig. 4, defined as \((\int _{14}^{t}y^{2}(s)\,\mathrm{d}s/\int _{14}^{t}u_{d}^{2}(s)\,\mathrm{d}s)^{\frac{1}{2}}\) under the initial condition \(\phi (\theta )\), which is less than \(\gamma ^{*}=1\) and is of almost the same form as \(\gamma _{0}(t)\). However, before the system is stabilized for the first time, i.e. during the transient period, the ES cannot be ensured, see \(\gamma _{1}(t)\) of each case in Fig. 4, defined as \((\int _{0}^{t}y^{2}(s)\,\mathrm{d}s/\int _{0}^{t}u_{d}^{2}(s)\,\mathrm{d}s)^{\frac{1}{2}}\) under the initial condition \(\phi (\theta )\), which is larger than γ around \(t=0~\mbox{s}\).
5 Conclusion
The ES and \(H_{\infty }\) control problem of SSs with delay and impulse has been investigated in this paper. After introducing the definitions of the maximum, minimum DT, we have applied the relation between the number of switchings and the maximum, minimum DT to prove the ES of SSs consisting of subsystems that are all Hurwitz stable. For those SSs comprised of subsystems that are not all Hurwitz stable, a realizable switching law has been employed to study their ES. And then the normal \(L_{2}\) norm constraint has been derived. The label “weighted” has been removed properly in this paper. Finally, these results have been applied to \(H_{\infty }\) control and illustrated by a numerical example. In the future, we will first study the ES of nonlinear switching control systems without impulse or with impulse, then investigate the stability of SSs with switching signals driven by stochastic processes.
Availability of data and materials
The data and material used to support the findings of this study are included within the article.
References
Morris, K.A.: Introduction to Feedback Control. Academic Press, San Diego (2001)
Lin, P.Y., Liu, J.Y.: Analysis of resistance factors for LFRD of soil nail walls against external stability failures. Acta Geotech. 12, 157–169 (2017)
Zheng, W., Sandip, R., Ali, S.: On the disturbance response and external stability of a saturating static-feedback-controlled double integrator. Automatica 44, 2191–2196 (2008)
Khalil, H.K.: Nonlinear Systems, 3rd edn. Prentice Hall, New York (2002)
Liberzon, D.: Switching in Systems and Control. Birkhaüser, Boston (2003)
Zhang, L.X., Ning, Z.P., Shi, Y.: Analysis and synthesis for a class of stochastic switching systems against delayed mode switching: a framework of integrating mode weights. Automatica 99, 99–111 (2019)
Vargas, A.N., Caruntu, C.F., Ishihara, J.Y.: Stability of switching linear systems with switching signals driven by stochastic processes. J. Franklin Inst. 356, 31–41 (2019)
Sun, Y.G., Tian, Y.Z., Xie, X.J.: Stabilization of positive switched linear systems and its application in consensus of multiagent systems. IEEE Trans. Autom. Control 62(12), 6608–6613 (2017)
Li, P.S., Lam, J., Lu, R.Q., Kwok, K.W.: Stability and \(L_{2}\) synthesis of a class of periodic piecewise time-varying systems. IEEE Trans. Autom. Control 64(8), 3378–3384 (2019)
Li, P.S., Lam, J., Kwok, K.W., Lu, R.Q.: Stability and stabilization of periodic piecewise linear systems: a matrix polynomial approach. Automatica 94, 1–8 (2018)
Liu, X.Z., Wu, C.: Fault-tolerant synchronization for nonlinear switching systems with time-varying delay. Nonlinear Anal. Hybrid Syst. 23, 91–110 (2017)
Zhou, Y.H., Li, C.D., Huang, T.W., Wang, X.: Impulsive stabilization and synchronization of Hopfield-type neural networks with impulse time window. Neural Comput. Appl. 28, 775–782 (2017)
Tian, Y.Z., Cai, Y.L., Sun, Y.G.: Asymptotic behavior of switched delay systems with nonlinear disturbances. Appl. Math. Comput. 268, 522–533 (2015)
Li, C.D., Huang, T.W., Feng, G., Chen, G.R.: Exponential stability of time-controlled switching systems with time delay. J. Franklin Inst. 349, 216–233 (2012)
Wang, G., Xie, R.Q., Zhang, H.B., Yu, G.J., Dang, C.Y.: Robust exponential \(H_{\infty }\) filtering for discrete-time switched fuzzy systems with time-varying delay. Circuits Syst. Signal Process. 35, 117–138 (2016)
Sun, X.M., Zhao, J., Hill, D.J.: Stability and \(L_{2}\)-gain analysis for switched delay systems: a delay-dependent method. Automatica 42, 1769–1774 (2006)
Wu, L.G., Zheng, W.X.: Weighted \(H_{\infty }\) model reduction for linear switched systems with time-varying delay. Automatica 45, 186–193 (2009)
Liu, X.Z., Yuan, S.: Reduced-order fault detection filter design for switched nonlinear systems with time delay. Nonlinear Dyn. 67, 601–617 (2012)
Syed, A.M., Saravanan, S., Cao, J.: Finite-time boundedness, \(L_{2}\) gain analysis and control of Markovian jump switched neural networks with additive time-varying delays. Nonlinear Anal. Hybrid Syst. 23, 27–43 (2017)
Yuan, S., Liu, X.Z.: Fault estimator design for a class of switched systems with time-varying delay. Int. J. Syst. Sci. 42, 2125–2135 (2011)
Liu, X.Z., Zhu, H., Zhong, S.M., Wu, C.: Exponential \(H_{\infty }\) synchronization of switching fuzzy systems with time-varying delay and impulses. Fuzzy Sets Syst. 365, 116–139 (2019)
Zhai, G.S., Hu, B., Yasuda, K., Michel, A.N.: Disturbance attenuation properties of time-controlled switched systems. J. Franklin Inst. 338, 765–779 (2001)
Shi, P., Su, X., Li, F.: Dissipativity-based filtering for fuzzy switched systems with stochastic perturbation. IEEE Trans. Autom. Control 61, 1694–1699 (2016)
Hua, D.L., Wang, W.Q., Yao, J., Ren, Y.H.: Non-weighted \(H_{\infty }\) performance for 2-D FMLSS switched system with maximum and minimum dwell time. J. Franklin Inst. 356, 5729–5753 (2019)
Wu, C., Liu, X.Z.: External stability of switching control systems. Syst. Control Lett. 106, 24–31 (2017)
Zhang, H.B., Mao, Y.B., Gao, Y.S.: Exponential stability and asynchronous stabilization of switched systems with stable and unstable subsystems. Asian J. Control 15, 1–8 (2013)
Long, L.J.: Input/output-to-state stability for switched nonlinear systems with unstable subsystems. Int. J. Robust Nonlinear Control 29 3093–3110 (2019)
Sun, Y.W., Zhao, J., Dimirovski, G.M.: Adaptive control for a class of state-constrained high-order switched nonlinear systems with unstable subsystems. Nonlinear Anal. Hybrid Syst. 32, 91–105 (2019)
Wei, J.M., Zhi, H.M., Liu, K., Mu, X.W.: Stability of mode-dependent linear switched singular systems with stable and unstable subsystems. J. Franklin Inst. 356, 3102–3114 (2019)
Francis, A.B.: A Course in \(H_{\infty }\) Control Theory. Springer, Berlin (1987)
Teolis, C.A.: Robust \(H_{\infty }\) output feedback control. Ph.D. thesis, University of Maryland (1994)
Tannenbaum, A.: Feedback stabilization of linear dynamical plants with uncertainty in the gain factor. Int. J. Control 32, 1–16 (1980)
Boyd, S., Ghaoui, L.E., Feron, E., Balakrishnan, V.: Linear Matrix Inequalities in System and Control Theory. SIAM, Philadelphia (1994)
Acknowledgements
The authors would like to thank the editor and the anonymous referees for their helpful comments.
Funding
This work was supported by Opening Fund of Geomathematics Key Laboratory of Sichuan Province (scsxdz2019yb03).
Author information
Authors and Affiliations
Contributions
All authors drafted the manuscript, and they read and approved the submitted version.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Ren, J., Wu, C. External stability and \(H_{\infty }\) control of switching systems with delay and impulse. Adv Differ Equ 2020, 652 (2020). https://doi.org/10.1186/s13662-020-03098-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03098-7