1 Introduction

The soliton theory is an important tool in describing various phenomena of wave propagation. Recently, several nonlinear equations have been successfully developed to investigate wave propagation. For instance, the Korteweg–de Vries (KdV) equation is mainly used to investigate the propagation of shallow water waves in one dimension, whereas the bad Boussinesq (BSQ) equation describes the wave propagation in two dimensions. The BSQ equation is also used in studying different processes appearing in electromagnetic waves in dielectrics [1], magnetosound waves in plasma [2], and the magnetoelastic waves in antiferromagnetic [3]. These equations and others have attracted the attention of a massive number of mathematicians and physicists since the 1970s due to their use in revealing the internal mechanisms of some sophisticated natural phenomena. Therefore numerous scientists have invented and discovered a wide variety of new methods to develop the soliton solutions for most NLPDEs. Some developed techniques and principles include the inverse scattering transform [4], the trial function process [5], the sine–cosine principle [6], the Weierstrass elliptic function approach [7], the tanh–sech technique [8], the F-expansion technique [9], Hirota’s bilinear principle [10], the modified tanh-function technique [11], the extended tanh-technique [12], the \(\exp (-f(\zeta ))\)-expansion process [13, 14], and the truncated Painleve expansion [15]. More information about other techniques can be obtained in [16–27].

The Boussinesq equation is given by

$$ u_{tt}-u_{xx}-u_{xxxx}- \bigl(u^{2}\bigr)_{xx}=0, $$
(1)

where \(u(x,t)\) is a real-valued function, and subscripts represent partial derivatives. This equation models the propagation of shallow water waves in both directions. If the sign associated to \(u_{xxxx}\) is changed, then we end up with a linearly stable equation, and the numerical computation can be achieved. Therefore the good Boussinesq (GB) equation is given by

$$ u_{tt}-u_{xx}+u_{xxxx}- \bigl(u^{2}\bigr)_{xx}=0. $$
(2)

According to [28], the solitary waves described by the GB equation solely occur for a finite range of velocities and can merge into one solitary wave. The Boussinesq equation has been exactly and numerically solved using different approaches. For example, the modified decomposition method is applied in [29] to develop soliton solutions and periodic solutions, whereas a simplified version of the Hirota technique is used in [30] to extract several exact solutions for the GB problem. Furthermore, in [31], N-soliton solutions are determined by using the bilinear form. Nguyen [32] has employed the Hirota direct bilinear process to find the soliton solution of the GB problem. The power-law nonlinearity [33] and the variational iteration techniques [34] are derived to obtain solitary wave solutions for the Boussinesq equation and the GB equation, respectively. On the other hand, the GB equation is solved numerically by Ismail and Bratsos [35]. They have presented a conditionally stable scheme that is second-order in space and fourth-order in time. The authors in [36] have applied a finite difference process to the GB equation and discovered that the used technique is unconditionally stable and is fourth-order in space and second-order in time. Other numerical methods can be found in [8, 37–45].

In this work, we employ the He semiinverse approach and the moving mesh process [46] to construct the soliton and numerical solutions, respectively, for the GB equation. The numerical method followed in this paper uses a monitor function and moving mesh partial differential equations (MMPDEs) to distribute the grid of the points in the area where the error is high. The main advantage of this approach is the reduction of the error, especially in the curvature and variation regions, by distributing more points in such regions.

The boundary constraints are graphically deduced from the behavior of the exact traveling wave solutions as the time changes. The exact solutions vanish at the boundaries of the physical domain. As a result, the relevant boundary conditions are constants. In other words, \(u_{x}=0\) and \(u_{xxx}=0\) as \(x\to \pm \infty \).

2 Traveling wave solution

In this part, we focus on extracting the exact solution of the GB equation using the He semiinverse process [47, 48]. Plugging the traveling wave transformation

$$ u(x,t)=\rho (\xi ),\qquad \xi = x -w t, $$

were w plays the role of the speed wave, into Eq. (2) and integrating twice with respect to ξ give

$$ \bigl(w^{2}-1\bigr)\rho +\rho _{\xi \xi }-\rho ^{2}=0. $$
(3)

Hence from Eq. (3) we obtain the following variational formulation:

$$ J= \int _{0}^{\infty } \biggl[ \frac{w^{2}-1}{2} \rho ^{2}-\frac{1}{3} \rho ^{3}-\frac{1}{2} \rho _{\xi }^{2} \biggr]\,d\xi. $$
(4)

Next, we utilize a Ritz-like process to invoke bright optical solitons in the following form:

$$ \rho (\xi )=\beta \operatorname {sech}^{2} (\alpha \xi ), $$
(5)

where β and α are constants to be found later. Plugging Eq. (5) into Eq. (4) leads to

$$ J=-\frac{8 \beta ^{3}}{45 \alpha }+\frac{\beta ^{2} w^{2}}{3 \alpha }- \frac{4 \beta ^{2} \alpha }{15}- \frac{\beta ^{2}}{3 \alpha }. $$

To find the stationary points (fixed points) β and α of J, we differentiate J with respect to β and α and equate the results to zero:

$$\begin{aligned} &\frac{\partial J}{\partial \beta }=- \frac{8 \beta ^{2}}{15 \alpha }+\frac{2 \beta w^{2}}{3 \alpha }- \frac{8 \beta \alpha }{15}-\frac{2 \beta }{3 \alpha }=0, \\ &\frac{\partial J}{\partial \alpha }= \frac{8 \beta ^{3}}{45 \alpha ^{2}}- \frac{\beta ^{2} w^{2}}{3 \alpha ^{2}}+ \frac{\beta ^{2}}{3 \alpha ^{2}}- \frac{4 \beta ^{2}}{15}=0. \end{aligned}$$

The solutions of this system are as follows:

$$\begin{aligned} & \beta=\frac{3}{2} \bigl(w^{2}-1 \bigr), \\ &\alpha= \pm \frac{\sqrt{1-w^{2}}}{2}. \end{aligned}$$

Substituting these values of β and α into Eq. (5) yields

$$ \rho (\xi )=\frac{3}{2} \bigl(w^{2}-1 \bigr) \operatorname {sech}^{2} \biggl(\pm \frac{1}{2} \sqrt{1-w^{2}} \xi \biggr). $$

Hence the exact solutions of Eq. (2) can be simply expressed as

$$ u(x,t)=\frac{3}{2} \bigl(w^{2}-1 \bigr) \operatorname {sech}^{2} \biggl(\pm \frac{1}{2} \sqrt{1-w^{2}} (x+x_{0}-w t ) \biggr), $$
(6)

where w indicates the speed parameter, and \(x_{0}\) is a constant.

2.1 Stability analysis

We study the stability of the accomplished exact traveling wave results by employing the Hamiltonian system expression given by

$$ \varphi (w)= \int _{-\infty }^{\infty }\frac{1}{2} \rho ^{2} \,d\xi , $$

where w plays the role of the speed parameter, \(\varphi (w)\) is the momentum, and ρ indicates the obtained exact solution of Eq. (3). A sufficient condition for testing the stability is given by

$$ \frac{\partial \varphi }{\partial w}> 0. $$

Applying the Hamiltonian system to Eq. (6) gives

$$ \varphi (w)=-3 \bigl(1 - w^{2} \bigr)^{3/2}. $$

Taking the derivative with respect to w yields

$$ \frac{\partial \varphi }{\partial w}= 9 w \sqrt{1 - w^{2}}. $$

Hence we clearly observe that the exact solution is stable for all \(\xi \in (-\infty , +\infty )\) under the parameter value \(|w|<1\). The sign of w plays a crucial role in determining the direction of the time evolution of the traveling wave solution. Consequently, we take \(w=0.5\) and \(x_{0}=-10\) to plot the following figures.

3 Numerical investigation

In this section, we numerically solve GB equation via the adaptive moving mesh method. This novel approach uses a monitor function, which distributes the mesh nodes along the evolving solution at each time step. To discretize in space, we utilize the central finite differences. To study Eq. (2) numerically, we assume that

$$ u_{t}=v_{xx}. $$
(7)

Differentiating Eq. (7) with respect to t and substituting the result into Eq. (2) lead to

$$ (v_{t})_{xx}= \bigl(-u_{xx}+u+u^{2}\bigr)_{xx}. $$

Hence Eq. (2) is converted to the following system:

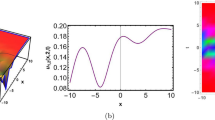
$$ \begin{aligned} &u_{t}-v_{xx}=0, \\ &v_{t} +u_{xx}-u-u^{2}=0. \end{aligned} $$
(8)

The relevant boundary conditions are obtained from Fig. 1, from which we observe that

$$ u_{x}=v_{x}=0,\qquad x=a, b, $$

where a and b are the endpoints of the physical domain. To find the numerical solutions of system (8), we first obtain the exact solution of \(v(x,t)\):

$$ v(x,t)= \int \int _{a}^{x} \frac{\partial u(\eta ,t)}{\partial t} \,d\eta. $$

Hence the exact solution of \(v(x,t)\) is given by

$$ v(x,t)=w \sqrt{1-w^{2}} \tanh \biggl( \frac{1}{2} \sqrt{1-w^{2}} (x+x_{0}-w t ) \biggr). $$
(9)

Thus the initial conditions are given by

$$ \begin{aligned}& u(x,0)=\frac{3}{2} \bigl(w^{2}-1 \bigr) \operatorname {sech}^{2} \biggl(\frac{1}{2} \sqrt{1-w^{2}} (x+x_{0} ) \biggr), \\ &v(x,0)=w \sqrt{1-w^{2}} \tanh \biggl(\frac{1}{2} \sqrt{1-w^{2}} (x+x_{0} ) \biggr). \end{aligned} $$
(10)

Applying the adaptive moving mesh process to build the numerical solution of the GB problem requires equal subintervals for the movement of the mesh. Thus the physical domain \([a, b]\) is first transformed into a computational domain, which is \([0,1]\), using the following transformation:

$$ x=x(\zeta , t)\colon [0,1] \rightarrow [a, b],\quad t>0. $$

Employing the physical coordinate x and the computational coordinate ζ leads to

$$ u=u\bigl(x(\zeta , t), t\bigr),\qquad v=v\bigl(x(\zeta , t), t\bigr),\quad \text{where } x=x(\zeta ,t). $$

Thus the moving mesh connecting with the solutions u and v is formed as

$$ x_{m}(\zeta )= x(\zeta _{m},t),\quad m=0, 1, \dots , N_{x}, $$

and the computational domain is formed as

$$ \zeta _{m}=m \Delta \zeta ,\qquad \Delta \zeta = \frac{1}{N_{x}},\quad m=0, 1, \dots , N_{x}. $$

Since the solution u and the mesh x are functions of the variable t, applying the chain rule to system (8), we have

$$ \begin{aligned}& u_{t}-u_{x} \dot{x}=v_{xx}, \\ &v_{t}-v_{x} \dot{x}= -u_{xx}+u+u^{2}. \end{aligned} $$
(11)

In the moving mesh method the error indicator is selected to redistribute the mesh nodes where the solution presents large curvatures or variations. We attempted different MMPDEs and monitor functions and we found that the obtained results are similar. As a result, we use the MMPDE5 [46, 49, 50] given by

$$ \tau \dot{x}=\frac{1}{\Phi } (\Phi x_{\zeta } )_{\zeta }, $$
(12)

where \(\tau \in (0,1)\) is called a relaxation parameter, and \(\Phi (u,v)\) denotes the monitor function. A successful selection for this function often gives effective and dependable results. This can be attributed to the fact that the monitor function feeds the bending and variation regions in the solution with more nodes. Therefore we apply an exceptional function given by

$$ \Phi (u,v)=\sqrt{1+u_{xx}^{2}+v_{xx}^{2}}. $$
(13)

The discretization of the mesh Eq. (12) is given by

$$ \frac{x_{j}^{n+1}-x_{j}^{n}}{ \Delta t}= \frac{1}{\tau \Phi _{j}^{n} \Delta \zeta ^{2} } \bigl[\Phi ^{n}_{j+1/2} \bigl(x_{j+1}^{n+1}-x_{j}^{n+1} \bigr)-\Phi ^{n}_{j-1/2} \bigl(x_{j}^{n+1}-x_{j-1}^{n+1} \bigr) \bigr] $$
(14)

subject to the boundary conditions

$$ x_{0}=a \quad\text{and}\quad x_{N_{x}}=b. $$

The initial condition is given by splitting the physical domain into \(N_{x}\) identical intervals as follows:

$$ a=x_{0}< x_{1}< x_{2}< \cdots < x_{j}< \cdots < x_{N_{x}}=b, $$

where \(x_{j}=a+j \Delta x\) with \(\Delta x=\frac{b-a}{N_{x}}\) and \(j=1, 2,\dots , N_{x}-1\). Moreover, the discretizations of the coupled equations (11) are given by

$$\begin{aligned} &\frac{u_{j}^{n+1}-u_{j}^{n}}{ \Delta t}=\frac{1}{2} \biggl[ \frac{u_{j+1}^{n+1}-u_{j-1}^{n+1}}{x_{j+1}^{n+1}-x_{j-1}^{n+1}}+ \frac{u_{j+1}^{n}-u_{j-1}^{n}}{x_{j+1}^{n}-x_{j-1}^{n}} \biggr] \dot{x}_{j+1/2} \\ &\phantom{ \frac{u_{j}^{n+1}-u_{j}^{n}}{ \Delta t}=}{}+ \frac{1}{x_{j+1}^{n+1}-x_{j-1}^{n+1}} \biggl[ \frac{v_{j+1}^{n+1}-v_{j}^{n+1}}{x_{j+1}^{n+1}-x_{j}^{n+1}}- \frac{v_{j}^{n+1}-v_{j-1}^{n+1}}{x_{j}^{n+1}-x_{j-1}^{n+1}} \biggr] \\ &\phantom{ \frac{u_{j}^{n+1}-u_{j}^{n}}{ \Delta t}=}{}+\frac{1}{x_{j+1}^{n}-x_{j-1}^{n}} \biggl[\frac{v_{j+1}^{n}-v_{j}^{n}}{x_{j+1}^{n}-x_{j}^{n}}- \frac{v_{j}^{n}-v_{j-1}^{n}}{x_{j}^{n}-x_{j-1}^{n}} \biggr], \end{aligned}$$
(15)
$$\begin{aligned} & \frac{v_{j}^{n+1}-v_{j}^{n}}{ \Delta t}=\frac{1}{2} \biggl[ \frac{v_{j+1}^{n+1}-v_{j-1}^{n+1}}{x_{j+1}^{n+1}-x_{j-1}^{n+1}}+ \frac{v_{j+1}^{n}-v_{j-1}^{n}}{x_{j+1}^{n}-x_{j-1}^{n}} \biggr] \dot{x}_{j+1/2} \\ &\phantom{\frac{v_{j}^{n+1}-v_{j}^{n}}{ \Delta t}=}{}+ \frac{1}{x_{j+1}^{n+1}-x_{j-1}^{n+1}} \biggl[ \frac{u_{j+1}^{n+1}-u_{j}^{n+1}}{x_{j+1}^{n+1}-x_{j}^{n+1}}- \frac{u_{j}^{n+1}-u_{j-1}^{n+1}}{x_{j}^{n+1}-x_{j-1}^{n+1}} \biggr] \\ &\phantom{\frac{v_{j}^{n+1}-v_{j}^{n}}{ \Delta t}=}{}+\frac{1}{x_{j+1}^{n}-x_{j-1}^{n}} \biggl[\frac{u_{j+1}^{n}-u_{j}^{n}}{x_{j+1}^{n}-x_{j}^{n}}- \frac{u_{j}^{n}-u_{j-1}^{n}}{x_{j}^{n}-x_{j-1}^{n}} \biggr] \\ &\phantom{\frac{v_{j}^{n+1}-v_{j}^{n}}{ \Delta t}=}{}+\frac{u_{j}^{n+1}+u_{j}^{n}}{2}+ \frac{(u^{2})_{j}^{n+1}+(u^{2})_{j}^{n}}{2},\quad j=1, 2, 3,\ldots , N_{x}-1, \end{aligned}$$
(16)

subject to the boundary conditions

$$ u_{x}=v_{x}=0 \quad\text{at } x=a,b. $$

It is to be highlighted that the initial conditions are chosen by Eqs. (10) at \(t=0\). Here Δt presents the step size of time t. To evaluate the boundaries of \(u_{xx}\) and \(v_{xx}\), we require some fictitious points

$$ u_{-1}=u_{1},\qquad v_{-1}=v_{1},\qquad u_{N_{x}+1}=u_{N_{x}-1},\qquad v_{N_{x}+1}=v_{N_{x}-1}, \quad\forall t. $$

Here we list the procedure of the alternating solution as follows:

  1. 1.

    At the time step \(t_{n}\) the monitor function Eq. (13) is computed using the solutions \(u^{n}\) and \(v^{n}\).

  2. 2.

    A new mesh at the time step \(t_{n+1}\) is obtained by solving scheme (14) using the monitor function \(\Phi ^{n}\). The monitor function is fixed during the computation.

  3. 3.

    The solutions \(u^{n+1}\) and \(v^{n+1}\) are obtained by solving the numerical schemes (15) and (16) simultaneously using \(x^{n}\) and \(x^{n+1}\).

  4. 4.

    This procedure is repeated from step 1.

Figure 1
figure 1

(a) The exact solution of \(u(x,t)\) is plotted in 3D diagram; (b) shows a 2D graph for the time evolution of a single solitary wave for \(u(x,t)\)

Full size image

3.1 Accuracy of the numerical schemes

This subsection is devoted to introducing the accuracy of the adaptive mesh schemes (14), (15) and scheme (16). The approximated solutions \(u^{n}_{j}\) and \(v^{n}_{j}\) are replaced throughout by \(u(x_{j},t_{n})\) and \(v(x_{j},t_{n})\), respectively, at the point \((x_{j},t_{n})\). Then we introduce the step size for both the time and spatial variables. They are presented by \(\Delta t=t_{n+1}-t_{n}\), \(\Delta x^{+}=x_{j+1}-x_{j}\), and \(\Delta x^{-}=x_{j}-x_{j-1}\). Taylor series expansion is used to determine \(x_{j+1}^{n+1}\) and \(x_{j-1}^{n+1}\) as follows:

$$ \begin{aligned} &x_{j+1}^{n+1}=x_{j}^{n+1}+ \biggl[ \Delta \zeta x_{\zeta }+ \frac{1}{2}\Delta \zeta ^{2} x_{\zeta \zeta }+ \frac{1}{6} \Delta \zeta ^{3} x_{\zeta \zeta \zeta }+ \frac{1}{24}\Delta \zeta ^{4} x_{\zeta \zeta \zeta \zeta } +\cdots \biggr]^{n+1}_{j}, \\ &x_{j-1}^{n+1}=x_{j}^{n+1}+ \biggl[ - \Delta \zeta x_{\zeta }+ \frac{1}{2}\Delta \zeta ^{2} x_{\zeta \zeta }- \frac{1}{6} \Delta \zeta ^{3} x_{\zeta \zeta \zeta }+ \frac{1}{24}\Delta \zeta ^{4} x_{\zeta \zeta \zeta \zeta }-\cdots \biggr]^{n+1}_{j}. \end{aligned} $$

Adding these expressions and simplifying, we get

$$ \frac{x_{j+1}^{n+1}-2 x_{j}^{n+1}+x_{j-1}^{n+1}}{\Delta \zeta ^{2}}- x_{ \zeta \zeta }= \biggl[ \frac{1}{12}\Delta \zeta ^{2} x_{\zeta \zeta \zeta \zeta } + \frac{1}{360}\Delta \zeta ^{4} x_{\zeta \zeta \zeta \zeta \zeta \zeta }+\cdots \biggr]^{n+1}_{j}. $$

In the same manner, we have

$$ \tau \frac{x_{j}^{n+1}-x_{j}^{n}}{ \Delta t} -\tau x_{t}= \biggl[ \frac{1}{2}\Delta t x_{tt} + \frac{1}{6}\Delta t^{2} x_{ttt}+ \cdots \biggr]^{n}_{j}. $$

Consequently, the truncation error of the implicit scheme (14) is

$$ T^{n}_{j}=\tau \frac{x_{j}^{n+1}-x_{j}^{n}}{ \Delta t} - \frac{x_{j+1}^{n+1}-2 x_{j}^{n+1}+x_{j-1}^{n+1}}{\Delta \zeta ^{2}}-( \tau x_{t}- x_{\zeta \zeta }). $$

Thus

$$ T^{n}_{j}=O(\Delta t)+O\bigl(\Delta x^{2}\bigr). $$
(17)

To investigate the accuracy of schemes (15) and (16), we use Taylor series expansions for \(u_{j}^{n+1}\) and \(u_{j}^{n}\) with respect to \(\Delta t/2\) as follows:

$$ \begin{aligned}& u_{j}^{n+1}= \biggl[ u+\frac{\Delta t}{2} u_{t}+ \frac{\Delta t^{2}}{8} u_{tt} + \frac{\Delta t^{3}}{48} u_{ttt}+ \frac{\Delta t^{4}}{348} u_{tttt}+\cdots \biggr]_{j}^{n+1/2}, \\ &u_{j}^{n}= \biggl[ u-\frac{\Delta t}{2} u_{t}+ \frac{\Delta t^{2}}{8} u_{tt} -\frac{\Delta t^{3}}{48} u_{ttt}+ \frac{\Delta t^{4}}{348} u_{tttt}+\cdots \biggr]_{j}^{n+1/2}. \end{aligned} $$

Subtracting these expansions and simplifying lead to

$$ \frac{u_{j}^{n+1}-u_{j}^{n}}{ \Delta t}-u_{t}= \biggl[ \frac{\Delta t^{2}}{24} u_{ttt}+ \frac{\Delta t^{4}}{1920} u_{ttttt}+ \cdots \biggr]_{j}^{n+1/2}. $$

The spatial first and second derivatives for u are approximated by the average of finite differences at \(t_{n}\) and \(t_{n+1}\) as follows:

$$\begin{aligned} & u_{j+1}^{n+1}= \biggl[ u+ \Delta x^{+} u_{x}+\frac{1}{2}\bigl( \Delta x^{+} \bigr)^{2} u_{xx}+\frac{1}{6}\bigl(\Delta x^{+}\bigr)^{3} u_{xxx}+ \frac{1}{24}\bigl( \Delta x^{+}\bigr)^{4} u_{xxxx}+\cdots \biggr]_{j}^{n+1}, \\ &u_{j-1}^{n+1}= \biggl[ u- \Delta x^{-} u_{x}+\frac{1}{2}\bigl( \Delta x^{-} \bigr)^{2} u_{xx}-\frac{1}{6}\bigl(\Delta x^{-}\bigr)^{3} u_{xxx}+ \frac{1}{24}\bigl( \Delta x^{-}\bigr)^{4} u_{xxxx}-\cdots \biggr]_{j}^{n+1}, \\ &\frac{u_{j+1}^{n+1}-u_{j-1}^{n+1}}{\Delta x^{+}_{n} + \Delta x^{-}_{n}}-u_{x}|_{j}^{n+1}= \biggl[\frac{1}{6} \biggl( \frac{ (\Delta x^{+}_{n} )^{3}+ (\Delta x^{-}_{n} )^{3}}{\Delta x^{+}_{n} +\Delta x^{-}_{n}} \biggr) u_{xxx}+ \cdots \biggr]_{j}^{n+1}, \\ &\frac{2}{\Delta x^{+}+\Delta x^{-}} \biggl( \frac{u_{j+1}^{n+1}-u_{j}^{n+1}}{\Delta x^{+}}- \frac{u_{j}^{n+1}-u_{j-1}^{n+1}}{\Delta x^{-}} \biggr)-u_{xx}|_{j}^{n+1}\\ &\quad= \biggl[ \frac{1}{24} \biggl( \frac{ (\Delta x^{+}_{n} )^{3}+ (\Delta x^{-}_{n} )^{3}}{\Delta x^{+}_{n} +\Delta x^{-}_{n}} \biggr)u_{xxxx}+ \cdots \biggr]_{j}^{n+1}. \end{aligned}$$

Similarly, we can construct the approximation of \(u_{x}\) and \(u_{xx}\) at the time level \(t_{n}\). In the same manner, we can derive the second derivative for v at \(t_{n}\) and \(t_{n+1}\). Hence the truncation error of the adaptive moving mesh schemes (15) and (16) is given by

$$ T_{j}^{n+1/2}=O \bigl(\Delta t^{2} \bigr) +O \biggl( \frac{ (\Delta x^{+} )^{3}+ (\Delta x^{-} )^{3}}{\Delta x^{+} +\Delta x^{-}} \biggr). $$

As a result, the accuracy of the adaptive mesh scheme is of the second order in time and roughly more than the second order in space when \(\Delta x^{+}=\Delta x^{-}\), that is,

$$ T_{j}^{n+1/2}=O \bigl(\Delta t^{2} \bigr) +O \bigl(\Delta x^{2} \bigr). $$
(18)

3.2 Stability of the numerical schemes

Here we use the von Neumann analysis to examine the stability of the numerical scheme (14). We ignore the boundary conditions and consider \((t_{n},\zeta _{j})\) with \(t_{n}=n \Delta t\), \(\zeta _{j}=j \Delta \zeta \), and \(x_{j}=j\Delta x\). Rearranging Eq. (14) yields

$$ x_{j}^{n}=- \gamma x_{j+1}^{n+1} +(1+2 \gamma ) x_{j}^{n+1}- \gamma x_{j-1}^{n+1}, $$
(19)

where \(\gamma =\frac{\Delta t}{\tau \Delta \zeta ^{2}}\). To employ the von Neumann technique, we assume that

$$ x^{n}_{j}=\rho ^{n} e^{i k \Delta \zeta j}, $$
(20)

where k is a constant. Substituting Eq. (20) into Eq. (19) gives

$$ 1=\rho -\bigl( e^{i k \Delta \zeta }-2+e^{-i k \Delta \zeta } \bigr) \rho. $$

Since \(( e^{i k \Delta \zeta }-2+e^{-i k \Delta \zeta })=-4\sin ^{2}(k \Delta \zeta /2)\), we have

$$ \rho = \frac{1}{1+4 \gamma \sin ^{2}(\frac{k \Delta \zeta }{2})}\leq 1. $$

Hence Eq. (14) is unconditionally stable for \(\gamma \geq 0\).

Now, to study the stability of scheme (15) and scheme (16), we assume that the mesh is fixed. Then the schemes are expressed by

$$ \begin{aligned}& u_{j}^{n+1}-u_{j}^{n}= \frac{\mu }{2}\delta _{x}^{2} \bigl(v_{j}^{n+1}+v_{j}^{n} \bigr), \\ &v_{j}^{n+1}-v_{j}^{n}=\frac{\mu }{2} \delta _{x}^{2} \bigl(u_{j}^{n+1}+u_{j}^{n} \bigr)+\frac{\alpha }{2} \bigl(u_{j}^{n+1}+u_{j}^{n} \bigr), \end{aligned} $$
(21)

where \(\delta _{x}^{2}=u^{n}_{j+1}-2u^{n}_{j}+u_{j-1}^{n}\), \(\mu =\Delta t/\Delta x^{2}\), and \(\alpha =\Delta t \max_{{0\leq j\leq N_{x}}} (1+u^{n}_{j} )\). We assume that

$$ u_{j}^{n}=\lambda ^{n} e^{i k \Delta x j},\qquad v_{j}^{n}= \beta ^{n} e^{i k \Delta x j}. $$
(22)

Substituting Eqs. (22) into schemes (21) leads to

$$\begin{aligned} & 2\mu \sin ^{2} \biggl( \frac{1}{2} k \Delta x \biggr)\beta + \lambda = 1-2\mu \sin ^{2} \biggl(\frac{1}{2}k \Delta x \biggr), \\ &\beta + \biggl(2\mu \sin ^{2}\biggl(\frac{1}{2} k \Delta x \biggr)-\alpha /2 \biggr)\lambda= 1-2\mu \sin ^{2} \biggl( \frac{1}{2} k \Delta x \biggr)+\alpha /2. \end{aligned}$$

Solving this system gives

$$ \begin{aligned} &\lambda = \frac{-(\alpha +4) \mu \sin ^{2}(\frac{1}{2} k \Delta x)+4 \mu ^{2} \sin ^{4}(\frac{1}{2} k \Delta x)+1}{\alpha \mu \sin ^{2}(\frac{1}{2} k \Delta x)-4 \mu ^{2} \sin ^{4}(\frac{1}{2} k \Delta x)+1}, \\ &\beta = \frac{-\alpha \mu \sin ^{2}(\frac{1}{2} k \Delta x)+\alpha + (1-2 \mu \sin ^{2}(\frac{1}{2} k \Delta x) )^{2}}{\alpha \mu \sin ^{2}(\frac{1}{2} k \Delta x)-4 \mu ^{2} \sin ^{4}(\frac{1}{2} k \Delta x)+1}. \end{aligned} $$

Since the required conditions for the stability of the numerical schemes are \(|\lambda |\leq 1\), \(|\beta |\leq 1\), \(\sin ^{2}(\frac{1}{2} k \Delta x)\leq 1\), and \(\alpha =\Delta t \max_{{0\leq j\leq N_{x}}} (1+u^{n}_{j} )\), the schemes are unconditionally stable for \(\mu \geq 0\). In this work, we used MATLAB software for running the numerical schemes to obtain numerical results.

Figures 2(a), (b) illustrate 3D surfaces for the exact traveling wave solution and the numerical solution. These figures show one wave. The exact and numerical results seem to be identical. In Fig. 2(c), we plot the numerical solution of \(v(x,t)\), which is used as an auxiliary equation for converting the original equation. The obtained exact and numerical results have very similar behaviors, as illustrated in Fig. 3(a). The achieved solutions are also shown similarly in 2D figures given in Figs. 4(a), (b). This leads to the conclusion that the used methods are applicable, powerful, and useful in solving other nonlinear PDEs.

Figure 2
figure 2

A 3D surface that shows one traveling wave for the exact solution \(u(x,t)\) is depicted in Figure (a), whereas the surface in (b) illustrates the numerical solutions for \(u(x,t)\). Figures (c) and (d) show 3D surfaces for the evolution time and the numerical solution of \(v(x,t)\), respectively

Full size image
Figure 3
figure 3

A graphical comparison of the exact and numerical solutions is presented in (a) \(u(x,t)\) and (b) \(v(x,t)\). The exact solutions for both \(u(x,t)\) and \(v(x,t)\) seem identical to numerical results. The curvature regions clearly show the match of solutions

Full size image
Figure 4
figure 4

Diagrams (a) and (b) illustrate the time development of a single traveling wave for the exact and numerical solutions of \(u(x,t)\), respectively. In (c), we present the time evolution of the corresponding mesh x

Full size image

Table 1 presents a brief description of \(L_{2}\) errors and CPU times consumed to arrive at \(t = 5\) for the adaptive technique. Various values of Δx were used. The error decreases to reach \(4.715\times 10^{-6}\) when \(\Delta x=1.0\times 10^{-2}\) for a long time (\(0.819\times 10^{+1}\) s). However, the method gives a small and acceptable error \(2.19\times 10^{-5}\) in short time \(7.7 \times 10^{-1}\) when \(\Delta x=2.5\times 10^{-2}\). The increase in the CPU time is due to the additional functions, which altogether evaluated along with the PDE. We can observe from Fig. 5 that the \(L_{2}\) error dramatically decreases when the number of mesh points increases. However, the CPU time slightly increases. As a result, the adaptive moving mesh method is reliable and more computationally effective.

Figure 5
figure 5

\(L_{2}\) error measured for u obtained by the numerical process against the grid of nodes N with \(w=0.5\) and \(x_{0}=-10\)

Full size image
Table 1 \(L_{2}\) errors and CPU times consumed to arrive at \(t = 5\) for the numerical technique
Full size table

4 Discussion and results

In this paper, we successfully employed a novel technique to construct the numerical solutions of Eq. (2). This method distributes the mesh points into the regions in which the error is high. Taylor expansion was specifically applied on Eq. (14). The accuracy is of the first order in time and of the second order in space, as shown in Eq. (17). Furthermore, the accuracy of schemes (15) and (16) is of the second order in time and of slightly more than the second order in space when \(\Delta x^{+}=\Delta x^{-}\), as described in Eq. (18). Moreover, the von Neumann stability showed that for Eq. (14), schemed (15) and (16) are unconditionally stable.

It is well known that the numerical solutions of PDEs are established by approximating the relevant equation on a mesh. Some solutions may contain dramatic spatial change. Hence a fine number of nodes is required on a small enough domain. However, this procedure is often extensive in computation. Consequently, we employed the adaptive moving mesh method, which sends more points into the regions in which there is a variation. The authors in [36] used the finite difference method to extract the numerical solution of the GB equation. The points are distributed on a uniform mesh. However, the adaptive moving mesh method gave new and more general results than those presented in [36]. We obtained more successful results during an acceptable time.

5 Conclusions

In this work, we discussed the traveling wave solutions and the numerical results of the good Boussinesq equation using the He semiinverse and the adaptive moving mesh methods, respectively. The accomplished exact solution was determined in the form of a hyperbolic trigonometric function. The exact solution was stable for all \(x \in (-\infty , +\infty )\) under the parameter values \(-1< w<1\). The exact and numerical solutions were compared in some 3D figures, which showed that the solutions were almost the same. The stability and accuracy of the numerical scheme were studied. The \(L_{2}\) error was measured to illustrate the accuracy of the adaptive moving mesh approach. The error vanished for a large number of mesh nodes, as shown in Fig. 5. The used methods gave successful and effective results for most nonlinear partial differential equations.