Abstract
In this paper, based on Galerkin–Legendre spectral method for space discretization and a linearized Crank–Nicolson difference scheme in time, a fully discrete spectral scheme is developed for solving the strongly coupled nonlinear fractional Schrödinger equations. We first prove that the proposed scheme satisfies the conservation laws of mass and energy in the discrete sense. Then a prior bound of the numerical solutions in \(L^{\infty }\)-norm is obtained, and the spectral scheme is shown to be unconditionally convergent in \(L^{2}\)-norm, with second-order accuracy in time and spectral accuracy in space. Finally, some numerical results are provided to validate our theoretical analysis.
Similar content being viewed by others
1 Introduction
The space fractional Schrödinger equation (FSE) is a natural extension of the classic Schrödinger equation, and it has been successfully used to describe the fractional quantum phenomena. Laskin [1, 2] originally derived the Riesz space FSE via replacing the Brownian trajectories with Levy flights in the Feynman path integrals. Some physical applications of the FSE were presented in [3, 4]. For the well-posedness, global attractor, soliton dynamics and ground states related to the FSE, we refer to Refs. [5–7] and the references therein.
The current paper is devoted to deriving a linearized conservative Galerkin–Legendre spectral method for solving the strongly coupled fractional Schrödinger equations (SCFSEs) with extended Dirichlet boundary conditions [8–10]
where \(i^{2}=-1\), \(1<\alpha \leq 2\), \(\Omega =(a,b)\) with \(a\ll 0\) and \(b\gg 0\), and the parameters \(\gamma >0\), κ, ρ, β and ϱ are given real constants. \(u_{0}(x)\) and \(v_{0}(x)\) are given initial functions. The Riesz fractional derivative is defined as
where the left and right Riemann–Liouville fractional derivatives [11] are given as
In particular, the Schrödinger system (1)–(4) preserves two invariant quantities, i.e., the mass-conservation law
and the energy-conservation law
Since it is hard to obtain the analytical solution of the FSE, the idea of developing numerical methods has drawn a growing number of researchers’ attention. Up to now, many efforts have been made to develop finite difference methods for the FSE, including the compact difference scheme [12], the mass-preserving schemes [13–15], and the mass- and energy-preserving schemes [16–20]. Li et al. [21–23] investigated a series of Galerkin finite element methods for the FSE, and they discussed the conservation, well-posedness and convergence properties of the discrete systems. In addition, spectral methods have also been applied in solving the nonlocal FSE, including spectral Galerkin schemes [24–30] and collocation schemes [31–35]. On the other hand, numerical studies of the FSE with Caputo fractional derivative in time were considered in [36–39].
The motivations of the current work are as follows. Firstly, since the conservative method performs better than the general goal method in long-time simulation, the discrete scheme which can preserve the invariant quantities of the original system is desirable. Moreover, to avoid time-consuming iterative process at each time step, an interesting topic is to construct a linearly implicit scheme for the SCFSEs. Furthermore, we intend to consider the unconditionally convergent spectral method, which takes advantage of spectral accuracy in space. Based on these considerations, the main objective of this paper is to develop a linearized Galerkin–Legendre spectral scheme for solving the SCFSEs. The derived scheme can preserve both the mass- and the energy-conservation laws in the discrete sense. Based on the discrete energy-conservation law, we show that the numerical solutions are bounded in \(L^{\infty }\)-norm. Moreover, the discrete scheme is proved to be unconditionally convergent with second-order accuracy in time and spectral accuracy in space by the energy method.
The outline of this paper is given as follows. In Sect. 2, some useful definitions and lemmas are recalled. In Sect. 3, a linearized Legendre spectral scheme is constructed for the SCFSEs. In Sect. 4, the conservation, boundedness and convergence properties of the proposed scheme are analyzed theoretically. Some numerical results are presented in Sect. 5, and some conclusions are drawn in the last section.
2 Preliminaries
In this section, before deriving the fully discrete Legendre spectral scheme for the SCFSEs, we first introduce some notations, definitions and lemmas which play an important role in subsequent theoretical analysis.
2.1 Notation
Define the inner product in the space \(L^{2}(\Omega )\) as \((v, u):=\int _{\Omega }v\bar{u}\,dx\) and the associated \(L^{2}\)-norm is denoted by \(\|\cdot \|\). Besides, define the \(L^{p}\)-norm \((1\leq p<\infty )\) and \(L^{\infty }\)-norm as follows:
2.2 Fractional derivative spaces
Definition 1
For \(\alpha >0\), define the semi-norms and norms of the left, right and symmetric fractional derivative spaces on Ω as
and \(J_{L,0}^{\alpha }(\Omega )\), \(J_{R,0}^{\alpha }(\Omega )\), \(J_{S,0}^{\alpha }(\Omega )\) denote the closure of \(C_{0}^{\infty }(\Omega )\) with respect to the above norms, respectively.
Definition 2
For \(\alpha >0\), define the semi-norm
and the norm
and \(H_{0}^{\alpha }(\Omega )\) denotes the closure of \(C^{\infty }(\Omega )\) with respect to \(\|\cdot \|_{H^{\alpha }(\Omega )}\), where ξ and v̂ represent the Fourier transform parameter and the Fourier transform of v, respectively.
Next we recall some useful properties of the above semi-norms, norms and spaces.
Lemma 1
For \(\alpha >0\) and \(\alpha \neq n-\frac{1}{2}\), \(n\in \mathbb{N}\), then \(J_{L,0}^{\alpha }(\Omega )\), \(J_{R,0}^{\alpha }(\Omega )\), \(J_{S,0}^{\alpha }(\Omega )\) and \(H^{\alpha }_{0}(\Omega )\) are equal with equivalent norms and semi-norms.
Lemma 2
(Fractional Poincaré–Friedrichs inequality [40, 41])
For \(v\in J_{L,0}^{\alpha }(\Omega )\), \(0<\mu <\alpha \), we have
Besides, for \(v\in J_{R,0}^{\alpha }(\Omega )\), \(0<\mu <\alpha \), we have
Similar conclusion can be established for \(v\in H^{\alpha }_{0}(\Omega )\) with \(\alpha \neq n-\frac{1}{2}\), \(n\in \mathbb{N}\).
Lemma 3
([42])
Let \(1<\alpha \leq 2\), for \(v, w\in J_{L}^{\alpha }(\Omega )\) (or \(J_{R}^{\alpha }(\Omega ) \)), \(v|_{\partial \Omega }=0\), \(w|_{\partial \Omega }=0\), then we have
3 Fully discrete Legendre spectral scheme
In this section, we will construct a Legendre spectral method for numerically solving the SCFSEs (1)–(4).
3.1 The semi-discrete variational scheme
The Legendre polynomials \(L_{k}(s)\) are determined by the following recurrence relation:
Denote
Then the approximate function space \(V_{N}^{0}\) is given as
The semi-discrete variational scheme for the SCFSEs (1)–(4) is to find \(u_{N}, v_{N} :[0,T]\rightarrow V^{0}_{N}\) such that
where \(I_{N}\) represents the Legendre–Gauss–Lobatto (LGL) interpolation operator [43]. The bilinear form \(B(\cdot ,\cdot )\) in (19) and (20) is defined as
where Lemma 3 has been used in deriving (22). For convenience of theoretical analysis, one can define the following semi-norm and norm:
By virtue of Lemma 1, \(|v|_{\frac{\alpha }{2}}\) and \(\|v\|_{\frac{\alpha }{2}}\) are equivalent with the semi-norms and norms of \(J_{L}^{\frac{\alpha }{2}}(\Omega )\), \(J_{R}^{\frac{\alpha }{2}}(\Omega )\), \(J_{S}^{\frac{\alpha }{2}}(\Omega )\) and \(H^{\frac{\alpha }{2}}(\Omega )\).
3.2 The fully discrete Galerkin–Legendre spectral scheme
For a given positive constant T and any positive integer M, let \(\tau =T/M\) and denote \(t_{n}=n\tau\) (\(0\leq n\leq M\)). For any function sequence \(\{\lambda ^{n}\}\) defined on Ω, when \(0\leq n\leq M-1\), we denote
Based on Legendre spectral method for space discretization and a linearized Crank–Nicolson difference scheme in time, we develop a linearized spectral scheme for the Schrödinger system (1)–(4), which is to find \(u_{N}^{n+1},v_{N}^{n+1}\in V_{N}^{0}\) such that
To obtain the first step approximate solutions \(u_{N}^{1}\) and \(v_{N}^{1}\), we employ the following Crank–Nicolson scheme:
with the initial conditions
4 Theoretical analysis
This section is devoted to discussing the theoretical analysis of the spectral scheme (24)–(28), including the discrete mass- and energy-conservation laws, boundedness and the unconditional convergence.
4.1 Conservative properties of the spectral scheme
Theorem 1
The fully discrete spectral scheme (24)–(28) is conservative in the sense that
where \(M^{n}\) and \(E^{n}\) are defined, respectively, as
Proof
Taking \(w=\tilde{u}_{N}^{n}\) in (24) gives
As a result
and
then considering the imaginary part of (33) yields
It further means that
Taking \(w=\tilde{v}_{N}^{n}\) in (25), we arrive at
Similarly, we take the imaginary part of (38) to get
Combining (37) and (39), we can conclude that the discrete mass conservation law (29) holds.
On the other hand, substituting \(w=\delta _{\hat{t}} u_{N}^{n}\) in (24), we arrive at
It is easy to get
and
Taking the real part of (40), and combining with (41)–(43), we have
Denoting \(w=\delta _{\hat{t}} v_{N}^{n}\) in (25), we obtain
Analogously, taking the real part of the above equation yields
It is easy to get from (44) and (46)
Noticing the definition of \(E^{n}\), it follows from (47) that \(E^{n}=E^{n-1}\) for \(1\leq n\leq M-1\), which further implies that (30) holds. Therefore, we complete the proof. □
4.2 A prior bound
Lemma 4
([44])
If \(\frac{1}{2}-\frac{1}{p}<\alpha \leq 1\) and \(2\leq p\leq \infty \), then there exists a positive constant \(C_{\alpha }\) such that
Lemma 5
([44])
If \(0\leq \alpha _{0}\leq \alpha \leq 1\), \(\frac{1}{2}-\frac{1}{p}<\alpha _{0}\leq 1\) and \(2\leq p\leq \infty \), there exists a constant \(C_{\alpha _{0}}>0\) such that
Based on the discrete mass- and energy-conservation laws, we can establish a prior bound for the numerical solutions of the scheme (24)–(28) in both \(L^{2}\)- and \(L^{\infty }\)-norms.
Theorem 2
The solutions of the fully discrete spectral scheme (24)–(28) are bounded in the sense that
Proof
It is easy to deduce that
Combining with the discrete mass conservation law (29), we have
When \(\tau \leq \frac{1}{2|\varrho |}\), it follows from (53) that (50) holds.
Noticing the energy-conservation law (30), we have
where the Cauchy–Schwartz inequality, (50) and Lemma 5 have been used in deriving the above inequalities. Since the semi-norm \(|\cdot |_{\frac{\alpha }{2}}\) is equivalent to the semi-norm \(|\cdot |_{H^{\frac{\alpha }{2}}}\), and noticing Lemma 2, it follows that there exists a positive constant \(C_{1}\) such that
In view of (30), (54) and (55), we obtain
Noticing that \(1<\alpha \leq 2\), when taking \(\frac{1}{4}<\alpha _{0}<\frac{\alpha }{4}\), it follows from (56) that \(E^{1}\rightarrow +\infty \) if \(\|u^{n}_{N}\|_{H^{\frac{\alpha }{2}}}^{2}+\|u^{n+1}_{N}\|_{H^{ \frac{\alpha }{2}}}^{2} +\|v^{n}_{N}\|_{H^{\frac{\alpha }{2}}}^{2}+\|v^{n+1}_{N} \|_{H^{\frac{\alpha }{2}}}^{2}\rightarrow +\infty \). However, we can conclude that \(E^{1}\) is bounded by the discrete conservation law (30). It will lead to a contradiction. Therefore, we can deduce that
According Lemma 4, we can further deduce from (57) that (51) holds, which completes the proof. □
4.3 Convergence analysis
Now we turn to discuss the convergence analysis of the discrete spectral scheme (24)–(28). To this end, we first introduce the projection operator \(\Pi _{N}^{\frac{\alpha }{2},0}:H_{0}^{\frac{\alpha }{2}}(\Omega ) \rightarrow V_{N}^{0}\), which satisfies
The error estimate of the projection operator \(\Pi _{N}^{\frac{\alpha }{2},0}\) is given in the following lemma.
Lemma 6
([25])
Let \(v\in H_{0}^{\frac{\alpha }{2}}(\Omega )\bigcap H^{s}(\Omega )\), we have
Lemma 7
([45])
For any complex functions V, W, v and w, we have
Lemma 8
(Grönwall inequality [46])
Suppose that \(\{g_{l}| l\geq 0\}\) is a nonnegative sequence, \(\beta >0\), and the sequence \(\{\varepsilon _{l}| l\geq 0\}\) satisfies
If \(p_{l}\geq 0\) for any \(l\geq 0\), \(\varepsilon _{0}\leq \beta \), then we have
For notation convenience, let \(u^{\frac{1}{2}}:=u(x,\frac{1}{2})\) and \(v^{\frac{1}{2}}:=v(x,\frac{1}{2})\), and we also use \(u^{n}\) and \(v^{n}\) to represent the analytical solutions \(u(x,t_{n})\) and \(u (x,t_{n})\), respectively. In view of (24) and (25), the exact solutions \(u^{n}\) and \(v^{n}\) satisfy the equations
where the local truncation errors \(R^{n}_{u}\) and \(R^{n}_{v}\) are defined as
From (26) and (27), we can also deduce that
where the local truncation errors \(R^{0}_{u}\) and \(R^{0}_{v}\) are given as
By virtue of a Taylor expansion, we can deduce that
Next, we focus on a rigorous convergence analysis for the spectral scheme (24)–(28).
Theorem 3
Assume that the analytical solutions of the Schrödinger system (1)–(4) satisfy \(u,v\in C^{3} (0,T;H^{\frac{\alpha }{2}}_{0}(\Omega )\bigcap H^{s}( \Omega ) )\). Then there exists a positive constant \(\tau _{0}\) such that when \(\tau <\tau _{0}\), the solutions of the fully discrete spectral scheme (24)–(28) satisfy
where C is a positive constant which is independent of τ and N.
Proof
We first consider the case of \(\alpha \neq \frac{3}{2}\). To derive the convergence result of the spectral scheme (24)–(28), we split the errors into
Subtracting (24) from (61) and subtracting (25) from (62), we arrive at
where
By virtue of (58), (72) and (73), the above equations (74) and (75) can be rewritten in the following equivalent form:
where
Analogously, it follows from (26), (27), (65) and (66) that
where
Thanks to Lemma 6 and (69), we obtain
Now taking \(w=\hat{\theta }^{\frac{1}{2}}\) in (81) and \(w=\hat{\eta }^{\frac{1}{2}}\) in (82), and then considering the imaginary part of the resulting equations, we have
It is obvious that \(\operatorname{Im}(\hat{\eta }^{\frac{1}{2}},\hat{\theta }^{\frac{1}{2}})+\operatorname{Im}( \hat{\theta }^{\frac{1}{2}},\hat{\eta }^{\frac{1}{2}})=0\), then adding (87) and (88) leads to
Noticing the definition of \(G_{u}^{\frac{1}{2}}\), and using Lemma 7 as well as Theorem 2, we observe that
where \(C_{4}\) denotes a positive constant. Following a similar analysis, we also conclude that
Therefore, we further deduce that
Analogously, we find that
Obviously, we can also deduce that
Substituting (92)–(94) into (89), we have
This, combined with Lemma 6 and (86), gives
Moreover, one easily gets
Therefore, when the time step τ in (96) is chosen sufficiently small such that \(\tau \leq \frac{1}{(12C_{4}+1)}\), it follows from (96)–(98) that
This together with Lemma 6 and the triangle inequality implies that (70) holds for \(n=1\).
By mathematical induction, we assume that (70) is valid for \(1\leq n\leq m\). Now we turn to a proof that the stated conclusion still holds for \(n=m+1\). To this end, taking \(w=\tilde{\theta }^{n}\) in (78) and \(w=\tilde{\eta }^{n}\) in (79), respectively, and considering the imaginary part of the resulting equations, we have
Combining (100) and (101) gives
In view of the definition of \(G_{u}^{n}\), Lemma 7 and Theorem 2,
and
Hence, we furthermore obtain
and
Also, we can conclude that
and
Substituting (105)–(108) into (102), we obtain
By virtue of Lemma 6 and (86), it follows from (109) that
Summing (111) for n from 1 to m leads to
This combined with (97)–(99) gives
Consequently, when \(\tau \leq \frac{1}{2(10C_{4}+2|\varrho |+1)}\), from Lemma 8
which further indicates that
where Lemma 6 and the triangle inequality have been used. It means that the conclusion (70) still holds for \(n=m+1\), which completes the proof of Theorem 3 for \(\alpha \neq \frac{3}{2}\).
For the case of \(\alpha =\frac{3}{2}\), the stated result (71) can be obtained by a similar analysis. Hence, we have completed the proof of Theorem 3. □
5 Numerical experiment
In this section, we present some numerical results to confirm our theoretical analysis of the spectral scheme (24)–(28).
Example 1
Consider the following strongly coupled fractional Schrödinger system:
subject to the initial conditions
and the homogeneous boundary conditions
where the computation domain is chosen sufficiently large as \(\Omega =(-25,25)\).
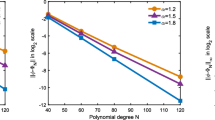
The first objective is to check the convergence behavior of the spectral scheme (24)–(28). Since the analytical solutions of the system (116)–(119) are difficult to find, we take the numerical solutions computed by fixed \(\tau =10^{-5}\) and \(N=512\) as the “exact” solutions. When fixing \(N=512\), we present the \(L^{2}\)-errors with different time steps in Fig. 1. It can be observed that the derived spectral scheme has second-order temporal accuracy. Moreover, we fix \(\tau =10^{-5}\) and plot the \(L^{2}\)-errors with the change of N in Fig. 2. It shows that the errors are exponentially decaying with N increases, and this indicates the spectral accuracy in space.
Now we turn to a validation of the discrete conservation laws of Theorem 1. To the end, we take \(\tau =0.001\) and \(N=256\) and depict the mass \(M^{n}\) and the energy \(E^{n}\) as well as corresponding error functions for different α in Figs. 3–6. It can be found that the spectral scheme preserves the total discrete mass and energy very well. Moreover, it can be observed that the values of the mass \(M^{n}\) are independent of α, while the values of the energy \(E^{n}\) are dependent of α. These numerical results are all in line with our theoretical analysis. Finally, we plot the graphs of the numerical solutions for \(\alpha =1.6\) and \(\alpha =1.95\) in Figs. 7 and 8. It shows that the value of α affects the shape of wave functions dramatically.
6 Conclusion
In the current work, we have constructed a linearized Galerkin–Legendre spectral method for solving the strongly coupled nonlinear fractional Schrödinger equations. The main novelty of this paper is that the proposed scheme can preserve both the mass- and the energy-conservation laws in the discrete sense, and the optimal error estimate is established rigorously without imposing any restriction on the grid ratio. The discrete scheme is efficient in the sense that only a linear system needs to be solved at each time step. Theoretical results show that our scheme is second-order convergent in time and at the same time has the advantage of spectral accuracy in space. Numerical results show that the derived scheme is quite efficient and exhibits remarkable mass- and energy-preserving properties. The spectral method and corresponding theoretical analysis for high-dimensional SCFSEs is worth of further investigation.
References
Laskin, N.: Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 268, 298–305 (2000)
Laskin, N.: Fractional Schrödinger equation. Phys. Rev. E 66, 056108 (2002)
Longhi, S.: Fractional Schrödinger equation in optics. Opt. Lett. 40, 1117–1120 (2015)
Zhang, Y., Liu, X., Belić, M.R., Zhong, W., Zhang, Y., Xiao, M.: Propagation dynamics of a light beam in a fractional Schrödinger equation. Phys. Rev. Lett. 115, 180403 (2015)
Cho, Y., Hwang, G., Kwon, S., Lee, S.: Well-posedness and ill-posedness for the cubic fractional Schrödinger equations. Discrete Contin. Dyn. Syst. 35, 2863–2880 (2015)
Guo, B., Han, Y., Xin, J.: Existence of the global smooth solution to the period boundary value problem of fractional nonlinear Schrödinger equation. Appl. Math. Comput. 204(1), 468–477 (2008)
Guo, B., Huo, Z.: Global well-posedness for the fractional nonlinear Schrödinger equation. Commun. Partial Differ. Equ. 36, 247–255 (2010)
Defterli, O., D’Elia, M., Du, Q., Gunzburger, M., Lehoucq, R., Meerschaert, M.M.: Fractional diffusion on bounded domains. Fract. Calc. Appl. Anal. 18(2), 342–360 (2015)
Du, Q., Gunzburger, M., Lehoucq, R., Zhou, K.: Analysis and approximation of nonlocal diffusion problems with volume constraints. SIAM Rev. 54(4), 667–696 (2012)
Deng, W., Li, B., Tian, W., Zhang, P.: Boundary problems for the fractional and tempered fractional operators. Multiscale Model. Simul. 16(1), 125–149 (2018)
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1999)
Zhao, X., Sun, Z., Hao, Z.: A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J. Sci. Comput. 36(6), 2865–2886 (2014)
Wang, D., Xiao, A., Yang, W.: Crank–Nicolson difference scheme for the coupled nonlinear Schrödinger equations with the Riesz space fractional derivative. J. Comput. Phys. 242, 670–681 (2013)
Wang, P., Huang, C.: A conservative linearized difference scheme for the nonlinear fractional Schrödinger equation. Numer. Algorithms 69, 625–641 (2015)
Wang, P., Huang, C.: Split-step alternating direction implicit difference scheme for the fractional Schrödinger equation in two dimensions. Comput. Math. Appl. 71, 1114–1128 (2016)
Wang, D., Xiao, A., Yang, W.: A linearly implicit conservative difference scheme for the space fractional coupled nonlinear Schrödinger equations. J. Comput. Phys. 272, 644–655 (2014)
Wang, D., Xiao, A., Yang, W.: Maximum-norm error analysis of a difference scheme for the space fractional CNLS. Appl. Math. Comput. 257, 241–251 (2015)
Wang, P., Huang, C.: An energy conservative difference scheme for the nonlinear fractional Schrödinger equations. J. Comput. Phys. 293, 238–251 (2015)
Wang, P., Huang, C., Zhao, L.: Point-wise error estimate of a conservative difference scheme for the fractional Schrödinger equation. J. Comput. Appl. Math. 306, 231–247 (2016)
Ran, M., Zhang, C.: A conservative difference scheme for solving the strongly coupled nonlinear fractional Schrödinger equations. Commun. Nonlinear Sci. Numer. Simul. 41, 64–83 (2016)
Li, M., Huang, C., Wang, P.: Galerkin finite element method for nonlinear fractional Schrödinger equations. Numer. Algorithms 74, 499–525 (2017)
Li, M., Gu, X., Huang, C., Fei, M., Zhang, G.: A fast linearized conservative finite element method for the strongly coupled nonlinear fractional Schrödinger equations. J. Comput. Phys. 358, 256–282 (2018)
Li, M., Huang, C., Ming, W.: A relaxation-type Galerkin FEM for nonlinear fractional Schrödinger equations. Numer. Algorithms 83(1), 99–124 (2020)
Zhang, H., Jiang, X., Wang, C., Chen, S.: Crank–Nicolson Fourier spectral methods for the space fractional nonlinear Schrödinger equation and its parameter estimation. Int. J. Comput. Math. 96, 238–263 (2019)
Zhang, H., Jiang, X., Wang, C., Fan, W.: Galerkin–Legendre spectral schemes for nonlinear space fractional Schrödinger equation. Numer. Algorithms 79, 337–356 (2018)
Liang, X., Khaliq, A.Q.M.: An efficient Fourier spectral exponential time differencing method for the space-fractional nonlinear Schrödinger equations. Comput. Math. Appl. 75, 4438–4457 (2018)
Wang, Y., Meng, L.: A conservative spectral Galerkin method for the coupled nonlinear space-fractional Schrödinger equations. Int. J. Comput. Math. 96, 2387–2410 (2019)
Zhang, H., Jiang, X.: Spectral method and Bayesian parameter estimation for the space fractional coupled nonlinear Schrödinger equations. Nonlinear Dyn. 95(2), 1599–1614 (2019)
Wang, Y., Mei, L., Li, Q., Bu, L.: Split-step spectral Galerkin method for the two-dimensional nonlinear space-fractional Schrödinger equation. Appl. Numer. Math. 136, 257–278 (2019)
Wang, Y., Li, Q., Mei, L.: A linear, symmetric and energy-conservative scheme for the space-fractional Klein–Gordon–Schrödinger equations. Appl. Math. Lett. 95, 104–113 (2019)
Amore, P., Fernández, F.M., Hofmann, C.P., Sáenz, R.A.: Collocation method for fractional quantum mechanics. J. Math. Phys. 51, 122101 (2010)
Duo, S., Zhang, Y.: Mass-conservative Fourier spectral methods for solving the fractional nonlinear Schrödinger equation. Comput. Math. Appl. 71, 2257–2271 (2016)
Wang, P., Huang, C.: Structure-preserving numerical methods for the fractional Schrödinger equation. Appl. Numer. Math. 129, 137–158 (2018)
Huang, Y., Li, X., Xiao, A.: Fourier pseudospectral method on generalized sparse grids for the space-fractional Schrödinger equation. Comput. Math. Appl. 75, 4241–4255 (2018)
Fei, M., Huang, C., Wang, P.: Error estimates of structure-preserving Fourier pseudospectral methods for the fractional Schrödinger equation. Numer. Methods Partial Differ. Equ. 36(2), 369–393 (2020)
Wei, L., Zhang, X., Kumar, S., Yildirim, A.: A numerical study based on an implicit fully discrete local discontinuous Galerkin method for the time-fractional coupled Schrödinger system. Comput. Math. Appl. 64, 2603–2615 (2012)
Ran, M., Zhang, C.: Linearized Crank–Nicolson scheme for the nonlinear time-space fractional Schrödinger equations. J. Comput. Appl. Math. 355, 218–231 (2019)
Li, D., Wang, J., Zhang, J.: Unconditionally convergent L1-Galerkin FEMs for nonlinear time-fractional Schrödinger equations. SIAM J. Sci. Comput. 39, 3067–3088 (2017)
Fei, M., Wang, N., Huang, C., Ma, X.: A second-order implicit difference scheme for the nonlinear time-space fractional Schrödinger equation. Appl. Numer. Math. 153, 399–411 (2020)
Ervin, V.J., Roop, J.P.: Variational formulation for the stationary fractional advection dispersion equation. Numer. Methods Partial Differ. Equ. 22(3), 558–576 (2006)
Roop, J.P.: Variational solution of the fractional advection dispersion equation. PhD thesis, Clemson University, South Carolina (2004)
Zhang, H., Liu, F., Anh, V.: Galerkin finite element approximation of symmetric space-fractional partial differential equations. Appl. Math. Comput. 217(6), 2534–2545 (2010)
Shen, J., Tang, T., Wang, L.: Spectral Methods: Algorithms, Analysis and Applications. Springer Series in Computational Mathematics, vol. 41. Springer, Berlin Heidelberg (2011)
Li, M., Huang, C., Wang, N.: Galerkin finite element method for the nonlinear fractional Ginzburg–Landau equation. Appl. Numer. Math. 118, 131–149 (2017)
Sun, Z., Zhao, D.: On the \(l_{\infty}\) convergence of a difference scheme for coupled nonlinear Schrödinger equations. Comput. Math. Appl. 59, 3286–3300 (2010)
Quarteroni, A., Valli, A.: Numerical Approximation of Partial Differential Equations. Springer, Berlin (1994)
Acknowledgements
The authors wish to thank the editor for taking time to handle the manuscript and the anonymous referees for their valuable comments and suggestions which lead to an improvement of this paper.
Availability of data and materials
Not applicable.
Funding
This work was supported by NSF of China (Nos. 11771163 and 12011530058), China Postdoctoral Science Foundation (No. 2019M662506), Natural Science Foundation of Hunan Province (No. 2020JJ5612), Scientific Research Fund of Hunan Provincial Education Department (Nos. 19B064 and 19C0181) and Hunan Province Key Laboratory of Industrial Internet Technology and Security (2019TP1011).
Author information
Authors and Affiliations
Contributions
All authors contributed equally significantly in this manuscript and they read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fei, M., Zhang, G., Wang, N. et al. A linearized conservative Galerkin–Legendre spectral method for the strongly coupled nonlinear fractional Schrödinger equations. Adv Differ Equ 2020, 661 (2020). https://doi.org/10.1186/s13662-020-03017-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-03017-w