Abstract
In this study, we examine the stabilization of fractional-order chaotic nonlinear dynamical systems with model uncertainties and external disturbances. We used the sliding mode controller by a new approach for controlling and stabilization of these systems. In this research, we replaced a continuous function with the sign function in the controller design and the sliding surface to suppress chattering and undesirable vibration effects. The advantages of the proposed control method are rapid convergence to the equilibrium point, the absence of chattering and unwanted oscillations, high resistance to uncertainties, and the possibility of applying this method to most fractional order chaotic systems. We applied the direct method of Lyapunov stability theory and the frequency distributed model to prove the stability of the slip surface and closed loop system. Finally, we simulated this method on two commonly used and practical chaotic systems and presented the results.
Similar content being viewed by others
1 Introduction
Fractional-order calculations play an important role in various scientific fields. Recently the application of fractional-order is known as an important topic in engineering [1]. The problem of fractional-order equations was first raised by Leibniz in a letter in September 1695 on the fractional-order derivative, and has become an issue for research that is still under investigation [2]. This branch of science had long been a theoretical subject, but there was no application to it. Deficit computing have attracted the interest of many scholars in recent decades [3]. Scientists have recently shown that fractional order equations are capable of modeling different phenomena more accurately than the integer-order equations and are a powerful tool for describing the structures of a system with complex dynamics. Most systems in nature obey fractional dynamics, and their approximations are considered integer. For example, Brownian fractional motion [4], porous media dynamics [5], time-lapse random walk theory [6], heat transfer process [7], electrochemical processes and flexible structures [8] and chaos theory are among these. The ability of fractional order calculators to improve the performance of controllers has been demonstrated [9]. In 1988, Oustaloup introduced a robust fractional-order controller called Crown, and created a starting point for entering fractional-order relationships into control. Then in 1994, Podlubny introduced a PID fractional-order controller, which is one of the best-known fractional-order controllers today. Since then, many different methods have been investigated with respect to fractional-order controllers, including optimal fractional-order controllers, adaptive controllers, and fractional sliding mode controllers [10].
In recent years, fractional-order systems have been used in numerous fields of sciences. For instance, in physics: nonlinear optics [11] and quantum mechanics [12] in electronics: electromagnetic waves [13] electrodynamics [14], and electrical circuits [15, 16], in medical and biological sciences: modeling of HIV infection [17], modeling of muscular blood vessels [18] and the movement of bacteria and food seeking of microbes [19], in psychology and social sciences: modeling of love [20] and modeling of happiness [21]. Moreover, the role of FDEs in the control engineering and renewable energy is well known in the related literature [22–31].
Chaotic behavior has been observed in various fields of science such as mechanics, electricity, physics, medicine, biology, and economics. The main goal of control engineers is chaos control, means, stopping chaotic oscillations or reducing them to normal oscillations. Various methods for controlling fractional-order chaotic systems have been presented so far, including feedback linearization [32, 33], fuzzy control [34–36], optimal control [37, 38], sliding mode control [39–41] and adaptive control [42–44].
Sliding mode control (SMC) is a nonlinear control strategy expressing considerable properties such as robustness, accuracy, simple implementation and immutability to uncertainties [45–47]. As is known, SMC includes two steps as follows.
-
The first one is to design appropriate sliding surface.
-
The second one is designing control input for the closed-loop system to change to the desired system specified by the sliding surface.
In recent years, a lot of works about control and stabilization of fractional-order systems have been designed by SMC in the literature. For instance, in [48], a fuzzy fractional-order sliding mode controller is designed for a group of nonlinear systems and a fractional-order sliding-surface is used to design the control law. Two robot arm systems and interconnected tanks were investigated by this method and it revealed that the control system by using the fractional-order sliding surface can provide a more robust and faster response in tracking the desired path. In [49] the sliding mode control method based on parameter setting with fuzzy control method is proposed for controlling a mechanical system. We also use fractional-order sliding surface in designing the sliding mode control law. Also, in [50] a fractional-order sliding mode control method is proposed for fractional adjustment of an ABS braking system that uses a \(PD^{\alpha }\) sliding surface in the design of the sliding mode control law. The results of experimental experiments show that this method performs better than deploying the integer sliding surface PI and P counteracting uncertainty in the ABS brake system and delivering the slip speed to the desired level.
One of the main issues in controller design is control under uncertain conditions and uncertainties in parameters. So, there has been a great deal of research and study of uncertain processes in recent years. Among the advanced control methods, sliding mode control is more prominent than other methods due to its high robustness to uncertainties and unmodified dynamics [51]. But despite its high capabilities, this method has one major drawback: it is the oscillation at the control input that is known as the chattering phenomenon. The chattering phenomenon can lead to unwanted and undesirable oscillations in the control system and make the behavior of the system nonideal [52, 53].
There are several ways to prevent the chattering. One of the most commonly used methods for smoothing unwanted oscillations is to apply a fuzzy algorithm to determine the amplitude of a narrow boundary layer around the slip surface, but slowing control is a problem of this method [54].
Another way is to exert high-order sliding mode control. In this way, we can maintain the main feature of the standard sliding mode control and prevent the chattering phenomenon without reducing accuracy [55]. But, in this method, when high-order slider dynamics increase the relative degree of the system, the algorithm of high-order sliding mode algorithm also faces the problem of chattering. Also, it is so hard to design control law to guarantee system convergence properties using systematic methods for controlling high-order and even second-order sliding modes [56]. The continuous approximation method is more applicable to reduce chattering than other methods. This method designs the control signal discontinuity by creating a narrow boundary layer around the sliding surface and no problems have been reported so far [57].
In this paper, fractional integral sliding mode control (FISMC) is applied to the control of nonlinear chaotic fractional order dynamical systems. Also, the continuous function has been exerted instead of the sign function in sliding surface design and control input to prevent fluctuation and chattering. The advantages of the proposed control method are rapid convergence to the equilibrium point, the absence of chattering and unwanted oscillations, high resistance to uncertainties, and the possibility of applying this method to most fractional order chaotic systems.
Briefly, the main contributions of the paper are as follows:
-
1.
Designing a novel chattering-free fractional-integral-based SMC approach, by which can be accomplished the stabilization of a vast class of fractional-order chaotic nonlinear systems.
-
2.
The proposed FISMC is robust against the system uncertainties and external disturbances.
-
3.
The global stability and asymptotic stability of the controlled closed-loop fractional-order chaotic nonlinear systems are concluded according to frequency distributed model and fractional version of the Lyapunov stability theorem.
-
4.
Using two applicable examples, the validation of the proposed method is guaranteed.
The article continues with the second part of this article, which contains the system’s definitions, descriptions and theorems. In the third section, we introduce the sliding mode control method and prove its stability. The fourth section contains two popular fractional order systems that are investigated based on the proposed control input and the simulation results confirm speed and accuracy of this method. Finally, the concluding section is presented.
2 Introductory concepts and system descriptions
2.1 Introductory concepts
Definition 1
The Riemann–Liouville fractional integral of the order α is defined as follows [58]:
where \(\Gamma (\cdot)\) is Euler’s gamma function.
Definition 2
The Caputo fractional derivative of a continuous function \(f(t):R^{ +} \to R\) of the order α is defined as follows [58]:
Property 1
If c is a fixed number, then \({}_{t_{0}}^{C}D_{t}^{\alpha } c = 0\).
In the rest of the paper, \(D^{\alpha } \) is the Caputo fractional derivative.
2.2 System description
Since in practical application the system dynamics is often affected by the uncertainty of the model and the external disturbances, in this paper a nonlinear fractional order system has been shown with the model uncertainties and the external disturbances as follows [59, 60]:
where \(\alpha \in (0,1)\) is the order of derivative and \(x(t) = [ x_{1}(t),x_{2}(t),\ldots,x_{n}(t) ]^{T} \in R^{n}\) denote the system state vector, \(f_{i}(t,x(t)) \in R\) is the given nonlinear function of t and \(x(t)\), \(\Delta f_{i}(t,x(t))\) is the uncertainty term, \(d_{i}(t) \in R\) is the external disturbance term of the system and \(u_{i}(t) \in R\) is the control input.
Because in practice system uncertainties and external disturbances can never be infinite, in this paper the uncertainties \(\Delta f_{i}(t,x(t))\) and external disturbances \(d_{i}(t)\) are assumed to be bounded as follows [61]:
where the constant coefficients \(\rho _{1}, \rho _{2}, \ldots, \rho _{n}\) are positive and these upper bounds are used in the controller design.
Now, suppose that
then the fractional order system (3) can be rewritten as follows:
The following theorem is presented to illustrate the method of converting the fractional order differential equation system to the frequency distributed model (FDM) model.
Theorem 1
([62])
Set
and define the function \(\varphi (\omega ,t)\)as follows:
then the fractional-order system (5) is equivalent to the following system:
To find the stability condition of the fractional order system, Theorem 2 is stated.
Remark 1
Actually, the FDM model, by converting a fractional derivative to an ordinary one, causes reduction of the complexity and difficulty of fractional calculations. On the other hand, it can provide a new Lyapunov function to prove the stability of fractional differential equations.
Theorem 2
([63])
The fractional-order system (3) is Mittag-Leffler stable at the equilibrium point \(\bar{x} = 0\)if there exists a continuous function \(V(t,x(t))\)that satisfies
in which \(V(t,x(t)):[0,\infty ) \times D \to R\)satisfies locally Lipschitz condition on x, \(\dot{V}(t,x(t))\)is piecewise continuous, and \(\lim_{\tau \to t^{ +}} \dot{V}(\tau ,x(\tau ))\)exists for any \(t \in [0,\infty )\), \(D \subset R^{n}\)is a domain containing the origin and for \(t \ge 0\)
where \(\beta \in (0,1)\)and \(\alpha _{1}\), \(\alpha _{2}\), \(\alpha _{3}\), a and b are arbitrary positive constants.
Theorem 3
([36])
If \(x(t)\)denotes a continuously differentiable function, the following inequality holds almost everywhere:
in which \(x(t^{ +} ) = \lim_{\tau \to t^{ +}} x(\tau )\).
3 Controller design
For the fractional-order system (3) we define the sliding surface as follows:
where \(k_{i} > 1\), \(0 < \eta < 1\).
The following equations are met when the system works on the sliding mode:
So, the dynamics of sliding surface (11) is obtained as follows:
Now it will be shown that the proposed sliding surface is stable.
Theorem 4
If the sliding surface is selected in the form (11), then the sliding dynamics (12) is stable and its state trajectories will converge to zero.
Proof
According to Theorem 1, one can convert (12) to the distributed frequency model as follows:
We know that, to prove the stability of the above sliding surface, by using the direct method of the Lyapunov theory, it is sufficient to select a positive-definite function as Lyapunov function, and show that its derivative is a negative-definite function, so the following Lyapunov function has been chosen:
The above function is clearly positive-definite. By deriving this function will be obtained
Note that \(x_{i}(t)\) and \(\tanh (x_{i}(t))\) are always of the same sign, then the expression \(x_{i}(t) \tanh (x_{i}(t))\) will always have a positive value, and therefore the derivative of the Lyapunov function is negative-definite, and the proof of the stability of the sliding surface is completed. □
Now design the control input as follows:
Here \(\rho _{i}\), \(\gamma _{i}\), \(\lambda _{i}\) are positive parameters and \(0 < \delta < 1\).
We now show that the system (3) will converge with the designed input (15) to the sliding surface (11).
Theorem 5
Consider the fractional order system (3) and the sliding surface (11). If the system is controlled by the controller (15), then its state trajectories will converge to the sliding surface in a short time.
Proof
We have defined the Lyapunov function as
According to Theorem 3
By deriving the Lyapunov function
Since \(\tanh (S_{i}(t))\) and \(\operatorname{sgn} (S_{i}(t))\) are always of the same sign, their product is always positive, and therefore the derivative of the Lyapunov function is a negative-definite function and this completes this proof. □
Remark 2
The parameter \(k_{i}\) and η in (11) and (15) is actually the gain of the sliding surface, which should be set to a value of \(k_{i} >0\) and \(0 <\eta <1 \) to ensure the stability of the sliding surface’s equilibrium point. According to (11) and (15), one sees that the bigger value of the parameter \(k_{i}\) affects the control effort applied in the proposed approach.
Remark 3
The parameters \(\rho _{i}\), \(\gamma _{i}\), \(\lambda _{i}\) and δ in (15) are some gains for the control method. It is seen that Eq. (15) is proportional to the values of all \(\rho _{i}\), \(\gamma _{i}\), \(\lambda _{i}\) and δ. This means that larger values for \(\rho _{i}\), \(\gamma _{i}\), \(\lambda _{i}\) may make the value of the magnitude of oscillations increase, which is appropriate for the cases with large bounds of the system dynamics. However, according to (15) the larger δ (near 1) the larger control effort. Thus, a trade-off between unknown dynamics cancelation and control effort may be taken into account.
Remark 4
In a real application, since most of complex fractional-order systems cannot be modeled and unknown uncertainties always exist, this FISMC controller can apply for these kinds of FO systems. As one can see, the simulation results indicate the efficiency of the proposed method. In addition, the method can be easily implemented by using digital devices, like FPGA (Field-Programmable gate array) or DSP (Digital signal processing), with only the state of the systems.
Remark 5
Because of using fractional version of Lyapunov stability theorem for the stability analysis of the close-loop systems, we can be sure that the initial solution is feasible.
4 Numerical simulation
The effectiveness of the FISMC control method is illustrated by two practical examples. The first one is about controlling the chaotic fractional-order Lu and the second one is about controlling the fractional-order Arneodo system. Also, it should be clear that the numerical simulations are provided based on a modification of Adams–Bashforth–Moulton algorithm [57, 64], in the MATLAB software with \(h = 0.001\) as a time step.
Example 1
This example applies the chaotic fractional order system Lu. It is widely used in the power industries and distribution of power electricity systems. Figure 1 shows an example of a power electricity transmission and distribution system.
The differential equations of this system are expressed as follows:
Consider the system uncertainties and external disturbances
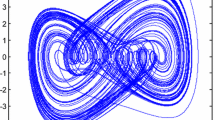
This system as \(0.91 < \alpha \le 1\) has chaotic behavior [37]. Figures 2 and 3 show the chaotic behavior of this system by selecting \(\alpha = 0.98\) in 3D and 2D plot modes, respectively. The initial states \(x_{1}(0)\), \(x_{2}(0)\) and \(x_{3}(0)\) are considered 10, 5- and 5, respectively. Obviously, extreme fluctuations in state variables cause a lot of energy to be consumed and the device to be consumed.
To control this system, we describe the sliding surface as follows:
For the appropriate control parameters, we apply the following control rules to the system:
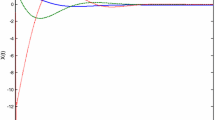
The stability of the primary system (17) is shown by using the control input (20) in Fig. 4. Very fast convergence to the equilibrium point about 0.1 second as well as the absence of noise in the closed-loop system behavior diagram indicates the high efficiency of the controller (20).
Closed-loop system states after applying the controller (20)
Figure 5 shows the convergence of the sliding surface (19) to zero and the control signal (20) is shown in Fig. 6. As it reveals, the state variables of the controlled system and the sliding surface and controller converge to zero in a short time of about 0.1 second, which will save energy and reduce device depreciation.
Time response of the sliding surface (19)
Time history of the FISMC controller (20)
In the following example, we intend to compare our sliding mode control method with another sliding mode controller. The method was designed in 2016 to stabilize fractional-order devices by Wang et al. [62].
This method is as follows:
Here \(S(t)\) is the sliding surface and \(u(t)\) is the control signal. By selecting \(\alpha = 0.98\) as the differential order, \(k_{1} = k_{2} = 3\), \(\eta _{1} = 2\), \(\xi _{1} = 10\), \(\xi _{2} = 5\), \(L = 8\) and \(k_{ 3} = 5\) as the controlling parameters, the state trajectories of this example occur as in Fig. 7. Figure 7 presents the comparison between the proposed FISMC method in this paper and the method [62]. As can be seen in Fig. 7, the continuous line shapes converge faster than the dotted lines to the equilibrium point.
Comparison of the proposed FISMC method with the method in Ref. [62]
In addition, more precisely in Fig. 7, we can see that the state variables are oscillating and noisy with the use of the sliding mode controllers [62], and this created chattering may create long-term problems for the device and the stability of the device will be destroyed. While the proposed method performs stabilization without any fluctuation or noise. Also, a discussion about this comparison is summarized in Table 1.
Example 2
In this example, we use our FISMC method to control the chaotic system of the Arneodo fractional order. This system is widely used in hydraulic dynamics. The Arneodo fractional order differential equation system is as follows [62]:
We consider external uncertainties and disturbances as follows:
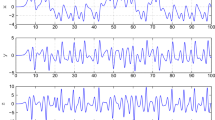
By selecting \(\alpha = 0.96\) the starting points are selected as \(x_{1}(0) = - 2\), \(x_{ 2} (0) = 5\), \(x_{ 3} (0) = 2\). Figures 8 and 9 show the instability and turbulence of the uncontrolled system in both three-dimensional and two-dimensional views.
Chaos in the behavior of Arneodo fractional order system (22)
To use the proposed controller, we describe the sliding surface as follows:
By choosing the appropriate parameters, we provide the controller as follows:
Figure 10 shows the state trajectories of the system over time after the proposed controller has been implemented. It is clear that all system state variables have converged to the equilibrium point rapidly and without fluctuation and the system has stabilized.
Figure 11 illustrates the sliding surface stability (24) and Fig. 12 illustrates the controller behavior (25) over time. It is observed that the controller components also converge to zero in a very short time. Therefore, the controller will consume very little energy, so the proposed method is consistent and practicable.
Stability of sliding surface (24)
Remark 6
Based on Eq. (15), and the concept of the tracking control, we can see in Figs. 4 and 10 that the tracking control converges to zero. Moreover, since the equilibrium point of the system equals zero, the asymptotic stability will be implied.
5 Conclusion
The present paper investigates a new method for stabilizing fractional-order chaotic nonlinear systems by using a sliding mode controller. A continuous function is replaced with the sign function in the controller design and the sliding surface to suppress chattering. Rapid convergence to the equilibrium point, high resistance to system uncertainties and external disturbances are main features of this method. The direct method of Lyapunov stability theory and the frequency distributed model (FDM) are applied to prove the stability of the sliding surface and closed-loop system. Two illustrative examples of the fractional order chaotic systems show the efficiency and applicability of the FISMC control method. It is noteworthy that the results and diagrams demonstrate appropriate performance, high speed of the control and the absence of oscillations. The proposed control scheme will significantly reduce the energy loss and depreciation of the device.
References
Roohi, M., Aghababa, M.P., Haghighi, A.R.: Switching adaptive controllers to control fractional-order complex systems with unknown structure and input nonlinearities. Complexity 21(2), 211–223 (2015)
Pham, V.-T., Kingni, S.T., Volos, C., Jafari, S., Kapitaniak, T.: A simple three-dimensional fractional-order chaotic system without equilibrium: dynamics, circuitry implementation, chaos control and synchronization. AEÜ, Int. J. Electron. Commun. 78, 220–227 (2017)
Asl, M.S., Javidi, M.: Numerical evaluation of order six for fractional differential equations: stability and convergency. Bull. Belg. Math. Soc. Simon Stevin 26(2), 203–221 (2019)
Biagini, F., Øksendal, B., Sulem, A., Wallner, N.: An introduction to white-noise theory and Malliavin calculus for fractional Brownian motion. Proc. R. Soc. Lond., Ser. A, Math. Phys. Eng. Sci. 460(2041), 347–372 (2004)
Kam, S.I., Nguyen, Q.P., Li, Q., Rossen, W.R.: Dynamic simulations with an improved model for foam generation. SPE J. 12(1), 35–48 (2007)
Shi, L., Yu, Z., Mao, Z., Xiao, A.: A directed continuous time random walk model with jump length depending on waiting time. Sci. World J. 2014, Article ID 182508 (2014)
Gabano, J.-D., Poinot, T., Kanoun, H.: Identification of a thermal system using continuous linear parameter-varying fractional modelling. IET Control Theory Appl. 5(7), 889–899 (2011)
Ivanov, D.V., Sandler, I.L., Kozlov, E.V.: Identification of fractional linear dynamical systems with autocorrelated errors in variables by generalized instrumental variables. IFAC-PapersOnLine 51(32), 580–584 (2018)
Hu, X., Zou, H., Tao, J., Gao, F.: Multimodel fractional predictive functional control design with application on an industrial heating furnace. Ind. Eng. Chem. Res. 57(42), 14182–14190 (2018)
Wang, Y., Luo, G., Gu, L., Li, X.: Fractional-order nonsingular terminal sliding mode control of hydraulic manipulators using time delay estimation. J. Vib. Control 22(19), 3998–4011 (2016)
Weitzner, H., Zaslavsky, G.M.: Some applications of fractional equations. Commun. Nonlinear Sci. Numer. Simul. 8(3–4), 273–281 (2003)
Laskin, N.: Fractional Schrödinger equation. Phys. Rev. E 66(5), 056108 (2002)
Zubair, M., Mughal, M.J., Naqvi, Q.A.: Electromagnetic wave propagation in fractional space. In: Electromagnetic Fields and Waves in Fractional Dimensional Space, pp. 27–60. Springer, Berlin (2012)
Tarasov, V.E., Trujillo, J.J.: Fractional power-law spatial dispersion in electrodynamics. Ann. Phys. 334, 1–23 (2013)
Luo, Y., Chen, Y.Q., Pi, Y.G.: Experimental study of fractional order proportional derivative controller synthesis for fractional order systems. Mechatronics 21(1), 204–214 (2011)
Gheisarnejad, M., Khooban, M.H.: Design an optimal fuzzy fractional proportional integral derivative controller with derivative filter for load frequency control in power systems. Trans. Inst. Meas. Control 41(9), 2563–2581 (2019)
Yan, Y., Kou, C.: Stability analysis for a fractional differential model of HIV infection of CD4+ T-cells with time delay. Math. Comput. Simul. 82(9), 1572–1585 (2012)
Aghababa, M.P., Borjkhani, M.: Chaotic fractional-order model for muscular blood vessel and its control via fractional control scheme. Complexity 20(2), 37–46 (2014)
Cohen, I., Golding, I., Ron, I.G., Ben-Jacob, E.: Biofluiddynamics of lubricating bacteria. Math. Methods Appl. Sci. 24(17–18), 1429–1468 (2001)
Ahmad, W.M., El-Khazali, R.: Fractional-order dynamical models of love. Chaos Solitons Fractals 33(4), 1367–1375 (2007)
Song, L., Xu, S., Yang, J.: Dynamical models of happiness with fractional order. Commun. Nonlinear Sci. Numer. Simul. 15(3), 616–628 (2010)
Teng, L., Iu, H.H., Wang, X., Wang, X.: Chaotic behavior in fractional-order memristor-based simplest chaotic circuit using fourth degree polynomial. Nonlinear Dyn. 77(1–2), 231–241 (2014)
Hasani-Marzooni, M., Hosseini, S.H.: Trading strategies for wind capacity investment in a dynamic model of combined tradable green certificate and electricity markets. IET Gener. Transm. Distrib. 6(4), 320–330 (2012)
Khooban, M.H., Gheisarnejad, M., Farsizadeh, H., Masoudian, A., Boudjadar, J.: A new intelligent hybrid control approach for DC–DC converters in zero-emission ferry ships. IEEE Trans. Power Electron. 35(6), 5832–5841 (2019)
Khooban, M.-H., Gheisarnejad, M., Vafamand, N., Boudjadar, J.: Electric vehicle power propulsion system control based on time-varying fractional calculus: implementation and experimental results. IEEE Trans. Intell. Veh. 4(2), 255–264 (2019)
Azami, A., Naghavi, S.V., Tehrani, R.D., Khooban, M.H., Shabaninia, F.: State estimation strategy for fractional order systems with noises and multiple time delayed measurements. IET Sci. Meas. Technol. 11(1), 9–17 (2017)
Khooban, M.-H., Gheisarnejad, M., Vafamand, N., Jafari, M., Mobayen, S., Dragicevic, T., Boudjadar, J.: Robust frequency regulation in mobile microgrids: HIL implementation. IEEE Syst. J. 13(4), 4281–4291 (2019)
Dehghani, M., Khooban, M.H., Niknam, T., Rafiei, S.M.R.: Time-varying sliding mode control strategy for multibus low-voltage microgrids with parallel connected renewable power sources in islanding mode. J. Energy Eng. 142(4), 05016002 (2016)
Veysi, M., Soltanpour, M.R., Khooban, M.H.: A novel self-adaptive modified bat fuzzy sliding mode control of robot manipulator in presence of uncertainties in task space. Robotica 33(10), 2045–2064 (2015)
Khooban, M.H., Niknam, T., Blaabjerg, F., Dehghani, M.: Free chattering hybrid sliding mode control for a class of non-linear systems: electric vehicles as a case study. IET Sci. Meas. Technol. 10(7), 776–785 (2016)
Khooban, M.: Secondary load frequency control of time-delay stand-alone microgrids with electric vehicles. IEEE Trans. Ind. Electron. 65(9), 7416–7422 (2018). https://doi.org/10.1109/TIE.2017.2784385
Dabiri, A., Butcher, E.A., Poursina, M., Nazari, M.: Optimal periodic-gain fractional delayed state feedback control for linear fractional periodic time-delayed systems. IEEE Trans. Autom. Control 63(4), 989–1002 (2017)
Haghighi, A.R., Pourmahmood Aghababa, M., Roohi, M.: Robust stabilization of a class of three-dimensional uncertain fractional-order non-autonomous systems. Int. J. Ind. Math. 6(2), 133–139 (2014)
Lin, D., Wang, X., Yao, Y.: Fuzzy neural adaptive tracking control of unknown chaotic systems with input saturation. Nonlinear Dyn. 67(4), 2889–2897 (2012)
Shi, K., Wang, J., Zhong, S., Tang, Y., Cheng, J.: Non-fragile memory filtering of T–S fuzzy delayed neural networks based on switched fuzzy sampled-data control. Fuzzy Sets Syst. 394, 40–64 (2020). https://doi.org/10.1016/j.fss.2019.09.001
Shi, K., Wang, J., Tang, Y., Zhong, S.: Reliable asynchronous sampled-data filtering of T–S fuzzy uncertain delayed neural networks with stochastic switched topologies. Fuzzy Sets Syst. 381, 1–25 (2020). https://doi.org/10.1016/j.fss.2018.11.017
Shi, K., Wang, J., Zhong, S., Tang, Y., Cheng, J.: Hybrid-driven finite-time \(H_{\infty}\) sampling synchronization control for coupling memory complex networks with stochastic cyber attacks. Neurocomputing 387, 241–254 (2020). https://doi.org/10.1016/j.neucom.2020.01.022
Esfahani, Z., Roohi, M., Gheisarnejad, M., Dragičević, T., Khooban, M.-H.: Optimal non-integer sliding mode control for frequency regulation in stand-alone modern power grids. Appl. Sci. 9(16), 3411 (2019)
Cai, N., Jing, Y., Zhang, S.: Modified projective synchronization of chaotic systems with disturbances via active sliding mode control. Commun. Nonlinear Sci. Numer. Simul. 15(6), 1613–1620 (2010)
Zare, K., Mardani, M.M., Vafamand, N., Khooban, M.H., Sadr, S.S., Dragičević, T.: Fuzzy-logic-based adaptive proportional-integral sliding mode control for active suspension vehicle systems: Kalman filtering approach. Inf. Technol. Control 48(4), 648–659 (2019)
Khooban, M.H., Niknam, T., Sha-Sadeghi, M.: A time-varying general type-II fuzzy sliding mode controller for a class of nonlinear power systems. J. Intell. Fuzzy Syst. 30(5), 2927–2937 (2016)
Xi, H., Yu, S., Zhang, R., Xu, L.: Adaptive impulsive synchronization for a class of fractional-order chaotic and hyperchaotic systems. Optik, Int. J. Light Electron Opt. 125(9), 2036–2040 (2014)
Roohi, M., Zhang, C., Chen, Y.: Adaptive model-free synchronization of different fractional-order neural networks with an application in cryptography. Nonlinear Dyn. 100(4), 3979–4001 (2020). https://doi.org/10.1007/s11071-020-05719-y
Aghababa, M.P., Haghighi, A.R., Roohi, M.: Stabilisation of unknown fractional-order chaotic systems: an adaptive switching control strategy with application to power systems. IET Gener. Transm. Distrib. 9(14), 1883–1893 (2015)
Yin, C., Dadras, S., Zhong, S.-M., Chen, Y.: Control of a novel class of fractional-order chaotic systems via adaptive sliding mode control approach. Appl. Math. Model. 37(4), 2469–2483 (2013). https://doi.org/10.1016/j.apm.2012.06.002
Yin, C., Dadras, S., Zhong, S.-M.: Design an adaptive sliding mode controller for drive-response synchronization of two different uncertain fractional-order chaotic systems with fully unknown parameters. J. Franklin Inst. 349(10), 3078–3101 (2012). https://doi.org/10.1016/j.jfranklin.2012.09.009
Mofid, O., Mobayen, S., Khooban, M.H.: Sliding mode disturbance observer control based on adaptive synchronization in a class of fractional-order chaotic systems. Int. J. Adapt. Control Signal Process. 33(3), 462–474 (2019)
Lin, T.-C., Lee, T.-Y.: Chaos synchronization of uncertain fractional-order chaotic systems with time delay based on adaptive fuzzy sliding mode control. IEEE Trans. Fuzzy Syst. 19(4), 623–635 (2011)
Wang, Y., Gu, L., Xu, Y., Cao, X.: Practical tracking control of robot manipulators with continuous fractional-order nonsingular terminal sliding mode. IEEE Trans. Ind. Electron. 63(10), 6194–6204 (2016)
Yin, C., Huang, X., Chen, Y., Dadras, S., Zhong, S.-M., Cheng, Y.: Fractional-order exponential switching technique to enhance sliding mode control. Appl. Math. Model. 44, 705–726 (2017)
Yu, X., Kaynak, O.: Sliding-mode control with soft computing: a survey. IEEE Trans. Ind. Electron. 56(9), 3275–3285 (2009)
Boiko, I., Fridman, L., Pisano, A., Usai, E.: Analysis of chattering in systems with second-order sliding modes. IEEE Trans. Autom. Control 52(11), 2085–2102 (2007)
Ziaratban, R., Haghighi, A.R., Reihani, P.: Design of a no-chatter fractional sliding mode control approach for stabilization of non-integer chaotic systems. Int. J. Ind. Math. 12(3), 215–223 (2020)
Soltanpour, M.R., Khooban, M.H.: A particle swarm optimization approach for fuzzy sliding mode control for tracking the robot manipulator. Nonlinear Dyn. 74(1–2), 467–478 (2013)
Bartolini, G., Pisano, A., Usai, E.: Second-order sliding-mode control of container cranes. Automatica 38(10), 1783–1790 (2002)
Fridman, L., Levant, A.: Higher order sliding modes. In: Sliding Mode Control in Engineering, vol. 11, pp. 53–102 (2002)
Asl, M.S., Javidi, M.: An improved PC scheme for nonlinear fractional differential equations: error and stability analysis. J. Comput. Appl. Math. 324, 101–117 (2017). https://doi.org/10.1016/j.cam.2017.04.026
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, vol. 198. Elsevier, Amsterdam (1998)
Tian, X., Fei, S.: Robust control of a class of uncertain fractional-order chaotic systems with input nonlinearity via an adaptive sliding mode technique. Entropy 16(2), 729–746 (2014)
Roohi, M., Khooban, M.-H., Esfahani, Z., Aghababa, M.P., Dragicevic, T.: A switching sliding mode control technique for chaos suppression of fractional-order complex systems. Trans. Inst. Meas. Control 41(10), 2932–2946 (2019). https://doi.org/10.1177/0142331219834606
Aghababa, M.P.: A novel terminal sliding mode controller for a class of non-autonomous fractional-order systems. Nonlinear Dyn. 73(1–2), 679–688 (2013)
Wang, B., Ding, J., Wu, F., Zhu, D.: Robust finite-time control of fractional-order nonlinear systems via frequency distributed model. Nonlinear Dyn. 85(4), 2133–2142 (2016)
Zhang, S., Yu, Y., Wang, H.: Mittag-Leffler stability of fractional-order Hopfield neural networks. Nonlinear Anal. Hybrid Syst. 16, 104–121 (2015). https://doi.org/10.1016/j.nahs.2014.10.001
Diethelm, K., Ford, N.J., Freed, A.D.: A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29(1–4), 3–22 (2002)
Acknowledgements
The authors gratefully acknowledge the editor and anonymous reviewers.
Availability of data and materials
All the data and materials of this paper are available.
Funding
The authors received no financial support for the research, authorship, and/or publication of this article.
Author information
Authors and Affiliations
Contributions
The authors have equally made contributions to this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no conflict of interest related the publication of this manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Haghighi, A., Ziaratban, R. A non-integer sliding mode controller to stabilize fractional-order nonlinear systems. Adv Differ Equ 2020, 503 (2020). https://doi.org/10.1186/s13662-020-02954-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02954-w