1 Introduction

Nowadays, the study of bio-mathematical models is considered as an original icon in the investigation of the dynamical and physical behavior of many biological models such as DNA [1], viruses [2, 3], the nerve system, the bacteria cell [4, 5] and their distribution, and the transmission of their impulses, and so on. These models are mathematically formulated depending on laboratory experiments and statistics [6–8]. These bio-models are expressed in nonlinear evaluation equations and system with integer and fractional order. However, studying the fractional bio-models is more important than the models with an integer order because of the nonlocal property that appears only in the fractional models [9–11].

The nervous system is one of these bio-models that are attractive to many researchers; it is a sophisticated collection of neurons and nerves [12–14]. The neuron cells transmit signals between different parts of the body. It mostly looks like an electrical wiring system in the human body. According to the National Institute of Health, this system contains two essential components which are the peripheral nervous system and the central nervous system. The brain, nerves, and spinal cord are primary components of the central nervous system [15].

In contrast, the ganglia (clusters of neurons), the sensory neurons, and nerves are primary components of the peripheral nervous system [16, 17]. These nerve cells contact each other and the central nervous system. Functionally, the nervous system has two main subdivisions: the somatic, or voluntary, component and the autonomic, or involuntary, part. There are two types of movement performed by the living body, namely the voluntary action and the inadvertent movement such as blood pressure, respiratory rate, heartbeat, etc., and all these movements are regulated by the autonomic nervous system, according to Merck Manuals [18, 19]. The somatic system is full of nerves that connect the spinal cord and muscles with the brain that are considered to be a sensory receptor in the skin [20].

The patients with nerve disorders experience functional difficulties according to the Mayo Clinic, which result in conditions such as [ epilepsy, multiple sclerosis (MS), amyotrophic lateral sclerosis (ALS), Huntington’s disease, Alzheimer’s disease, stroke, transient ischemic attack (TIA), and sub-arachnoid hemorrhage ] [21]. The mathematical model of the transmission for the nerve impulses of a nervous system is the FN equation [22–24] which looks like another form of the Hodgkin–Huxley model [25]

$$\begin{aligned} \textstyle\begin{cases} \mathcal{Q}_{i}=\varphi _{i} (\mathcal{E}_{m}-\mathcal{E}_{i}), \\ \mathcal{Q}=\mathcal{M}_{m} \,\frac{d \mathcal{E}_{m}}{d t}+\varphi _{ \mu } (\mathcal{E}_{m}-\mathcal{E}_{\mu })+\varphi _{\nu _{a}} ( \mathcal{E}_{m} -\mathcal{E}_{\nu _{a}}) +\varphi _{i} (\mathcal{E}_{m}- \mathcal{E}_{\nu _{i}}), \\ \mathcal{Q}_{c}=\mathcal{T}_{m} \, \frac{d \mathcal{L}_{m}}{d t}, \end{cases}\displaystyle \end{aligned}$$
(1)

where \(\mathcal{E}_{\nu _{a}}\), \(\mathcal{E}_{m}\), \(\varphi _{E}\), \(\mathcal{T}_{m}\), \(\mathcal{E}_{\mu }\), \(\varphi _{i}\), \(\mathcal{E}_{i}\) respectively describe sodium reversal potentials, ion pumps, leak channels, the lipid bilayer, the potassium, the leak conductance per unit area, and membrane potential.

In this context, we study the AB time-fractional FN equation [26, 27]

$$\begin{aligned} \mathcal{N}_{x x}-\mathcal{N} (1-\mathcal{N}) (\rho - \mathcal{N})- \mathcal{D}^{\alpha } _{t} \mathcal{N}=0,\quad 0< \alpha < 1, \end{aligned}$$
(2)

where ρ is an arbitrary constant. Equation (2) takes the Newell–Whitehead (\(\mathcal{NW}\)) equation’s form when \(\rho =0\).

Recently, many research papers have investigated the analytical and numerical solutions of the time fractional FN equation [28–37] for discovering novel properties of the transmission for the nerve impulses of a nervous system. These solutions are very useful tools for better understanding of the transmission attitude.

In this research paper, the improved Riccati expansion method is applied to the nervous biological fractional FN equation to investigate the analytical solutions of it. Many novel computational solutions are obtained, then they are used to evaluate the initial and boundary conditions. These conditions are employed to handle the numerical solutions of this biological model to show the accuracy of the obtained analytical solutions by calculating the absolute value of error. The obtained solutions are successfully sketched to show the physical and dynamical behavior of these solutions. Moreover, the stability feature of solutions is investigated to demonstrate their applicability in its applications where many analytical and numerical schemes have been derived to construct the exact and numerical schemes of this kind of nonlinear evolutions equations [38–49].

The rest of paper is as follows. Section 2 applies computational and numerical schemes [50–56] to the AB time-fractional FN equation for constructing exact and numerical wave solutions. Section 3 illustrates the stability characteristic of the evaluated computational solutions. Section 4 shows, explains, and discusses the relation between our calculated solutions and previously gained solutions by other schemes. Section 5 gives the conclusion.

2 Application

This section employs the improved Riccati expansion method and B-spline schemes to find the analytical and numerical solutions. Using the following AB wave transformation , , where λ, k [56–58] are arbitrary constants, yields

$$\begin{aligned} k^{2} \mathcal{Q}''- \mathcal{Q} (1-\mathcal{Q}) (\rho -\mathcal{Q})- \omega \mathcal{Q}'=0. \end{aligned}$$
(3)

Employing the homogeneous balance principles for Eq. (3) yields \(\mathcal{Q}'', \mathcal{Q}^{3} \Rightarrow n+2=3 n \Rightarrow n=1\).

2.1 Analytical explicit wave solution

The general solutions of Eq. (3) based on the improved Riccati expansion method are given by [57, 58]

(4)

where \(a_{i}\), (\(i=0, 1\)) are arbitrary constants to be determined later. Also, satisfies the following ODE:

where σ, ϱ, δ are arbitrary constants. Substituting Eq. (4) into Eq. (3), gathering all coefficients with the same power of \((i=-3, -2, -1, 0, 1, 2, 3)\), and equating them to zero lead to a system of algebraic equations. Solving this system to get the above-mentioned parameters yields:

Family I:

$$ \biggl[ a_{0}= \frac{1}{2} (\sqrt{2} \delta k+1 ),a_{1}= \sqrt{2} k \sigma ,\omega = \frac{1}{2} (2 \sqrt{2} k \rho - \sqrt{2} k ),\varrho = \frac{2 \delta ^{2} k^{2}-1}{8 k^{2} \sigma }. \biggr] $$

Consequently, the computational solutions of the AB time-fractional FN equation are given by the following:

For \([ \delta ^{2}-4 \sigma \varrho >0\ \&\ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] \mathcal{N}_{1}(x,t)={}&\frac{1}{2}- \frac{k \sqrt{\delta ^{2}-4 \sigma \varrho }}{\sqrt{2}} \\ &{}\times\tanh \biggl( \frac{1}{2} \sqrt{\delta ^{2}-4 \sigma \varrho } \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr), \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned}& \begin{aligned}[b] \mathcal{N}_{2}(x,t)={}&\frac{1}{2}- \frac{k \sqrt{\delta ^{2}-4 \sigma \varrho }}{\sqrt{2}} \\ &{}\times\coth \biggl( \frac{1}{2} \sqrt{\delta ^{2}-4 \sigma \varrho } \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr). \end{aligned} \end{aligned}$$
(6)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \&\ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] \mathcal{N}_{3}(x,t)={}&k \sqrt{2 \sigma \varrho -\frac{\delta ^{2}}{2}}\\ &{}\times\tan \biggl(\frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+ \frac{1}{2}, \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}& \begin{aligned}[b] \mathcal{N}_{4}(x,t)={}&\frac{1}{2}-k \sqrt{2 \sigma \varrho - \frac{\delta ^{2}}{2}} \\ &{}\times\cot \biggl(\frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr). \end{aligned} \end{aligned}$$
(8)

For \([ \delta ^{2}-4 \sigma \varrho >0\ \&\ \sigma \varrho \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{5}(x,t)\\ &\quad =\frac{k }{\sqrt{2}} \biggl(\delta - \frac{4 \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \tanh (\frac{1}{2} \sqrt{\delta ^{2}-4 \sigma \varrho } (k x-\frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )} \biggr)\\ &\qquad {}+\frac{1}{2}, \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{6}(x,t)\\ &\quad =\frac{k}{\sqrt{2}} \biggl(\delta - \frac{4 \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \coth (\frac{1}{2} \sqrt{\delta ^{2}-4 \sigma \varrho } (k x-\frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )} \biggr)\\ &\qquad {}+\frac{1}{2}. \end{aligned} \end{aligned}$$
(10)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \& \ \sigma \varrho \neq 0 ]\),

$$\begin{aligned} &\mathcal{N}_{7}(x,t) \\ &\quad = \frac{\delta k}{\sqrt{2}}+ \frac{1}{2} \\ &\qquad {}- \biggl[ {\biggl(} 2 \sqrt{2} k \sigma \varrho \cos \biggl( \frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ {\biggl(} \sqrt{4 \sigma \varrho -\delta ^{2}} \sin {\biggl(} \frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} {\biggl(}k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} {\biggr)} {\biggr)} \\ &\qquad {} +\delta \cosh \biggl(\frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr], \end{aligned}$$
(11)
$$\begin{aligned} &\mathcal{N}_{8}(x,t) \\ &\quad = \frac{\delta k}{\sqrt{2}}+ \frac{1}{2} \\ &\qquad {}+ \biggl[ {\biggl(} 2 \sqrt{2} k \sigma \varrho \sin \biggl(\frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ {\biggl(} \sqrt{4 \sigma \varrho -\delta ^{2}} \cos \biggl( \frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \\ &\qquad {}-\delta \sinh \biggl(\frac{1}{2} \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(k x- \frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr]. \end{aligned}$$
(12)

For \([ \delta ^{2}-4 \sigma \varrho =0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \mathcal{N}_{9}(x,t)= \frac{\delta k (\exp (\frac{\delta k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} )-\varOmega e^{\delta k x} )}{\sqrt{2} (\exp (\frac{\delta k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} )+\varOmega e^{\delta k x} )}+ \frac{1}{2}, \end{aligned}$$
(13)
$$\begin{aligned}& \mathcal{N}_{10}(x,t)=\frac{\delta k }{\sqrt{2}} \biggl( \frac{2 \varOmega }{\exp (\delta (k x-\frac{k (2 \rho -1) (\vartheta -1) t^{-m \vartheta }}{\sqrt{2} B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )+\varOmega }-1 \biggr)+\frac{1}{2}. \end{aligned}$$
(14)

Family II:

$$ \biggl[ a_{1}= -\sqrt{2} k \sigma ,\omega = k \bigl(\sqrt{2} (a_{0}-1 )+\delta k \bigr),\rho = 2 a_{0}+\sqrt{2} \delta k,\varrho = \frac{ (-\sqrt{2} ) a_{0} \delta k-a_{0}^{2}}{2 k^{2} \sigma }. \biggr] $$

Consequently, the computational solutions of the AB time-fractional FN equation are given by the following:

For \([ \delta ^{2}-4 \sigma \varrho >0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{11}(x,t)\\ &\quad = \frac{k }{\sqrt{2}} \biggl(\sqrt{ \delta ^{2}-4 \sigma \varrho }\\ &\qquad {}\times \tanh \biggl(\frac{1}{2} k \sqrt{ \delta ^{2}-4 \sigma \varrho } \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}, \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{12}(x,t)\\ &\quad = \frac{k }{\sqrt{2}} \biggl(\sqrt{ \delta ^{2}-4 \sigma \varrho }\\ &\qquad {}\times \coth \biggl(\frac{1}{2} k \sqrt{ \delta ^{2}-4 \sigma \varrho } \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}. \end{aligned} \end{aligned}$$
(16)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{13}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl( \delta -\sqrt{4 \sigma \varrho -\delta ^{2}} \\ &\qquad {}\times\tan \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \biggr) +a_{0}, \end{aligned} \end{aligned}$$
(17)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{14}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl(\sqrt{4 \sigma \varrho -\delta ^{2}} \\ &\qquad {}\times\cot \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}. \end{aligned} \end{aligned}$$
(18)

For \([ \delta ^{2}-4 \sigma \varrho >0\ \& \ \sigma \varrho \neq 0 ]\),

$$\begin{aligned}& \mathcal{N}_{15}(x,t)= \frac{2 \sqrt{2} k \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \tanh (\frac{1}{2} k \sqrt{\delta ^{2}-4 \sigma \varrho } (x-\frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )}+a_{0}, \end{aligned}$$
(19)
$$\begin{aligned}& \mathcal{N}_{16}(x,t)= \frac{2 \sqrt{2} k \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \coth (\frac{1}{2} k \sqrt{\delta ^{2}-4 \sigma \varrho } (x-\frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )}+a_{0}. \end{aligned}$$
(20)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \& \ \sigma \varrho \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{17}(x,t)\\ &\quad = a_{0}+ \biggl[ {\biggl(} 2 \sqrt{2} k \sigma \varrho \cos \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ \biggl( \sqrt{4 \sigma \varrho -\delta ^{2}} \sin \biggl( \frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \\ &\qquad {} +\delta \cosh \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr], \end{aligned} \end{aligned}$$
(21)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{18}(x,t)\\ &\quad = a_{0}+ \biggl[ {\biggl(} 2 \sqrt{2} k \sigma \varrho \sin \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ {\biggl(} \delta \sinh \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \\ &\qquad {}-\sqrt{4 \sigma \varrho -\delta ^{2}} \cos \biggl( \frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr]. \end{aligned} \end{aligned}$$
(22)

For \([ \delta ^{2}-4 \sigma \varrho =0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \mathcal{N}_{19}(x,t)= \frac{\sqrt{2} \delta k \varOmega }{\exp (\delta (-k) (x-\frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )+\varOmega }+a_{0}, \end{aligned}$$
(23)
$$\begin{aligned}& \mathcal{N}_{20}(x,t)=\sqrt{2} \delta k \biggl(1- \frac{\varOmega }{\exp (\delta k (x-\frac{(\vartheta -1) (\sqrt{2} (a_{0}-1 )+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )+\varOmega } \biggr)+a_{0}. \end{aligned}$$
(24)

Family III:

$$ \biggl[ a_{1}= -\sqrt{2} k \sigma ,\omega = k (\sqrt{2} a_{0}+ \delta k ),\rho = 2 a_{0}+\sqrt{2} \delta k-1, \varrho = - \frac{ (a_{0}-1 ) (a_{0}+\sqrt{2} \delta k-1 )}{2 k^{2} \sigma }. \biggr] $$

Consequently, the computational solutions of the AB time-fractional FN equation are given by the following:

For \([ \delta ^{2}-4 \sigma \varrho >0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{21}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl(\sqrt{ \delta ^{2}-4 \sigma \varrho } \\ &\qquad {}\times\tanh \biggl(\frac{1}{2} k \sqrt{ \delta ^{2}-4 \sigma \varrho } \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}, \end{aligned} \end{aligned}$$
(25)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{22}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl(\sqrt{ \delta ^{2}-4 \sigma \varrho } \\ &\qquad {}\times\coth \biggl(\frac{1}{2} k \sqrt{ \delta ^{2}-4 \sigma \varrho } \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}. \end{aligned} \end{aligned}$$
(26)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{23}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl( \delta -\sqrt{4 \sigma \varrho -\delta ^{2}} \\ &\qquad {}\times\tan \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \biggr) +a_{0}, \end{aligned} \end{aligned}$$
(27)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{24}(x,t)\\ &\quad = \frac{k}{\sqrt{2}} \biggl(\sqrt{4 \sigma \varrho -\delta ^{2}}\\ &\qquad {}\times \cot \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr)+\delta \biggr) +a_{0}. \end{aligned} \end{aligned}$$
(28)

For \([ \delta ^{2}-4 \sigma \varrho >0\ \& \ \sigma \varrho \neq 0 ]\),

$$\begin{aligned}& \mathcal{N}_{25}(x,t)= \frac{2 \sqrt{2} k \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \tanh (\frac{1}{2} k \sqrt{\delta ^{2}-4 \sigma \varrho } (x-\frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )}+a_{0}, \end{aligned}$$
(29)
$$\begin{aligned}& \mathcal{N}_{26}(x,t)= \frac{2 \sqrt{2} k \sigma \varrho }{\delta -\sqrt{\delta ^{2}-4 \sigma \varrho } \coth (\frac{1}{2} k \sqrt{\delta ^{2}-4 \sigma \varrho } (x-\frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )}+a_{0}. \end{aligned}$$
(30)

For \([ \delta ^{2}-4 \sigma \varrho <0\ \& \ \sigma \varrho \neq 0 ]\),

$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{27}(x,t)\\ &\quad = a_{0}+ \biggl[ {\biggl(} 2 \sqrt{2} k \sigma \varrho \cos \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ \biggl( \sqrt{4 \sigma \varrho -\delta ^{2}} \sin \biggl( \frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \\ &\qquad {}+\delta \cosh \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr], \end{aligned} \end{aligned}$$
(31)
$$\begin{aligned}& \begin{aligned}[b] &\mathcal{N}_{28}(x,t)\\ &\quad = a_{0}+ \biggl[ \biggl( 2 \sqrt{2} k \sigma \varrho \sin \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho - \delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \\ &\qquad \biggm/ \biggl( \delta \sinh \biggl(\frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) \\ &\qquad {}-\sqrt{4 \sigma \varrho -\delta ^{2}} \cos \biggl( \frac{1}{2} k \sqrt{4 \sigma \varrho -\delta ^{2}} \biggl(x- \frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} \biggr) \biggr) {\biggr)} \biggr]. \end{aligned} \end{aligned}$$
(32)

For \([ \delta ^{2}-4 \sigma \varrho =0\ \& \ \delta \sigma \neq 0 ]\),

$$\begin{aligned}& \mathcal{N}_{29}(x,t)= \frac{\sqrt{2} \delta k \varOmega }{\exp (\delta (-k) (x-\frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )+\varOmega }+a_{0}, \end{aligned}$$
(33)
$$\begin{aligned}& \mathcal{N}_{30}(x,t)=\sqrt{2} \delta k \biggl(1- \frac{\varOmega }{\exp (\delta k (x-\frac{(\vartheta -1) (\sqrt{2} a_{0}+\delta k ) t^{-m \vartheta }}{B(\vartheta ) \sum_{m=0}^{\infty } (-\frac{\vartheta }{1-\vartheta } )^{m} \varGamma (1-m \vartheta )} ) )+\varOmega } \biggr)+a_{0}. \end{aligned}$$
(34)

2.2 Numerical simulation

In this section, the B-spline scheme is applied to the fractional biological FN equation to evaluate the numerical solution of it and also to show the accuracy of the gained analytical solutions that are evaluated in Sect. 2.1 by employing the improved Riccati expansion method under the following conditions on Eq. (5):

$$ \biggl[ \delta =5, k=\frac{1}{\sqrt{2}}, \rho =-1, \sigma =1, \omega =- \frac{3}{2}, \varrho =6. \biggr] $$

These conditions allow applying the B-spline family in the following forms.

2.2.1 Cubic-spline

This scheme formulates the general solution of Eq. (2) in the form

(35)

where \(\mho _{\jmath }\), \(\eth _{\jmath }\) are given in the following mathematical forms, respectively:

and

(36)

where \(\jmath \in [-2,m+2]\). Thus, we obtain

(37)

Substituting Eq. (37) into Eq. (3) yields \((m+3)\) of equations. Using Mathematica 11.3 to solve this system to get the value of \(\mho _{\jmath }\) leads to the following analytical, numerical values under the different values of in Table 1.

Table 1 Analytical, numerical, and absolute values in different values of via cubic B-spline scheme, showing the accuracy of the obtained analytical solution
Full size table

2.2.2 Quantic-spline

This scheme formulates the general solution of Eq. (2) in the form

(38)

where \(\mho _{\jmath }\), \(\eth _{\jmath }\) are given in the following mathematical forms, respectively:

and

(39)

where \(\jmath \in [-2,m+2]\). Thus, we obtain

(40)

Substituting Eq. (40) into Eq. (3) yields \((m+5)\) of equations. Using Mathematica 11.3 to solve this system to get the value of \(\mho _{\jmath }\) leads to the following analytical, numerical values under the different values of in Table 2.

Table 2 Analytical, numerical, and absolute values in different values of via quantic B-spline scheme, showing the accuracy of the obtained analytical solution
Full size table

2.2.3 Septic-spline

This scheme formulates the general solution of Eq. (2) in the form

(41)

where \(\mho _{\jmath }\), \(\eth _{\jmath }\) are given in the following mathematical forms, respectively:

and

(42)

where \(\jmath \in [-3,m+3]\). Thus, we obtain

(43)

Substituting Eq. (43) into Eq. (3) yields \((m+7)\) of equations. Using Mathematica 11.3 to solve this system to get the value of \(\mho _{\jmath }\) leads to the following analytical, numerical values under the different values of in Table 3.

Table 3 Analytical, numerical, and absolute values in different values of via septic B-spline scheme, showing the accuracy of the obtained analytical solution
Full size table

3 Stability characteristic

Investigation of the stability of the obtained analytical solutions by employing the properties of the Hamiltonian system that gives the momentum Ξ in the form

(44)

leads to the stable condition of the solution given by

$$\begin{aligned} \text{Re} \biggl( \frac{\partial \varXi }{\partial \omega } \biggr) >0, \end{aligned}$$
(45)

where ω is the wave velocity. Thus, the investigation of the stability characteristic for Eq. (5) is formulated as follows:

$$\begin{aligned} \varXi =& \frac{1}{\omega ^{2}} \bigl[ (\sqrt{2}-i \sqrt{10} \omega ) \text{Li}_{2} \bigl(-e^{i \omega \sqrt{5}+ \frac{5}{\sqrt{2}}} \bigr)-\sqrt{2} \text{Li}_{3} \bigl(-e^{\omega \sqrt{5}+\frac{5}{\sqrt{2}}} \bigr)-\sqrt{2} \text{Li}_{3} \bigl(-e^{i \sqrt{5} \omega -\frac{5}{\sqrt{2}}} \bigr) \\ &{} +\sqrt{2} (\sqrt{5} \omega -1 ) \text{Li}_{2} \bigl(-e^{\omega \sqrt{5}+\frac{5}{\sqrt{2}}} \bigr)+ \sqrt{2} (1-\sqrt{5} \omega ) \text{Li}_{2} \bigl(-e^{\sqrt{5} \omega -\frac{5}{\sqrt{2}}} \bigr) \\ &{}+\sqrt{2} (-1+i \sqrt{5} \omega ) \text{Li}_{2} \bigl(-e^{i \sqrt{5} \omega -\frac{5}{\sqrt{2}}} \bigr) +\sqrt{2} \text{Li}_{3} \bigl(-e^{\sqrt{5} \omega - \frac{5}{\sqrt{2}}} \bigr)+ \sqrt{2} \text{Li}_{3} \bigl(-e^{i \omega \sqrt{5}+\frac{5}{\sqrt{2}}} \bigr) \\ &{}+50 \omega ^{2}+\sqrt{5} \omega {\bigl(}-i \sqrt{2} \log \bigl(e^{\frac{5}{\sqrt{2}}}+e^{i \sqrt{5} \omega } \bigr)-\sqrt{2} \log \bigl(e^{\sqrt{5} \omega +\frac{5}{\sqrt{2}}}+1 \bigr) \\ &{}+\sqrt{2} \log \bigl(e^{\sqrt{5} \omega }+e^{ \frac{5}{\sqrt{2}}} \bigr)+i \sqrt{2} \log \bigl(1+e^{ \frac{5}{\sqrt{2}}+i \sqrt{5} \omega } \bigr)+(-5+5 i) {\bigr)} \bigr], \end{aligned}$$
(46)

and thus

$$\begin{aligned} \text{Re} \biggl( \frac{\partial \varXi }{\partial \omega }|_{\omega =- \frac{3}{2}} \biggr) =70.4226 >0. \end{aligned}$$
(47)

This result shows that the stable property of Eq. (5) is accomplished. Therefore, applying the same steps to the other analytical solution explains the stability characteristic of each of them.

4 Discussion

Studying the novelty of our solutions is shown in this section by giving more explanation of them and confirming the comparison between our solutions and those obtained in the previous article. Our investigation has two main steps, which are studying the analytical solutions and then surveying the numerical solutions. This process takes the following steps:

  1. 1.

    Obtained analytical solutions

    • Using a new fractional operator [ Atangana–Baleanu derivative operator ] for the first time to transform the nervous biological fractional FN equation into the ordinary differential equation.

    • Applying the improved Riccati expansion method to the obtained ODE leads to many analytical solutions of this model.

    • Comparing the obtained solutions with the previous ones in the following steps:

      1. (a)

        In [26], Dumitru Baleanu et al. used the extended simplest equation method and the sinh-cosh expansion method to find the analytical wave solutions of the FN model with the integer order. Some of their solutions are equal to our obtained solutions such as [26, Eq. (10)] is equal to Eq. (5) when \([ \vartheta =1, k= \frac{\sqrt{2 (\delta ^{2}-4 \sigma \varrho )}}{2} . ] \)

      2. (b)

        In [27], Abdel-Haleem Abdel-Aty et al. employed the modified Khater (mK) method and B-spline schemes to find the analytical and numerical schemes of the FitzHugh–Nagumo (FN) equation with the integer order. Some of their solutions are equal to our obtained solutions such as Eq. (7, [27]) is equal to Eq. (5) when \([ \vartheta =1, k= \frac{\sqrt{2 (\delta ^{2}-4 \sigma \varrho )}}{2} . ] \)

  2. 2.

    Obtained numerical solutions

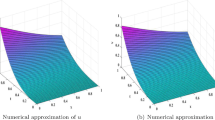
    Applying the B-spline schemes on the fractional biological FN model shows the accuracy of the obtained analytical solutions, but it also explains the superiority of the cubic B-spline scheme over the other two applied methods: the absolute value of error obtained by using it is smaller than the absolute value of error calculated by the other two applied schemes. This accuracy of the cubic-B-spline is shown in Fig. 6.

5 Conclusion

This paper has successfully performed the improved Riccati expansion method for constructing the exact traveling wave solutions of the nervous biological fractional FN equation that have been represented in Figs. 1, 2. These solutions have been used to evaluate the initial and boundary conditions that have allowed applying the B-spline collection schemes (cubic, quantic, and septic). Referring to these numerical schemes has shown the absolute value of error between the obtained exact and numerical solutions. These values have explained the accuracy of the obtained solutions as shown in Figs. 3, 4, 5. The stability property of the obtained solutions has been investigated based on the Hamiltonian system’s features and their ability to use into the biological model’s applications. Three- and two-dimensional and contour plots have been given for the obtained exact and numerical solutions to show the physical and dynamical behavior of these solutions. The comparison between the obtained solutions and the previous solutions was shown to explain the novelty of our research.

Figure 1
figure 1

Breath solitary wave of Eq. (5) in three distinct plots (three- and two-dimensional and contour plot) when \([ \delta =5, k=\frac{1}{\sqrt{2}}, \rho =-1, \sigma =1, \omega =-\frac{3}{2}, \varrho =6 ]\)

Full size image
Figure 2
figure 2

Solitary wave of Eq. (6) in three distinct plots (three- and two-dimensional and contour plot) when \([ \delta =5, k=\frac{1}{\sqrt{2}}, \rho =-1, \sigma =1, \omega =-\frac{3}{2}, \varrho =6 ]\)

Full size image
Figure 3
figure 3

A comparison representation between analytical and numerical solutions of Eq. (2) according to the cubic-B-spline simulation

Full size image
Figure 4
figure 4

A comparison representation between analytical and numerical solutions of Eq. (1) according to the quantic-B-spline simulation

Full size image
Figure 5
figure 5

A comparison representation between analytical and numerical solutions of Eq. (1) according to the septic-B-spline simulation

Full size image
Figure 6
figure 6

A comparison representation of absolute value of error of Eq. (2) according to the obtained values via cubic, quantic, and septic B-spline schemes

Full size image