Abstract
This paper is concerned with the number of limit cycles bifurcating from a period annulus for some planar piecewise smooth non-Hamiltonian systems. We construct a planar piecewise quadratic system with multiple parameters, obtain its lower bound for the maximum number of limit cycles by using Melnikov function method, and find more limit cycles than (Li and Liu in J. Math. Anal. Appl. 428:1354–1367, 2015).
Similar content being viewed by others
1 Introduction
In the last decades, the study of piecewise smooth systems has attracted great interest for their wider range of application in modeling real phenomena [2, 3]. Quite a few methods and interesting results have been obtained on limit cycle bifurcations of piecewise smooth systems. For example, the authors in [4, 5] studied the problem of homoclinic bifurcation of piecewise smooth systems and the authors in [6, 7] studied the problem of Hopf bifurcations of piecewise smooth systems. Many research works concerned planar piecewise quadratic systems with two zones separated by a straight line. For example, the authors in [8] studied the maximum number of limit cycles which can bifurcate from the periodic orbits of the quadratic isochronous centers perturbed inside discontinuous quadratic polynomial differential systems. By perturbing a center of discontinuous Bautin system, nine limit cycles have been found in [9] and ten limit cycles have been obtained in [10]. Recently, the authors in [11] claimed the lower bound for the Hilbert number is 16 in piecewise quadratic systems with two zones.
Roughly speaking, there are several methods to estimate the number of limit cycles of planar piecewise smooth systems. For example, by computing Lyapunov constants to study the maximal number of limit cycles obtained in switching systems, see [9, 10]. By using the averaging theory to study the periodic solutions of discontinuous piecewise systems, see [8, 12–14] etc. In [15], an expression of the first order Melnikov function is derived to study the number of limit cycles bifurcated from the periodic orbits of piecewise Hamiltonian systems. Later, the authors [16, 17] developed the Melnikov function method to near-Hamiltonian systems with multiple parameters. Specifically, for the following system:
where \(0<\varepsilon \ll \lambda \ll 1\), \(H^{ \pm }\), \(p^{ \pm }\), and \(q^{ \pm }\) are \(C^{\infty }\) functions in \((x, y)\) and depend on small parameter λ. In this case, the first order Melnikov function M of (1.1) depends on parameter λ and it has an expansion of the form
The formulas for \(M_{1}\) and \(M_{2}\) were deduced in [17] under some conditions. When \(M_{0}(h)\) is not zero identically, then for \(0<\lambda \ll 1\) one can study the number of limit cycles by using \(M_{0}(h)\). When \(M_{0}(h)\equiv 0\) and \(M_{1}(h)\) is not zero identically, then for \(0<\lambda \ll 1\) one can study the number of limit cycles by using \(M_{1}(h)\), and so forth.
The authors [1] considered the following planar piecewise smooth system:
where
It is not hard to see that system \(\mbox{(1.3)}|_{\varepsilon =0}\) has a first integral of the form \(H(x, y)=\frac{1}{2}(x^{2}+y^{2})\) and the origin is a center. Let \(L_{h}\) denote the periodic orbit of \(\mbox{(1.3)}|_{\varepsilon =0}\), given by \(L_{h} =L_{h}^{+} \cup L_{h}^{-}\) for \({h \in (0,\frac{1}{2} \eta ^{2})}\), where
and
The authors in [1] gave a linear estimation of the maximum number (denoted by \(H(n)\)) of limit cycles which bifurcate from any compact region of the period annulus of system (1.3) for all possible bounded coefficients \(p_{i j}^{\pm }\) and \(q_{i j}^{\pm }\) independent of the small parameter ε up to the first order averaging method, and proved the following results:
-
(i)
If \(a b \neq 0 \) and \(a \neq -b\), then \(H(n)=2 [\frac{n+1}{2} ]+n+1\).
-
(ii)
If \(a b \neq 0 \) and \(a = -b\), then \(H(n)= [\frac{n+1}{2} ]+n\).
-
(iii)
If \(a \neq 0\), \(b=0\) or \(a=0\), \(b \neq 0\), then \(H(n)= [\frac{n+1}{2} ]+n+1\).
Clearly, for the case of \(n=2\), one has particularly
Inspired by [15, 17], we construct a system with multiple parameters and obtain its lower bound for the maximum number of limit cycles by using \(M_{1}(h)\) in (1.2). Our main result can be stated in the following.
Theorem 1.1
There is a system of the form (1.3) with\(n=2\)and\(|\varepsilon |\)sufficiently small such that it has
-
(i)
seven limit cycles for\(a b \neq 0 \)and\(a \neq -b\);
-
(ii)
four limit cycles for\(a b \neq 0 \)and\(a = -b\);
-
(iii)
five limit cycles for\(a \neq 0\), \(b=0\)or\(a=0\), \(b \neq 0 \).
We remark that for \(a=b=0\) system (1.3) is a piecewise smooth near-Hamiltonian system and can have n limit cycles, which has already been studied in [15]. Comparing with [1], for the case of \(n=2\), our lower bound for the maximum number of limit cycles is one or two bigger for each case.
This paper is organized as follows. In Sect. 2, we introduce a second small parameter λ to (1.3) with \(n=2\) and give some preliminaries. In Sect. 3, we calculate the function \(M_{1}(h)\) for each case and prove our main result.
2 Preliminaries
Consider the following piecewise quadratic polynomial system with multiple parameters:
where \(0<|\varepsilon |\ll \lambda \ll 1\), \(H_{1}^{{\pm }}(x,y)=\sum_{i+j=1}^{2} h_{i j}^{\pm } x^{i} y^{j}\), and
Obviously, (2.1) is a piecewise smooth near-integrable system. In the region \(\{ L_{h} | h\in (0, \frac{1}{2}\eta ^{2}) \} \), system (2.1) is equivalent to the following near-Hamiltonian differential system:
Therefore, by [15], the first order Melnikov function of (2.3) can be expressed as
where
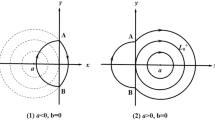
and \(A_{\lambda }=(0, a(h, \lambda ))\), \(B_{\lambda }=(0, b(h, \lambda ))\) with \(a(h, \lambda )>b(h, \lambda )\) satisfying \(H^{+}(A_{\lambda })=H^{+}(B_{\lambda })=h\), \(H^{-}(A_{\lambda })=H^{-}(B_{ \lambda }) \) for \(h\in (0, \frac{1}{2}\eta ^{2})\). \(\widehat{A_{\lambda } B_{\lambda }}\) is an orbital arc starting from \(A_{\lambda }\) and ending at \(B_{\lambda }\) defined by \(H^{+}(x, y, \lambda )=h\), \(x > 0\); \(\widehat{B_{\lambda } A_{\lambda }}\) is an orbital arc starting from \(B_{\lambda }(h)\) and ending at \(A_{\lambda }(h)\) defined by \(H^{-}(x, y, \lambda )=H^{-}(B_{\lambda }(h))\), \(x\leq 0\). Clearly, for given \(h\in (0, \frac{1}{2}\eta ^{2})\), \(\widehat{A_{\lambda } B_{\lambda }}\) and \(\widehat{B_{\lambda } A_{\lambda }}\) form a closed orbit \(L_{\lambda }\) with clockwise orientation(see Fig. 1).
By [17], for \(0<\lambda \ll 1\), (2.4) has an expansion of the form (1.2), where
with \(A=A_{\lambda } \vert _{\lambda =0}\), \(B=B_{\lambda } \vert _{\lambda =0}\). Obviously, for given \(h\in (0, \frac{1}{2}\eta ^{2})\), \(\widehat{A B}\) and \(\widehat{B A}\) form a closed orbit \(L_{0}(h)\), defined by \(\frac{1}{2} (x^{2}+y^{2} )=h\).
Suppose \(h_{0 j}^{-}=h_{0 j}^{+} \) (\(j=1,2 \)), so that the points on \(\widehat{A_{\lambda } B_{\lambda }}\) and \(\widehat{B_{\lambda } A_{\lambda }}\) satisfy
\(H^{\pm }(x, y,\lambda )= h\), \(\pm x\geq 0\), \(h\in (0, \frac{1}{2}\eta ^{2})\). Then, by Theorem 1.1 of [17], \(M_{1}(h)\) has the form
where
with
for a \(C^{\infty }\) function \(r(x,y)\).
Since the authors in [18] have proved the equivalence of the Melnikov function method and the averaging method, by using \(M_{0}(h)\) we can obtain the same number of limit cycles as that obtained by using the first order averaging method in [1]. By formula (15) of [1], it is not hard to obtain the following lemma that gives the necessary and sufficient conditions for \(M_{0}(h)\equiv 0\).
Lemma 2.1
For\(a b \neq 0 \)and\(a \neq -b\), \(M_{0}(h)\equiv 0\)if and only if
For\(a b \neq 0 \)and\(a = -b\), \(M_{0}(h)\equiv 0\)if and only if
For\(a \neq 0\), \(b=0 \), \(M_{0}(h)\equiv 0\)if and only if
For\(b \neq 0\), \(a=0 \), \(M_{0}(h)\equiv 0\)if and only if
3 Proof of the main result
In this section we prove Theorem 1.1. By (2.7), we know that \(M_{1}(h)=M_{11}(h)+M_{12}(h)+M_{13}(h)\). In the following, we first divide three cases to calculate \(M_{1i}(h)\) (\(i=1,2,3\)).
Case 1.\(a b \neq 0 \) and \(a \neq -b\)
Suppose that (2.10) holds, so that \(M_{0}(h)\equiv 0\). Let \(\sqrt{2 h}= r\). Then \(L_{0}(h)\) can be represented as \(x = r \cos \theta \), \(y=r \sin \theta \), \(r \in (0, \eta )\), \(\theta \in [- \frac{\pi }{2},\frac{3\pi }{2} ]\). Then, by (2.8), we rewrite
where
and
For the sake of convenience, introduce some notations as follows:
where \(ab\neq 0 \) and \(i \in \mathbb{Z}\), \(j \in \mathbb{N}\).
By [1] and some simple definite integral calculations, we have
where
with
Moreover, noting that \(a^{j} r^{j} \cos ^{j} \theta = (1+a r \cos \theta -1 )^{j}\), then by using the binomial expansion
it is easy to deduce the following relationship:
It is direct that
In the following we will use \(I_{i,j}^{\pm }\) instead of \(I_{i,j}^{\pm }(r)\) for simplicity.
Now, coming back to \(M_{11}^{\pm }(h)\), (3.1) and (3.2) can be read as
where
Obviously, \(\gamma _{1i}^{\pm }\) (\(i=0,1,2,3\)) can be taken as free parameters.
By (3.5) we have
Inserting (3.6) and (3.10) into (3.7) and (3.8) respectively yields
where
Clearly, \(d_{1i}^{\pm }\), \(b_{1i}^{\pm }\) (\(i=1,2\)) can be taken as free parameters.
Next, we calculate \(M_{12}(h)\). Note that along the curve \(L_{0}(h)\), \(d t=-\frac{1}{x} \,d y\). Hence, by (2.8), we have
where
Through a direct computation, we obtain
and
where
Further, by (3.3), one achieves
where
In view of (3.5), we have
It follows from (3.10) and (3.17) that
where
with
Now we are in the position to calculate \(M_{13}(h)\). Recall that
Thus, we have from (2.5)
where
Consequently,
and
Therefore, by (2.8) and (2.10), we obtain
Noting that \(h_{02}^{-}=h_{02}^{+}\), by (3.16), (3.20) and (3.21), (3.24) reads
Hence, combining (3.11), (3.12), (3.18), (3.19), and (3.25), we find that
where
Case 2. \(a b \neq 0 \) and \(a = - b\)
Suppose that (2.11) holds, so that \(M_{0}(h)\equiv 0\). If \(a = - b\), then \(I_{i,0}^{-}=I_{i,0}^{+}\) (\(i=1,2\)). By (3.26), we have
where
Case 3. \(a \neq 0\), \(b=0 \) or \(b \neq 0\), \(a=0 \)
Suppose that (2.12) holds, so that \(M_{0}(h)\equiv 0\). Note that, for \(a \neq 0\), \(b=0 \), \(M_{11}^{+}(h)\), \(M_{12}^{+}(h)\), and \(M_{13}(h)\) are identical to (3.11), (3.18), and (3.24) respectively. Hence, in order to give \(M_{1}(h)\), it suffices to calculate \(M_{11}^{-}(h)\) and \(M_{12}^{-}(h)\).
We have from (3.2)
Through a direct computation,
Thus, (3.30) becomes
By (3.15), together with (3.31), we have
Combining (3.11), (3.18), (3.24), (3.32), and (3.33), one can obtain
where
Similarly, suppose that (2.13) holds to ensure \(M_{0}(h)\equiv 0\). Then, for the case \(b \neq 0\), \(a=0 \), we can obtain
where
We can prove the following theorem.
Theorem 3.1
Suppose that\(M_{0}(h)\equiv 0\)and\(M_{1}(h)\)is not zero identically. Denote by\(Z_{1}(2)\)the maximum number of zeros of\(M_{1}(h)\)with\(0< \lambda \ll 1\). Then
Proof
First, for the case \(ab\neq 0\) and \(a\neq -b\), we study the number of zeros of \(M_{1}(h)\) in (3.26). We introduce the following coefficients:
Since \(p_{1ij}^{\pm }\) and \(q_{1ij}^{\pm }\) are independent of \(p_{0ij}^{\pm }\) and \(q_{0ij}^{\pm }\), so by (3.13) it is easy to see \(c_{i}\) (\(i=1,2,\ldots ,10\)) can be taken as free parameters as long as \(h_{0i}^{\pm }\neq 0\) (\(i=1,2\)). Under condition (2.10), for \(ab\neq 0\), one can obtain by (3.16), (3.20), (3.21), and (3.27)
Similar to the proof of Corollary 2.4.1 in [19], one knows that \(l_{i}\) (\(i=1,2,\ldots ,10\)) in (3.26) can be taken as free parameters.
For \(0< r \ll 1\), we have the following Taylor expansions:
Inserting (3.36) into (3.26), we get
where
and \(A_{i} \) (\(i\geq 9\)) are linear combinations of \(l_{i}\) (\(i=1,2,\ldots ,10\)).
By direct computation, for \(ab\neq 0\) and \(a\neq -b\), we have by (3.38)
Fix \(l_{1}\) and \(l_{7}\). Take \(l_{2}=- l_{3}=-\frac{1}{a^{2}}l_{1}\), \(l_{8}=-l_{9}=-\frac{1}{b^{2}}l_{7}\), and \(l_{4}=l_{5}=l_{6}=l_{10}=0\) such that \(A_{1}=A_{2}=\cdots =A_{8}=0 \). Thus, by (3.39), (3.38) has the inverse \(l_{i}=l_{i}(A_{1}, A_{2},\ldots , A_{8})\), \(i=1,2,\ldots ,10\), and consequently \(A_{i}=0 \) (\(i\geq 9\)) as \(A_{1}=A_{2}=\cdots =A_{8}=0 \). It follows that (3.38) can be rewritten as
where \(P_{i}(r)=O(r)\), \(i=1,2,\ldots ,8\). Hence, by Rolle’s theorem, (3.40) implies that \(M_{1}(h)\) has at most seven zeros in h for \(0<\sqrt{2 h}\ll 1\).
On the other hand, (3.39) implies that \(A_{1},A_{2},\ldots ,A_{8}\) can be taken as free parameters. Letting \(\delta =(l_{2}, l_{3},l_{4},l_{5},l_{6},l_{8},l_{9},l_{10})\) and taking \(\delta _{0}=(-\frac{1}{a^{2}}l_{1},\frac{1}{a^{2}}l_{1},0,0,0,- \frac{1}{b^{2}}l_{7},\frac{1}{b^{2}}l_{7},0)\), we can choose proper value δ near \(\delta _{0}\) such that
which ensures that \(M_{1}(h)\) has seven zeros in h for \(0<\sqrt{2 h}\ll 1\).
Second, consider the case \(ab\neq 0\) and \(a=-b\). Obviously, \(\widetilde{l}_{i}\) (\(i=1,2,\ldots ,6\)) in (3.29) can be taken as free parameters.
Inserting (3.36) into (3.28), we get
where
and \(\widetilde{A}_{i}\) (\(i\geq 6\)) are linear combinations of \(\widetilde{l}_{i}\) (\(i=1,2,\ldots ,6\)). Moreover, for \(ab\neq 0\) and \(a=-b\), we have by (3.42)
Similar to the above case, \(\widetilde{A}_{i}=0\) (\(i\geq 6\)) if \(\widetilde{A}_{1}=\widetilde{A}_{2}=\cdots =\widetilde{A}_{5}=0\). Thus, \(M_{1}(h)\) in (3.41) has at most four zeros in h for \(0<\sqrt{2 h}\ll 1\).
Also, (3.43) implies that \(\widetilde{A}_{1},\widetilde{A}_{2},\ldots ,\widetilde{A}_{5}\) can be taken as free parameters. Let \(\widetilde{\delta }= (\widetilde{l}_{2}, \widetilde{l}_{3}, \widetilde{l}_{4},\widetilde{l}_{5},\widetilde{l}_{6})\) and take \(\widetilde{\delta }_{0}=(-\frac{1}{a^{2}}\widetilde{l}_{1}, \frac{1}{a^{2}}\widetilde{l}_{1},0,0,0)\). Then \(\widetilde{A}_{1}=\widetilde{A}_{2}=\cdots =\widetilde{A}_{5}=0 \) if \(\widetilde{\delta }=\widetilde{\delta }_{0}\). Hence, we can choose proper value δ̃ near \(\widetilde{\delta }_{0}\) such that
which ensures that \(M_{1}(h)\) has four zeros in h for \(0<\sqrt{2 h}\ll 1\).
For the case \(a\neq 0\), \(b=0\), it is easy to see \(\overline{l}_{i}\) (\(i=1,2,\ldots ,7\)) in (3.34) can be taken as free parameters. Then, by inserting (3.36) into (3.34), we get the expansion
where
and \(\overline{A}_{i}\) (\(i\geq 7\)) are linear combinations of \(\overline{l}_{i}\) (\(i=1,2,\ldots ,7\)). By calculation, for \(a\neq 0\) and \(b=0\), we have by (3.45)
By using the similar analysis, one can obtain that \(M_{1}(h)\) in (3.44) has at most five zeros in h for \(0<\sqrt{2 h}\ll 1\). Moreover, (3.46) implies that \(\overline{A}_{1},\overline{A}_{2},\ldots ,\overline{A}_{6}\) can be taken as free parameters. Let \(\overline{\delta }=(\overline{l}_{2}, \overline{l}_{3},\overline{l}_{4}, \overline{l}_{5},\overline{l}_{6},\overline{l}_{7})\) and take \(\overline{\delta }_{0}=(-\frac{1}{a^{2}}\overline{l}_{1}, \frac{1}{a^{2}}\overline{l}_{1},0,0,0,-\frac{2}{a}\overline{l}_{1})\). Then \(\overline{A}_{1}=\overline{A}_{2}=\cdots =\overline{A}_{5}= \overline{A}_{6}=0 \) if \(\overline{\delta }=\overline{\delta }_{0}\). Hence, we can choose proper value δ̅ near \(\overline{\delta }_{0}\) such that
which ensures that \(M_{1}(h)\) has five zeros in h for \(0<\sqrt{2 h}\ll 1\). In the case of \(b \neq 0\), \(a=0 \), the proof is similar. Theorem 3.1 is proved. □
Proof of Theorem 1.1
It is not hard to see that system (2.1) can be rewritten as
where
and
with \(0<|\varepsilon |\ll \lambda \ll 1\) and \(\sigma =\frac{\varepsilon }{\lambda }\). Obviously, \(0<|\sigma |\ll 1\).
By Theorem 3.1, there exists \(\lambda _{0}>0\) such that, for any \(\lambda \in (0,\lambda _{0}]\), \(M(h,\lambda )\) for system (3.47) has k (\(k=7,4,5\) for each case) zeros in h for \(0<\sqrt{2 h}\ll 1\). It follows that, for any \(\lambda \in (0,\lambda _{0}]\) and \(0<|\varepsilon |\ll \lambda \), system (3.47) can have k limit cycles. That is to say, for any \(\lambda \in (0,\lambda _{0}]\), there exist \(\varepsilon _{0} \) and \(\sigma _{0}=\frac{\varepsilon _{0}}{\lambda }\) satisfying \(0<|\varepsilon _{0} |\ll \lambda \) and \(0<|\sigma _{0}|\ll 1\) such that system (3.47) can have k limit cycles. Note that system (3.47) has the form of (2.1) with \(n=2\). The proof is then completed. □
References
Li, S., Liu, C.: A linear estimate of the number of limit cycles for some planar piecewise smooth quadratic differential system. J. Math. Anal. Appl. 428, 1354–1367 (2015)
Di Bernardo, M., Budd, C.J., Champneys, A.R., et al.: Piecewise-Smooth Dynamical Systems: Theory and Applications. Springer, New York (2008)
Di Bernardo, M., Budd, C.J., Champneys, A.R., et al.: Bifurcations in nonsmooth dynamic systems. SIAM Rev. 50, 629–701 (2008)
Liang, F., Han, M.: Limit cycles near generalized homoclinic and double homoclinic loops in piecewise smooth systems. Chaos Solitons Fractals 45, 454–464 (2012)
Liang, F., Han, M., Zhang, X.: Bifurcation of limit cycles from generalized homoclinic loops in planar piecewise smooth systems. J. Differ. Equ. 255, 4403–4436 (2013)
Han, M., Sheng, L.: Bifurcation of limit cycles in piecewise smooth systems via Melnikov function. J. Appl. Anal. Comput. 5, 809–815 (2015)
Han, M., Zhang, W.: On Hopf bifurcation in non-smooth planar systems. J. Differ. Equ. 248, 2399–2416 (2010)
Llibre, J., Mereu, A.C.: Limit cycles for discontinuous quadratic differential systems with two zones. J. Math. Anal. Appl. 413, 763–775 (2014)
Chen, X., Du, Z.: Limit cycles bifurcate from centers of discontinuous quadratic systems. Comput. Math. Appl. 59, 3836–3848 (2010)
Tian, Y., Yu, P.: Center conditions in a switching Bautin system. J. Differ. Equ. 259, 1203–1226 (2015)
Da Cruz, L.P.C., Novaes, D.D., Torregrosa, J.: New lower bound for the Hilbert number in piecewise quadratic differential systems. J. Differ. Equ. 266, 4170–4203 (2019)
Llibre, J., Mereu, A.C., Novaes, D.D.: Averaging theory for discontinuous piecewise differential systems. J. Differ. Equ. 458, 4007–4032 (2015)
Llibre, J., Novaes, D.D., Teixeira, M.A.: On the birth of limit cycles for non-smooth dynamical systems. Bull. Sci. Math. 139, 229–244 (2015)
Han, M.: On the maximum number of periodic solutions of piecewise smooth periodic equations by average method. J. Appl. Anal. Comput. 7, 788–794 (2017)
Liu, X., Han, M.: Bifurcation of limit cycles by perturbing piecewise Hamiltonian systems. Int. J. Bifurc. Chaos 5, 1379–1390 (2010)
Han, M., Xiong, Y.: Limit cycle bifurcations in a class of near- Hamiltonian systems with multiple parameters. Chaos Solitons Fractals 68, 20–29 (2014)
Xiong, Y.: Limit cycle bifurcations by perturbing piecewise smooth Hamiltonian systems with multiple parameters. J. Math. Anal. Appl. 421, 260–275 (2015)
Han, M., Romanovski, V., Zhang, X.: Equivalence of the Melnikov function method and the averaging method. Qual. Theory Dyn. Syst. 15, 471–479 (2016)
Han, M.: Bifurcation Theory of Limit Cycles. Science Press, Beijing (2013)
Acknowledgements
The authors would like to thank the anonymous referees for their valuable suggestions, which have greatly helped in improving the presentation of this paper.
Availability of data and materials
Not applicable.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 11931016 and Nos. 11771296).
Author information
Authors and Affiliations
Contributions
The two authors worked together in the derivation of the mathematical results. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gong, S., Han, M. Limit cycle bifurcations in a planar piecewise quadratic system with multiple parameters. Adv Differ Equ 2020, 366 (2020). https://doi.org/10.1186/s13662-020-02827-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02827-2