Abstract
In this work, optimal control for a fractional-order nonlinear mathematical model of cancer treatment is presented. The suggested model is determined by a system of eighteen fractional differential equations. The fractional derivative is defined in the Atangana–Baleanu Caputo sense. Necessary conditions for the control problem are derived. Two control variables are suggested to minimize the number of cancer cells. Two numerical methods are used for simulating the proposed optimal system. The methods are the iterative optimal control method and the nonstandard two-step Lagrange interpolation method. In order to validate the theoretical results, numerical simulations and comparative studies are given.
Similar content being viewed by others
1 Introduction
It is well known that one of the most dangerous diseases all over the world is cancer ([1–4]). Modeling and simulations are important tools to discover tumor cells ([5–7]). Well-known treatment modalities are surgery, radiotherapy and chemotherapy. Sadly, every of those varieties of treatment has its own disadvantages, for more details see [5–20]. However, progress within the fight against cancer continues to be made with novel modes; for more details see [12–19].
In [21] an interesting mathematical model for cancer treatment is presented. This model is governed by a system of eighteen differential equations. The first aim of this paper is to develop this model in order to control the cancer cells. In [22], optimal control of a fractional-order delay model for cancer treatment is presented. Here the fractional-order derivative is defined in the Caputo sense.
Applications of fractional calculus have increased in the last few decades, after centuries of small advancements. Examples can be found in a variety of scientific areas: engineering, biology, epidemiology, amongst others ([23–37]). In most cases, the fractional-order differential equations (FODEs) models seem more consistent with the real phenomena than the integer order models. This is due to the fact that fractional derivatives and integrals enable the description of the memory and hereditary properties inherent in various materials and processes that exist in most biological systems.
In [14–16, 38], some fractional optimal control problems (FOCPs) have been introduced. Sweilam and AL-Mekhlafi, studied optimal control of some biology models in [22, 30, 39–42]. In [2], Torres et al. introduced and analyzed a multiobjective formulation of an optimal control problem, where the two conflicting objectives are minimization of the number of HIV-infected individuals with AIDS clinical symptoms and co-infected with AIDS and active TB and costs related to prevention and treatment of HIV and/or TB measures. More recently, in the Atangana–Baleanu Caputo sense (ABC) one defined a modified Caputo fractional derivative by introducing a generalized Mittag-Leffler function as the nonlocal and non-singular kernel ([43]). These new types of derivatives have been used in modeling of real life applications in different fields ([44, 45]). In [46–49] necessary optimality conditions for FOCPs are obtained in the Riemann–Liouville sense and numerically studied by a finite difference method. In [50], the spectral method is developed for a distributed-order fractional optimal control problem. In [51] Baleanu et al., used a central difference scheme for solving FOCPs.
In this paper, we introduced the fractional mathematical model without singular kernel for a cancer treatment model with modified parameters ([52]). Minimizating of tumor cells of FOCPs for the proposed model is the aim of this article. Two numerical techniques are introduced to study the nonlinear FOCPs. The techniques are: the iterative optimal control method (IOCM) ([22, 30, 42]) and the nonstandard two-step Lagrange interpolation method (N2LIM), which is presented here as an adaptation for the two-step Lagrange interpolation method. Numerical simulations are given. To the best of our knowledge the fractional optimal control without singular kernel for cancer treatment based on synergy between anti-angiogenic model was never explored before.
This paper organized as follows: The fractional-order model with two controls is given in Sect. 2. In Sect. 3, the optimality conditions are derived. In Sect. 4, numerical methods for FOCPs are presented. In Sect. 5, numerical experiments and simulations are presented. Finally the conclusions are given in Sect. 6.
2 The model problem
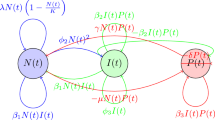
In the following, the cancer treatment fractional model based on synergy between immune cell therapies and an anti-angiogenic method with modified parameters is presented. It is important to notice that all the parameters here depend on the fractional order α as an extension of the model of integer order which is given in [21]. The model consists of eighteen variables dependent on the time. Two control variables \(u_{M} ( t )\), \(u_{A} ( t )\) are given for measuring the immunotherapy and the anti-angiogenic therapy, respectively. The variables can be identified as follows:
-
\(T ( t )\): Number of cancer cells.
-
\(U ( t )\): Number of mature unlicensed dendritic cells.
-
\(D ( t )\): Number of mature licensed dendritic cells.
-
\(A_{E} ( t )\): Number of activating/proliferating effector memory \(CD 8^{+} T\) cells.
-
\(E ( t )\): Number of activated effector memory \(CD 8^{+} T\) cells.
-
\(A_{H} ( t )\): Number of activating/proliferating memory helper \(CD 4^{+} T\) cells.
-
H: Number of activated memory helper \(CD 4^{+} T\) cells.
-
\(A_{R} ( t )\): Number of activating/proliferating regulatory T cells.
-
\(R ( t )\): T cells number of activated regulatory.
-
\(Y ( t )\): Endothelial cells number.
-
\(C ( t )\): Concentration of \(IL- 2\).
-
\(S ( t )\): Concentration of \(TGF-\beta\).
-
\(I ( t )\): Concentration of \(IL- 10\).
-
\(A_{1} ( t )\): Concentration of angiopoietin-1.
-
\(A_{2} ( t )\): Concentration of angiopoietin-2.
-
\(V ( t )\): Concentration of free \(VEGF\).
-
\(V_{a} ( t )\): Concentration of anti-\(VEGF\).
-
\(B ( t )\): Length of tumor vasculature.
The parameters of the model are described in [21, 53, 54]. The new system can be described by fractional-order differential equations as follows:
The parameters \(\omega_{1}^{\alpha}\) and \(\omega_{2}^{\alpha}\) are the weight factors.
3 The FOCPs
Consider the state system (1)–(18), in \(R^{18}\), let
be the admissible control set. The objective functional is defined as follows:
where the weight constant of cancer cell numbers is A. Moreover, \(B_{1}\), is the weight constant of immunotherapy and C is the weight constant of anti-angiogenic therapy.
Now, the aim is to minimize the following objective functional:
subject to the constraints
where
with the following initial conditions:
The modified objective functional is defined as follows ([30]):
where the Hamiltonian is given as follows:
From (21) and (22) the necessary conditions for FOPCs ([46–49]) are
where \(\lambda_{j}\), \(j =1,2,3,\ldots,18\), are the Lagrange multipliers.
Theorem 3.1
If\(u_{M}^{*}\), \(u_{A}^{*}\)be the optimal controls with corresponding states\(T^{*}\), \(U^{*}\), \(D^{*}\), \(A_{E}^{*}\), \(E^{*}\), \(A_{H}^{*}\), \(H^{*}\), \(A_{R}^{*}\), \(R^{*}\), \(C^{*}\), \(S^{*}\), \(I^{*}\), \(A_{1}^{*}\), \(A_{2}^{*}\), \(V^{*}\), \(Y^{*}\), \(B^{*}\), and\(V_{a}^{*}\), then there exist adjoint variables\(\lambda_{j}^{*}\), \(j =1,2,3,\ldots,18\), satisfying the following. (i) Adjoint equations:
(ii) Transversality conditions
(iii) Optimality conditions:
Furthermore, the control functions\(u_{A}^{*}\), \(u_{M}^{*}\)are given by
Proof
We can claim (27)–(44) using the conditions (23) where the Hamiltonian \(H_{a}^{*}\) is given by
Moreover, \(\lambda_{j}^{*} ( T_{f} )=0\), \(j =1,\ldots,18\), hold. The optimal controls (47)–(48) can be claimed from the minimization condition (46). Substituting \(u_{A}^{*}\), \(u_{M}^{*}\) in (1)–(18), we get the state system as follows:
□
3.1 Existence of an optimal control pair
The existence of the optimal control pair can be directly obtained using the results in Fleming and Rishel [55] and Lukes [56]; more precisely, we have the following theorem.
Theorem 3.2
There exists an optimal control pair \(( u_{M}^{*}, u_{A}^{*} ) \in \varOmega\) such that
Proof
To prove the existence of an optimal control, we use the result in [56]. Note that the control and the state variables are nonnegative values. In this minimizing problem, the necessary convexity of the objective functional in \(u_{A}\), \(u_{M}\) are satisfied. The set of all the control variables \(( u_{M}, u_{A} ) \in \varOmega\) is also convex and closed by definition. The optimal system is bounded, which determines the compactness needed for the existence of the optimal control. In addition, the integrand in functional (19), “\(AT+ u_{A}^{2} +C u_{M}^{2}\),” is convex on the control set Ω. Also we can claim that there exist a constant \(\mu >1\) and numbers \(c_{1}\), \(c_{2}\) such that
because the state variables are bounded, it completes the existence of an optimal control. □
4 Numerical method for solving FOCP
4.1 Nonstandard two-step Lagrange interpolation method
For simplicty consider the FODEs in the following general form:
The Atangana–Baleanu fractional-order derivative in the Caputo sense is given as follows ([43]):
where \(M ( \alpha )=1 -\alpha+ \frac{\alpha}{\varGamma( \alpha )}\) is the normalization function, \(E_{\alpha}\) is the Mittag-Leffler function.
Thanks to the fundamental theorem of fractional calculus with (69), we have
at \(t_{n+ 1}\) we have
The two-step Lagrange interpolation is given as follows:
Equation (71) is replaced in (70) and performing the same steps as in [57], we obtain
To obtain high stability [58], we used a simple modification in (72). This modification is to replace the step size h with \(\phi ( h )\) such that \(\phi ( h )= h+O ( h^{2} )\), \(0< \phi ( h ) \leq 1\). For more details on NSFDM see [40, 59–62]. The nonstandard two-step Lagrange interpolation method (NS2LIM) is given as follows:
Then we use the new scheme to numerically solve the state system (50)–(67) and we use the nonstandard implicit finite difference method to solve the co-state system (27)–(44) with transversality conditions \(\lambda_{i} ( T_{f} )=0\), \(i =1,\ldots,18\).
4.2 Construction of the N2LIM for the fraction order cancer model
Using the nonstandard technique and Eq. (73) we obtain the following nonstandard scheme for system (50)–(67). Let in system (50)–(67)
where
5 Numerical results
In the following, N2LIM is applied to solve the optimality system (50)–(67) and (27)–(44) with the transversality conditions \(\lambda_{j}^{*} ( T_{f} )=0\), \(j =1,\ldots,18\). The state Eqs. (50)–(67) have initial conditions \(T^{*} (0)=1\), \(U^{*} (0)=0\), \(D^{*} (0)=1\), \(A_{E}^{*} (0)=0\), \(E^{*} (0)=1\), \(A_{H}^{*} (0)=0\), \(H^{*} (0)=0\), \(A_{R}^{*} (0)=0\), \(R^{*} (0)=0\), \(Y^{*} (0)=10{,}000\), \(C^{*} (0)=1\), \(S^{*} (0)=0\), \(I^{*} (0)=1\), \(A_{1}^{*} (0)=10\), \(A_{2}^{*} (0)=1\), \(V^{*} (0)=0\), \(V_{a}^{*} (0)=0\), \(B^{*} (0)=1000\), \(\omega_{1} =1000\), \(\omega_{2} =1000\). The values of the parameters are taken from [21] with the power α, \(0< \alpha\leq 1\). These state equations are initially solved by the proposed methods. Then we will solve the co-state equations (27)–(44) by using a nonstandard finite difference method with back step in the time.
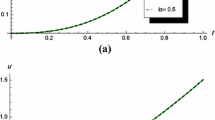
Figure 1 shows the approximate solutions at \(\alpha =0.96\) of the state variables without controls. Figure 2 shows the behavior of approximate solutions \(E ( t )\), \(I ( t )\) and \(T ( t )\) in two cases with and without controls using N2LIM. We noted that, in controlled case the increment of \(E ( t )\) and \(Y ( t )\) lead to decrease the number of cancer cells \(T ( t )\).
Figure 3 shows the approximate solutions of the state variables T, U, E, Y, S and R with control case and \(B_{1} =100\), \(C =1000\) at different α using N2LIM. It is clear that the best result is at \(\alpha =0.98\) because the number of cancer cells is minimal. Also, these results show the fractional model is more general than the integer model. Figure 4, shows the values of \(u_{A}^{*}\), \(u_{M}^{*}\) in a units of days with different values of α by using N2LIM. It is clear that the best result at \(\alpha =0.98\) in (a) and in (b) is at \(\alpha =0.7\). Table 1 shows the comparison between the values of the objective functional using N2LIM with and without controls at \(T_{f} =100\) and different values of α and \(\phi ( h )\). We note that the best result is at \(\phi ( h )=0.025(1 - e^{-h} )\). The values of objective functional (19) by the IOCM ([22, 30, 42]) and N2LIM at different values of α are shown in Table 2. We note that the N2LIM results are better than the IOCM results. We use Matlab on a computer with Windows 7 home premium, RAM 4 GB and system type 64-bit operating system.
6 Conclusions
In this paper, numerical solutions for optimal control of fractional order with generalized Mittag-Leffler function for cancer treatment based on synergy between anti-angiogenic and immune cell therapies are presented. The necessary optimality conditions are proved, where two controls \(u_{A} ( t )\), \(u_{M} ( t )\) are added to reduce the cancer cells number. N2LIM is developed to study the model problem. We present some simulations that support our theoretical findings and show the effectiveness of the model. Comparative studies with IOCM are implemented, it is found that the values of the objective functional which are obtained by N2LIM are better than the results obtained by IOCM. Moreover, N2LIM can be applied to solve the fractional optimal control problem simply and effectively.
References
Jemal, A., Center, M.M., DeSantis, C., Ward, E.M.: Global patterns of cancer incidence and mortality rates and trends. Cancer Epidemiol. Biomark. Prev. 19, 1893–1907 (2010). https://doi.org/10.1158/1055-9965.EPI-10-0437
Denysiuk, R., Silva, C.J., Torres, D.F.M.: Multiobjective optimization to a TB-HIV/AIDS coinfection optimal control problem. Comput. Appl. Math. 37 2112–2128 (2018). https://doi.org/10.1007/s40314-017-0438-9
Mathers, C.D., Boschi-Pinto, C., Lopez, A.D., Murray, C.J.L.: Cancer incidence, mortality and survival by site for 14 regions of the world. Global Programme on Evidence for Health Policy Discussion Paper No. 13, World Healh Organization (2001)
Hayat, M.J., Howlader, N., Reichman, M.E., Edwards, B.K.: Cancer statistics, trends, and multiple primary cancer analyses from the Surveillance Epidemiology, and End Results (SEER) Program. The Oncologist 12, 20–37 (2007). https://doi.org/10.1634/theoncologist.12-1-20
Poleszczuk, J., Hahnfeldt, P., Enderling, H.: Therapeutic implications from sensitivity analysis of tumor angiogenesis models. PLoS ONE 10, Article ID e0120007 (2015). https://doi.org/10.1371/journal.pone.0120007
Arciero, J., Jackson, T., Kirschner, D.: A mathematical model of tumor-immune evasion and SIRNA treatment. Discrete Contin. Dyn. Syst., Ser. B 4, 39–58 (2004)
Stevens, A., Mackey, M.C. (eds.): Mathematical Methods and Models in Biomedicine. Springer, New York (2013)
Hodgson, D.C., Gilbert, E.S., Dores, G.M., Schonfeld, S.J., Lynch, C.F., et al.: Longterm solid cancer risk among 5-year survivors of Hodgkin’s lymphoma. J. Clin. Oncol. 25, 1489–1497 (2007). https://doi.org/10.1200/JCO.2006.09.0936
Palumbo, M.O., Kavan, P., Miller, W.H., Panasci, L., Assouline, S., et al.: Systemic cancer therapy: achievements and challenges that lie ahead. Front. Pharmacol. 4, Article ID 57 (2013). https://doi.org/10.3389/fphar.2013.00057
Bokemeyer, C., Schmoll, H.: Treatment of testicular cancer and the development of secondary malignancies. J. Clin. Oncol. 13, 283–292 (1995)
Azim, H., de Azambuja, E., Colozza, M., Bines, J., Piccart, M.J.: Long-term toxic effects of adjuvant chemotherapy in breast cancer. Ann. Oncol. 22, 1939–1947 (2011). https://doi.org/10.1093/annonc/mdq683
Enderling, H., Chaplain, M.A.J.: Mathematical modeling of tumor growth and treatment. Curr. Pharm. Des. 20, 4934–4940 (2014)
Louzoun, Y., Xue, C., Lesinski, G.B., Friedman, A.: A mathematical model for pancreatic cancer growth and treatments. J. Theor. Biol. 351, 74–82 (2014). https://doi.org/10.1016/j.jtbi.2014.02.028
Salati, A.B., Shamsi, M., Torres, D.F.M.: Direct transcription methods based on fractional integral approximation formulas for solving nonlinear fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. (2018). https://doi.org/10.1016/j.cnsns.2018.05.011
Khan, A., Zaman, G.: Optimal control strategy of SEIR endemic model with continuous age-structure in the exposed and infectious classes. Optim. Control Appl. Methods 39(5), 1716–1727 (2018). https://doi.org/10.1002/oca.2437
Yildiz, T.A.: A fractional dynamical model for honeybee colony population. Int. J. Biomath. 11(5), Article ID 1850063 (2018). https://doi.org/10.1142/S1793524518500638
Joshi, B., Wang, X., Banerjee, S., Tian, H., Matzavinos, A., et al.: On immunotherapies and cancer vaccination protocols: a mathematical modelling approach. J. Theor. Biol. 259, 820–827 (2009). https://doi.org/10.1016/j.jtbi.2009.05.001
Eftimie, R., Bramson, J.L., Earn, D.J.D.: Interactions between the immune system and cancer: a brief review of non-spatial mathematical models. Bull. Math. Biol. 73, 2–32 (2011). https://doi.org/10.1007/s11538-010-9526-3
Wilson, S., Levy, D.: A mathematical model of the enhancement of tumor vaccine efficacy by immunotherapy. Bull. Math. Biol. 74, 1485–1500 (2012). https://doi.org/10.1007/s11538-012-9722-4
Scherer, R., Kalla, S., Tang, Y., Huang, J.: The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 62, 902–917 (2011)
Soto-Ortiz, L.: A cancer treatment based on synergy between anti-angiogenic and immune cell therapies. J. Theor. Biol. 394, 197–211 (2016). https://doi.org/10.1016/j.jtbi.2016.01.026
Sweilam, N.H., Rihan, F.A., AL-Mekhlafi, S.M.: A fractional-order delay differential model with optimal control for cancer treatment based on synergy between anti-angiogenic and immune cell therapies. Discrete Contin. Dyn. Syst., Ser. S 13(9), 2403–2424 (2020). https://doi.org/10.3934/dcdss.2020120
Carvalho, A.R.M., Pinto, C.M.A.: Non-integer order analysis of the impact of diabetes and resistant strains in a model for TB infection. Commun. Nonlinear Sci. Numer. Simul. 61, 104–126 (2018)
Pintoa, C.M.A., Carvalho, A.R.M.: The HIV/TB coinfection severity in the presence of TB multi-drug resistant strains. Ecol. Complex. 32, 1–20 (2017)
Cole, K.S.: Electric conductance of biological systems. In: Cold Spring Harbor Symposium on Quantitative Biology, pp. 107–116 (1993)
Caponetto, R., Dongola, G., Fortuna, L.: Fractional Order Systems: Modeling and Control Applications. World Scientific, London (2010)
El-Sayed, A., El-Mesiry, A., El-Saka, H.: On the fractionalorder logistic equation. Appl. Math. Lett. 20(7), 817–823 (2007)
Machado, J.A.T.: Analysis and design of fractional order digital control systems. Syst. Anal. Model. Simul. 27, 107–122 (1997)
Machado, J.A.T.: Fractional-order derivative approximations in discrete-time control systems. Syst. Anal. Model. Simul. 34, 419–434 (1999)
Sweilam, N.H., AL-Mekhlafi, S.M.: On the optimal control for fractional multi-strain TB model. Optim. Control Appl. Methods 37(6), 1355–1374 (2016). https://doi.org/10.1002/oca.2247
Sweilam, N.H., AL-Mekhlafi, S.M., Hassan, A.N.: Numerical treatment for solving the fractional two-group influenza model. Prog. Fract. Differ. Appl. 4, 503–517 (2018)
Xu, H.: Analytical approximations for a population growth model with fractional order. Commun. Nonlinear Sci. Numer. Simul. 14, 1978–1983 (2009)
Jajarmia, A., Yusuf, A., Baleanu, D., Inc, M.: A new fractional HRSV model and its optimal control: a non-singular operator approach. Phys. A, Stat. Mech. Appl. 547, Article ID 123860 (2020)
Baleanu, D., Jajarmi, A., Mohammadi, H., Rezapour, S.: A new study on the mathematical modelling of human liver with Caputo–Fabrizio fractional derivative. Chaos Solitons Fractals 134, Article ID 109705 (2020)
Alijani, Z., Baleanu, D., Shiri, B., Wu, G.-C.: Spline collocation methods for systems of fuzzy fractional differential equations. Chaos Solitons Fractals 131, Article ID 109510 (2020)
Shiri, B., Baleanu, D.: Numerical solution of some fractional dynamical systems in medicine involving non-singular kernel with vector order. Results Nonlinear Anal. 2(4), 160–168 (2019)
Baleanu, D., Shiri, B., Srivastava, H.M., Al Qurashi, M.: A Chebyshev spectral method based on operational matrix for fractional differential equations involving non-singular Mittag-Leffler kernel. Adv. Differ. Equ. 2018, Article ID 353 (2018). https://doi.org/10.1186/s13662-018-1822-5
Baleanu, D., Jajarmi, A.: On the fractional optimal control problems with a general derivative operator. Asian J. Control (2019). https://doi.org/10.1002/asjc.2282
Sweilam, N.H., AL-Mekhlafi, S.M.: Optimal control for a time delay multi-strain tuberculosis fractional model: a numerical approach. IMA J. Math. Control Inf. 36(1), 317–340 (2019)
Sweilam, N.H., AL-Mekhlafi, S.M.: Optimal control for a nonlinear mathematical model of tumor under immune suppression: a numerical approach. Optim. Control Appl. Methods 39(5), 1581–1596 (2018). https://doi.org/10.1002/oca.2427
Sweilam, N.H., AL-Mekhlafi, S.M., Baleanu, D.: Efficient numerical treatments for a fractional optimal control nonlinear tuberculosis model. Int. J. Biomath. 11(8), Article ID 1850115 (2018)
Sweilam, N.H., AL-Mekhlafi, S.M., Alshomrani, A.S., Baleanu, D.: Comparative study for optimal control nonlinear variable-order fractional tumor model. Chaos Solitons Fractals 136, Article ID 109810 (2020). https://doi.org/10.1016/j.chaos.2020.109810
Atangana, A., Baleanu, D.: New fractional derivatives with non-local and non-singular kernel theory and application to heat transfer model. Therm. Sci. 20(2), 763–769 (2016)
Baleanu, D., Fernandez, A.: On some new properties of fractional derivatives with Mittag-Leffler kernel. Commun. Nonlinear Sci. Numer. Simul. 18(59), 444–462 (2018)
Fernandez, A., Ozarslan, M.A., Baleanu, D.: On fractional calculus with general analytic kernels. Appl. Math. Comput. 354, 248–265 (2019)
Agrawal, O.P.: On a general formulation for the numerical solution of optimal control problems. Int. J. Control 28(1–4), 323–337 (2004)
Agrawal, O.P.: Formulation of Euler–Lagrange equations for fractional variational problems. J. Math. Anal. Appl. 272(1), 368–379 (2002)
Agrawal, O.P.: A formulation and numerical scheme for fractional optimal control problems. IFAC Proc. Vol. 39(11), 68–72 (2006)
Agrawal, O.P., Defterli, O., Baleanu, D.: Fractional optimal control problems with several state and control variables. J. Vib. Control 16(13), 1967–1976 (2010)
Zaky, M.A., Tenreiro Machado, J.A.: On the formulation and numerical simulation of distributed-order fractional optimal control problems. Commun. Nonlinear Sci. Numer. Simul. 52, 177–189 (2017)
Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus: Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos, vol. 3. World Scientific, Hackensack (2012)
Arenas, A.J., Gonzàlez-Parra, G., Chen-Charpentierc, B.M.: Construction of nonstandard finite difference schemes for the SI and SIR epidemic models of fractional order. Math. Comput. Simul. 121, 48–63 (2016)
Robertson-Tessi, M., El-Kareh, A., Goriely, A.: A mathematical model of tumor-immune interactions. J. Theor. Biol. 294, 56–73 (2012). https://doi.org/10.1016/j.jtbi.2011.10.027
Cameron, M.A., Davis, A.L.: A mathematical model of angiogenesis in glioblastoma multiforme. Arizona State University (2009)
Fleming, W.H., Rishel, R.W.: Deterministic and Stochastic Optimal Control. Springer, New York (1975)
Lukes, D.L.: Differential Equations: Classical to Controlled. Mathematics in Science and Engineering, vol. 162. Academic Press, New York (1982)
Solís-Pérez, J.E., Gómez-Aguilar, J.F.: Novel numerical method for solving variable-order fractional differential equations with power, exponential and Mittag-Leffler laws. Chaos Solitons Fractals 14, 175–185 (2018)
Sweilam, N.H., AL-Mekhlafi, S.M., Baleanu, D.: Optimal control for a fractional tuberculosis infection model including the impact of diabetes and resistant strains. J. Adv. Res. 17, 125–137 (2019)
Mickens, R.E.: Nonstandard Finite Difference Models of Differential Equations. World Scientific, Singapore (2005)
Mickens, R.E.: Calculation of denominator functions for nonstandard finite difference schemes for differential equations satisfying a positivity condition. Numer. Methods Partial Differ. Equ. 23, 672–691 (2007)
Patidar, K.C.: Nonstandard finite difference methods: recent trends and further developments. J. Differ. Equ. Appl. 22(6), 817–849 (2016). https://doi.org/10.1080/10236198.2016.1144748
Sweilam, N.H., Soliman, I.A., AL-Mekhlafi, S.M.: Nonstandard finite difference method for solving the multi-strain TB model. J. Egypt. Math. Soc. 25(2), 129–138 (2017). https://doi.org/10.1016/j.joems.2016.10.004
Acknowledgements
The authors would like to thanks the anonymous reviewers very much for their positive comments, careful reading and useful suggestions on improving this article.
Availability of data and materials
Please contact the corresponding author for data requests.
Funding
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sectors.
Author information
Authors and Affiliations
Contributions
The authors contributed equally to this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sweilam, N.H., Al-Mekhlafi, S.M., Assiri, T. et al. Optimal control for cancer treatment mathematical model using Atangana–Baleanu–Caputo fractional derivative. Adv Differ Equ 2020, 334 (2020). https://doi.org/10.1186/s13662-020-02793-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02793-9