1 Introduction

Fractional calculus has been concerned with integrals and derivatives of arbitrary non-integer order of functions. In recent years, several researchers in the field of fractional calculus have brought attention to the search for the best fractional derivative, which will be used to model real world problems. Fractional calculus is as old as the classical calculus whose equations are often considered unable to model certain complex systems and it turned out that the methods used in the fractional calculus are splendid when modeling long-memory processes and many phenomena that occur in physics, chemistry, electricity, mechanics and many other disciplines [10, 13, 17, 21, 31, 32, 34, 35, 38–40].

However, scientists felt the need for other types of fractional operators restricted to Riemann–Liouville fractional operators and Caputo fractional derivatives until the turn of this century. Many scientists proposed a variety of new fractional operators which contributed to the growth of the field of fractional calculus [9, 14, 15, 24, 25, 27–29, 37]. It is worth noting that the fractional operators proposed in this work are unique instances of fractional integrals/derivatives in relation to another function described in [4, 5, 22, 41]. But all of these operators possess one of the most important peculiarities of fractional operators: nonlocality.

In [30], the authors introduced a local derivative with a non-integer order and called it a conformable derivative. The process of conceptualization of these local derivatives will lead to the rediscovery of the nonlocal fractional operators described in [28, 29]. We explain the key principles of the conformable derivative and suggest a derivative consistent with the left and right versions. Once again, the nonlocal fractional version as proposed in [1, 12] is found in [27].

In all types of fractional calculus or calculus with derivative, the order zero for a function should be equal to the function. The conformable derivative lacks this essential property of every derivative and in fact it is a deficit. In order to circumvent this deficit, the authors in [6, 7] redefined the conformal derivative to yield the function itself when this local derivative is of the order of zero. Following this was work by Jarad et al. [23] where the authors suggested the fractional version of the redefined conformable derivative. The existence and uniqueness of solutions belong to the most important qualitative properties of fractional differential equations. The existence and uniqueness of solutions to fractional differential equations that include different types of fractional derivatives and initial/boundary conditions were tackled by several mathematicians (see [2, 3, 8, 11, 16, 19, 20, 26, 42–45] and the references cited therein).

Motivated by [18, 36], we propose a new fractional derivative (simply known as Hilfer generalized proportional fractional derivative). Therefore, in the context of the defined derivative, we discuss the existence and uniqueness of solutions for a certain type of nonlinear fractional differential equations with nonlocal initial condition. The Hilfer generalized proportional fractional differential equation is of the following form:

$$ \textstyle\begin{cases} \mathcal{D}^{p,q,\rho }_{a^{+}}x(t)=f(t, x(t)),\quad t\in J=[a, T], T>a\ge 0,&\\ \mathcal{I}^{1-\gamma , \rho }_{a^{+}}x(a) =\sum_{i=1}^{m}c_{i}x( \tau _{i}), \quad p\leq \gamma =p+q-pq, \tau _{i}\in (a, T), \end{cases} $$
(1.1)

where \(\mathcal{D}^{p,q,\rho }_{a^{+}}(\cdot )\) is the Hilfer generalized proportional fractional derivative of order \((0< p<1)\), \(\mathcal{I}^{1-\gamma , \rho }_{a^{+}}(\cdot )\) is the generalized proportional fractional integral of order \(1-\gamma >0\), \(c_{i}\in \mathbb{R}\), \(f: J\times \mathbb{R}\rightarrow \mathbb{R}\) is a continuous function and \(\tau _{i}\in J\) satisfying \(a<\tau _{1}<\cdots <\tau _{m}<T\) for \(i=1,\ldots, m\). To the best of our knowledge no one has discussed the existence and uniqueness of solutions of (1.1).

The rest of the paper is structured as follows. In Sect. 2, we shall review some basic definitions and theoretical results that we need to proceed. We describe our proposed derivatives in Sect. 3, the Hilfer generalized proportional derivatives along with some of the preliminary properties. In addition, we also investigate the comparability between an initial value problem and an integral equation of Volterra, from which we prove the existence and uniqueness of the solution using fixed point theorems of Banach and Kransnoselskii’s. Moreover, two examples were given to clarify the results. The conclusion of the paper is given in Sect. 4.

2 Preliminaries and theoretical results

We offer some preliminary details, results and definitions of fractional calculus in this section, which are important throughout this paper.

Let \(-\infty < a< b<\infty \) be finite and infinite intervals on \(\mathbb{R}_{+}\). Denote by \(\mathcal{C}[a, b]\), the spaces of the continuous function f on \([a, b]\) with norm defined by [32]

$$ \Vert f \Vert _{\mathcal{C}[a, b]}= \max_{t\in [a, b]} \bigl\vert f(t) \bigr\vert , $$

and \(\mathcal{AC}^{n}[a, b]\), the space of n times absolutely continuous differentiable functions, given by

$$ {\mathcal{AC}}^{n}[a, b]=\bigl\{ f: (a, b]\rightarrow \mathbb{R}; f^{n-1} \in \mathcal{AC}\bigl([a, b]\bigr)\bigr\} . $$

The weighted space \(\mathcal{C}_{\gamma }[a, b]\) of a functions f on \((a, b]\) is defined by

$$ {\mathcal{C}}_{\gamma }[a, b]=\bigl\{ f: (a, b]\rightarrow \mathbb{R}; (t-a)^{ \gamma }f(t)\in \mathcal{C}\bigl([a, b]\bigr)\bigr\} , \quad 0\leq \gamma < 1, $$

with the norm

$$ \Vert f \Vert _{\mathcal{C}_{\gamma }[a, b]}= \bigl\Vert (t-a)^{\gamma }f(t) \bigr\Vert _{ \mathcal{C}[a, b]}= \max_{t\in [a, b]} \bigl\vert (t-a)^{\gamma }f(t) \bigr\vert . $$

The weighted space \(\mathcal{C}_{\gamma }^{n}[a, b]\) of the functions f on \((a, b]\) is defined by

$$ {\mathcal{C}}_{\gamma }^{n}[a, b]=\bigl\{ f: (a, b]\rightarrow \mathbb{R}; f(t) \in \mathcal{C}^{n-1}\bigl([a, b]\bigr); f^{n}(t)\in \mathcal{C}_{\gamma }\bigl([a, b]\bigr) \bigr\} ,\quad 0 \leq \gamma < 1, $$

with the norm

$$ \Vert f \Vert _{\mathcal{C}^{n}_{\gamma }[a, b]}= \sum_{k=0}^{n-1} \bigl\Vert f^{k} \bigr\Vert _{\mathcal{C}[a, b]}+ \bigl\Vert f^{n} \bigr\Vert _{\mathcal{C}_{\gamma }[a, b]}. $$

Clearly, \(\mathcal{C}^{0}_{\gamma }[a, b]=\mathcal{C}_{\gamma }[a, b]\), if \(n=0\).

Definition 2.1

([32])

Suppose \(f\in L^{1}([a, b], \mathbb{R})\). Then the fractional operator

$$ I^{p}_{a^{+}}f(t)=\frac{1}{\varGamma (p)} \int _{a}^{t}(t-\mu )^{p-1}f( \mu )\,d\mu , \quad p>0, t>a, n\in \mathbb{N}, $$

is referred to as the Riemann–Liouville integral of order p with the lower limit \(a^{+}\) of the function f, where \(\varGamma (\cdot )\) denotes the classical gamma function.

Definition 2.2

([32])

Let \(f\in \mathcal{C}([a, b])\). Then the fractional operator

$$ {}^{L}D^{p}_{a+}f(t)=\frac{1}{\varGamma (n-p)} \frac{d^{n}}{dt^{n}} \int _{a}^{t}(t- \mu )^{n-p-1}f(\mu )\,d\mu , \quad p>0, t>a, n-1< p< n, n\in \mathbb{N}, $$

is called the Riemann–Liouville fractional derivative of order p with the lower limit \(a^{+}\) of the function f, where \(\varGamma (\cdot )\) denotes the gamma function.

Definition 2.3

([32])

Let \(f\in \mathcal{C}^{n}([a, b])\). Then the fractional operator

$$ {}^{C}D^{p}_{a+}f(t)=\frac{1}{\varGamma (n-p)} \int _{a}^{t}(t-\mu )^{n-p-1}f^{n}( \mu )\,d\mu , \quad p>0, n-1< p< n, n\in \mathbb{N}, $$

is referred to the Caputo fractional derivative of order p with the lower limit \(a^{+}\) of the function f.

Definition 2.4

([23])

If \(\rho \in (0, 1]\) and \(p\in \mathbb{C}\), \(\operatorname{Re}(p)>0\). Then the fractional operator

$$ I_{a^{+}}^{p, \rho }f(t)=\frac{1}{\rho ^{p}\varGamma (p)} \int _{a}^{t}e^{{ \frac{\rho -1}{\rho }}(t-\mu )}(t-\mu )^{p-1}f(\mu )\,d\mu , \quad t>a, $$
(2.1)

is called the left-sided generalized proportional integral of order p of the function f.

Definition 2.5

([23])

The left generalized proportional fractional derivative of order p and \(\rho \in (0, 1]\) of a function f is defined by

$$ D_{a^{+}}^{p, \rho }f(t)=\frac{D^{n, \rho }}{\rho ^{n-p}\varGamma (n-p)} \int _{a}^{t}e^{{\frac{\rho -1}{\rho }}(t-\mu )}(t-\mu )^{n-p-1}f(\mu )\,d \mu , \quad p\in \mathbb{C}, \operatorname{Re}(p)>0, $$
(2.2)

where \(\varGamma (\cdot )\) is the Gamma function and \(n=[p]+1\).

Definition 2.6

([23])

Let \(\rho \in (0, 1]\). Then the fractional operator

$$ \begin{aligned}[b] {}^{C}D_{a^{+}}^{p, \rho }f(t)&= \frac{1}{\rho ^{n-p}\varGamma (n-p)}\\ &\quad {}\times \int _{a}^{t}e^{{ \frac{\rho -1}{\rho }}(t-\mu )}(t-\mu )^{n-p-1}\bigl(D^{n, \rho }f\bigr) (\mu )\,d \mu , \quad p\in \mathbb{C}, \operatorname{Re}(p)>0, \end{aligned} $$
(2.3)

is referred to as the left-sided generalized proportional fractional derivative in the sense of Caputo of order p of the function f, where \(\varGamma (\cdot )\) is the gamma function and \(n=[p]+1\).

Remark 2.7

Note that if \(\rho =1\) Definitions 2.4, 2.5 and 2.6 coincide with the classical definitions of the Riemann–Liouville fractional integral, the Riemann–Liouville fractional derivative and the Caputo fractional derivative (see Definitions 2.1, 2.2 and 2.3).

The following are certain important properties of the generalized proportional fractional integral and derivative.

Proposition 2.8

([23])

Let\(p, \delta \in \mathbb{C}\)such that\(\operatorname{Re}(p)\ge 0\)and\(\operatorname{Re}(\delta )>0\). Then for any\(\rho \in (0,1]\)we have

$$ \begin{gathered} \bigl( I_{a^{+}}^{p, \rho }e^{{\frac{\rho -1}{\rho }}s}(s-a)^{ \delta -1} \bigr) (t)= \frac{\varGamma (\delta )}{\rho ^{p}\varGamma (\delta +p)}e^{{ \frac{\rho -1}{\rho }}t}(t-a)^{\delta +p-1}, \\ \bigl( D_{a^{+}}^{p, \rho }e^{{\frac{\rho -1}{\rho }}s}(s-a)^{\delta -1} \bigr) (t)=\frac{\rho ^{p}\varGamma (\delta )}{\varGamma (\delta -p)}e^{{ \frac{\rho -1}{\rho }}t}(t-a)^{\delta -p-1}, \\ \bigl( I_{b}^{p, \rho }e^{{\frac{\rho -1}{\rho }}(b-s)}(b-s)^{\delta -1} \bigr) (t)=\frac{\varGamma (\delta )}{\rho ^{p}\varGamma (\delta +p)}e^{{ \frac{\rho -1}{\rho }}(b-t)}(b-t)^{\delta +p-1}, \\ \bigl( D_{b}^{p, \rho }e^{{\frac{\rho -1}{\rho }}(b-s)}(b-s)^{q-1} \bigr) (t)=\frac{\rho ^{p}\varGamma (\delta )}{\varGamma (\delta -p)}e^{{ \frac{\rho -1}{\rho }}(b-t)}(b-t)^{\delta -p-1}. \end{gathered} $$
(2.4)

Theorem 2.9

([23])

Let\(\rho \in (0, 1]\), \(\operatorname{Re}(p)>0\)and\(\operatorname{Re}(q)>0\). If\(f\in \mathcal{C}([a, b], \mathbf{R})\), then

$$ I^{p, \rho }_{a^{+}}\bigl(I_{a^{+}}^{q, \rho }f\bigr) (t)=I_{a^{+}}^{q, \rho }\bigl(I_{a^{+}}^{p, \rho }f\bigr) (t)=\bigl(I_{a^{+}}^{p+q, \rho }f\bigr) (t),\quad t\ge a. $$
(2.5)

Theorem 2.10

([23])

Suppose\(\rho \in (0, 1]\)and\(0\leq m<[\operatorname{Re}(p)]+1\). If\(f\in L^{1}([a, b])\). Then

$$ D_{a^{+}}^{m, \rho }\bigl(I_{a^{+}}^{p, \rho }f\bigr) (t) =\bigl(I_{a^{+}}^{p-m, \rho }f\bigr) (t), \quad t>a. $$
(2.6)

Corollary 2.11

([23])

If\(0<\operatorname{Re}(q)<\operatorname{Re}(p)\)and\(m-1<\operatorname{Re}(q)\leq m\). Then we get

$$ D_{a^{+}}^{q, \rho }I_{a^{+}}^{p, \rho }f(t) =I_{a^{+}}^{p-q, \rho }f(t). $$

Theorem 2.12

([23])

Let\(f\in L^{1}([a, b])\), \(\operatorname{Re}(p)>0\)and\(\rho \in (0, 1]\). Then

$$ D_{a^{+}}^{p, \rho }I_{a^{+}}^{p, \rho }f(t)=f(t),\quad t\ge a, n=\bigl[\operatorname{Re}(p)\bigr]+1. $$

Lemma 2.13

([23])

If\(p>0\), \(\rho \in (0, 1]\)and\(m\in \mathbb{Z}_{+}\). Then

$$ \bigl(I_{a^{+}}^{p, \rho }D_{a^{+}}^{m, \rho }f\bigr) (t)=\bigl(D_{a^{+}}^{m, \rho }I_{a^{+}}^{p, \rho }f\bigr) (t)- \sum_{k=0}^{m-1} \frac{e^{{\frac{\rho -1}{\rho }}(t-a)}(t-a)^{p-m+k}}{\rho ^{p-m+k}\varGamma (p+k-m+1)} \bigl(D_{a^{+}}^{k, \rho }f\bigr) (a). $$
(2.7)

In particular, if\(m=1\), we obtain

$$ \bigl(I_{a^{+}}^{p, \rho }D_{a^{+}}^{\rho }f\bigr) (t)=\bigl(D_{a^{+}}^{\rho }I_{a^{+}}^{p, \rho }f\bigr) (t)- \frac{e^{{\frac{\rho -1}{\rho }}(t-a)}(t-a)^{p-1}}{\rho ^{p-1}\varGamma (p)}f(a). $$
(2.8)

Theorem 2.14

([23])

Let\(\operatorname{Re}(p)>0\), \(n=-[-\operatorname{Re}(p)]\), \(f\in L_{1}(a, b)\)and\((I_{a^{+}}^{p, \rho }f)(t)\in AC^{n}[a, b]\). Then

$$ \bigl(I_{a^{+}}^{p, \rho }D_{a^{+}}^{p, \rho }f\bigr) (t)=f(t)-e^{{ \frac{\rho -1}{\rho }}(t-a)} \sum_{j=1}^{n} \frac{(t-a)^{p-j}}{\rho ^{p-j}\varGamma (p-j+1)}\bigl(I_{a}^{j-p, \rho }f\bigr) \bigl(a^{+}\bigr). $$
(2.9)

3 Main results

We introduce the Hilfer generalized proportional fractional derivative in this section and discuss some of its properties. Additionally, we demonstrate the equivalence between the proposed problem (1.1) and the integral equation of Volterra type. In addition, we prove the existence and uniqueness of solutions of problem (1.1) by employing the fixed point theorems.

Definition 3.1

Let \(n-1< p< n\), \(\rho \in (0, 1]\) and \(0\le q\le 1\), with \(n\in \mathbb{N}\). The left-sided/right-sided Hilfer generalized proportional fractional derivative of order p and type q of a function f is defined by

$$ \bigl( \mathcal{D}_{a^{\pm }}^{p,q,\rho }f \bigr) (x)= \mathcal{I}_{a^{\pm }}^{q(n-p),\rho } \bigl[D^{\rho } \bigl( \mathcal{I}_{a^{\pm }}^{(1-q)(n-p), \rho }f \bigr) \bigr](x), $$
(3.1)

where \(D^{\rho }f(x)=(1-\rho )f(x)+\rho f^{\prime }(x)\) and \(\mathcal{I}\) is the generalized proportional fractional integral defined in Eq. (2.1).

In particular, if \(n=1\), Definition 3.1 is equivalent with

$$ \bigl( \mathcal{D}_{a^{\pm }}^{p,q,\rho }f \bigr) (x)= \mathcal{I}_{a^{\pm }}^{q(1-p),\rho } \bigl[D^{\rho } \bigl( \mathcal{I}_{a^{\pm }}^{(1-q)(1-p), \rho }f \bigr) \bigr](x). $$
(3.2)

Thus, throughout this paper, we discuss the case where \(n=1\), \(0< p<1\), \(0\le q\le 1\) and \(\gamma =p+q-pq\).

Remark 3.2

It is worthwhile to specify that:

  • The derivative is used as an interpolator between the Riemann–Liouville and Caputo generalized proportional fractional derivative, respectively, since

    $$ \mathcal{D}^{p,q,\rho }_{a^{\pm }}f= \textstyle\begin{cases} {D^{\rho }}\mathcal{I}_{a^{\pm }}^{(1-p),\rho }f,\quad q=0 \text{ ({see Definition 2.5})}, \\ \mathcal{I}_{a^{\pm }}^{(1-p),\rho }D^{\rho }f, \quad q=1\text{ ({see Definition 2.6})}. \end{cases} $$
    (3.3)

  • The parameter γ satisfies

    $$ 0< \gamma \le 1,\qquad \gamma \ge p,\qquad \gamma >q, \qquad 1-\gamma < 1-q(1-p). $$

Property 3.3

The operator \(\mathcal{D}_{a^{+}}^{p,q,\rho }\) can be simplified as

$$ \mathcal{D}_{a^{+}}^{p,q,\rho }f=\mathcal{I}_{a^{+}}^{q(1-p),\rho } D^{\rho}\mathcal{I}_{a^{+}}^{(1-\gamma ),\rho }f= \mathcal{I}_{a^{+}}^{q(1-p), \rho }\mathcal{D}^{\gamma ,\rho }_{a^{+}}f, \quad \gamma =p+q-pq. $$

Proof

In view of Equation (3.2) and Definition 2.5,

$$ \begin{aligned}[b] \bigl( \mathcal{D}_{a^{+}}^{p,q,\rho }f \bigr) (x) &= \mathcal{I}_{a^{+}}^{q(1-p),\rho } \bigl[ \mathcal{D}^{\rho } \bigl( \mathcal{I}_{a^{+}}^{(1-q)(1-p),\rho }f \bigr) \bigr](x) \\ &=\mathcal{I}_{a^{+}}^{q(1-p),\rho } \biggl\lbrace \frac{D^{\rho}}{\rho ^{(1-\gamma )}\varGamma ((1-\gamma ))} \int _{a}^{t}e^{\frac{\rho -1}{\rho }(t-\tau )}(t-\tau )^{(1-\gamma )-1}f( \tau )\,d\tau \biggr\rbrace \\ &= \bigl( \mathcal{I}_{a^{+}}^{q(1-p),\rho }\mathcal{D}^{\gamma ,\rho }f \bigr) (x). \end{aligned} $$

 □

We consider the following weighted spaces of continuous function on \((a, b]\):

$$ \mathcal{C}_{1-\gamma }^{p,q}[a, b]=\bigl\{ f\in \mathcal{C}_{1-\gamma }[a, b], \mathcal{D}_{a^{+}}^{p,q,\rho }f\in \mathcal{C}_{1-\gamma }[a, b]\bigr\} $$

and

$$ \mathcal{C}_{1-\gamma }^{\gamma }[a, b]=\bigl\{ f\in \mathcal{C}_{1-\gamma }[a, b], \mathcal{D}_{a^{+}}^{\gamma ,\rho }f\in \mathcal{C}_{1-\gamma }[a, b] \bigr\} . $$

Since \(\mathcal{D}_{a^{+}}^{p,q,\rho }=\mathcal{I}_{a^{+}}^{q(1-p),\rho } \mathcal{D}^{\gamma ,\rho }_{a^{+}}\),

$$ \mathcal{C}_{1-\gamma }^{\gamma }[a, b]\subset \mathcal{C}_{1-\gamma }^{p,q}[a, b]. $$

Lemma 3.4

Suppose\(0< p<1\), \(\rho \in (0, 1]\)and\(0\le \gamma <1\). If\(f\in \mathcal{C}_{\gamma }[a, b]\)then

$$ \mathcal{I}_{a^{+}}^{p,\rho }f(a)=\lim_{x\rightarrow a^{+}} \mathcal{I}_{a^{+}}^{p,\rho }f(x)=0,\quad 0\le \gamma < p. $$

Proof

Considering \(f\in \mathcal{C}[a, b]\), it implies that \(f\in \mathcal{C}_{\gamma }[a, b]\) and \((x-a)^{\gamma }\in \mathcal{C}[a, b]\). Therefore, there exists \(M>0\) for which

$$ (x-a)^{\gamma }f(x)< M, \quad \text{for all } x\in [a, b], $$

and

$$ \bigl\vert \mathcal{I}_{a^{+}}^{p,\rho }e^{\frac{\rho -1}{\rho }x}f(x) \bigr\vert < M \bigl[ \mathcal{I}_{a^{+}}^{p,\rho }e^{\frac{\rho -1}{\rho }t}(t-a)^{-\gamma } \bigr](x). $$

It follows from Proposition 2.8, that

$$ \bigl\vert \mathcal{I}_{a^{+}}^{p,\rho }e^{\frac{\rho -1}{\rho }x}f(x) \bigr\vert < M \biggl[ \frac{\varGamma (1-\gamma )}{\varGamma (p+1-\gamma )}e^{ \frac{\rho -1}{\rho }x}(x-a)^{p-\gamma } \biggr], $$

which implies that the right-hand side →0 as \(x\rightarrow a^{+}\). □

Lemma 3.5

Let\(0< p<1\), \(\rho \in (0, 1]\), \(0\le q\le 1\)and\(\gamma =p+q-pq\). If\(f\in \mathcal{C}_{1-\gamma }^{\gamma }[a, b]\)then

$$ \mathcal{I}_{a^{+}}^{\gamma ,\rho }\mathcal{D}_{a^{+}}^{\gamma ,\rho }f= \mathcal{I}_{a^{+}}^{p,\rho }\mathcal{D}_{a^{+}}^{p,q,\rho }f $$

and

$$ \mathcal{D}_{a^{+}}^{\gamma ,\rho }\mathcal{I}_{a^{+}}^{p,\rho }f= \mathcal{D}_{a^{+}}^{q(1-p),\rho }f. $$

Proof

Making use of Theorem 2.9 and Property 3.3,

$$ \begin{aligned}[b] \mathcal{I}_{a^{+}}^{\gamma ,\rho } \mathcal{D}_{a^{+}}^{ \gamma ,\rho }f&=\mathcal{I}_{a^{+}}^{\gamma ,\rho } \bigl(\mathcal{I}_{a^{+}}^{-q(1-p), \rho }\mathcal{D}_{a^{+}}^{p,q,\rho }f \bigr) \\ &=\mathcal{I}_{a^{+}}^{p+q-pq,\rho }\mathcal{I}_{a^{+}}^{-q(1-p),\rho } \mathcal{D}_{a^{+}}^{p,q,\rho }f \\ &=\mathcal{I}_{a^{+}}^{p,\rho }\mathcal{D}_{a^{+}}^{p,q,\rho }f. \end{aligned} $$

Furthermore, in view of Theorem 2.9 and Eq. (3.2), we can see that

$$ \begin{aligned}[b] \mathcal{D}_{a^{+}}^{\gamma ,\rho } \mathcal{I}_{a^{+}}^{p, \rho }f&=\mathcal{D}_{a^{+}}^{\rho } \mathcal{I}_{a^{+}}^{1-\gamma ,\rho } \mathcal{I}_{a^{+}}^{p,\rho }f \\ &=\mathcal{D}_{a^{+}}^{\rho }\mathcal{I}_{a^{+}}^{1-q+pq,\rho }f \\ &=\mathcal{D}_{a^{+}}^{q(1-p),\rho }f. \end{aligned} $$

 □

Lemma 3.6

Suppose\(f\in L^{1}(a, b)\)such that\(\mathcal{D}_{a^{+}}^{q(1-p),\rho }f\)exists in\(L^{1}(a, b)\). Then

$$ \mathcal{D}_{a^{+}}^{p,q,\rho }\mathcal{I}_{a^{+}}^{p,\rho }f= \mathcal{I}_{a^{+}}^{q(1-p),\rho }\mathcal{D}_{a^{+}}^{q(1-p),\rho }f. $$

Proof

It follows from Definition 2.5 and Eq. (3.2) that

$$ \begin{aligned}[b] \mathcal{D}_{a^{+}}^{p,q,\rho } \mathcal{I}_{a^{+}}^{p, \rho }f&=\mathcal{I}_{a^{+}}^{q(1-p),\rho } \mathcal{D}_{a^{+}}^{\rho } \mathcal{I}_{a^{+}}^{(1-q)(1-p),\rho } \\ &=\mathcal{I}_{a^{+}}^{q(1-p),\rho }\mathcal{D}_{a^{+}}^{\rho } \mathcal{I}_{a^{+}}^{1-q(1-p),\rho } \\ &=\mathcal{I}_{a^{+}}^{q(1-p),\rho }\mathcal{D}_{a^{+}}^{q(1-p),\rho }f. \end{aligned} $$

 □

Lemma 3.7

Let\(0< p<1\), \(\rho \in (0, 1]\), and\(0\le \gamma <1\). If\(f\in \mathcal{C}_{\gamma }[a, b]\)and\(\mathcal{I}_{a^{+}}^{1-p,\rho }f\in \mathcal{C}^{1}_{\gamma }[a, b] \), then

$$ \mathcal{I}_{a^{+}}^{p,\rho }\mathcal{D}_{a^{+}}^{p,\rho }f(x)=f(x)-e^{{ \frac{\rho -1}{\rho }}(x-a)} \frac{(x-a)^{p-1}}{\rho ^{p-1}\varGamma (p)}\bigl(I_{a}^{1-p, \rho }f\bigr) \bigl(a^{+}\bigr), $$

for all\(x\in (a, b]\).

Proof

The proof is similar to the ones in [23]. □

Lemma 3.8

Let\(0< p<1\), \(\rho \in (0, 1]\), \(0\le q\le 1\)and\(\gamma =p+q-pq\). If\(f\in \mathcal{C}_{1-\gamma }[a, b]\)and\(\mathcal{D}_{a^{+}}^{p,q,\rho }f\)then\(\mathcal{D}_{a^{+}}^{p,q,\rho }\mathcal{I}_{a^{+}}^{p,\rho }f\)exists in\((a, b)\)and

$$ \mathcal{D}_{a^{+}}^{p,q,\rho }\mathcal{I}_{a^{+}}^{p,\rho }f(x)=f(x), \quad x\in (a, b]. $$

Proof

Now, using Lemmas 3.4, 3.6 and 3.7, we have

$$ \begin{aligned}[b] \bigl( \mathcal{D}_{a^{+}}^{p,q,\rho } \mathcal{I}_{a^{+}}^{p, \rho }f \bigr) (x)&= \bigl( \mathcal{I}_{a^{+}}^{q(1-p),\rho } \mathcal{D}_{a^{+}}^{q(1-p),\rho }f \bigr) (x) \\ &=f(x)-e^{{\frac{\rho -1}{\rho }}(x-a)} \frac{(x-a)^{q(1-p)-1}}{\rho ^{q(1-p)-1}\varGamma (q(1-p))}\bigl(I_{a}^{1-q(1-p), \rho }f \bigr) \bigl(a^{+}\bigr) \\ &=f(x). \end{aligned} $$

 □

Lemma 3.9

Let\(0< p<1\), \(\rho \in (0, 1]\), \(0\le q\le 1\)and\(0<\gamma <1\). If\(f\in \mathcal{C}_{1-\gamma }[a, b]\)and\(\mathcal{I}_{a^{+}}^{1-\gamma ,\rho }f\), then

$$ \mathcal{I}_{a^{+}}^{p,\rho }\mathcal{D}_{a^{+}}^{p,q,\rho }f(x)=f(x)-e^{{ \frac{\rho -1}{\rho }}(x-a)} \frac{(x-a)^{\gamma -1}}{\rho ^{\gamma -1}\varGamma (\gamma )}\bigl(I_{a}^{1- \gamma , \rho }f\bigr) \bigl(a^{+}\bigr), \quad x\in (a, b]. $$

Proof

It follows from Definition 3.1 and Lemma 3.7 that

$$ \begin{aligned}[b] \bigl(\mathcal{I}_{a^{+}}^{p,\rho } \mathcal{D}_{a^{+}}^{p,q, \rho }f \bigr) (x)&=\mathcal{I}_{a^{+}}^{p,\rho } \bigl( \mathcal{I}_{a^{+}}^{ \gamma -p,\rho }\mathcal{D}_{a^{+}}^{\gamma ,\rho }f \bigr) (x) \\ &=\mathcal{I}_{a^{+}}^{\gamma ,\rho }\mathcal{D}_{a^{+}}^{\gamma ,\rho }f(x) \\ &=f(x)-e^{{\frac{\rho -1}{\rho }}(x-a)} \frac{(x-a)^{\gamma -1}}{\rho ^{\gamma -1}\varGamma (\gamma )}\bigl(I_{a}^{1- \gamma , \rho }f \bigr) \bigl(a^{+}\bigr). \end{aligned} $$

 □

3.1 Equivalent mixed-type Volterra integral equation

The following lemma shows the equivalence between the proposed problem (1.1) and the Volterra integral equation.

Lemma 3.10

Let\(0< p<1\), \(0\le q\leq 1\)and\(\gamma =p+q-pq\)and let\(f:J\times \mathbb{R}\rightarrow \mathbb{R}\)be a function such that\(f\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\)for any\(x\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\). If\(x\in \mathcal{C}_{1-\gamma }^{\gamma }[J, \mathbb{R}]\)thenxsatisfies problem (1.1) if and only ifxsatisfies the mixed-type integral equation:

$$ \begin{aligned}[b] x(t)&=\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(t-a)}(t-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}( \tau _{i}-s)^{p-1}f\bigl(s, x(s)\bigr)\,ds \\ &\quad{}+\frac{1}{\rho ^{p}\varGamma (p)} \int _{a^{+}}^{t}e^{ \frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f \bigl(s, x(s)\bigr)\,ds, \end{aligned} $$
(3.4)

where

$$ \varLambda = \frac{1}{\rho ^{\gamma -1}\varGamma (\gamma )- \sum_{i=1}^{m}c_{i}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-a)}(\tau _{i}-a)^{\gamma -1}}. $$
(3.5)

Proof

Suppose, \(x\in \mathcal{C}_{1-\gamma }^{\gamma }[J, \mathbb{R}]\) be a solution of (1.1). We show that x is also a solution of (3.4). In view of Lemma 3.9, we have

$$ \begin{aligned}[b] x(t)&=\frac{(t-a)^{\gamma -1}}{\rho ^{\gamma -1}\varGamma (\gamma )}e^{ \frac{(\rho -1)}{\rho }(t-a)}\mathcal{I}_{a^{+}}^{1-\gamma ,\rho }x \bigl(a^{+}\bigr)\\ &\quad {}+ \frac{1}{\rho ^{p}\varGamma (p)} \int _{a^{+}}^{t}e^{ \frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f \bigl(s,x(s)\bigr)\,ds. \end{aligned} $$
(3.6)

Now, substituting \(t=\tau _{i}\) and multiplying both sides by \(c_{i}\) in (3.6), we get

$$ c_{i}x(\tau _{i})= \frac{(\tau _{i}-a)^{\gamma -1}}{\rho ^{\gamma -1}\varGamma (\gamma )}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-a)}c_{i} \mathcal{I}_{a^{+}}^{1- \gamma ,\rho }x\bigl(a^{+} \bigr)+c_{i}\mathcal{I}^{p,\rho }_{a^{+}}f(\tau _{i}), $$
(3.7)

which implies that

$$ \begin{aligned}[b] \sum_{i=1}^{m}c_{i}x( \tau _{i})&=\frac{1}{\rho ^{\gamma -1}\varGamma (\gamma )} \sum_{i=1}^{m}c_{i}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-a)}( \tau _{i}-a)^{\gamma -1}\mathcal{I}_{a^{+}}^{1-\gamma ,\rho }x \bigl(a^{+}\bigr) \\ &\quad{}+\frac{1}{\rho ^{p}\varGamma (p)} \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}( \tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds. \end{aligned} $$
(3.8)

From the initial condition \(\mathcal{I}^{1-\gamma , \rho }_{a^{+}}x(a) =\sum_{i=1}^{m}c_{i}x( \tau _{i})\), we get

$$ \mathcal{I}_{a^{+}}^{1-\gamma , \rho }x\bigl(a^{+} \bigr)= \frac{\rho ^{\gamma -1}\varGamma (\gamma )}{\rho ^{p}\varGamma (p)}\varLambda \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds. $$
(3.9)

Therefore, the result follows by substituting (3.9) in (3.6). This shows that \(x(t)\) satisfies (3.4).

Conversely, suppose that \(x\in \mathcal{C}_{1-\gamma }^{\gamma }\) satisfies Eq. (3.4), then we show that x also satisfies Eq. (1.1). Applying \(\mathcal{D}_{a^{+}}^{\gamma ,\rho }\) to both sides of (3.4) and in view of Proposition 2.8, Lemma 2.10 and Definition 3.1, we have

$$ \begin{aligned}[b] &\mathcal{D}_{a^{+}}^{\gamma ,\rho }x(t)\\ &\quad = \mathcal{D}_{a^{+}}^{ \gamma ,\rho } \Biggl(\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(t-a)}(t-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}( \tau _{i}-s)^{p-1}f\bigl(s, x(s)\bigr)\,ds \Biggr) \\ &\qquad{}+\mathcal{D}_{a^{+}}^{\gamma ,\rho } \biggl( \frac{1}{\rho ^{p}\varGamma (p)} \int _{a^{+}}^{t}e^{ \frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f \bigl(s, x(s)\bigr)\,ds \biggr) \\ &\quad = \bigl( \mathcal{D}_{a^{+}}^{q(1-p),\rho }f\bigl(t,x(t)\bigr) \bigr) (x). \end{aligned} $$
(3.10)

Since \(\mathcal{D}_{a^{+}}^{p,q,\rho }x\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\), by the definition of \(\mathcal{C}_{1-\gamma }^{\gamma }[J, \mathbb{R}]\) Eq. (3.10) implies that

$$ \mathcal{D}_{a^{+}}^{q(1-p),\rho }f=D^{\rho } \mathcal{I}_{a^{+}}^{1-q(1- \rho ),\rho }f\in \mathcal{C}_{1-\gamma ,\rho }[J, \mathbb{R}]. $$

For \(f\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\) and from Lemma 2.12, we can see that \(\mathcal{I}_{a^{+}}^{1-q(1-p),\rho }f\in \mathcal{C}_{1-\gamma ,\rho }[J, \mathbb{R}]\), this implies that \(\mathcal{I}_{a^{+}}^{1-q(1-p),\rho }f\in \mathcal{C}^{1}_{1-\gamma }[J, \mathbb{R}]\) from the definition of \(\mathcal{C}^{n}_{\gamma }[J, \mathbb{R}]\).

Applying \(\mathcal{I}_{a^{+}}^{q(1-p),\rho }\) on both sides of (3.10) and in view of Proposition 2.8, Lemma 3.7 and Definition 3.1,

$$ \begin{aligned}[b] \mathcal{I}_{a^{+}}^{q(1-p),\rho } \mathcal{D}_{a^{+}}^{ \gamma ,\rho }x(t)&=\mathcal{I}_{a^{+}}^{q(1-p),\rho } \mathcal{D}_{a^{+}}^{q(1-p), \rho }f\bigl(t,x(t)\bigr). \\ &=f\bigl(t,x(t)\bigr)- \frac{ ( \mathcal{I}_{a^{+}}^{1-q(1-p),\rho }f ) (a)}{\varGamma (q(1-p))}(t-a)^{q(p-1)-1} \\ &=f\bigl(t,x(t)\bigr). \end{aligned} $$
(3.11)

Hence, its remains to show that if \(x\in \mathcal{C}_{1-\gamma }^{\gamma }[J, \mathbb{R}]\) satisfies (3.4), it also satisfies the initial condition. So, by applying \(\mathcal{I}_{a^{+}}^{1-\gamma ,\rho }\) to both sides of (3.4) and using Proposition 2.8, Theorem 2.9 and 2.11, we obtain

$$ \begin{aligned}[b] &\mathcal{I}_{a^{+}}^{1-\gamma ,\rho }x(t)\\ &\quad = \mathcal{I}_{a^{+}}^{1- \gamma ,\rho } \Biggl(\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(t-a)}(t-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}( \tau _{i}-s)^{p-1}f(s)\,ds \Biggr) \\ &\qquad{}+\mathcal{I}_{a^{+}}^{1-\gamma ;\varphi } \biggl( \frac{1}{\rho ^{p}\varGamma (p)} \int _{a^{+}}^{t}e^{ \frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f(s) \,ds \biggr) \\ &\quad =\frac{\rho ^{\gamma -1}\varGamma (\gamma )}{\rho ^{p}\varGamma (p)} \varLambda e^{\frac{(\rho -1)}{\rho }(t-a)} \sum _{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}( \tau _{i}-s)^{p-1}f(s)\,ds \\ &\qquad{}+\mathcal{I}_{a^{+}}^{1-q(1-p),\rho }f(t). \end{aligned} $$
(3.12)

Taking the limit as \(t\rightarrow a^{+}\) in Eq. (3.12) and the fact that \(1-q<1-p(1-r)\) give

$$ \mathcal{I}_{a^{+}}^{1-\gamma ,\rho }x\bigl(a^{+} \bigr)= \frac{\rho ^{\gamma -1}\varGamma (\gamma )}{\rho ^{p}\varGamma (p)}\varLambda \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds. $$
(3.13)

Substituting \(t=\tau _{i}\) and multiplying through by \(c_{i}\) in (3.4),

$$ \begin{aligned}[b] c_{i}x(\tau _{i})&=\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-a)}(\tau _{i}-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f(s)\,ds \\ &\quad{}+\frac{c_{i}}{\rho ^{p}\varGamma (p)} \int _{a^{+}}^{\tau _{i}}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds, \end{aligned} $$
(3.14)

which implies that

$$ \begin{aligned}[b] \sum_{i=1}^{m}c_{i}x( \tau _{i})&=\varLambda \sum_{i=1}^{m}c_{i} \mathcal{I}^{p,\rho }_{a^{+}}f(\tau _{i}) \sum _{i=1}^{m}c_{i}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-a)}( \tau _{i}-a)^{\gamma -1}+ \sum_{i=1}^{m}c_{i} \mathcal{I}^{p,\rho }_{a^{+}}f(\tau _{i}) \\ &= \sum_{i=1}^{m}c_{i} \mathcal{I}^{p,\rho }_{a^{+}}f( \tau _{i}) \Biggl( 1+ \varLambda \sum_{i=1}^{m}c_{i}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-a)}( \tau _{i}-a)^{\gamma -1} \Biggr). \end{aligned} $$
(3.15)

Thus

$$ \sum_{i=1}^{m}c_{i}x( \tau _{i})= \frac{\rho ^{\gamma -1}\varGamma (\gamma )}{\rho ^{p}\varGamma (p)}\varLambda \sum _{i=1}^{m}c_{i} \int _{a^{+}}^{\tau _{i}}e^{ \frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds. $$
(3.16)

So, in view of (3.13) and (3.16), we have

$$ \mathcal{I}_{a^{+}}^{1-\gamma , \rho }x\bigl(a^{+}\bigr)= \sum _{i=1}^{m}c_{i}x( \tau _{i}). $$
(3.17)

Hence, the proof is completed. □

Remark 3.11

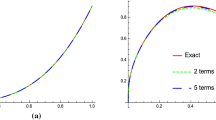
As shown below, the proposed Hilfer generalized proportional fractional derivative (see Definition 3.1) unifies the existing ones of Riemann–Liouville, the generalized proportional and the Hilfer fractional derivatives. We present the approximate numerical solution of Eq. (3.4) and present these solutions in Figs. 1–3.

Figure 1
figure 1

Graph of \(x(t)\), for the Hilfer fractional derivatives (\(\rho =1\)) and Hilfer generalized proportional fractional derivatives (\(\rho \in (0,1)\))

Full size image

3.2 Uniqueness result

This subsection will a detailed proof of the uniqueness of solutions of the proposed problem (1.1) using the concepts of the Banach contraction principle. Thus, we need the following assumptions.

\((H_{1})\):

Let \(f:J\times \mathbb{R}\rightarrow \mathbb{R}\) be a function such that \(f\in \mathcal{C}^{q(1-p)}_{1-\gamma }[J, \mathbb{R}]\) for any \(x\in \mathcal{C}^{\gamma }_{1-\gamma }[J, \mathbb{R}]\).

\((H_{2})\):

There exists a constant \(K>0\) such that

$$ \bigl\vert f(t,u)-f(t,\bar{u}) \bigr\vert \leq K \vert u-\bar{u} \vert , $$

for any \(u,\bar{u}\in \mathbb{R}\) and \(t\in J\).

\((H_{3})\):

Suppose that

$$ K\psi < 1, $$

where

$$ \psi =\frac{\mathcal{B}(\gamma , p)}{\rho ^{p}\varGamma (p)} \Biggl( \vert \varLambda \vert \sum _{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} +(T-a)^{p} \Biggr) $$
(3.18)

and \(\mathcal{B}(\gamma , p)\) is the Beta function defined by [32]

$$ \mathcal{B}(\gamma , p)= \int _{0}^{1}x^{\gamma -1}(1-x)^{p-1} \,dx,\quad \operatorname{Re}( \gamma ),\operatorname{Re}(p)>0. $$

Theorem 3.12

Let\(0< p<1\), \(0\leq q\leq 1\)and\(\gamma =p+q-pq\). Suppose that the assumptions\((H_{1})\)–\((H_{3})\)are satisfied. Then problem (1.1) has a unique solution in the space\(\mathcal{C}^{\gamma }_{1-\gamma }[J, \mathbb{R}]\).

Proof

Define the operator \(T:\mathcal{C}_{1-\gamma }[J, \mathbb{R}]\rightarrow \mathcal{C}_{1- \gamma }[J, \mathbb{R}]\) by

$$ \begin{aligned}[b] (Tx) (t)&=\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(t-a)}(t-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds \\ &\quad{}+\frac{1}{\rho ^{p}\varGamma (p)} \int _{a}^{t}e^{\frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f \bigl(s,x(s)\bigr)\,ds. \end{aligned} $$
(3.19)

It follows that the operator T is well defined. Now for any \(x_{1},x_{2}\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\) and \(t\in J\), this gives

$$ \begin{aligned}[b] \bigl\vert \bigl((&Tx_{1}) (t)-(Tx_{2}) (t)\bigr) (t-a)^{1-\gamma } \bigr\vert \\ &\leq \frac{ \vert \varLambda \vert }{\rho ^{p}\varGamma (p)} \bigl\vert e^{ \frac{(\rho -1)}{\rho }(t-a)} \bigr\vert \sum _{i=1}^{m}b_{i} \int _{a}^{\tau _{i}} \bigl\vert e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)} \bigr\vert (\tau _{i}-s)^{p-1} \bigl\vert f \bigl(s,x_{1}(s)\bigr)-f\bigl(s,x_{2}(s)\bigr) \bigr\vert \,ds \\ &\quad{}+\frac{1}{\rho ^{p}\varGamma (p)} \int _{a}^{t} \bigl\vert e^{ \frac{(\rho -1)}{\rho }(t-s)} \bigr\vert (t-s)^{p-1} \bigl\vert f\bigl(s,x_{1}(s)\bigr)-f \bigl(s,x_{2}(s)\bigr) \bigr\vert \,ds. \end{aligned} $$
(3.20)

Since \(|e^{\frac{(\rho -1)}{\rho }t}|<1\), we get

$$ \begin{aligned}[b] \bigl\vert \bigl((&Tx_{1}) (t)-(Tx_{2}) (t)\bigr) (t-a)^{1-\gamma } \bigr\vert \\ &\leq \frac{K \vert \varLambda \vert }{\rho ^{p}\varGamma (p)} \Biggl( \sum_{i=1}^{m}b_{i} \int _{a^{+}}^{\tau _{i}}(\tau _{i}-s)^{p-1}(s-a)^{ \gamma -1} \,ds \Biggr) \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\quad{}+\frac{K}{\rho ^{p}\varGamma (p)}(t-a)^{1-\gamma } \biggl( \int _{a^{+}}^{t}(t-s)^{p-1}(s-a)^{ \gamma -1} \,ds \biggr) \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\leq \frac{K \vert \varLambda \vert }{\rho ^{p}\varGamma (p)}\mathcal{B}(\gamma , p) \sum _{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\quad{}+\frac{K}{\rho ^{p}\varGamma (p)}(T-a)^{p}\mathcal{B}(\gamma , p) \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]}. \end{aligned} $$
(3.21)

Therefore,

$$ \begin{aligned}[b] \bigl\Vert (&Tx_{1})-(Tx_{2}) \bigr\Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\leq \frac{K}{\rho ^{p}\varGamma (p)}\mathcal{B}(\gamma ,p) \Biggl( \vert \varLambda \vert \sum_{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} +(T-a)^{p} \Biggr) \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\le K\psi \Vert x_{1}-x_{2} \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]}. \end{aligned} $$
(3.22)

Hence, it follows from (3.18) that T is a contraction map. Thus, as a consequence of the Banach contraction principle, problem (1.1) has a unique solution. □

3.3 Existence result

In this subsection, we prove the existence of solutions of problem (1.1) using the concepts of Kransnoselskii’s fixed point theorem [33].

\((H_{4})\):

Suppose that

$$ K\Delta < 1, $$

where

$$ \Delta =\frac{\mathcal{B}(\gamma , p)}{\rho ^{p}\varGamma (p)} \vert \varLambda \vert \sum _{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1}. $$
(3.23)

Theorem 3.13

Let\(0< p<1\), \(0\leq q\leq 1\)and\(\gamma =p+q-pq\). Suppose that the hypotheses\((H_{1})\), \((H_{2})\)and\((H_{4})\)are satisfied. Then problem (1.1) has at least one solution in the space\(\mathcal{C}^{\gamma }_{1-\gamma }[J, \mathbb{R}]\).

Proof

We have \(\|\eta \|_{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]}=\sup_{t\in J}|(t-a)^{1-\gamma }\eta (t)|\) and choose \(\kappa \ge M\|\eta \|_{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]}\), where

$$ M=\frac{\mathcal{B}(\gamma , p)}{\rho ^{p}\varGamma (p)} \Biggl( \vert \varLambda \vert \sum _{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} +(T-a)^{p} \Biggr), $$
(3.24)

we consider \(\mathbf{B}_{\kappa }=\{x\in \mathbb{C}[J, \mathbb{R}]: \|x\|_{ \mathcal{C}_{1-\gamma }[J, \mathbb{R}]}\le \kappa \}\). Define the operators \(\mathbb{T}_{1}\) and \(\mathbb{T}_{2}\) on \(\mathbf{B}_{\kappa }\) by

$$ \begin{aligned}[b] \mathbb{T}_{1}x(t)&=\frac{1}{\rho ^{p}\varGamma (p)} \int _{a}^{t}e^{ \frac{(\rho -1)}{\rho }(t-s)}(t-s)^{p-1}f \bigl(s,x(s)\bigr)\,ds, \\ \mathbb{T}_{2}x(t)&=\frac{\varLambda }{\rho ^{p}\varGamma (p)}e^{ \frac{(\rho -1)}{\rho }(t-a)}(t-a)^{\gamma -1} \sum_{i=1}^{m}c_{i} \int _{a}^{\tau _{i}}e^{\frac{(\rho -1)}{\rho }(\tau _{i}-s)}(\tau _{i}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds, \end{aligned} $$

for all \(t\in [a, T]\). Now, for every \(x,y\in \mathbf{B}_{\kappa }\),

$$ \begin{aligned}[b] &\bigl\vert \bigl(\mathbb{T}_{1}x(t)+ \mathbb{T}_{2}y(t)\bigr)(t-a)^{1-\gamma } \bigr\vert \\ &\quad \leq \frac{(t-a)^{1-\gamma }}{\rho ^{p}\varGamma (p)} \int _{a}^{t}(t-s)^{p-1}(s-a)^{ \gamma -1} \bigl\vert f\bigl(s,x(s)\bigr) (s-a)^{1-\gamma } \bigr\vert \,ds \\ &\qquad{}+\frac{ \vert \varLambda \vert }{\rho ^{p}\varGamma (p)} \sum_{i=1}^{m}c_{i} \int _{a}^{\tau _{i}}(\tau _{i}-s)^{p-1}( \tau _{i}-a)^{\gamma -1} \bigl\vert f\bigl(s,y(s)\bigr) ( \tau _{i}-a)^{1-\gamma } \bigr\vert \,ds \\ &\quad \leq \Vert \eta \Vert \Biggl[ \frac{\mathcal{B}(\gamma , p)}{\rho ^{p}\varGamma (p)} \vert \varLambda \vert \sum_{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} + \frac{\mathcal{B}(\gamma , p)}{\rho ^{p}\varGamma (p)}(T-a)^{p} \Biggr] \\ &\quad \le \Vert \eta \Vert M \\ &\quad \leq \kappa < \infty . \end{aligned} $$
(3.25)

This implies that \(\mathbb{T}_{1}x+\mathbb{T}_{2}y\in \mathbf{B}_{\kappa }\).

Step 2. We show that \(\mathbb{T}_{2}\) is a contraction.

Now, let \(x,y\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\) and \(t\in J\), then

$$ \begin{aligned}[b] &\bigl\vert \bigl(\mathbb{T}_{2}x(t)- \mathbb{T}_{2}y(t)\bigr) (t-a)^{1- \gamma } \bigr\vert \\ &\quad = \Biggl\vert \varLambda e^{\frac{(\rho -1)}{\rho }(t-a)} \sum_{i=1}^{m}c_{i} \mathcal{I}^{p,\rho }_{a^{+}}\bigl(f\bigl(s,x(s)\bigr)-f\bigl(s,y(s) \bigr)\bigr) (\tau _{i}) \Biggr\vert \\ &\quad \le \frac{K \vert \varLambda \vert }{\rho ^{p}\varGamma (p)} \sum_{i=1}^{m}c_{i} \int _{a}^{\tau _{i}}(\tau _{i}-s)^{p-1}( \tau _{i}-s)^{\gamma -1} \bigl\vert x(s)-y(s) \bigr\vert \,ds \\ &\quad \leq \Biggl[ \frac{K \vert \varLambda \vert }{\rho ^{p}\varGamma (p)}\mathcal{B}( \gamma ,p) \sum _{i=1}^{m}c_{i}(\tau _{i}-a)^{p+\gamma -1} \Biggr] \Vert x-y \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]} \\ &\quad \le K\Delta \Vert x-y \Vert _{\mathcal{C}_{1-\gamma }[J, \mathbb{R}]}. \end{aligned} $$
(3.26)

Hence, it follows from \((H_{4})\) that \(\mathbb{T}_{2}\) is a contraction.

Step 3. We show that the operator \(\mathbb{T}_{1}\) is continuous and compact.

Clearly, the operator \(\mathbb{T}_{1}\) is continuous, due to the fact that the function f is continuous. Thus, for any \(x\in \mathcal{C}_{1-\gamma }[J, \mathbb{R}]\), we have

$$ \Vert \mathbb{T}_{1}x \Vert \leq \Vert \eta \Vert \frac{\mathcal{B}( \gamma , p)}{\rho ^{p}\varGamma (p)}(T-a)^{p}< \infty . $$

This shows that the operator \(\mathbb{T}_{1}\) is uniformly bounded on \(\mathbf{B}_{\kappa }\). Thus, it remains to shows that \(\mathbb{T}_{1}\) is compact. Denoting \(\sup_{(t, x)\in J\times \mathbf{B}_{\kappa }}|f(t, x(t))|= \delta <\infty \) and for any \(a<\tau _{1}<\tau _{2}<T\),

$$ \begin{aligned}[b] &\bigl\vert (\tau _{2}-a)^{1-\gamma } \bigl(\mathbb{T}_{1}x(\tau _{2})\bigr)+( \tau _{1}-a)^{1-\gamma }\bigl(\mathbb{T}_{1}x(\tau _{1})\bigr) \bigr\vert \\ &\quad = \biggl\vert \frac{(\tau _{2}-a)^{1-\gamma }}{\rho ^{p}\varGamma (p)} \int _{a}^{ \tau _{2}}e^{\frac{(\rho -1)}{\rho }(\tau _{2}-s)}(\tau _{2}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds \\ &\qquad{}-\frac{(\tau _{1}-a)^{1-\gamma }}{\rho ^{p}\varGamma (p)} \int _{a}^{ \tau _{1}}e^{\frac{(\rho -1)}{\rho }(\tau _{1}-s)}(\tau _{1}-s)^{p-1}f\bigl(s,x(s)\bigr)\,ds \biggr\vert \\ &\quad \leq \frac{1}{\rho ^{p}\varGamma (p)} \int _{a}^{\tau _{2}}\bigl[(\tau _{2}-a)^{1- \gamma }( \tau _{2}-s)^{p-1}-(\tau _{1}-a)^{1-\gamma }( \tau _{1}-s)^{p-1}\bigr] \bigl\vert f\bigl(s,x(s)\bigr) \bigr\vert \,ds \\ &\qquad{}+\frac{1}{\rho ^{p}\varGamma (p)} \int _{\tau _{1}}^{\tau _{2}}(\tau _{2}-a)^{1- \gamma }( \tau _{2}-s)^{p-1} \bigl\vert f\bigl(s,x(s)\bigr) \bigr\vert \,ds \\ &\quad \longrightarrow 0, \quad \text{as } \tau _{2}\rightarrow \tau _{1}. \end{aligned} $$
(3.27)

As a consequences of Arzelá–Ascoli theorem, the operator \(\mathbb{T}_{1}\) is compact on \(\mathbf{B}_{\kappa }\). Thus, problem (1.1) has at least one solution. □

3.4 Examples

Example 3.14

Consider the fractional differential equation which involves the Hilfer generalized proportional derivative of the form

$$ \textstyle\begin{cases} \mathcal{D}^{\frac{2}{3},\frac{1}{2},1}_{0^{+}}x(t)= \frac{1}{25e^{2t}} ( \frac{\cos 2t}{1+ \vert x(t) \vert } ) + \frac{3}{2},\quad t\in J=[0, 2],&\\ \mathcal{I}^{1-\gamma ,1}_{0^{+}}x(0) =2x(\frac{2}{5}). \end{cases} $$
(3.28)

By comparing (1.1) with (3.28), we get \(p=\frac{2}{3}\), \(q=\frac{1}{2}\), \(\rho =1\), \(\gamma =\frac{5}{6}\), \(a=0\), \(T=2\), \(c_{1}=2\) since \(m=1\), \(\tau _{1}=\frac{2}{5}\in J\) and \(f: J\times \mathbb{R}\rightarrow \mathbb{R}\) is a function defined by

$$ f(t, u)=\frac{1}{25e^{2t}} \biggl( \frac{\cos 2t}{1+ \vert u \vert } \biggr) + \frac{3}{2}, \quad t\in J, u\in \mathbb{R}_{+}. $$

Thus, f is continuous and for all \(u,v\in \mathbb{R}_{+}\) and \(t\in J\), we have \(|f(t, u)-f(t, v)|\leq \frac{1}{25}|u-v|\). Thus, it follows that conditions \((H_{1})\) and \((H_{3})\) are true with \(K=\frac{1}{25}\). Therefore, by simple calculation, we can see that \(|\varLambda |\approx 0.8325\) and \(\psi \approx 3.3628\), which implies that

$$ K\psi \approx 0.1345< 1. $$

Hence, all the assumptions of Theorem 3.12 are satisfied. So, problem (1.1) has a unique solution on J.

Similarly, we find that \(\Delta \approx 1.3413>0\) and \(K\Delta \approx 0.0537<1\). Since all the hypotheses of Theorem 3.13 hold, we conclude that problem (1.1) has at least one solution on J.

Example 3.15

Consider the Hilfer generalized proportional fractional differential equation described by

$$ \textstyle\begin{cases} \mathcal{D}^{\frac{2}{3},\frac{1}{2},\frac{1}{5}}_{0^{+}}x(t)= \frac{1}{25e^{2t}} ( \frac{\cos 2t}{1+ \vert x(t) \vert } ) + \frac{3}{2},\quad t\in J=[0, 2],&\\ \mathcal{I}^{1-\gamma ,\frac{1}{5}}_{0^{+}}x(0) =2x(\frac{2}{5}). \end{cases} $$
(3.29)

Repeating application of the same procedure as Example 3.14 above, we get the values \(|\varLambda |\approx 0.9943\), \(\psi \approx 10.5950\) and \(\Delta \approx 4.6839\). Thus

$$ K\psi \approx 0.4238< 1. $$

According to Theorem 3.12, problem (1.1) has a unique solution on J. In addition,

$$ K\Delta \approx 0.1874< 1, $$

hence, by Theorem 3.13, problem (1.1) has at least one solution on J.

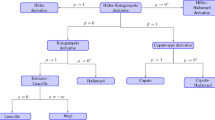
It should be noted here that the proposed Hilfer generalized proportional derivative (3.1) unifies the existing ones in the sense of Riemann–Liouville and Caputo generalized proportional fractional derivative, respectively. In addition:

  • If \(\rho \rightarrow 1\) and \(q\in [0, 1]\), the formulation for this problem, reduce to Hilfer fractional derivative [18, 32, 44] (see Fig. 1).

  • If \(\rho \in (0, 1)\) and \(q\in [0, 1]\), we obtain the proposed Hilfer generalized proportional fractional derivative, which we can see that it covers the classical Hilfer fractional derivative, as shown in Fig. 1.

  • If \(\rho \rightarrow 1\) and \(q=0\), the formulation for this problem reduces to the Riemann–Liouville fractional derivative [32] (see Fig. 2).

    Figure 2
    figure 2

    Graph of \(x(t)\), for the Riemann–Liouville fractional derivatives (\(q=0\), \(\rho =1\)), and generalized proportional fractional derivatives (\(q=0\), \(\rho \in (0,1)\))

    Full size image

  • If \(\rho \rightarrow 1\) and \(q=1\), we obtain the Caputo fractional derivative [32].

  • If \(\rho \in (0, 1)\) and \(q=0\), we obtain the Riemann–Liouville generalized proportional fractional derivative [23], which we can see from Fig. 2 to cover the Riemann–Liouville fractional derivative.

  • If \(\rho \in (0, 1)\) and \(q=1\), we obtain the Caputo generalized proportional fractional derivative [23].

  • If \(q,\rho \in (0, 1)\), it is easily to observe from Fig. 3 that the newly proposed derivative unifies the ones in the setting of the Hilfer, Riemann–Liouville and generalized proportional fractional derivatives.

    Figure 3
    figure 3

    Graph of \(x(t)\), for the Riemann–Liouville fractional derivatives (\(q=0\), \(\rho =1\)), generalized proportional fractional derivatives (\(q=0\), \(\rho =0.8\)) and Hilfer generalized proportional fractional derivatives (\(q\in (0,1)\), \(\rho \in (0,1)\))

    Full size image

4 Conclusions

In this paper, we defined the proportional fractional derivatives in the Hilfer setting. We used some known theorems from the fixed point theory that enabled us to prove the existence and uniqueness of solutions to a specific type of fractional initial value problem involving the Hilfer proportional fractional derivative. Furthermore, to show the effectiveness of our results, we presented some examples. In fact, the Hilfer proportional derivative contains three parameters. The existence of more parameters is useful especially when one considers the stability and other qualitative aspects of differential equations involving fractional derivative.