Abstract
In this paper, we investigate the existence of mild solutions for neutral Hilfer fractional evolution equations with noninstantaneous impulsive conditions in a Banach space. We obtain the existence results by applying the theory of resolvent operator functions, Hausdorff measure of noncompactness, and Sadovskii’s fixed point theorem. We also present an example to show the validity of obtained results.
Similar content being viewed by others
1 Introduction
Fractional calculus primarily involves the description of fractional-order derivatives and integral operators [28]. In the last few decades, it has gained significant importance because of its wide range of applicability in diverse scientific domains. Fractional differential equations (FDEs) are among the strongest tools of mathematical modeling and are successfully employed to model complex physical and biological phenomena like anomalous diffusion, viscoelastic behavior, power laws, and automatic remote control systems. In the available literature, notable definitions of fractional derivatives were given by famous mathematicians, but the most commonly used are the Riemann–Liouville (RL) and Caputo derivatives [1, 2, 21, 22, 24, 26, 29, 39]. Thus FDEs involving the RL fractional derivative or Caputo derivative have considered frequently for investigating the existence of mild solutions. However, little attention has been devoted to FDEs with generalized fractional derivatives. The Hilfer fractional derivative (HFD), a generalization of the RL fractional derivative was first introduced by Hilfer [4, 11, 15, 16]. The existence and uniqueness of general initial and boundary value problems involving HFD were first examined by Furati and Kassim [10] and Wang and Zhang [36], respectively. Thereafter, by means of the noncompact measure method Gu and Trujilo [13] defined mild solutions for FDEs involving HFD. Later on, Gou and Li [12] proved the existence of mild solutions for Sobolev-type Hilfer fractional evolution equations with boundary conditions. In [17, 32, 33] the authors considered Hilfer FDEs with nonlocal conditions for investigating approximate controllability and existence of solutions. Recently, Subashini et al. [34] obtained mild solutions for Hilfer integro-differential equations of fractional order by means of Monch’s fixed point technique and noncompact measure. FDEs involving HFD are widely applicable in biomedical research. These equations are successfully employed to model the irregular boundaries of biological cells and microscopic fluctuations of biomedical matters [37].
Hernandez et al. [14] first introduced the concept of noninstantaneous impulsive conditions. These conditions appeared in the mathematical description of real-world dynamical processes experiencing a sudden change over a short interval of time like DNA sequences, heart beat intervals, optimal control models, and so on [19]. In the published work, FDEs involving either RL or Caputo derivative are commonly considered with impulsive conditions for obtaining mild solutions [5, 7, 20, 27, 30]. However, Sousa et al. [31] for the first time obtained the mild solutions for Hilfer FDEs with noninstantaneous impulsive conditions. Similalrly, no existence results have been established for neutral Hilfer FDEs in contrast to neutral FDEs with RL or Caputo derivative [9, 25, 35, 40]. Such equations have a bundle of applications in physics, biology, and electrical engineering. Thus, to make a little contribution to existing works, we consider the neutral Hilfer FDEs with impulsive conditions of the mentioned form for obtaining mild solutions. We obtain an existence result with the help of fixed point theory, which is proven to be an authoritative modeling tool for obtaining exact or approximate solutions of FDEs

where \({\mathcal{I}}_{0^{+}}^{1-\theta }\) is the RL fractional integral, \({}^{H}{\mathcal{D}}^{\mathfrak{p}, \mathfrak{q}}_{0^{+}}\) is the HFD of order \((\mathfrak{p},\mathfrak{q})\) with \(0\le \mathfrak{p}<1\), \(0\le \mathfrak{q}\le 1\), and \(0 \le \theta =\mathfrak{p} +\mathfrak{q}- \mathfrak{p}\mathfrak{q}\le 1\), the linear operator  is the infinitesimal generator of a strongly continuous semigroup
is the infinitesimal generator of a strongly continuous semigroup  in a Banach space
in a Banach space  , \(0=\mathfrak{t}_{o}=\mathfrak{s}_{o}<\mathfrak{t}_{1}<\mathfrak{s}_{1}< \mathfrak{t}_{2}<\cdots<\mathfrak{t}_{\mathfrak{l}}<\mathfrak{s}_{\mathfrak{l}}<\mathfrak{t}_{\mathfrak{l}+1}=\mathfrak{a}\) is a partition of \([0, \mathfrak{a}]\), \(\mathfrak{a}>0\), \(\mathfrak{l}=1, 2, \ldots, m\),
, \(0=\mathfrak{t}_{o}=\mathfrak{s}_{o}<\mathfrak{t}_{1}<\mathfrak{s}_{1}< \mathfrak{t}_{2}<\cdots<\mathfrak{t}_{\mathfrak{l}}<\mathfrak{s}_{\mathfrak{l}}<\mathfrak{t}_{\mathfrak{l}+1}=\mathfrak{a}\) is a partition of \([0, \mathfrak{a}]\), \(\mathfrak{a}>0\), \(\mathfrak{l}=1, 2, \ldots, m\),  and
and  are appropriate functions satisfying some assumptions to be discussed later, and a continuous function
are appropriate functions satisfying some assumptions to be discussed later, and a continuous function  characterizes the impulsive conditions and
characterizes the impulsive conditions and  . The properties of functions \(\vartheta :\Delta \longrightarrow \mathbb{R}\) and
. The properties of functions \(\vartheta :\Delta \longrightarrow \mathbb{R}\) and  , \(\Delta =(\mathfrak{t}, \mathfrak{s}) \in [0, \mathfrak{a}]\times [0, \mathfrak{a}]\) are specified in later section.
, \(\Delta =(\mathfrak{t}, \mathfrak{s}) \in [0, \mathfrak{a}]\times [0, \mathfrak{a}]\) are specified in later section.
This manuscript is structured as follows. In Sect. 2, we discuss the Hilfer fractional derivative, Hausdorff measure of noncompactness, and mild solutions of equation (1.1) along with some basic results and lemmas. In later section, we obtain existence results by means of fixed point technique, measure of noncompactness, and Lebesgue dominated convergence theorem. We confirm the validity of obtained results by offering an example in the last section.
2 Preliminaries
Let  denote the complete normed linear space of continuous functions \(\mathfrak{z}(\mathfrak{t})\) defined on the interval \(\mathcal {J}=[0, \mathfrak{a}]\) with \(\|\mathfrak{z}\|=\sup{\mathfrak{t}\in \mathcal {J}}\| \mathfrak{z}(\mathfrak{t})\|\). We define the Banach space
denote the complete normed linear space of continuous functions \(\mathfrak{z}(\mathfrak{t})\) defined on the interval \(\mathcal {J}=[0, \mathfrak{a}]\) with \(\|\mathfrak{z}\|=\sup{\mathfrak{t}\in \mathcal {J}}\| \mathfrak{z}(\mathfrak{t})\|\). We define the Banach space  with norm \(\|\mathfrak{z}\|_{\mathcal{C}_{1-\theta }}= [4] \sup_{0\le \mathfrak{t}\le \mathfrak{a}}|\mathfrak{t}^{1- \theta }\mathfrak{z}(\mathfrak{t})|\).
with norm \(\|\mathfrak{z}\|_{\mathcal{C}_{1-\theta }}= [4] \sup_{0\le \mathfrak{t}\le \mathfrak{a}}|\mathfrak{t}^{1- \theta }\mathfrak{z}(\mathfrak{t})|\).
We will establish the existence results in the Banach space

for \(\mathfrak{l}=1,2, \ldots,m\) with the corresponding norm
By  we denotes the family of bounded linear operators defined on
we denotes the family of bounded linear operators defined on  , and by \(\{{\mathcal{W}}_{\mathfrak{p}, \mathfrak{q}}({\mathfrak{t}}) \}_{{ \mathfrak{t}}\ge 0}\) the \((\mathfrak{p} -\mathfrak{q})\)-resolvent operator or the \(\mathfrak{q}\)-times integrated \(\mathfrak{p}\)-resolvent operator generated by
, and by \(\{{\mathcal{W}}_{\mathfrak{p}, \mathfrak{q}}({\mathfrak{t}}) \}_{{ \mathfrak{t}}\ge 0}\) the \((\mathfrak{p} -\mathfrak{q})\)-resolvent operator or the \(\mathfrak{q}\)-times integrated \(\mathfrak{p}\)-resolvent operator generated by  .
.
Definition 2.1
([16])
The Hilfer fractional derivative of order \(n-1 \le \mathfrak{p} < n\), \(n\in \mathbb{N}\); \(0\le \mathfrak{q} \le 1\), with lower limit \(\mathfrak{c}\) is defined as
where \({\mathcal{I}}^{\mathfrak{p} (n-\mathfrak{q})}_{\mathfrak{c}^{+}}\) is the RL integral, and \({\mathcal{D}}^{\mathfrak{q}+\mathfrak{p} n-\mathfrak{p} \mathfrak{q}}_{ \mathfrak{a}^{+}}\) is the RL derivative.
Lemma 2.1
([10])
Let\(0<\mathfrak{p}<1\), \(0\leq \mathfrak{q}\leq 1\), and\(\theta =\mathfrak{p}+\mathfrak{q}-\mathfrak{p}\mathfrak{q}\). If\(f \in {\mathcal{C}}_{1-\theta }[\mathfrak{c}, \mathfrak{d}]\)is such that\({\mathcal{D}}_{\mathfrak{c}^{+}}^{\theta }f\in {\mathcal{C}}_{1-\theta }[ \mathfrak{c}, \mathfrak{d}]\), then
Lemma 2.2
([18])
Let\(0<\mathfrak{p}<1\)and\(0\le \theta \leq 1\). If\(f\in {\mathcal{C}}_{1-\theta }[\mathfrak{c}, \mathfrak{d}]\)and\({\mathcal{I}}_{\mathfrak{c}^{+}}^{1-\mathfrak{p}}f\in {\mathcal{C}}_{ \theta }^{1}[\mathfrak{c}, \mathfrak{d}]\), then
Definition 2.2
([3])
The Hausdorff measure of noncompactness on a bounded subset  of Banach space
of Banach space  is the mapping
is the mapping  defined as
defined as
Lemma 2.3
The measure of noncompactnessζdefined on bounded subsets\(\mathcal{ P}\)and\(\mathcal{ Q }\)of a Banach space has following properties:
has following properties:
- 1
\(\zeta (\mathcal{P}) = 0\)iff\({ \mathcal{P}}\)is a relatively compact set.
- 2
\(\mathcal{\mathcal{P}} \subset \mathcal{Q} \implies \zeta (\mathcal{P}) \le \zeta (\mathcal{Q})\).
- 3
\(\zeta (\bar{\mathcal{P}})=\zeta (\mathcal{P})\).
- 4
\(\zeta (\mathcal{P}\cup \mathcal{Q})= \max \lbrace \zeta ( \mathcal{P}), \zeta (\mathcal{Q}) \rbrace \).
- 5
\(\zeta (\mathfrak{a}\mathcal{P})= |\mathfrak{a}|\zeta (\mathcal{P})\), \(\forall \mathfrak{a} \in \mathbb{R} \).
Lemma 2.4
For a bounded set , there is a denumerable set\({\mathcal{D}}_{o} \subset {\mathcal{D}}\)such that\(\zeta ({\mathcal{D}}_{o})\le \zeta ({\mathcal{D}})\).
, there is a denumerable set\({\mathcal{D}}_{o} \subset {\mathcal{D}}\)such that\(\zeta ({\mathcal{D}}_{o})\le \zeta ({\mathcal{D}})\).
Lemma 2.5
([38])
For a bounded and equicontinuous function , the Hausdorff measure of noncompactness\(\zeta (\mathcal{G}({\mathfrak{t}}) )\)is continuous on\(\mathcal {J}\), and\(\zeta (\mathcal{G})= \max_{{\mathfrak{t}}\in \mathcal {J}} \zeta ( \mathcal{G}({\mathfrak{t}}) )\).
, the Hausdorff measure of noncompactness\(\zeta (\mathcal{G}({\mathfrak{t}}) )\)is continuous on\(\mathcal {J}\), and\(\zeta (\mathcal{G})= \max_{{\mathfrak{t}}\in \mathcal {J}} \zeta ( \mathcal{G}({\mathfrak{t}}) )\).
Lemma 2.6
([23])
Let be a bounded denumerable subset of
be a bounded denumerable subset of . Then\(\zeta (\mathcal{D}({\mathfrak{t}}) )\)is Lebesgue integrable on
. Then\(\zeta (\mathcal{D}({\mathfrak{t}}) )\)is Lebesgue integrable on , and
, and
Lemma 2.7
([31])
After applying Lemmas2.1and2.2, the system of fractional nonlinear differential equations (1.1) reduces to the following integral equation:

Definition 2.3
A mild solution  of problem (1.1) is the solution of the corresponding its integral form (2.1)
of problem (1.1) is the solution of the corresponding its integral form (2.1)

where \(\mathcal{M}_{\mathfrak{p}}(\nu )\) is the Wright function defined as
and satisfying the equality
This definition of a mild solution is obtained by means of the Laplace transform of the Hilfer fractional derivative.
Remark 2.1
The Laplace transform of the Hilfer derivative of a function \({f(\mathfrak{t})}\) of order \(0<\mathfrak{p}<1\) and \(0<\mathfrak{q}<1\) is as follows [15]:
where \({\mathcal{I}}_{0+}^{(1-\mathfrak{p})(1-\mathfrak{q})}f(0+)\) is the RL fractional integral of order \((1-\mathfrak{p})(1-\mathfrak{q})\).
Remark 2.2
Let us assume
- 1
The strong continuity of linear operators \(\lbrace {\mathcal{W}}_{\mathfrak{p}, \mathfrak{q}}(\mathfrak{t}) \rbrace _{\mathfrak{t}>0}\) and \(\lbrace {\mathcal{Y}}_{\mathfrak{p}}(\mathfrak{t}) \rbrace _{ \mathfrak{t}>0}\) with
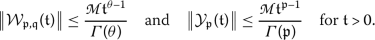
- 2
The norm continuity of family
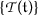 for \(\mathfrak{t}>0\).
for \(\mathfrak{t}>0\).
3 Existence result
In the beginning of this section, we introduce some assumptions required to obtain the desired result:
(H1)  is a Carathéodory function, that is,
is a Carathéodory function, that is,  is measurable for all
is measurable for all  ,
,  is continuous a.e. for \(\mathfrak{t}\in \mathcal {J}\), and there exist \(\psi _{1}\in L_{\frac{1}{\mathsf{r}}}( \mathcal {J}, \mathbb{R}^{+})\), \(\frac{1}{\mathsf{r}}>1\), and a continuous function \(\psi _{2}\) such that
is continuous a.e. for \(\mathfrak{t}\in \mathcal {J}\), and there exist \(\psi _{1}\in L_{\frac{1}{\mathsf{r}}}( \mathcal {J}, \mathbb{R}^{+})\), \(\frac{1}{\mathsf{r}}>1\), and a continuous function \(\psi _{2}\) such that

for almost all \(\mathfrak{t}\in \mathcal {J}\).
(H2) There exist functions \({\hat{\phi }}_{1}\), \({\hat{\phi }}_{2}\in L_{\frac{1}{\mathsf{r}}}( \mathcal {J}, \mathbb{R}^{+})\) and constants  such that
such that

for any bounded, equicontinuous, and countable sets  , \({\mathfrak{l}}=1, 2\).
, \({\mathfrak{l}}=1, 2\).
(H3)  is bounded and Lipschitz continuous, that is, there exist
is bounded and Lipschitz continuous, that is, there exist  and such that
and such that

(H4) The impulsive function  is Lipschitz continuous, that is, there exist \(\mathcal{K}_{\eta _{\mathfrak{l}}}>0\), \(\mathfrak{l}=1, 2, \ldots, m\), such that for all
is Lipschitz continuous, that is, there exist \(\mathcal{K}_{\eta _{\mathfrak{l}}}>0\), \(\mathfrak{l}=1, 2, \ldots, m\), such that for all  ,
,
(H5)  is a Carathéodary function, and there exist \(\mathfrak{\bar{m}}:\Delta \longrightarrow \mathbb{R}\) with
is a Carathéodary function, and there exist \(\mathfrak{\bar{m}}:\Delta \longrightarrow \mathbb{R}\) with

(H6) For a bounded set  and \(0\le \mathfrak{s}\le \mathfrak{t}\le \mathfrak{a}\), there exists a function \(\xi : \Delta \longrightarrow \mathbb{R}\) such that
and \(0\le \mathfrak{s}\le \mathfrak{t}\le \mathfrak{a}\), there exists a function \(\xi : \Delta \longrightarrow \mathbb{R}\) such that
where
(H7) \(\vartheta ^{*}=\sup \lbrace \vartheta (\mathfrak{t}, \mathfrak{s}): 0\le \mathfrak{s} \le \mathfrak{t} \rbrace \) is bounded and measurable on \(\mathcal {J}\) along with the continuity of the function \(\vartheta _{\mathfrak{t}}: \mathcal {J}\longrightarrow L^{\infty }( \mathcal {J}, \mathbb{R})\) defined as \(\vartheta _{t}(s)=\vartheta (t, s)\).
Theorem 3.1
The equation system (1.1) has at least one mild solution in the space\({\mathcal{PC}}_{1-\theta }\)if assumptions (H1)–(H7) hold along with the following conditions:

Proof
To prove the existence of a mild solution for equation system (1.1), it is sufficient to prove the existence of a solution the corresponding integral form (2.2).
Define

Clearly, \(\varOmega _{\delta }\) is a closed convex bounded subset of  . Define the operator
. Define the operator

The operator Θ is well defined.
We establish our results in six steps.
Step 1. We show that \({\varTheta }\mathfrak{z} \in \mathcal{P\mathcal{C}}_{1-\theta }\) for \(\mathfrak{z} \in {\mathcal{P}\mathcal{C}}_{1-\theta }\), that is, \({\mathfrak{t}}^{1-\theta }{\varTheta }\mathfrak{z}(\mathfrak{t})\) is a continuous function for \(\mathfrak{t}\in (\mathfrak{t_{l}}, \mathfrak{t_{l+1}}]\), \(\mathfrak{l}=0,1,2,\ldots,m\). For \(0\le \tilde{\mathfrak{t}}\le \mathfrak{t} <\mathfrak{t}_{1}\), we consider

Substituting \(\tilde{\mathfrak{t}}-\mathfrak{s}=\mathfrak{s}_{1}\) into the third and fifth terms, we have

This proves the continuity of \(\mathfrak{t}^{1-\theta } { \varTheta }\mathfrak{z}(\mathfrak{t})\) for \(\mathfrak{t}\in [0, \mathfrak{t}_{1}]\), that is,  .
.
Using the continuity of noninstantaneous impulsive functions \(\eta _{\mathfrak{l}} (\mathfrak{t}, \mathfrak{z}(\mathfrak{t}) )\) for \(\mathfrak{l}=1,2,\ldots,m\) and applying the similar procedure as before, we easily see that  and
and  . Thus we conclude that \({\varTheta }\mathfrak{z}\in {\mathcal{P}\mathcal{C}}_{1-\theta }\) for \(\mathfrak{z} \in {\mathcal{P}\mathcal{C}}_{1-\theta }\).
. Thus we conclude that \({\varTheta }\mathfrak{z}\in {\mathcal{P}\mathcal{C}}_{1-\theta }\) for \(\mathfrak{z} \in {\mathcal{P}\mathcal{C}}_{1-\theta }\).
Step 2. We show that Θ maps the bounded closed convex set \({\varOmega _{\delta }}\) onto itself, that is, \({\varTheta }\mathfrak{z}\in \varOmega _{\delta }\) for \(\mathfrak{z} \in \varOmega _{\delta }\). Suppose the contrary, that is, there are \(\mathfrak{z}\in \varOmega _{\delta }\) and \(\mathfrak{t} \in \mathcal {J}\) such that \(\|{\varTheta }\mathfrak{z}\|_{\mathfrak{C}_{1-\theta }}> \delta \). Let us evaluate \(\|{\varTheta }\mathfrak{z}\|\) for \(\mathfrak{t}\in [0, \mathfrak{t}_{1}]\), \((\mathfrak{t}_{\mathfrak{l}}, \mathfrak{s}_{\mathfrak{l}}]\), and \((\mathfrak{s}_{\mathfrak{l}}, \mathfrak{t}_{\mathfrak{l}+1}]\), \(\mathfrak{l}=1, 2, \ldots, m\).
For \(\mathfrak{t}\in [0, \mathfrak{t}_{1}]\), we have

For \(\mathfrak{t}\in (\mathfrak{t}_{\mathfrak{l}}, \mathfrak{s}_{\mathfrak{l}}]\), \({\mathfrak{l}}=1, 2, \ldots, m\), we have
For \(\mathfrak{t}\in (\mathfrak{s}_{\mathfrak{l}}, \mathfrak{t}_{\mathfrak{l}+1}]\), \({\mathfrak{l}}=1, 2, \ldots, m\), we have


By our assumptions we have

Dividing both sides by δ and taking the limits of both sides as \(\delta \to \infty \), we have

which is a contradiction. Hence
This proves that Θ maps bounded sets to bounded sets.
Step 3. We prove that \({\varTheta }_{1}\) is Lipschitz continuous. For \(\mathfrak{t}\in [0, \mathfrak{t}_{1}]\), we have

For \(\mathfrak{t}\in (\mathfrak{t}_{\mathfrak{l}}, \mathfrak{s}_{\mathfrak{l}}]\), \(\mathfrak{l}=1, 2,\ldots, m\), we have
For \(\mathfrak{t}\in (\mathfrak{s}_{\mathfrak{l}}, \mathfrak{t}_{\mathfrak{l}+1}]\), we have

Combining Eqs. (3.4)–(3.6), we get

This proves that \({\varTheta }_{1}\) is a Lipschitz function with Lipschitz constant  .
.
Step 4. Let \(\{\mathfrak{z}_{n}(\mathfrak{t})\}\) be a sequence in \(\varOmega _{\delta }\) such that
Since  and
and  are continuous functions with respect to the second and third variables, it follows that
are continuous functions with respect to the second and third variables, it follows that

By assumptions (H1) and (H3) we have

Since \(\psi _{1}\in L_{\frac{1}{\mathsf{r}}[0, \mathfrak{a}]}\) and \(\psi _{2}(\mathfrak{t})\) is continuous, both functions on the right-hand side are integrable.
For all \(\mathfrak{t}\in \mathcal {J}\), \(\mathfrak{z}_{n}, \mathfrak{z} \in \varOmega _{\mathfrak{\delta }} \), consider

By the Lebesgue dominated convergence theorem
This proves the continuity of the operator \({\varTheta }_{2}\).
Step 5. Let us prove that \({\varTheta }_{2}\) is equicontinuous. For any \(\mathfrak{z} \in \varOmega _{\delta }\) and \(\mathfrak{s}_{\mathfrak{l}}< \mathfrak{t}_{1}< \mathfrak{t}_{2}< \mathfrak{t}_{\mathfrak{l}+1}\), \(\mathfrak{l}=0, 1, 2,\ldots, m\), we have

By substituting \((\mathfrak{t}_{1}-\mathfrak{s})=\mathfrak{s}_{1}\) into \(\mathcal{I}_{1}\) and \(\mathcal{I}_{3}\) we have

By the equicontinuity of \((\mathfrak{p}-\mathfrak{q})\)-resolvent operator and the Lebesgue dominated convergence theorem both the integrals \(\mathcal{I}_{1}\), \(\mathcal{I}_{3} \longrightarrow 0\) as \(\mathfrak{t}_{2}\longrightarrow \mathfrak{t}_{1}\).
Clearly, \(\mathcal{I}_{2}\), \(\mathcal{I}_{4}\longrightarrow 0\) as \(\mathfrak{t}_{2}\longrightarrow \mathfrak{t}_{1}\), from which it follows that
This proves the equicontinuity of \({\varTheta }_{2}\).
Step 6. Let us prove that Θ is a condensing operator. We have to show that for any bounded subset \(\mathcal{D}\subset \varOmega _{\delta }\),
Since \({\varTheta }_{2}\) is a continuous map, for any bounded set \(\mathcal{D} \subset \varOmega _{\delta }\), there exists a countable set \(\mathcal{D}_{o}= \lbrace \mathfrak{z}_{n} \rbrace \subset \mathcal{D}\) such that \(\zeta ( {\varTheta }_{2}(\mathcal{D}) )_{\mathcal{PC}_{1- \theta }} = \zeta ( {\varTheta }_{2}(\mathcal{D}_{o}) )_{ \mathcal{PC}_{1-\theta }}\).
Since \({\varTheta }_{2}\) is a bounded and equicontinuous operator, it follows that

Equation (3.6) implies

Since \({\varTheta }_{1}\) is a Lipschitz function with Lipschitz constant  , for any bounded set \(\mathcal{D}\in \varOmega _{\delta }\),
, for any bounded set \(\mathcal{D}\in \varOmega _{\delta }\),

As \({\varTheta }= {\varTheta }_{1}+{\varTheta }_{2}\), we have

Thus \({\varTheta }: \varOmega _{\delta }\longrightarrow \varOmega _{\delta }\) is a condensing operator. Hence by Sadovskii’s fixed point theorem [8] operator Θ has at least one fixed point \(\mathfrak{z}\in \varOmega _{\delta }\), which is a \(\mathcal{PC}_{1-\theta }\) mild solution of the given system of equations. □
4 Applications
Consider the following neutral Hilfer FDE with noninstantaneous impulsive condition on \(\mathcal {J}=[0, 1]\):

Let  and
and  with
with

The operator  generates an equicontinuous \(C_{o}\)-semigroup \(\mathcal{W}(\mathfrak{t})\), (\(\mathfrak{t}\ge 0\)) on
generates an equicontinuous \(C_{o}\)-semigroup \(\mathcal{W}(\mathfrak{t})\), (\(\mathfrak{t}\ge 0\)) on  with \(\|\mathcal{W}(\mathfrak{t})\|\le 1\) for \(\mathfrak{t}\ge 0\). On comparing with equation system (1.1), we have
with \(\|\mathcal{W}(\mathfrak{t})\|\le 1\) for \(\mathfrak{t}\ge 0\). On comparing with equation system (1.1), we have

Put \(\mathfrak{z}(\mathfrak{t}, \mathfrak{x})= \mathfrak{z}(\mathfrak{t})\). It is easy to see that

Similarly,

In particular, take \(\mathsf{r}=\frac{1}{4}\):
Both  and \(\eta _{\mathfrak{l}} ( \mathfrak{t}, \mathfrak{z}(\mathfrak{t}) )\) are Lipschitz functions with Lipschitz constants and \(\mathcal{L}_{\eta _{\mathfrak{l}}}= \frac{1}{25}\). Thus we have \(\mathfrak{p}= \frac{1}{2}\), \(\mathfrak{q}= \frac{1}{8}\), \(\theta = \frac{9}{16}\), \(\mathsf{r}=\frac{1}{4}\),
and \(\eta _{\mathfrak{l}} ( \mathfrak{t}, \mathfrak{z}(\mathfrak{t}) )\) are Lipschitz functions with Lipschitz constants and \(\mathcal{L}_{\eta _{\mathfrak{l}}}= \frac{1}{25}\). Thus we have \(\mathfrak{p}= \frac{1}{2}\), \(\mathfrak{q}= \frac{1}{8}\), \(\theta = \frac{9}{16}\), \(\mathsf{r}=\frac{1}{4}\),  , \(\vartheta ^{*}=1\),
, \(\vartheta ^{*}=1\),  ,
,  , , \(\mathcal{L}_{\eta _{\mathfrak{l}}}= \frac{1}{25}\), \(\|\psi _{1}\|=\|{ \hat{\phi }}_{1}\|= 0.063\), \(\|\psi _{2}\|= \|{\hat{\phi }}_{2}\|=0.102\), \(\eta ^{*}= \mathfrak{\bar{m}}^{*}=0.63212\).
, , \(\mathcal{L}_{\eta _{\mathfrak{l}}}= \frac{1}{25}\), \(\|\psi _{1}\|=\|{ \hat{\phi }}_{1}\|= 0.063\), \(\|\psi _{2}\|= \|{\hat{\phi }}_{2}\|=0.102\), \(\eta ^{*}= \mathfrak{\bar{m}}^{*}=0.63212\).
For these values, the first condition of Theorem 3.1 is satisfied:

Similarly, we have the second condition:

Thus both conditions of Theorem 3.1 are satisfied. So the equation system (4.1) has at least one mild solution in \(\mathcal{PC}_{1-\theta }(\mathcal {J})\).
5 Conclusion
We established the existence of mild solutions for neutral fractional-order system involving the Hilfer fractional derivative in a Banach space by converting it into an integral form and hence applying Sadovskii’s fixed point technique. For future research work, for the proposed problem, we suggest stability analysis, multiple solutions, and singular solutions.
References
Abdeljawad, T., Al-Mdallal, Q.M., Jarad, F.: Fractional logistic models in the frame of fractional operators generated by conformable derivatives. Chaos Solitons Fractals 119, 94–101 (2019). https://doi.org/10.1016/j.chaos.2018.12.015
Atangana, A., Gómez-Aguilar, J.F.: Numerical approximation of Riemann–Liouville definition of fractional derivative: from Riemann–Liouville to Atangana–Baleanu. Numer. Methods Partial Differ. Equ. 34(5), 1502–1523 (2018). https://doi.org/10.1002/num.22195
Banas, J.: Measures of noncompactness in the study of solutions of nonlinear differential and integral equations. Open Math. 10, 2003–2011 (2012). https://doi.org/10.2478/s11533-012-0120-9
Belmor, S., Ravichandran, C., Jarad, F.: Nonlinear generalized fractional differential equations with generalized fractional integral conditions. J. Taibah Univ. Sci. 14(1), 114–123 (2020). https://doi.org/10.1080/16583655.2019.1709265
Chalishajar, D., Ravichandran, C., Dhanalakshmi, S., Murugesu, R.: Existence of fractional impulsive functional integro-differential equations in Banach spaces. Appl. Syst. Innov. 2(2), 1–17 (2019). https://doi.org/10.3390/asi2020018
Chen, C., Li, M.: On fractional resolvent operator functions. Semigroup Forum 80, 121–142 (2010). https://doi.org/10.1007/s00233-009-9184-7
Chen, P., Zhang, X., Li, Y.: Existence of mild solutions of partial differential equations with non-instantaneous impulses. Electron. J. Differ. Equ. 2016, 241 (2016), 1–11, http://ejde.math.txstate.edu or http://ejde.math.unt.edu
Daher, S.J.: On a fixed point principle of Sadovskii. Nonlinear Anal., Theory Methods Appl. 2, 643–645 (1978). https://doi.org/10.1016/0362-546X(78)90012-3
Fu, X., Huang, R.: Existence of solutions for neutral integro-differential equations with state-dependent delay. Appl. Math. Comput. 224, 743–759 (2013). https://doi.org/10.1016/j.amc.2013.09.010
Furati, K.M., Kassim, M.D.: Existence and uniqueness for a problem involving Hilfer fractional derivative. Comput. Math. Appl. 64, 1616–1626 (2012). https://doi.org/10.1016/j.camwa.2012.01.009
Gambo, Y.Y., Ameen, R., Jarad, F., Abdeljawad, T.: Existence and uniqueness of solutions to fractional differential equations in the frame of generalized Caputo fractional derivatives. Adv. Differ. Equ. 2018, 134, 1–13 (2018). https://doi.org/10.1186/s13662-018-1594-y
Gou, H., Li, B.: Existence of mild solutions for Sobolev-type Hilfer fractional evolution equations with boundary conditions. Bound. Value Probl. 2018, 48 (2018). https://doi.org/10.1186/s13661-018-0965-3
Gu, H., Trujillo, J.J.: Existence of mild solution for evolution equations with Hilfer fractional derivative. Appl. Math. Comput. 257, 344–354 (2015). https://doi.org/10.1016/j.amc.2014.10.083
Hernández, E., ÓRegan, D.: On a new class of abstract impulsive differential equations. Proc. Am. Math. Soc. 141, 1641–1649 (2013). https://doi.org/10.1090/S0002-9939-2012-11613-2
Hilfer, R.: Fractional time evolution. In: Applications of Fractional Calculus in Physics, pp. 87–130 (2000). https://doi.org/10.1142/9789812817747_0002
Hilfer, R.: Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Jarad, F., Harikrishnan, S., Shah, K., Kanagarajan, K.: Existence and stability results to a class of fractional random implicit differential equations involving a generalized Hilfer fractional derivative. Discrete Contin. Dyn. Syst., Ser. S 13(3), 723–739 (2020). https://doi.org/10.3934/dcdss.2020040
Kilbas, A.A.A., Srivastava, H.M., Trujillo, J.J.: Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier, Amsterdam (2006)
Lakshmikantham, V., Simeonov, P.S.: Theory of Impulsive Differential Equations. World Scientific Series on Modern Applied Mathematics, vol. 6. World Scientific, Singapore (1989). https://doi.org/10.1142/0906
Mophou, G.M.: Existence and uniqueness of mild solutions to impulsive fractional differential equations. Nonlinear Anal., Theory Methods Appl. 72, 1604–1615 (2010). https://doi.org/10.1016/j.na.2009.08.046
Morales-Delgado, V.F., Gómez-Aguilar, J.F., Escobar-Jimenez, R.F.: Fractional conformable attractors with low fractality. Math. Methods Appl. Sci. 41(16), 6378–6400 (2018). https://doi.org/10.1002/mma.5146
Morales-Delgado, V.F., Gómez-Aguilar, J.F., Escobar-Jiménez, R.F., Taneco-Hernández, M.A.: Fractional conformable derivatives of Liouville Caputo type with low-fractionality. Phys. A, Stat. Mech. Appl. 503, 424–438 (2018). https://doi.org/10.1016/j.physa.2018.03.018
Mursaleen, M., Noman, A.K.: The Hausdorff measure of noncompactness of matrix operators on some BK spaces. Oper. Matrices 5, 473–486 (2011)
Panda, S.K., Abdeljawad, T., Ravichandran, C.: Novel fixed point approach to Atangana–Baleanu fractional and \(L_{p}\)-Fredholm integral equations. Alex. Eng. J., 1–12 (2020, in press). https://doi.org/10.1016/j.aej.2019.12.027
Pandey, D.N., Das, S., Sukavanam, N.: Existence of solution for a second-order neutral differential equation with state dependent delay and non-instantaneous impulses. Int. J. Nonlinear Sci. 18, 145–155 (2014)
Perez, J.E.S., Gómez-Aguilar, J.F., Baleanu, D., Tchier, F.: Chaotic attractors with fractional conformable derivatives in the Liouville–Caputo sense and its dynamical behaviors. Entropy 20(5), 384 (2018). https://doi.org/10.3390/e20050384
Pierri, M., ÓRegan, D., Rolnik, V.: Existence of solutions for semi-linear abstract differential equations with non-instantaneous impulses. Appl. Math. Comput. 219, 6743–6749 (2013). https://doi.org/10.1090/S0002-9939-2012-11613-2
Podlubny, I.: Fractional Differential Equations. Academic Press, San Diego (1998). https://doi.org/10.2307/2653160
Ravichandran, C., Logeswari, K., Jarad, F.: New results on existence in the framework of Atangana–Baleanu derivative for fractional integro-differential equations. Chaos Solitons Fractals 125, 194–200 (2019). https://doi.org/10.1016/j.chaos.2019.05.014
Shu, X.B., Lai, Y., Chen, Y.: The existence of mild solutions for impulsive fractional partial differential equations. Nonlinear Anal., Theory Methods Appl. 74, 2003–2011 (2011). https://doi.org/10.1016/j.na.2010.11.007
Sousa, J.: Existence of mild solutions to Hilfer fractional evolution equations in Banach space (2018). arXiv:1812.02213. arXiv preprint
Subashini, R., Jothimani, K., Saranya, S., Ravichandran, C.: On the results of Hilfer fractional derivative with nonlocal conditions. Int. J. Pure Appl. Math. 118(11), 277–289 (2018). https://doi.org/10.12732/ijpam.v118i11.33
Subashini, R., Ravichandran, C.: On the results of nonlocal Hilfer fractional semilinear differential inclusions. Proc. Jangjeon Math. Soc. 22(2), 249–267 (2019). https://doi.org/10.17777/pjms2019.22.2.249
Subashini, R., Ravichandran, C., Jothimani, K., Baskonus, H.M.: Existence results of Hilfer integro-differential equations with fractional order. Discrete Contin. Dyn. Syst., Ser. S 13(3), 911–923 (2020). https://doi.org/10.3934/dcdss.2020053
Suganya, S., Baleanu, D., Kalamani, P., Arjunan, M.M.: On fractional neutral integro-differential systems with state-dependent delay and non-instantaneous impulses. Adv. Differ. Equ. 2015, 372, 1–39 (2015). https://doi.org/10.1186/s13662-015-0709-y
Wang, J., Zhang, Y.: Nonlocal initial value problems for differential equations with Hilfer fractional derivative. Appl. Math. Comput. 266, 850–859 (2015). https://doi.org/10.1016/j.amc.2015.05.144
Yang, M., Wang, Q.: Existence of mild solutions for a class of Hilfer fractional evolution equations with nonlocal conditions. Fract. Calc. Appl. Anal. 20, 679–705 (2017). https://doi.org/10.1515/fca-2017-0036
Ye, R.: Existence of solutions for impulsive partial neutral functional differential equation with infinite delay. Nonlinear Anal., Theory Methods Appl. 73, 155–162 (2010). https://doi.org/10.1016/j.na.2010.03.008
Yépez-Martínez, H., Gómez-Aguilar, J.F.: Fractional sub-equation method for Hirota–Satsuma-coupled KdV equation and coupled mKdV equation using the Atanganás conformable derivative. Waves Random Complex Media 29(4), 678–693 (2019). https://doi.org/10.1080/17455030.2018.1464233
Zhou, Y., Jiao, F.: Existence of mild solutions for fractional neutral evolution equations. Comput. Math. Appl. 59, 1063–1077 (2010). https://doi.org/10.1016/j.camwa.2009.06.026
Acknowledgements
The first author is highly thankful to the Council of Scientific and Industrial Research (CSIR)-New Delhi, India, for their financial support with grant no. 09/1051(0017)/2018-EMR-I. The third author (Thabet Abdeljawad) would like to thank Prince Sultan University for funding this work through research group in Applied Mathematics (NAMAM) group number RG-DES-201701-17.
Availability of data and materials
Not applicable.
Funding
Prince Sultan University for funding this work through research group in Applied Mathematics (NAMAM) group number RG-DES-201701-17.
Author information
Authors and Affiliations
Contributions
All authors have equal contributions in this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors have no competing interests regarding the publication of this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bedi, P., Kumar, A., Abdeljawad, T. et al. Existence of mild solutions for impulsive neutral Hilfer fractional evolution equations. Adv Differ Equ 2020, 155 (2020). https://doi.org/10.1186/s13662-020-02615-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-02615-y




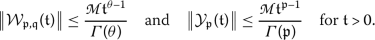
 for
for